moltiplicazione
moltiplicazione
moltiplicazione operazione dell’aritmetica, denotata col segno · (oppure ×, ma se vi sono lettere il segno è anche omesso), il cui risultato è detto prodotto mentre i singoli operandi sono detti fattori. Così, indicati con a e b i due fattori e con p il loro prodotto, in simboli si ha
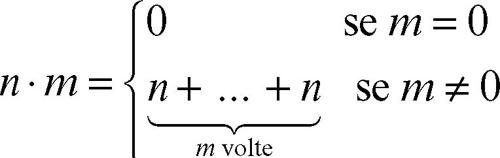
La moltiplicazione può essere definita formalmente in N, insieme dei numeri naturali, in modo induttivo a partire dall’operazione di addizione, ponendo
che si legge «n per m», dove n e m sono due numeri naturali; la moltiplicazione definisce così una legge di composizione interna ⋅: N × N → N sull’insieme dei numeri naturali. La moltiplicazione viene poi estesa, in opportuni modi, a tutti gli insiemi numerici che ampliano quello dei naturali, cioè all’insieme dei numeri interi Z, a quello dei numeri razionali Q, a quello dei numeri reali R e a quello dei numeri complessi C.
La moltiplicazione gode della proprietà commutativa
e della proprietà associativa
Nell’esecuzione delle operazioni, la moltiplicazione ha precedenza rispetto all’addizione; le due operazioni sono comunque legate dalla proprietà distributiva della moltiplicazione rispetto all’addizione
e determina gli elementi privilegiati 1 (detto elemento neutro della moltiplicazione e definito dalla proprietà n ⋅ 1 = n per ogni numero n) e 0 (detto elemento assorbente della moltiplicazione e definito dalla proprietà n ⋅ 0 = 0 per ogni numero n). Valgono la legge di → annullamento del prodotto e la legge di → cancellazione.
Moltiplicazione in Z, insieme degli interi relativi
La moltiplicazione di due numeri relativi si effettua facendo il prodotto dei loro valori assoluti e aggiungendo l’opportuno segno: se essi sono concordi (hanno lo stesso segno) il segno è positivo, se discordi, è negativo (→ regola dei segni per il prodotto).
Moltiplicazione in Q, insieme dei numeri razionali
Il prodotto di due numeri razionali (rappresentati mediante due frazioni) è una frazione che ha come numeratore il prodotto dei numeratori e come denominatore il prodotto dei denominatori (effettuate le semplificazioni). Se le frazioni sono dotate di segno, si segue la regola dei segni.
Moltiplicazione in R, insieme dei numeri reali
Per l’estensione dell’operazione di moltiplicazione ai numeri reali, si veda → R (insieme dei numeri reali).
Moltiplicazione in C, insieme dei numeri complessi
Per l’estensione dell’operazione di moltiplicazione ai numeri complessi, si veda → C (insieme dei numeri complessi).
Inverso rispetto alla moltiplicazione
Dato un numero a, il suo inverso rispetto alla moltiplicazione è un numero b tale che a ⋅ b = 1; se esiste, tale numero è unico. Negli insiemi numerici fondamentali, tranne nei casi in cui la moltiplicazione è considerata come operazione su N o Z, l’inverso di un numero a diverso da zero esiste sempre ed è indicato con il simbolo a−1; due numeri inversi l’uno dell’altro sono detti reciproci. Se n è un numero intero non nullo, allora il suo inverso coincide con il numero razionale 1/n: esso non è mai intero, a meno che non sia n = 1 oppure n = −1. Tutti gli insiemi numerici sopra elencati, tranne N e Z, sono chiusi rispetto all’operazione unaria che associa a un elemento non nullo il suo inverso. Indicati con i simboli N0, Z0, Q0, R0, C0 i rispettivi insiemi privati dello zero, ciò si traduce nel fatto che N0 e Z0 sono dei monoidi rispetto alla moltiplicazione (detti il monoide moltiplicativo del relativo insieme), mentre Q0, R0 e C0 sono dei gruppi rispetto alla moltiplicazione (detti il gruppo moltiplicativo del relativo insieme). Per la determinazione dell’inverso di un numero reale o di un numero complesso si vedano rispettivamente → R (insieme dei numeri reali) e → C (insieme dei numeri complessi).
Moltiplicazione in un insieme qualunque
Il termine moltiplicazione, indicato con gli stessi simboli, può denotare operazioni in insiemi qualunque, per le quali di volta in volta si postulano tutte o in parte le proprietà della moltiplicazione tra numeri; in particolare è detta moltiplicazione una delle due operazioni di un anello. In un gruppo di sostituzioni la moltiplicazione non si identifica con l’operazione aritmetica sin qui definita, ma è l’esecuzione successiva di due sostituzioni del gruppo.
Moltiplicazione per uno scalare
In uno spazio vettoriale V definito su un campo K è detta moltiplicazione per uno scalare la legge di composizione esterna che a ogni coppia (λ, v) costituita da uno scalare λ appartenente a K e da un vettore v appartenente a V associa il vettore w = λv appartenente a V, ottenuto moltiplicando ogni componente del vettore v per λ. In R3 il vettore λv ha direzione uguale a quella di v e verso uguale o opposto a quello di v a seconda che λ sia rispettivamente positivo o negativo e il suo modulo è |λ| ⋅ |v|.