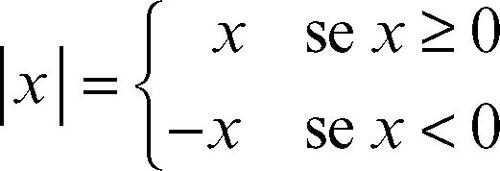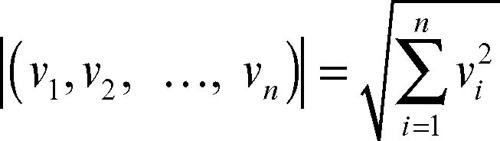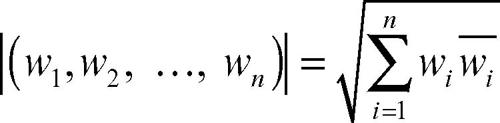modulo

modulo

modulo termine usato in matematica con significati diversi.

Modulo di un numero reale (o valore assoluto)

). II modulo di un numero reale x, indicato con il simbolo |x|, è un numero reale non negativo definito da

Valgono le seguenti proprietà:

• |x| ≥ 0

• |x| = 0 se e solo se x = 0

• |xy| = |x| ⋅ |y|

• |x + y| ≤ |x| + |y| (disuguaglianza triangolare)

È così definita una funzione (funzione modulo) che a ogni numero reale associa il suo modulo.

Modulo di un numero complesso

Dato un numero complesso della forma z = a + ib, dove a e b sono rispettivamente la parte reale e la parte immaginaria di z, si definisce suo modulo la radice quadrata della somma dei quadrati di a e b:

Nel caso in cui b = 0, cioè se z = a è un numero reale, allora il modulo di un numero complesso coincide con il modulo di un numero reale sopra definito. In questo modo la funzione sopra definita è estesa all’insieme dei numeri complessi e continua a soddisfare le proprietà formali sopra enunciate e in più soddisfa le ulteriori proprietà (che nel caso reale risultano banalmente verificate):

• |z̄| = |z|, dove con z̄ si indica il numero complesso coniugato di z;

• se z = a + ib, allora |z| ≤ |a| + |b|.

Rappresentando C mediante il piano di → Argand-Gauss, il modulo di un numero complesso a + ib esprime la lunghezza del vettore (a, b) associato, calcolata per mezzo del teorema di Pitagora; la disuguaglianza triangolare esprime invece il fatto geometrico che in ogni triangolo la lunghezza di un lato è minore della somma delle lunghezze degli altri. La funzione modulo così definita su C coincide con la forma quadratica associata al prodotto scalare standard definito su R².

Il modulo definisce in modo naturale una distanza d su C (e in particolare su R), attraverso la formula d(w, z) = |w − z|, dove w e z sono arbitrari numeri complessi; tale distanza è usualmente chiamata distanza euclidea.

Modulo di un vettore

In uno spazio vettoriale reale (rispettivamente complesso) V dotato di un prodotto scalare (rispettivamente, di un prodotto hermitiano), che qui si indica con u ⋅ w, essendo u e w due vettori, si definisce modulo di un vettore v ∈ V, indicato con il simbolo |v|, il numero reale non negativo √(v ⋅ v). Il modulo è lo strumento fondamentale che permette di definire in uno spazio vettoriale nozioni metriche quali la lunghezza di un vettore v (definita come il suo modulo |v|) e la distanza tra due vettori v e w (definita come il modulo della loro differenza |v – w|).

Esso soddisfa le seguenti proprietà:

• |v| ≥ 0

• |v| = 0 se e solo se v = 0

• |v + w| ≤ |v| + |w| (disuguaglianza triangolare)

Nel caso in cui V = Rⁿ e il prodotto scalare è quello standard, allora il modulo del vettore v di n componenti v_i è:

nel caso in cui V = Cⁿ e il prodotto hermitiano è quello standard, allora il modulo del vettore w di n componenti w_i è:

Modulo su un anello A (o A-modulo)

Si veda il lemma specifico → modulo su un anello.

Modulo di una congruenza

Due interi a e b sono detti congruenti modulo n se n divide la differenza a − b. Si scrive a ≡ b (mod n) e si legge: «a congruo b modulo n»; n è detto modulo della congruenza (→ congruenza modulo n; → aritmetica modulare).