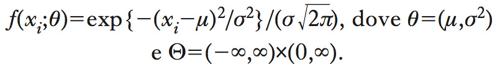modello statistico

modello statistico

Famiglia di meccanismi probabilistici che si presume approssimi sufficientemente bene, o addirittura contenga, il meccanismo probabilistico che ha generato i dati disponibili (➔ dati). La specificazione di un m. s. dipende dall’obiettivo dell’analisi e dalle informazioni che a priori si hanno sulla popolazione da cui i dati sono tratti e sul tipo di campionamento (➔ campione statistico). Formalmente, un m. s. per la distribuzione di probabilità (➔) dei dati osservati è definito da una famiglia di distribuzioni F={f_n(x₁,…,x_n;θ),θ∈Θ}, dove la funzione f_n(x₁,…,x_n;θ) rappresenta una possibile densità di probabilità congiunta X₁,…,X_n, corrispondente al punto θ nello spazio dei parametri Θ. In particolare, nel caso in cui i dati siano ottenuti tramite campionamento casuale semplice da una popolazione, vale la fattorizzazione f_t,(x₁,…,x_n;θ)=f (x₁;θ)... f(x_n;θ), dove f(x_i;θ) è la densità di una singola osservazione.

I modelli parametrici

Un m. s. si dice parametrico se lo spazio dei parametri Θ (➔ parametro) è finito dimensionale. Per es., un m. parametrico per dati di tipo continuo è il modello gaussiano (➔ gaussiana, distribuzione), che, nel caso di campionamento casuale semplice, assume che la densità di una singola osservazione sia

Un altro esempio è il m. multinomiale, basato sulla distribuzione multinomiale, la quale generalizza la distribuzione binomiale a variabili categoriche con k>2 categorie. Nell’approccio bayesiano (➔ inferenza statistica), la definizione di un m. parametrico richiede, oltre alla definizione di una famiglia parametrica di distribuzioni di probabilità per il campione osservato, anche la definizione di una distribuzione di probabilità per il parametro θ.

I modelli non parametrici

Un m. F è non parametrico se lo spazio dei parametri Θ è di dimensione infinita. I m. non parametrici vengono generalmente utilizzati per evitare di porre troppe restrizioni sulla distribuzione dei dati, specialmente quando le informazioni a priori sono limitate. Un esempio può essere il m. F costituito da tutte le distribuzioni di probabilità con media zero e varianza finita. L’utilizzo di m. non parametrici tende a essere complicato nel caso di dati multivariati, a meno che il numero di variabili sia molto ridotto. Per questo motivo si preferisce talvolta utilizzare m. intermedi, detti semiparametrici, che cercano di mantenere parte della flessibilità di un m. non parametrico, ma introducono anche una componente parametrica allo scopo di limitare la dimensione dello spazio dei parametri.

Altre tipologie di modelli statistici

M. s. possono essere definiti anche per specifici aspetti di una distribuzione. Un esempio è un modello lineare per la media condizionata o funzione di regressione (➔ regressione, modelli e stimatori di), cioè, nel caso di un solo regressore,

M={E(Y∣X=x)=α+βx,−∞<α,β<∞}.

Sebbene M sia un m. parametrico perché lo spazio dei parametri è finito dimensionale, nulla impedisce di considerare anche m. non parametrici o semiparametrici per la media condizionata. Un esempio di m. non parametrico è quello definito da tutte le funzioni μ(x) crescenti in x, mentre un esempio di m. semiparametrico è il m. single-index in cui, ipotizzando che x=(x₁,x₂) la media condizionata viene rappresentata come trasformazione non lineare della combinazione lineare o ‘indice’ α+β₁₁+β₂₂, cioè μ(x)=g(α+β₁₁+β₂₂), dove la funzione g non è specificata. Due m. s. si dicono annidati se il primo è incluso nel secondo. Per es., il m. gaussiano con media ignota e varianza nota è annidato nel m. gaussiano con media e varianza ignote, mentre il m. di regressione lineare è annidato nel m. single-index (infatti, basta scegliere g(x)=x per ottenere il m. lineare).