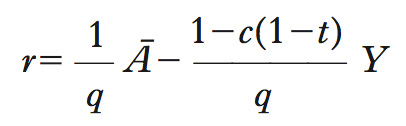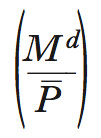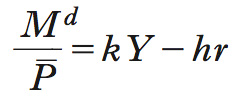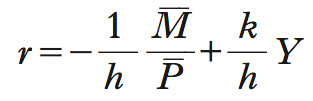IS-LM, modello
IS-LM, modello
Il più noto modello macroeconomico elementare, relativo a un’economia chiusa agli scambi con l’estero, di ispirazione keynesiana. Esso consente di determinare il PIL – o output o spesa o reddito aggregato – e il tasso di interesse in condizioni di equilibrio generale sul mercato dei beni e della moneta (ma non su quello del lavoro) nell’ipotesi che il livello dei prezzi sia fisso (breve periodo). La relazione tra reddito e tasso di interesse di equilibrio per il mercato dei beni (ossia di equilibrio tra investimenti desiderati, investimenti relativi e risparmio o Investment-Saving) è la curva IS. La relazione tra reddito e tasso di interesse di equilibrio per il mercato della moneta (ossia di equilibrio tra domanda e offerta di moneta o Liquidity preference e Money) è la curva LM.
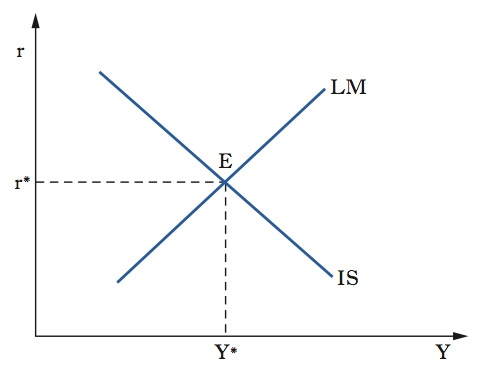
Nella figura 1, sull’asse orizzontale si misura il PIL reale (Y), sul quello verticale si misura il tasso di interesse reale (r), ossia la differenza tra il tasso di interesse nominale e il tasso di inflazione (poiché il modello IS-LM è a prezzi fissi, il tasso di inflazione è nullo, e il tasso di interesse reale coincide con quello nominale). L’intersezione delle curve IS e LM identifica la coppia di valori del tasso di interesse reale (r*) e della produzione (Y*), che rappresentano l’equilibrio macroeconomico (E), ossia l’equilibrio simultaneo per il mercato dei beni e per il mercato della moneta. In condizioni standard questo equilibrio è unico.
Curva IS
È inclinata negativamente sul piano (Y, r) ed è il luogo dei punti che rappresentano combinazioni di tasso di interesse e livello del reddito di equilibrio per il mercato dei beni. In altre parole, la curva IS è il luogo dei punti sul piano (Y, r) in cui la spesa totale, rappresentata dalla somma dei consumi (C), degli investimenti privati (I) e della spesa pubblica (G), è uguale alla produzione totale realizzata da un’economia, ossia il PIL reale (Y). Pertanto, la curva IS è il luogo dei punti di equilibrio per l’economia ‘reale’ (chiusa). In simboli: Y=C+I+G. Si ipotizzi che i consumi siano definiti dalla relazione C=C0+cYd, dove C0 è detta componente autonoma dei consumi (in quanto non dipende dal PIL reale), 0<c<1 rappresenta la propensione marginale al consumo e Yd è il reddito disponibile, ossia il reddito complessivo (Y) al netto della tassazione (T=tY; 0<t<1) e dei trasferimenti pubblici (TR). Pertanto, i consumi possono essere definiti come segue: C=C0+c(1−t)Y+cTR, ossia come una funzione lineare crescente del reddito complessivo. In altre parole, all’aumentare del reddito il consumo aggregato aumenta. Si assume, inoltre, che gli investimenti privati siano una funzione lineare decrescente del tasso di interesse I=I0−qr, dove q è un parametro positivo che rappresenta la sensibilità degli investimenti privati a variazioni del tasso di interesse. Infatti, se il tasso di interesse aumenta, poiché cresce anche il costo medio del finanziamento di un investimento, gli investimenti privati si riducono e viceversa. Infine, G rappresenta la spesa pubblica e costituisce una esogena nel modello, cioè uno strumento di politica economica (al pari di TR e di t). La curva IS, pertanto, è rappresentata dalla seguente equazione:
dove Ā=C0+cTR+I0+G rappresenta la spesa autonoma (ossia indipendente dal livello del reddito aggregato). Un incremento (decremento) della spesa pubblica ha, a parità di tutte le altre condizioni, l’effetto di fare traslare verso l’alto (basso) la curva IS.
Curva LM
È inclinata positivamente sul piano (Y, r) e rappresenta il luogo dei punti che costituiscono combinazioni di tasso di interesse e di reddito di equilibrio per il mercato della moneta, ossia il luogo dei punti in cui la domanda di moneta in termini nominali (Md) è uguale all’offerta nominale di moneta (Ms). Si ipotizzi che l’offerta di moneta in termini nominali sia esogena (dunque sia uno strumento di politica economica) e sia costante e pari a Ms=M−. La domanda di moneta in termini reali
dove P− è il livello generale dei prezzi (fisso per ipotesi) – dipende dal reddito ed è inversamente correlata al tasso di interesse, ossia formula
dove h è un parametro positivo che rappresenta la sensibilità della domanda di moneta a variazioni del tasso di interesse. Dalla condizione di equilibrio per il mercato della moneta Md=Ms si ottiene l’equazione che rappresenta la curva LM:
Un aumento (riduzione) dell’offerta di moneta ha, a parità di tutte le altre condizioni, l’effetto di fare traslare verso il basso (l’alto) la curva LM.
Applicazioni del modello
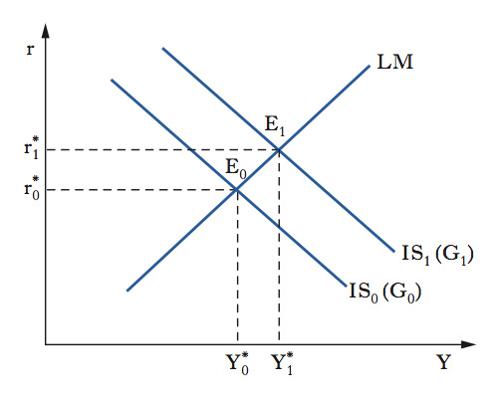
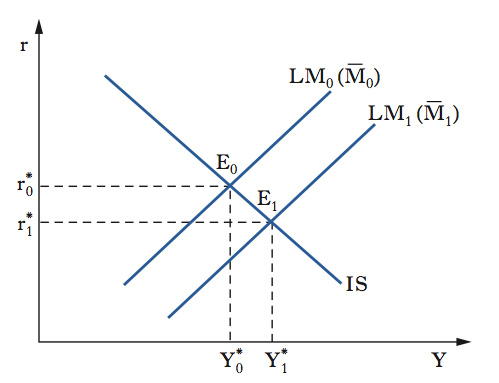
Il modello IS-LM può essere utilizzato per analizzare gli effetti della politica fiscale e della politica monetaria sull’equilibrio macroeconomico, definito come la coppia di valori del tasso di interesse e del reddito di equilibrio contemporaneo per il mercato dei beni e per quello della moneta. La politica fiscale (➔) si traduce in variazioni della spesa pubblica (G) o del livello della pressione fiscale (t) o dei trasferimenti (TR). In caso di un incremento della spesa pubblica G da un livello iniziale G0 a un certo livello G1>G0 (politica di bilancio espansiva), la curva IS si sposta verso destra fino a IS1(G1) (figura 2). L’aumento della spesa pubblica provoca contemporaneamente un incremento del reddito di equilibrio da Y*0 a Y*1 e del tasso di interesse di equilibrio da r*0 a r*1. Il nuovo equilibrio macroeconomico, pertanto, sarà rappresentato dal punto E1. Poiché il costo degli investimenti privati cresce all’aumentare del tasso di interesse, ciò comporta una riduzione parziale degli investimenti: si ha pertanto un effetto di parziale spiazzamento (crowding out) degli investimenti privati da parte della spesa pubblica. Poiché gli investimenti rappresentano una componente della domanda aggregata (➔), l’incremento del tasso di interesse provocherà un effetto negativo sulla domanda aggregata e sul reddito di equilibrio. Il reddito di equilibrio, a seguito di una politica fiscale espansiva, si accresce in misura minore rispetto a quanto aumenterebbe se il tasso di interesse rimanesse invariato. La politica monetaria (➔) si traduce in variazioni dell’offerta di moneta in termini nominali (M−). Dato il livello dei prezzi, fisso per ipotesi, una variazione dell’offerta nominale di moneta implica una variazione dello stesso segno dell’offerta reale di moneta. In caso di un aumento dell’offerta di moneta in termini nominali M− da un livello iniziale M−0 a un certo livello M−1>M−0 (politica monetaria espansiva) la curva LM si sposta in basso fino a LM1 (M−1) in figura 3. La crescita dell’offerta di moneta in termini nominali provoca un aumento del reddito di equilibrio da Y*0 a Y*1 e una riduzione del tasso di interesse di equilibrio da r*0 a r*1. Il nuovo equilibrio macroeconomico, pertanto, è rappresentato dal punto E1. Il più basso tasso di interesse comporta un incremento degli investimenti e, conseguentemente, della domanda aggregata e del reddito di equilibrio. A seguito di una politica monetaria espansiva, dunque, si osserva un aumento del reddito di equilibrio e un decremento del tasso di interesse di equilibrio.
