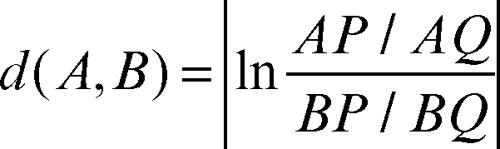Poincare, modello di
Poincare, modello di
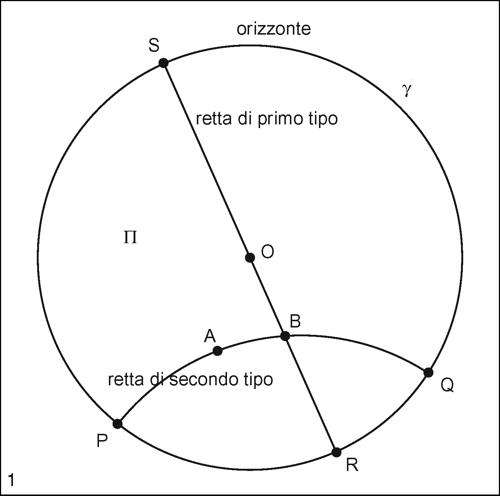
Poincaré, modello di in ambiente euclideo, modello coerente di geometria non euclidea di tipo iperbolico (→ geometria non euclidea; → geometria iperbolica). Detto anche disco di Poincaré, esso è costituito dalla regione interna a una circonferenza γ, detta orizzonte. Le rette del piano sono i diametri di γ, dette anche rette di primo tipo, oppure archi di circonferenze ortogonali all’orizzonte γ (cioè archi di circonferenza che incontrano l’orizzonte in modo tale che nei punti d’intersezione le rispettive tangenti siano tra loro perpendicolari), dette anche rette di secondo tipo. In questo modello valgono tutti gli assiomi della geometria euclidea, tranne il quinto postulato, sostituito dall’assioma: «per un punto P non appartenente a una retta r si possono tracciare infinite parallele a r».
La distanza tra due punti A e B del disco di Poincaré può essere definita come
dove P e Q indicano le intersezioni della retta AB con l’orizzonte. In tale modo, si può infatti verificare che se A e B coincidono la distanza è nulla e se A, B o entrambi i punti si avvicinano all’orizzonte la distanza tende ad avvicinarsi all’infinito (e le rette sono perciò di lunghezza infinita).
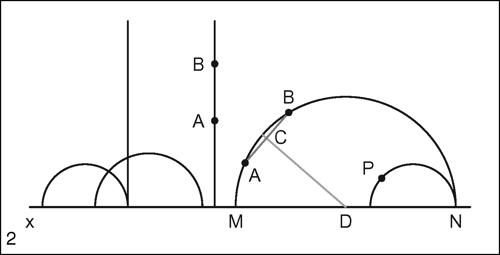
Un altro modello di Poincaré di geometria iperbolica è il cosiddetto piano di Poincaré: è in realtà un semipiano in cui le rette sono le semicirconferenze con centro sulla retta frontiera del semipiano e, quindi, ortogonali a essa, oppure, come loro casi limite, semirette ortogonali alla frontiera. Anche in questo caso gli assiomi di appartenenza, dell’ordine, della continuità sono verificati, ma non quello della parallela; si definisce poi una metrica particolare tale che il percorso di minor lunghezza per andare da un punto all’altro sia quello su tali rette.
