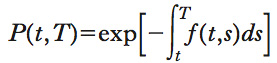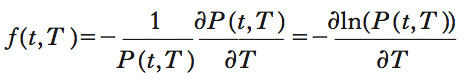HJM, modello di
HJM, modello di
Uno dei modelli di maggiore importanza per lo studio delle dinamiche evolutive della struttura dei tassi di interesse, perfezionato in alcuni lavori della fine del 20° sec. dagli studiosi D. Heath, R. Jarrow e A. Morton, da cui viene l’acronimo HJM. Contrariamente all’approccio, fino ad allora prevalente, di modellare l’evoluzione aleatoria delle intensità di interesse basandosi sull’evoluzione dei tassi a pronti, il modello di HJM propone di dedurla dai movimenti (coerenti con l’ipotesi dell’assenza di opportunità di arbitraggio) della intera curva dei tassi (intensità) istantanei a termine. L’intensità istantanea a termine f(t,T) è intuitivamente quella che descrive il rendimento istantaneo, negoziato sui mercati in modo vincolante al tempo t, di un buono senza cedola in un tempo infinitesimo da T a T+dt. Esso è legato al prezzo del buono dalle relazioni
Ovvero
L’ipotesi del modello di HJM è che le intensità a termine soddisfino al tempo t il sistema di equazioni differenziali stocastiche (una per ogni s>t): df(t,s)=μ(t,s)dt+ξ(t,s)dW(t).