minimi quadrati, metodo dei
minimi quadrati, metodo dei
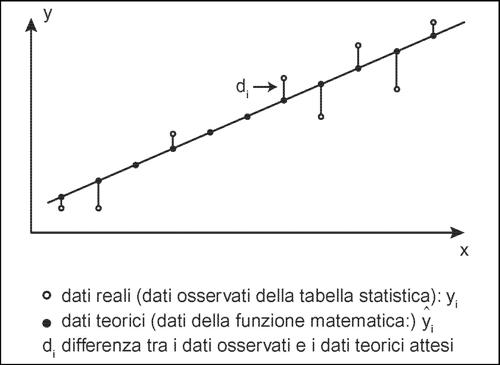
minimi quadrati, metodo dei metodo di stima usato nei modelli di → regressione, in cui una variabile dipendente Y è espressa attraverso una funzione (lineare o non lineare) di una o più variabili indipendenti. Esso consiste nello scegliere, come stime dei parametri che figurano nell’equazione, i valori che rendono minima la somma dei quadrati delle differenze fra i valori della variabile Y stimata come dipendente (valori osservati yi in corrispondenza di valori xi) e quelli stimati mediante la funzione. Per esempio, se (xi, yi) sono n coppie di osservazioni sulle variabili X e Y e la relazione ipotizzata fra X e Y è di tipo lineare, la funzione che lega le due variabili è allora del tipo Y = a + bX. In corrispondenza di ogni valore xi si avrà quindi un valore reale osservato (yi) e un valore teorico, detto anche valore atteso ŷi = a + bxi Tra ogni valore teorico e ogni valore atteso c’è uno scarto di, espresso dalla formula
La somma dei quadrati di tutti questi scarti dà una misura della distanza tra il modello teorico scelto e i dati effettivi.
Il metodo di stima dei minimi quadrati porta quindi a scegliere a e b in modo tale che sia minima la quantità
La retta individuata dai parametri a e b così ottenuti prende il nome di retta dei minimi quadrati o retta di regressione. Nel caso generale, la funzione che si sceglie a priori non è necessariamente lineare: potrebbe essere quadratica, logaritmica, esponenziale o di altro tipo ancora. Se comunque il metodo di scelta dei particolari parametri è effettuato con il metodo dei minimi quadrati, si parla, in generale, di funzione di regressione dei minimi quadrati. Tra tutte le funzioni in cui siano stati determinati i particolari parametri con tale metodo, si sceglierà quella per cui risulta minima l’espressione con la sommatoria qui indicata.
In termini più generali, il principio dei minimi quadrati assicura di determinare il valore o la legge funzionale che con maggiore probabilità si adatta ai dati rilevati statisticamente, sempre ammettendo, in via d’ipotesi, che i dati ubbidiscano a qualche legge di regolarità e non siano meramente casuali. Il metodo dei minimi quadrati consiste in un procedimento matematico di approssimazioni successive che, partendo dal valore della media dei valori osservati, attraverso il calcolo degli scarti e successive correzioni della media, permette di stabilire il valore, e quindi la legge, più probabile (e un indice della sua precisione: → scarto).