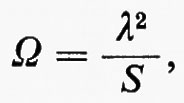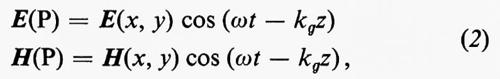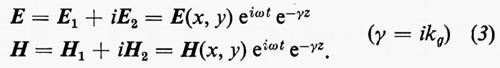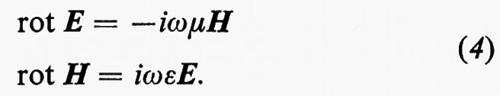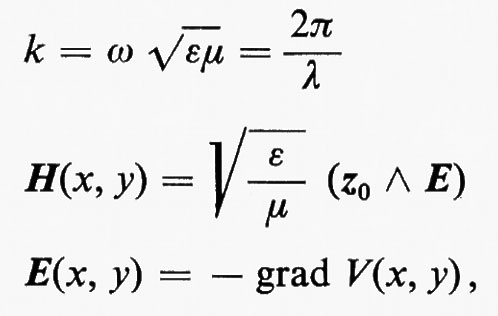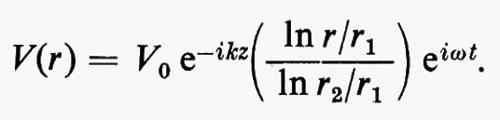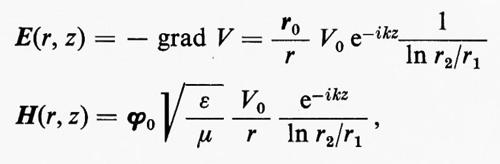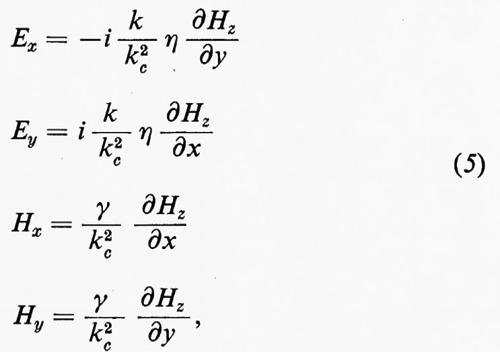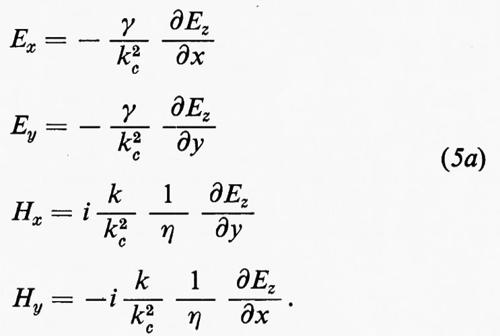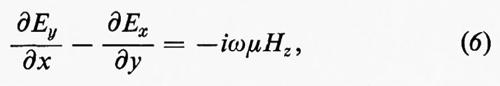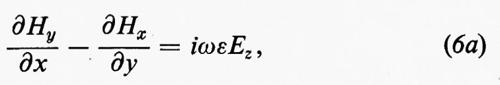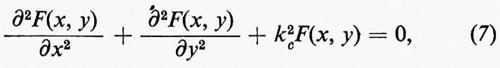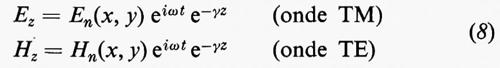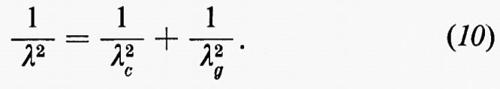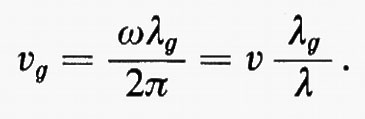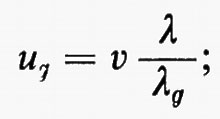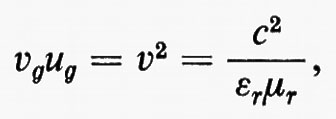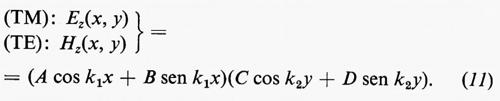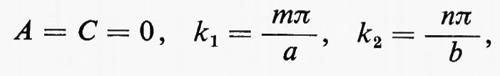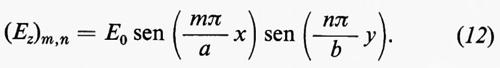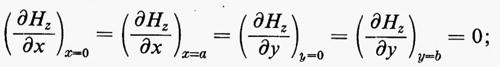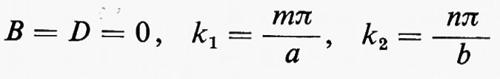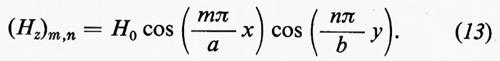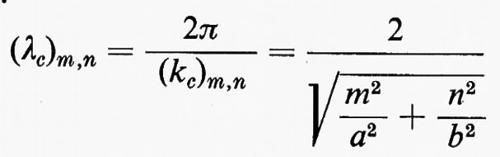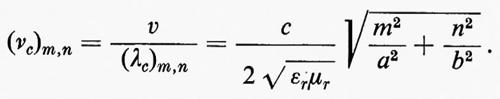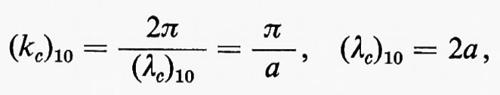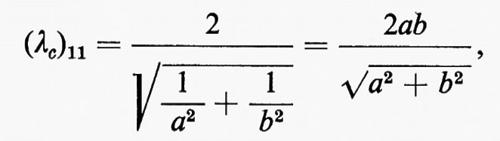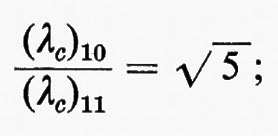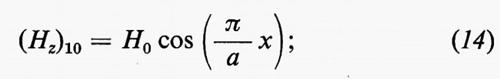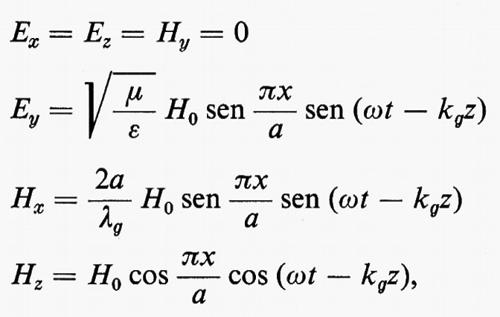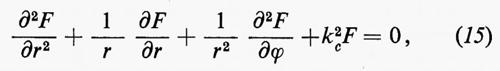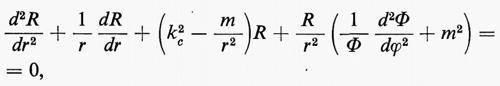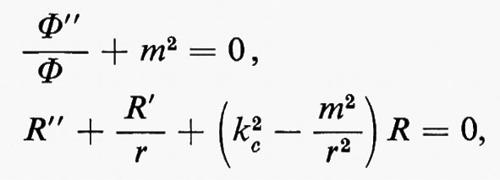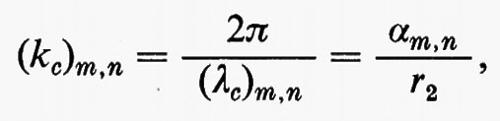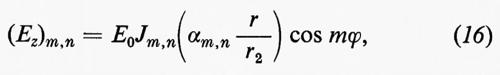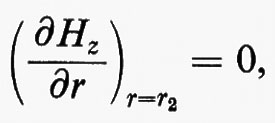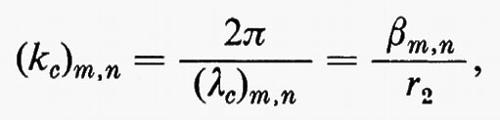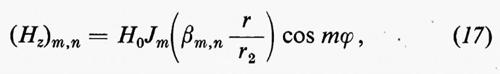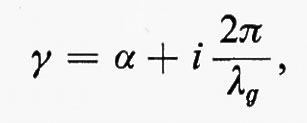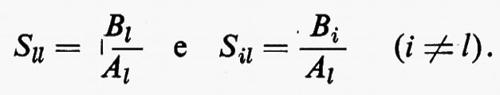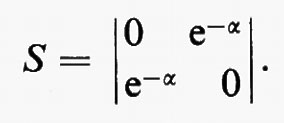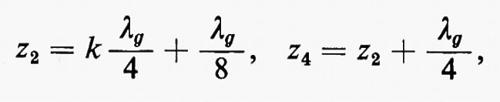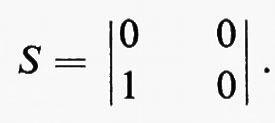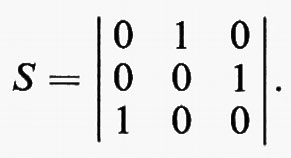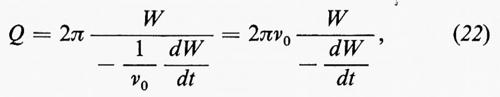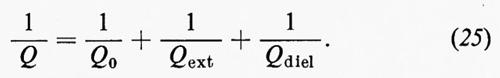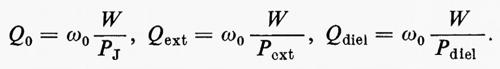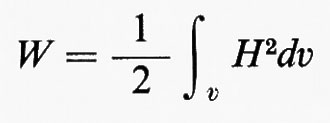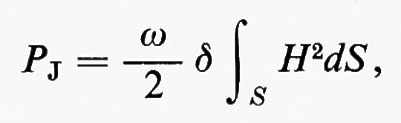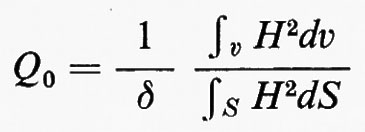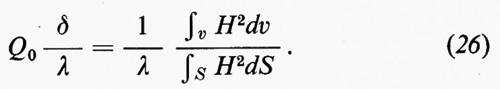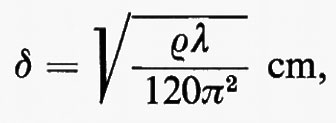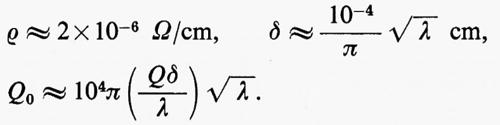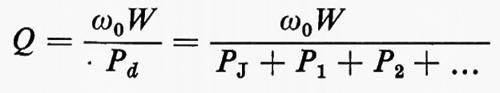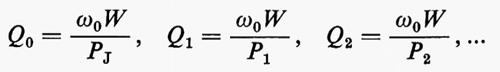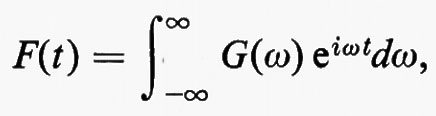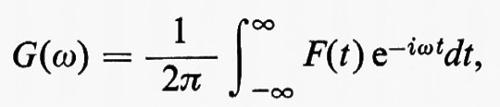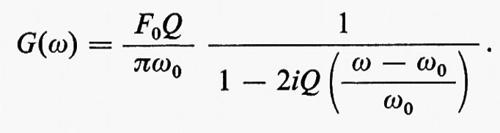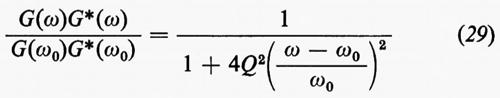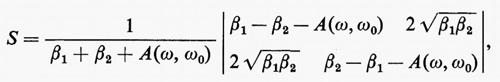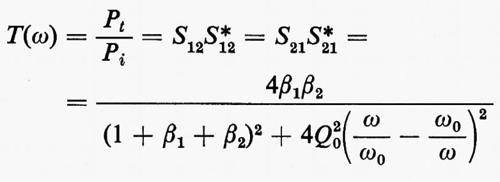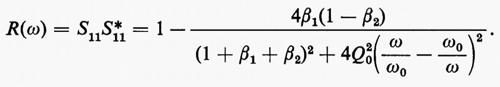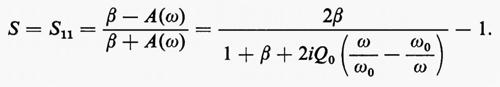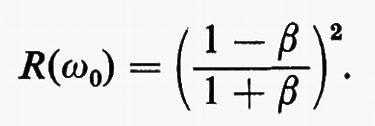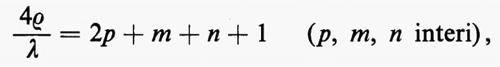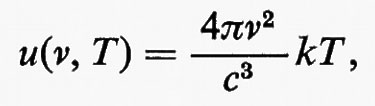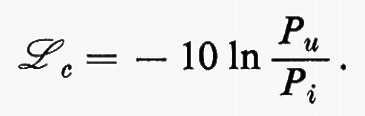Microonde

Microonde

di Adriano Gozzini

Microonde

sommario: 1. Introduzione. 2. Propagazione delle microonde. a) Propagazione libera. b) Propagazione guidata. 3. Circuiti a microonde. a) Multipoli. b) Matrice di scattering. c) Proprietà generali della matrice S. d) Dipoli e quadrupoli. e) Esapoli. f) Ottupoli. g) Multipoli di ordine più elevato. h) Multipoli non reciproci. 4. Cavità risonanti. a) Frequenze di risonanza e struttura dei campi. b) Il fattore di merito Q. c) Accoppiamento delle cavità. d) Curva di risposta. e) Cavità a trasmissione e a riflessione. f) Cavità particolari. 5. Generazione delle microonde. a) Prime esperienze. b) Il klystron. c) Il klystron reflex. d) Stabilizzazione di frequenza. e) Il magnetron. f) Il maser. 6. Rivelazione delle microonde. a) Sensibilità limite nella rivelazione di segnali radioelettrici. b) La conversione di frequenza. c) Rivelazione supereterodina. d) Ricevitori a microonde. e) Metodi di integrazione nella spettroscopia. 7. Applicazioni delle microonde. a) Il radar. b) Spettroscopia a microonde. c) Orologi atomici e standard di frequenza. □ Bibliografia.

1. Introduzione

Nella seconda metà del secolo scorso numerose esperienze avevano reso ben chiaro ai fisici che la luce era un fenomeno di tipo ondulatorio, che il ‛colore' era associato alla lunghezza d'onda e l'intensità era proporzionale al quadrato dell'ampiezza della perturbazione, la quale si propaga, nel vuoto, con la velocità c=3•10¹⁰ cm/s. La misura della velocità di propagazione e delle lunghezze d'onda permise di determinare le frequenze associate ai diversi colori, che risultarono comprese fra 3•10¹⁴ e 10¹⁵ oscillazioni al secondo. Fu anche chiaro che esistevano oscillazioni della stessa natura, di frequenza inferiore e superiore a quelle della luce visibile, che potevano essere rivelate attraverso effetti termici o chimici. Cosi lo spettro della radiazione ottica fu diviso in tre regioni: infrarossa, visibile e ultravioletta.

In base alla teoria elettromagnetica introdotta da Maxwell nel 1865 la perturbazione fu identificata in un'oscillazione periodica di campi elettrici e magnetici, e si comprese anche che la regione ottica non era che una piccola parte dello spettro elettromagnetico. La teoria elettromagnetica fu confermata sperimentalmente: fu provato che oscillazioni elettriche, prodotte in laboratorio, si propagavano con la velocità c e che davano luogo ai fenomeni di diffrazione, interferenza, polarizzazione ecc., caratteristici delle radiazioni luminose.

Parimenti si identificarono con oscillazioni della stessa natura le radiazioni X, scoperte da Röntgen verso la fine del secolo, con le quali von Laue riuscì ad ottenere fenomeni di diffrazione.

Identificata così la natura della luce come quella di campi elettrici e magnetici oscillanti periodicamente, le teorie esistenti agli inizi del secolo si rivelarono incapaci di interpretare alcuni fatti sperimentali, quali la distribuzione in frequenza della radiazione emessa da un corpo portato a temperatura elevata, l'emissione fotoelettrica e, più generalmente, i processi associati all'interazione di sistemi microscopici, atomi o molecole, con la radiazione. La necessità di superare tali difficoltà portò, nei primi decenni del secolo, all'edificazione della meccanica quantistica. I fisici scoprirono un mondo nuovo, descritto da leggi più generali, comprendenti le leggi della fisica classica come casi particolari, leggi che interpretavano in un quadro coerente i risultati sperimentali delle osservazioni di fenomeni elementari e che permettevano di prevederne dei nuovi.

In particolare, la radiazione elettromagnetica veniva ad assumere una struttura ‛quantizzata', cioè a essere costituita da ‛fotoni' o quanti di luce, a ciascuno dei quali era associata una energia hν e una quantità di moto, o, come oggi si dice, un momento hν/c, proporzionali alla frequenza ν, e un momento angolare ℏ=h/2π indipendente dalla frequenza (h=6,6•10^-27 erg•s è una costante universale, detta di Planck, avente le dimensioni di un'azione). Parallelamente l'ipotesi di de Broglie (1925), che a una particella in moto con momento mv fosse associato un treno di onde di lunghezza d'onda λ=h/mv (ipotesi confermata dalle esperienze di Davisson e Germer che riprodussero con elettroni i fenomeni di interferenza e diffrazione caratteristici del moto ondulatorio), portò al ben noto dualismo onda-corpuscolo, cioè alla necessità di descrivere (a seconda dei fenomeni investigati) con l'uno o l'altro dei modelli il campo elettromagnetico e le particelle.

La struttura corpuscolare della radiazione elettromagnetica permise di identificare come tale anche la radiazione γ emessa nel decadimento delle sostanze radioattive e presente nella radiazione cosmica, la cui natura ondulatoria è molto difficile dimostrare sperimentalmente.

In tal modo lo spettro della radiazione elettromagnetica si estende dalle frequenze basse (corrispondenti a quelle delle correnti alternate di uso industriale) a quelle corrispondenti alle energie più elevate delle particelle γ, e si divide convenzionalmente in regioni, a seconda della frequenza delle oscillazioni o dell'energia dei fotoni associati. La regione delle frequenze inferiori a 10¹² Hz è detta hertziana o delle radiofrequenze, quelle delle frequenze superiori sono le regioni ottica, X e γ. La distinzione è importante da un punto di vista pratico, in quanto distingue i fenomeni di interazione della radiazione con la materia, nei quali il campo elettromagnetico può essere descritto dalla teoria ondulatoria o classica, da quelli nei quali è necessario considerarne la struttura quantizzata.

Tale differenza si riflette anche nelle tecniche sperimentali che è necessario usare per rivelare la radiazione. Alle basse frequenze la radiazione è rivelata da un indicatore di corrente o di tensione, dal suono di un altoparlante, dallo spostamento del fascio di elettroni in un tubo a raggi catodici, ecc.: in sostanza, dall'azione meccanica che il campo elettrico o magnetico dell'onda produce sulle cariche libere, nel vuoto o nei conduttori di un circuito elettrico. Alle frequenze ottiche e a quelle superiori la radiazione è invece rivelata attraverso l'emissione di elettroni in una cella fotoelettrica, i processi chimici che avvengono in una emulsione fotografica, ecc.; attraverso processi, cioè, puramente quantistici, la cui descrizione è possibile con il modello corpuscolare della radiazione elettromagnetica.

La regione delle microonde comprende le frequenze più elevate dello spettro hertziano, estendendosi da frequenze di qualche gigahertz (10⁹ Hz) a frequenze di qualche centinaio di gigahertz (0,1 cm〈λ〈30 cm). Dal punto di vista storico questa è stata la prima regione dello spettro hertziano a essere studiata. Le prime esperienze sulle onde elettromagnetiche furono eseguite da Hertz, Righi, Lebedev, ecc., con onde prodotte in laboratorio per mezzo di scariche. Si trattava di oscillazioni smorzate della lunghezza d'onda di alcuni centimetri, cioè di quelle che oggi chiamiamo microonde. Con tali onde furono riprodotti i fenomeni caratteristici dell'ottica, a conferma della teoria elettromagnetica della luce. Con l'invenzione del triodo la possibilità di produrre oscillazioni di minor frequenza e maggiore potenza polarizzò le ricerche verso la produzione di onde di frequenza minore, le quali suscitarono particolare interesse per le possibili applicazioni alle radiocomunicazioni.

Negli anni immediatamente precedenti e durante la seconda guerra mondiale lo sforzo gigantesco compiuto soprattutto in America e in Inghilterra per la realizzazione del radar ha portato a un progresso prodigioso nelle tecniche per la produzione, la trasmissione e la ricezione di queste onde. Tale sforzo è documentato dai ventotto volumi della monumentale opera del Columbia Radiation Laboratory, i quali a tutt'oggi contengono le informazioni più dettagliate sull'argomento. Negli anni successivi alla fine della seconda guerra mondiale le tecniche sperimentali per lo studio di questa regione dello spettro sono state rese disponibili per la ricerca di base e hanno permesso la realizzazione di alcune esperienze fondamentali della fisica moderna.

2. Propagazione delle microonde

a) Propagazione libera

La propagazione di onde elettromagnetiche nello spazio è ampiamente trattata in altri articoli di questa Enciclopedia (v. radiotelevisione). Ci limitiamo qui pertanto ad analizzare le caratteristiche peculiari della propagazione delle microonde nell'atmosfera.

La caratteristica principale per le applicazioni risiede nel fatto che le microonde possono essere irradiate in fasci ben collimati. Un'antenna alimentata da un generatore costituisce una sorgente di radiazione elettromagnetica. È noto dai principi generali dell'ottica che un fascio di onde monocromatiche di lunghezza d'onda λ non può avere un'apertura angolare inferiore a

dove S è l'area della sorgente che irradia il fascio considerato. Per lunghezze d'onda di qualche centimetro e sorgenti (o antenne) del diametro di 1 m, Ω risulta dell'ordine di 10^-3 steradianti. Collimazioni di quest'ordine di grandezza possono essere effettivamente realizzate; pertanto è possibile inviare nello spazio energia elettromagnetica in fasci ben collimati (pencil beams), nei quali è contenuta quasi tutta l'energia irradiata da un generatore.

Una seconda importante caratteristica della propagazione atmosferica delle microonde risiede nel fatto che, a differenza delle onde di frequenza più bassa, esse non sono riflesse dagli strati ionizzati della ionosfera e quindi possono propagarsi nello spazio rendendo possibili comunicazioni con oggetti extraterrestri, ad esempio con satelliti. Reciprocamente, la radiazione a microonde proveniente dagli spazi cosmici può pervenire sulla Terra e fornire numerose informazioni di grande interesse per l'astronomia (v. telescopi: Radiotelescopi).

Molto importanti per il radar e la radioastronomia sono le proprietà dielettriche dell'aria alle frequenze delle microonde. L'ossigeno presenta numerose righe di assorbimento nella regione attorno a 60 GHz (λ=0,5 cm), dovute al paramagnetismo della molecola O₂, e anche una riga a 120 GHz (λ=2,5 mm). Oltre alla molecola O₂, la molecola H₂O presenta risonanze dovute ai livelli rotazionali, in corrispondenza di λ=1,25 cm e λ=1,8 mm (v. fig. 1). Questi assorbimenti limitano la distanza utile per il funzionamento del radar in tali regioni. Nelle altre parti dello spettro delle microonde l'atmosfera è perfettamente trasparente, per cui la radiazione ‛nera' ricevuta da un'antenna altamente direttiva non è quella che compete alla temperatura dell'atmosfera, ma quella della regione di spazio verso la quale è orientata l'antenna.

b) Propagazione guidata

Guide d'onda. - Alle frequenze elevate non è possibile trasmettere l'energia elettromagnetica lungo fili conduttori, come avviene alle frequenze di uso industriale, poiché le perdite per radiazione divengono importanti. Si ricorre allora a linee di trasmissione che impediscono l'irraggiamento nello spazio. Una linea di trasmissione è un sistema ‛cilindrico' (cioè dotato di un asse longitudinale z e avente una sezione S indipendente da z), formato da uno o più conduttori che costituiscono la superficie chiusa di contorno di un volume riempito con un dielettrico. Se il sistema comprende un solo conduttore, esso viene denominato ‛guida d'onda'. Questa è quindi semplicemente costituita da un tubo metallico che racchiude un dielettrico (generalmente aria). Le altre linee (linee coassiali) sono formate generalmente da uno o più conduttori posti all'interno di un tubo metallico e isolati dalla parete del tubo dal dielettrico. In tutti i casi l'energia elettromagnetica si propaga all'interno della regione dielettrica contornata dalla superficie conduttrice che ne impedisce la propagazione nello spazio. Nel caso delle linee coassiali la presenza del dielettrico, supporto del conduttore interno, comporta un'attenuazione supplementare rispetto a quella dovuta alla conducibilità finita dei conduttori, causata dalle perdite nel dielettrico. Tali perdite diventano importanti alle frequenze elevate, per cui le linee di trasmissione usate per le microonde sono generalmente costituite da guide d'onda. D'altra parte, affinché la propagazione possa avvenire all'interno di un tubo metallico, è necessario, come vedremo, che le dimensioni della sezione trasversale di questo siano dell'ordine della lunghezza d'onda della radiazione che si propaga. Ciò limita l'impiego delle guide alla regione delle onde centimetriche o millimetriche. Ne consegue che la trasmissione di microonde è generalmente realizzata con linee coassiali nella regione delle frequenze più basse (ν〈3•10⁹ Hz, λ>10 cm) e con guide d'onda alle frequenze più elevate.

La trasmissione di onde elettromagnetiche all'interno di un conduttore cavo è stata oggetto di numerose ricerche da parte di molti autori, fin dagli inizi della teoria elettromagnetica. Già nel 1897 lord Rayleigh fornì un'analisi matematica rigorosa della propagazione all'interno di tubi metallici con sezione circolare o rettangolare, riempiti con un dielettrico. Tali studi, di interesse puramente accademico fino all'avvento dei moderni generatori di microonde, sono stati ripresi intensivamente negli anni immediatamente precedenti la seconda guerra mondiale.

Tratteremo succintamente tale problema, facendo, per semplicità, l'ipotesi di assenza di perdite di conduzione (conducibilità infinita per i conduttori e nulla per i dielettrici) e dielettriche (costanti ε e μ del dielettrico reali). Tale ipotesi è giustificata dall'alta conducibilità dei conduttori (argento, rame) e dalle proprietà dei dielettrici (aria per le guide d'onda) generalmente usati. La presenza di perdite si traduce in una costante di propagazione complessa, la cui parte reale rappresenta un'attenuazione esponenziale con la distanza z lungo la linea.

Il campo elettrico e il campo magnetico di un'onda elettromagnetica che si propaga in un dielettrico devono soddisfare in ogni punto della regione dielettrica le equazioni di Maxwell che, nel caso ipotizzato di assenza di perdite, si scrivono:

dove E, H, ε e μ sono misurati nelle unità del sistema internazionale. Sulla superficie della regione dielettrica racchiusa dal conduttore deve essere inoltre

J=σE,

dove J è la densità di corrente nel conduttore. Dovendo J essere finito e avendo supposto la conducibilità infinita, la componente del campo elettrico tangenziale alle pareti deve essere nulla.

Il problema è quindi ricondotto alla ricerca di funzioni E, H che soddisfino le (1) nella regione dielettrica e le condizioni al contorno sulla sua superficie.

Soluzioni monocromatiche. - In un punto P(x, y, z) della sezione della linea percorsa da un'onda elettromagnetica progressiva, i campi E e H saranno funzioni periodiche del tempo, che potremo decomporre mediante uno sviluppo in serie di Fourier in una sovrapposizione di componenti monocromatiche del tipo

dove k_g è la costante di fase della linea. Viceversa, poiché le equazioni (1) sono lineari, una qualunque combinazione lineare di soluzioni del tipo (2) è anch'essa una soluzione, per cui potremo costruire tutte le soluzioni possibili se abbiamo quelle del tipo (2). Il problema è quindi ricondotto alla ricerca delle soluzioni armoniche monocromatiche.

Notiamo che, se

E₁=E(x, y) cos (ωt−k_gz)

H₁=H(x, y) cos (ωt−k_gz)

è una soluzione, lo è anche

E₂=E(x, y) sen (ωt−k_gz)

H₂=H(x, y) sen (ωt−k_gz)

e così anche la loro combinazione

Tale soluzione rappresenta un vettore complesso che non ha alcun senso fisico, ma la cui parte reale o il coefficiente di quella immaginaria rappresentano le soluzioni del problema.

Il vantaggio della ricerca delle soluzioni complesse (3) risiede nel fatto che per tale tipo di soluzione le equazioni (1) risultano indipendenti dal tempo (∂/∂t=iω) e si scrivono

Le equazioni vettoriali (4), proiettate sugli assi di un sistema di riferimento con l'asse z coincidente con l'asse della guida, si traducono in sei equazioni scalari che pongono delle relazioni fra le componenti dei campi E e H e le loro derivate. Si dimostra facilmente che: a) se si pongono identicamente nulle le componenti trasversali (E_x=E_y=H_x=H_y=0), risultano nulle anche quelle longitudinali; quindi non possono esistere onde puramente longitudinali; b) possono esistere onde trasversali elettromagnetiche (o TEM), nelle quali cioè le componenti longitudinali dei due campi sono entrambe nulle (E_z=H_z=0); c) possono esistere onde trasversali magnetiche (o TM, o onde E, con H_z=0, E_z≠0) e onde trasversali elettriche (o TE, o onde H, con E_z=0, H_z≠0) nelle quali cioè solo una delle componenti longitudinali è nulla.

Tale classificazione delle soluzioni in TEM, TM e TE è esauriente poiché tutte le possibili soluzioni possono essere costruite con combinazioni lineari di onde elementari TEM, TM e TE. Quindi il problema è ricondotto alla ricerca di soluzioni dei tre tipi descritti.

Onde TEM. - Ponendo H_z=E_z=0 si ottiene facilmendalle (4) per soluzioni del tipo 3), a meno del fattore e^iωt:

E(x, y, z)=E(x, y) e^-ikz

H(x, y, z)=H(x, y) e^-ikz

con

dove z₀ è un vettore unitario nella direzione z, e V è un potenziale scalare che soddisfa l'equazione di Laplace ΔV=0 in tutti i punti della regione dielettrica e assume valori costanti sulle superfici dei conduttori. In una guida d'onda, che ha una sola superficie conduttrice, il potenziale è costante su ogni sezione e quindi è E=H=0. Onde TEM non possono propagarsi entro una guida d'onda, ma solo lungo una linea che comprenda due o più conduttori, fra i quali possa sussistere una differenza di potenziale. La costante di propagazione k=2π/λ e il rapporto E/H=√-μ-/-ε (impedenza caratteristica del mezzo) sono per le onde TEM gli stessi che si hanno nel caso della propagazione delle onde piane in un dielettrico illimitato. Il problema della determinazione dei campi di un'onda TEM è quindi quello di determinare la funzione V che soddisfi l'equazione di Laplace ΔV=0 nella regione dielettrica e assuma valori costanti sui conduttori che ne formano il contorno (problema di Dirichlet). La soluzione dipende ovviamente dalla geometria della linea.

La più comune linea di questo tipo è il ‛cavo coassiale', costituito da due cilindri coassiali di raggio r₁ e r₂ isolati dal dielettrico, fra i quali è applicata una differenza di potenziale V₀e^iωt. La differenza di potenziale fra il conduttore interno e un punto alla distanza r dall'asse risulta:

A meno del fattore e^iωt, i campi risultano

dove r₀ e ϕ₀ sono i vettori unitari del sistema di coordinate cilindriche r, ϕ.

Onde TE e TM. - Proiettando le (4) sugli assi cartesiani si può verificare immediatamente che per soluzioni del tipo (3) si ottengono delle relazioni fra le diverse componenti dei campi che permettono di esprimere tali componenti in funzione della sola componente longitudinale E_z o H_z diversa da zero. Si ha precisamente, per onde TE (E_z=0):

e per onde TM (H_z=0):

Inoltre:

per le prime, e

per le seconde, dove k=2π/λ=ω √-ε-μ è la costante di propagazione nel dielettrico illimitato, η=√-ε-μ è l'impedenza caratteristica del mezzo e k²_c=k²+γ².

Sostituendo nella (6) i valori di E_x e E_y dati dalla (5) e nella (6a) i valori di H_x e H_y dati dalla (5a), si ricava che le componenti longitudinali devono nei due casi soddisfare l'equazione di Helmholtz, o delle onde:

in tutti i punti della sezione della guida, e le condizioni al contorno imposte dalle pareti conduttrici.

Si può dimostrare che soluzioni non nulle della (7) che soddisfano a tali condizioni esistono solo per particolari valori (reali>0) del parametro k_c (autovalori), formanti una successione discreta (k_c)₀, (k_c)₁, ..., (k_c)_n, ... . A ognuno di tali autovalori corrisponde almeno una funzione F (auto-funzione) che soddisfa il problema e che permette, attraverso le (5) o le (6) di determinare le componenti dei campi. Si ha così, per ciascun tipo di onda TE e TM, un'infinità di configurazioni (o ‛modi') e di frequenze possibili per le onde che possono propagarsi nella guida. La ricerca degli autovalori e delle autofunzioni della (7) è un problema di analisi matematica la cui complessità dipende dal contorno Γ della sezione della guida.

Condizioni di propagazione. - A ogni autovalore della (7) è associata una soluzione del tipo

che permette di determinare le altre componenti e che soddisfa le condizioni al contorno. Avendo posto

k²_c=k²+γ², (9)

a ogni autovalore corrisponde una costante di propagazione diversa.

Se è k>k_c, la costante di propagazione è immaginaria pura. Le (8) rappresentano allora un'onda elettromagnetica che si propaga senza attenuazione nella direzione z. Essendo k=2π/λ la costante di propagazione libera nel dielettrico, se si pone k_c=2π/λ_c, γ=i 2π/λ_g=ik_g, dalla (9) si ottiene la seguente relazione generale fra la lunghezza d'onda λ_g nella guida e la lunghezza d'onda λ nella propagazione libera, per la propagazione guidata con la configurazione corrispondente all'autovalore k_c:

Da tale relazione appare che la lunghezza d'onda λ_g e la velocità di fase v_g dell'onda guidata risultano rispettivamente maggiori di λ e v, lunghezza d'onda e velocità di fase della propagazione libera nel dielettrico illimitato, essendo

La velocità di gruppo u_g, ovvero la velocità con cui si propaga l'energia, risulta invece inferiore nella propagazione guidata che nella propagazione libera:

da cui

dove ε_r e μ_r sono rispettivamente la costante dielettrica e la permeabilità del mezzo relative al vuoto. Per k=k_c la lunghezza d'onda λ_g e la velocità di fase divengono infinite. I campi in tutti i punti della guida oscillano in fase. La velocità di gruppo risulta nulla e non vi è propagazione d'energia.

Quando infine è k〈k_c la costante di propagazione è reale e l'ampiezza dei campi decresce esponenzialmente con z. Tale attenuazione non può essere attribuita alle perdite nelle pareti o nel dielettrico (che si sono ipotizzate assenti), ma al fatto che, alle frequenze alle quali k〈k_c, il campo non può propagarsi nella guida.

Possiamo visualizzare il comportamento dell'onda TE o TM all'interno della guida decomponendo il campo che si propaga in una sovrapposizione di onde piane che si propagano con la velocità v=1/√-ε-μ =c/√-ε-_r-μ-_r dell'onda nel dielettrico illimitato e si riflettono secondo un angolo ϕ sulle pareti della guida (v. fig. 3). L'angolo di propagazione ϕ risulta

Per k→k_c, è anche ϕ→π/2, cioè la direzione di propagazione dell'onda tra le pareti della guida tende a essere normale alle pareti stesse e diviene normale quando k=k_c. In tal caso il campo elettromagnetico si riflette fra le pareti della guida senza propagarsi secondo z. La lunghezza d'onda λ_g diviene infinita, cioè il campo oscilla in fase su tutti i punti della linea.

Per k〈k_c, ϕ è immaginario e non vi è propagazione: in queste condizioni il fenomeno è analogo a quello delle onde evanescenti nel caso della riflessione totale.

Determinazione degli autovalori e struttura dei campi. - Ordinando i possibili autovalori k_c (reali e positivi) secondo una successione crescente,

(k_c)₀, (k_c)₁, ..., (k_c)_n, ... ,

le corrispondenti lunghezze d'onda ‛critiche', o di ‛taglio', associate, λ_c=2π/k_c, formano una successione decrescente:

(λ_c)₀, (λ_c)₁, ..., (λ_c)_n, ... .

Un'onda che si propaghi nel dielettrico illimitato con lunghezza d'onda λ può propagarsi nella guida se e solo se esiste una (λ_c)_r tale che (λ_c)_r>λ. Se tale condizione è soddisfatta l'onda può propagarsi nella guida in una qualunque delle configurazioni associate agli autovalori (k_c)₀, (k_c)₁, ..., (k_c)_r, o anche con la configurazione risultante dalla sovrapposizione di diverse di tali configurazioni. Se invece è (λ_c)₀〈λ, l'onda non può propagarsi nella guida. Ne risulta che una guida agisce da filtro ‛taglia basso', impedisce cioè la propagazione di tutte le componenti del campo elettromagnetico la cui frequenza sia inferiore alla frequenza corrispondente alla lunghezza d'onda critica dell'autovalore più basso.

La determinazione degli autovalori permette quindi di determinare le frequenze che si possono propagare nella guida. Ne diamo la soluzione per i casi semplici delle guide più comunemente usate: la guida rettangolare e la guida circolare.

1. Guida rettangolare. Questa guida è costituita da un tubo metallico la cui sezione retta è un rettangolo di lati a e b. Nel riferimento cartesiano più appropriato l'asse z coincide con l'asse del tubo e gli assi x e y sono paralleli ai lati a e b (a>b) della sezione. L'equazione (7), nella quale F(x, y) rappresenta la componente longitudinale E_z del campo elettrico per i modi TM e del campo magnetico H_z per i modi TE si integra col metodo della separazione delle variabili, ponendo F(x, y)=ϕ(x)ψ(y). La soluzione, per l'una e l'altra delle funzioni ϕ e ψ è data da:

ϕ(x)=A cos k₁x+B sen k₁x

ψ(y)=C cos k₂y+D sen k₂y,

con A, B, C e D costanti arbitrarie e k²_c=k²₁+k²₂.

La soluzione generale è quindi:

Per i modi TM le condizioni al contorno sono:

E_z(0, y)=E_z(a, y)=E_z(x, 0)=E_z(x, b)=0;

da esse si ricava:

con m ed n interi. La soluzione per il campo E_z risulta quindi:

Introducendo questa soluzione nelle (5) si ottengono le altre componenti e si verifica che anch'esse soddisfano le condizioni al contorno

E_x(x, 0)=E_x(x, b)=E_y(0, y)=E_y(a, y)=0.

Per i modi TE le condizioni al contorno risultano invece:

da queste si ottiene:

e la soluzione per il campo H_z risulta:

Attraverso le (5) si determinano quindi le altre componenti e si verifica che anch'esse soddisfano le medesime condizioni al contorno.

Ad ogni coppia di numeri interi m ed n corrisponde un autovalore

che è determinato, oltre che dagli indici m ed n, anche dalle dimensioni a e b dei lati della sezione della guida. Gli indici m ed n non possono essere entrambi nulli e a ogni autovalore (k_c)_m,n corrispondono una soluzione TM e una soluzione TE che si ottengono dalle (12) e (13) e dalle (5) e (5a), salvo il caso m=m, n=0 per il quale la soluzione TM è nulla ed esiste solo la (TE)_m,0 (m≠0).

Le lunghezze d'onda critiche dei vari modi m, n risultano date da:

e le corrispondenti frequenze critiche da:

La lunghezza d'onda λ_c più grande, cui corrisponde la frequenza più bassa che può propagarsi nella guida, corrisponde all'autovalore m=1, n=0:

che è indipendente dalla lunghezza b del lato più corto della sezione della guida. A tale autovalore è associata una sola soluzione, corrispondente al modo TE₁₀, che è quindi il modo fondamentale della guida rettangolare. All'auto- valore successivo (k_c)₁₁ corrispondono un modo TE e un modo TM, i quali hanno entrambi una lunghezza d'onda critica

che dipende da entrambe le dimensioni a e b della sezione del tubo.

In una guida in cui sia b=a/2, il rapporto fra le lunghezze d'onda critiche dei due primi modi risulta

pertanto un'onda la cui frequenza sia compresa fra ν_c e 2 ν_c può propagarsi in tale guida con una configurazione soltanto, quella del modo fondamentale TE₁₀. Per questo motivo la guida generalmente usata nei circuiti per microonde è la guida rettangolare, con dimensioni approssimativamente nel rapporto di 1 a 2.

Per il modo fondamentale TE₁₀ la soluzione (13) si scrive:

da questa, attraverso le equazioni (5) si ottengono per le componenti dei campi le seguenti espressioni:

nelle quali si sono espressi i campi mediante l'ampiezza della componente H_z del campo magnetico sulle pareti (x=0).

La configurazione del campo elettromagnetico nel modo TE₁₀ in una guida rettangolare è la più semplice possibile. Il campo elettrico è polarizzato linearmente, e sul- l'asse della guida esso oscilla in fase con il campo magnetico, che ivi è puramente trasversale. Al centro della guida, quindi, l'onda elettromagnetica ha la struttura di un'onda piana. Il campo magnetico giace sul piano xz: la componente trasversale H_x è nulla sulle pareti laterali, in x=0 e x=a, ed è massima al centro, in x=a/2, mentre la componente longitudinale H_z è nulla al centro e massima sulle pareti; essa inoltre a ogni istante ha lo stesso valore ma verso opposto in punti simmetrici rispetto all'asse della guida. Le due componenti H_x e H_z oscillano con una differenza di fase di π/2: ne consegue che il campo magnetico risultante oscilla secondo una direzione rettilinea in x=0, x=a, x=a/2, dove una delle due componenti è nulla, ed è un campo polarizzato ellitticamente sul piano xz negli altri punti della guida, la polarizzazione essendo di segno contrario in due punti simmetrici rispetto all'asse. A una certa distanza dall'asse le ampiezze delle due componenti sono eguali e il campo magnetico in tali punti è un campo ruotante con velocità angolare opposta nelle due posizioni simmetriche, il segno della polarizzazione, nell'una e nell'altra posizione, essendo determinato dal segno di k_g, cioè dalla direzione di propagazione dell'onda nella guida. Kastler (1952) propose di utilizzare questa particolare struttura del modo TE₁₀ per discriminare la propagazione secondo i due possibili versi lungo z: vedremo nel seguito come ciò sia stato utilizzato nei circuiti a microonde.

2. Guida circolare. Questa guida è costituita da un tubo metallico a sezione circolare di raggio r₂ . In coordinate cilindriche r, ϕ, z l'equazione (7) si scrive:

che si può integrare per separazione delle variabili ponendo F(r, ϕ)=R(r)Φ(ϕ). Così facendo, l'equazione precedente può scriversi:

dove m² è una costante arbitraria. Φ e R devono quindi separatamente soddisfare le equazioni seguenti:

le cui soluzioni sono rispettivamente

Φ(ϕ)=A cos (mϕ)+B sen (mϕ),

R(r)=CJ_m(k_cr)+DN_m(k_cr),

con A, B, C, D costanti arbitrarie, e dove J_m ed N_m sono funzioni di Bessel di prima e seconda specie, d'ordine m, dell'argomento k_cr, per le quali, in virtù della continuità della funzione Φ, m deve essere un numero intero: m=0, 1, 2, ... . Poiché in r=0 la funzione N_m→∞, dev'essere D=0; inoltre possiamo fissare arbitrariamente l'origine degli angoli ϕ in modo da rendere nulla la costante B. La soluzione è quindi

F(r, ϕ)=F₀J_m(k_cr) cos (mϕ).

Modi TM. - Per tali modi sarà F(r, ϕ)=E_z(r, ϕ)=E₀J_m(k_cr) cos (mϕ) e, dovendo essere E_z(r₂, ϕ)=0, ne consegue:

J_m(k_cr₂)=0,

da cui

dove α_m,n è la n-esima radice dell'equazione J_m(x)=0. Sono così determinati gli autovalori e le lunghezze d'onda critiche delle configurazioni, o modi, TM_m,n in una guida circolare. La componente E_z risulta

dalla quale, attraverso le (5), si possono ricavare le altre componenti E_r, E_ϕ, H_r, H_ϕ.

Modi TE. - Per tali modi si trova F(r, ϕ)=H_z(r, ϕ)=H₀J_m(k_c, r) cos mϕ. Affinché le componenti tangenziali del campo elettrico siano nulle sulle pareti, deve essere:

da cui

J_m′ (k_cr₂)=0.

Pertanto, deve essere

dove β_m,n e l'n-esima radice dell'equazione J_m′ (x)=0. La soluzione H_z risulta quindi data da

dalla quale, mediante la (5), si ottengono le altre componenti dei campi E_r, E_ϕ, H_r, H_ϕ.

I valori più piccoli non nulli delle soluzioni delle equazioni J_m(x)=0 e J_m′ (x)=0 sono:

β₁₁=1,841, α₀₁=2,405, β₂₁=3,054, β₀₁=α₁₁=3,832...;

dall'esame di questa successione si deduce che il modo fondamentale nella guida circolare è il modo TE₁₁, al quale corrisponde la lunghezza d'onda critica λ_c=2πr₂/1,84=3,4 r₂. La configurazione del campo per tale modo è simile a quella del modo TE₁₀ in una guida rettangolare. La configurazione dei campi per i modi più bassi è illustrata dalla fig. 7. Dall'esame di tali configurazioni appare chiaro il significato fisico degli indici m, n, che rappresentano il numero degli zeri che i campi hanno secondo le coordinate x e y (guida rettangolare) o r e ϕ (guida circolare) della sezione della guida.

Attenuazione nelle guide. - Nei paragrafi precedenti si è assunto che qualunque componente di un'onda propagantesi lungo una guida indefinita sia espressa dalla parte reale A della funzione

A=A₀ e^iωt-γz,

dove, per una guida priva di perdite, si è posto γ=ik_g= i 2π/λ_g. In una guida reale la costante di propagazione è complessa:

per cui il campo si attenua esponenzialmente secondo la direzione z. La costante di attenuazione a, misurata in cm^-1 o m^-1, dipende dalla geometria della guida, dal modo di propagazione, dalla frequenza e dalla resistività del metallo di cui è fatta la guida; 2α rappresenta la costante di attenuazione in potenza. Per λ=1 cm, una guida a sezione rettangolare di 1×0,5 cm presenta, per onde TE₁₀, un'attenuazione in potenza 2α pari a 10^-3 cm^-1, cioè l'intensità del campo si riduce di un fattore e, dopo un percorso di 10 m. Tranne in alcuni casi particolari (spettrometri), la lunghezza dei circuiti per guide d'onda è molto minore e ciò giustifica l'approssimazione di assenza di perdite precedentemente formulata.

3. Circuiti a microonde

a) Multipoli

Un circuito a microonde comprende molti elementi, ciascuno dei quali è progettato per adempiere a una funzione particolare. Ad esempio, può essere necessario suddividere l'energia che si propaga in una guida in diverse guide, oppure prelevarne una frazione, ovvero attenuarla, ecc. Ciò si realizza con combinazioni di guide che prendono il nome di ‛multipoli'.

Un multipolo è costituito da un certo numero di guide che convergono tutte verso una stessa regione (‛giunzione'; v. fig. 8). Scegliamo su ciascuna guida un piano normale all'asse piano di riferimento) come origine della coordinata z. Ogni guida costituisce una ‛porta' o ‛braccio' del multipolo. Il multipolo può essere rappresentato mediante un ‛circuito equivalente' fittizio, a costanti concentrate, nel quale a ogni piano di riferimento corrisponde una coppia di terminali. Perciò un multipolo con un solo braccio è un dipolo, con due bracci un quadrupolo ecc. Considereremo per semplicità multipoli ‛passivi' (che non contengono cioè nessuna sorgente di energia), costituiti da guide rettangolari, nelle quali sia possibile solo la propagazione di onde TE₁₀. Si suppone inoltre che i bracci del multipolo siano ‛adattati', cioè che il coefficiente di rifiessione verso la giunzione dei circuiti esterni connessi ai vari bracci sia zero. Chiameremo incidenti le onde che si propagano verso la giunzione, emergenti quelle che si propagano secondo il verso opposto e useremo la notazione A per le prime, B per le seconde. A_i rappresenterà quindi, nella notazione complessa, l'ampiezza e la fase (sul piano di riferimento del braccio i-esimo del multipolo, cioè in z_i=0) del campo elettrico di un'onda che si propaga verso la giunzione, B_i quelle del campo di un'onda che ne emerge. Le proprietà fisiche del multipolo saranno determinate se si conoscono le relazioni che legano le variabili A e B delle onde incidenti ed emergenti dai vari bracci del multipolo.

b) Matrice di scattering

Poiché le equazioni di Maxwell sono lineari, potremo scrivere che nel piano di riferimento del braccio i-esimo il campo dell'onda emergente B_i sarà dato da una combinazione lineare dei campi delle onde incidenti sulla giunzione dai diversi rami, sarà cioè:

B_i=S_i1A₁+S_i2A₂+...+S_inA_n (i=1, 2, ... n). (18)

I coefficienti S_ik sono numeri complessi adimensionali, che caratterizzano il comportamento del multipolo.

Le relazioni (18) possono essere scritte nella forma matriciale

B=SA,

in cui le matrici a n righe e i colonna A e B rappresentano le onde incidenti ed emergenti dalla giunzione e la matrice quadrata S a n righe ed n colonne è la ‛matrice di scattering' o di trasmissione, che caratterizza completamente il multipolo. Il significato fisico degli elementi S_ik della matrice S è immediato. Ponendo infatti nelle (18) A_k=0, per ogni k≠l, cioè eccitando un solo braccio della giunzione, si ottiene:

B_i=S_ilA_l, (i=1, 2, ..., n)

da cui:

Così gli elementi diagonali della matrice di scattering rappresentano per ciascun braccio il rapporto fra il campo riflesso dalla giunzione e quello che incide su essa, cioè il coefficiente di riflessione in ampiezza della giunzione considerata come una discontinuità della guida che costituisce il braccio (il quadrato ∣S_ll∣²=S_llS*_ll è il coefficiente di riflessione in potenza; gli elementi S_il rappresentano il rapporto fra le ampiezze del campo emergente dal ramo i, a causa di un'eccitazione nel ramo l, e l'ampiezza ditale eccitazione, cioè il coefficiente di trasmissione tra i bracci l e i (il quadrato ∣S_il∣²=S_ilS*_il rappresenta la frazione della potenza incidente sul braccio l che emerge dal braccio i).

Gli elementi della matrice di scattering hanno quindi un preciso significato fisico e possono essere determinati sperimentalmente con misure di ampiezza e fase nei diversi bracci del multipolo. Il problema quindi di avere un dispositivo che realizzi determinate funzioni si riduce a quello di progettare un multipolo in modo che sia descritto dalla matrice S appropriata, agendo sui diversi parametri da cui dipendono, nei vari casi, i coefficienti S_ik. Tali parametri sono in numero di n², se il multipolo ha n bracci, e, poiché ciascuno di essi è un numero complesso a+ib, il numero dei parametri che caratterizzano il multipolo è 2n². Poiché il numero di condizioni che si impongono è pari a 2n (ampiezza e fase per ogni B_i), può sembrare che vi sia ridondanza. Tuttavia, le proprietà generali della matrice S riducono fortemente il numero dei parametri da cui dipendono le proprietà di un multipolo (parametri fisici).

c) Proprietà generali della matrice S

Parametri liberi. - La fase delle onde B_i emergenti dai vari bracci del multipolo dipende dalla scelta (arbitraria) dei piani di riferimento, mentre ovviamente le proprietà fisiche del multipolo non dipendono da tale scelta. Tali piani sono in numero di n, per cui in realtà le proprietà del multipolo sono descritte da 2n²−n parametri anziché da 2n².

Assenza di perdite. - Se il multipolo è privo di perdite, n² parametri risultano determinati. Ciò deriva dal fatto che in questo caso deve essere verificata la relazione

Σ A_iA*_i=Σ B_jB*_j (19)

che esprime l'eguaglianza fra la potenza della radiazione incidente e quella della radiazione emergente dalla giunzione. Affinché la (19) sia verificata è necessario che fra i coefficienti S_ik intercorrano n² relazioni, per cui la matrice S è determinata da soli n² parametri.

Reciprocità. - Un sistema fisico soddisfa al principio di reciprocità se la risposta in un punto B del sistema a una sollecitazione applicata in un altro punto A è la stessa che si osserva in A quando la medesima sollecitazione sia applicata in B. Mediante le equazioni di Maxwell si può dimostrare che un sistema lineare, isotropo e passivo, nel quale si propaga un campo elettromagnetico soddisfa a tale principio (teorema di Lorentz). Ciò si traduce nella proprietà di simmetria della matrice S:S_ik=S_ki. Perciò la matrice di un multipolo reciproco privo di perdite ha solo (n²−n)/2+n elementi distinti e, tenuto conto della arbitrarietà dell'origine delle coordinate, le proprietà fisiche di un tale multipolo sono descritte da (n²−n)/2=n(n−1)/2 parametri distinti.

Proprietà di simmetria. - Le proprietà sopra descritte della matrice S di un multipolo reciproco e privo di perdite sono proprietà generali, che non dipendono dalla realizzazione materiale del multipolo. Se questa presenta caratteri di simmetria geometrica, tali caratteri si ritrovano nella matrice S. Se la struttura del multipolo non cambia per riflessione rispetto a un piano o per rotazione attorno a un asse, ciò significa che deve essere S_ik=S_pq. Tali condizioni si aggiungono a quelle intrinseche e riducono ancora il numero dei parametri che descrivono il multipolo; può anche accadere che tali proprietà descrivano completamente la struttura. In altri casi restano alcuni parametri che possono essere fissati in modo che il dispositivo funzioni nel modo desiderato. In tutti i casi non è possibile imporre a un multipolo più condizioni di quelle consentite dalle sue caratteristiche intrinseche e dal numero dei parametri fisici. Descriviamo nel seguito alcuni multipoli di uso frequente nei circuiti a microonde.

d) Dipoli e quadrupoli

Un dipolo è costituito da un semplice tratto di guida che termina in un modo qualsivoglia: la matrice S in tal caso è costituita da un unico elemento che rappresenta il coefficiente di riflessione della terminazione. Casi interessanti sono quelli per i quali è S₁₁=0 e S₁₁=−1: il primo rappresenta una terminazione assorbente o adattata, il secondo un cortocircuito perfetto. Si realizza il primo caso chiudendo una guida con materiale assorbente opportuna- mente sagomato in modo da ridurre al massimo la discontinuità; il secondo caso cortocircuitando la guida con una parete metallica. In quest'ultimo caso nella guida si forma un sistema di onde stazionarie: la posizione dei massimi e dei minimi è determinata dalla distanza z dal cortocircuito. È di grande interesse poter variare tali posizioni, il che si ottiene, in generale, realizzando le terminazioni con pistoni mobili che permettono di modificare la configurazione del campo nei diversi punti della guida. La realizzazione di terminazioni perfettamente assorbenti o riflettenti non è possibile, ma è possibile realizzare tali dispositivi con valori del rapporto d'onda stazionaria (o ROS: rapporto fra il quadrato dell'ampiezza del campo in un ventre e in un nodo, pari a 1 per un'onda progressiva e ∞ per un sistema di onde stazionarie prodotte da un corto circuito perfetto) di 1,01 in un caso e 10⁴ nell'altro.

Altri dipoli sono i rivelatori e le cavità a riflessione. Un rivelatore è un tratto di guida che contiene un elemento capace di convertire l'energia della microonda in un segnale elettrico di bassa frequenza o continuo. Ciò si realizza mediante un diodo a semiconduttore o un bolometro inserito in un ponte. L'elemento rivelatore è racchiuso in una cartuccia ceramica, inserita all'interno di una guida. Il sistema deve costituire una terminazione adattata, tale da convertire la maggior parte possibile dell'energia incidente. Per questo la guida che alloggia il rivelatore è chiusa su un cortocircuito mobile (pistone), che permette di situare il rivelatore in un ventre di campo elettrico, ed è munita di viti d'accordo che minimizzano le riflessioni.

Una cavità posta come terminazione di una guida (‛cavità a riflessione') costituisce un dipolo il cui coefficiente di riflessione dipende dalla frequenza dell'onda incidente. Se la cavità è accoppiata a due guide (‛cavità a trasmissione') costituisce un quadrupolo che si comporta come un filtro che trasmette una banda stretta di frequenze. Tali dispositivi saranno trattati nel seguito.

Un quadrupolo è praticamente costituito da un tratto di guida contenente all'interno alcune discontinuità, costituite da ostacoli, cambiamenti di sezione, ecc. La trattazione generale è assai complessa; pertanto, ci limiteremo a dare una descrizione sommaria di alcuni di essi. Un tipo importante di quadrupolo è l'attenuatore, usato per controllare la potenza che si propaga in una guida. Esso è un quadrupolo con perdite, la cui matrice di scattering deve quindi essere del tipo:

Si deve inoltre poter variare l'attenuazione 2α senza variare la lunghezza elettrica della guida equivalente. Ciò si realizza mediante una lama molto sottile di materiale dielettrico con forti perdite, sagomata in modo da minimizzare le riflessioni. Il dispositivo può essere realizzato come è indicato nella fig. 12: in tal caso la lama si sposta all'interno della guida parallelamente al lato corto. L'attenuazione è molto piccola quando la lama è in x=0 o in x=a ed è massima quando è al centro (x=a/2), dove è massimo il campo elettrico dell'onda TE₁₀.

e) Esapoli

Gli esapoli sono sistemi a tre bracci. Gli esapoli a T sono costituiti da una guida principale alla quale è saldata perpendicolarmente una seconda guida. A seconda che la saldatura sia realizzata in modo che le facce strette o quelle larghe delle due guide siano complanari, i T sono denominati E o H. Questa denominazione è dovuta al fatto che nel primo caso il piano determinato dagli assi delle due guide contiene in tutti i rami il campo elettrico, nell'altro il campo magnetico. La potenza che incide dal ramo 1 adattato si suddivide in due parti uguali. Il campo, a uguale distanza dalla giunzione, è in fase nel tipo H, in opposizione di fase nel tipo E.

Le giunzioni Y sono realizzate, come le T, nei piani E e H, ma dispongono di una simmetria più elevata. Dovendo essere eguali i termini diagonali della matrice di scattering, S₁₁=S₂₂=S₃₃, tali giunzioni non possono essere adattate: un terzo dell'energia di un'onda che incide da uno dei rami si riflette, mentre gli altri due terzi si suddividono in parti uguali nei rimanenti due rami.

f) Ottupoli

Di questi dispositivi a 4 bracci descriviamo brevemente i più importanti: il T magico e l'accoppiatore direzionale.

T magico. - La combinazione di due T, uno nel piano E, l'altro nel piano H, come indicato nella fig. 14, è detta T ibrido. Oltre alle condizioni imposte dalla reciprocità e dall'assenza di perdite, la simmetria del sistema impone le condizioni supplementari:

S₁₁=S₂₂; S₃₁=S₃₂; S₄₁=−S₄₂.

Per la disposizione relativa delle guide 3-4 deve essere inoltre S₃₄=S₄₃=0; pertanto, i parametri fisici che caratterizzano il circuito sono solo due.

Essi possono essere opportunamente scelti per adattare i rami E e H, imponendo cioè S₃₃=S₄₄=0. In tal caso, il dispositivo prende il nome di ‛T magico'. Con un'opportuna scelta dei piani di riferimento, la matrice S può essere scritta nella forma

dal cui studio si possono individuare le seguenti proprietà del T magico.

1. Un'onda incidente dal braccio 3 si suddivide nei bracci 1 e 2 in due onde di uguale ampiezza e in fase fra loro, in due punti qualunque equidistanti dalla giunzione. Nessuna onda si propaga nel braccio 4, né è riflessa nel braccio 3.

2. Se l'onda incide dal braccio 4, essa ancora si suddivide in due onde nei bracci 1 e 2, in opposizione di fase a uguale distanza dalla giunzione, e nessuna onda è riflessa in 4 né si propaga lungo il braccio 3.

3. Se l'onda incide dai rami 1 o 2, eccita con uguale ampiezza due onde nei rami 3 e 4, che sono in fase se l'eccitazione viene dal braccio i, in opposizione di fase se viene dal braccio 2.

In conclusione, nel T magico ciascun ramo è completamente disaccoppiato da un altro e l'energia proveniente da un ramo si equipartisce negli altri due in due onde che sono in fase o in opposizione di fase a seconda dei casi.

Tali proprietà rendono questa struttura preziosa nei circuiti a microonde, dove trova numerose applicazioni: ad esempio, essa costituisce l'analogo a microonde di un ponte di impedenze. Se un generatore alimenta, infatti, il braccio 3 e i bracci 1 e 2 sono terminati con una impedenza uguale, nessuna onda si propaga in 4, poiché le onde riflesse dai due bracci interferiscono in 4. Si può così misurare l'impedenza (o ‛coefficiente di riflessione') di un qualunque circuito connettendolo a uno dei bracci allineati e terminando l'altro con un'impedenza campione. Altri impieghi del T magico saranno illustrati nel seguito di questo articolo.

Accoppiatori direzionali. - Questi sono elementi di circuito molto importanti, che servono a trasmettere una frazione dell'energia che si propaga in una guida (guida principale) entro una seconda guida, in modo che l'onda eccitata in questa si propaghi secondo una sola direzione. Sono quindi degli ottupoli nei quali due bracci sono costituiti dalla guida principale e due dalla guida secondaria. Essi sono ovviamente sistemi reciproci, nei quali cioè i ruoli delle guide principale e secondaria possono essere scambiati. Le proprietà di un accoppiatore direzionale sono descritte dal coefficiente di accoppiamento

C=−10 ln (S₄₁)² (in decibel),

che rappresenta la frazione della potenza che viene immessa nella guida secondaria, e dalla direttività

D=10 ln (S₄₁/S₂₁)² (in decibel),

che rappresenta il rapporto tra la potenza che si propaga nella guida secondaria secondo la direzione voluta e secondo la direzione opposta. Per un accoppiatore ideale dev'essere D=∞, cioè S₂₁=0.

La teoria degli accoppiatori direzionali è complessa e di tali circuiti esistono molte realizzazioni. Ci limitiamo all'esempio dell'acooppiatore a due fori usato nei dispositivi con piccoli accoppiamenti, per il quale è immediata la comprensione del principio fisico di funzionamento. Consiste in due guide sovrapposte e accoppiate fra loro mediante due piccoli fori, posti a distanza λ_g/4 l'uno dall'altro.

Consideriamo un'onda incidente dal braccio 1. Il primo foro costituisce una sorgente che eccita un'onda nella guida secondaria. Poiché l'accoppiamento è assai piccolo, dell'ordine di 20 dB, anche il secondo foro costituisce una sorgente praticamente di uguale intensità. Poiché però i due fori sono praticati a distanza λ_g/4 l'uno dall'altro, l'onda eccitata dal primo foro è in anticipo di fase di un quarto di periodo rispetto a quella eccitata dal secondo foro. Ne consegue che le due onde, emesse da ciascun foro nelle due direzioni, interferiscono positivamente sul secondo foro, dando luogo a un'onda che si propaga nel braccio 4, e negativamente sul primo foro, così che nessuna energia si propaga nel braccio 2.

g) Multipoli di ordine più elevato

Nella fig. 16 è illustrato l'esempio di un decapolo costituito da una giunzione di 5 guide. Se questa è adattata (S_ii=0) la potenza di un'onda che incide da un ramo si suddivide in parti uguali negli altri 4 rami.

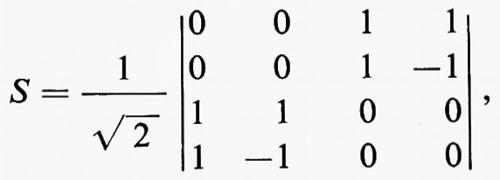
Il multipolo della fig. 17 (giunzione turnstile) è invece un dodecapolo, molto usato nei lavori di polarimetria a microonde. I sei bracci sono costituiti da 4 guide rettangolari che formano una croce nel piano H e da una guida circolare il cui asse è perpendicolare al piano che contiene la guida rettangolare. Il diametro della guida circolare è scelto in modo che, alla frequenza per la quale è progettato il dispositivo, sia possibile solo la propagazione del modo TE₁₁, che è degenere, per via dell'arbitrarietà della scelta dell'origine della coordinata angolare. Tale guida può essere pertanto considerata equivalente a due guide, una adatta alla propagazione di un'onda col vettore elettrico parallelo agli assi dei bracci 1-3, l'altra di un'onda col vettore elettrico parallelo all'asse dei bracci 2-4. Poiché in realtà le due onde coesistono nella stessa guida, esse possono formare un'onda polarizzata ellitticamente con qualunque valore della ellitticità e segno della polarizzazione.

La giunzione può essere adattata e in questo caso presenta le proprietà seguenti.

1. Eccitando con onde di uguale ampiezza e fase i rami 5 e 6, cioè eccitando la guida circolare con un'onda polarizzata rettilinearmente secondo la bisettrice 5-6, la potenza si distribuisce in parti uguali nei quattro bracci 1, 2, 3 e 4.

2. Chiudendo il braccio 2 con un corto circuito a distanza kλ_g/4 (con k intero) dalla giunzione e il braccio 4 a distanza (k+1)λ_g/4, si ottiene un ottupolo nel quale i bracci 1-5 e 3-6 sono completamente disaccoppiati. Un'onda che incida con polarizzazione rettilinea qualunque dalla guida circolare si ripartisce nelle guide 1 e 3 con ampiezze proporzionali alle componenti dell'onda incidente lungo gli assi 5 e 6. Ciò permette di determinare la polarizzazione dell'onda nella guida circolare.

3. Reciprocamente, eccitando i bracci 1 e 3 con onde in fase, si ottiene nella guida circolare un'onda polarizzata rettilinearmente secondo una direzione determinata dalle ampiezze delle onde incidenti.

4. Se i bracci 2 e 4 sono cortocircuitati a distanze rispettivamente eguali a

un'onda che incida dal braccio 1 eccita nella guida circolare un'onda polarizzata circolarmente, mentre il braccio 3 è disaccoppiato. Se viceversa essa incide dal braccio 3, nella guida circolare si eccita ancora un'onda polarizzata circolarmente, ma questa volta in senso contrario al caso precedente. Si può quindi sintetizzare una qualunque polarizzazione ellittica eccitando i bracci 1 e 3 con onde di opportuna ampiezza e, viceversa, analizzare lo stato di polarizzazione di un'onda che si propaga nella guida circolare con misure sulle onde che emergono dai bracci 1 e 3.

h) Multipoli non reciproci

È molto importante nei circuiti a microonde far sì che la propagazione in un tratto di circuito sia indipendente da quanto accade nei tratti successivi. Ad esempio, è necessario ‛isolare' un generatore, cioè evitare che un cambiamento di impedenza in un tratto di circuito produca riflessioni verso il generatore, che lo possano danneggiare. È evidente che un sistema in grado di assolvere a questo compito non può essere descritto da un multipolo reciproco. Prima degli anni cinquanta a tale scopo venivano usati assorbitori che minimizzavano l'effetto delle riflessioni attenuando l'onda riflessa. Ovviamente un tale dispositivo, reciproco, attenua anche l'onda diretta, per cui solo una frazione della potenza disponibile (tanto più piccola quanto più grande è la necessità di isolare) può essere utilizzata.

Negli anni cinquanta, però, lo studio dei fenomeni magneto-ottici associati alla risonanza magnetica portò alla realizzazione di dispositivi non reciproci. Già lord Rayleigh aveva proposto un dispositivo ottico unidirezionale basato sull'effetto Faraday. Come è noto, l'effetto Faraday consiste nella rotazione del piano di polarizzazione di un'onda elettromagnetica polarizzata linearmente che si propaga in un dielettrico trasparente magnetizzato parallelamente alla direzione di propagazione. A differenza del potere rotatorio naturale, il potere rotatorio magnetico è un effetto non reciproco. La rotazione del piano di polarizzazione è descritta da un vettore parallelo o antiparallelo al campo applicato e non dipende quindi dalla direzione di propagazione dell'onda, ma solo dalla direzione del campo.

Il dispositivo proposto da Rayleigh è illustrato nella fig. 18: esso consiste di due nicol N₁ e N₂ con gli assi orientati a 45° fra loro e posti agli estremi di uno spessore d di un dielettrico trasparente sottoposto a un campo H longitudinale, di intensità talè da produrre una rotazione Faraday di 45° dopo un percorso d nel mezzo. La luce che si propaga nella direzione N₁→N₂ è polarizzata da N₁, perviene a N₂ con la polarizzazione corretta ed è trasmessa. Quella che si propaga da N₂ a N₁ perviene a N₁ polarizzata nella direzione ortogonale all'asse di N₁ ed è estinta dal nicol. Tale dispositivo ottico non è stato realizzato a causa della piccola entità dell'effetto Faraday nei dielettrici trasparenti.

Il medesimo principio, tuttavia, è stato applicato nei circuiti per microonde, sfruttando certi materiali, le ferriti, che sono sostanze ferromagnetiche isolanti. Un'onda elettromagnetica polarizzata circolarmente che si propaghi in un tale mezzo, magnetizzato da un campo esterno, è fortemente assorbita se la propagazione avviene nella direzione del campo e il vettore magnetico ruota alla frequenza della precessione attorno al campo dei momenti magnetici del mezzo. Se la polarizzazione è opposta, l'onda non è assorbita. La frequenza di tale precessione, per campi magnetici di qualche migliaio di gauss, cade nella regione delle microonde. All'assorbimento (risonanza ferromagnetica) è associata una diversa velocità di propagazione per le due polarizzazioni circolari, che si traduce in un forte effetto Faraday. Con campi di qualche centinaio di gauss, un'onda che si propaghi in una ferrite non è praticamente assorbita ma subisce una rotazione Faraday di alcune decine di gradi per centimetro di percorso. Questo ha permesso la realizzazione di molti dispositivi non reciproci.

Isolatori uniline. - Nella fig. 19 è rappresentato un isolatore a effetto Faraday, versione a microonde del dispositivo di lord Rayleigh. L'ingresso del dispositivo è costituito da una guida rettangolare che si raccorda gradualmente con una guida circolare. Un'onda TE₁₀ incidente si trasforma in un'onda TE₁₁ nella guida circolare. L'uscita del dispositivo è ancora costituita da una guida rettangolare raccordata con continuità alla guida circolare. Le due guide rettangolari di ingresso e di uscita sono ruotate di 45° una rispetto all'altra attorno al loro asse comune, realizzando così un sistema che è l'analogo a microonde di due polarizatori ottici con gli assi ruotati di 45°. La guida circolare contiene una bacchetta di ferrite magnetizzata che produce una rotazione di 45° del vettore elettrico dell'onda TE₁₁ in modo da assicurare la trasmissione completa dal braccio 1 al braccio 2. Un'onda che si propaghi da 2 a 1, viceversa, a causa della rotazione Faraday, non può propagarsi nel braccio 1 ed è assorbita da una sottile lamina assorbente. Questa non perturba la propagazione nella direzione 1→2, poiché in tal caso il campo elettrico oscilla perpendicolarmente al piano della lamina, mentre assorbe completamente l'onda proveniente da 2, il cui vettore elettrico, oscilla parallelamente al piano della lamina.

Un isolatore perfetto è rappresentato dalla seguente matrice:

Il rapporto fra la trasmissione nella direzione inversa e quella nella direzione diretta, in un isolatore reale, può essere pari a circa 10^-3 con una trasmissione diretta del 90%. Se il campo magnetizzante è prodotto da un solenoide è possibile realizzare con tale dispositivo attenuatori variabili, o modulare in ampiezza o controllare automaticamente la potenza trasmessa agendo sulla corrente che percorre il solenoide.

Isolatori ad assorbimento. - La necessità di impiegare guide circolari per permettere la rotazione rende l'isolatore a effetto Faraday di realizzazione assai delicata. Data la degenerazione del modo TE₁₁ in una guida circolare, le transizioni devono essere particolarmente accurate per impedire l'eccitazione di altri modi. Perciò sono stati realizzati isolatori ad assorbimento, di realizzazione molto più semplice, nei quali il campo magnetico esterno è trasversale anziché longitudinale, e che non comportano transizioni né cambiamenti di modo. L'asimmetria necessaria per ottenere la non reciprocità risiede in questo caso nella particolare struttura che ha il campo magnetico di un modo TE₁₀ in una guida rettangolare. Abbiamo visto che il campo magnetico di un'onda TE₁₀ è un campo puramente trasversale al centro della guida (x=a/2), puramente longitudinale sulla parete piccola (x=0, x=a), mentre nelle altre posizioni ha una componente longitudinale e una trasversale che si compongono in una polarizzazione ellittica, l'ellitticità essendo la stessa e la polarizzazione di segno contrario in due posizioni simmetriche rispetto all'asse della guida. Per due valori particolari di x la polarizzazione è circolare e il campo magnetico dell'onda è un campo ruotante attorno alla direzione y, coincidente con quella del campo statico esterno. Il segno della polarizzazione circolare è determinato, in ciascuna di tali posizioni, dalla direzione di propagazione dell'onda. Se un piccolo campione di ferrite è posto in una di queste posizioni e se il campo magnetico esterno ha il valore della risonanza magnetica per la frequenza dell'onda che si propaga, la ferrite assorbirà l'onda che si propaga in un verso e sarà praticamente trasparente per l'onda che si propaga nel verso opposto e il cui campo magnetico ruota in senso contrario a quello della precessione di Larmor.

Circolatori. - Un circolatore è un multipolo a più bracci, non reciproco e privo di perdite. Un circolatore ideale a n bracci è descritto da una matrice S i cui termini soddisfano le equazioni seguenti:

S_i+1,i=1, S_k,i=0, per k≠i+1 (i=1, 2, ... n−1)

e

S_1,n=1, S_k,n=0, per k≠1.

Nella fig. 21 è schematizzato un circolatore a tre bracci la cui matrice S è data da:

Un'onda incidente da 1 è trasmessa completamente nel braccio 2, quella incidente da 2 nel braccio 3 e quella da 3 nel braccio 1.

Il funzionamento di un circolatore sfrutta gli effetti dispersivi associati alla risonanza ferromagnetica. Nella fig. 21 è illustrato il funzionamento di un circolatore a 3 bracci che utilizza l'effetto Faraday. Il braccio 1 si affaccia su una guida circolare. Un'onda TE₁₀ proveniente da 1 eccita un'onda TE₁₁ nella guida circolare, polarizzata col vettore elettrico parallelo al lato largo della guida che costituisce il braccio 2. Essa non può quindi propagarsi in 2 e si propaga verso 3 dove perviene col vettore elettrico ruotato di 45°, parallelo al lato largo del braccio 3, da cui pertanto viene ancora riflessa per riattraversare una seconda volta la ferrite ruotando ancora di 45°. Nei due percorsi l'onda ritorna al braccio 2 avendo subito una rotazione di 90°, così che è trasmessa nel braccio 2. I bracci 2 e 3 costituiscono un isolatore a effetto Faraday privo della lama assorbente, per cui si ha trasmissione completa nella direzione 2→3 e non si ha trasmissione nella direzione 3→2 poiché l'onda giunge in 2 con la polarizzazione non adatta per l'eccitazione.

4. Cavità risonanti

a) Frequenze di risonanza e struttura dei campi

Alle frequenze molto elevate i circuiti risonanti a ‛costanti concentrate', costituiti da una capacità C e da un'induttanza L, non possono funzionare, sia perché non è possibile realizzare tali costanti L, C sufficientemente piccole, sia perché le perdite per radiazione sono troppo elevate. Si ricorre allora, come per la propagazione, a sistemi nei quali l'energia elettromagnetica è confinata in una regione racchiusa da pareti conduttrici che ne impediscono la dispersione nello spazio. Tale regione è generalmente realizzata con un tratto di guida d'onda di lunghezza L terminata da due pareti conduttrici, normali all'asse della guida. Ne risulta una ‛cavità risonante' le cui frequenze proprie sono quelle per le quali il campo elettromagnetico all'interno può assumere una configurazione stazionaria.

Un'onda elettromagnetica che soddisfi queste condizioni, una volta eccitata all'interno della cavità, si riflette continuamente fra le pareti terminali e vi si manterrebbe indefinitamente in assenza di perdite. Una cavità risonante è quindi l'analogo a microonde del risuonatore ottico: l'interferometro di Fabry-Perot.

Le caratteristiche di una cavità vengono espresse da due parametri: le frequenze proprie di risonanza ν_r e il fattore di merito Q del risuonatore, che ne misura le perdite.

Frequenze di risonanza. - Per determinare le frequenze di risonanza e la struttura del campo elettromagnetico in una cavità si devono trovare le soluzioni delle equazioni di Maxwell che soddisfano le opportune condizioni al contorno: che cioè in ogni punto delle pareti conduttrici il campo E sia normale e il campo H tangenziale alla parete stessa. In generale, se la geometria della cavità non è semplice, il problema è matematica:mente complesso. Noi lo tratteremo per i casi di cavità di forma parallelepipeda e cilindrica, che sono quelle generalmente usate.

Consideriamo una guida indefinita nella quale si propaga un'onda TE_m,n (TM_m,n) e immaginiamo di cortocircuitarla in A mediante una parete conduttrice perpendicolare all'asse z (v. fig. 22). I campi elettrico e magnetico si riflettono sulla parete con coefficiente di riflessione pari a ±1, in modo da soddisfare le condizioni al contorno e da determinare nella guida un sistema di onde stazionarie. Nei piani nodali A, B, C, ... distanti tra loro λ_g/2 la componente trasversale del campo elettrico è nulla e quindi, se poniamo in una qualunque di tali posizioni una seconda parete conduttrice, le condizioni al contorno restano ancora soddisfatte e le oscillazioni, una volta innescate, continueranno a sussistere indefinitamente (se la cavità è priva di perdite). Quindi, fissata una frequenza che può propagarsi secondo un modo ben determinato in una determinata guida, possiamo avere infinite cavità che risuonano a tale frequenza e, precisamente, tutte quelle ottenute chiudendo la guida con una parete conduttrice in uno qualunque dei piani nodali del campo stazionario prodotto dalla riflessione sulla prima parete. Tali cavità saranno contraddistinte da un indice l che misura, in unità λ_g/2, la distanza fra le due pareti trasversali. Viceversa, per una cavità assegnata, di lunghezza L, e per ciascun modo di propagazione, vi sono infinite frequenze per le quali le condizioni al contorno risultano soddisfatte; tutte quelle per le quali la lunghezza d'onda nella cavità soddisfa la condizione

dove l è un intero. I modi e le frequenze di risonanza di una cavità saranno quindi contraddistinti da tre indici. I primi due caratterizzano il modo TE o TM, il terzo è l'indice l.

La configurazione del campo all'interno di un risuonatore è quella del campo stazionario. Il rapporto fra l'ampiezza del campo riflesso e quella del campo incidente è −1 per le componenti trasversali di E e longitudinali di H, +1 per quelle longitudinali di E e trasversali di H. La dipendenza da z del campo stazionario all'interno della cavità sarà pertanto data, per le prime, da

e^ikgz−e^-ikgz=2i sen k_gz

e, per le seconde, da

e^ikgz+e^-ikgz=2 cos k_gz.

Ricordando che è k_g=2π/λ_g e tenendo conto della (20) si ricava che i campi all'interno della cavità si ottengono da quelli dei modi corrispondenti nella guida moltiplicando le ampiezze delle componenti trasversali di E e longitudinali di H per 2i sen (πlz/L) e quelle delle componenti longitudinali di E e trasversali di H per 2 cos (πlz/L).

b) Il fattore di merito Q

Il Q di un risuonatore è definito da

cioè da

dove ν₀ è la frequenza di risonanza. Se l'energia contenuta nel risuonatore al tempo t =0 è W₀, la (22) permette di ricavare l'energia contenuta al tempo t:

W(t)=W₀e^-(2πν0/Q)t. (23)

Q/2π rappresenta, quindi, il numero di periodi del campo elettromagnetico dopo i quali, in oscillazione libera, l'energia immagazzinata nel risuonatore si sarà ridotta di un fattore e.

Se il risuonatore è eccitato da una sorgente esterna e P_c è l'energia introdotta nell'unità di tempo, l'energia all'interno del risuonatore aumenta fino a un valore di regime, quando si sarà raggiunta la condizione per cui la potenza dissipata è pari alla potenza di eccitazione. Allora sarà:

cioè Q può essere anche definito come il prodotto della frequenza di risonanza per il rapporto fra l'energia immagazzinata e la potenza dissipata, in regime di oscillazione stazionaria.

Le perdite di un risuonatore hanno diverse cause: perdite per effetto Joule sulle pareti conduttrici, perdite per radiazione all'esterno, perdite nel dielettrico contenuto nella cavità; si può cioè genericamente scrivere:

P_d=P_J+P_ext+P_diel.

Introducendo tale espressione nella (24), potremo scrivere:

e conseguentemente introdurre, per ciascun tipo di perdita, un fattore Q, da definirsi attraverso la relazione:

Sarà cioè

Il Q definito dalla (25) è l'effettivo Q del risuonatore, mentre Q₀ è il valore teorico del risuonatore isolato e vuoto, che può essere calcolato teoricamente dalla geometria del risuonatore e dalla conducibilità del metallo che ne costituisce le pareti. L'energia immagazzinata è, infatti:

e la potenza dissipata per effetto Joule:

dove δ è la profondità di penetrazione del campo elettromagnetico nel metallo che forma la parete. Gli integrali sono estesi rispettivamente al volume e alla superficie interna della cavità. Dalla (24) si ottiene quindi:

che può essere scritta nella forma:

Per un'assegnata geometria e configurazione del campo tutte le dimensioni della cavità e il rapporto fra i due integrali sono proporzionali a λ, per cui Q₀δ/λ dipende solo dalla geometria e dal modo ed è detto ‛fattore di forma'.

La penetrazione δ del campo all'interno del conduttore dipende dalla conducibilità 1/ρ e da λ:

se ρ è dato in Ω/cm e λ in cm. Per i metalli più usati, rame, argento, alluminio, si ha come ordine di grandezza:

Con Qδ/λ=1, il Q₀ di una cavità che risuona alla lunghezza d'onda di 1 cm risulta pari a 30.000.

Nei grafici della fig. 23 è riportato il valore del fattore di forma Qδ/λ, per cavità di forma cilindrica, in funzione dei rapporto D/L tra il diametro e l'altezza del risuonatore, per i primi tre modi TE_01l.

c) Accoppiamento delle cavità

Una cavità può contenere energia elettromagnetica solo alle frequenze corrispondenti a uno dei modi propri. Per poter eccitare uno di questi modi occorre introdurre energia dall'esterno in modo tale che la cavità abbia praticamente la stessa frequenza propria della cavità imperturbata. A tal fine è sufficiente praticare nella cavità un piccolo foro che si affacci all'interno di una guida d'onda. Normalizzando a 1 il valore massimo del campo elettrico (magnetico) all'interno della cavità e nella guida di eccitazione, l'accoppiamento risulta proporzionale al prodotto scalare

E_g•E_c (H_g•H_c)

nella posizione del foro, all'interno della guida e della cavità, rispettivamente. Risultano quindi eccitati i modi per i quali tali prodotti sono diversi da zero e l'efficienza dell'eccitazione è proporzionale ai valore di tali prodotti. La sorgente costituita da un piccolo foro può essere rappresentata da un dipolo oscillante e l'accoppiamento risultante dipende dalla sesta potenza del diametro. Se occorre, oltre che introdurre, prelevare energia dalla cavità e distribuirla in diversi circuiti, ciò può farsi con altri fori che si affacciano in altre guide. L'accoppiamento di un circuito con una cavità abbassa il Q di questa, poiché alle perdite Joule si aggiungono quelle per radiazione attraverso i fori di accoppiamento. Indicando con P_J le perdite Joule e con P₁, P₂, ... le potenze irradiate attraverso i fori, dalla definizione del Q:

possiamo definire l'accoppiamento con altrettanti Q che rappresentano le perdite per radiazione nei diversi circuiti esterni in regime di funzionamento stazionario, alla frequenza di risonanza. Posto

si ottiene

e di qui

Q₀=Q(1+β₁+β₂ ...),

con β_i=Q₀/Q_i=P_i/P_J rapporto fra la potenza persa attraverso il foro i-esimo e quella dissipata per effetto Joule. Tali parametri (parametri di accoppiamento) descrivono quindi il ‛carico' dato alla cavità dai diversi accoppiamenti con l'esterno. Le cavità sono generalmente munite di uno (cavità a riflessione) o due (cavità a trasmissione) accoppiamenti; per esse si avrà rispettivamente:

e

d) Curva di risposta

Una cavità ideale, priva di perdite, avrebbe uno spettro di frequenze a righe, ciascuna riga corrispondendo a un possibile modo di risonanza del campo elettromagnetico al suo interno. A causa delle perdite, invece, essa può risuonare anche a frequenze prossime a quelle di risonanza.

Consideriamo una cavità in regime di oscillazione stazionario, alla frequenza propria ω₀, e supponiamo di interrompere l'eccitazione all'istante t=0. L'energia immagazzinata all'interno decrescerà esponenzialmente nel tempo con costante ω₀/Q e una qualunque componente F₀(x, y, z, t) del campo elettromagnetico sarà descritta dalla parte reale della funzione

F(t)=F₀ e^-(ω0/2Q)t e^iω0t,

che può scriversi come

dove G(ω) è la trasformata di Fourier della funzione F(t):

cioè

La parte reale di G(ω) fornisce l'ampiezza delle componenti monocromatiche presenti nella cavità in regime di oscillazione smorzata, mentre il suo quadrato dà l'intensità ditali componenti. In regime di funzionamento stazionario, sotto un'eccitazione esterna di frequenza ω, l'espressione

rappresenta l'intensità del campo all'interno della cavità rapportata all'intensità che si avrebbe con pari eccitazione alla frequenza di risonanza ω₀, cioè la ‛curva di risposta' del risuonatore.

Alle frequenze ω=ω₀(1±1/2Q) la risposta della cavità è pari a nietà della risposta che si ha alla frequenza di risonanza. Il Q di una cavità è quindi anche eguale al rapporto ω₀/Δω fra la frequenza di risonanza e la differenza Δω fra le due frequenze alle quali la risposta è metà della risposta alla risonanza (‛larghezza della risonanza').

e) Cavità a trasmissione e a riflessione

Una cavità con un solo accoppiamento può essere inserita quale terminazione di una linea (‛cavità a riflessione') o in parallelo alla linea dalla quale preleva una frazione dell'energia quando la frequenza dell'onda che si propaga è prossima alla frequenza di risonanza ω₀ (‛cavità ad assorbimento'). Se è accoppiata a due guide è una cavità a ‛trasmissione' (v. fig. 24) e costituisce un quadrupolo che agisce come un filtro che trasmette nella guida di uscita una stretta banda di frequenza centrata attorno alla frequenza ω₀. Gli elementi S_ik risultano funzioni della frequenza e la matrice S risulta, per il quadrupolo, data da:

dove si è posto A(ω, ω₀) =1+2iQ₀(ω/ω₀−ω₀/ω) e β₁, β₂ sono i parametri di accoppiamento. Si ottiene, pertanto, per la potenza trasmessa, l'espressione

e, per quella riflessa, l'espressione

La cavità a riflessione è descritta dalla stessa matrice nella quale si ponga β₁=β e β₂=0:

Alla frequenza di risonanza, S₁₁ è reale e la cavità si comporta come un carico puramente resistivo, mentre a frequenze prossime a quella di risonanza la fase dell'onda riflessa è in anticipo o in ritardo rispetto a quella dell'onda incidente, a seconda che ω sia rispettivamente minore o maggiore di ω₀. La potenza riflessa risulta, per ω=ω₀:

Per β=1 (accoppiamento critico) è R=0; in tal caso la cavità si comporta come una terminazione adattata.

f) Cavità particolari

Cavità toroidali. - In alcuni casi è necessario che alcune dimensioni della cavità siano molto piccole. Ad esempio nei generatori ‛klystron' gli elettroni devono attraversare una cavità in un tempo pari a una piccola frazione del periodo della radiazione per la quale sono progettati, cioè in un tempo dell'ordine di 10^-11 s o anche minore. Ciò non può essere realizzato con cavità cilindriche o rettangolari. Si ricorre allora a strutture del tipo di quella illustrata nella fig. 25, che si possono considerare come ottenute da un circuito a costanti concentrate nel quale le armature del condensatore CC sono collegate da una distribuzione continua di spire L. Il campo elettrico nel risuonatore è localizzato nella regione CC, mentre quello magnetico è localizzato nella regione toroidale. La frequenza di questi risuonatori può essere variata variando leggermente la distanza CC. Il Q di un tale circuito può essere di qualche centinaio.

Risuonatori aperti. - Alle frequenze più elevate, corrispondenti a lunghezze d'onda millimetriche, le dimensioni di una cavità divengono troppo piccole e il Q troppo basso. Si ricorre allora a risuonatori aperti, del tipo FabryPerot, quali sono usati in ottica (v. fig. 26A). La radiazione è eccitata in una regione limitata da due specchi tra i quali si riflette continuamente. Se le dimensioni degli specchi sono grandi rispetto alla lunghezza d'onda, le perdite per diffrazione sono piccole e il Q elevato. In tali risuonatori mancano le pareti laterali e la configurazione dei campi non può essere determinata dalle condizioni al contorno come nelle cavità chiuse.

Fox e Lee (1961) hanno determinato le frequenze di risonanza e le perdite per diffrazione di un tale risuonatore con un metodo molto originale. Se è nota la distribuzione dei campi su uno specchio S₁ al tempo t=0, il principio di Huyghens permette di determinare quella sul secondo specchio, S₂, al tempo t=d/c, dove d è la distanza fra i due specchi e c la velocità di propagazione della radiazione. Da questa è possibile allora determinare la distribuzione su S₁ al tempo t=2d/c, ecc. Mediante un calcolatore elettronico, partendo da una distribuzione iniziale, corrispondente ad esempio a un'eccitazione impulsiva del risuonatore, dopo un numero più o meno grande di riflessioni sui due specchi si ottengono delle configurazioni stazionarie, nelle quali cioè i rapporti fra le ampiezze delle varie componenti dei campi rimangono inalterate nel corso delle successive riflessioni, mentre le ampiezze stesse decrescono con legge esponenziale. Tali configurazioni costituiscono i modi propri del risuonatore (v. fig. 26B-D) mentre la costante di tempo del decadimento esponenziale ne caratterizza le perdite.

Per i sistemi costituiti da specchi sferici è stata data una soluzione analitica da Boyd e Gordon (1962). Nel caso di un risuonatore confocale, nel quale cioè i vertici dei due specchi sferici sono a una distanza pari al loro raggio di curvatura ρ, le lunghezze d'onda di risonanza sono quelle che soddisfano alla condizione

dove 2p è il numero di zeri del campo elettrico lungo l'asse del risuonatore, m il numero di zeri lungo la coordinata x ed n il numero di quelli lungo la coordinata y. Le configurazioni dei campi sono, con buona approssimazione, configurazioni trasversali elettromagnetiche e vengono contraddistinte dagli indici p, m, n: TEM_pmn.

Le espressioni analitiche dei campi all'interno dell'interferometro sono date da un prodotto di esponenziali e di polinomi di Hermite nelle variabili x, y e z. Le superfici di eguale fase sono piani al centro del risuonatore e sfere sugli specchi, cosicché la distanza fra due nodi consecutivi lungo l'asse decresce leggermente andando dal centro agli specchi. Poiché p è un numero dell'ordine di 100 o maggiore, per i modi m, n più bassi la lunghezza d'onda del risuonatore è molto prossima a quella nello spazio libero.

La struttura del campo in un risuonatore Fabry-Perot, per i modi più bassi, è stata verificata sperimentalmente con molta precisione (v. fig. 26B-D). Se il parametro, detto ‛numero di Fresnel', N=a²/(dλ) (a diametro degli specchi, d distanza fra essi, eguale, nella posizione confocale, a ρ, raggio di curvatura) è grande, pari a circa 1,5÷2, le perdite per diffrazione sono trascurabili e il Q dei risuonatori può raggiungere valori assai grandi, dell'ordine di 10⁵÷10⁶, a seconda della lunghezza d'onda e della geometria.

Nel concludere questo capitolo sulle cavità risonanti è da dire che le loro applicazioni nella tecnica e nella ricerca sono troppo numerose per poterne dare un'esposizione particolareggiata. Quali elementi nei circuiti a microonde, tali cavità sono utilizzate come filtri, quali ondametri, per la stabilizzazione della frequenza, ecc. Nella ricerca fisica, in particolare nella spettroscopia a microonde, esse costituiscono generalmente la cella di assorbimento che racchiude il campione. Troveremo nel seguito di questo articolo numerosi esempi di impiego delle cavità risonanti.

5. Generazione delle microonde

a) Prime esperienze

Il primo a produrre e rivelare in laboratorio onde elettromagnetiche fu Hertz, il quale verificò le deduzioni teoriche di Maxwell con esperienze magistrali e decisive. Il problema di Hertz era anzitutto quello di produrre e quindi di rivelare le onde elettromagnetiche.

L'oscillatore di Hertz è schematizzato nella fig. 27A: esso consiste in un condensatore C le cui armature AA′ sono connesse a una sorgente d'alta tensione attraverso una resistenza R. Le armature sono anche connesse a due sferette metalliche ravvicinate, a a′, che costituiscono un interruttore automatico. Se all'istante iniziale t=0 si inserisce la sorgente d'alta tensione, la differenza di potenziale tra le armature, e quindi fra le sferette aa′, cresce esponenzialmente con la costante di tempo RC fino al valore al quale fra a e a′ scocca una scintilla che cortocircuita le armature del condensatore. Questo allora si scarica attraverso il circuito Aaa′A′ che è percorso da una corrente oscillante la cui frequenza ω=1/√-L-Cè determinata dall'induttanza del circuito di scarica. Due conduttori rettilinei connessi alle armature costituiscono un dipolo che durante la scarica irradia onde elettromagnetiche nello spazio.

Per la rivelazione Hertz usò il ‛risuonatore' (v. fig. 27B), dispositivo costituito da un'induttanza, realizzata con una spira circolare. La spira è interrotta e munita di due sferette molto ravvicinate che costituiscono una capacità C. Il tutto è aggiustato in modo che il periodo proprio del circuito sia quello delle onde generate dall'oscillatore. Disponendo la spira in modo che l'antenna dell'oscillatore giaccia sul piano della spira, questa si concatena col campo magnetico dell'onda irradiata ed è percorsa da una corrente oscillante che produce piccole scintille fra le due sferette. È così possibile rivelare la presenza delle onde elettromagnetiche a una certa distanza dall'oscillatore. L'oscillatore di Hertz emette treni d'onda smorzati che si susseguono a una cadenza determinata dalla costante di tempo RC, costituiti da oscillazioni della lunghezza d'onda di qualche centimetro.

Con dispositivi di questo tipo, i fisici della fine del secolo mostrarono non solo che le onde elettromagnetiche esistono ma che si propagano con la velocità c e che con esse possono riprodursi tutti i fenomeni caratteristici della radiazione ottica. Nel suo libro L'ottica delle oscillazioni elettriche Righi descrive tutta una serie di esperienze d'interferenza, diffrazione, doppia rifrazione, polarizzazione, ecc., eseguite con onde generate da dispositivi del genere. Tali esperienze costituirono una conferma sperimentale dell'ipotesi della natura elettromagnetica della luce.

Con l'invenzione del triodo da parte di De Forest (1907) fu possibile generare onde elettromagnetiche persistenti e di potenza elevata (v. elettronica). La frequenza delle onde prodotte da un oscillatore a tubi elettronici, però, non può essere molto elevata, non superiore cioè a qualche decina di MHz, a causa delle caratteristiche intrinseche al funzionamento di un tubo elettronico.

Le cause che impediscono tale funzionamento alle frequenze elevate sono essenzialmente due. La prima risiede nella necessità di accedere dall'esterno agli elettrodi interni del tubo. Ogni coppia di elettrodi all'interno del tubo costituisce un condensatore di capacità C, cosicché una differenza di potenziale applicata ai terminali griglia-catodo del tubo è in realtà applicata a un circuito costituito da un'induttanza L e da una capacità C in serie (l'induttanza L essendo quella dei conduttori che collegano gli elettrodi ai terminali del tubo). Ne consegue che l'effettiva differenza di potenziale fra i due elettrodi è la frazione 1/(1+ω²LC) di quella applicata ai terminali e tende a zero al crescere di ω.

La seconda causa che impedisce il funzionamento dei tubi alle frequenze elevate risiede nel tempo di transito degli elettroni nello spazio fra due elettrodi. In un triodo, ad esempio, la griglia ha la funzione di controllare il numero di elettroni che attraversano lo spazio tra catodo e anodo. Se il campo fra la griglia e il catodo varia durante il tempo necessario agli elettroni per attraversare lo spazio tra griglia e catodo, essi risentono del valore medio del campo durante tale tempo così che il tubo cessa di funzionare quando tale tempo è superiore al periodo dell'oscillazione.

Il tempo di transito degli elettroni è dell'ordine di 10^-8 s. Nella tecnologia del 1930 un triodo di grossa potenza, di 500 kW, cessava di funzionare alla frequenza di qualche decina di MHz e solo tubi molto piccoli e opportunamente studiati potevano essere fatti funzionare a frequenze dell'ordine di 1.000 MHz (corrispondenti a lunghezze d'onda di 30 cm). L'ostacolo fu superato nella seconda metà degli anni trenta, quando furono sviluppati dispositivi molto ingegnosi che utilizzano il tempo di transito stesso per controllare la corrente elettronica in un tubo termoionico. Si realizzarono così diversi tubi elettronici funzionanti sul principio della modulazione di velocità, tra i quali va ricordato il klystron, che è senza dubbio quello più usato.

b) Il klystron

Nel klystron lo spazio catodo-anodo del triodo è sostituito da tre regioni distinte (v. fig. 28). In una prima regione gli elettroni sono accelerati da una differenza di potenziale di alcune centinaia o migliaia di volt e, passando per piccoli fori, attraversano lo spazio compreso fra due elettrodi piani G₁ G₂. Questi formano le pareti di una cavità risonante che ha forma tale da permettere l'eccitazione di un modo nel quale il campo elettrico oscilla nella direzione parallela alla velocità degli elettroni. Attraversata tale regione, gli elettroni si propagano liberamente per una distanza opportuna, quindi attraversano una seconda cavità C₂ identica alla prima per essere infine raccolti da un elettrodo collettore. L'esatta descrizione del funzionamento del dispositivo è molto complessa ma possiamo darne una schematizzazione semplice che ne rende chiaro il principio. Supponiamo che all'interno della prima cavità C₁ esista un campo elettrico oscillante parallelo alla direzione della velocità degli elettroni e che questi incidano su G₁ tutti con la stessa velocità v₀; ne emergeranno con velocità diverse, a seconda della fase del campo durante il tempo di transito fra le due pareti di C₁.

La distanza G₁G₂=d fra tali pareti è dell'ordine di una frazione di millimetro, assai piccola rispetto alla lunghezza d'onda della radiazione per la quale è progettato il dispositivo. Possiamo quindi per semplicità supporre che il campo E sia costante durante il tempo di transito degli elettroni. Questi allora emergeranno da G₂ con velocità

dove si è posto V₁=E₁/d≪V₀(Δv/v≪1) E₁, ω ampiezza e frequenza del campo fra G₁ e G₂. Consideriamo gli elettroni che emergono da G₂ un quarto di periodo l'uno dopo l'altro, agli istanti ai quali rispettivamente il campo E è minimo, nullo e massimo. La loro velocità sarà v₀(1−Δv/v₀), v₀ e v₀(1+Δv/v₀), rispettivamente.

Se prendiamo come origine dei tempi t=0 l'istante al quale gli elettroni più lenti, di velocità v₀(1−Δv/v₀), emergono da G₂, allora all'istante t essi si troveranno alla distanza

Quelli che emergono da G2 al tempo τ/4 (con τ periodo del campo in C₁), con velocità v₀, allo stesso istante t avranno percorso la distanza

S(t)=v₀(t−τ/4)

e quelli che emergono da G₂ al tempo τ/2, con velocità v₀(1+Δv/v₀), al tempo t si troveranno alla distanza

e

Gli elettroni più lenti e quelli più veloci distano da quelli emersi con velocità inalterata v₀ di un tratto

Tutti gli altri elettroni, che sono transitati durante il semiperiodo considerato, sono compresi entro tale intervallo.

In conclusione, gli elettroni che prima del passaggio attraverso la cavità erano distribuiti su un intervallo v₀ τ/2 si trovano distribuiti in un intervallo molto più breve, pari a Δv τ/4, a una distanza v₀²τ/(4Δv) da G₂. A tale distanza la densità elettronica sarà molto elevata e varierà periodicamente con frequenza ω/2π. Tale effetto, detto di bunching, avviene a diverse distanze da G₂: quelle alle quali gli elettroni più veloci emersi durante un periodo raggiungono i più lenti emersi nei periodi precedenti. La densità elettronica in tali regioni è tanto più elevata quanto più la regione è distante da C₁ (v. fig. 29). In ciascuna di tali regioni la densità di carica varia periodicamente da valori molto elevati a valori bassi, alla frequenza del campo esistente in C₁.

Da quanto precede è chiara la funzione dello spazio fra C₁ e C₂ (drift space): esso permette agli elettroni di raggrupparsi formando regioni con densità di carica elevata. Se la distanza C₁C₂ fosse troppo piccola, gli elettroni arriverebbero in C₂ senza essersi potuti addensare; se fosse troppo grande si addenserebbero prima di C₂, dopodiché gli elettroni veloci sorpasserebbero i più lenti e il pacchetto si disgregherebbe. Se C₂ è a distanza opportuna, la densità fra le pareti G₃G₄ varia fortemente alla frequenza ω/(2π)=1/τ inducendo un campo elettromagnetico all'interno di C₂. Una frazione dell'energia elettromagnetica presente in C₂ è prelevata e inviata in C₁ con un'opportuna relazione di fase, in modo da assicurare il funzionamento stazionario. I primi elettroni emessi all'accensione del tubo innescano al loro passaggio un debole campo in C₁ da cui ha inizio il processo. Da C₂ l'energia elettromagnetica è prelevata opportunamente e trasferita all'esterno.

Il klystron può essere fatto funzionare, oltre che come generatore, anche come amplificatore: difatti, introducendo energia elettromagnetica in C₁, essa può essere prelevata da C₂ amplificata.

c) Il klystron reflex

Nei casi in cui non si richieda una grande potenza si usano klystron nei quali le funzioni delle due cavità C₁ e C₂ sono espletate da una sola cavità C (v. fig. 30). Ciò elimina la difficoltà di mantenere le due cavità esattamente alla stessa frequenza e soprattutto permette di variare la frequenza di oscillazione variando la tensione di un elettrodo. Gli elettroni che escono dalla cavità C con velocità diversa si propagano in una regione nella quale c'è un campo elettrico che li frena, E_R, prodotto da una differenza di potenziale applicata fra la cavità e un elettrodo R (repeller). Tale campo è sufficientemente elevato da impedire agli elettroni di raggiungere R. Gli elettroni più veloci, che emergono al tempo t=0, invertono la loro velocità all'istante t₁ e attraversano nuovamente la cavità all'istante 2t₁ pari a:

Quelli più lenti, usciti con un ritardo di un semiperiodo rispetto ai più veloci, ripassano per la cavità al tempo

e quelli usciti con velocità inalterata e ritardo τ/4 la riattraversano all'istante

Se E_R è tale che

i tre tipi di elettroni ripassano per la cavità allo stesso istante e nello stesso istante la riattraversano anche tutti gli elettroni che l'avevano attraversata durante il semiperiodo considerato.

Se il potenziale all'elettrodo repulsore e la velocità degli elettroni sono tali da far sì che il passaggio avvenga con opportuna relazione di fase, il sistema entra in oscillazione trasformando in energia elettromagnetica l'energia usata per accelerare gli elettroni alla velocità v₀.

La frequenza di oscillazione di un klystron reflex può essere variata variando la tensione dell'elettrodo repulsore, in modo che il passaggio per C dei pacchetti degli elettroni riflessi avvenga a una frequenza compresa nella banda della cavità. Questa in genere è tale da permettere l'oscillazione in una regione di circa 50÷100 MHz attorno alla frequenza centrale, alla quale la potenza della radiazione emessa è massima.

Sono stati realizzati altri dispositivi basati sul principio della modulazione di velocità, i quali non utilizzano tuttavia cavità risonanti e quindi possono funzionare in un intervallo di frequenze molto più ampio.

d) Stabilizzazione di frequenza.

Una delle caratteristiche più interessanti del klystron reflex risiede nella possibilità che esso offre di variare la frequenza variando la tensione applicata all'elettrodo repulsore, consentendone così un controllo automatico. Un sistema di stabilizzazione di frequenza è un sistema che confronta la frequenza di un oscillatore con quella di un campione esterno (cavità risonante, riga spettroscopica) e ne minimizza la differenza.

La frequenza di un klystron è determinata dalla sua cavità e può variare a causa di fluttuazioni della tensione, della presenza di campi magnetici, di vibrazioni meccaniche, di variazioni della temperatura, ecc. L'ampiezza di tali fluttuazioni è inversamente proporzionale al Q della cavità del klystron, che non è molto elevato, per cui è difficile, anche prendendo le dovute precauzioni, mantenere la frequenza di oscillazione di un klystron entro una parte su 10⁵ o 10⁶ della frequenza centrale. Ciò corrisponde a una fluttuazione di qualche decina di kHz alla frequenza di 10.000 MHz.

Se nel sistema di stabilizzazione si utilizza una cavità a Q elevato è possibile ridurre tale fluttuazione a qualche decina di Hz, o anche meno, con una stabilità della frequenza dell'oscillatore pari a 10^-8 o anche migliore.

Nella fig. 31A è schematizzato il circuito di stabilizzazione: una frazione della radiazione emessa dal klystron è inviata al circuito discriminatore, che ne confronta la frequenza ω con la frequenza ω₀ di una cavità e fornisce una differenza di potenziale proporzionale in valore e segno ω−ω₀. Tale differenza di potenziale è amplificata e usata per controllare la tensione dell'elettrodo repulsore e quindi la frequenza del klystron.

Nella fig. 31B è schematizzato il funzionamento di un discriminatore (‛discriminatore di Pound') che utilizza un T magico come un ponte per confrontare la potenza riflessa da una cavità con quella riflessa da un corto circuito. Una frazione dell'energia del klystron è immessa, attraverso un accoppiatore direzionale AD, nel ramo 3 (ramo H) del T. Alla giunzione essa si suddivide in parti uguali nei rami simmetrici 1 e 2. Uno di questi si chiude su un corto circuito, posto a distanza d dalla giunzione, l'altro su una cavità C accordata alla frequenza ω₀ sulla quale si vuole stabilizzare il klystron. La distanza della cavità dalla giunzione è d+λ_g/8. Se la frequenza ω del segnale è uguale alla frequenza ω₀ della cavità, questa si comporta come una resistenza e l'onda riflessa torna alla giunzione sfasata di π/2 rispetto a quella riflessa dal corto circuito. Per la proprietà del T le onde eccitate nei rami 3 e 4 hanno uguale ampiezza e i potenziali ai capi dei due rivelatori X_a e X_b, che costituiscono il carico adattato dei rami 3 e 4, sono uguali. Se è ω≠ω₀, l'impedenza costituita dalla cavità ha componenti capacitiva (ω〈ω₀) o induttiva (ω>ω₀) e le onde riflesse si sommano nei rami E e H con diversa ampiezza. La differenza di potenziale fra X_a e X_b risulta positiva o negativa, a seconda del segno di ω−ω₀.

Nella fig. 31C è riportato l'andamento della differenza di potenziale in funzione di ω−ω₀.

e) Il magnetron

Assieme al klystron, il ‛magnetron' è il tubo che ha permesso la realizzazione del radar. Questo dispositivo, infatti, permette di generare impulsi di energia elettromagnetica di potenza molto elevata (0,1−10 MW) di durata dell'ordine del microsecondo, quali sono gli impulsi che vengono inviati nello spazio nei trasmettitori radar. In realtà, il magnetron è stato il primo dispositivo elettronico capace di produrre energia elettromagnetica a frequenze molto elevate. Esso consiste sostanzialmente di un diodo cilindrico posto in un campo magnetico parallelo all'asse del diodo.

Già nel 1921 Hull aveva osservato che, in certe condizioni, si potevano generare delle oscillazioni di frequenza molto elevata entro un dispositivo costituito da un diodo cilindrico sottoposto a un campo magnetico assiale. Sotto l'azione combinata del campo elettrico radiale e del campo magnetico longitudinale gli elettroni emessi dal catodo percorrono traiettorie che sono approssimativamente delle cicloidi, alla frequenza di ciclotrone ν=eH/mc; questa fu approssimativamente la frequenza osservata da Hull in certe condizioni.

Lo studio di tali oscillazioni portò nel 1927 i fisici giapponesi alla realizzazione del magnetron ad anodo sezionato, che, inserito in un circuito risonante, permise di realizzare degli oscillatori di potenza utilizzabile. Il funzionamento di tale dispositivo, illustrato nella fig. 32, è molto complesso ma può essere schematizzato nel modo seguente. Sotto l'azione combinata di un campo magnetico assiale e di un campo elettrico radiale gli elettroni percorrono traiettorie complesse prima di arrivare all'una o all'altra sezione dell'anodo. Se l'intensità del campo magnetico supera un certo valore la corrente è interdetta e gli elettroni tornano al catodo. Esiste quindi un valore critico,

(dove r_c e r_a sono i raggi del catodo e dell'anodo), che interdice la corrente. Per valori di H molto prossimi al valore critico la corrente anodica è assai sensibile a piccole variazioni della tensione. Supponiamo allora che H sia prossimo a tale valore e che nel circuito oscillante si siano innescate delle oscillazioni, per cui uno dei due anodi è a ogni istante a una tensione leggermente diversa da quella dell'altro. Ciò produce una differenza fra l'intensità della corrente che attraversa una metà dell'anodo e quella che attraversa l'altra metà e potremo scrivere, tenuto conto del tempo di transito τ:

ρi₁(t)=V₁(t−τ)

ρi₂(t)=V₂(t−τ),

dove ρ è la resistenza interna del diodo.

Il circuito oscillante sarà percorso dalla corrente i₁−i₂ e si avrà, tenuto conto del senso della corrente:

V₁−V₂=−Z(i₁−i₂),

dove Z è l'impedenza del circuito risonante. Alla frequenza di risonanza questa si riduce a una pura resistenza R e potremo scrivere quindi:

ρ(V₁−V²)_t+R(V₁−V₂)_(t-τ)=0. (30)

Supponiamo che all'istante t=0 si instauri tra i due settori dell'anodo una differenza di potenziale V₁−V₂=V₀. Negli istanti successivi tale differenza di potenziale varierà nel tempo secondo un'oscillazione smorzata, alla frequenza del circuito risonante:

V₁−V₂=V₀ e^αt e^-iωt. (31)

Sostituendo la (31) nella (30) si ottiene:

ρ+R e^-αt e^-iωt=0;

se è ωτ=π,

La frequenza delle oscillazioni è determinata dal tempo di transito τ e risulta pari alla metà dell'inverso di tale tempo. Occorre quindi che il circuito oscillante sia accordato a questa frequenza. Se è R〈ρ, cioè se la resistenza interna del diodo è più grande di quella del circuito, α è negativa e le oscillazioni non possono autosostenersi. Se, al contrario, è ρ〈R, α è positiva e una minima instabilità induce un'oscillazione, la cui ampiezza aumenta esponenzialmente fino a un valore di regime, determinato dai valori dei parametri del sistema (corrente erogabile dal tubo, differenza di potenziale applicata, intensità del campo magnetico, ecc.). Variando la tensione applicata al tubo si varia, come in ogni diodo, la resistenza interna. Quando questa è minore di R una qualunque eccitazione del circuito risonante porta a un aumento della differenza di potenziale che si produce fra i due anodi e all'indursi delle auto-oscillazioni.

Questi calcoli sono in realtà troppo qualitativi e il funzionamento di un magnetron è molto più complesso. Essi fanno tuttavia comprendere che le oscillazioni sono caratterizzate dal tempo di transito e dalla disposizione a settori dell'anodo. Per creare le condizioni di autoscillazione occorre che un eccesso di elettroni arrivi su uno dei due anodi, quello a potenziale più basso, producendo una ulteriore caduta del potenziale con una reazione positiva. Diversi altri perfezionamenti furono introdotti negli anni trenta. Furono usati quattro e più anodi e il circuito risonante fu incluso all'interno del tubo. Negli anni quaranta e durante la seconda guerra mondiale il magnetron fu perfezionato e portato alla forma attuale soprattutto ad opera dei ricercatori dell'Università di Birmingham, che realizzarono il magnetron a cavità risonante, per il funzionamento pulsato, di grande potenza. In tale tubo l'anodo è costituito da un grosso blocco di rame nel quale sono ricavate alcune cavità, di forma cilindrica, accoppiate mediante fessure alla regione di interazione. L'impiego di catodi di grande superficie e rivestiti con ossidi ad alta emissività permette di ottenere impulsi di onde elettromagnetiche della durata di uno o due microsecondi e con potenza di cresta pari ad alcune decine di megawatt, a frequenze comprese fra 1 e 30 GHz. Gli impulsi si susseguono a intervalli di qualche millisecondo l'uno dall'altro cosicché la potenza media è dell'ordine di qualche chilowatt o anche di qualche decina di chilowatt.

f) Il maser

La parola maser è formata con le iniziali dell'espressione Microwave Amplification by Stimulated Emission of Radiation, che significa amplificazione di microonde attraverso il processo di emissione stimolata e denota una classe di dispositivi elettronici (amplificatori, oscillatori) nei quali gli elementi attivi (i tubi elettronici) sono sostituiti da atomi o molecole e il cui funzionamento è determinato dai processi di interazione degli atomi con la radiazione. La natura ditali processi è quantica e il funzionamento di questi dispositivi può essere studiato solo coi metodi della meccanica quantistica. Le ricerche in questo settore costituiscono una nuova disciplina, l'‛elettronica quantistica', attualmente in pieno sviluppo. Il primo maser fu realizzato negli Stati Uniti da Gordon, Zeiger e Townes nel 1954. Contemporaneamente i fisici sovietici Basov e Prochorov proponevano lo stesso dispositivo. Negli anni successivi furono realizzati diversi dispositivi del genere funzionanti nella regione delle microonde. Negli anni sessanta il funzionamento di tali apparati fu esteso alle frequenze ottiche ed ebbe così origine il maser ottico o laser (da Light Amplification by Stimulated Emission of Radiation), la cui importanza in numerosi campi della tecnica e della ricerca è ben nota e non necessita di commenti.

La realizzazione di un maser è concettualmente più semplice di quella di un amplificatore elettronico convenzionale: consiste sostanzialmente nel ‛preparare' un sistema di atomi o di molecole in modo tale che il campo elettromagnetico risulti amplificato dall'interazione con tale sistema. Per comprenderne il funzionamento è necessario pertanto considerare i processi mediante i quali un sistema microscopico (atomo, molecola) può interagire con il campo elettromagnetico. Tali processi sono trattati estesamente in altri articoli (v. atomo; v. ottica quantistica); ne richiamiamo qui solo le carattenstiche che è necessario conoscere per comprendere il funzionamento del maser.

I processi mediante i quali un sistema microscopico scambia energia con il campo elettromagnetico sono: l'emissione spontanea, l'emissione indotta e l'assorbimento. Nell'emissione spontanea il sistema decade spontaneamente da uno stato di energia interna E_i a uno stato di energia inferiore E_k emettendo radiazione elettromagnetica sotto forma di un fotone di energia hν_ik=E_i−E_k. In presenza di radiazione elettromagnetica di frequenza ν_ik, la transizione tra i due livelli può essere indotta dalla presenza del campo. In questo caso, a seconda che il sistema si trovi al livello di energia superiore o a quello di energia inferiore, si ha rispettivamente il processo di emissione stimolata o di assorbimento. Nel processo di assorbimento un fotone di energia hν_ik è assorbito, cioè annichilato, e la sua energia è trasformata in energia interna del sistema. In quello di emissione indotta, invece, il sistema cede al campo elettromagnetico l'energia E_i−E_k sotto forma di un fotone di energia hν_ik, come nel caso dell'emissione spontanea. Fra i due possibili processi di emissione vi è però una differenza sostanziale. Nell'emissione spontanea, infatti, il fotone è emesso in una direzione e con uno stato di polarizzazione casuale, che dipendono dallo stato dell'atomo all'istante del decadimento e la distribuzione in frequenza della luce emessa copre una regione spettrale più o meno estesa (larghezza della transizione), determinata dalla probabilità del processo (larghezza naturale) e dalla distribuzione di velocità degli atomi (effetto Doppler). Nell'emissione stimolata, invece, il fotone emesso è fisicamente indistinguibile da quello che ha indotto il processo: ha esattamente la stessa frequenza, lo stesso stato di polarizzazione e la stessa direzione di propagazione. Nella descrizione ondulatoria del campo elettromagnetico si tratta quindi di un vero e proprio processo di amplificazione. Il campo elettromagnetico che interagisce con un sistema di atomi a causa di processi stimolati (emissione indotta e assorbimento) risulta modificato solo nella sua intensità, mentre rimangono inalterati gli altri parametri che lo caratterizzano (direzione di propagazione, stato di polarizzazione, frequenza).

I processi sono descritti dai ‛coefficienti di Einstein':

A_ik, B_ik, B_ki,

il primo dei quali rappresenta la probabilità per unità di tempo che avvenga una transizione spontanea fra due stati di energia E_i ed E_k (E_i>E_k), mentre B_ik ρ(ν_ik), B_ki ρ(ν_ik) rappresentano le probabilità di una transizione di emissione o di assorbimento indotta dalla presenza di energia elettromagnetica di densità spettrale ρ(ν_ik) alla frequenza della transizione. Risulta inoltre B_ik=B_ki,cioè la probabilità di una transizione indotta dal campo è la stessa nei due sensi. La probabilità di emissione spontanea è proporzionale alla terza potenza della frequenza della transizione, così che tale processo, predominante nella regione ottica, è assolutamente trascurabile alle frequenze delle microonde o inferiori. I coefficienti B_ik sono invece indipendenti dalla frequenza. Alle basse frequenze l'emissione indotta e l'assorbimento sono praticamente i soli processi attraverso i quali il campo elettromagnetico interagisce con la materia. Poiché da un processo di emissione stimolata il campo elettromagnetico risulta amplificato e da un processo di assorbimento attenuato, dall'interazione con un sistema di atomi il campo sarà globalmente attenuato o amplificato a seconda che il numero di processi di assorbimento sia maggiore o minore del numero dei processi di emissione, cioè, essendo la probabilità dei processi la stessa, a seconda che il numero degli atomi che si trovano nello stato di energia più bassa sia maggiore o minore del numero degli atomi che si trovano nello stato di energia più elevata. In un sistema all'equilibrio termico alla temperatura T gli atomi sono distribuiti fra i diversi stati di energia con ripartizione di Boltzmann. Il rapporto, cioè, fra il numero degli atomi che si trovano nello stato di energia E_i e quello degli atomi nello stato di energia E_k è n_i/n_k=exp [−(E_i−E_k]/kT)≃1−(E_i−E_k)/kT, se E_i−E_k≪kT (dove k è la costante di Boltzmann). Lo stato di energia più elevata è meno popolato e pertanto un campo elettromagnetico di frequenza ν_ik=(E_i−E_k)/h che interagisca col sistema indurrà un numero di processi di assorbimento maggiore del numero dei processi di emissione e risulterà attenuato dall'interazione. Se però si riesce a ottenere uno stato stazionario descritto da una distribuzione degli atomi fra i due livelli tale che il livello superiore sia più popolato di quello inferiore, sia cioè (n_i−n_k)>0, il numero dei processi d'emissione stimolata sarà più elevato di quello dei processi di assorbimento e il sistema sarà capace di amplificare la radiazione.

Il guadagno di un qualunque amplificatore, in condizioni opportune, può essere reso infinito. In tal caso l'amplificatore diviene un generatore, cioè emette radiazione senza dover essere stimolato all'ingresso da alcun segnale. Se il numero di atomi che si trovano al livello eccitato è molto grande, il numero di quelli che decadranno per emissione spontanea nell'unità di tempo sarà sufficiente a produrre un campo elettromagnetico che induce l'emissione di altri atomi, innescando un processo a cascata. Se la popolazione degli atomi al livello eccitato è mantenuta costante mediante un dispositivo opportuno, si avrà emissione di radiazione alla frequenza della transizione. L'energia spesa per mantenere il sistema in tali condizioni sarà in parte convertita in energia elettromagnetica. Pertanto per realizzare un maser, amplificatore o oscillatore, è necessario produrre e mantenere un'‛inversione' fra le popolazioni di due livelli in un insieme di atomi o di molecole, cioè realizzare uno stato stazionario del sistema nel quale la popolazione di un livello sia maggiore di quella di un altro livello d'energia inferiore, verso il quale sia permessa una transizione radiativa.

Il primo maser realizzato fu quello ad ammoniaca, nel quale l'inversione delle popolazioni è ottenuta mediante un campo elettrico. Il gas NH₃ presenta nella regione compresa fra 20 e 30 GHz numerose e intense risonanze (spettro di inversione). In presenza di un campo elettrico E l'energia di ciascuno dei due stati fra i quali avviene una di queste transizioni è modificata: quella degli stati di energia più elevata aumenta di ΔW=μ²E²/(hν₀), mentre quella degli stati di energia più bassa diminuisce della stessa quantità (μ momento elettrico della molecola, hν₀ separazione energetica tra i due stati in assenza di campo). Ne consegue che, in presenza di un campo elettrico non uniforme, le molecole sono sollecitate da una forza verso la regione dove E è più grande o più piccolo, a seconda che la molecola si trovi nello stato di energia più bassa o più elevata e ciò permette di separare nello spazio le molecole che si trovano nello stato di energia più bassa da quelle che si trovano nello stato di energia più elevata.

Nella fig. 34 è riportato lo schema di un maser a NH₃. Le molecole di NH₃, emesse da una sorgente S, per mezzo di opportuni diaframmi vengono collimate in un fascio che si propaga nella direzione z, traversano quindi una cavità risonante e vengono pompate fuori. Lungo la traiettoria le molecole subiscono l'azione di un campo elettrico che non dipende da z e che varia linearmente con la distanza r dall'asse del fascio: ∣E∣=ar. Tale campo focalizza sull'asse del fascio le molecole che si trovano negli stati eccitati e allontana dal fascio quelle che si trovano negli stati di energia inferiore. Dopo un percorso di alcune decine di centimetri il fascio risulta formato prevalentemente da molecole che si trovano negli stati eccitati. La cavità funziona a trasmissione e la sua frequenza può essere variata dall'esterno. Se essa è eccitata da un'onda elettromagnetica la cui frequenza è quella propria di una transizione, il campo interagisce fortemente con le molecole stimolando l'emissione e la radiazione all'uscita della cavità è più intensa che all'ingresso. Si può anzi dire che, variando la frequenza della radiazione all'ingresso, si osserva un brusco aumento del livello di uscita quando la frequenza coincide con quella di una transizione e lo strumento funziona allora come uno spettrometro con potere risolutivo estremamente elevato. A causa della radiazione termica presente nella cavità, alcune delle molecole del fascio decadono durante il tempo di transito e, se il fascio è sufficientemente intenso, il campo elettromagnetico prodotto sarà sufficiente a indurre transizioni nelle molecole successive e le oscillazioni potranno autosostenersi anche in assenza di radiazione dall'esterno. In tal caso il sistema funziona come un generatore di energia elettromagnetica di grande purezza spettrale.

Come amplificatore, la banda del dispositivo è determinata dal tempo di transito delle molecole nella cavità. Tale tempo è dell'ordine di 5×10^-4 s e la banda corrispondente è di 2 kHz, dell'ordine di quella che si osserva sperimentalmente. Alla frequenza di funzionamento di 2,4×10¹⁰ Hz il Q corrispondente risulta dell'ordine di 10⁷. La fiuttuazione percentuale della frequenza di un oscillatore è una piccola frazione di 1/Q, per cui un maser a NH₃ è stabile entro 1 parte su 10¹⁰. La potenza erogata, dell'ordine di 10^-8÷10^-9 watt nei primi dispositivi realizzati, è dell'ordine di 10^-6 watt in quelli attuali. I diversi tipi di maser si diversificano, oltre che per il metodo usato per ottenere l'inversione degli stati, anche per la natura delle transizioni e trovano numerose applicazioni, di alcune delle quali sarà fatto cenno nel seguito di questo articolo.

6. Rivelazione delle microonde

a) Sensibilità limite nella rivelazione di segnali radioelettrici

L'informazione, o ‛segnale', portata da un'onda elettromagnetica è costituita da una variazione temporale dell'ampiezza, o della frequenza, o dello stato di polarizzazione dell'onda. Per ‛rivelare' il segnale tale variazione è tradotta, in ogni caso, in una variazione ΔP della potenza che incide su un ricevitore.

La ‛potenza del segnale', ΔP, è trasportata da componenti monocromatiche, le cui frequenze sono distribuite in un intorno più o meno esteso della frequenza ν dell'onda. Il ricevitore deve quindi avere una ‛banda' Δν, deve cioè accettare tutte le frequenze che contribuiscono sostanzialmente alla potenza del segnale. La presenza all'ingresso del ricevitore di fluttuazioni di natura fondamentale pone un limite inferiore alla potenza ΔP rivelabile in un intorno di frequenze Δν, cioè alla ‛sensibilità' del ricevitore.

Ogni ricevitore è fornito di un ingresso, cioè di un dispositivo che permette di trasferire energia elettromagnetica da una sorgente esterna al ricevitore. Senza perdita di generalità, possiamo schematizzare tale ingresso come un'antenna caratterizzata da un'area S (area equivalente) che trasferisce al ricevitore la potenza che incide su di essa sotto un angolo solido Ω=λ²/S=c²/ν²S.

In assenza di radiazione esterna diversa da quella termica, se tutto il sistema è in equilibrio termico alla temperatura T, l'antenna riceve (e irradia) nell'intervallo di frequenze Δν, attorno a una frequenza ν, la potenza

dove u(ν, t) è la densità spettrale della radiazione termica alla temperatura T e alla frequenza ν che, alle frequenze dello spettro hertziano, vale, per un definito stato di polarizzazione:

con k=1,48×10^-23 joule/°K costante di Boltzmann. Sostituendo nella (32) e ricordando che è SΩ=c²/ν² si ottiene, per la potenza all'ingresso del ricevitore, il risultato seguente (teorema di Nyquist):

P_R=kTΔν. (33)

Se il ricevitore è ‛ideale' (cioè non introduce fluttuazioni proprie), alla sua uscita, in assenza di ogni segnale all'ingresso, è quindi presente un segnale aleatorio indipendente dalla frequenza (rumore bianco) corrispondente alla potenza di rumore termico (33) presente al suo ingresso.

Supponiamo ora che all'ingresso del ricevitore sia presente, oltre alla potenza di rumore termico P_R, una potenza di segnale P_S. L'accoppiamento del ricevitore col campo elettromagnetico avviene attraverso il campo elettrico o il campo magnetico dell'onda; in altre parole, la potenza trasferita al ricevitore è proporzionale alla seconda potenza del campo elettrico (o magnetico) presente all'ingresso del ricevitore. Poiché tale campo è dato dalla somma dei campi associati alle potenze P_R e P_S: E=E_R+E_S, e poiché la potenza di un'onda elettromagnetica è proporzionale al quadrato del campo dell'onda, risulta che la potenza P_r trasferita al ricevitore è data da:

P_r∝(E_S+E_R)²=P_S+2√-P-_S-k-T-Δ-ν +kTΔν. (34)

Il secondo e il terzo termine della (34) rappresentano potenze di rumore e pongono un limite al minimo segnale rivelabile.

A seconda della natura del segnale da rivelare occorre considerare due casi distinti. Il primo caso è quello della rivelazione dei segnali radar, della radioastronomia, delle telecomunicazioni ecc., e consiste nel rivelare radiazione di intensità la più debole possibile. Assumiamo convenzionalmente che il minimo segnale rivelabile sia quello che raddoppia il valore quadratico medio del segnale che è presente all'uscita del ricevitore in assenza di segnale all'ingresso. Ponendo, per tale caso, nell'equazione (34) P_S=0, si ottiene:

(P_S)_min=kTΔν=4×10^-21Δν watt, per T=300°K. (35)

Il secondo caso è quello della spettroscopia ad assorbimento. In questo caso il ricevitore è alimentato con una potenza P relativamente elevata, la cui frequenza è variata lentamente. Il segnale consiste in una piccola variazione ΔP della potenza che si ha quando la frequenza dell'onda passa per il valore di risonanza. Il problema quindi è quello di rivelare una variazione percentualmente piccola di una potenza relativamente elevata. In tal caso, l'ultimo termine della (34) è trascurabile rispetto al secondo e si ha:

(ΔP)_min=2√-P-_S-k-T-Δ-ν (36)

o

Le (35) e (36a) si riferiscono alla sensibilità di un ricevitore ‛ideale', il cui rumore cioè sia quello termico, di natura fondamentale, e nel quale tutta la potenza del segnale presente all'ingresso sia utilizzata. In un ricevitore reale parte della potenza all'ingresso è perduta e rumore supplementare viene introdotto dai processi di rettificazione, di amplificazione, ecc. Se S_u=P_u/N è il rapporto fra la potenza del segnale P_u e quella del rumore N all'uscita del ricevitore e S_i=P_i/kTΔν l'analogo rapporto all'ingresso, il rumore aggiunto a quello termico introdotto dal ricevitore è descritto dalla ‛figura di rumore' F, definita da F=S_i/S_u, che descrive come il rapporto segnale/rumore venga deteriorato dai processi interni al ricevitore. Riferita all'ingresso, la potenza di rumore risulta espressa da P_R=FkTΔν e il minimo segnale rivelabile risulta nei due casi:

P_min=FkTΔν (37)

(ΔP)_min=√-P-_S-F-k-T-Δ-ν. (38)

Per la ricezione di segnali deboli occorre quindi usare la banda più piccola possibile, compatibilmente con la riproduzione del segnale, e rendere più piccola possibile la figura di rumore.

b) La conversione di frequenza

La rivelazione di microonde viene realizzata convertendo l'energia di alta frequenza in energia di frequenza più bassa e amplificando tale segnale fino al livello sufficiente per azionare un indicatore. La conversione è realizzata mediante diodi particolari. I diodi usati (cristalli rivelatori) sono diodi a semiconduttore, versione perfezionata del rivelatore a galena usato nei primi radioricevitori, consistenti in un blocco di materiale semiconduttore (generalmente silicio), posto in contatto con la punta di un sottile filo metallico. La resistenza del contatto è diversa a seconda della polarità della tensione applicata fra il metallo e il semiconduttore, cosicché il sistema può rettificare una tensione alternata. Poiché il contatto è realizzato mediante una punta molto sottile, la capacità in parallelo ai terminali è molto piccola e il diodo è in grado di rettificare anche tensioni alternate di frequenza assai elevata. Il sistema filo-semiconduttore è racchiuso in una cartuccia che gli conferisce stabilità meccanica e che viene inserita in una guida d'onda.

Nel processo di conversione non tutta la potenza del segnale a microonde è convertita in potenza del segnale a bassa frequenza; inoltre, viene introdotto del rumore in aggiunta a quello termico. L'efficienza del diodo è descritta dalle ‛perdite di conversione', ℒ_c, e dalla ‛temperatura di rumore', t_c. Se P_i è la potenza a microonde assorbita dal diodo e P_u è quella del segnale a bassa frequenza trasferita dal diodo a un carico adattato, la perdita di conversione, espressa in decibel, è definita come

Quando la potenza a microonde incidente è piccola, inferiore a 10^-5 watt, un diodo a cristallo si comporta come un generatore di forza elettromotrice proporzionale alla potenza incidente e di resistenza interna indipendente da tale potenza. Valori tipici di questi parametri sono rispettivamente 1 volt per mW di potenza assorbita e alcune migliaia di ohm. Ne consegue che la potenza del segnale rettificato è proporzionale al quadrato della potenza a microonde assorbita e le perdite di conversione risultano molto elevate. A tali livelli di potenza è cioè:

P_u=AP_i², con A≅10³ watt^-1. (39)

Per P_i=10^-5 watt, risulta P_u/P_i=10^-2, cioè è convertito solo 1/100 della potenza incidente (ℒ_c=20 dB). Le perdite di conversione aumentano fortemente per potenze incidenti ancora inferiori. All'aumentare della potenza incidente (≅10^-3 watt) diminuisce la resistenza interna del cristallo, la potenza di uscita tende ad essere proporzionale a quella incidente e la perdita di conversione diminuisce. Un buon rivelatore per la banda K (frequenze comprese tra 20 e 30 GHz) sul quale incida 1 mW di potenza a microonde, eroga una corrente di 1 mA su un carico di 200 ohm, con un rendimento del 20%, cioè con perdite di conversione di 7 dB.

La temperatura di rumore t_c è definita da

in cui T_R è data da

P_R=kT_RΔν,

e P_r è la potenza di rumore generata dal diodo alla temperatura T•t_c rappresenta quindi quante volte la temperatura del laboratorio dovrebbe essere aumentata affinché la potenza di rumore ai terminali di un diodo ideale (t_c=1) fosse quella del diodo considerato.

La potenza di rumore generata da un diodo può essere suddivisa in due parti

dove i è la corrente che attraversa il diodo, f la frequenza del segnale di uscita e a una costante dell'ordine di 10^-7 ohm per un buon diodo. La prima parte è la potenza di rumore termico, la seconda, in 1/f, è il cosiddetto ‛rumore flicker', caratteristico dei semiconduttori e dei tubi elettronici alle basse frequenze.

c) Rivelazione supereterodina.Dalle (39) e (40) si ricava che, se la potenza incidente è piccola, la temperatura di rumore t_c è praticamente eguale a 1, ma le perdite di conversione divengono molto elevate. Inoltre, se il segnale rettificato è di bassa frequenza, il rumore flicker dell'amplificatore è elevato. La sensibilità di un ricevitore costituito da un diodo connesso con un amplificatore di bassa frequenza (‛ricevitore video') è dell'ordine di 10^-10 watt per hertz di banda passante. Tale sensibilità non è sufficiente per la maggior parte delle applicazioni. Si ricorre in tal caso ai cosiddetti ricevitori ‛supereterodina'.

In un ricevitore supereter6dina sul diodo a cristallo è inviata la radiazione generata da un oscillatore interno al ricevitore (‛oscillatore locale') con potenza di qualche milliwatt, alla quale le perdite di conversione del dio- do sono piuttosto piccole. Se ν_S è la frequenza per la quale è progettato il ricevitore, la frequenza dell'oscillatore locale è regolata su un valore ν_OL=ν_S+f e l'uscita del diodo è connessa all'ingresso di un amplificatore (amplificatore a media frequenza) accordato alla frequenza f (media frequenza). La media frequenza f è di qualche decina di MHz, tale cioè da rendere trascurabile rispetto a quello termico il rumore in 1/f che compare nella (40) e da ridurre la figura di rumore degli amplificatori molto prossima a 1. La ricezione in supereterodina consiste nel convertire la potenza del segnale in potenza a media frequenza f, nell'amplificare a tale frequenza f e nel convertire ancora il segnale amplificato a frequenza f nel segnale a bassa frequenza. Il principio di funzionamento supereterodina può essere compreso tenendo presente le considerazioni precedenti sul rumore introdotto dalla presenza di potenza di segnale all'ingresso del rivelatore.

Abbiamo visto dall'equazione (34) che, in presenza di potenza P all'ingresso del ricevitore, all'uscita del rivelatore è presente un segnale di rumore corrispondente alla potenza dell'ingresso P_R=2√-P-_S-k-T-Δ-ν. Il battimento del segnale a frequenza ν_S con la componente a frequenza ν_S±δ del rumore termico dà origine a un segnale alla frequenza δ e la potenza P_R è quella risultante da tali battimenti, sommati su tutte le frequenze δ〈Δν.

La potenza di oscillatore locale P_OL produce quindi un segnale di rumore pari a 2√-P-_S-_L-k-T-Δ-ν nella banda Δν dell'amplificatore di media frequenza. Quando è presente anche un debole segnale P_S≪P_OL, il rumore resta praticamente lo stesso ma è presente il segnale alla frequenza f, di battimento fra la potenza P_OL, a frequenza ν_S+f; e la potenza P_S a frequenza ν_S. La potenza ditale segnale corrisponde a una potenza all'ingresso P=√-P-_O-_L-P-_S. Ne consegue che il rapporto segnale/rumore all'ingresso dell'amplificatore di media frequenza è

Se P_S≅kTΔν, è S=1/2 ed è come se nella conversione si perdesse la metà del segnale, per cui il rendimento di conversione supereterodina non può essere migliore del 50%. Ciò traduce il fatto che metà della potenza del segnale è perduta nel battimento alla frequenza ν_S+ν_OL=2ν_S+f, non accettata dall'amplificatore. Tale rendimento è ad ogni modo enorme confrontato con quello che si ottiene convertendo direttamente la piccola potenza P_S a microonde in potenza a bassa frequenza. In tale risultato si è trascurato il contributo delle altre potenze di rumore, per cui la perdita di conversione 1/2 è un limite asintotico cui tende un rivelatore perfetto, all'aumentare della potenza P_OL. All'aumentare di questa, aumenta la temperatura di rumore t_c del cristallo e la figura complessiva di rumore è ottenuta per un valore ottimale della potenza dell'oscillatore locale. La figura di rumore del sistema risulta:

dove F′ è la figura di rumore dell'amplificatore di media frequenza ed F, F′ sono espressi in numeri e non in dB. F raggiunge un valore ottimale per un determinato livello della potenza dell'oscillatore locale. Nella fig. 35A è mostrata la perdita di conversione (in dB), la temperatura di rumore t_c e la figura totale di rumore F (in dB) del ricevitore, in funzione della potenza P_OL. Al valore ottimale di questa la figura di rumore complessiva del ricevitore risulta pari a F =11 dB, cioè il ricevitore può rivelare segnali circa 10 volte più grandi del rumore termico. Si sono ottenute figure di rumore più basse e un buon ricevitore supereterodina ha una sensibilità dell'ordine di 10^-20 watt per hertz di banda passante, molto prossima a quella di rumore termico (4•10^-21 W/Hz).

Nella fig. 35B è illustrato il circuito mediante il quale si effettua la conversione in un ricevitore supereterodina (circuito ‛mescolatore' o mixer). Esso è un T magico nel quale due diodi rivelatori sono alloggiati nei rami allineati 1 e 2. Le uscite dei diodi sono connesse agli ingressi di un amplificatore differenziale alla frequenza f. Il segnale è inviato dal ramo 4 e perviene ai diodi in opposizione di fase mentre la potenza dell'oscillatore locale è inviata dal ramo 3 ed è ricevuta dai diodi in fase. Ne consegue che il segnale di battimento ai terminali dei diodi è in opposizione di fase e viene amplificato mentre il rumore a frequenza f generato da fluttuazioni della potenza dell'oscillatore locale, in fase, viene soppresso dall'amplificatore differenziale.

d) Ricevitori a microonde.

Ricevitori radar. - Un ricevitore radar deve rivelare segnali costituiti da treni d'onda di durata dell'ordine del microsecondo, che si susseguono alla cadenza di qualche centinaio al secondo. Il segnale di uscita è costituito da impulsi di tensione di forma rettangolare, costituenti l'inviluppo di tali treni d'onde. Si usano ricevitori supereterodina con larghezza di banda Δν=1/τ (τ durata del treno) dell'ordine del megahertz, sufficiente per la riproduzione dell'impulso. Con tale larghezza di banda la sensibilità è dell'ordine di 10^-14 W.

Radiometri. - Un radiometro è un ricevitore usato per rivelare la presenza di radiazione di debole intensità, emessa da una sorgente a temperatura diversa dalla temperatura ambiente. È il ricevitore usato per lo studio della radiazione proveniente dallo spazio. Esso consiste in un ricevitore supereterodina, connesso a un'antenna altamente direttiva. Questa trasmette al ricevitore la potenza incidente dalle direzioni comprese entro un angolo solido Ω attorno a una data direzione z, nell'intervallo di frequenze Δν, attorno a una frequenza ν. Abbiamo visto che questa potenza è P_a=kT_aΔν, dove T_a è la temperatura della regione di spazio verso la quale è orientata l'antenna. A differenza dei segnali radar, tale potenza è un segnale continuo che provoca all'uscita del ricevitore un segnale di rumore. Per rivelarlo con alta sensibilità, nella guida che connette l'antenna al ricevitore è inserito un modulatore meccanico costituito da materiale assorbente (‛corpo nero') che viene periodicamente inserito e tolto dalla guida. Esso costituisce una sorgente di rumore alla temperatura del laboratorio: quando è inserito la potenza all'ingresso del ricevitore è kTν, quando è tolto è kT_aΔν. Il segnale ottenuto dopo la seconda rivelazione consiste quindi in una tensione di rumore, modulata alla frequenza f d'inserimento del modulatore meccanico, di ampiezza corrispondente a una potenza di ingresso k(T−T_a)Δν, dove Δν è la banda dell'amplificatore a media frequenza. Tale banda è scelta più grande possibile compatibilmente con l'informazione richiesta, in modo da raccogliere la massima potenza. Se tale informazione è quella della temperatura nella direzione z la banda Δν può essere di qualche decina o centinaia di MHz. Dopo la seconda rivelazione, il segnale è amplificato da un amplificatore di frequenza f e banda δν la più stretta possibile per rendere minimo il rumore. La banda di rumore non risulta però δν. Battimenti fra le frequenze dell'intervallo Δν che occorrono nella seconda rivelazione producono potenza di rumore nell'intervallo δν, per cui l'effettiva banda di rumore del sistema risulta eguale alla media geometrica tra le bande Δν e δξ degli amplificatori a media e bassa frequenza. La sensibilità del radiometro risulta quindi:

k(T−T_a)Δν=FkTδν,

cioè

Con δν=0,1 Hz, Δν=10⁷ Hz e F=10 è possibile rivelare la radiazione emessa da un corpo nero che si trovi a una temperatura diversa di una frazione di grado dalla temperatura ambiente.

Quando il radiometro è utilizzato per lo studio di sorgenti a bassa temperatura, come nella radioastronomia, il confronto è eseguito con la temperatura T più vicina possibile a quella della sorgente. Ciò aumenta la sensibilità e la precisione nella misura assoluta di T, che viene realizzata commutando alla frequenza f la radiazione proveniente dall'antenna a temperatura T_a con quella proveniente da una sorgente mantenuta alla ‛temperatura di confronto' T_c, più vicina possibile a T_a.

Nella spettroscopia a microonde del gas interstellare le risonanze appaiono come picchi (positivi o negativi a seconda che si tratti di emissione o di assorbimento) nello spettro bianco corrispondente alla potenza termica alla temperatura T_a. Occorre in questo caso che la banda Δν dell'amplificatore a media frequenza sia piccola rispetto alla larghezza della riga di risonanza (qualche decina di kHz). Il confronto in questo caso si esegue cambiando periodicamente la frequenza dell'oscillatore locale da un valore ν₁ a un valore ν₂=ν₁+δ, con una variazione δ che è maggiore della larghezza di ogni possibile riga di risonanza. Ciò equivale a confrontare la potenza emessa alla frequenza ν₁ con quella emessa alla frequenza ν₂. In assenza di risonanze alle frequenze ν₁ o ν₂ la potenza si mantiene costante e nessun segnale è presente all'uscita del radiometro. Una risonanza all'una o all'altra frequenza produce invece una modulazione della potenza all'ingresso, alla frequenza f di modulazione della frequenza dell'oscillatore locale.

Nella misura di basse temperature, la principale sorgente di rumore è costituita dall'emissione della guida che connette l'antenna col ricevitore. La guida irradia verso l'antenna e verso il ricevitore la potenza αkTδν, dove α è l'assorbimento della guida e T la temperatura del laboratorio. Con α≅10^-2 e T≅300 °K la potenza di rumore sempre presente all'ingresso del rivelatore corrisponde a una temperatura di qualche grado kelvin, che può essere ridotta raffreddando la guida. Si ricorre allora a un'amplificazione della potenza a microonde, che si ottiene interponendo fra l'antenna e il rivelatore un amplificatore maser. La figura di rumore di un maser è molto prossima a 1 e permette di innalzare il livello della potenza del segnale a un valore tale da rendere trascurabile la potenza di rumore all'ingresso.

Nella fig. 36 è schematizzato un radiometro per radio-astronomia, la cui descrizione è data nella didascalia.

Spettrometri a microonde. - Uno spettrometro a microonde per gas è costituito da un generatore che alimenta un ricevitore attraverso una cella di assorbimento contenente il campione (v. fig. 37). La cella è costituita da un tratto di guida d'onda di lunghezza L. La frequenza del generatore è fatta variare periodicamente alla frequenza f in un intervallo di frequenze entro il quale si prevede sia compresa la frequenza di risonanza del gas. Se l'assorbimento per unità di lunghezza della cella è α_c e quello del gas è α_g≪α_c, la potenza trasmessa al ricevitore è

P_t=P₀ e^-(αc+αg)L=P₀ e^-αcL(1−α_gL),

dove P₀ è la potenza all'ingresso della cella. In un intervallo di frequenze di qualche MHz o decina di MHz, P₀ e α_c sono indipendenti dalla frequenza, mentre l'assorbimento del gas a bassa pressione avviene solo in un intervallo di qualche decina o centinaia di kHz attorno alla frequenza di risonanza ν. Al passaggio per la frequenza di risonanza la potenza all'ingresso del ricevitore varia quindi di

ΔP_t=−α_gLP₀ e^-α_c^L

e il problema è quello di rivelare tale piccola variazione ΔP, della potenza P₀ e^-αcL.

Abbiamo visto che la sensibilità limite per tale problema è data dalla (38) da cui risulta per il minimo coefficiente di assorbimento rivelabile

La lunghezza ottimale della cella risulta allora

L_opt=2/α_c,

da cui

Come sarà visto in seguito, il coefficiente di assorbimento di un gas non dipende dall'intensità della radiazione che lo attraversa solo nel caso in cui tale intensità sia sufficientemente debole e tende a zero all'aumentare di questa. Ciò limita la potenza P₀, all'ingresso della guida che costituisce la cella, a qualche microwatt. La banda passante Δν deve essere sufficientemente ampia da permettere la riproduzione del segnale di assorbimento. Questo è un segnale periodico di frequenza f, di forma lorentziana, che può essere riprodotto senza apprezzabile distorsione con una banda Δν pari a 10 volte la frequenza f (frequenza di sweep). Se questa è pari a 20 Hz si ottiene, con P₀=10^-5 watt: α_c=10^-3 cm^-1, Δν=200 Hz, (α_g)_min=10^-9√-F cm^-1.

La figura di rumore del cristallo e degli amplificatori è elevata alle frequenze basse, perciò il valore (α_g)_min di uno spettrometro semplice, costituito da un rivelatore a cristallo connesso con un amplificatore a bassa frequenza (spettrometro video), è dell'ordine di 10^-6÷10^-7 cm^-1.

Gli spettrometri più sofisticati si distinguono per la maniera in cui si ottimizzano F e Δν. Negli ‛spettrometri Stark' il gas è sottoposto a una differenza di potenziale alternata di frequenza elevata, dell'ordine della larghezza della risonanza, cioè di un centinaio di kHz. La forma d'onda di tale tensione è rettangolare, cosicché il gas è sottoposto a un campo elettrico di valore costante durante un semiperiodo e a un campo nullo nell'altro semiperiodo. Nel semiperiodo durante il quale il campo è presente la curva di risonanza è modificata in frequenza e intensità (effetto Stark) e l'assorbimento del gas risulta pertanto ‛modulato' alla frequenza del campo applicato producendo sul rivelatore un segnale a tale frequenza. Poiché tale frequenza è elevata, la potenza di rumore aggiunta a quella termica, che secondo la (40) è inversamente proporzionale alla frequenza, è molto ridotta. Inoltre, poiché la frequenza del segnale di assorbimento è quella del campo applicato, la banda Δν può essere resa molto stretta attorno a tale frequenza e il segnale può essere confrontato in fase con quello della modulazione Stark, rendendo la banda di rumore non più ampia di 1 Hz o anche meno. Con tali spettrometri si possono misurare coefficienti di assorbimento dell'ordine di 10^-9÷10^-10 cm^-1. Tali assorbimenti sono estremamente deboli, se si pensa che l'intensità di un'onda piana che si propaga in un gas con α=10^-9 cm^-1 si riduce in ampiezza di un fattore e, dopo un percorso di 10.000 km.

Per campioni solidi piccoli di volume, ad esempio nelle esperienze di risonanza paramagnetica elettronica, la cella di assorbimento è generalmente costituita da una cavità posta in un campo magnetico statico. La frequenza della risonanza è la frequenza di Larmor dei momenti magnetici contenuti nel campione (v. atomo) e può quindi essere variata variando l'intensità del campo statico. Per campi magnetici di alcune migliaia di gauss la frequenza di risonanza cade nella regione delle microonde. Variando l'intensità H del campo esterno è quindi possibile far coincidere la frequenza della risonanza magnetica con quella della cavità. Quando ciò avviene, alle perdite proprie della cavità si aggiungono quelle del campione e si osserva una variazione relativa del Q:

dove P_c è la potenza assorbita dal campione e P_d la potenza totale dissipata nella cavità. L'assorbimento quindi è rivelato dalla misura della variazione del Q, attraverso la misura della variazione della potenza trasmessa o riflessa. La sensibilità di uno spettrometro a cavità è dello stesso ordine di grandezza di quella degli spettrometri in guida. Nella risonanza paramagnetica elettronica questa sensibilità è misurata dal numero dei centri paramagnetici che è possibile rivelare: tale numero dipende dalla larghezza della riga di risonanza, cioè dalla natura del campione. Nei casi più favorevoli è possibile rivelare a temperatura ambiente la presenza in un campione di 10¹⁰÷10¹¹ centri paramagnetici.

e) Metodi di integrazione nella spettroscopia.

Un esperimento di spettroscopia a microonde consiste nel variare la frequenza del generatore da un valore ν₁ a un valore ν₂, passando attraverso il valore ν₀, al quale è prevista la risonanza, e nel registrare la potenza trasmessa dal campione al ricevitore per ogni frequenza ν di tale intervallo. Il tempo necessario per eseguire l'esperimento è quello τ impiegato dal generatore a ‛spazzare' l'intervallo ν₁−ν₂ ed è in generale stabilito dallo sperimentatore. All'aumentare di τ diminuisce proporzionalmente la larghezza della banda di frequenze Δν nella quale è contenuto il segnale e aumenta conseguentemente la sensibilità dello spettrometro. Un limite inferiore alla larghezza di banda è imposto dalle fiuttuazioni della frequenza e della potenza del generatore. A causa di queste fiuttuazioni, infatti, la potenza del generatore, a ogni frequenza ν, è distribuita in un intervallo δν intorno al valore ν e nessun guadagno si ottiene riducendo Δν al di sotto di δν.

Un metodo per aumentare la sensibilità di uno spettro- metro oltre tale limite è quello di mediare il risultato di N esperimenti consecutivi. Se τ è il tempo necessario per eseguire un esperimento, si possono eseguire f=1/τ esperimenti nell'unità di tempo, modulando in frequenza il generatore alla frequenza f, con ampiezza di modulazione δ=ν₁−ν₂. L'istante iniziale e finale di ogni esperimento, cioè il passaggio per le frequenze ν₁ e ν₂ (e, conseguentemente, per ogni frequenza ν dell'intervallo esplorato) può essere deterininato con precisione mediante dispositivi elettronici e si può, a ogni esperimento, registrare il segnale presente all'uscita in corrispondenza di ogni frequenza ν e sommare i segnali ottenuti in N esperimenti consecutivi.

La risposta di uno spettrometro consiste in una differenza di potenziale che contiene informazione (la potenza trasmessa alla frequenza ν) e rumore. Nella differenza di potenziale ottenuta come somma delle risposte di N esperimenti consecutivi, il valore quadratico medio del rumore, che è aleatorio, è √-N volte quello del singolo esperimento, mentre il segnale, che si mantiene lo stesso in ogni esperimento, è moltiplicato per N. Il rapporto segnale/rumore risulta migliorato del fattore √-N. Ciò equivale ad avere ridotto di un fattore N la banda di rumore dello spettrometro. Il ‛prezzo' di tale guadagno è costituito dal tempo N volte maggiore che è necessario per eseguire la misura.

Un metodo diverso per ottenere lo stesso risultato in un tempo τ anziché Nτ è quello di mediare i risultati di N esperimenti contemporanei. Nella spettroscopia a micro,onde la potenza assorbita da un campione è proporzionale alla potenza incidente su esso, pur che questa sia piccola; all'aumentare della potenza incidente, infatti, la potenza assorbita tende ad un valore limite e l'assorbimento percentuale ΔP/P tende a zero (‛saturazione'). Questo limita a qualche microwatt la potenza utilizzabile in una cella di assorbimento costituita da una guida d'onda. Tale potenza è molto piccola rispetto a quella ottenibile da un oscillatore klystron (10^-2÷10^-1 watt). E possibile perciò suddividere la potenza dell'oscillatore in N celle di assorbimento, ciascuna chiusa su un diodo connesso con un primo stadio di amplificazione. Il sistema risultante è un insieme di N spettrometri, alimentati da un unico generatore, con i quali è possibile eseguire N esperimenti contemporaneamente. Se le caratteristiche dei diodi usati sono le stesse e si inviano le uscite ditali spettrometri a un circuito di somma, il rapporto segnale/rumore all'uscita di questo circuito è √-N volte quello all'uscita di ogni spettrometro. Il ‛prezzo' del guadagno consiste questa volta nella complicazione delle apparecchiature e nella quantità di sostanza che è necessaria.

La dipendenza del guadagno da N² rende difficile l'uso di entrambi i metodi quando si richieda un aumento considerevole della sensibilità. L'uso del primo richiede infatti che i passaggi consecutivi del generatore per ciascuna frequenza dell'intervallo esplorato avvengano con periodicità rigorosamente costante. All'aumentare di N si sommano gli effetti dovuti alle fluttuazioni di tale periodicità, il segnale si deforma e appare distribuito in un intervallo di frequenze maggiori di quello reale. Col secondo tipo di media la complicazione delle apparecchiature diviene proibitiva se N è elevato. Possiamo convenzionalmente dire che, con l'una o l'altra tecnica, le difficoltà da superare o il ‛prezzo' da pagare per ottenere un guadagno N nella sensibilità sono proporzionali a N². Conviene allora combinare le due tecniche mediando i risultati di N1² esperimenti consecutivi, ciascun esperimento essendo il risultato della media di N2² esperimenti contemporanei. Il guadagno ottenuto è N₁N₂ e sarà pagato un prezzo N1²+N2², mentre lo stesso guadagno sarà pagato, usando una sola tecnica, (N₁N₂)². Se è N₁=N₂=√-, il guadagno N sarà ottenuto al prezzo di 2N anziché di N² (v. fig. 38).

7. Applicazioni delle microonde.

a) Il radar.

Formata con le iniziali dell'espressione Radio Detection And Ranging, la parola radar è la denominazione più generale di sistemi che permettono di rivelare la presenza e di determinare la posizione e la velocità di oggetti mediante onde elettromagnetiche. Tentativi di determinare la distanza di un oggetto mediante il tempo intercorrente fra l'emissione di un segnale elettromagnetico e la ricezione della sua eco furono fatti non appena furono disponibili generatori di onde elettromagnetiche di potenza elevata. Nel 1925 Appleton riuscì a rivelare l'esistenza e a determinare l'altezza di diversi strati ionizzati nella ionosfera facendovi riflettere brevi impulsi di onde radio emessi in direzione verticale. Negli anni trenta fu evidenziato che potevano essere rivelati segnali elettromagnetici riflessi da navi o da aerei; in Inghilterra furono installate varie stazioni per il controllo del traffico aereo e marittimo e furono intensificati gli sforzi per ottenere con tali tecniche informazioni sempre più precise. In Italia, invece, ricerche del genere, condotte soprattutto dalla Marina Militare nei suoi laboratori presso l'Accademia Navale, furono sospese perché giudicate d'interesse ‛puramente accademico'.

Negli anni immediatamente precedenti e durante la seconda guerra mondiale l'impiego di generatori e ricevitori a microonde, perfezionati negli Stati Uniti e in Inghilterra, permise di realizzare dispositivi estremamente precisi che contribuirono largamente all'esito del conflitto. L'uso di microonde permette infatti di realizzare fasci molto direttivi e, quindi, di ottenere localizzazioni molto precise. Nel dopoguerra l'impiego del radar si estese dalle applicazioni militari a quelle civili ed è oggi largamente adottato nella navigazione marittima e aerea, nelle osservazioni meteorologiche, ecc. Tra i molti tipi di radar, illustreremo il funzionamento di quello più usato: il radar a impulsi.

Radar a impulsi. - Consideriamo un'antenna che irradi nella direzione z un impulso di onde elettromagnetiche di potenza P₀ e lunghezza d'onda λ. Sia G il guadagno dell'antenna, definito come il rapporto fra l'intensità del campo elettromagnetico in un punto P dell'asse z, a grande distanza dall'antenna, e l'intensità che si avrebbe nello stesso punto se la potenza P₀ fosse irradiata isotropicamente in tutto lo spazio. Le leggi della diffrazione danno

dove S è l'area della superficie emittente. La potenza intercettata da una superficie σ normale alla direzione z a distanza R dall'antenna risulta

Se tale superficie è un diffusore perfetto che diffonde la potenza ricevuta su tutto l'angolo solido 4π, la potenza dell'eco che torna all'antenna risulta

la (41) è l'‛equazione del radar' che ne determina la portata in funzione delle caratteristiche del sistema e della natura del bersaglio. Quest'ultimo, comunque, non è mai un diffusore isotropo e la potenza dell'eco dipende, oltre che dalla superficie dell'oggetto, anche dal materiale di cui è formato, dall'angolo di incidenza della radiazione, ecc. La ‛superficie apparente' σ viene determinata sperimentalmente per i diversi tipi di ostacoli che interessano e varia da una decina di m² per un piccolo aereo a 10.000 m² per una grande nave. Per λ=3 cm e S=1 m² si ha G=10⁴. Con P₀=10⁵ watt la distanza alla quale un piccolo aereo (σ=10 m²) produce un'eco della potenza 10^-11watt (rivelabile con un rapporto segnale/rumore migliore di 10²) risulta R=50 km. L'impulso è ricevuto dopo un tempo τ=330 μs dall'istante di emissione. La misura del ritardo e dell'ampiezza con cui è ricevuta l'eco fornisce l'informazione, oltre che della distanza, anche della natura del bersaglio. (Si veda lo schema dato nella fig. 39).

Un modulatore alimenta un oscillatore magnetron (o klystron di potenza elevata) con impulsi della durata di 0,5÷2 μs, che si susseguono alla cadenza di alcune centinaia di impulsi al secondo. Il modulatore è generalmente costituito da una linea di ritardo che viene caricata durante il tempo intercorrente fra un impulso e l'altro e successivamente scaricata sul primario di un trasformatore di impulsi, il cui secondario è connesso al catodo del magnetron. Durante il tempo di scarica della linea il magnetron emette un treno d'onde. L'energia è convogliata a un'antenna mediante una guida d'onda ed è quindi irradiata nello spazio.

Un'unica antenna è usata sia per la trasmissione sia per la ricezione dell'eco. Generalmente l'antenna che irradia l'impulso costituisce anche l'ingresso del ricevitore. Per questo è necessario che il ricevitore sia perfettamente isolato dalla linea durante la trasmissione dell'impulso, per non essere danneggiato dall'elevata potenza. Ciò si realizza mediante una giunzione che connette l'antenna al trasmettitore e al ricevitore e che contiene dei tubi a gas (TR e ATR) situati in tratti opportuni della guida.

In condizioni normali, cioè quando il magnetron non oscilla, uno dei tubi (ATR) rende infinita l'impedenza della linea del trasmettitore verso la giunzione, cosicché questa è isolata dall'antenna che risulta invece adattata al ricevitore. Durante la formazione dell'impulso il gas viene completamente ionizzato e costituisce un corto circuito che adatta l'antenna al circuito trasmettitore e isola invece il ricevitore dalla linea di trasmissione.

La potenza degli impulsi è compresa fra 10⁵ e 10⁷ watt, ma, poiché il tempo di funzionamento dell'oscillatore magnetron è una piccola frazione del tempo totale, la potenza media necessaria non supera qualche kW o decina di kW anche negli apparati più potenti. Il ricevitore è un ricevitore supereterodina molto sensibile. L'impulso di eco viene tradotto in segnale sullo schermo di un tubo a raggi catodici sul quale vengono fornite le informazioni.

b) Spettroscopia a microonde.

Cenni storici. - La spettroscopia può essere definita come lo studio dei possibili stati di energia nei quali può trovarsi un sistema microscopico e dei processi mediante i quali il sistema si porta da uno a un altro di tali stati scambiando energia col campo elettromagnetico. Nella regione hertziana dello spettro la maggior parte dei sistemi microscopici interagisce con il campo elettromagnetico. Lo studio di tali processi e della struttura degli stati energetici interessati costituisce la spettroscopia a radiofrequenza o hertziana, la cui nascita può essere fatta risalire agli anni seguenti la fine della seconda guerra mondiale. Già nel 1928 Gotrian segnalava l'interesse dello studio delle transizioni fra livelli atomici molto vicini, ad esempio della transizione 2P_3/2-2P_1/2 dell'atomo di idrogeno, che si prevedeva dovesse avvenire a circa 10 GHz. Tentativi per rivelare tale transizione furono fatti in Germania negli anni trenta, senza successo. La prima transizione a microonde fu osservata nel 1934 in gas di ammoniaca da Cleeton e Williams. Questi autori misero in evidenza la banda di inversione a 1,25 cm di lunghezza d'onda, usando come generatore un magnetron ad anodo sezionato, da essi stessi costruito.

Negli stessi anni (1936) fallirono i tentativi di Görter per rivelare la risonanza magnetica, che fu messa in evidenza per la prima volta nel 1938 da Rabi, negli Stati Uniti, applicando campi a radiofrequenza a fasci atomici, in dispositivi del tipo di quelli di Stern e Gerlach (v. atomo).

Dal 1945, da quando cioè le tecniche sviluppate per la realizzazione del radar furono a disposizione della ricerca fondamentale, la spettroscopia hertziana ebbe un rapido sviluppo. Tra il 1945 e il 1946 fu rivelata sperimentalmente la risonanza paramagnetica elettronica (REP) da Zavoisky, nell'Unione Sovietica, mentre negli Stati Uniti Purcell e Bloch, indipendentemente, scoprirono la risonanza magnetica nucleare (RMN) e Griffith in Inghilterra la risonanza ferromagnetica. Negli stessi anni in Inghilterra (Bleaney-Penrose) e negli Stati Uniti (Townes, Gordy, Strandberg) sorse la spettroscopia molecolare a microonde. Un ruolo particolare va assegnato ad alcune esperienze di quegli anni (l'esperienza di Lamb e Retherford sulla struttura fine dello spettro dell'idrogeno, la determinazione da parte di Kusch del momento magnetico anomalo dell'elettrone, la misura dell'intervallo di struttura fine del positronio da parte di Deutch) che permisero all'elettrodinamica quantistica di uscire dalla situazione di stasi nella quale si trovava da molti anni (v. atomo; v. quanti, teoria dei).

Nel 1950, ad opera di Kastler, Brossel e Bitter, furono introdotti i metodi ottici della spettroscopia hertziana, che permisero di studiare sistemi isolati con tecniche sensibili e relativamente semplici, che hanno portato a un prodigioso sviluppo delle nostre conoscenze sulla struttura degli atomi. L'invenzione del maser (1954) permise di ottenere radiazioni di eccezionale purezza spettrale, di grande interesse per la metrologia, e di amplificare la radiazione proveniente dal cosmo, di grande interesse per l'astrofisica. Alla fine degli anni cinquanta furono osservati, negli atomi orientati otticamente, nella risonanza magnetica e nella spettroscopia molecolare, fenomeni non lineari: processi che coinvolgono più di un fotone e che dettero origine alla spettroscopia non lineare, successivamente estesa, con la realizzazione del maser ottico o laser, al campo ottico e ai nuovi campi di ricerca dell'ottica e dell'elettronica quantistica (v. ottica quantistica).

La grande diversità dei sistemi e dei fenomeni studiati ha portato nella letteratura scientifica a una suddivisione della spettroscopia a radiofrequenza in diverse parti, che costituiscono ormai delle direzioni di ricerca a sé stanti. Generalmente la suddivisione è stabilita in base al criterio della natura dei livelli fra i quali avvengono le transizioni. Così la risonanza magnetica è lo studio delle transizioni fra i sottolivelli magnetici di uno stesso stato paramagnetico, la cui degenerazione è eliminata dall'applicazione di un campo esterno. A seconda poi che il paramagnetismo dello stato sia di origine elettronica o sia dovuto allo spin dei nuclei, si parla rispettivamente di risonanza paramagnetica elettronica (RES, RPE) o nucleare (RMN). Nei nuclei con spin I≥1, che possiedono un momento di quadrupolo elettrico, la degenerazione fra i sottolivelli nucleari può essere tolta dal gradiente del campo elettrico degli elettroni più vicini al nucleo, che interagiscono col momento di quadrupolo elettrico del nucleo stesso, quantizzandone l'orientazione rispetto a tale gradiente. Il fenomeno delle transizioni fra i sottolivelli magnetici del nucleo così separati costituisce la ‛risonanza quadrupolare pura' (RQM). Transizioni fra stati non degeneri di struttura fine o iperfine degli atomi sono pure ampiamente studiate.

Capitoli a parte sono costituiti dalla spettroscopia molecolare dei gas (nella quale le transizioni studiate sono quelle fra i livelli rotazionali, di inversione, ecc.), le risonanze di ciclotrone, i fenomeni di rilassamento dielettrico, ecc. Oltre al ruolo occupato nella ricerca fondamentale quale scienza a sé stante, la spettroscopia a radiofrequenza è diventata una tecnica ausiliare in molte altre parti della fisica: dalla fisica delle particelle elementari, cui fornisce ‛targhette' polarizzate, alla fisica dello stato solido, alla fisica nucleare, alla metrologia, alla radioastronomia e, infine, anche all'ingegneria, alla chimica, alla biofisica, ecc.

Caratteristiche della spettroscopia hertziana. - Nonostante la grande varietà dei sistemi (che vanno dai preparati biologici, ai solidi e ai liquidi, fino agli atomi praticamente isolati) e dei fenomeni studiati, alcune caratteristiche comuni si presentano in tutte le esperienze di spettroscopia a radiofrequenza e si riflettono nei metodi di indagine e di rivelazione.

1. Nei sistemi costituiti da molte particelle all'equilibrio termico, tale equilibrio è caratterizzato da una ripartizione pressoché uguale delle particelle negli stati interessati alle transizioni. Il fattore di Boltzmann, exp(−ΔE/kT), a temperatura ambiente differisce dall'unità per 1/10² nella regione delle frequenze più elevate e per 1/10⁹ nella regione delle frequenze più basse, cosicché il numero di transizioni indotte dalla radiazione nei due sensi è quasi lo stesso.

2. Nella regione delle basse frequenze la probabilità di emissione spontanea

(μ momento di dipolo della transizione; v. atomo) risulta molto piccola e conseguentemente la vita media τ dei livelli risulta molto grande. Per ν=10¹⁰ hertz e μ=10^-18 u.e.s. è

un tempo che praticamente diventa infinito a frequenze più basse e per transizioni di dipolo magnetico. Ne consegue che l'emissione spontanea è un fenomeno assolutamente trascurabile, rispetto all'assorbimento e all'emissione stimolata.

L'assenza del decadimento spontaneo implica quale conseguenza che, eccitando il sistema, l'energia fornita agli atomi non sarà riemessa sotto forma di radiazione elettromagnetica, ma sarà dissipata sotto forma di calore nel campione. Salvo eventualità molto particolari, non potremo cioè fare della spettroscopia in emissione ma, come già nel caso della regione infrarossa, unicamente una spettroscopia in assorbimento.

3. A causa della piccola differenza fra le popolazioni degli stati e della piccola energia associata alle transizioni, l'assorbimento risulta estremamente basso e, nonostante la grande sensibilità delle tecniche, per la rivelazione dei segnali sono necessari campioni contenenti un numero relativamente elevato di atomi, specialmente nei casi nei quali i tempi di rilassamento sono lunghi e quindi la potenza utilizzabile è piccola.

4. Nella regione delle radiofrequenze le sorgenti della radiazione sono costituite da oscillatori elettronici che producono radiazione altamente monocromatica e di densità spettrale molto elevata. Alla frequenza di 1 GHz, o di qualche decina di GHz, a qualche milliwatt di potenza elettromagnetica che si propaghi in una guida di 1 cm² di sezione è associato un flusso di fotoni pari a 10²⁰÷10²¹ fotoni al secondo, cui corrisponderebbe nella regione ottica una densità di potenza dell'ordine del kW/cm². Con densità così elevate è facile perturbare l'equilibrio termico del sistema e distruggere la ripartizione di Boltzmann; di qui nasce allora la necessità in molti casi di lavorare a livelli di potenza estremamente bassi.

Questa stessa caratteristica d'altra parte rende possibile provocare e studiare processi nei quali intervengono due o più quanti di energia elettromagnetica, in generale, cioè, quei processi caratteristici della non linearità del mezzo.

Da quanto sopra esposto possiamo suddividere i problemi sperimentali da risolvere nella spettroscopia a radio- frequenza in due classi: a) problemi nei quali il sistema studiato è composto da molte particelle interagenti e in cui l'assorbimento di energia elettromagnetica risulta rilevabile direttamente; b) problemi nei quali si studiano sistemi costituiti da poche particelle che non interagiscono fra loro, o interagiscono solo debolmente.

La prima classe di problemi comprende la maggior parte dei casi. Le tecniche impiegate sono quelle della spettroscopia in assorbimento, opportunamente adattate a questa regione particolare dello spettro. Sostanzialmente in tal caso si rivela il processo studiato attraverso la modificazione che esso produce sul campo elettromagnetico.

Nel secondo caso la perturbazione prodotta dall'interazione sul campo elettromagnetico non è assolutamente rilevabile. L'interazione però produce anche una perturbazione sul campione e la risonanza può essere studiata osservando per quale frequenza del campo qualche proprietà del campione viene modificata. Abragam ha denominato tali classi di tecniche rispettivamente ‛rivelazione per radiazione' e ‛rivelazione per materia'. I metodi di rivelazione per materia sono i soli utilizzabili nel caso di sistemi isolati, ma possono naturalmente essere usati anche nello studio di sistemi condensati. Salvo casi particolari, però, questi sono studiati con le tecniche proprie del primo tipo, già sinteticamente descritte nei capitoli sulla rivelazione dei segnali a microonde.

c) Orologi atomici e standard di frequenza.

‟Il tempo può essere definito come un parametro che compare nelle leggi della fisica". Adottando questa definizione di Townes, un orologio è un qualunque sistema che evolve secondo una di tali leggi. La distanza temporale fra due eventi può essere misurata determinando lo stato del sistema in coincidenza con l'uno e l'altro degli eventi. Affinché sia possibile fare la storia, è necessario che il sistema evolva secondo una legge periodica e che si possano contare con precisione i periodi. Per molto tempo il campione di tempo è stato fornito dal moto di rivoluzione della Terra attorno al proprio asse. A causa dei moti interni, però, come maree, venti, ecc., la Terra converte continuamente in calore parte della sua energia cinetica di rotazione. Il suo moto pertanto non è esattamente periodico, se confrontato ad esempio con quello di altri moti astronomici, e l'‛orologio Terra' rallenta. Dalla nascita di Cristo a oggi la Terra è in ritardo di 1/8 di giro rispetto a una Terra che avesse continuato a ruotare con velocità angolare rigorosamente costante. Ciò ha portato alla necessità di definire il secondo come una frazione di un particolare anno.

L'avvento della spettroscopia a microonde ha permesso di utilizzare per la misura del tempo i moti periodici estremamente regolari che avvengono all'interno di un sistema microscopico, atomo o molecola.

Il funzionamento di un orologio atomico è concettualmente assai semplice. La radiazione, di frequenza ν₀, generata da un oscillatore elettronico, è fatta interagire con un sistema di atomi o molecole che presentano una transizione alla stessa frequenza ν₀. Una variazione della frequenza dell'oscillatore si traduce in un segnale su un ricevitore, che è utilizzato per riportare l'oscillatore alla frequenza ν₀. Così i primi orologi atomici realizzati furono semplicemente spettrometri a microonde nei quali il segnale di risonanza veniva utilizzato per stabilizzare la frequenza del klystron, con tecniche analoghe a quelle usate per la stabilizzazione di frequenza mediante cavità risonanti. La stabilità della frequenza in un dispositivo di questo tipo dipende dall'intensità e dalla larghezza della riga di risonanza utilizzata. Per una riga ‛intensa' in un gas a bassa pressione essa è migliore di 10^-8, cioè la frequenza dell'oscillatore fluttua in modo aleatorio in un intervallo di ampiezza 10^-8 ν₀ attorno a ν₀. La frequenza ν₀ viene poi demoltiplicata con dispositivi elettronici e utilizzata per controllare la marcia di un orologio, con la stessa precisione percentuale.

L'impiego di fasci atomici e delle tecniche di pompaggio ottico ha permesso di utilizzare risonanze molto più strette e di migliorare il rapporto segnale/rumore, così che la precisione degli attuali orologi atomici è migliorata di diversi ordini di grandezza: per l'orologio al cesio si ha Δν/ν≅10^-13÷10^-14.

Nelle figg. 40 e 41 sono illustrati due orologi prodotti commercialmente, al rubidio e al cesio. Naturalmente la marcia di un orologio atomico non può essere confrontata che con quella di un altro orologio atomico, non esistendo altri orologi più precisi, e tale confronto implica l'uso di tecniche assai sofisticate. Si pensi che con precisioni di tali ordini di grandezze, due orologi siffatti scarterebbero l'uno rispetto all'altro di 1 secondo dopo un tempo di funzionamento di alcune cèntinaia di migliaia di anni.

Oltre a tali orologi ‛passivi', nei quali cioè si confronta la radiazione prodotta da un oscillatore elettronico con quella di una transizione atomica, vi sono i maser, orologi ‛attivi', che generano cioè direttamente radiazione di grande purezza spettrale. In tal caso si parla di ‛standard di frequenza'. Dei diversi tipi di maser, quello a idrogeno è oggi il più preciso (Δν/ν=10^-14). La transizione utilizzata è la transizione fra i due stati iperfini, F=1→F=0, dello stato fondamentale dell'idrogeno atomico, che occorre alla frequenza ν₀=1.420.405.751 Hz.

Le applicazioni di questi strumenti sono svariate, nel campo delle comunicazioni, della navigazione, dei collegamenti, della misura interferometrica a grandi distanze, della guida dei satelliti, ecc. Due orologi atomici usati quali campioni di frequenza possono fornire un oscillatore locale comune a ricevitori diversi posti a grande distanza e permettere precise misure geodetiche e astronomiche.

Nel campo della metrologia va considerato che l'orologio atomico è lo strumento più preciso che sia mai stato realizzato dall'uomo ed è prevedibile che il tempo o la frequenza saranno il fondamento di una metrologia per la misura di altre grandezze.

Nella ricerca fondamentale gli orologi atomici renderanno e hanno già reso possibili molte ‛espenenze ideali', per la verifica della teoria della relatività, della gravitazione, ecc.

Nel 1967 la precisione allora già raggiunta da questi dispositivi indusse il Comitato Internazionale Pesi e Misure a dare una nuova definizione dell'unità legale di tempo: il secondo, prima definito come la frazione 1/31.556.925,9747 dell'anno solare medio è oggi pari a 9.192.631.770 periodi della radiazione emessa nella transizione tra i due livelli iperfini F=4, m_F=0→F=3, m_F=0 dello stato fondamentale dell'atomo di ¹³⁷Cs.

Così lo sviluppo della spettroscopia a microonde ha portato a un curioso drastico cambiamento nella scelta dell'‛orologio naturale' e del ‛campione naturale' di tempo.

Il sistema solare, orologio naturale in unico esemplare, di dimensioni astronomiche, la cui marcia è perfettamente descritta dalle leggi della meccanica classica, è stato sostituito da un sistema quantomeccanico (l'atomo di ¹³⁷Cs), di dimensioni atomiche, reperibile in natura in un numero praticamente illimitato di esemplari identici. Il rapporto di ~10¹⁷ tra il vecchio e il nuovo campione di tempo è dello stesso ordine di grandezza del rapporto tra le dimensioni dei due sistemi.

bibliografia.

Argence, E., Kahan, Th., Théorie des guides et cavités électromagnétiques, Paris 1964.

Boudouris, G., Cavités électromagnétiques, Paris 1971.

Harvey, A. F., Microwave engineering, New York 1963.

Ingram, D. J. E., Spectroscopy at radio and microwave frequencies, London 1967.

Lawson, J. L., Uhlenbeck, G. E. (a cura di), Threshold signals, New York 1950.

Montgomery, C. G., Technique of microwave measurements, New York 1947.

Reintjes, J. F., Coate, G. T., Principles of radar, New York 1952.

Thorp, J. S., Masers and lasers, New York 1967.

Townes, C. H., Schawlow, A. L., Microwave spectroscopy, New York 1955.

Vuxlsteke, A. A., Elements of maser theory, New York 1960.