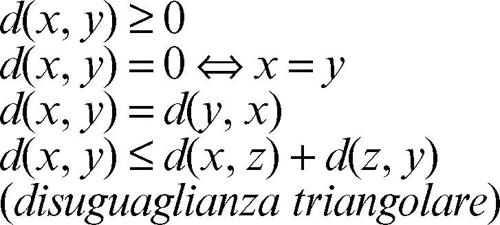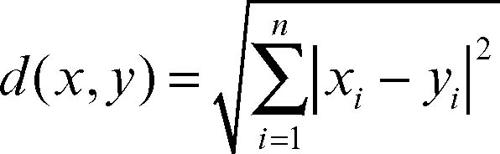metrica

metrica

metrica su un insieme X è così detta una funzione d: X × X → R tale che, comunque si prendano x, y, z ∈ X, si abbia:

Il numero reale non negativo d definito da una metrica e associato a una coppia di punti è detto distanza tra i due punti. L’insieme X con una metrica d costituisce uno spazio metrico.

Data una norma ‖...‖: X → R, resta definita una metrica d in X assumendo d(x, y) = ‖x − y‖, detta metrica indotta dalla norma. In uno stesso insieme X possono essere introdotte metriche diverse. Per esempio nell’insieme Rⁿ delle n-ple ordinate di numeri reali si possono introdurre la metrica euclidea

che definisce la distanza pitagorica, così detta perché consiste nell’applicazione n − 1 volte del teorema di Pitagora, o anche altre metriche, come per esempio la seguente:

che definisce la cosiddetta distanza del taxista perché, nel caso n = 2, è interpretabile come distanza percorsa da un taxi in una città il cui schema viario è a maglie rigorosamente rettangolari (a volte è detta anche geometria di Manhattan, data la struttura regolare delle vie di quel settore di New York). In termini astratti si può definire anche una metrica di tipo discreto, per esempio stabilendo che d(x, y) = 1 se x ≠ y e d(x, y) = 0 se x = y; si verifica che tale definizione soddisfa tutte le condizioni che caratterizzano una metrica.

Se X è uno spazio metrico, la sua metrica definisce per ogni suo elemento P e per ogni numero reale r > 0, l’insieme

detto disco (o palla) aperto di raggio r e centro P (se la disuguaglianza non è stretta si definisce un disco chiuso).

Due metriche d₁ e d₂ si dicono equivalenti se esistono due numeri reali positivi m e M tali che per ogni x e y di X risulti m ≤ d₁(x, y)/d₂(x, y) ≤ M. Questa relazione indica che ogni insieme aperto rispetto a una metrica è aperto anche rispetto all’altra e viceversa.