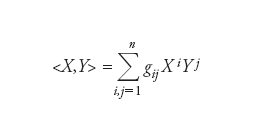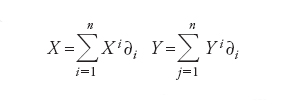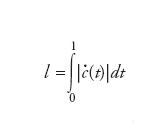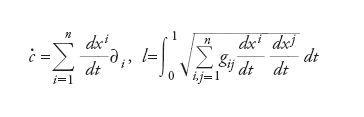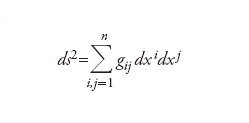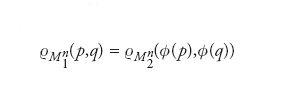metrica riemanniana
metrica riemanniana
Un tensore g di rango 2 definito su una varietà differenziabile n-dimensionale che sia covariante, simmetrico e definito positivo. In ogni spazio tangente TπMν nel punto p∈Mν il tensore g determina un prodotto scalare 〈∙,∙> definito dalla formula 〈X,Y>=g(X,Y) per X,Y∈TπMν. Viceversa se per ogni p∈Mν è definito un prodotto scalare sullo spazio vettoriale TπMν che dipende in maniera differenziabile dal punto p stesso, ciò definisce un campo tensoriale g con le proprietà precedenti. In coordinate locali xι (i=1,…,n), definite in un intorno U di Mν, che definiscono su TπMν (per p∈Mν) la base locale ∂ι (i=1,…,n), le componenti di g prendono la forma gιξ=〈∂ι,∂ξ> così che
dove
Se il prodotto scalare 〈∙,∙> non è definito positivo ma semplicemente non degenere (ovvero 〈X,Y>=0 per ogni Y∈TπMν implica X=0), oltre che covariante e simmetrico, la metrica è detta semiriemanniana. L’esistenza di una metrica riemanniana su una varietà Mν permette di definire una lunghezza l di una curva regolare c:[0,1]→Mν
dove c∙ indica il vettore tangente alla curva c(t). La lunghezza di una curva regolare a tratti è definita come somma delle lunghezze delle sue parti regolari. Se xι= xι(t) (con i=1,…,n) è l’equazione di c(t) in coordinate locali, allora
In analogia con la formula precedente, spesso la metrica su Mν è scritta nella forma
dove ds è detto elemento di lunghezza e le funzioni gιξ(x) sono le componenti del tensore g nelle coordinate locali scelte. La distanza ϱ(p,q) tra due punti p,q∈Mν è definita come la più piccola delle lunghezze delle curve regolari a tratti con estremi p,q. Con questa distanza la varietà Mν diviene uno spazio metrico. Due varietà riemanniane Mν1 e Mν2 si dicono isometriche se esiste un mappa ϕ:Mν1→Mν2 tale che
Una curva che minimizzi il funzionale l è detta geodetica e ogni curva di lunghezza minima tra due punti p,q∈Mν è tale. Viceversa, solo gedetiche di lunghezza sufficientemente piccola sono curve di lunghezza minima.
→ Geometria differenziale; Variazioni, calcolo delle