Viete, metodo di

Viete, metodo di

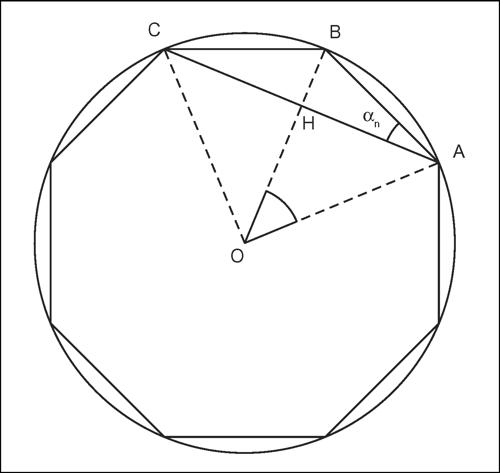
Viète, metodo di (per pi greco) metodo numerico per il calcolo approssimato di π, dovuto al matematico francese F. Viète. La procedura si basa sul considerare π come lunghezza della semicirconferenza di raggio unitario e sul costruire la successione dei semiperimetri di poligoni regolari a essa inscritti, con un numero sempre maggiore di lati. I poligoni regolari inscritti che si considerano sono quelli che hanno 2ⁿ lati (con n > 1): il quadrato, l’ottagono, il poligono regolare di 16 lati ecc. A ogni successiva iterazione della procedura, si esprimono le misure del poligono regolare di 2ⁿ lati a partire da quelle del poligono di 2ⁿ⁻¹ lati. Indicato con O il centro della circonferenza, si considerino tre vertici consecutivi, A, B e C di un poligono regolare inscritto di 2ⁿ lati (per esempio un ottagono) e si indichi con α_n l’angolo alla circonferenza formato dal lato AB e dalla diagonale AC. L’angolo alla circonferenza α_n = BÂC è metà dell’angolo al centro BÔC ed è un quarto dell’angolo al centro AÔC. Questa relazione si ripete per ogni poligono successivo.

Indicata con H l’intersezione della diagonale AC e del raggio OB e con x_n la lunghezza del lato AB del poligono regolare di 2ⁿ lati, AH risulta essere la metà del lato del poligono di 2ⁿ⁻¹ lati e α_n = 180°/2ⁿ (per esempio, per un ottagono, n = 3 e α₃ = 180°/8); inoltre AH = AB cosα_n. Quindi: x_n = x_n−1/(2cosα_n), da cui moltiplicando per 2ⁿ si ottiene:

e, quindi, si può scrivere

dove p_n indica il semiperimetro del poligono di n lati. Il limite della successione dei semiperimetri per n tendente all’infinito è π (lunghezza della semicirconferenza di raggio unitario):

Sapendo che α_n = α_n−1/2, si applica la formula di bisezione per il → coseno, ottenendo:

A ogni iterazione è così possibile calcolare il semiperimetro del poligono a partire dai valori (del semiperimetro e del coseno dell’angolo alla circonferenza) del poligono “precedente”.

Per costruire un algoritmo per il calcolo approssimato di π seguendo il metodo di Viète, si consideri inizialmente n = 2: il poligono in questo caso è un quadrato, il suo semiperimetro p₂ è 2√(2), l’angolo α₂ ha ampiezza di 45° e cosα₂ = √(2/2). La procedura è così formalizzabile (i è un contatore inizialmente posto uguale a 3 e che si incrementa fino a n; la variabile informatica p contiene i successivi valori del semiperimetro, mentre c contiene cosα_i):

L’algoritmo permette di scrivere una successione di valori del semiperimetro; all’aumentare di n, fornisce un’approssimazione sempre più accurata di π. Si può dimostrare che l’errore analitico commesso con questo metodo, ossia la quantità e_n = |π − p_n| alla n-esima iterazione è circa un quarto di quello commesso dall’iterazione precedente e_n ≅ e_n−1/4.

L’algoritmo così costruito risulta molto più stabile (→ algoritmo, stabilità di un) rispetto a quello costruito con altri metodi, per esempio con il metodo di → Archimede.