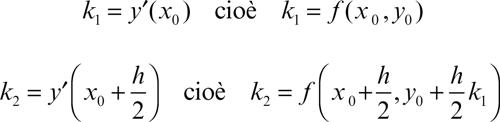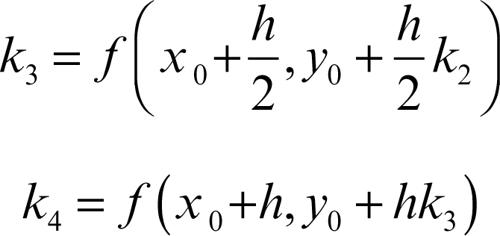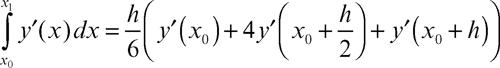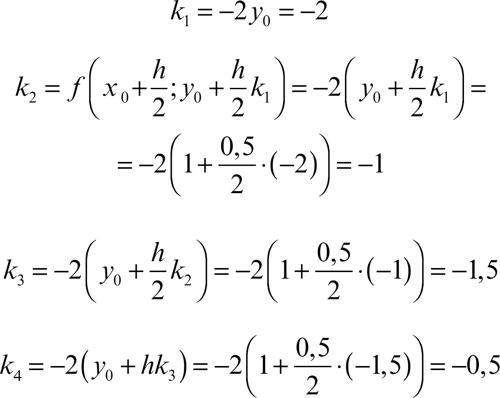Runge-Kutta, metodo di

Runge-Kutta, metodo di

Runge-Kutta, metodo di locuzione che indica una famiglia di metodi numerici per la risoluzione di equazioni differenziali i quali, per la stima dell’integrale soluzione dell’equazione, usano il metodo di quadratura noto come metodo di → Cavalieri-Simpson. Tutti i metodi di Runge-Kutta che risolvono numericamente il problema di → Cauchy y' = ƒ(x, y) con la condizione iniziale y' (x₀) = y₀ possono essere ricondotti alla formula generale:

dove Φ(x_i, y_i, h) è detta funzione incremento. In Φ compaiono i valori della pendenza della curva integrale calcolati in punti diversi e indicati con k₁, k₂, ..., k_i; h è il passo dell’integrazione. Il valore di k₁ = ƒ(x_i, y_i) viene usato per il calcolo di k₂ in un punto intermedio tra x_i e x_i+1; k₁ e k₂ si utilizzano per calcolare k₃ e così via con iterazioni successive. A seconda del tipo di funzione incremento che si usa (ossia di quanti valori di k si utilizzano), si ha un metodo di Runge-Kutta di ordine differente. Nel metodo di Runge-Kutta del primo ordine la funzione incremento si scrive Φ = ƒ(x_i, y_i) e il metodo si riduce in pratica al metodo di → Eulero. All’aumentare dell’ordine del metodo, aumenta la precisione dell’approssimazione, ma anche la complessità del calcolo. Il metodo più usato è del quarto ordine, perché non richiede calcoli troppo complicati e dà risultati molto precisi. Per determinare il valore y₁ a partire dalle condizioni iniziali y' (x₀) = y₀, si approssima la pendenza della curva integrale nei punti di rispettiva ascissa

Il metodo richiede il calcolo di quattro valori di k:

e analogamente:

Si osservi che nel calcolo di k_i compare il valore precedente k_i−1. Per integrare la y' (x₀) tra x₀ e x_i, si utilizza il metodo di Cavalieri-Simpson:

Si assume poi come stima del termine centrale la media tra i valori di k₂ e di k₃:

L’approssimazione di y₁ risulta quindi:

Successivamente, dall’approssimazione così ottenuta di y₁ si può ricavare y₂, da questa y₃, e così via. Si consideri per esempio l’equazione differenziale y′ = −2y, con condizione iniziale y(0) = y₀ = 1. Si vuole stimare il valore y(1), utilizzando il metodo di Runge-Kutta di ordine 4, con un passo di integrazione h = 0,5. Dopo il primo passo di integrazione si ottiene la stima per y(0,5):

dove

Ripetendo il procedimento con il valore

si ottiene l’approssimazione desiderata:

Confrontando il risultato ottenuto con il valore della funzione y = e^−2x, che è l’esatta curva integrale dell’equazione differenziale data, y ≅ 0,135335, si ottiene un errore assoluto pari a 0,00529 e un errore relativo pari al 3,9%: un risultato apprezzabile, considerato che è stato ottenuto con due soli passi di integrazione. Diminuendo il passo di integrazione, per esempio ponendo h = 0,1, con calcoli analoghi a quelli precedentemente effettuati, si può verificare che gli errori relativi diminuiscono sino a un valore dello 0,005%.