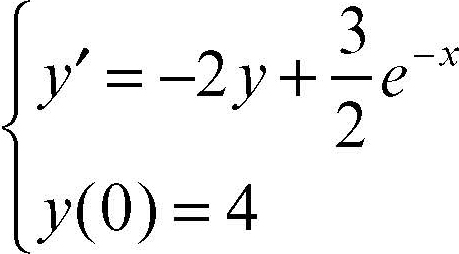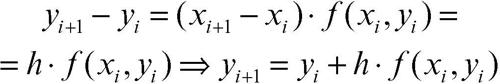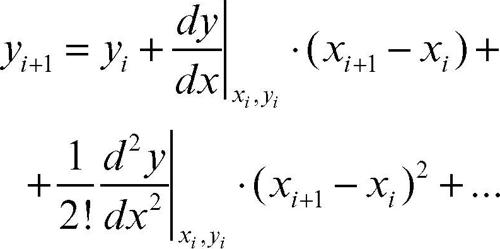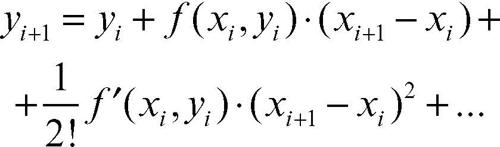Eulero, metodo di
Eulero, metodo di
Eulero, metodo di (per la risoluzione di una equazione differenziale) procedimento numerico per la ricerca della soluzione approssimata di una equazione differenziale. In particolare, il metodo di Eulero si applica alle equazioni differenziali del tipo
con y = y(x) definita nell’intervallo [a, b], con la condizione iniziale y(x0) = y0. Per esempio, un’equazione differenziale quale
con y(0) = 4, si può scrivere nella forma
In questo caso
Se si considera una partizione di [a, b] in n sottointervalli, presi per semplicità tutti di uguale lunghezza
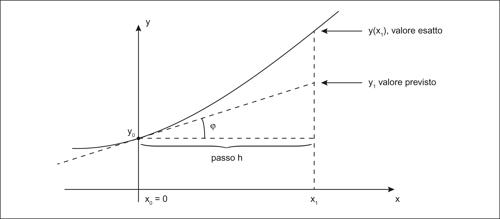
detto passo di integrazione, ciascuno di estremi {x0, x1, …, xn} con xi+1 − xi = h, i = 0, ..., n − 1, x0 = a e xn = b, da cui xi = x0 + ih, il metodo di Eulero consiste nella previsione del valore della funzione y(x) attraverso la sostituzione con la retta passante per i due estremi dell’intervallo (per questo motivo è anche chiamato metodo della pendenza puntuale). Esistono diverse varianti del metodo: il metodo di Eulero in avanti presuppone la seguente approssimazione in ciascun sottointervallo:
per i = 0, ..., n −1, da cui
In tal modo si ottiene esplicitamente il valore approssimato yi+1 di y(xi+1) calcolato nell’estremo superiore dell’intervallo considerato. Per il primo sottointervallo di estremi [x0, x1] la (2) si scrive:
Per il secondo intervallo vale l’analoga equazione:
Ricavando dalla prima equazione y1 e sostituendo nella seconda, si ricava y2; sostituendo nella terza si ricava y3 e così via. Ricorsivamente si ottiene quindi l’espressione finale:
Il metodo di Eulero è uno dei metodi numerici a passo singolo (single-step), perché genera la soluzione approssimata dell’equazione differenziale a ogni passo, usando incrementi finiti nell’intervallo d’integrazione: alla fine produce un insieme discreto di valori approssimati della funzione, rappresentante la soluzione dell’equazione differenziale nell’intervallo considerato.
L’altra variante del metodo di Eulero, detta metodo di Eulero all’indietro, è un metodo implicito nel quale la soluzione approssimata è ottenuta, a ogni passo, estrapolando il valore lungo la retta tangente, la cui pendenza è ottenuta usando il valore della funzione ƒ(x, y) nel punto non ancora calcolato, e non già nel punto calcolato precedentemente come accade nel metodo in avanti. In altre parole, si ottiene la formula
Poiché nella maggior parte dei casi l’equazione ottenuta può essere non lineare, la sua soluzione generalmente richiede ulteriori metodi iterativi. Ne consegue l’importanza di stimare l’errore nella risoluzione delle equazioni differenziali. Tale operazione dipende dal metodo numerico usato e dall’ordine dell’equazione differenziale. Nel caso in questione, l’errore che si commette usando il metodo di Eulero si ricava dai primi due termini dello sviluppo di → Taylor della funzione y(x) nel punto di ascissa xi :
per cui operando la sostituzione derivata dalla (1) nel secondo termine dello sviluppo si ottiene:
Ne segue:
Si deduce che, troncando lo sviluppo al termine di primo grado in h, l’errore che si commette nell’approssimazione di y(x) con il metodo di Eulero è dell’ordine di h2.
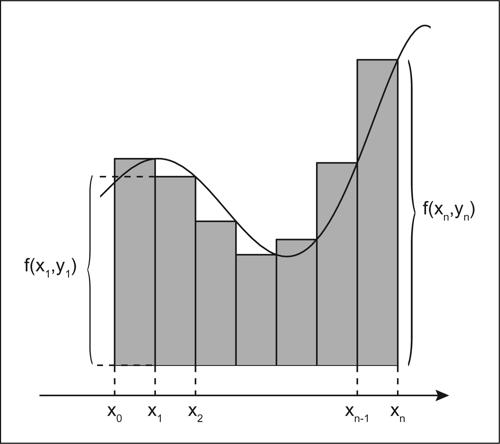
Si può interpretare geometricamente la soluzione data dalla (3) come l’approssimazione di una funzione integrale ottenuta attraverso il metodo dei rettangoli (→ integrazione numerica). Infatti, come è mostrato in figura, il valore yn è uguale all’area totale dei rettangoli di base h e altezza rispettivamente uguale a ƒ(xi, yi), a meno della costante additiva y0. Si dimostra che anche nel metodo di integrazione numerica dei rettangoli l’errore commesso nella stima dell’area è proporzionale al quadrato del passo d’integrazione.