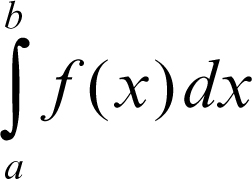Cavalieri-Simpson, metodo di
Cavalieri-Simpson, metodo di
Cavalieri-Simpson, metodo di metodo numerico di approssimazione (→ Cavalieri Simpson, approssimazione di) dell’integrale definito
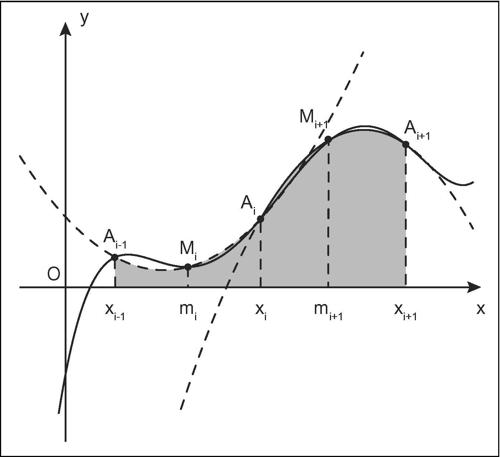
di una funzione ƒ(x) continua in un intervallo [a, b] dell’asse reale. Tale metodo consiste nel suddividere l’intervallo di integrazione in sottointervalli uguali e nell’approssimare l’andamento della funzione in ciascun sottointervallo con opportuni segmenti parabolici. Il risultato finale si ottiene sommando le aree che ciascun segmento parabolico forma con l’asse delle ascisse. Oltre al calcolo diretto di un integrale definito, il metodo può essere applicato anche per risolvere numericamente equazioni differenziali scritte in forma di differenze finite, come avviene nel metodo di → Runge-Kutta.