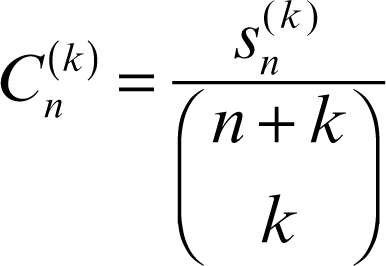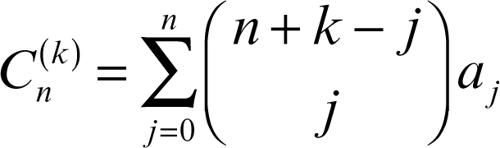sommazione, metodi di
sommazione, metodi di
sommazione, metodi di metodi volti a estendere la definizione di somma di una → serie numerica, allo scopo di assegnare un valore anche a serie che non risultano convergenti in senso classico. Ciò non viene fatto a puro scopo di generalità, ma in vista di importanti applicazioni. È essenziale che un nuovo metodo di sommazione M soddisfi il principio di permanenza: una serie convergente in senso classico a S deve ammettere con il nuovo metodo la stessa somma S. Si dice in tal caso che la serie è sommabile M a S e si scrive
Naturalmente il nuovo metodo deve assegnare una somma ad almeno una serie non convergente in senso classico. I più importanti di questi metodi sono dovuti ad Abel, a Hölder e a Cesàro. Nel metodo di Abel alla serie
si assegna la somma S se la funzione
ammette limite finito S per x → 1− in cui il segno meno a esponente indica un limite “da sinistra”, cioè per intervalli che hanno sempre 1 come estremo destro. Il teorema di → Abel garantisce la permanenza. Per esempio, la serie di → Grandi
è oscillante; essa corrisponde alla serie geometrica
che ha per somma ƒ(x) = 1/(1 + x). Risulta dunque
cioè la serie data converge secondo Abel al valore 1/2.
Il metodo di Cesàro e il metodo di Hölder hanno infiniti ordini di iterazione. Nel primo essi coincidono, e consistono nel considerare le medie aritmetiche delle somme parziali
Se queste medie ammettono limite S per n → ∞ si dice che la serie
è sommabile secondo Cesàro o secondo Hölder al valore S, e si scrive
Per esempio, le somme parziali della serie
valgono alternativamente 1 e 0; perciò la loro media tende a 1/2 per n → ∞. Dunque è anche
Il metodo di Hölder può essere iterato costruendo le medie delle medie,
e in generale
Se tali medie generalizzate convergono si dice che la serie data è sommabile secondo Hölder di ordine k e si scrive
Si dimostra che se una serie è H(k−1)-sommabile è anche Hk-sommabile con la stessa somma. Anche il metodo di Cesàro può essere iterato, costruendo, a partire dalle somme parziali
le somme delle somme
e in generale
si considerano poi i numeri
Se esiste il limite S di Cn(k) per n → ∞, la serie si dice sommabile secondo Cesàro all’ordine k. A differenza del metodo di Hölder è agevole dare un’espressione analitica ai termini Cn(k), risultando
Si dimostra che se una serie è C(k−1)-sommabile è anche Ck-sommabile con la stessa somma. I due metodi in realtà hanno esattamente la stessa potenza, nel senso che se una serie è Hk-sommabile è anche Ck-sommabile con la stessa somma e viceversa. Per esempio, la serie 1 − 2 + 3 − 4 + 5 − … è sommabile C2 al valore 1/4. Si dimostra pure che se una serie è Ck-sommabile, sia i suoi termini an sia le somme parziali sn sono o(nk) (si veda → o piccolo). Viceversa, se
è Ck-sommabile e an = O(1/n) (si veda → O grande), la serie è sommabile in senso classico. Analogamente, se una serie è sommabile secondo Abel e i suoi termini sono an = O(1/n), la serie è sommabile in senso classico.
Importanti applicazioni del metodo di Cesàro sono il teorema di Fejér sulle serie di Fourier (→ Fejér, integrale di) e il teorema sul prodotto di serie: infatti il prodotto secondo Cauchy di due serie A e B non è necessariamente convergente, ma lo è sempre (e al valore AB) se sommato in senso C1. In generale, se A è sommabile Ck e B è sommabile Cj il loro prodotto è sommabile Ck+j+1.
I metodi di Hölder e di Cesàro sono tuttavia meno potenti del metodo di Abel, che implica la Ck-sommabilità per ogni k, ma non viceversa.
Si deve notare che alcune proprietà delle serie si possono perdere adottando una definizione generalizzata di somma. Per esempio, non è lecito inserire degli addendi uguali a zero. In particolare, se nella serie di Grandi 1 − 1 + 1 − 1 + … si inserisce uno zero dopo ciascun termine positivo si ha 1 + 0 − 1 + 1 + 0 − 1 + …, che corrisponde alla serie di potenze
e quindi la nuova serie è A-sommabile al valore 2/3. Mettendo gli zeri dopo i termini negativi si ottiene la somma 1/3, e in generale si può ottenere qualsiasi somma compresa tra 0 e 1 con un opportuno inserimento di zeri.