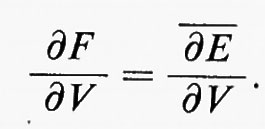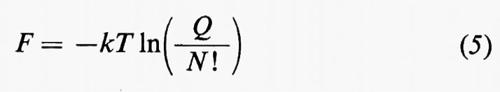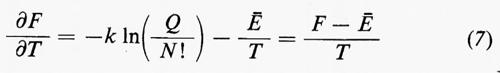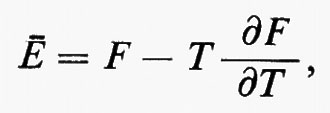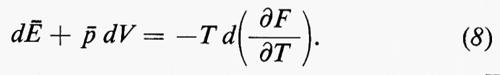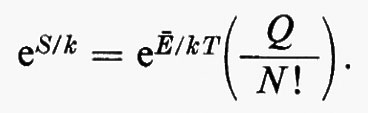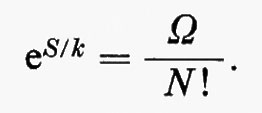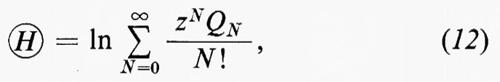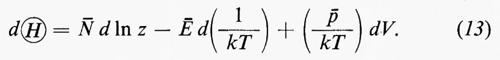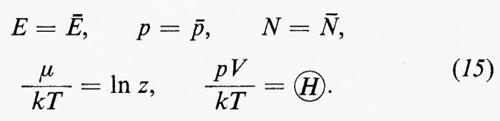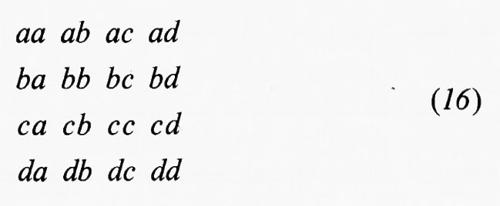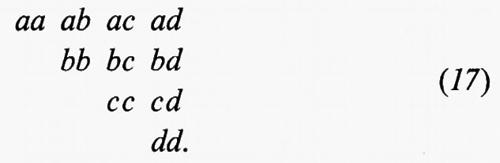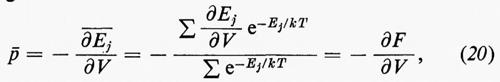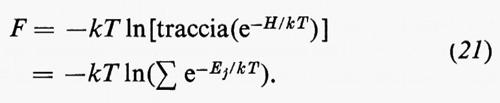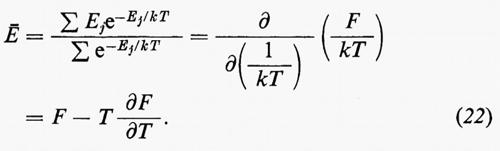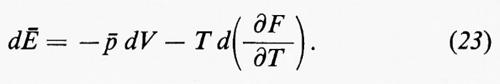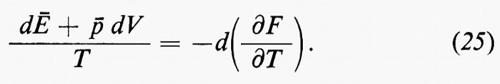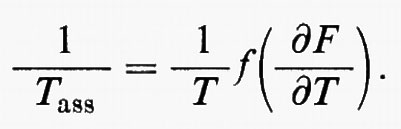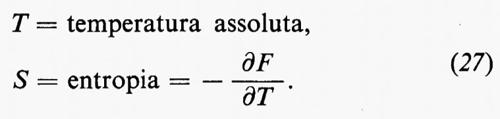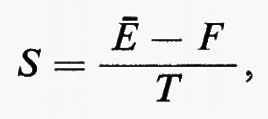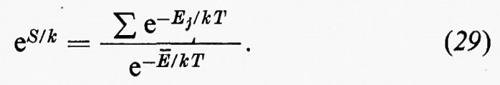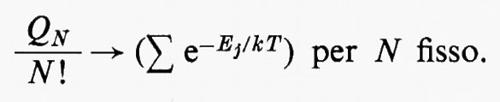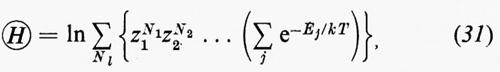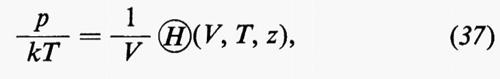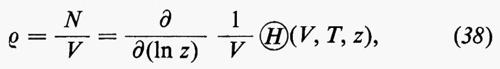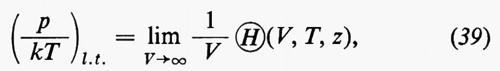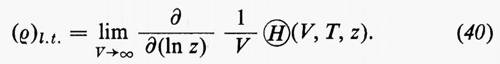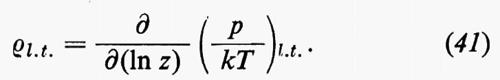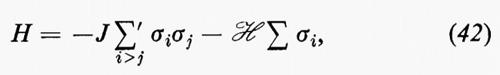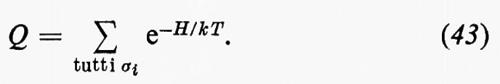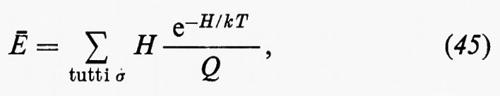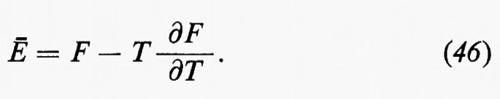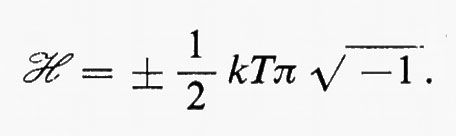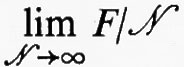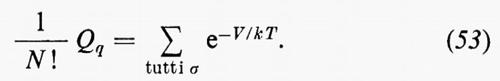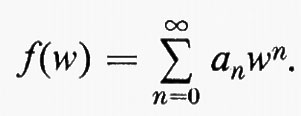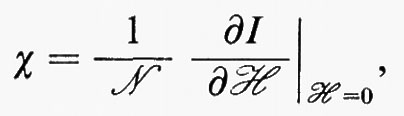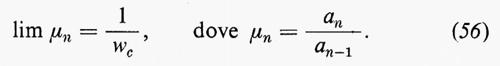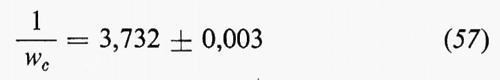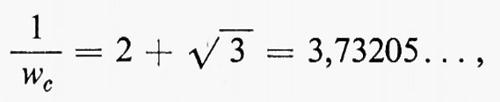Meccanica statistica

Meccanica statistica

di Chen Ning Yang

SOMMARIO: 1. Introduzione. □ 2. La meccanica statistica prima della meccanica quantica: a) storia; b) la formulazione di Gibbs; c) rapporto con la formula dell'entropia di Boltzmann; d) insieme macrocanonico; e) validità della formulazione di Gibbs. □ 3. Meccanica statistica quantica: a) statistica di Bose-Einstein; b) statistica di Fermi-Dirac; c) sviluppi ulteriori; d) meccanica statistica quantica; e) insieme macrocanonico nella meccanica statistica; f) miscela di vari tipi di atomi e molecole; g) applicazione della meccanica statistica quantica dell'equilibrio; h) limite di validità della meccanica statistica quantica. □ 4. Teoria delle transizioni di fase: a) storia; b) meccanica statistica dell'equilibrio e transizioni di fase; c) modello di Ising e gas a reticolo; d) determinazione numerica delle proprietà al punto critico; e) esponenti critici. □ 5. Transizioni di fase quantiche. □ Bibliografia.

1. Introduzione.

La meccanica statistica è quel ramo della fisica che si occupa del fondamento statistico, dal punto di vista molecolare, delle leggi fisiche che riguardano corpi macroscopici. Essa costituisce il punto d'incontro tra la fisica microscopica (cioè quella degli atomi, delle molecole e dei nuclei) e la fisica macroscopica (ossia la termodinamica, l'idrodinamica, la fisica dello stato solido, la fisica dei plasmi, ecc.) e, per grandi linee, si suddivide in meccanica statistica dell'equilibrio e meccanica statistica del non equilibrio. Quest'ultima si occupa di fenomeni che avvengono in condizioni di non equilibrio, in particolare dei processi irreversibili; essa è trattata in altre voci di questa enciclopedia (v. termodinamica irreversibile e sinergetica; v. fluidi, dinamica dei; v. criofisica; v. plasmi in fisica).

In questo articolo ci proponiamo di esaminare lo sviluppo storico delle idee più importanti della meccanica statistica dell'equilibrio verificatosi negli ultimi 75 anni, tralasciando però le applicazioni a sistemi specifici, che costituiscono invece l'oggetto della fisica chimica, della fisica dello stato solido, della criofisica, della fisica dei plasmi e di altri campi ancora.

Tale storia, sulla quale ci tratterremo più diffusamente nei capp. 2 e 3, può essere così brevemente riassunta: prima del 1901, teoria cinetica dei gas, relazione di Boltzmann tra entropia e probabilità; 1901, formulazione di Gibbs della meccanica statistica classica; 1924, statistica di Bose-Einstein; 1926, statistica di Fermi-Dirac e meccanica statistica quantica. Dopo il 1926 la meccanica statistica fu applicata con grande successo in vari settori della fisica, in particolare ai gas e alle soluzioni diluite, alla teoria delle transizioni di fase e alla teoria delle transizioni di fase quantiche. Questi ultimi due tipi di applicazioni saranno trattati nei capp. 4 e 5, mentre tralasceremo quelle del primo tipo.

2. La meccanica statistica prima della meccanica quantica.

a) Storia.

La fondazione dell'elettromagnetismo e quella della termodinamica statistica costituirono gli eventi più importanti della fisica del secolo scorso. La termodinamica nacque dallo studio delle proprietà termiche della materia; intorno al 1860, dopo un lungo lavoro che aveva condotto a precisare idee già note da molto tempo, sia pure solo intuitivamente, si era giunti a una chiara formulazione delle due leggi fondamentali: cioè quella della conservazione dell'energia e quella dell'aumento continuo dell'entropia di un sistema isolato. Il termine entropia fu introdotto nel 1865 da Clausius con la seguente giustificazione: ‟Per grandezze come queste, di grande importanza per la scienza, è meglio scegliere nomi tratti dalle lingue antiche in modo da renderne possibile l'introduzione, senza cambiamento, in tutte le lingue moderne; io propongo di chiamare la grandezza S ‛entropia' del corpo, seguendo la parola greca ἐντροπή, che significa trasformazione. Ho formato intenzionalmente la parola entropia in modo da renderla il più possibile simile a energia, proprio perché le due quantità che verranno designate con questi nomi sono così strettamente legate dal punto di vista del loro significato fisico da renderne vantaggiosa una somiglianza nei nomi" (W. F. Magie, A source book in physics, Cambridge, Mass., 1969, p. 234).

Parallelamente allo sviluppo della termodinamica, veniva studiata la teoria cinetica dei gas, il cui scopo è quello di fornire un modello molecolare per i gas. Di particolare importanza per questi studi fu l'introduzione di metodi statistici, sfruttati da Maxwell e in seguito da Boltzmann, il quale, negli anni successivi al 1870, si rese conto che essi avrebbero potuto essere utilizzati per fornire una base alla termodinamica. I lavori di Boltzmann in quel periodo contribuirono alla nascita della meccanica statistica. In particolare, si deve a lui la profonda intuizione della relazione che lega l'entropia S di un sistema in equilibrio termico alla probabilità W dello stato di equilibrio, che, nella terminologia moderna, viene espressa nel modo seguente:

S=k ln W, (1)

in cui k=1,38•10^-16 erg/°C è detta ‛costante di Boltzmann'.

Ugualmente a Boltzmann si deve l'altra importante idea contenuta nel suo famoso teorema H, che ebbe un ruolo di grande rilevanza in tutti i successivi sviluppi della termodinamica irreversibile (v. termodinamica irreversibile e sinergetica).

Sebbene Maxwell e Boltzmann siano stati i fondatori della meccanica statistica, i successivi sviluppi in questo campo furono però più direttamente influenzati dalla formulazione che della meccanica statistica dell'equilibrio dette Gibbs, il quale, nella sua opera Elementary principles in statistical mechanics, developed with special reference to the rational foundation of thermodynamics, del 1901, introdusse l'importante concetto di ‛insieme canonico' per un sistema termodinamico in equilibrio a temperatura T.

b) La formulazione di Gibbs.

Per un sistema dinamico di N particelle identiche (quale ad esempio un gas reale in un dato volume V) aventi coordinate q₁, q₂, ..., q_N e quantità di moto, o momenti, p₁, p₂, ...., p_N. Gibbs definì insieme canonico con parametro T l'insieme degli stati del sistema aventi varie assegnazioni dei valori q_i e p_j e funzione di distribuzione

e^-E/kT dτ, (2)

dove dτ = dq₁ dq₂ ... dq_N dp₁ dp₂ ... dp_N è il cosiddetto ‛elemento di volume dello spazio delle fasi' ed E rappresenta l'energia del sistema. Ogni stato è uno stato del gas nel volume V. La media calcolata sull'insieme di una qualunque grandezza fisica A che dipenda da q₁, q₂, ..., p_N è uguale ad:

À=Q^-1 ∫ Ae^-E/kT dτ, (3)

dove si ponga:

Q=∫ e^-E/kT dτ. (4)

Se si definisce:

e si considera F come funzione di T e del volume V del sistema, diviene facile calcolare ∂F/∂T e ∂F/∂V. Si ottiene:

Poiché −∂Ε/∂V è la pressione del sistema, −-∂-E-/-∂-V rappresenta la pressione media, ä, e sarà:

Si ha inoltre:

oppure

per cui è:

T^-1 è dunque un fattore integrante per dÄ+ä dV.

Secondo Gibbs, il fondamento razionale della termodinamica consiste nell'identificazione di Ä e ä con l'energia e la pressione di equilibrio del sistema. Dal momento che T^-1 è un fattore integrante per dE+ä dV, T si deve identificare con la temperatura assoluta e per l'entropia S deve aversi:

La combinazione delle equazioni (9) e (6) mostra che:

dF=−S dT−ä dV, (10)

da cui si deduce che F rappresenta l'energia libera.

c) Rapporto con la formula dell'entropia di Boltzmann.

Dalle equazioni (7) e (9) si deduce che S=(Ä−F)/T; per cui, facendo uso della (5), si ottiene:

Se si definisce ora il volume medio Ω dello spazio delle fasi mediante la seguente relazione:

Q=Ωe-^Ä/kT,

si ottiene

Confrontando quest'ultima relazione con l'equazione (1) di Boltzmann si vede che è:

o, in altri termini, che la probabilità di Boltzmann è proporzionale al volume medio di spazio delle fasi Ω.

d) Insieme macrocanonico.

Gibbs introdusse anche il concetto, che fu largamente utilizzato in seguito, d'insieme macrocanonico (che egli chiamava ‟grand ensemble" o macroinsieme), con il quale s'intende un insieme d'insiemi canonici con valori diversi di N, ma con il medesimo valore di T e di V. Il peso dei sistemi con N particelle è dato da Q_Nz^N/N!, dove z è un parametro e Q_N è l'espressione di Q definita dalla (4) per un sistema di N particelle. È semplice calcolare le medie Ò, ä ed Ä su tutto l'insieme macrocanonico; definendo una funzione ???51??? con la formula:

si trova facilmente che:

Partendo dalla relazione termodinamica

dF=−S dT−p dV+μdN,

si può arrivare alla seguente relazione:

Un confronto tra le relazioni (13) e (14) suggerisce che il fondamento razionale della termodinamica consiste nelle seguenti identificazioni:

e) Validità della formulazione di Gibbs.

Oggi si sa che Gibbs raggiunse lo scopo che si era proposto nel suo lavoro, in quanto l'espressione (5) per l'energia libera F di un sistema termodinamico in funzione di un integrale Q eseguito sullo spazio delle fasi (dato dall'espressione 4) costituisce effettivamente il fondamento razionale della termodinamica. Le imperfezioni della sua formulazione non erano dovute alle considerazioni statistiche, quanto piuttosto alla meccanica newtoniana che all'epoca del lavoro di Gibbs non era in grado di spiegare la fisica atomica e rendeva quindi talmente difficile comprendere l'intera portata delle leggi della natura da non permettere ai fisici di verificare sperimentalmente la fondatezza della formulazione di Gibbs. È stato recentemente detto che ‟se si dovesse riassumere in un'unica conclusione quanto è avvenuto in questo campo negli ultimi settant'anni, si dovrebbe dire che la base statistica della meccanica ha trionfato brillantemente" (v. Domb e Green, 1972, vol. I, p. 1).

A questo proposito, è importante ricordare che lo stesso Gibbs non aveva, né avrebbe potuto avere, una visione così positiva del suo lavoro, quale l'abbiamo noi oggi. Quando nel 1901 egli pubblicò i suoi Elementary principles of statistical mechanics, il mondo della fisica stava vivendo, per una parte, le grandi scoperte sperimentali, quali quella dell'elettrone, della radioattività e dei raggi X, che portarono all'era della fisica atomica, cioè microscopica, per l'altra, le forti contraddizioni inerenti alla fisica classica quando viene applicata all'atomo. Nella prefazione del suo libro Gibbs scrisse, per esempio: ‟Allo stato attuale della scienza, non sembra quasi possibile formulare una teoria dinamica dell'azione molecolare in grado di abbracciare i fenomeni della termodinamica, della radiazione e dell'elettricità, che accompagnano le unioni di atomi; eppure, qualunque teoria che non dia conto di tutti questi fenomeni è senza dubbio inadeguata. Pur se ci limitiamo ai soli fenomeni della termodinamica, non riusciamo a sfuggire alle difficoltà neppure nel caso di problemi semplici, quale quello del numero dei gradi di libertà di un gas diatomico. E ben noto che, mentre la teoria assegnerebbe al gas sei gradi di libertà per molecola, i nostri esperimenti sul calore specifico danno un valore pari a cinque. Sicuramente, chi basa il suo lavoro su ipotesi circa la costituzione della materia costruisce su fondamenta poco sicure".

È veramente sorprendente che, pur ‟costruendo su fondamenta poco sicure", Gibbs sia potuto arrivare a un simile ‛fondamento razionale della termodinamica'. Forse, i fisici oggi impegnati ad affrontare le grandi complessità della fisica delle particelle elementari potrebbero trovare motivo di coraggio proprio riflettendo sulle difficoltà passate che hanno caratterizzato la storia della fisica. (Si veda Ch. N. Yang, Introductory note in Phase transitions and critical phenomena, a cura di C. Domb e M. S. Green, New York 1972).

Particolarmente importante nel libro di Gibbs era anche il tipo di ragionamento matematico, la cui eleganza, combinata con la profondità delle argomentazioni fisiche, fu probabilmente alla base della grande ammirazione che Einstein nutriva per Gibbs.

3. Meccanica statistica quantica.

a) Statistica di Bose-Einstein.

Il fattore N! nell'equazione (5) fu introdotto da Gibbs per arrivare a un'espressione estensiva per F, tale cioè che, per T fisso, raddoppiando contemporaneamente N e V, raddoppiasse anche F. Questo problema, trattato nell'ultimo capitolo del libro, divenne noto come ‛paradosso di Gibbs': benché l'introduzione del fattore N! rendesse effettivamente la F della (5) una grandena estensiva, la ragione dell'introduzione del fattore non fu però considerata soddisfacente e fu oggetto di lunghe argomentazioni negli anni successivi.

La costante di Planck h, naturalmente, era già stata introdotta all'inizio del secolo e apparve presto che per motivi dimensionali il fattore N! della (5) e della (11) andava moltiplicato per h^3N; doveva cioè aversi:

Seguirono tentativi di discutere la termodinamica di un gas di quanti non interagenti per arrivare alla legge della radiazione di Planck; essi, tuttavia, non ebbero mai alcun successo.

Il metodo corretto fu trovato nel 1924 da Bose, il quale fece l'importante constatazione che non bisognava partire da quanti tra loro distinguibili, distribuirli nello spazio delle fasi, calcolare Q e dividere poi il risultato per N!, come nella (5) e nella (11); ma che bisognava invece partire da quanti non distinguibili e distribuirli nello spazio delle fasi, tralasciando la divisione per N!. Per esempio, se si distribuiscono 2 quanti in quattro celle nello spazio delle fasi, chiamate a, b, c, d (in questo esempio si suppone che competa a tutte la stessa energia), il vecchio calcolo comporterebbe la somma delle sedici possibilità:

e poi la divisione per 2!=2. Il calcolo di Bose, invece, richiede soltanto la somma di 10 possibilità o stati:

È chiaro che questi procedimenti forniscono gli stessi contributi per i 6 stati non degeneri ab, ac, ecc., cioè per gli stati in cui i due quanti non occupano la stessa cella; ma per gli stati degeneri aa, bb, cc e dd il calcolo di Bose dà un peso 1 a ciascuno di essi, invece del peso 1/2 del vecchio metodo. Tale metodo per il calcolo degli stati portò a quella che fu detta la statistica di Bose-Einstein.

b) Statistica di Fermi-Dirac.

Negli anni tra il 1923 e il 1925 si ebbero altri sviluppi molto importanti nella fisica statistica, primo fra i quali la formulazione del principio di esclusione di Pauli. Con i suoi studi sulla costante assoluta dell'entropia - problema strettamente collegato al paradosso di Gibbs (si veda The collected papers of Enrico Fermi, Chicago 1965, vol. I, pp. 30 e 31) - Fermi fu tra coloro che maggiormente contribuirono a tali sviluppi e all'inizio del 1926 egli mostrò che la termodinamica di un gas di particelle monoatomiche che soddisfi il principio di esclusione è molto diversa da quella che si ottiene mediante i calcoli usuali. Il punto essenziale di tale scoperta può essere illustrato ricorrendo ancora all'esempio usato nel precedente paragrafo, in cui si considerano 2 particelle distribuite su quattro celle a, b, c, d nello spazio delle fasi; se esse soddisfano il principio di esclusione, il calcolo di Fermi implica allora 6 stati possibili e precisamente:

cioè i medesimi stati dati dalla statistica di Bose-Einstein, con l'esclusione di quelli per i quali la medesima cella è occupata da più d'una particella. Questo metodo introdotto da Fermi per il calcolo degli stati portò in seguito alla cosiddetta statistica di Fermi-Dirac.

c) Sviluppi ulteriori.

Di enorme importanza sono entrambe le statistiche di Bose-Einstein e di Fermi-Dirac. Einstein, il quale si rese immediatamente conto dell'importanza della prima, ne continuò le ricerche e a sua volta influenzò Schrödinger nella scoperta della meccanica ondulatoria (M. Klein, Einstein and the wave particle duality in The natural philosopher, Waltham, Mass., 1964, vol. III, p. 3). Inoltre, Einstein, applicando la statistica di Bose-Einstein a un sistema gassoso in cui il numero totale di particelle non varia con il tempo, arrivò all'ardita conclusione che sarebbe dovuto esistere un fenomeno di condensazione, noto come condensazione di Bose-Einstein, che in seguito risultò essere alla base della spiegazione dei fenomeni della superfluidità e della superconduttività (v. cap. 5).

La statistica di Fermi-Dirac, per altro verso, condusse all'idea assai importante di gas ‛degenere' di elettroni, limitato nello spazio dei momenti da una superficie chiamata ora ‛superficie di Fermi'. Questa terminologia può purtroppo generare confusione perché, a differenza di quanto avviene nella statistica di Bose-Einstein, in questo caso il termine degenerazione non sta a significare che più particelle occupano il medesimo stato (il che è vietato dal principio di esclusione), ma indica invece una situazione in cui il principio di esclusione svolge un ruolo dominante. Il concetto di gas degenere di elettroni si pose ben presto alla base della fisica dei metalli e questo tipo di degenerazione acquistò in seguito anche un'importanza fondamentale per la comprensione della fisica della materia in condizioni di alte densità, quali ad esempio si hanno all'interno di stelle nane bianche.

d) Meccanica statistica quantica.

Nel 1926 Dirac dimostrò che le statistiche di Bose-Einstein e di Fermi-Dirac derivavano dalla simmetria e dall'antisimmetria delle funzioni d'onda che descrivono un sistema quantomeccanico. Divenne così possibile formulare la meccanica statistica quantica qual è alla base della concezione attuale del fondamento microscopico della termodinamica. Ne riassumeremo ora brevemente i concetti essenziali.

Consideriamo un sistema quantomeccanico, quale un insieme di atomi contenuti in un volume V descritto dall'hamiltoniana H(p_i, q_i), in cui p_i, q_i (i=1 ...) indicano i momenti e le coordinate canoniche del sistema; domandiamoci quali ne siano le proprietà macroscopiche alla temperatura assoluta T. È importante tenere presente che, quando si specifica la temperatura di un sistema, s'intende che quest'ultimo è immerso in un bagno termostatico che scambia energia a caso con il sistema attraverso un meccanismo di accoppiamento debole e che quindi il sistema stesso non ha un'energia fissa. Dimostreremo ora che, statisticamente, il sistema si comporta come un insieme incoerente (cioè come una collezione indipendente e non interferente) di tutti gli autostati ψ_j di H, con una probabilità relativa per lo stato ψ_j uguale a

cost e-^Ej/kT, (19)

dove E_j rappresenta l'autovalore di H per ψ_j. Consideriamo soltanto gli stati ψ_j che obbediscono alla statistica appropriata (di Bose-Einstein o di Fermi-Dirac). La dimostrazione è del tutto simile a quella che è stata data sopra (v. cap. 2, È b) per il caso della meccanica classica. Per cominciare, si noti che la pressione p del sistema nello stato E_j è uguale a

dal che discende che la pressione media su tutto l'insieme è uguale a

dove:

La traccia qui è definita prendendo soltanto quelle autofunzioni di H che obbediscono alla statistica appropriata (Bose-Finstein o Fermi-Dirac). L'energia mediata sull'insieme è:

Le equazioni (20) e (22) permettono un calcolo esplicito di dÄ che dà:

Quindi, per l'insieme, il differenziale

dÄ+ä dV (24)

ha un fattore integrante 1/T che dà:

Prima di poter identificare il fattore integrante 1/T con l'inverso della temperatura assoluta, occorre fare un'ulteriore considerazione che, pur essendo stata tralasciata per brevità, era necessaria anche per la meccanica statistica classica riassunta sopra (v. sopra, cap. 2, È b). Due insiemi descritti dalla distribuzione di probabilità (19) per diversi parametri T e T′, presi insieme, formano un insieme più grande se e soltanto se T=T′; quindi, se s'identifica l'insieme in modo che descriva statisticamente un sistema a una data temperatura, T deve essere identificato con una funzione della temperatura empirica, quindi della temperatura assoluta T_ass.

Secondo la termodinamica, identificando le proprietà medie dell'insieme con le proprietà termodinamiche di equilibrio si ha che:

Confrontando l'espressione (25) con la (26) si vede che

Ma T/T_ass è funzione soltanto di T_ass. Poiché ∂F/∂T e T_ass sono variabili indipendenti, si conclude che la f è una costante e che T è proporzionale alla temperatura assoluta T_ass. Se nell'espressione (19) si sceglie k in modo che coincida con la costante di Boltzmann, la costante di proporzionalità diventa uguale a 1 e l'espressione (25) mostra quindi che:

Si è così dimostrato che l'insieme descrive statisticamente il sistema alla temperatura assoluta T. Le espressioni (22), (25) e (27) mostrano che:

dF=−S dT−ä dV, (28)

il che permette di identificare F con l'energia libera. Dalle espressioni (22) e (27) si ha inoltre che

da cui si ottiene:

In altri termini si ha che e^S/k è pari al numero effettivo di termini che compaiono nella somma Σ e-^Ej/kT e si ha quindi un'interpretazione quantomeccanica della formula (1) di Boltzmann, dove:

W=numero effettivo di termini nella somma e-^Ej/kT. (30)

e) Insieme macrocanonico nella meccanica statistica.

La considerazione fatta sopra (v. sopra, cap. 2, È d) per la meccanica statistica classica può essere applicata anche in questo caso con la seguente semplice sostituzione:

f) Miscela di vari tipi di atomi e molecole.

La generalizzazione è immediata; invece dell'espressione (12) si ha ora la seguente:

dove N₁, N₂, ... sono i numeri delle diverse specie di particelle ed E_j è l'autovalore dell'hamiltoniana del sistema in un volume V con N₁, N₂, ... particelle di ciascuna specie. Si considerano qui soltanto quelle autofunzioni (e quegli autovalori) che obbediscono alla statistica appropriata per le varie particelle.

Un caso particolare importante è quello dei fotoni, perché per questi ultimi, quando interagiscono con la materia, l'hamiltoniana non commuta con il numero dei fotoni, il che, in altri termini, significa che il numero dei fotoni non è una costante del moto. L'espressione (31) può quindi essere utilizzata soltanto se si tiene presente che in N₁, N₂, ... non è compreso il numero di fotoni; mentre E_j comprende la loro energia e la loro interazione con la materia. Tutto ciò si può formulare in maniera equivalente dicendo che per il fotone

z_fotone=1. (32)

Una situazione simile si ha anche in un sistema a temperatura molto alta quando diventano importanti gli effetti di creazione di coppie, per esempio di elettroni e positroni. In un problema di questo tipo, N_- ed N₊, ossia i numeri di elettroni e di positroni, non si conservano separatamente, si conserva invece

N_c=N₊−N_-,

per cui occorre introdurre un fattore z⁽c^Nc) nell'espressione (31) per il sistema elettrone-positrone. Il termine Σ_j deve allora comprendere tutti gli stati con N_c fisso, ma con numeri arbitrari di coppie. L'espressione (31) si può anche riformulare in questo caso mantenendo sia z⁽+^N+) che z⁽_^N-), ma ponendo

z₊=(z_-)^-1=z_c. (33)

g) Applicazione della meccanica statistica quantica dell'equilibrio.

L'applicazione della meccanica statistica quantica alle molecole biatomiche, come ad esempio H₂, ha permesso di spiegare i problemi relativi al calore specifico alle basse temperature che erano apparsi particolarmente difficili da risolvere ai fisici del secolo scorso (v. sopra, cap. 2, È e) e ha fornito analoghi successi anche in altri campi della termodinamica e della chimica dei gas diluiti (v. Fowler e Guggenheim, 1939).

Per quanto fondamentalmente soddisfacente e benché si ritenga in genere che essa descriva accuratamente tutti i fenomeni di equilibrio (v. solidi, fisica dei; v. criofisica) l'applicazione della statistica quantomeccanica ai liquidi, ai solidi e ai gas densi non è priva di difficoltà, dal momento che il calcolo dell'energia libera (21) per un liquido o un solido con, per esempio, 10²³ gradi di libertà, presenta delle difficoltà matematiche enormi. Ci occuperemo più avanti di alcuni tra i progressi che si sono compiuti in questo campo.

h) Limite di validità della meccanica statistica quantica.

Fino a oggi non si conoscono casi in cui la meccanica statistica dell'equilibrio, quando è applicabile, conduca a risultati errati. Di recente sono state avanzate ipotesi su eventuali limiti superiori della temperatura assoluta T, oltre i quali il possibile instaurarsi rapidissimo di nuovi gradi di libertà ne renderebbe impossibile un ulteriore aumento (v. Hagedorn, 1968). Queste ipotesi non sono per ora nulla più che semplici speculazioni non fondate né su prove sperimentali, né su concezioni teoriche generalmente accettate, anche se fino a oggi non sono ancora incorse in difficoltà logiche.

4. Teoria delle transizioni di fase.

a) Storia.

Cercheremo ora di vedere se la meccanica statistica sia in grado di fornire una base solida per la spiegazione delle transizioni di fase che, sia dal punto di vista sperimentale sia da quello teorico, costituiscono uno degli aspetti più importanti della termodinamica. Prima del 1937 questo problema era affrontato in vari modi, tutti assai approssimativi, che rientravano in una classe di teorie oggi note con il nome di ‛teorie di campo medio'. L'idea su cui si basavano deriva dalla teoria del ferromagnetismo di Weiss (v. Weiss, 1907), nella quale l'influenza degli altri atomi su di un dato atomo è sostituita da un campo locale medio H_l. Dato un campo locale medio H_l, la meccanica statistica permette di calcolare l'orientazione media e quindi il momento magnetico atomico m del singolo atomo e di arrivare pertanto alla seguente espressione:

m=f(H_l). (34)

Weiss dimostrò che, se si attribuisce a ogni atomo un momento magnetico medio m, il campo locale medio H_l è determinato da m, ossia è:

H_l=g(m). (35)

Weiss euristicamente suppose che g fosse una funzione lineare ed è questa ipotesi che caratterizza la teoria che porta il suo nome.

L'importanza della teoria di Weiss consiste nella sua stretta relazione con concetti come quello di costante dielettrica e di suscettività magnetica. Negli ultimi settan- t'anni sono state formulate, per numerosi problemi fisici, altre teorie di campo medio che rappresentano delle variazioni delle idee fondamentali della teoria di Weiss. In tutte viene introdotto un campo medio a partire dal quale si calcola la risposta del sistema locale con i metodi della meccanica statistica, come nell'espressione (34).

Nella prima parte, queste considerazioni sono quindi esattamente uguali, nello spirito, alla teoria di Weiss, ma esse impiegano procedimenti diversi per arrivare alla generalizzazione dell'espressione (35) e conducono quindi a teorie diverse.

Sebbene assai utili, le teorie di campo medio si basano fin dall'inizio su concetti approssimati e sono quindi poco adatte a fornire il fondamento per un'analisi più precisa. Un nuovo indirizzo fu tentato da Mayer (v., 1937) il quale per primo sistematicizzò il calcolo dei coefficienti del viriale dei gas diluiti nella meccanica statistica classica (per l'effetto della meccanica quantica si veda più sotto il cap. 5). In base a tale sistematicizzazione, egli tentò di discutere le transizioni gas-liquido senza introdurre campi medi e, quando al Congresso per il centenario di Van der Waals, il 26 novembre 1937, ad Amsterdam, si discusse il lavoro di Mayer, nacque ‟una vivace discussione sull'esattezza della spiegazione che Mayer aveva dato dei fenomeni della condensazione. Furono espressi dubbi su questo punto in quanto era difficile comprendere come un metodo approssimato come quello di Mayer potesse, partendo dallo stato gassoso, arrivare alla discontinuità della densità presente su una curva isotermica in corrispondenza del punto di condensazione. Mentre i metodi usuali con cui si tratta l'equilibrio di due fasi introducono l'equazione di stato di ambedue le fasi e deducono la condizione per la loro coesistenza, la teoria di Mayer non fa nulla di tutto questo ma tratta tutte le possibili configurazioni molecolari con il loro peso appropriato come se fossero una sola fase. Come possono le molecole ‛sapere' quando debbono coagularsi per formare un liquido o un solido? Il metodo matematico di Mayer è troppo complicato per permettere di chiarire completamente questo punto" (v. Born e Fuchs, 1938, p. 391).

Il problema essenziale è in realtà se l'energia libera F data sopra nelle equazioni (5) o (21) descriva sia la fase liquida che quella gassosa e, in caso affermativo, come possa comparire nell'energia libera una discontinuità, dal momento che alla transizione di fase qualche grandezza termodinamica o qualche sua derivata deve diventare discontinua.

Come fu dimostrato già poco dopo il Congresso Van der Waals (v. Kahn e Uhlenbeck, 1938), la risposta al primo problema è affermativa e più tardi ambedue i problemi ricevettero una risposta formulata in termini rigorosi (v. Van Hove, 1949; v. Yang e Lee, 1952). Le idee e le conclusioni principali su questo problema saranno tracciate più avanti nel cap. 4, È b.

Mentre questi risultati dimostrarono che la meccanica statistica è in grado di spiegare le transizioni di fase, essa tuttavia non riusciva a chiarire quale ne fosse l'intima natura. Dal punto di vista teorico questo è un problema assai difficile perché occorre conoscere il comportamento matematico preciso dell'energia libera (5) o (21) per un liquido o per un solido. Per lungo tempo la discussione su questo problema e su quello dei fenomeni critici fu dominata dalle prime idee euristiche che classificavano le transizioni di fase in transizioni di primo ordine, di secondo ordine, ecc. (v. Ehrenfest, 1933; v. Landau e Lifschitz, 1958). Tali idee erano assai largamente accettate per vari motivi e precisamente: a) per mancanza di prove sperimentali che dimostrassero il contrario; b) per l'utilità empirica della teoria di Van der Waals; c) per coerenza con le teorie di campo medio, assai seducenti dal punto di vista fisico; d) per l'esistenza di fasi metastabili, come il vapore supersaturo, che suggerivano una continuità delle funzioni termodinamiche in queste fasi.

La prima, e fino a oggi ancora la più importante, soluzione teorica esatta di un modello di transizione di fase la si deve a Onsager (v., 1944), il quale risolse la termodinamica del ‛modello di Ising' per un problema d'interazione spin-spin in un reticolo bidimensionale (v. sotto, cap. 4, È c). Egli trovò che il calore specifico vicino alla temperatura di transizione T_c diverge proporzionalmente alla funzione

ln ∣T−T_c∣ (36)

Prima degli studi di Onsager non si conosceva, né dal punto di vista teorico né da quello sperimentale, un comportamento divergente di questo tipo dei calori specifici. Benché la soluzione di Onsager sia stata in seguito molto perfezionata ed estesa (v. McCoy e Wu, 1973) e benché siano stati esattamente risolti altri problemi di transizioni di fase in reticoli bidimensionali (v. Lieb e Wu, 1972), a tutt'oggi non si è tuttavia ancora potuta dare una soluzione esatta di alcun problema tridimensionale non banale in meccanica statistica.

Nel 1951 Tisza suggeri che il calore specifico dell'He liquido potrebbe divenire infinito al punto di transizione λ ed esperimenti compiuti nel 1955 mostrarono che ciò è in effetti possibile (v. Atkins e Edwards, 1955). Poco più tardi, nel 1957, Fairbank, Buckingham e Kellers, con un bellissimo esperimento in cui riuscirono a misurare il calore specifico dell'⁴He con una risoluzione di temperatura del milionesimo di grado, stabilirono oltre ogni possibilità di dubbio che il calore specifico diverge effettivamente e si comporta secondo l'espressione (36) riportata sopra, dove T_c è uguale alla temperatura di transizione T_λ (v. fig. 1).

La transizione λ è una transizione quantomeccanica speciale (v. sotto, cap. 5; v. criofisica) diversa dalle transizioni magnetiche e da quelle liquido-gas e fu perciò assai interessante trovare, nelle transizioni di questo ultimo tipo (v. fig. 2), delle divergenze logaritmiche dei calori specifici nelle vicinanze dei punti critici (v. Robinson e Friedberg, 1960; v. Bagatskii e altri, 1962).

Dal 1960 in poi, a seguito di queste scoperte, sono state compiute moltissime ricerche sia teoriche che sperimentali di cui riassumeremo qui soltanto i punti fondamentali.

1. Sia nelle transizioni liquido-gas, sia in quelle magnetiche le grandezze termodinamiche nelle vicinanze dei punti critici sono rappresentabili mediante potenze di grandezze quali ∣T−T_c∣, il campo magnetico e ∣ρ−ρ_c∣, dove ρ rappresenta la densità.

Gli esponenti di tali potenze, generalmente non interi, vengono detti ‛esponenti critici'; in questo contesto ln ∣T−T_c∣ viene considerato come ∣T−T_c∣⁰ (v. sotto, cap. 4, È e).

2. Dal punto di vista teorico è stato sviluppato un modello di ‛gas a reticolo', matematicamente equivalente al modello semplice del magnetismo, cioè al ‛modello di Ising', il quale, a sua volta, è legato a più complicati modelli di magnetismo, quali, per esempio, il ‛modello di Heisenberg'. Tali modelli presentano fenomeni critici caratterizzati da esponenti critici α, α′, β, γ, γ′, δ, ν, ecc., i quali, data la relazione matematica intercorrente tra il modello del gas a reticolo e quello di Ising, consentono una discussione unificata.

3. È stato sviluppato un metodo numerico approssimato basato su uno sviluppo in serie (v. Domb, 1949) che permette di ottenere risultati molto attendibili per i parametri e gli esponenti critici. L'applicazione frequente di questo metodo a molti casi ha fatto pensare che gli esponenti critici dei modelli siano uguali per tutti i reticoli di diversi tipi (quali quelli a corpo centrato, a facce centrate, cubico, ecc.) per dimensioni assegnate.

4. Si è inoltre trovato che gli esponenti critici determinati sperimentalmente per varie transizioni, sia liquido-gas sia magnetiche, sono sorprendentemente uguali fra loro e inoltre che esse sono generalmente uguali a quelle ottenute per modelli teorici a tre dimensioni. Ciò induce a pensare che il modello di gas a reticolo si adatti molto bene a spiegare i fenomeni della fisica delle transizioni liquido-gas.

5. Le disuguaglianze termodinamiche necessarie per la stabilità termodinamica portano a molte disuguaglianze tra gli esponenti critici (v. Rushbrooke, 1963; v. Fisher, 1964; v. Griffith, 1965), le quali, oltre a presentare interesse teorico, sono interessanti anche dal punto di vista sperimentale, in quanto permettono di determinare gli esponenti critici.

6. Nel 1965 Widom propose un metodo basato su una legge di scala (v. Widom, 1965) che si rivelò poi molto utile nell'analisi sia teorica che sperimentale delle transizioni di fase.

7. Recentemente Wilson ha proposto l'introduzione dei concetti di gruppo di rinormalizzazione per la discussione dei fenomeni critici e questo campo è, al momento attuale, oggetto di molte ricerche.

8. Dal 1960 in poi si è venuta sempre più estendendo la simulazione, mediante elaboratori elettronici, di sistemi dinamici in equilibrio e tendenti all'equilibrio ed è probabile che, con l'aumentare della velocità e della capacità di memoria degli elaboratori, gli studi di questo tipo contribuiranno ancora in maniera considerevole a spiegare la meccanica statistica delle transizioni di fase.

La nostra attuale concezione delle transizioni liquido-gas e di quelle magnetiche si può quindi riassumere dicendo che la meccanica statistica quantica dell'equilibrio fornisce effettivamente una descrizione esatta di tutte le fasi e del punto di transizione. Nelle vicinanze del punto critico, si è trovato sperimentalmente che le funzioni termodinamiche assumono la forma dileggi di potenza i cui esponenti sono detti esponenti critici. Sebbene non si sia ancora riusciti a risolvere esattamente alcun problema di transizione in tre dimensioni (neppure in casi ideali), sono stati tuttavia trovati dei metodi approssimati abbastanza sicuri per il calcolo degli esponenti critici, con i quali si ottengono risultati che concordano assai bene con quelli sperimentali. Tale accordo sembra così confermare l'idea intuitiva secondo cui l'aspetto essenziale delle transizioni liquido-gas è contenuto nel modello di gas a reticolo e vi è una notevole somiglianza tra le transizioni liquido-gas e quelle magnetiche, così da permettere di studiarle entrambe in una maniera unificata.

b) Meccanica statistica dell'equillbrio e transizioni di fase.

Per un sistema con un numero N finito di particelle in un volume finito V, l'energia libera F data dall'equazione (21) è una funzione analitica di T e di V. Sorge allora il problema di come essa possa descrivere più di una fase e, a maggior ragione, le transizioni che avvengono tra le fasi stesse. Questo era in sostanza il problema alla base delle discussioni del Congresso del Centenario di Van der Waals del 1937, cui si è accennato nel cap. 4, È a. Il punto essenziale della risposta, peraltro assai semplice, a tale problema è che si deve prima passare al ‛limite termodinamico', che è definito come il limite per N→∞ e V→∞, con ρ=N/V determinato; ne risulta che è più facile trattare con l'insieme macrocanonico il cui limite termodinamico è V→∞, per un valore fisso della fugacità z, quale è stata definita nelle equazioni (12) e (15).

Passando ora a delineare lo sviluppo della meccanica statistica classica, consideriamo un insieme macrocanonico di atomi in un recipiente di volume V. Secondo l'equazione (15) si ha:

dove ???51??? è dato dall'equazione (12).

Il limite termodinamico (l.t.) in questo caso è il limite V→∞, per T e z fissi, cioè:

È stato dimostrato che, sotto condizioni molto generali per le interazioni tra gli atomi: 1) tali limiti termodinamici esistono; 2) il limite (p/kT)_l.t. è una funzione continua monotona crescente di ln z con la possibile eccezione di punti singolari ln z₁, ln z₂, ..., tra i quali (p/kT)_l.t. è analitico in ln z. Tra i punti singolari nell'equazione (40) il passaggio al limite è intercambiabile con la derivata, di modo che si ha:

La fig. 3 illustra tali risultati e mostra che nei punti A e B avvengono transizioni di fase.

Tali risultati sono stati estesi alla meccanica statistica quantica; inoltre, le condizioni che devono essere soddisfatte dalle interazioni atomiche - prima ancora di dimostrare l'esistenza di un limite termodinamico - sono state via via indebolite in vari modi (v. Rouelle, 1969). Tuttavia, nessuna di queste estensioni riesce a coprire un caso molto importante, ossia quello di una collezione di nuclei e di elettroni in interazione coulombiana. Tale interazione ha un raggio d'azione (relativamente) lungo e richiede una trattazione particolare. Anzi, è stato dimostrato (v. Dyson, 1967) che, se tanto i nuclei quanto gli elettroni obbediscono alla statistica di Bose-Einstein, il sistema non ha limite termodinamico e ciò perché in tal caso sarebbe possibile costruire una funzione d'onda con un alto grado di correlazione nuclei-elettrone. In realtà, gli elettroni obbediscono alla statistica di Fermi-Dirac, secondo la quale due elettroni non possono occupare la stessa posizione (v. sopra, cap. 3, È b), e si è dimostrato che tale impedimento al raggrupparsi di tutti i nuclei e di tutti gli elettroni in un piccolo volume è sufficiente per portare all'esistenza di un limite termodinamico (v. Dyson e Lenard, 1967; v. Lieb e Lebowitz, 1972).

Di recente, prendendo le mosse da alcune importanti idee contenute in precedenti lavori (v. Peierls, 1936; v. Mermin e Wagner, 1966), si son fatti notevoli progressi nello studio di un problema strettamente collegato a questo, relativo all'esistenza di una transizione di fase per interazioni atomiche specifiche.

c) Modello di Ising e gas a reticolo.

Il modello di Ising è un modello di magnetismo consistente in un reticolo di spins con momento magnetico. La configurazione in un punto i è descritta da una variabile σ_i=±1, con σ_i=1 o −1 a seconda che lo spin nel punto i sia rivolto verso l'alto o verso il basso. I momenti magnetici interagiscono fra di loro ed eventualmente anche con un campo magnetico esterno ℋ. La versione più comunemente studiata del modello di Ising ha come hamiltoniana la

dove la prima sommatoria Σ′ è estesa a tutte le coppie degli spins più vicini nel reticolo e rappresenta un'energia +J per ogni coppia di spins antiparalleli e −J per ogni coppia di spins paralleli. Il caso in cui sia J>0 rappresenta quindi un modello in cui gli spins paralleli sono energeticamente preferiti a quelli antiparalleli per gli stati più vicini, come avviene nel caso di un reticolo con interazioni ferromagnetiche. Similmente, J〈0 rappresenta il caso di un modello con interazioni antiferromagnetiche. La seconda sommatoria che appare nell'equazione (42) rappresenta l'energia addizionale del sistema dovuta al campo magnetico esterno ℋ, espresso in unità appropriate. I fenomeni fisici del modello di Ising si ottengono calcolando la funzione di partizione

L'energia libera, secondo la formula (21), è data da:

F=−kT ln Q=F(T, ℋ). (44)

Le singole configurazioni hanno probabilità relativa eguale a e^-H/kT e l'energia media del sistema è data da:

che, per analogia con quanto detto a proposito dell'equazione (22), è uguale a

Come già si era ottenuto in precedenza,

rappresenta l'entropia. Da una valutazione diretta si ottiene:

dove

rappresenta la magnetizzazione totale media. Riassumendo, si può scrivere che:

dF=−S dT−I dℋ. (50)

Il calcolo dell'energia libera (44) per un reticolo unidimensionale è assai semplice e mostra che non vi è transizione di fase a nessuna temperatura e per nessun valore del campo magnetico. Dal punto di vista fisico ciò è spiegabile semplicemente osservando che le interazioni reciproche tra spins più vicini sono legate insieme in maniera poco stretta e non si propagano a grandi distanze. Se si prende, per esempio, il caso di un campo esterno uguale a zero, ℋ=0, l'influenza di uno spin in A su di uno spin in G distante (v. fig. 4) avviene attraverso l'influenza di A su B, il quale a sua volta influenza C, e così via. Tale catena d'influenze può essere completamente alterata in un punto qualsiasi da una variazione finita di energia che non aumenta con il crescere delle dimensioni del reticolo: per esempio, un'inversione di tutti gli spins alla destra di C cambia il segno della correlazione fra gli spins in A e G, ma per tale inversione occorre soltanto una variazione dell'energia pari a ±2J, la quale è finita.

Ciò non vale però per un reticolo a due o più dimensioni. Nella fig. 5 lo spin in Ainfluenza quello in G attraverso un gran numero di catene d'influenza tra spins contigui, alcune delle quali sono indicate in figura, che non possono però essere interrotte con una variazione finita dell'energia. In effetti, in questo caso si verificano delle transizioni di fase (v. Peierls, 1936). Tuttavia, fino a oggi una valutazione esplicita dell'energia libera F è stata ottenuta soltanto per reticoli a due dimensioni, con ℋ=0 (v. Onsager, 1944) o con ℋ avente il valore, privo di senso fisico:

Onsager trovò che per un reticolo quadrato con campo esterno nullo la funzione termodinamica

dove  rappresenta il numero di punti del reticolo, è analitica in T per ogni T>0 a eccezione di T=T_c, dove vale:

e-^2J/kTc=√-2 −1.

(Per ragioni di chiarezza consideriamo qui il caso ferro magnetico, ossia quello in cui J>0). Vi è dunque una transizione di fase ad ℋ=0 e T=T_c; ed è stato anche dimostrato che esistono discontinuità in alcune funzioni termodinamiche e nelle loro derivate per ogni ℋ=0, T≤T_c, e che le funzioni termodinamiche sono analitiche per tutti gli altri valori.

Un gas a reticolo è un modello di gas i cui atomi sono costretti a muoversi su punti del reticolo stesso. Si fa ricorso a questo modello perché nel gas classico (cioè non quantomeccanico) l'energia cinetica contribuisce all'energia libera per una parte additiva priva di singolarità e indipendente dal volume; quindi, per studiare le relazioni p- V-T, è possibile sottrarre dall'energia E che compare nella funzione di partizione Q dell'espressione (4) l'energia cinetica e sostituire perciò Q con Q_q:

Q→Q_q= ∫ e^-V/kT dτ, (51)

dove V rappresenta l'energia potenziale. La sostituzione dell'integrale con la somma

Q_q=Σ e^-V/kT (52)

conduce al modello di gas a reticolo.

Le configurazioni di un gas a reticolo possono essere specificate mediante variabili σ_i in cui con i=1, 2, ...,  si rappresentano i punti del reticolo. Il valore di σ_i è ±1, con σ_i=−1 che rappresenta un punto reticolare occupato e σ_i=+1 che rappresenta un punto vacante. In un gas a reticolo non può aversi un punto occupato da più di un atomo, in quanto in tutti i gas reali l'energia potenziale tende a infinito quando i due atomi si avvicinano indefinitamente l'uno all'altro. L'energia potenziale V dell'espressione (51) è una funzione di σ₁, σ₂, ..., σ_ e, se vi sono N atomi, si ha evidentemente Σ σ_i=N. Per valori fissi di σ₁, σ₂, ..., σ_, la permutazione degli N atomi porta a N! termini identici nella espressione (52) e si ha così:

Il confronto dell'espressione (53) con la (43) mostra che identificando le configurazioni di un gas a reticolo con il corrispondente modello di Ising descritto dal medesimo insieme di σ₁, σ₂, ..., σ_ si hanno due problemi matematicamente identici. Se, per esempio, si considera il problema di Ising descritto dall'espressione (42), si vede che esso corrisponde al problema di un gas a reticolo con interazioni interatomiche V_g(g=gas a reticolo) descritte da:

Le grandezze fisiche dei due problemi sono correlate tra loro dalla tabella I d'identificazione. Occorre notare che la parte orizzontale dell'isoterma nel diagramma p-V del gas a reticolo corrisponde al tratto rettilineo dell'isoterma nel diagramma 1-ℋ, che va da −I₀ a I₀ per ℋ=0, dove con I₀ si indichi il momento magnetico permanente a campo nullo.

d) Determinazione numerica delle proprietà al punto critico.

Benché la valutazione esatta della funzione di partizione sia in generale impossibile, si possono però fare delle stime numeriche assai accurate dei parametri e degli esponenti critici con un metodo dovuto originariamente a Domb (v. Domb, 1949). Tale metodo consiste nei due passaggi seguenti:

1) si valutano i primi m termini dello sviluppo di qualche grandezza termodinamica in serie di potenze di una variabile w nel modo seguente:

Per esempio, per il modello di Ising di un reticolo triangolare, se χ è la suscettività per ℋ=0, cioè:

il valore di kTχ può essere sviluppato in serie di potenze di

w=tanh(J/kT)

e il risultato finale è (v. Gaunt e Guttmann, 1974):

2) lo sviluppo in serie valido per piccoli valori positivi di w rappresenta una funzione con una singolarità nel punto di transizione

w_c=tanh(J/kT_c);

ci si attende quindi che i coefficienti a_n della serie soddisfino la condizione:

Il valore di μ_n che si ottiene dalla (55) è indicato nel diagramma della fig. 6 e la sua estrapolazione porta a un valore

(v. Gaunt e Guttmann, 1974). L'entità dell'errore viene calcolata mediante un confronto tra i vari metodi di estrapolazione.

Per questo problema è possibile calcolare il valore esatto di w_c estendendo il metodo di Onsager per il reticolo quadrato: il valore,

è in perfetto accordo con l'espressione (57).

Il metodo che si è appena descritto è fino a oggi l'unico in grado di fornire stime numeriche dei parametri e degli esponenti critici e con l'aiuto dei calcolatori esso è stato ulteriormente sviluppato, pur mantenendo l'idea fondamentale cui si è sopra accennato, sì da permettere il calcolo dei coefficienti a_n coi metodi di approssimazione di Pade (v. Baker, 1961) e con altri miglioramenti. Nei casi in cui si conoscono i valori esatti, come in quello dell'esempio che si è riportato, i risultati ottenuti coll'impiego di tale metodo si dimostrano in ottimo accordo con essi, mentre nei casi in cui i valori esatti non sono noti, il metodo ha permesso di calcolare delle costanti critiche, le quali sono considerate attendibili da tutti i fisici impegnati in questo campo.

e) Esponenti critici.

Gli esponenti critici α, β, γ, δ sono definiti come l'esponente B nella formula empirica

ξ∝η^B,

vicino al punto critico o al punto di Curie nelle transizioni liquido-gas e nelle transizioni ferromagnetiche. I diversi esponenti sono definiti nella tab. II.

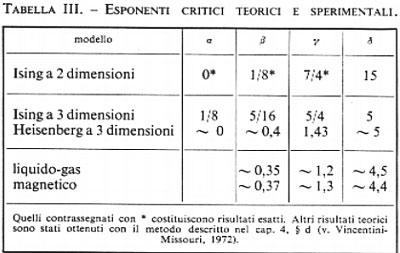
Le misure degli esponenti critici per diverse transizioni liquido-gas portano a valori sorprendentemente identici e lo stesso vale per i valori sperimentali degli esponenti critici per sostanze ferromagnetiche diverse. Nella tab. III sono riportati alcuni valori tipici e anche gli esponenti critici teorici per modelli diversi (v. sopra, cap. 4, È a).

5. Transizioni di fase quantiche.

Come si è detto nell'ultimo capitolo, i fenomeni fisici delle transizioni liquido-gas sono in gran parte descritti dal modello di gas a reticolo, nel quale non sono presenti effetti quantici, come si deduce chiaramente dal fatto che in essi non appare la costante di Planck. Le transizioni liquido-gas non sono dunque fenomeni quantici: i fenomeni essenziali di tali transizioni sono di origine classica, anche se correzioni quantiche intervengono negli aspetti quantitativi dei parametri critici di gas leggeri, quali l'⁴He e l'³He (v. de Boer, 1948).

La possibilità che esistano transizioni di fase puramente quantiche fu discussa teoricamente per la prima volta da Einstein, il quale osservò che un sistema di particelle non interagenti che obbediscano alla statistica di Bose-Einstein dovrebbe presentare strane proprietà termodinamiche a basse temperature o ad alte densità. Tali proprietà sono prodotte dall'occupazione di uno stato di particella singola da parte di un numero finito di particelle del sistema: tale fenomeno, noto oggi come ‛condensazione di Bose-Einstein', è un fenomeno quantico.

Esperimenti compiuti sin dall'inizio del secolo mostrarono che l'⁴He liquido a temperature inferiori a ~2 °K passa, attraverso una transizione λ, in una fase con proprietà superfluide e che a temperature basse, di pochi gradi assoluti, molte altre sostanze passano a una fase avente proprietà superconduttrici (v. criofisica). Di recente è stato scoperto che, a temperature estremamente basse, di ~2×10^-3 °K, l'³He liquido passa attraverso una serie di transizioni in fasi che probabilmente presentano proprietà superfiuide (v. Wheatley, 1975).

La spiegazione teorica delle fasi superfluide e superconduttrici si basa su generalizzazioni del concetto di condensazione di Bose-Einstein, rese necessarie dal fatto che nel caso dei superconduttori e dell'³He la condensazione di Bose-Einstein è una condensazione di coppie di particelle di Fermi-Dirac (v. Bardeen, Cooper e Schrieffer, 1957). La condensazione di Bose-Einstein conduce a proprietà quantomeccaniche di coerenza nel comportamento globale del sistema, le quali sono molto simili alle proprietà di coerenza che s'incontrano nella fisica dei laser.

La generalizzazione della condensazione di Bose-Einstein porta a trasformazioni di fase quantiche di origine totalmente diversa da quella delle transizioni classiche, del tipo liquido-gas, ad esempio. Un aspetto importante della fase quantica con condensazione di Bose-Einstein è l'esistenza di ulteriori variabili termodinamiche macroscopiche, che portano al fenomeno dei ‛due fluidi', originariamente proposto per descrivere la superfluidità dell'⁴He liquido. La relazione tra la teoria dei due fluidi, i concetti di superfluidità e di superconduttività, da un lato, e la condensazione di Bose-Einstein, dall'altro, è stata oggetto di lunghi studi, ma, sebbene molte delle idee più importanti siano senza dubbio corrette, resta ancora da formulare una trattazione completa a partire dai principi fondamentali, per fornire quello che Gibbs definirebbe un ‛fondamento razionale' della termodinamica delle fasi con proprietà superfluide o superconduttrici.

Bibliografia.

Atkins, K. R., Edwards, M. H., Coefficient of expansion of liquid helium II, in ‟Physical review", 1955, XVCII, pp. 1429-1434.

Bagatskii, M. I., Voronel, A. V., Gusak, V. G., Measurement of the specific heat C_v of argon in the immediate vicinity of the critical point, in ‟Journal of experimental and theoretical physics", 1962, XVI, pp. 517-518.

Baker, G. A., Application of the Pade approximant method to the investigation of the some magnetic properties of the Ising model, in ‟Physical review", 1961, CXXIV, pp. 768-774.

Bardeen, J., Cooper, L. N., Schrieffer, J. R., Theory of superconductivity, in ‟Physical review", 1957, CVIII, pp. 1175-1200.

Boer, J. de, Quantum theory of condensed permanent gases. I. The law of corresponding states, in ‟Physica", 1948, XIV, pp. 139-164.

Boer, J. de, Lunbeck, R. J., The properties of the condensed phase of the light helium isotope, in ‟Physica", 1948, XIV, pp. 510-519.

Born, M., Fuchs, K., The statistical mechanisms of condensing systems, in ‟Proceedings of the Royal Society" (Series A), 1938, CLXVI, pp. 391-414.

Domb, C., Order-disorder statistics. II. A two-dimensional model, in ‟Proceedings of the Royal Society" (Series A), 1949, CIL, pp. 199-221.

Domb, C., Green M. S. (a cura di), Phase transitions and critical phenomena, 3 voll., New York 1972.

Dyson, F. J., Ground-state energy of a finite system of charged particles, in ‟Journal of mathematical physics", 1967, VIII, pp. 1538-1545.

Dyson, F. J., Lenard, A., Stability of matter I, in ‟Journal of mathematical physics", 1967, VIII, pp. 423-434.

Ehrenfest, P., Collected science papers, Leiden communication supplement 85 B., 1933.

Fisher, M. E., Correlation functions and the critical region of simple fluids, in ‟Journal of mathematical physics", 1964, V, pp. 944-962.

Fowler, R., Guggenheim, E. A., Statistical thermodynamics, Cambridge 1939.

Gaunt, D. S., Guttmann, A. J., Asymptotic analysis of coefficients, in Critical phenomena, vol. III, London 1974, pp. 181-243.

Gibbs, J. W., Elementary principles in statistical mechanics, New York 1901.

Griffith, R. B., Ferromagnets and simple fluids near the critical point: some thermodynamic inequalities, in ‟Journal of chemical physics", 1965, XLIII, pp. 1958-1968.

Griffith, R. B., Rigorous results and theorems, in Phase transitions and critical phenomena (a cura di C. Domb, M. S. Green), vol. I, New York 1972, pp. 7-109.

Hagedorn, R., Observations on the π⁺→r⁺→e⁺ angular correlation in nuclear emulsion, in ‟Nuovo cimento", suppl. 1968, VI, pp. 311-354.

Kahn, B., Uhlenbeck, G. E., On the theory on condensation, in ‟Physica", 1938, V, pp. 399-416.

Landau, L. D., Lifschitz, E. M., Statistical physics, London 1958.

Lieb, E. H., Lebowitz, J., The constitution of matter: existence of thermodynamics for systems composed of electrons and nuclei, in Advances in mathematics, vol. IX, New York-London 1972, pp. 316-398.

Lieb, E. H., Wu Fa Yueh, Two-dimensional ferroelectric models, in Phase transitions and critical phenomena (a cura di C. Domb, M. S. Green), vol. I, New York 1972, pp. 332-490.

McCoy, B. M., Wu Tai Tsun, The two-dimensional Ising model, Cambridge, Mass., 1973.

Mayer, J. E., The statistical mechanics of condensing systems, in ‟Journal of chemical physics", 1937, V, pp. 67-73, 74-83, 87-104.

Mermin, N. D., Wagner, H., Absence of ferromagnetism or antiferromagnetism in one- or 2-dimensional isotropic Heisenberg models, in ‟Physical review letters", 1966, XVII, pp. 1133-1136.

Onsager, L., Crystal statistics. I. A two-dimensional model with an order-disorder transition, in ‟Physical review", 1944, LXV, pp. 117-149.

Peierls, R., On Ising's model of ferromagnetism, in ‟Proceedings of the Cambridge Philosophical Society", 1936, XXXII, pp. 477-481.

Robinson, W. K., Friedberg, S. A., Specific heats of NiCl₂•6H₂O and CoCl₂•6H₂O between 1,4^o and 20°K, in ‟Physical review", 1960, CXVII, pp. 402-408.

Rouelle, D., Statistical mechanics, rigorous results, New York 1969.

Rushbrooke, G. S., On the thermodynamics of the critical region for the Ising problem, in ‟Journal of chemical physics", 1963, XXXIX, pp. 842-843.

Van Hove, L., Quelques propriétés générales de l'intégrale de configuration d'un système de particules avec interaction, in ‟Physica", 1949, XV, pp. 951-961.

Vincentini-Missouri, M., Equilibrium scaling in fluids and magnets, in Phase transitions and critical phenomena (a cura di C. Domb, M. S. Green), vol. II, New York 1972, pp. 415-470.

Weiss, P., Hypothesis of the molecular field and ferromagnetic properties, in ‟Journal de physique", 1907, VI, pp. 661-690.

Wheatley, J. C., Experimental properties of superfluid ³He, in ‟Reviews of modern physics", 1975, XLVII, pp. 415-470.

Widom, R., Equation of state in the neighborhood of the critical point, in ‟Journal of chemical physics", 1965, XLIII, pp. 3898-3905.

Yang Chen Ning, Lee Tsung Dao, Statistical theory of equation of state and phase transitions. I. Theory of condensation, in ‟Physical review", 1952, LXXXVII, pp. 404-410.