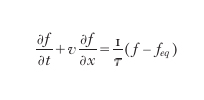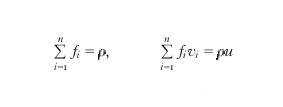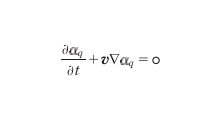Fluidi, meccanica dei
Fluidi, meccanica dei
La m. dei f. è la branca della fisica che si occupa del comportamento dei fluidi, ossia delle sostanze liquide e gassose, dal punto di vista statico e dinamico. Gli inizi della m. dei f., modernamente intesa, risalgono alla metà del 17° sec., epoca in cui alcuni matematici cominciarono a enunciarne le leggi.
Nella m. dei f., coerentemente al classico approccio della meccanica del continuo, il fluido è considerato assimilabile a un continuo, cui sono associabili proprietà caratteristiche variabili con continuità da punto a punto. In effetti la materia (solidi, liquidi, aeriformi) è composta da particelle distinte situate a distanze reciproche grandi rispetto alle loro dimensioni: alla scala delle molecole lo schema di continuo matematico non è affatto significativo, visto che il valore di ogni grandezza è più o meno definito e varia bruscamente da punto a punto e da istante a istante, a seconda della presenza o meno di una molecola nel punto considerato. È peraltro vero che, per la maggior parte dei problemi pratici, la minima scala di osservazione è enormemente maggiore di quella molecolare, sicché ogni (piccolo) volume di interesse contiene un grandissimo numero di molecole; associando a tale volume opportune caratteristiche medie della materia contenuta, le proprietà così definite variano con continuità nello spazio e al variare delle dimensioni del volume medesimo. È dunque possibile considerare la materia come sistema continuo e descriverne il comportamento con gli strumenti della matematica del continuo. In seguito, pertanto, il concetto di particella fluida farà riferimento a un volume di fluido, per quanto piccolo, contenente un elevato numero di molecole, da considerarsi come unità puntuale di un sistema continuo, cui sono univocamente associate le grandezze fisiche densità, velocità, temperatura, pressione e così via.
L'utilizzo dell'ipotesi del continuo nello studio della m. dei f. si è sempre rivelato più che accettabile; infatti la maggior parte dei problemi analizzati presenta numeri di Knudsen sufficientemente piccoli. Il numero di Knudsen (Kn) è un numero adimensionale definito come il rapporto tra il libero cammino medio molecolare λ e una lunghezza caratteristica L del problema fisico: Kn=λ/L. Tale grandezza viene usata per definire il campo di validità dell'ipotesi del continuo nel fluido e quindi l'applicabilità delle sue leggi ed equazioni: problemi per cui tale numero risulta essere dell'ordine di grandezza dell'unità o superiore non possono essere studiati con la suddetta ipotesi. Specialmente per un gas, i valori di λ (nel caso di aria in condizioni atmosferiche vale circa 10−5 cm) sono talmente piccoli che certamente nelle applicazioni pratiche risulta valida l'ipotesi del continuo. Soltanto con la produzione di microsistemi elettromeccanici detti MicroElectroMechanical System (MEMS), si sono aperti campi nei quali la classica teoria del continuo non può essere applicata: tali problemi si classificano come problemi di nanofluidodinamica e vengono analizzati utilizzando la teoria cinetica dei gas. La m. dei f. trova moltissime applicazioni in svariati campi dell'ingegneria chimica, civile e meccanica, ed è fondamentale in aeronautica, in meteorologia, in architettura e ingegneria navale, in oceanografia e in molti altri settori delle scienze applicate. Tra le varie applicazioni sembra opportuno menzionare la propulsione a getto, le turbine, i compressori e le pompe.
Da quanto detto appare evidente l'importanza che la m. dei f. ha in molte branche dell'ingegneria moderna: certamente le equazioni che la governano, ricavate dalla trascrizione matematica delle leggi fondamentali, ossia i principi di conservazione della massa, della quantità di moto e dell'energia, sono note già da molto. Purtroppo la loro applicazione diretta è possibile solo in alcuni semplici casi di trascurabile interesse pratico. Grazie agli enormi passi in avanti fatti nel campo dei calcolatori, è stata sviluppata, dalla metà del 20° sec., una nuova scienza detta meccanica computazionale, che ha in comune elementi di fisica (m. dei f.), di matematica (risoluzione di equazioni differenziali), di informatica (linguaggi di programmazione e strumenti hardware e software) e come scopo l'integrazione per via numerica delle equazioni differenziali che governano la meccanica dei fluidi.
Fluidodinamica. - Le leggi che regolano il comportamento dei fluidi in moto sono piuttosto complesse, per cui, nonostante la notevole importanza pratica della fluidodinamica, si potranno esporre soltanto alcuni concetti di base sui quali sono fondate le equazioni che ne regolano l'evoluzione. Un campo di moto fluido è compiutamente descritto dal punto di vista cinematico quando sia noto il vettore velocità in ogni punto del campo (definito dal vettore r, ossia dalle sue componenti cartesiane x, y, z al variare del tempo t); ogni altra grandezza cinematica (spostamenti, accelerazioni, deformazioni, traiettorie ecc.) può essere dedotta per derivazione o integrazione del campo di velocità. Come ogni grandezza vettoriale, la velocità può essere descritta in termini delle sue tre componenti scalari, anch'esse funzioni dello spazio e del tempo. Indicando con s l'ascissa curvilinea lungo la traiettoria, il modulo della velocità risulta, conseguentemente, essere pari a ds/dt. Per la definizione di ogni grandezza del campo fluidodinamico possono essere utilizzati due diversi approcci. La descrizione lagrangiana identifica un sistema materiale (particella, insieme di particelle, corpo rigido ecc.) e ne segue gli spostamenti nello spazio; in ogni istante e per ogni punto materiale sono descritti i valori delle grandezze di interesse e la posizione del punto medesimo, ottenendo una completa descrizione spazio-temporale del campo. Nella descrizione euleriana, viceversa, si identifica un riferimento geometrico (per es., punto, volume ecc.) fisso nello spazio, e se ne descrivono i valori delle grandezze di interesse in ogni istante; a causa del movimento, però, i diversi valori per i diversi tempi sono riferiti a punti materiali (particelle fluide) diverse. Le leggi della fisica (conservazione della massa, bilanci di quantità di moto, conservazione dell'energia ecc.) vengono tipicamente formulate per un sistema materiale, ossia in un riferimento lagrangiano. Per lo studio della fluidodinamica, però, si rivela di solito più vantaggiosa una descrizione euleriana: a causa della possibilità di deformazioni illimitate, nello studio dei fluidi risulta complesso seguire la storia delle diverse porzioni di materia, e conviene invece fissare l'attenzione su punti (linee, superfici, volumi) prefissati a priori nello spazio.
Dalle equazioni di conservazione della massa, quantità di moto ed energia, scritte in un qualsiasi sistema di riferimento (lagrangiano o euleriano) si deduce un sistema di equazioni differenziali che, una volta integrato, consente la valutazione degli andamenti delle grandezze cinematiche e termodinamiche nello spazio e nel tempo. Vale la pena notare, da un lato, l'enorme importanza che la risoluzione di tali sistemi di equazioni ha in moltissime applicazioni industriali (aeronautiche, automobilistiche, chimiche, farmaceutiche, navali ecc.), dall'altro, l'impossibilità di trovare soluzioni analitiche per problemi applicativi di interesse. Le due considerazioni esposte spiegano l'enorme sviluppo che hanno avuto, e continuano ad avere, le metodologie di risoluzione numerica di tali sistemi, comunemente denominate CFD (Computational Fluid Mechanics). L'utilizzo della CFD nella progettazione ha permesso di riformulare completamente moltissime procedure di disegno e di ottimizzare notevolmente le prestazioni dei dispositivi.
Moto turbolento
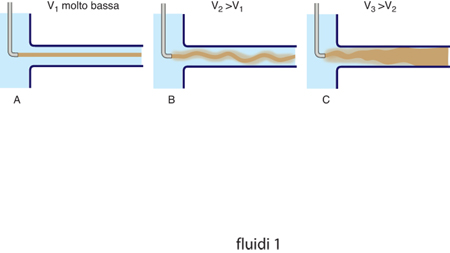
In un fluido viscoso all'interno di un condotto, a basse velocità le particelle seguono le linee di flusso (regime laminare), secondo le previsioni delle equazioni analitiche, mentre a più alte velocità il flusso si rompe in una serie di gorghi (regime turbolento) non perfettamente prevedibili neppure con le moderne teorie. La transizione dal regime laminare a quello turbolento dipende da un solo parametro, detto numero di Reynolds, che può essere calcolato moltiplicando il prodotto della velocità e della densità del fluido per il diametro del condotto e dividendo il risultato ottenuto per la viscosità. Se per un certo sistema fluidodinamico il numero di Reynolds risulta minore di un valore critico pari a circa 2100, il flusso all'interno del condotto, è di tipo laminare; per valori più alti si instaura invece un regime di moto turbolento. Lo studio dei moti turbolenti non può essere unicamente teorico, ma dipende da una sintesi tra dati sperimentali e modelli teorici, che è ancora da perfezionare.Il fenomeno della transizione da regime laminare a regime turbolento e la complessità di quest'ultimo possono essere osservati nella diffusione di un tracciante colorato all'interno di un efflusso gassoso all'aumentare della velocità media del fluido. Come mostrato in fig. 1, a basse velocità i filetti fluidi colorati con il tracciante mantengono una traiettoria ben precisa parallela alle pareti del condotto (flusso laminare); in altre parole non ci sono scambi di massa tra i filetti fluidi colorati e quelli circostanti. Aumentando la velocità del gas, la traiettoria del colorante comincia a presentare alcune instabilità (transizione laminare-turbolenta), dovute all'instaurarsi di moti trasversali che fanno perdere al colorante il parallelismo con le pareti. Infine, un ulteriore aumento di velocità (moto turbolento) provoca una dispersione del colorante in tutta la zona interessata al moto in quanto questo non avviene più per filetti fluidi paralleli, ma con scambi di massa significativi nel verso normale alle pareti stesse.
Si può quindi affermare che il fenomeno della turbolenza si presenta quando una corrente regolare e ordinata si trasforma in un flusso caotico e irregolare. A caratterizzare in maniera sostanziale un flusso in regime turbolento rispetto a un flusso in regime laminare è la presenza all'interno del flusso stesso di un numero più o meno elevato di strutture vorticose, le quali, essendo di diverse dimensioni e muovendosi a velocità differenti, rendono il moto del fluido impredicibile nel tempo.
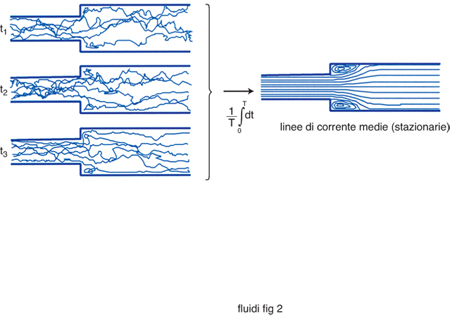
La turbolenza nei moti atmosferici, è, per fare un esempio, un elemento fondamentale nelle previsioni meteorologiche e ha anche importanti applicazioni nella diffusione in aria degli agenti inquinanti. I moti turbolenti si manifestano in altri ambiti: dall'astrofisica alla chimica, fino all'ingegneria, dove un controllo del regime turbolento può rendere migliori le prestazioni di un motore a combustione interna (aumentando la velocità di combustione) o l'efficienza aerodinamica di un autoveicolo. Il concetto di un moto turbolento come di un efflusso che è caratterizzato da un campo di moto caotico e imprevedibile non deve però portare a conclusioni affrettate ed errate. Si può definire con modalità statistiche una perturbazione a media nulla, ciò vuol dire (fig. 2), che mediando i campi di moto si ottiene una configurazione stazionaria nel tempo, ovviamente riferita al moto medio. L'analisi dei moti turbolenti, nel caso di flussi incomprimibili, può anche essere effettuata utilizzando l'equazione di Boltzmann:
dove f è la probabilità di trovare in una certa posizione spaziale una molecola con una data velocità, mentre τ è un tempo caratteristico di rilassamento per arrivare a condizioni di equilibrio feq. Tale approccio presenta notevoli vantaggi rispetto a quello tradizionale il quale utilizza le equazioni di Navier-Stokes. Il primo risiede nella capacità di descrivere una fisica particolarmente complessa mediante il termine τ, o meglio mediante il suo effetto sulle variabili idrodinamiche, in quanto le informazioni trasferite nel tempo τ sono riferite a una scala delle lunghezze estremamente ridotta rispetto a quella normalmente utilizzata nella risoluzione delle equazioni di Navier-Stokes.
Un altro vantaggio risiede nell'analogo trattamento matematico che le fluttuazioni di grandezze turbolente e termodinamiche hanno nell'approccio di Boltzmann, ciò permette di applicare gli stessi trattamenti matematici con le medesime ipotesi e approssimazioni. Un ulteriore vantaggio è insito nella definizione di τ, che include gli effetti viscosi molecolari e quelli turbolenti, per cui senza variazioni di modello di turbolenza si può estendere l'approccio di Boltzmann a problemi aventi scale metriche dei vortici estremamente differenziate. Risolvere, da un punto di vista matematico, l'equazione di Boltzmann vuol dire per ogni molecola integrare la sua equazione nel tempo e nello spazio nelle sei variabili indipendenti che identificano il suo moto, tre componenti di velocità e tre di posizione. Ovviamente la risoluzione di tali sistemi, nonostante il vertiginoso aumento delle potenze computazionali, è possibile solo in situazioni molto particolari, dove non è coinvolto un numero enorme di molecole. Per superare il problema citato, si è andata affermando una nuova metodologia di analisi dei flussi turbolenti; tale approccio si basa sull'ipotesi che sia sufficiente seguire non tutte le molecole, ma solo un certo numero, valutato per via statistica all'interno di un reticolo di velocità discreto. In questa formulazione il metodo di Boltzmann (LBE, Lattice Boltzmann Equation) è basato sulla valutazione della dinamica di una serie di particelle fittizie che si muovono su un reticolo discreto e interagiscono mediante alcune leggi le quali consentono di soddisfare i principi di conservazione di massa, quantità di moto ed energia. In altri termini, con la tecnica LBE l'evoluzione del fluido viene seguita attraverso l'evoluzione f(x,t) di una densità discreta di particelle, con velocità v prefissata, lungo la direzione x in un reticolo a un certo istante t. Oltre a muoversi, le particelle collidono tra di loro tendendo alla distribuzione di equilibrio in un tempo caratteristico τ. In queste condizioni è possibile dimostrare che il risultato è lo stesso che si può ottenere mediante un'integrazione numerica delle equazioni di Navier-Stokes ed è possibile ricavare le variabili idrodinamiche macroscopiche attraverso le seguenti relazioni:
dove ρ è la densità del fluido e u la velocità macroscopica del fluido. Il metodo LBE riesce, in tre dimensioni, con un numero di particelle fittizie minore di 20 a riprodurre con notevole fedeltà l'evoluzione di un fluido a livello tanto microscopico quanto macroscopico. le citate metodologie hanno avuto grande applicazione in ambito industriale, in particolare negli studi che sono relativi alla aerodinamica esterna degli autoveicoli, dove più del 50% del mercato mondiale utilizza metodologie che sono basate su tecniche cinetiche.
Teoria dello strato limite
La complessità del comportamento dei fluidi viscosi, in modo particolare in regime di moto turbolento, ha rappresentato un serio ostacolo ai progressi della fluidodinamica. In un gran numero di casi è possibile e conveniente suddividere il fluido in moto in due regioni distinte, vale a dire: la regione di fluido prossima alla superficie del condotto, che consiste di un sottile strato limite nel quale sono concentrati gli effetti della viscosità e all'interno del quale il modello matematico può essere semplificato significativamente, e la regione esterna a questo strato in cui, potendo trascurare gli effetti della viscosità, è possibile impiegare le più semplici equazioni matematiche per i fluidi privi di attrito interno. È proprio alla teoria dello strato limite che si deve lo sviluppo delle più moderne applicazioni ingegneristiche nel campo della fluidodinamica, quali ali dei velivoli, le turbine a gas e i compressori. Essa infatti non solo ha reso possibile una riformulazione più semplice delle equazioni di Navier-Stokes nella regione prossima alla superficie di corpo immerso in un fluido in moto, ma ha portato anche a ulteriori sviluppi della teoria sui fluidi ideali, nelle sue applicazioni alla regione esterna allo strato limite.
Moto di fluidi comprimibili
Uno dei principi che risulta fondamentale rispetto al comportamento dei fluidi comprimibili prevede che la densità di un gas vari quando esso è sottoposto a variazioni di pressione e di velocità. Contemporaneamente si manifestano, inoltre, anche variazioni di temperatura, ponendo problemi analitici ancora più complessi.
Il comportamento di un fluido comprimibile in moto dipende dalla velocità di flusso, e varia in modo sostanziale a seconda che questa sia maggiore o minore della velocità del suono. Il suono consiste nella propagazione di una piccola perturbazione, o onda di pressione, all'interno di un fluido, e si propaga con velocità proporzionale alla radice quadrata della temperatura assoluta. Se un aereo vola con velocità maggiore rispetto a quella del suono (volo supersonico), nelle estreme vicinanze dell'ala si verifica un'intensa compressione, detta anche onda d'urto, che può essere percepita da un osservatore a terra, sotto forma di bang sonico.
Moto di fluidi multifase
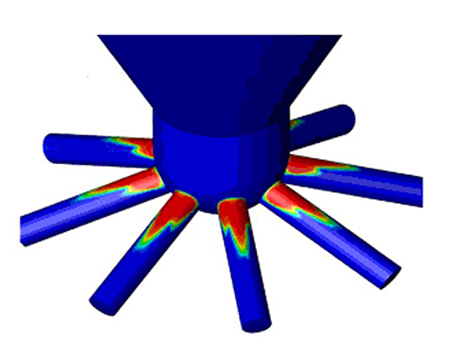
Un campo di sviluppo riguarda l'analisi dei fluidi multifase, ossia lo studio di tutti quei problemi dove coesistono fluidi in fasi diverse, per es., una fase liquida e una gassosa. Le applicazioni sono svariate e vanno dal settore automobilistico, dove sono particolarmente studiati gli iniettori dei motori diesel ad alta pressione, detti common rail, a settori che attengono all'ingegneria ambientale, come lo studio di onde di piena in un fiume o l'analisi degli effetti di una frana in un bacino. Per quanto riguarda l'analisi degli iniettori, si analizza il flusso di un liquido che ad altissima pressione (1500÷2000 bar) viene introdotto, attraverso un idoneo sistema di iniezione, nel cilindro di un motore a combustione interna. Durante il suo efflusso all'interno dell'iniettore il liquido raggiunge localmente elevate velocità e, quindi, pressioni inferiori alla sua tensione di vapore: nei punti dove ciò accade si instaura un fenomeno di cavitazione e parte del liquido cambia stato diventando vapore. Tale fenomeno assume una notevole rilevanza in quanto può variare sensibilmente le sezioni di efflusso disponibili per il liquido, con la conseguente modifica della sua velocità e quindi delle caratteristiche dell'evoluzione dello spray di combustibile in camera di combustione. A titolo di esempio si riporta, in fig. 3, la parte terminale di un iniettore ad alta pressione multiforo per motori diesel (in blu è stata evidenziata la parte liquida, in rosso il suo vapore). Si nota come passando dal corpo centrale degli iniettori ai condotti, nei punti dove presumibilmente si raggiungono le velocità più elevate, e quindi le pressioni più basse, si innesca la cavitazione con il cambio di fase da liquida a gassosa; quest'ultima viene riassorbita a causa dell'aumento locale di pressione durante l'evoluzione gas-liquido all'interno dei condotti. Certamente in questo caso gioca un ruolo fondamentale l'angolo di raccordo tra il corpo centrale dell'iniettore e i canali dei vari fori, ma le piccole dimensioni dei canali, valutabili nell'ordine di grandezza del decimo di millimetro, rendono particolarmente difficili e onerose lavorazioni meccaniche finalizzate a ottenere angoli di raccordi con elevati raggi di curvatura. Come ulteriore esempio di applicazione dell'analisi multifase si può considerare l'apertura veloce di una paratia incernierata in alto che separa due ambienti, occupati rispettivamente da un liquido (destra) e da aria (sinistra).
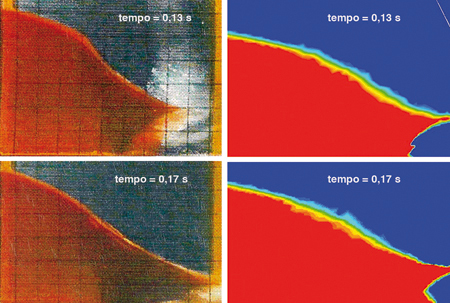
In fig. 4 si ha la sequenza di immagini ottenute sperimentalmente (a sinistra) e con valutazioni teoriche (a destra). È da notare come l'approccio matematico sia in grado di riprodurre con notevole fedeltà le forme assunte da un liquido in tale processo di dinamica veloce. Entrambe le applicazioni citate vengono analizzate utilizzando una metodologia VOF (Volume Of Fluid), che consiste nell'aggiunta, alle equazioni della m. dei f. che descrivono il fenomeno, di una ulteriore equazione di trasporto che esprime la dinamica della superficie di interfaccia tra le due fasi e che assume la forma
che descrive l'evoluzione della variabile αq che identifica la presenza della fase q: se αq assume valore unitario si ipotizza la sola presenza della fase q, mentre se il suo valore rimane nullo si ipotizza la sua totale assenza. La conoscenza delle zone con un valore intermedio permette, utilizzando particolari tecniche, di ricostruire con una buona precisione le superfici di interfaccia tra le varie fasi.
Bibliografia
C. Cercignani, Theory and application of the Boltzmann equation, Edinburgh-London 1975.
S. Succi, The lattice Boltzmann equation for fluid dynamics and beyond, Oxford 2001.