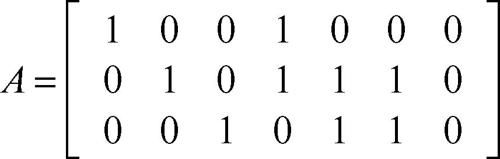matroide

matroide

matroide ente matematico che consente di generalizzare il concetto di indipendenza e dipendenza lineare; si applica a diversi contesti come la teoria dei → grafi o delle → matrici, e trova impiego nella soluzione di svariati problemi di ottimizzazione discreta. Il termine matroide fu usato la prima volta nel 1935 dal matematico H. Whitney nell’articolo Sulle proprietà astratte della dipendenza lineare. Nel definire una matroide, Whitney operò una sintesi delle proprietà fondamentali di dipendenza che sono comuni ai grafi e alle matrici. La teoria delle matroidi fornisce un’ipotesi di lavoro attraverso la quale molti problemi di ottimizzazione, di ricerca operativa, di teoria dei grafi diventano più semplici da analizzare e risolvere. Si consideri per esempio la matrice

e siano:

• E l’insieme {1, 2, 3, 4, 5, 6, 7} degli indici delle colonne di A;

• I l’insieme dei sottoinsiemi di E in cui le colonne risultino linearmente indipendenti: I contiene tutti i sottoinsiemi di E{7} con almeno tre elementi, tranne {1, 2, 4}, {2, 3, 5}, {2, 3, 6} e tranne inoltre ciascun sottoinsieme contenente la coppia {5, 6}.

L’insieme I ha le seguenti proprietà:

a) I non è vuoto;

b) ciascun sottoinsieme di un insieme elemento di I, appartiene anch’esso a I;

c) se X e Y appartengono a I e |X| = |Y| + 1, cioè se la cardinalità di X è uguale a quella di Y aumentata di 1 (X ha, quindi, un elemento in più di Y), allora esiste un elemento x ∈ X Y tale che Y ∪ {x} è elemento di I.

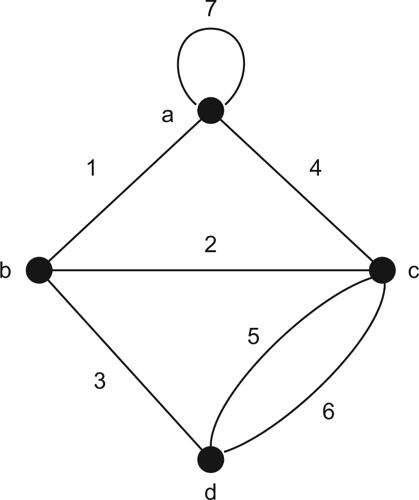
La coppia (E, I) è un esempio di matroide, e ogni coppia (E, I) avente le proprietà a), b) e c) è definita come matroide. Si noti che I rappresenta un sottoinsieme dell’insieme delle parti di E. Qualora valgano solo le proprietà a) e b) la coppia (E, I) prende il nome di sistema di indipendenza; l’essere matroide prevede anche la terza proprietà. L’insieme E è detto insieme fondamentale della matroide e gli elementi di I sono gli insiemi indipendenti della matroide. Se, date due matroidi M₁ e M₂, esiste una corrispondenza biunivoca tra l’insieme fondamentale di M₁ e l’insieme fondamentale di M₂ tale che un insieme è indipendente nella prima matroide se e solo se la sua immagine è indipendente nella seconda matroide, le due matroidi si dicono isomorfe. Per esempio, se E = ∅ c’è esattamente una matroide su E, quella che ha I = {∅}. Se E = {1}, allora ci sono esattamente due matroidi su E, una con I = {∅} e l’altra con I = {∅, {∅, 1}}. Se E = {1, 2}, ci sono esattamente cinque matroidi su E, ciascuna delle quali ha insiemi indipendenti uguali a {∅}, {∅, {1}}, {∅, {2}}, {∅, {1}, {2}} e {∅, {1}, {2}, {1, 2}}. La seconda e terza matroide sono isomorfe. Le matroidi si applicano anche alla teoria dei grafi. Si consideri il seguente grafo G con quattro nodi e 7 archi:

Sia E = {1, 2, 3, 4, 5, 6, 7} l’insieme degli archi di G e sia I l’insieme dei sottoinsiemi di E che non contengono tutti gli archi di ciascun cammino semplice chiuso di G. I cicli di G corrispondono agli insiemi degli archi {7}, {5, 6}, {1, 2, 4}, {2, 3, 5}, {2, 3, 6}, {1, 3, 4, 5}: non è difficile verificare che I coincide con l’insieme di sottoinsiemi di indici di colonne linearmente indipendenti della matrice A dell’esempio precedente: la coppia (E, I) derivata dal grafo G è quindi una matroide.