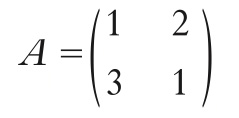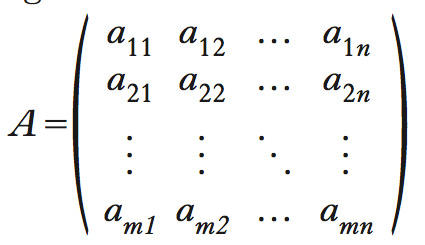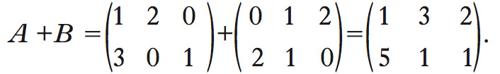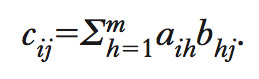matrice

matrice

Tabella rettangolare o quadrata di simboli, di solito rappresentativi di numeri reali o complessi, disposti per righe e per colonne, utilizzati per esprimere in forma compatta alcune proprietà o per eseguire certi tipi di calcoli. Per es., la m.

è costituita da 2 righe e 2 colonne (perciò è quadrata avendo un identico numero di righe e colonne), e ha come elemento della prima riga e della seconda colonna il numero 2. In quanto segue si considereranno solo m. numeriche, i cui elementi sono tutti numeri. Una matrice ha dimensione m×n se è composta da m ≥1 righe e n≥1 colonne. Un esempio è la m. formula

Di norma, si indica con a_ij il generico elemento della i-esima riga e j-esima colonna della m. A. Se m>1 e n=1 la m. si riduce a un vettore colonna di dimensione m (➔ vettore), mentre se m=1 e n>1 si riduce a un vettore riga di dimensione n. Se m=n. la m. è detta quadrata e la somma degli elementi a_ii sulla sua diagonale principale è detta traccia. Infine, se m=n=1, la m. si riduce a uno scalare (➔) e coincide con la nozione usuale di numero.

M. di particolare importanza sono la m. nulla, composta da tutti zeri, e la m. identità, m. quadrata avente tutti 1 sulla diagonale principale e zero altrove. La m. identità di dimensione n è indicata con I o con I_n. Essa ha funzione analoga a quella del numero 1 nel caso di scalari. Una m. che ha elementi diversi da 0 soltanto sulla diagonale principale è detta m. diagonale. Una m. che contiene tutti 0 al di sopra (al di sotto) della diagonale principale è detta matrice triangolare inferiore (superiore).

Operazioni tra matrici

Date due m. A e B aventi lo stesso numero di righe e lo stesso numero di colonne, la loro somma A+B è la m. i cui elementi sono uguali alla somma dei rispettivi elementi di A e di B. Così per es.,

Dato un numero scalare a e una m. B con elemento generico b_ij, si indica con aB la m. con elemento generico ab_ij. Per le m. è possibile definire diversi concetti di prodotto, ciascuno dei quali può essere visto come generalizzazione del prodotto tra scalari. Il concetto più comunemente utilizzato si basa sul prodotto scalare tra vettori: se A è una m. n×m e B è una m. m×l, la m. prodotto C=A. è la m. di dimensione n×l, il cui elemento (i,j)-esimo è ottenuto dal prodotto scalare di due vettori, il vettore corrispondente alla riga i-esima di A e quello corrispondente alla colonna j-esima di B, ossia

Il prodotto di m. gode della proprietà del prodotto tra scalari, a eccezione della commutatività, cioè A.≠B.. Altri due concetti di prodotto sono il prodotto di Hadamard e quello di Kronecker. Il prodotto di Hadamard è definito per due m. A e B con lo stesso numero di righe (m) e colonne (n) ed è uguale alla m. di dimensione m×n il cui elemento (i,j)-esimo è uguale al prodotto di a_ij per b_ij. Il prodotto di Kronecker è invece definito qualunque sia la dimensione delle matrici A e B. Se A ha dimensione n×m e B ha dimensione l×k, allora il prodotto di Kronecker A⊗B è la matrice di dimensione n.×mk, ottenuta moltiplicando ciascun elemento a_ij di A per la m. B.

Matrici trasposte e matrici inverse

Data una m. A, m×n, si definisce m. trasposta di A, indicata con A^T o con A., la m. di dimensione n×m ottenuta scambiando le righe con le colonne di A. Una m. quadrata si dice simmetrica se A=A.. Data una m. quadrata A, la sua inversa A⁻¹ è la m. tale che A⁻¹A=A.⁻¹=I. L’inversa non esiste sempre. Condizione necessaria e sufficiente per l’esistenza di A⁻¹ è che il determinante di A sia diverso da zero (➔ determinante) o, equivalentemente, che tutti gli autovalori di A (➔ autovettore) siano diversi da zero. Una m. invertibile è anche detta non singolare.

Matrici definite positive e definite negative

La generalizzazione a una m. quadrata del concetto di numero positivo o negativo conduce al concetto di m. definita positiva o definita negativa (➔ positivo definito). Esistono diversi modi di riscrivere una m. quadrata definita positiva come prodotto di m. più semplici. Uno di questi è la decomposizione spettrale, nella quale giocano un ruolo fondamentale gli autovettori e autovalori della m. stessa. Un altro tipo di decomposizione è quella di Cholesky (➔ Cholesky, decomposizione di).