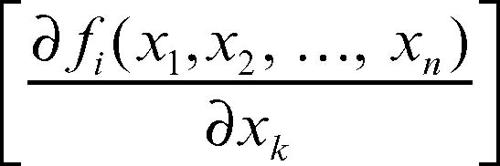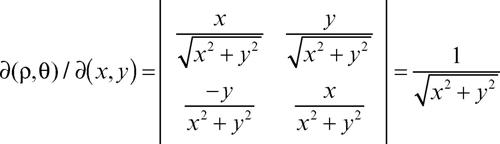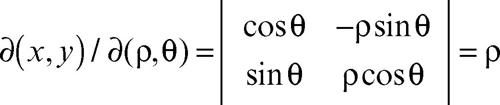matrice jacobiana

matrice jacobiana

matrice jacobiana matrice che generalizza a funzioni di più variabili la nozione di derivata prima. Si consideri una funzione ƒ: Rⁿ → R^m di n variabili reali, a valori vettoriali (il numero m di componenti di ƒ può essere diverso da quello n delle variabili indipendenti) e si supponga che tutte le componenti siano dotate di derivate parziali rispetto ai loro argomenti; si può allora costruire la matrice di tali derivate prime

Questa matrice è detta matrice jacobiana, ha dimensioni m × n, e viene designata in letteratura con simboli quali J, Dƒ(x), ∂ƒ /∂x, ∂[ƒ₁, ..., ƒ_m]/∂[x₁, ..., x_n]. Nel caso m = 1 la matrice si riduce a un vettore riga, che coincide col gradiente della funzione ƒ. Il differenziale di ƒ si ottiene moltiplicando J per il vettore dx ∈ Rⁿ.

Se si compongono le funzioni (di classe C¹) ƒ: Rⁿ → R^m e g: R^m → R^p si ottiene la funzione composta g ∘ ƒ: Rⁿ → R^p, z = g(ƒ(x)), la cui jacobiana è data dal prodotto delle jacobiane, nell’ordine:

generalizzando così il teorema di derivazione della funzione composta a funzioni vettoriali.

Il caso m = n è particolarmente importante, perché corrisponde a trasformazioni y = ƒ(x) dello spazio Rⁿ in sé. L’invertibilità locale della trasformazione è garantita, per il teorema di → Dini, dal fatto che la matrice jacobiana J sia non singolare, e quindi che il suo determinante, detto jacobiano e indicato con det(J) o con ∂(ƒ₁, ..., ƒ_n)/∂(x₁, ..., x_n), sia diverso da zero. Il suo segno dipende dalla permutazione degli assi (ogni scambio di assi corrisponde a uno scambio di colonne e quindi a un cambio di segno del determinante). La jacobiana della trasformazione inversa è J⁻¹, estendendosi in tal modo il teorema di derivazione delle funzioni inverse. Dal punto di vista geometrico, lo jacobiano rappresenta il rapporto tra le misure (n-dimensionali) di due elementi corrispondenti. Per esempio, in due variabili, se si considera il passaggio da coordinate cartesiane a polari, si hanno le formule

(valide per x > 0; per gli altri punti, tranne l’origine, si deve modificare l’espressione di θ, ma i calcoli sono analoghi). Le inverse sono x = ρcosθ, y = ρsinθ. Gli jacobiani sono rispettivamente

e

I due determinanti sono dunque l’uno l’inverso dell’altro (come lo sono le matrici); la biunivocità della corrispondenza è assicurata per ρ ≠ 0, cioè fuori dall’origine, ma solo localmente (l’argomento non è definito univocamente). L’elemento di area espresso da dT = dxdy in coordinate cartesiane diviene

in coordinate polari.