Matematica
Matematica
(XXII, p. 257; App. II, ii, p. 276; III, ii, p. 44; IV, ii, p. 414)
Nella voce matematica pubblicata nel vol. XXII della Enciclopedia Italiana, l'etimologia greca della parola introduce una stringata visione della storia della m. fino al 19° secolo, strettamente collegata a una riflessione sul suo significato e sulla sua natura nell'insieme dei saperi; vengono considerati anche alcuni aspetti psicologici dell'attività e del pensiero matematico, oltre ad alcune questioni relative all'insegnamento della matematica. Completano la voce una bibliografia ragionata e la classificazione dei rami della m. seguita nell'opera enciclopedica tedesca Encyclopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen (1898-1935). Nell'Enciclopedia questi settori classici sono oggetto di specifiche voci, sia nell'ambito delle 'matematiche pure' (aritmetica, IV, p. 362; combinatoria, analisi, X, p. 912; algebra, II, p. 421; probabilità, calcolo delle, XXVIII, p. 259; differenze, calcolo delle, XII, p. 790; integrale, calcolo, XIX, p. 364; differenziale, calcolo, XII, p. 792; funzione, XVI, p. 185; equazione, XIV, p. 132; variazioni, calcolo delle, XXXIV, p. 1001; funzionali, XVI, p. 180; geometria, XVI, p. 623; analysis situs, III, p. 87) sia in quello delle 'matematiche applicate' (i vari settori della meccanica e della fisica matematica: v. meccanica, XXII, p. 660; idrodinamica, XVIII, p. 735; elasticità, XIII, p. 606; e anche geodesia, XVI, p. 589; astronomia, V, p. 105).
La questione del valore e della natura della m. viene riesaminata nell'App. II alla luce delle tendenze che si affermano a partire dagli anni Trenta. Sulla scia dello sviluppo degli studi di logica matematica - volti a chiarire il problema dei fondamenti della disciplina - e dell'elaborazione dell'impostazione assiomatica, si diffonde una concezione della m. come sistema ipotetico-deduttivo, che trova una sua realizzazione negli Élements de mathématique, un'opera pubblicata sotto lo pseudonimo Bourbaki da un gruppo di ricercatori francesi a partire dal 1939 (v. bourbaki, nikolas, App. II, i, p. 441; matematica, ii, p. 276; logica matematica, ii, p. 266). Lo sviluppo dell'algebra moderna, l'algebrizzazione di molte teorie matematiche e la nascita di nuovi settori di ricerca, caratterizzati da una grande astrazione, portano a una radicale trasformazione dei metodi e dei confini disciplinari dell'analisi e della geometria nei decenni centrali del secolo: nelle voci matematica delle App. III e IV si sottolinea il contrasto con gli indirizzi classici, e in particolare con l'approccio che aveva caratterizzato la geometria e la m. italiana (v. anche algebra, App. III, i, p. 61; topologia, ii, p. 960; funzionale, analisi, App. IV, i, p. 883). Il quadro di questo periodo si completa considerando la crescita e il rinnovamento della m. applicata, dovuto all'avvento degli elaboratori elettronici e all'emergere di nuovi strumenti e teorie; le voci relative si trovano nell'App. III: informazione, teoria della (i, p. 874); operativa, ricerca (ii, p. 315; ma v. anche App. IV, ii, p. 669, V, iii, p. 768); programmazione lineare (ii, p. 494; ma v. anche App. IV, iii, p. 67; V, iv, p. 291); nell'App. IV: giochi, teoria dei (ii, p. 74); ottimizzazione (ii, p. 707); programmazione non lineare (iii, p. 70; ma v. anche App. V, iv, p. 292); sistemi (iii, p. 347; ma v. anche App. V, iv, p. 802); decisioni, teoria delle (i, p. 579). Vedi inoltre attuariale, matematica (App. III, i, p. 169; IV, i, p. 189); finanziaria, matematica (App. III, i, p. 615); statistica (App. IV, iii, p. 447).
Oltre alle voci dedicate alle diverse discipline matematiche, vengono esaminati in voci specifiche alcuni concetti matematici basilari, fra cui per es., nell'Enciclopedia: angolo, III, p. 335; cerchio, IX, p. 781; coordinate, XI, p. 294; curve, XII, p. 172; determinanti, XII, p. 691; frazione, XVI, p. 45; insieme, XIX, p. 358; numero, XXV, p. 31; punto, XXVIII, p. 548; superficie, XXXIII, p. 1; vettore, XXXV, p. 276; e nelle Appendici: frattali (V, ii, p. 329); gruppo (II, i, p. 1096; iii, i, p. 795; IV, ii, p. 119); matrice (IV, iii, p. 415); serie (III, ii, p. 699; IV, iv, p. 308); stocastici, processi (V, v, p. 275); varietà (II, ii, p. 1089; III, ii, p. 1069). Infine, per alcuni temi filosofici generali viene trattato l'aspetto fisico-matematico (infinito: L'infinito nella storia della fisica e della matematica, XIX, p. 206; spazio: Le teorie dello spazio e la geometria, XXXII, p. 316).
Negli ultimi decenni il grande dinamismo della m., come disciplina e come professione, si manifesta in una duplice tendenza: centrifuga, che porta alla frammentazione e alla specializzazione e centripeta, che opera nel conservare l'unità della matematica. *
La comunità matematica internazionale
Nel corso del Novecento si è consolidato un gran numero di comunità matematiche nazionali. Ai paesi con maggiore tradizione nella ricerca matematica, come la Francia, la Germania e la Gran Bretagna, si sono affiancate molte altre nazioni, fra cui alcune depositarie di una cultura matematica in grande misura indipendente, come il Giappone, la Cina e l'India. A questo sviluppo ha contribuito la fiducia nell'importanza della ricerca e dell'educazione matematica nel processo di modernizzazione di ogni paese, attraverso il loro ruolo nella formazione scientifica e nello sviluppo tecnologico, e di conseguenza nell'affermazione dell'identità nazionale. Una tale convinzione ha cominciato a diffondersi nel mondo intellettuale, ma anche fra le classi politiche, nell'Ottocento, e si è consolidata nel secolo 20° soprattutto a partire dalla Seconda guerra mondiale, durante la quale si sono avuti straordinari sviluppi della ricerca matematica che hanno mostrato la loro utilità in ambito militare e la potenziale applicabilità in molti altri settori (v. oltre).
La m. occidentale di radice greca si è imposta a conclusione di un lungo processo storico, nel corso del quale si sono sviluppate in diverse culture tradizioni matematiche le cui influenze reciproche non sono ancora ben conosciute. Alcune conoscenze matematiche delle antiche civiltà di Mesopotamia ed Egitto furono ereditate dalla m. greca, la quale a sua volta potrebbe aver avuto un influsso in epoca medievale sulla m. in India, ove esisteva una tradizione essenzialmente indipendente che era iniziata nel primo millennio a.C. con i testi vedici per la preparazione degli altari, i Śulbasūtras; d'altra parte, la m. araba è erede sia della tradizione greca che di quella sanscrita. Un'altra tradizione indipendente è quella della m. cinese, la cui opera classica - vale a dire, comparabile per la sua rilevanza in questo ambito culturale agli Elementi di Euclide per la m. occidentale -, Jiuzhang suanshu (I nove capitoli sulle procedure matematiche), fu scritta sotto la dinastia Han, attorno all'inizio dell'era volgare; oltre all'enorme influenza di questa tradizione nell'area culturale del cinese classico (Corea, Giappone, Tibet, Vietnam, Mongolia), diversi indizi permettono di congetturare che vi furono contatti sia con la m. indiana, sia con quella araba. La m. tradizionale giapponese, detta wasan, fu sviluppata in modo indipendente nel tentativo di 'decifrare' un'opera cinese, Suanxue qumeng (Introduzione agli studi matematici, 1299), che arrivò in Giappone attraverso la Corea dopo le spedizioni militari giapponesi nel continente alla fine del Cinquecento, in un periodo di decadenza degli studi matematici in Cina (Companion encyclopedia 1994; L'Europe mathématique 1996).
Negli ultimi anni si è rivolta una grande attenzione alla conoscenza delle varie tradizioni matematiche, alla circolazione delle idee e allo studio comparato delle varie forme di attività matematica. Oltre che sulle metodologie storiografiche di applicazione generale, nel caso della m. si lavora anche sulla tradizione antica e medievale dei problemi concreti, anche di tipo pratico o ricreativo, presenti nei testi di m., che si ritrovano nei contesti culturali più svariati; questi elementi hanno portato a pensare a una via secondaria nella trasmissione delle conoscenze matematiche di natura pratica, utili a commercianti, geometri e capomastri, quasi una 'via della seta' della matematica. Più in generale, le ricerche di etnomatematica, rivolte soprattutto allo studio di alcune culture indigene in Africa e in America, tentano di rintracciare attraverso la diversità culturale le idee matematiche, intese in un senso generale come quelle che coinvolgono il numero, la configurazione spaziale e la logica, e soprattutto la combinazione e organizzazione di queste idee in sistemi (Høyrup 1994; Ascher 1991; Gerdes 1994).
Lo sviluppo della m. nei singoli paesi è segnato da alcune iniziative ben definite, le quali, poiché si tratta di una delle discipline più consolidate, sono emblematiche dell'istituzionalizzazione scientifica moderna. Innanzitutto, sono state create numerose società nazionali dedicate specificamente alla m. e alle quali aderiscono liberamente quanti si interessano alla disciplina da una molteplicità di posizioni culturali e sociali; le prime società di questo genere, che hanno sostituito le accademie alle cui discussioni partecipava una cerchia limitata di 'saggi' e che avevano un carattere transdisciplinare, sono state create nell'Ottocento: nel 1864 la Società matematica di Mosca; nel 1865 la London Mathematical Society; nel 1872 la Société mathématique de France; nel 1884 la American Mathematical Society; nel 1890 la Deutsche Mathematiker-Vereinigung. Molte altre sono sorte nel seguito, come per es. l'Unione matematica italiana (1922), la Sociedad matemática argentina (1924), la Società matematica cinese (1935), fino alla European Mathematical Society (1990). Altre iniziative importanti sono la pubblicazione di riviste da parte di queste società e l'organizzazione di una ricerca matematica autonoma, in grado di produrre contributi originali, attraverso la creazione di nuovi posti accademici, la fondazione di istituti di ricerca (v. matematica, App. II) e la cura della formazione dei giovani studiosi (Parshall 1996; Companion encyclopedia 1994; Messengers of mathematics 1993).
Questo processo, che ha prodotto ovviamente una grande crescita del numero di matematici attivi in tutto il mondo, è stato accompagnato da numerose iniziative volte a favorire lo scambio internazionale. Se la circolazione internazionale delle idee è sentita come una condizione fondamentale del progresso della scienza, non è meno certo che i numerosi interessi economici, militari e anche politici legati alla ricerca scientifica contemporanea condizionano pesantemente la comunicazione fra gli scienziati di tutto il mondo. Questo è vero anche per la m.: valga come esempio un caso individuale, quello dei molti lavori di J. von Neumann, uno dei più importanti matematici del 20° secolo (App. III), che sono rimasti inediti, coperti dal segreto militare, per lunghi anni; questo problema si è riproposto anche per i lavori di crittografia, da quelli di C. Shannon fino al più recente cifrario RSA (dai nomi degli autori, R. Rivest, A. Shamir e L. Adelman). Di maggiore portata per quanto riguarda il numero di ricercatori coinvolti sono state le difficoltà provocate dalla Prima guerra mondiale nei contatti fra matematici tedeschi e non, e dalla Guerra fredda fra matematici dei paesi comunisti e non. Comunque, è forse lecito affermare che nell'ambito della m., più che in altre discipline, permane la convinzione di lavorare in un'impresa comune, attorno a problemi riconosciuti da tutti (anche ereditati da matematici del passato, come nel caso del teorema di Fermat recentemente dimostrato: v. numeri, teoria dei, in questa Appendice) e con metodi e tecniche ampiamente condivise. Difatti, alle riviste matematiche nazionali si è aggiunta un'imponente quantità di riviste altamente specializzate improntate a un genuino respiro internazionale, seguendo un'impostazione che fu aperta fra la fine dell'Ottocento e l'inizio del Novecento dalle riviste Acta mathematica, diretta da G. Mittag-Leffler, e Rendiconti del Circolo matematico di Palermo, diretta da G.B. Guccia (Brigaglia, Masotto 1982).
D'altra parte, mentre la ricerca scientifico-tecnologica presenta caratteri collettivi sempre più marcati, la ricerca matematica manifesta ancora una peculiare impronta individuale. Un buon esempio recente è dato dalla soluzione positiva per l'ultimo teorema di Fermat. Infatti, sebbene il risultato si basi su una serie di idee prodotte da autori diversi, è anche vero che il passo finale, densissimo sia da un punto di vista concettuale che tecnico, è stato compiuto da un solo uomo, A. Wiles, in sette anni di lavoro solitario e segreto. Un discorso analogo può farsi per le congetture di Weil (dimostrate da P.R. Deligne) o per la congettura di Mordell (dimostrata da G. Faltings).
La crescita fortissima del numero di articoli di ricerca matematica che vengono pubblicati mensilmente in tutto il mondo, negli ultimi anni anche all'interno degli electronic journals, rende necessario un lavoro di documentazione e di disseminazione dell'informazione che poggia fondamentalmente sulla rivista di recensioni Mathematical reviews, fondata nel 1940 e, dal 1996, su MathSciNet, che rende possibile accedere ai dati attraverso Internet. Strumenti di questo tipo sono stati approntati per tutte le discipline scientifiche, anche se hanno una funzione diversa a seconda dei casi. Uno studio sull'invecchiamento dei riferimenti bibliografici condotto dalla rivista di citazioni Science citation index nel 1990 ha mostrato che, mentre i lavori in biologia molecolare hanno una vita media per le citazioni di alcuni mesi, i lavori di m. sopravvivono in media almeno alcuni decenni. La società matematica statunitense AMS (American Mathematical Society) sostiene questa pubblicazione proprio in quanto considera essenziale conservare la memoria e la possibilità di reperire dei risultati che, a volte, dimostrano la loro fecondità molti anni dopo la loro produzione, e ciò nonostante l'enorme impegno: da un volume di 400 pagine contenente 2115 recensioni pubblicato nel primo anno di attività si è arrivati alle circa 7000 pagine (più altre 4000 di indici) pubblicate oggigiorno annualmente, per un totale di circa 50.000 recensioni.
La rivista Mathematical reviews fu fondata in pieno conflitto bellico come reazione all'espulsione dei matematici ebrei dal comitato scientifico che guidava la rivista di recensioni tedesca Zentralblatt für Mathematik und ihre Grenzgebiete, ancora oggi attiva e pubblicata da una delle case editrici di m. di più antica tradizione, Springer Verlag (Sarkowski, Gotze 1992-94). Il direttore dello Zentralblatt, O. Neugebauer, dimessosi ed emigrato negli Stati Uniti, diventò direttore della nuova rivista, la cui creazione segna la forte crescita professionale e culturale della m. americana, consolidata definitivamente proprio grazie all'emigrazione di gran parte dei matematici tedeschi. La comunità matematica tedesca mantenne fino all'esplodere della Seconda guerra mondiale una notevole influenza internazionale, e in particolare l'attività dell'Istituto di matematica dell'Università di Gottinga, sotto la guida di F. Klein e di D. Hilbert, è rimasta il modello accademico operante in tutti i paesi, relativamente all'equilibrio fra insegnamento e ricerca matematica e alla disponibilità di scambi internazionali di studenti e ricercatori. Tuttavia, nel dopoguerra gli Stati Uniti hanno sostituito la Germania nella leadership della comunità matematica internazionale. Un ruolo comparabile è stato svolto soltanto dall'Unione Sovietica, e soprattutto dalla scuola matematica di Mosca, che ha mantenuto una forte specificità culturale (v. oltre); il disagio politico nei confronti del regime comunista a partire dagli anni Sessanta (e soprattutto dopo la lettera di protesta firmata nel 1968 da un gruppo di matematici contro la reclusione del logico-matematico A. Essenin-Volpin), però, ha contribuito a indebolire la m. russa, almeno da un punto di vista istituzionale, e a partire dal 1985 molti fra i più insigni matematici russi si sono trasferiti all'estero, in particolare negli Stati Uniti.
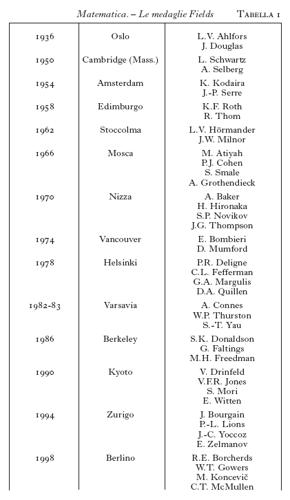
Le drammatiche vicende politiche del Novecento hanno minacciato fortemente la prospettiva globale e internazionale della m., rappresentata soprattutto dai convegni internazionali dei matematici (ICM, International Congress of Mathematicians) che hanno periodicità quadriennale: il primo di questa serie ebbe luogo a Zurigo nel 1897, e nel 1900 si tenne a Parigi il memorabile congresso nel quale Hilbert presentò una lista dei problemi aperti come proposta di lavoro per il nuovo secolo; nel 1990 è stata scelta per la prima volta una sede nel continente asiatico, Kyoto; nel 1998 la scelta di Berlino può essere considerata carica di implicazioni storiche per l'evoluzione della m. nel secolo che si chiude; nel 2002 il convegno si terrà a Pechino. Questa serie di riunioni scientifiche internazionali è organizzata dalla IMU (International Mathematical Union), creata nel 1920 e rifondata nel 1951 per iniziativa americana; i paesi socialisti europei vi hanno preso parte solo dopo la morte di Stalin (Lehto 1998). L'IMU, alla quale appartengono oggi sessanta paesi, assegna le medaglie Fields, il più importante riconoscimento nel campo della m. (istituito dal matematico canadese J.C. Fields nel 1932 e assegnato a due o più matematici di età inferiore ai 40 anni in occasione dei convegni internazionali; tab. 1), e a essa aderisce la ICMI (International Commission on Mathematical Instruction), fondata durante il convegno internazionale tenutosi a Roma nel 1908.
Particolarmente degna di nota in questo contesto generale risulta l'evoluzione che si è registrata in Cina, in Giappone e in India. Un fondamentale contributo per l'introduzione della m. occidentale in Cina fu dato dalle traduzioni di opere matematiche pubblicate verso la metà dell'Ottocento dal missionario inglese A. Lie e da Li Shan-lan, che posero le basi dell'attuale terminologia matematica in cinese; tuttavia solo all'inizio del Novecento, sulla scia del rifiuto della cultura classica cinese, dell'apertura alle idee occidentali e della nascita della Repubblica cinese dopo la rivoluzione del 1911, fu definitivamente abbandonato il simbolismo matematico tradizionale, fu inserita la m. moderna nei programmi di insegnamento e iniziò il contatto con i centri della ricerca in Europa e negli Stati Uniti. Benché la Cina abbia prodotto studiosi di fama internazionale, le vicende politiche hanno segnato lo sviluppo altalenante della ricerca matematica. Dopo la rivoluzione comunista del 1949 molti matematici si stabilirono all'estero, come il geometra S.S. Chern; quelli rimasti, come Hua Luo-geng, primo direttore dell'istituto di Matematica della rifondata Accademia cinese, riorientarono i contatti internazionali verso l'Unione Sovietica e i paesi comunisti europei e rivolsero molta della loro attenzione a problemi di natura applicativa, anche per esigenze ideologiche. Il periodo di più intenso sviluppo della m. cinese è iniziato a metà degli anni Settanta, grazie alla maggiore apertura nei rapporti internazionali (la Cina è stata ammessa all'IMU solo nel 1986), alla crescita dei finanziamenti destinati alla ricerca e allo sforzo nella formazione dei giovani, che hanno prodotto notevoli risultati.
Anche in Giappone lo sviluppo della m. moderna e l'abbandono della tradizione wasan è stato un aspetto culturale fondamentale nell'accelerato processo, iniziato nella seconda metà dell'Ottocento, di superamento dell'isolamento del paese e di conseguente modernizzazione e occidentalizzazione. La m. occidentale - a cominciare dai numerali indo-arabici e dai quattro simboli per le operazioni aritmetiche fondamentali, fino ad allora sconosciuti ai Giapponesi - fu introdotta nelle scuole elementari nel 1872 e all'università di Tokio nel 1877. Nella prima tappa evolutiva della m. moderna in Giappone, caratterizzata dall'organizzazione di un'attività di ricerca autonoma contrassegnata dall'influenza della Germania, ebbero un ruolo decisivo R. Fujisawa e il suo allievo T. Takagi. Una seconda fase si è aperta simbolicamente, finita la Seconda guerra mondiale, con la creazione della società matematica giapponese nel 1946 e la visita di M. Stone per invitare i matematici giapponesi a unirsi all'IMU. Ma è stato solo grazie ai contributi di studiosi come H. Hironaka, K. Kodaira e S. Mori che la ricerca matematica giapponese, in stretto collegamento con gli Stati Uniti, si è sviluppata in modo spettacolare, in particolare nei settori della teoria dei numeri e della geometria algebrica. Segni della maturità di questa comunità sono l'importante impresa culturale della pubblicazione di un monumentale dizionario enciclopedico della m., che costituisce oggi un'importante opera di riferimento (ha avuto varie edizioni, l'ultima nel 1985, ed è stato tradotto in inglese con il titolo Encyclopedic dictionary of mathematics), la creazione di nuovi istituti come l'Istituto di Kyoto e infine l'organizzazione del primo convegno internazionale tenutosi nell'emisfero orientale (1990), con sede proprio a Kyoto.
Lo sviluppo della m. è stato sentito anche in India come un aspetto fondamentale del progresso generale del paese, prima e dopo l'indipendenza. Si è trattato comunque di un processo più lento, contrassegnato dall'influenza della Gran Bretagna (come dimostra per es. l'importante contributo agli studi di statistica matematica), dall'attività di alcuni prestigiosi istituti di ricerca e da alcune personalità di primo piano, come S.A. Ramanujan, K. Chandrasekharan, Harish-Chandra, K.R. Parthasarathy e C.R. Rao.
La m. è un sapere con una storia plurimillenaria che attraversa molte culture; pur nelle sue diverse forme, le viene generalmente riconosciuto un valore culturale universale, in particolare per la cultura contemporanea. L'anno 2000 è stato dichiarato Anno internazionale della matematica sotto il patrocinio dell'UNESCO, anche in considerazione del ruolo chiave che la diffusione della cultura matematica svolge per lo sviluppo: le applicazioni della m. nella scienza e nella tecnologia sono in continua espansione, e la formazione matematica, che è stata uno dei pilastri dell'insegnamento fin dalla creazione delle prime scuole, continua a essere sentita come un'esigenza fondamentale nell'educazione dei futuri cittadini.
La ricerca matematica e le applicazioni nella scienza e nel mondo produttivo
La ricerca matematica del Novecento si è sviluppata secondo una nuova e cangiante articolazione del rapporto fra m. pura e m. applicata. La classica distinzione fra m. pura o teorica e m. mista (secondo l'esposizione del sistema delle conoscenze umane contenuta nell'Encyclopédie di d'Alembert e Diderot, la prima si occupa della quantità astratta, mentre la seconda si articola in tante divisioni e suddivisioni quanti sono gli enti reali nei quali la quantità può essere considerata) si è modificata per il riposizionamento della m. pura nei suoi rapporti con la meccanica, e in generale nei riguardi dello sforzo della scienza per spiegare il mondo fisico. J. Dieudonné, un illustre rappresentante di questa tendenza nel contesto del bourbakismo, scriveva nel 1964 che a una concezione platonica della m. come idealizzazione del mondo sensibile si era venuto a sostituire "un atteggiamento di completa indipendenza riguardo al 'concreto', rivendicando la possibilità di sviluppare nozioni puramente astratte rette da sistemi di assiomi quasi arbitrari e senza una necessaria corrispondenza con la realtà sperimentale; […] ci si è resi conto che le procedure che sembravano vincolate a certi tipi di oggetti nati dalla nostra intuizione sensibile (numeri, figure geometriche ecc.) avevano un campo di applicazione 'astratto' molto più vasto e superavano senza difficoltà le barriere che l'uso tradizionale sembrava imporre al suo impiego" (in Histoire générale des sciences 1964; trad. it. 1984, p. 20).
Ciononostante, un numero sempre maggiore di matematici svolge la propria attività in collegamento con le applicazioni in ambito scientifico (innanzitutto in fisica, ma anche in altre discipline che erano rimaste fino al Novecento estranee alla m., come l'economia o la biologia) e tecnologico (applicazioni militari e industriali). L'interesse per le applicazioni concrete si è mantenuto vivo nell'Unione Sovietica anche per motivi ideologici, fondamentali nel pensiero marxista, i quali hanno intralciato la pervasività dell'approccio bourbakista: ci si riferisce all'idea di sapore genericamente positivista e ottocentesco, secondo la quale l'importanza della m. (nel contesto dell'impresa scientifica) risiede nel contributo che essa porta al progresso materiale della società. Difatti i matematici sovietici hanno continuato a studiare, sotto la guida di A.N. Kolmogorov, problemi di analisi di equazioni differenziali non lineari (la non linearità si presenta spesso nelle applicazioni), altrove meno considerati fino ad anni recenti, quando tali questioni sono tornate di grande attualità (v. caos e complessità, App. V), e hanno dato grandi contributi alla teoria del controllo, alla programmazione lineare (sviluppata indipendentemente dallo statunitense G.B. Dantzig, che dal 1941 al 1946 era stato a capo del Combat Analysis Branch, in ambito militare, e dal sovietico L.V. Kantorovič, come risposta ai problemi della pianificazione dello sviluppo industriale dell'Unione Sovietica fra la fine degli anni Trenta e l'inizio degli anni Quaranta), alla teoria della turbolenza e così via (Golden years, 1993; Chaos et déterminisme, 1992).
La mobilitazione degli scienziati durante la Seconda guerra mondiale riguardò molti matematici: è emblematico il caso della Gran Bretagna, dove per es. il topologo M.H.A. Newman diresse una sezione del servizio di intelligence che si occupava di decifrare i codici del nemico; il logico matematico A. Robinson contribuì con le sue ricerche di aerodinamica per la British Royal Aircraft allo sviluppo di razzi per le forze alleate (sviluppo basato in parte sui dati relativi ai razzi tedeschi V1 e V2 forniti dallo spionaggio); J. Todd organizzò il servizio di calcolo numerico militare. Ma anche negli Stati Uniti, nell'ambito del Comitato di ricerche per la difesa nazionale organizzato nel 1940 dall'ingegnere V. Bush, fu organizzato un gruppo specifico di m. applicata, diretto da W. Weaver: il contributo dei matematici, fra cui von Neumann, N. Wiener e S. Ulam, spaziò dalla balistica alla progettazione degli aerei, alla lotta antiaerea, alla logistica, agli esplosivi e allo sviluppo del calcolo automatico. Questi successi spiegano il forte sostegno delle autorità militari alla ricerca matematica durante la guerra fredda; i finanziamenti, d'altra parte, non soltanto hanno portato a un notevole sviluppo della m. applicata, ma ne ha tratto beneficio anche la m. pura, in ragione della diffusa convinzione che gli sviluppi teorici avrebbero comunque trovato una futura applicazione (The history of modern mathematics, 1989, 2° vol.; A century of mathematics in America, 1988-89). Questa fiducia, propria anche dei bourbakisti e basata su quello che E. Wigner (1960) ha espressivamente descritto come l'"irragionevole efficacia della matematica", unita al fatto che le ricerche matematiche sono molto meno onerose di altre ricerche scientifiche, ha garantito una grande libertà negli indirizzi e nei temi, che solo di recente si comincia a vedere minacciata con il tentativo delle agenzie nazionali, come la statunitense National Science Foundation, di controllare la ricerca anche in termini di 'ritorno' e di risultati (Mumford 1998).
Alcune fra le più astratte ricerche in settori come la geometria algebrica, la topologia differenziale e la teoria della probabilità continuano a trovare importanti applicazioni nella fisica fondamentale, che sembrano prolungare una tradizione iniziata con lo sviluppo del calcolo infinitesimale in connessione con quello della meccanica e proseguita con l'applicazione della geometria nella teoria della relatività. La fisica continua a essere fonte di problemi matematici oltre che sorgente di nuove tecniche e punti di vista che si svelano fondamentali nella scoperta e dimostrazione di nuovi risultati del tutto interni alla matematica. Un esempio significativo è il ruolo delle teorie di gauge in un numero importante di risultati topologici e geometrici (v. fisica matematica, in questa Appendice). Tuttavia, lo sviluppo della m. 'in vista delle applicazioni' del Novecento ha delle caratteristiche concettuali e metodologiche proprie, in virtù dell'emergere dell'approccio modellistico (v. modellistica matematica, in questa Appendice). Esso è collegato alla nascita di branche completamente nuove, come la teoria dei giochi, la teoria dell'informazione, la ricerca operativa, l'ottimizzazione, la teoria delle decisioni (v. sopra); a ulteriori risultati in branche classiche come le equazioni differenziali, allo sviluppo della teoria del controllo, della teoria dei sistemi dinamici, e all'introduzione del tema della complessità nello studio dei sistemi (v. equazioni e complessità, in questa Appendice); allo sviluppo della probabilità e di metodi di statistica matematica che trovano applicazione nei più disparati settori di attività; all'emergere di una nuova m. numerica con lo sviluppo dei metodi computazionali, e di conseguenza all'approfondimento di campi come l'algebra lineare (v. computazionali, metodi, in questa Appendice; Hackbusch 1998); e alle ricerche di m. combinatoria sui problemi del finito, spesso richiamate con il nome di matematica discreta (v. finito, in questa Appendice).
Il lavoro dei matematici applicati, come quello degli informatici, non si svolge più soltanto nell'ambito accademico ma anche nell'industria (aeronautica, automobilistica, informatica, tessile, delle telecomunicazioni, chimica) e nei servizi, in stretta collaborazione con gli ingegneri industriali e gestionali e altri professionisti: negli Stati Uniti, circa il 44% dei giovani laureati in m. nel periodo 1988-92 e il 25% dei dottori di ricerca nello stesso periodo hanno lavorato in questo contesto.
Problematiche tipiche della m. applicata sono: la modellizzazione di fenomeni fisici, chimici e biomedici; la progettazione di elementi, strutture e sistemi in ingegneria per ottimizzare il rendimento produttivo; la pianificazione e la direzione di strategie di mercato e finanziarie; la comprensione e l'ottimizzazione dei processi di produzione (v. modellistica matematica; ottimizzazione; simulazione, in questa Appendice; v. anche tab. 2). Fra i problemi che si aprono verso il futuro si possono citare i modelli matematici per lo studio dei mutamenti climatici e per lo sviluppo di nuovi materiali, delle biotecnologie, degli strumenti multimediali. Un'associazione professionale fondata nel 1951 e che conta oggi più di 9000 soci, la SIAM (Society for Industrial and Applied Mathematics), grazie a un ampio programma editoriale e di riunioni scientifiche svolge un importante ruolo istituzionale in questo ambito, favorendo la circolazione interdisciplinare delle idee, non sempre facile (v. matematica, App. III); negli ultimi anni la SIAM si è occupata anche del problema della formazione che deve essere fornita a una figura professionale di 'matematico' il cui profilo è molto diverso da quella del matematico attivo in ambito accademico o nell'insegnamento (Friedman, Glimm, Lavery 1992; The Siam report, 1998).
Unità e diversità delle discipline matematiche
La classificazione adoperata dalle due principali riviste di recensioni della letteratura matematica, Mathematical Reviews e Zentralblatt, divide la m. in più di 60 rami, fino a un totale di più di 5000 settori specializzati di ricerca (v. tab. 3, dove si presenta la versione, con un solo livello di classificazione, introdotta a partire dal 2000). Si parte dalla logica matematica, la combinatoria e la teoria dei numeri; si continua con settori classici e moderni delle tre grandi aree dell'algebra, dell'analisi e della geometria, per arrivare a discipline il cui maggiore sviluppo si è registrato nel Novecento, come la topologia, la probabilità, la statistica e infine l'ultima arrivata, l'informatica, alla quale si fa riferimento in italiano anche con l'espressione scienze dell'informazione (computer science), con la quale si entra nei settori applicativi, in diversi ambiti della fisica, in economia, in biologia e così via.
La m. contemporanea appare attraversata da molte tensioni culturali, le cui origini risalgono a volte a tempi antichi: fra m. pura e applicata; fra m. del continuo, rappresentata dalle branche classiche dell'analisi e della geometria, e m. del finito, ritornata in primo piano anche per gli sviluppi dell'informatica teorica (v. informatica: Scienze dell'informazione, in questa Appendice); fra m. astratta (di stampo bourbakista, che tende alla massima generalità) e m. concreta (legata agli esempi, all'intuizione); fra m. strutturale, che punta alla dimostrazione di teoremi nel quadro di teorie assiomatizzate, e m. algoritmica, che sviluppa e analizza algoritmi (v. algoritmo, II; struttura: Matematica, App. V). Tuttavia, molti interessanti sviluppi teorici del Novecento sono proprio legati alle applicazioni, a volte sorprendenti, di risultati ottenuti in un settore entro un altro settore anche apparentemente lontano, come nel caso della dimostrazione dell'ultimo teorema di Fermat. La comunità matematica si confronta, alla pari con altre discipline scientifiche, con l'estrema specializzazione e con i problemi di comunicazione (Davis, Hersh 1982), ma forse anche in ragione della sua dimensione più ridotta (vi sono circa 50.000 ricercatori in m. attivi in tutto il mondo; Bourguignon 1998) tende ancora ad apprezzare le convergenze interdisciplinari e a lavorare per superare queste difficoltà. Un esempio attuale di un programma di ricerca trasversale a molti settori della m. è quello della 'quantizzazione', che prende le mosse proprio da alcuni sviluppi teorici legati all'apparato matematico della meccanica quantistica (v. matematica non commutativa, in questa Appendice). Anche la probabilità rappresenta un importante crocevia matematico: sono state date versioni 'stocastiche' di molte teorie matematiche o fisico-matematiche (equazioni differenziali stocastiche, meccanica stocastica, trasporto parallelo stocastico e così via); inoltre la teoria della probabilità appare come uno strumento cruciale in molte questioni che hanno un rilevante significato epistemologico, quali il problema della 'freccia del tempo' (contrasto tra microfisica reversibile e dinamica macroscopica irreversibile), il problema dell'esistenza di metodologie induttive nell'epistemologia contemporanea (si pensi alla polemica Popper-Carnap) e il significato dell'indeterminismo nella meccanica quantistica.
La ricchezza di approcci con la quale si presenta la ricerca matematica della fine del Novecento ha stimolato un crescente numero di studi analitici da un punto di vista filosofico, storico e anche sociologico. La riflessione sull'attività matematica si era concentrata nei primi decenni del secolo sul problema dei fondamenti logici del corpus teorico della matematica. Questa circostanza ha dato l'impulso iniziale a uno straordinario fiorire degli studi di logica matematica, i quali, con l'avvento degli elaboratori elettronici, si sono sviluppati anche in collegamento con i temi di base dell'informatica, per es. per quanto riguarda i concetti di algoritmo, di programma, di calcolabilità, e con le ricerche nel campo dell'intelligenza artificiale (v. logica matematica, App. IV; informatica: Scienze dell'informazione, in questa Appendice; intelligenza artificiale, App. V). Tuttavia, il programma filosofico teso a trovare dei solidi fondamenti per la m. ha subito numerosi insuccessi, a partire dalla dimostrazione dei teoremi di Gödel, e ha anche smesso di essere al centro della riflessione matematica. Negli ultimi anni è ritornato l'interesse per temi poco studiati dalla fine degli anni Trenta (v. matematica, XXII) quali lo studio della pratica matematica (per es. gli aspetti psicologici dell'invenzione matematica); il concetto effettivo di dimostrazione e il rapporto fra dimostrazione formale e informale, anche alla luce di alcune dimostrazioni moderne con l'ausilio del calcolatore o di una complessità e lunghezza che sembra al di là del controllo di un singolo individuo (v. finito, in questa Appendice); il rapporto della m. con il contesto culturale e sociale. Il problema dell'esistenza degli enti matematici e quello del confronto fra m. e altri aspetti del sapere scientifico (che mette in discussione la differenza fra la conoscenza matematica assoluta e certa e la conoscenza scientifica fallibile) sono altri temi sui quali si è tornato di recente; anche la moderna sociologia della scienza si è confrontata con la conoscenza matematica (Davis, Hersh 1982; New directions, 1986; Bloor 1991²; Cellucci 1998).
A un periodo di grande fioritura degli studi di storia della m., ovvero di uno dei settori di più antica tradizione della storia della scienza (v. scienza, App. V), rappresentato dalla monumentale opera di M. Cantor Vorlesungen über Geschichte der Mathematik (1898-1908) e da un notevole numero di edizioni critiche (riguardanti la m. sino alla fine del Settecento), è seguito un periodo di minore attività (una notevole eccezione è data dal lavoro di O. Neugebauer sulla m. antica). A partire dagli anni Settanta (nel 1972 K.O. May crea la International Commission on the History of Mathematics) si registra una ripresa dell'interesse per la ricerca storica. Tale ricerca, che ai primi del Novecento si concentrava sulla m. antica e medievale e sul periodo della Rivoluzione scientifica, si è aperto anche alla m. contemporanea, sia per quanto riguarda lo sviluppo delle idee, sia per gli aspetti sociali e di istituzionalizzazione scientifica. Il quadro storico si viene completando cronologicamente, ma anche culturalmente, prendendo in considerazione tradizioni matematiche diverse da quella occidentale (v. sopra), e alla considerazione degli aspetti teorici si è aggiunta l'analisi del ruolo della m. nello sviluppo materiale delle società (Kline 1972; The history of modern mathematics, 1989; Companion encyclopedia, 1994).
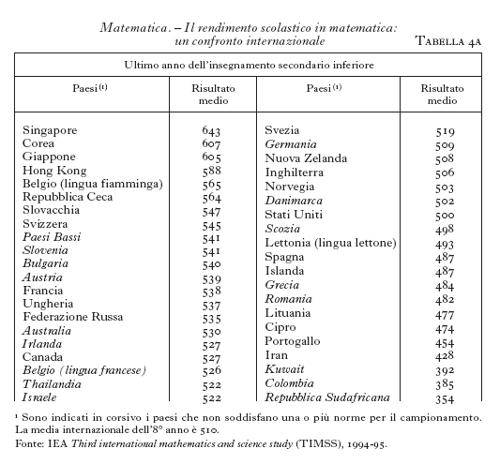
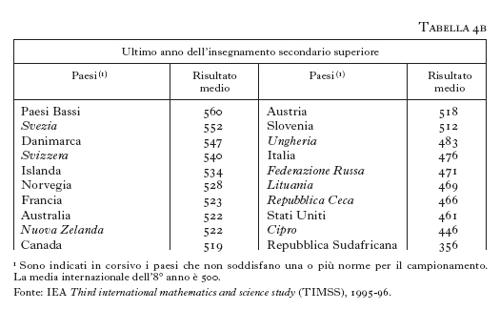
I mutamenti in atto nella m. e i recenti contributi sulla natura e il valore della m. si riflettono nel dibattito odierno sui problemi dell'educazione matematica. All'inizio del Novecento l'insegnamento elementare della m. era ancora basato essenzialmente sullo studio della geometria seguendo gli Elementi di Euclide e sull'acquisizione di alcune abilità aritmetiche, inclusa la soluzione di problemi legati alla proporzionalità, essenzialmente già codificate nelle scuole d'abaco italiane medievali. La trasformazione dell'insegnamento tradizionale nel mondo occidentale è stata segnata, da una parte, dall'eliminazione delle dimostrazioni e degli aspetti concettuali considerati difficili della geometria classica, soprattutto nei paesi anglosassoni, e, dall'altra, nelle aree dove si è sentito più fortemente l'influsso del bourbakismo, dall'introduzione della 'matematica moderna', vale a dire l'immissione anche a livelli elementari di concetti della teoria degli insiemi, e il rilievo dato agli aspetti astratti dell'algebra a scapito dell'aspetto concreto e intuitivo della geometria. Tuttavia, queste novità si sono dimostrate spesso fallimentari, sia per quanto riguarda il rendimento degli studenti, sia per le difficoltà incontrate nello studio della m. da molti di essi, che sembra aggravare la già tradizionale 'paura della matematica'. L'importanza assegnata internazionalmente al livello di cultura matematica in ogni singolo paese ha portato un notevole sviluppo delle ricerche sulla didattica della m. (per es., in Inghilterra, in Francia e negli Stati Uniti, anche promosse dalle autorità educative) e iniziative a livello internazionale, come i convegni ICMI (v. sopra: La comunità matematica internazionale), le Olimpiadi di matematica e gli studi di valutazione comparata sul rendimento scolastico in matematica. A partire dal 1964 la International Association for the Evaluation of the Educational Achievement ha promosso tre studi internazionali sulla m. e sulla scienza, allo scopo di confrontare i contenuti e la pratica dell'insegnamento e il rapporto fra rendimento e contesto sociale ed educativo. Si forniscono i risultati dello studio condotto negli anni 1994 e 1995 (risultati del 1996 e 1997) per quanto riguarda la m., sia per gli allievi di 13 anni (vale a dire l'età attorno alla quale finisce l'insegnamento obbligatorio nella maggioranza dei paesi, tab. 4a) sia per gli studenti dell'ultimo anno dell'insegnamento secondario (tab. 4b).
Per ogni paese è stato scelto un campione di studenti seguendo delle norme internazionali. Gli studenti sono stati sottoposti a una prova di rendimento costituita da una serie di domande, collocate in una scala relativa al grado di difficoltà. Il rendimento globale di ogni paese corrisponde al punteggio medio ottenuto dagli studenti in questa scala, calibrata in modo che il punteggio medio internazionale per gli studenti di 13 anni (7° e 8° anno di scuola) sia di 500, con un'oscillazione di 100.
Il recupero degli aspetti concreti e algoritmici della m., anche attraverso l'introduzione di temi della m. discreta e l'esplorazione delle procedure computazionali, il ritorno alla geometria e lo sviluppo dell'intuizione spaziale, l'avvicinamento ai processi del pensiero matematico nelle sue molte facce, inclusa la probabilità, e infine il lavoro sulle motivazioni, stimolando l'apprezzamento e l'interesse per la m., per le sue applicazioni e per il suo ruolo nella cultura umana, sono alcune delle proposte su cui si continuerà a lavorare nelle scuole nei prossimi anni (Reshaping school mathematics, 1990; International handbook of mathematics education, 1996).
bibliografia
G. Polya, Induction and analogy in mathematics, 2 voll., Princeton (N.J.) 1954.
N. Wiener, I am a mathematician, New York 1956.
E. Wigner, The unreasonable effectiveness of mathematics in the natural sciences, in Communications in pure and applied mathematics, 1960, pp. 1-14.
Histoire générale des sciences, éd. R. Taton, 2° vol., 3° t., Le XXe siècle, Paris 1964 (trad. it. Roma 1984).
M. Kline, Mathematical thought from ancient to modern times, New York 1972 (trad. it. Storia del pensiero matematico, 2 voll., Torino 1991).
D. Bloor, Knowledge and social imagery, London-Boston 1976, Chicago 1991² (trad. it. La dimensione sociale della conoscenza, Milano 1994).
I. Lakatos, Proofs and refutations. The logic of mathematical discovery, Cambridge 1976 (trad. it. Milano 1979).
S. Ulam, Adventures of a mathematician, New York 1976 (trad. it. Palermo 1995).
J. Dieudonné, Panorama des mathématiques pures: le choix bourbachique, Paris 1977.
N.C. Metropolis, J. Howlett, G.C. Rota, A history of computing in the twentieth century, New York 1980.
A. Brigaglia, G. Masotto, Il circolo matematico di Palermo, Bari 1982.
Ph.J. Davis, R. Hersh, The mathematical experience, Boston 1982.
P. Halmos, I want to be a mathematician: an automatography, New York 1985.
New directions in the philosophy of mathematics, ed. T. Tymoczko, Boston 1986.
K. Devlin, Mathematics: the new golden age, London-New York 1988 (trad. it. Dove va la matematica, Torino 1994).
A century of mathematics in America, ed. P.L. Duren, R.A. Askey, U.C. Merzbach, 3 voll., Providence (R.I.) 1988-89.
The history of modern mathematics, ed. D. Rowe, J. McClearly, 2 voll., Boston 1989.
E.E. David jr. et al., Renewing U.S. mathematics: a plan for the 1990s, Washington (D.C.) 1990.
P. Halmos, Has progress in mathematics slowed down?, in American mathematical monthly, 1990, pp. 561-88.
Ein Jahrhundert Mathematik 1890-1990. Festschrift zum Jubiläum der DMV, hrsg. G. Fischer, F. Hirzebruch, W. Scharlau et al., Braunschweig 1990.
Reshaping school mathematics: a philosophy and a framework for curriculum, Washington (D.C.) 1990.
M. Ascher, Ethnomathematics: a multicultural view of mathematical ideas, Pacific Grove (Calif.) 1991.
A. Weil, Souvenirs d'apprentissage, Bâle-Boston 1991 (trad. it. Torino 1994).
Chaos et déterminisme, éd. A. Dahan-Dalmedico, J.-L. Chabert, K. Chemla, Paris 1992.
A. Friedman, J. Glimm, J. Lavery, The mathematical and computational sciences in emerging manufacturing technologies and management practices, Philadelphia 1992.
Mathematics into the twenty-first century, ed. F.E. Browder, Providence (R.I.) 1992.
H. Sarkowski, H. Gotze, Der Springer-Verlag: Stationen seiner Geschichte, 2 voll., Berlin-New York 1992-94.
Golden years of Moscow mathematics, ed. S. Zdravkovska, P.L. Duren, Providence (R.I.) 1993.
Messengers of mathematics: European mathematical journals (1800-1946), ed. E. Ausejo, M. Hormigón, Madrid 1993.
G.C. Rota, Pensieri discreti, Milano 1993.
Companion encyclopedia of the history and philosophy of the mathematical sciences, ed. I. Grattan-Guinness, 2 voll., London-New York 1994.
Development of mathematics, 1900-1950, ed. J.-P. Pier, Basel 1994.
P. Gerdes, On mathematics in the history of sub-Saharan Africa, in Historia mathematica, 1994, pp. 345-76.
The history of modern mathematics, ed. E. Knobloch, J. Mc Cleary, D. Rowe, 3 voll., Boston 1994.
J. Høyrup, In measure, number and weight. Studies in mathematics and culture, New York 1994.
G. Israel, A. Millán Gasca, Il mondo come gioco matematico. John von Neumann, scienziato del Novecento, Roma 1994.
L'Europe mathématique: histoires, mythes, identités, éd. C. Goldstein, J. Gray, J. Ritter, Paris 1996.
International handbook of mathematics education, ed. A.J. Bishop, K. Clements, Ch. Keitel et al., 2 voll., Dordrecht 1996.
K.H. Parshall, How we got where we are: an international overview of mathematics in national contexts (1875-1900), in Notices of the American mathematical society, 1996, pp. 287-96.
L. Accardi, Urne e camaleonti, Milano 1997.
Many visions, many aims, ed. W.H. Schmidt et al., Dordrecht-Boston 1997.
J.P. Bourguignon, Enjeux des mathématiques dans la société d'aujourd'hui, preprint, Paris 1998.
C. Cellucci, Le ragioni della logica, Roma-Bari 1998.
O.E. Lehto, Mathematics without borders: A history of the International Mathematical Union, Berlin 1998.
Proceedings of the International congress of mathematicians (in partic.: W. Hackbusch, From classical numerical mathematics to scientific computing, in Documenta mathematica, Journal der Deutschen Mathematiker-Vereinigung, 1° vol., pp. 235-54.
L. Lovász, One mathematics, in The Berlin Intelligencer, 1° vol., pp. 10-15.
D. Mumford, Trends in the profession of mathematics, in The Berlin Intelligencer, 1° vol., pp. 2-5): Berlin 18-27 August 1998, Berlin-Heidelberg 1998.
SIAM, The SIAM report on mathematics in industry, Philadelphia 1998.