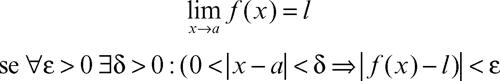matematica
matematica
matematica termine che deriva dal greco mathematiché (sottinteso téchne, dove máthema significa conoscenza, sapere) e dal corrispondente sostantivo neutro plurale latino mathematica (le cose che riguardano la conoscenza), da cui, probabilmente, la sua declinazione al plurale in molte lingue (in inglese: mathematics; in spagnolo: matemáticas; in francese: mathématiques) e talvolta, anche in italiano, le matematiche. L’incertezza sulla declinazione al singolare o al plurale del termine indica la difficoltà di caratterizzare tale disciplina: essa va considerata un corpus unitario, sia pure articolato, di concetti, procedure e metodi oppure un aggregato di teorie locali con contenuti differenti e alcuni tratti in comune? Qui si assumerà il punto di vista che la matematica possieda un corpus comune di concetti astratti, metodi di lavoro, indagine e validazione e un linguaggio altamente specializzato che permettono di stabilire oggi, con una certa precisione, se uno scritto sia di matematica o meno o se il problema di cui si occupa un ricercatore sia un problema matematico o meno. Tale caratterizzazione ha naturalmente un valore storico relativo perché contenuti, problemi, procedure, strumenti e forme espressive della matematica sono largamente variabili nel tempo. Da un punto di vista ingenuo, infatti, oggi si potrebbe riconoscere come matematico, o comunque a forte contenuto matematico, qualunque scritto in cui siano presenti formule e derivazioni da formule, anche se il suo oggetto riguarda questioni applicative attinenti ad altre scienze. Eppure la matematica esisteva anche prima dello sviluppo dell’algebra simbolica. Ancora da un punto di vista ingenuo, si potrebbe pensare che la matematica sia, in primo luogo, la scienza dei numeri e delle figure perché effettivamente l’aritmetica e la geometria hanno costituito storicamente i suoi primi terreni di applicazione, di problematizzazione e di riflessione. Eppure la vastità degli oggetti di cui si occupa oggi la matematica va molto oltre il mondo dei numeri e delle figure, che quasi costituiscono suoi territori periferici di specializzazione. Secondo una ulteriore vulgata assai diffusa, la matematica sarebbe inoltre il regno della certezza. Eppure è proprio una branca della matematica, la teoria della probabilità, a indagare il caso, il regno dell’incertezza, e a stabilirne delle regole. E ancora, è sotto il segno della matematica l’indagine su ciò che si trasforma e su come si trasforma: gli invarianti nelle trasformazioni geometriche, la derivata di una funzione, che ne esprime la variazione istantanea, o ancora l’evoluzione probabilistica di un fenomeno. Anche se si avvale di un metodo di ragionamento assai stringente, il metodo ipotetico-deduttivo, la matematica non pare ridursi a questo, sia perché nel suo processo inventivo di ricerca (euristica) tale metodo non appare essere il principale generatore di risultati sia perché comunque, nonostante i tentativi effettuati nell’ambito della corrente di pensiero denominata logicismo, la matematica non si riduce a logica. Di fronte alla difficoltà di precisare l’identità della matematica si è tentati di accettare due sue celebri definizioni, l’una di H. Poincaré, secondo il quale la matematica consiste nel «dare lo stesso nome a cose differenti», l’altra, più provocatoria, di B. Russell, secondo cui la matematica è «una scienza in cui non si sa mai di che cosa si parla né se ciò che si dice è vero». Prese insieme, tuttavia, queste due vaghe indicazioni forniscono un indizio di definizione, che si completa con le connotazioni parziali che i punti di vista ingenui individuano.
La matematica si occupa di enti di natura non precisata (e quindi potenzialmente di tutte le cose), ma ne considera gli aspetti astratti e strutturali comuni (attribuendo un nome uguale a cose diverse e riducendo ad astrazione gli innumerevoli concreti), utilizzando oggi un metodo rigoroso di ragionamento ipotetico-deduttivo. Ognuna delle diverse teorie di cui essa si compone è inoltre caratterizzata da un coerente sistema di assiomi che ne definiscono implicitamente gli oggetti, le operazioni e le relazioni (per tale caratterizzazione degli oggetti tramite definizioni implicite si veda → definizione). Ulteriore tipicità della matematica, dalla quale deriva l’attenzione al calcolo e ai suoi strumenti, dalla riga e il compasso dell’antica geometria greca fino all’attuale massiccia incorporazione della matematica stessa nei mezzi informatici e nelle apparecchiature digitali, è l’attenzione congiunta agli oggetti e alle procedure con cui essi si trasformano o si corrispondono, giacché ogni procedura possiede proprie regole, imposte da alcune delle caratteristiche degli oggetti stessi. Quando la matematica studia degli oggetti (numeri, figure ecc.) ne studia anche le relazioni, il modo in cui si possono organizzare, combinare e il modo in cui si possono effettuare calcoli con essi.
Settori di studio della matematica
Le aree d’interesse della matematica sono moltissime e in continua espansione, con una gamma di problemi inesauribile, sia interni alla matematica stessa (matematica pura) sia di interesse particolare per qualche altra disciplina o per le applicazioni (matematica applicata). Qui se ne ricordano le principali, rinviando ai relativi lemmi per una descrizione più dettagliata di ciascuna:
• aritmetica: studia i numeri naturali e le operazioni tra essi; a un livello più avanzato diventa teoria dei numeri e indaga sulle più profonde proprietà dei numeri, sui numeri primi, sulle applicazioni per costruire o decrittare codici segreti (crittografia);
• algebra: studia le procedure per risolvere equazioni e disequazioni e il problema della loro stessa risolubilità, le proprietà generali delle operazioni, le diverse strutture matematiche;
• geometria e topologia: studiano le proprietà delle figure e le loro relazioni, nel piano e nello spazio, ma anche spazi più generali e astratti, le loro possibili trasformazioni e i loro invarianti;
• trigonometria: studia le relazioni tra angoli e distanze, ma anche la costruzione di modelli per interpretare i numerosi fenomeni di natura ondulatoria (dal suono, alla luce, alle radiazioni elettromagnetiche);
• logica: studia i metodi del ragionare corretto per arrivare a conclusioni ineccepibili, e analizza i fondamenti stessi della matematica e i limiti della razionalità dell’uomo;
• analisi infinitesimale: è lo studio delle funzioni, cioè delle leggi di variabilità di un fenomeno, dei suoi comportamenti locali e degli andamenti all’infinito;
• analisi numerica e informatica: studiano le procedure di calcolo e come esse si implementano in una macchina, affrontando problemi di finitezza, approssimazione e complessità;
• teoria della probabilità e statistica: studiano gli eventi che dipendono dal caso e le loro relazioni, dando una misura della casualità;
• matematica finanziaria e attuariale: studia gli investimenti, le rendite, il costo di un’assicurazione, la rata di un mutuo;
• matematiche applicate: studiano l’applicazione della matematica all’ingegneria, alla fisica, alla biologia, all’economia, per arrivare alla costruzione di modelli di ricerca operativa per la risoluzione di problemi che vanno dall’analisi della dinamica di una popolazione all’evoluzione di fenomeni caotici, alla gestione delle risorse, alla distribuzione ottimale del traffico;
• matematiche finite o discrete: ne fanno parte l’analisi combinatoria e la teoria dei grafi, con applicazioni all’informatica, alla teoria dell’informazione, alla teoria dei giochi.
La matematica nell’antichità
Tecniche e procedure di tipo matematico risalgono agli albori dell’umanità e si sono sviluppate, in forma diversa, in vari territori e culture nel corso dei secoli: civiltà mesopotamiche, antico Egitto, Cina, India, antica Grecia, periodo ellenistico, cultura araba. Le prime conoscenze aritmetiche e geometriche sono documentate nelle civiltà preelleniche del Medio Oriente (assiro-babilonesi, egizi); sono perlopiù legate ad attività pratiche (commercio, agrimensura, navigazione), ma lasciano intuire anche probabili commistioni tra i primi germi di conoscenza razionale e pratiche magiche o rituali. È nella civiltà greca, ossia nell’area di lingua e cultura greca che comprende, oltre alla Grecia stessa, l’Italia meridionale, l’Asia minore, Alessandria d’Egitto, nel periodo che va dal vi al ii secolo a.C., che la matematica trova una prima caratterizzazione assiomatica, su base logico-deduttiva, con il fondamentale lavoro di Euclide di sistemazione della geometria del piano e dello spazio (Elementi) e lo studio delle coniche dovuto ad Apollonio, i primi approfondimenti teorici sui numeri (con la scoperta delle grandezze incommensurabili nell’ambito della scuola pitagorica o la dimostrazione, di Euclide stesso, della infinità dei numeri primi), lo sviluppo della trigonometria e, soprattutto con Archimede di Siracusa ed Eudosso di Cnido, l’utilizzo di primi procedimenti di tipo infinitesimale (metodo di → esaustione).
Nella civiltà greca, la matematica si struttura come una disciplina che, distinguendosi dalla filosofia, inizia a delineare propri autonomi contenuti di studio, un originale metodo di convalida dei risultati (la dimostrazione dei teoremi) e un quadro epistemologico di riferimento (per esempio, il rifiuto dell’infinito attuale). Occorre considerare che in altre civiltà, pur con tradizioni culturali e scientifiche millenarie, questa impostazione teorica non fu mai raggiunta: per esempio, tra gli antichi matematici cinesi le dimostrazioni non avevano un ruolo primario, ma erano considerate piuttosto mezzi retorici atti a convincere oppure strumenti didattici per meglio comprendere, ma non strumenti di validazione. Peraltro, è proprio in ambito greco che si ha una prima suddivisione interna della matematica: la scoperta degli incommensurabili portò infatti a incrinare la originaria visione unitaria del numero (aritmo-geometria) e a distinguere lo studio delle quantità discontinue (l’aritmetica) da quello delle quantità continue (la geometria).
Declino degli studi matematici in Occidente
Il i secolo a.C. vede affermarsi il dominio politico-militare di Roma sui territori dove era fiorito l’ellenismo; in campo filosofico e culturale, si registra la tendenza a una commistione tra sapere razionale e credenze magiche. In tale contesto, è emblematica la figura di Erone di Alessandria che, erede della cultura scientifica alessandrina, si segnala per l’invenzione di numerosi strumenti idraulici ma anche per l’ideazione di automi e congegni meccanici (come una rudimentale macchina a vapore) utilizzati non per scopi produttivi, ma come giochi ingegnosi volti a stupire la corte e il pubblico elegante e ad alimentare credenze irrazionali.
I primi tre secoli dell’era cristiana sono caratterizzati dal diffondersi di concezioni mistico-religiose che via via contaminano il pensiero razionale anche nella capitale della cultura scientifica, Alessandria. Claudio Tolomeo scrive la Sintassi matematica (nota con il titolo in arabo di Almagesto), opera in cui si trova una buona corrispondenza tra il modello del sistema solare (quello che poi sarà detto sistema tolemaico) ed effettive osservazioni astronomiche nonché uno sviluppo della trigonometria; ma Tolomeo è anche autore del Tetrabiblos, in cui studia l’influsso degli astri sulle vicende umane.
Nel iii secolo d.C. la matematica risente del clima culturale sincretistico e misticheggiante: si sviluppa una mistica dei numeri e i matematici si confondono con cabalisti, indovini e maghi. Unica figura di spicco di questo periodo, nel mondo occidentale, è l’alessandrino Diofanto, che nella sua Arithmetica giunge a una concezione puramente numerica dei problemi matematici, trattando le incognite come dati numerici conosciuti e non avvalendosi di procedimenti geometrici.
Come testimoniano i protagonisti dell’ultima fase dell’ellenismo alessandrino qui ricordati, Erone, Tolomeo e Diofanto, il sapere matematico e scientifico perde quel carattere sistematico e teorico che aveva assunto nel periodo aureo greco raggiungendo il culmine nell’opera di Euclide, per frammentarsi piuttosto in conoscenze specifiche e nell’esposizione di singoli problemi. Tutto il periodo romano, segnato da imponenti opere ingegneristiche che non potevano essere progettate e portate a termine senza un sapere tecnico-operativo, è caratterizzato dalla quasi assoluta mancanza di progressi nella ricerca matematica e scientifica più teorica.
Tre morti violente, avvenute a grande distanza di tempo, indicano simbolicamente come il mondo romano e poi cristiano fossero poco interessati alla ricerca matematica, il primo perché concentrato sulle imprese militari, il secondo perché impegnato nella sistemazione della propria teologia: l’uccisione di Archimede di Siracusa da parte di un soldato romano (212 a.C.), la lapidazione di Ipazia di Alessandria da parte di monaci cristiani (415 d.C.) e la condanna a morte di Boezio (524 d.C.) da parte dell’imperatore d’Occidente Teodorico. Boezio, nato nel 480, cioè quattro anni dopo che l’ultimo imperatore romano, Romolo Augustolo, era stato deposto da Odoacre, re dei goti, scrisse due compendi di aritmetica e geometria e fu probabilmente l’unico matematico di un certo livello espresso dall’antica Roma.
La matematica in India
Lo zero e il sistema posizionale decimale. Al declino della matematica in Occidente si contrappongono nei secoli successivi i notevoli risultati conseguiti nel mondo indiano e in quello arabo. Un interessante compendio delle conoscenze matematiche indiane risale al 499 ed è dovuto ad Aryabhata: è una breve opera in versi che espone molte regole di calcolo, senza darne alcuna giustificazione, e in cui non si rileva alcun interesse sistematico e teorico quale si trovava nei greci; si mescolano risultati esatti, approssimati ed errori e lo stesso linguaggio fiorito limita fortemente uno sviluppo matematico autonomo. Ecco per esempio come è spiegata da Aryabhata la regola per risolvere la proporzione a : b = c : x: «Nella regola del tre moltiplica il frutto per il desiderio e dividi per la misura. Il risultato sarà il frutto del desiderio». C’è tuttavia, in quest’opera, il primo esempio di notazione decimale posizionale che più tardi (nel 628) fu perfezionato da Brahmagupta nell’opera Brahma-Sphuta Sidd’hanta (Il sommario del verbo di Brahma), in cui lo zero è introdotto ed è utilizzato come vero e proprio numero e non soltanto come segnaposto (è da segnalare tuttavia il fatto che anche i maya avessero sviluppato una notazione posizionale comprendente lo zero).
Del xii secolo è un’altra significativa opera della matematica indiana, il Siddhanta Shiromani di Bhāskara, in cui per la prima volta si afferma che la divisione per zero dà una quantità infinita e si trattano equazioni numeriche di primo e secondo grado con soluzioni dell’ordine del miliardo. L’abilità di calcolo dei matematici indiani era sicuramente molto elevata; a differenza dei greci, essi trattavano i numeri irrazionali nello stesso modo di quelli razionali. Nonostante la loro indifferenza a qualunque sistemazione o dimostrazione dei risultati raggiunti, è pressoché certo che attraverso le loro opere il sistema di numerazione posizionale decimale sia stato assimilato dal mondo arabo. Agli indiani si deve inoltre lo sviluppo della trigonometria con la considerazione del seno di un angolo: prima di allora, infatti, in relazione agli angoli si erano considerate soltanto le lunghezze delle intere corde sottese agli archi di circonferenza corrispondenti agli angoli.
La matematica nel mondo arabo: l’algebra
Nel suo primo secolo, l’Islam (la cui data di nascita si fa risalire all’Egira, la fuga di Maometto a Medina nel 622) si distingue, come l’impero romano, più per le sue conquiste militari che per l’attenzione a questioni scientifiche o culturali. Il mondo islamico ben presto si estende oltre la penisola araba, dalla Spagna a tutta l’Africa settentrionale fino a lambire, a oriente, l’India. Già nell’viii secolo, tuttavia, Baghdad, fondata nel 762 dal califfo abbaside Al Mansur, diventa il nuovo centro internazionale degli studi matematici, dopo Atene e Alessandria: vi viene infatti istituita la Bayt al-Hikma (Casa della sapienza), dotata di una ricchissima biblioteca, che accoglie numerosi scienziati e filosofi provenienti dalla Siria, dall’Iran e dalla Mesopotamia e vengono avviate le traduzioni in arabo di molte fondamentali opere greche e indiane: tra queste, le opere di Platone e Aristotele, gli Elementi di Euclide e l’indiano Brahma-Sphuta Sidd’hanta di Brahmagupta. Proprio a quest’opera, a carattere algebrico-aritmetico, attinge il personaggio chiave dello sviluppo della matematica araba e della sua rinascita in Europa, al-Khuwārizmī, membro della Casa della sapienza, che nel suo fondamentale testo al-Kitāb al-mukhtasar fi hisab al-giabr wa’l-muqābala (da cui proviene il termine «algebra»), pur non utilizzando notazioni simboliche, espone sistematicamente i metodi per risolvere le equazioni di primo e secondo grado, superando lo stile frammentario delle opere del tardo ellenismo (come l’Aritmetica di Diofanto) o di quelle indiane. Altri studiosi del mondo arabo proseguirono l’opera di al-Khuwārizmī; tra questi, va ricordato il persiano ‘Omar Khayyām, che nel 1070 scrisse l’opera Algebra, in cui sono studiate anche le equazioni di terzo grado, risolte prevalentemente “alla greca” e cioè con metodi geometrici (e proprio per questo si limitò al terzo grado, ritenendo inconcepibile una quarta dimensione). Per Khayyām «l’algebra non è altro che la dimostrazione di fatti geometrici» ed è singolare che questa affermazione, mentre sembra precorrere Cartesio, abbia imposto limiti alle sue ricerche. Il cosmopolitismo e il plurilinguismo del mondo musulmano, legati anche all’espansione dei commerci, alimentò nel xii secolo, soprattutto in Spagna, un’intensa attività di traduzione. Fu così che furono conosciuti in Europa gli Elementi di Euclide, nella traduzione latina dall’arabo, e l’opera di al-Khuwārizmī.
La lenta rinascita della matematica in Europa
La divulgazione nel mondo occidentale delle opere degli studiosi delle scuole indiane e arabe, dedicate prevalentemente a questioni di algebra e di aritmetica, unitamente alla riscoperta delle opere greche, dette impulso in Europa a un nuovo interesse per gli studi matematici. L’introduzione in Europa del sistema di numerazione posizionale decimale (detto anche indo-arabo), propugnata già attorno all’anno Mille da papa Silvestro ii, il primo papa matematico e francese, ma con studi effettuati nella Spagna araba, si fa risalire in modo determinante alla pubblicazione nel 1202 del Liber abaci di Leonardo Pisano, detto il Fibonacci (perché figlio di tal Bonaccio, un mercante), in cui, oltre che del nuovo sistema numerico, si fa uso di dimostrazioni rigorose. In un’altra opera del 1220, Practica geometriae, Fibonacci inverte lo stile greco, utilizzando l’algebra per risolvere problemi geometrici. Altro personaggio di rilievo di questo periodo è Giordano Nemorario (m. 1283), che studia le leggi della meccanica, anche da un punto di vista matematico, e che nella sua opera Arithmetica utilizza le lettere al posto dei numeri per indicare grandezze variabili generiche. La ricerca ha tuttavia una battuta d’arresto: la società medievale occidentale attraversa una fase controversa e difficile, tra peste, conflitti, guerre, decremento demografico: astrologia e astronomia si confondono e all’osservazione diretta dei fatti naturali si sovrappone l’esaltazione dell’autorità aristotelica cui la chiesa d’Occidente si rifà per esprimere una continuità con la classicità. Più che problemi aritmetici o geometrici, emergono in tutto questo periodo, fino alla rivoluzione scientifica del xvii secolo, problematiche di logica legate alla filosofia, interessanti tuttavia perché riaprono, dopo Aristotele, un diverso campo di interesse della matematica, legato al suo intrinseco modo di procedere (→ logica). In questo quadro emerge la figura di Raimondo Lullo di Maiorca (1235-1315), che, intento a conquistare i musulmani alla verità cristiana, si propone di ideare, con l’ars magna, una forma di calcolo logico, una lingua universale, che, a partire dai termini semplici del mondo reale, costruisca un sapere universale valido tanto per i cristiani quanto per gli “infedeli”. Su basi religiose, e intento a conciliare fede e ragione, Lullo tenta quindi una sintesi tra la tradizione pitagorico-platonica e il pensiero cristiano di derivazione aristotelica; in tutto ciò, paradossalmente, il suo misticismo religioso pone le basi di un primo abbozzo di logica matematica che solo alcuni secoli dopo sarà ripreso da G.W. Leibniz.
Il rinascimento
Il Quattrocento segna uno spartiacque nella storia dell’Europa occidentale e convenzionalmente segna l’inizio di quello che viene chiamato rinascimento, per l’affacciarsi dei nuovi ceti produttivi imprenditoriali nati dalle corporazioni professionali artigianali, per lo sviluppo degli scambi commerciali e della finanza e per il dispiegarsi di energie intellettuali e artistiche che si manifestano anche in campo matematico. Luogo privilegiato di tale rinascita è l’Italia. Accanto a una matematica pratica, che s’avvale oramai con sicurezza del sistema di numerazione indo-arabico, sono affrontati problemi teorici più generali e si affermano figure poliedriche quali il filosofo Nicolò Cusano (1401-1464), che studia la quadratura del cerchio, il letterato Leon Battista Alberti (1404-1472), che nel trattato De pictura (1436) descrive le tecniche della prospettiva, e il pittore Piero della Francesca (1416?-1492), che in De prospectiva pingendi (1475) utilizza in modo consapevole la matematica per dedurre le regole della prospettiva. A Piero della Francesca si devono due altre interessanti opere matematiche: De quinque corporibus regularibus, sui → solidi platonici, e il Trattato d’abaco, in cui riprende lo studio delle equazioni di secondo grado con metodi geometrici. Questo intreccio di interessi geometrici e aritmetici, legati ai commerci, si trova anche in Luca Pacioli che pubblica Summa di Arithmetica, Geometria, Proportioni e Proportionalità, in cui oltre a questioni riguardanti i cambi di moneta, introduce la partita doppia, e il De Divina Proportione, arricchito dalle incisioni di poliedri del suo amico Leonardo da Vinci, in cui si occupa della → sezione aurea. Nel 1482, a Venezia viene pubblicata la prima versione a stampa in latino degli Elementi di Euclide.
Nel xvi secolo si assiste in Italia a una vera esplosione di ricerche algebriche, agevolate anche da una forma di scrittura che si avvale di convenzioni e abbreviazioni (l’algebra sincopata) che prelude alla successiva algebra simbolica. Scipione Dal Ferro scopre le soluzioni di alcune classi di equazioni di terzo grado, N. Tartaglia, L. Ferrari e il suo discepolo G. Cardano generalizzano il procedimento (e tra Cardano e Tartaglia scoppia un’aspra polemica perché Tartaglia accusa Cardano di aver tratto ispirazione da lui); Cardano stesso nella Ars magna pubblica le formule risolutive per le equazioni di quarto grado e risolve per radicali anche l’equazione generale di quarto grado. Infine, R. Bombelli, nel 1572, pubblica Algebra parte maggiore dell’aritmetica, in cui risolve anche quei casi di equazioni, di terzo e quarto grado, in cui è necessario operare con numeri complessi e ne indica esplicitamente le regole di calcolo. Oltre alle ricerche di contenuto, l’algebra in questo periodo registra l’importante contributo del francese F. Viète al simbolismo: egli infatti introduce le lettere per rappresentare numeri generici, le vocali per le incognite e le consonanti per i dati noti, dando così avvio alla moderna algebra simbolica.
Lo sviluppo delle scienze e il nuovo ruolo della matematica: il concetto di funzione
Il Seicento è il secolo della rivoluzione scientifica, tra le cui caratteristiche c’è, con Galilei, l’affermazione della supremazia, nell’indagare i fatti della natura, del ruolo diretto dell’uomo ricercatore rispetto a qualunque principio di autorità. Il metodo della ricerca scientifica deve unire il “discorso” con lo “sperimentare”, il ragionamento con l’esperienza, giacché l’universo, come scrive Galilei in una celebre frase del Saggiatore, «non si può intendere se prima non s’impara a intender la lingua e conoscer i caratteri ne’quali è scritto. Egli è scritto in lingua matematica e i caratteri son triangoli, cerchi ed altre figure geometriche, senza i quali mezzi è impossibile a intenderne umanamente parola; senza questi è un aggirarsi vanamente per un oscuro labirinto». La matematica si afferma quindi come la lingua privilegiata per descrivere i fatti della realtà fisica non soltanto per la sua naturale vocazione a esprimere i dati quantitativi che provengono dalle osservazioni sperimentali, ma anche per il rigore del suo assetto, di cui gli Elementi di Euclide costituiscono il modello. È infatti sul modello degli Elementi che I. Newton scrive i Philosophiae naturalis principia mathematica (1687) e il filosofo olandese Baruch Spinoza (1632-77) in Ethica more geometrico demonstrata (L’etica dimostrata con ordine geometrico) invoca il metodo dimostrativo della geometria euclidea addirittura per discutere di etica, procedendo per definizioni e proposizioni.
Dal punto di vista dei contenuti, la portata innovativa del secolo è testimoniata dalla nascita del → calcolo infinitesimale, dovuta in modo indipendente a Newton e Leibniz, dall’invenzione della → geometria analitica per opera di Cartesio e P. de Fermat, e dall’aprirsi della matematica a un nuovo campo di indagine, quello dei fenomeni casuali, attraverso la precisazione del concetto di → probabilità a opera di Fermat e Pascal. Complessivamente, questi risultati sono dovuti all’affermarsi, in connessione con lo studio dei corpi in movimento, di un nuovo e autonomo oggetto concettuale della matematica, quello di funzione, termine introdotto esplicitamente da Leibniz, insieme a variabile e parametro, in relazione alle curve e alle loro tangenti. La matematica non è più soltanto lo studio di relazioni numeriche statiche, quali sono anche quelle espresse da una equazione, oppure di proprietà di figure geometriche, ma diventa scienza di quantità variabili e delle loro reciproche relazioni.
Questa tendenza si rafforzerà nel secolo successivo con la ricerca di leggi funzionali per descrivere i diversi fenomeni della natura, con l’approfondimento dei metodi infinitesimali e con il progressivo affermarsi, anche in geometria, dell’idea di trasformazione che porterà allo sviluppo della geometria proiettiva. Si assiste quindi nel Settecento a una sistematica applicazione dei metodi dell’analisi infinitesimale, e più in generale della matematica, a tutti i possibili fenomeni della realtà fisica, e non soltanto alla meccanica, ma, per esempio con C.A. Coulomb (1736-1806), anche ai fenomeni elettrici. L’estensione dei settori di studio della matematica di questo periodo si può riassumere emblematicamente nella figura di Eulero, i cui lavori spaziarono dalla geometria al calcolo differenziale e integrale, dalla teoria dei numeri alle equazioni, dalla fisica all’astronomia, e che inoltre fu inventore di molti dei simboli matematici ancora oggi in uso. A Eulero si deve poi la definizione di funzione come espressione di una formula analitica: ciò porterà il nuovo concetto, e quindi l’analisi, nell’ambito dell’aritmetica e dell’algebra anziché, come in Leibniz, in quello della geometria.
Nuovi strumenti d’indagine
L’invenzione del calcolo infinitesimale. La moderna analisi matematica trae origine da problemi indotti dalla realtà fisica legati all’analisi del movimento. In particolare il calcolo infinitesimale, cioè lo studio relativo all’andamento di successioni all’infinito o al comportamento di funzioni nelle vicinanze dei punti in cui non sono definite nasce dal problema di definire che cosa si intenda per velocità istantanea di un mobile. Dato infatti che il modulo della velocità media si definisce come rapporto tra lo spazio percorso da un mobile e l’intervallo di tempo nel frattempo trascorso, sembrava fosse necessario per determinare il valore della velocità in un determinato istante riferirsi a un intervallo di tempo “nullo”, il che rendeva la definizione di velocità come rapporto tra spazio e tempo matematicamente problematica, giacché la divisione per zero di un numero non nullo è in matematica impossibile (infatti, se a ≠ 0, qualunque valore b si attribuisca al risultato di a : 0, si ha b ⋅ 0 = 0 ≠ a e quindi il numero b prescelto non può essere il risultato).
Si trattava quindi di approfondire il comportamento “locale” (cioè in “piccoli intervalli”) delle funzioni; intervalli “così piccoli” da doversi considerare, in qualche senso da specificare, “infinitesimi”, cioè “prossimi a zero, ma non nulli”. Tale specificazione non era semplice da effettuare giacché nei ragionamenti e nelle tecniche matematiche facilmente si insinuavano modelli legati al movimento nel tempo e soggetti a considerazioni fisico-meccaniche di tipo intuitivo e non poggianti su rigorose basi matematiche.
Lo sviluppo sistematico del calcolo infinitesimale si deve soprattutto, tra la fine del xvii e l’inizio del xviii secolo ai lavori di Leibniz e di Newton, tra i quali scoppiò anche un’aspra polemica sulla primogenitura (→ analisi).
Le impostazioni di Newton e Leibniz relative al calcolo infinitesimale erano in realtà alquanto differenti, sia concettualmente sia per i simbolismi utilizzati. Newton voleva mantenersi aderente ai problemi che poneva la realtà fisica, ma ciò fece sì che la sua definizione di velocità istantanea, basata sul concetto di «quantità evanescenti» («ultimo rapporto di quantità evanescenti inteso come il rapporto fra dette quantità non prima che siano svanite, e nemmeno dopo, ma nell’istante stesso in cui svaniscono») pecchi di rigore e sia fondamentalmente inconsistente. Leibniz pubblicò la prima esposizione del calcolo infinitesimale in Nova mehodus pro maximis et minimis, itemque tangentibus, qua nec irrationales quantitates moratur (Nuovo metodo per massimi, minimi, e anche per le tangenti, non ostacolato da quantità irrazionali, 1684) e la sua notazione per la derivata
si rivelò più efficace, grazie anche al disinvolto utilizzo degli infinitesimi.
Il nuovo calcolo infinitesimale, anche se dimostrava una indubbia efficacia, rimaneva tuttavia privo di rigorose basi matematiche e si prestava perciò anche a resistenze e critiche. Voltaire, per esempio, definì il calcolo infinitesimale come «l’arte di numerare e misurare con esattezza qualcosa la cui esistenza non può nemmeno essere concepita» e, nel 1734 il filosofo empirista George Berkeley, vescovo di Cloyne (Irlanda), pubblicò un libro dal significativo titolo The analist. A discours addressed to an infidel mathematician. Wherein it is examined wheter the objects, principles and inferences of the modern analysis are more distinctly conceived, or more ecidently deduced, the religious mysteriees and points of faith. (L’analista, ovvero discorso indirizzato a un matematico infedele nel quale si esamina se l’oggetto, i principi e le inferenze della moderna analisi siano più distintamente concepiti o evidentemente dedotti che non i misteri della religione o gli oggetti di fede).
È a Cauchy che si deve il merito di aver compreso che alla base dei nuovi strumenti infinitesimali si dovesse definire un nuovo concetto, il limite di una funzione; tuttavia ancora nel 1821, nel suo Cours d’analyse così definiva il limite: «Quando valori attribuiti successivamente a una stessa variabile si avvicinano indefinitamente a un valore fissato, in modo che finiscono per differirne tanto poco quanto si vuole, quest’ultimo è chiamato limite di tutti gli altri». Si può notare come nella nuova terminologia ci sia ancora una reminiscenza di una concezione legata a movimenti di tipo fisico-meccanico; tuttavia con la locuzione «tanto poco quanto si vuole», Cauchy mostra di avvicinarsi alla soluzione del problema, cioè al definitivo svincolarsi da approssimativi termini legati a un movimento fisico. Il passo decisivo lo compirà Weierstrass nel 1870 con la sua definizione, detta «ε − δ», di limite e oramai divenuta classica:
Si dice che l è il limite della funzione ƒ(x) per x tendente ad a e si scrive
Si può notare come nella definizione di Weierstrass tutti i termini e simboli che esprimono “tendenza” o “avvicinamento” (le parole limite, tendente ad a e la stessa freccia), cioè che esprimono una variabilità di tipo spazio-temporale, sono definiti attraverso i quantificatori universale ed esistenziale, collocandoli così all’interno di una variabilità logica, svincolata da realtà fisiche e matematicamente accettabile.
Le rivoluzionarie scoperte del XIX secolo
La teoria degli insiemi. L’enorme quantità di nuovi concetti e strumenti della matematica e le sempre più ampie applicazioni alle scienze che caratterizzano il xvii e il xviii secolo richiedevano una analisi più approfondita dei loro fondamenti e la loro unificazione da un nuovo punto di vista. Per mettere ordine nel tumultuoso sviluppo avvenuto nei secoli precedenti, nel corso dell’Ottocento la ricerca matematica volge lo sguardo prevalentemente al suo interno. Viene fornita da P.-S. de Laplace, peraltro sostenitore di un meccanicismo assolutamente deterministico, una prima sistemazione della teoria della probabilità, si sviluppa una intensa attività di ricerca sulle funzioni di variabile reale e complessa e, con J.-B.J. Fourier, si stabilisce un legame tra funzioni e serie.
Tale sguardo rivolto all’interno conduce a tre risultati di straordinaria importanza:
• la nascita delle geometrie non euclidee, che determina la fine dell’idea di uno spazio unico e assoluto, quello euclideo, all’interno del quale si situano i fenomeni studiati dalla fisica newtoniana;
• la scoperta, da parte di E. Galois, della irrisolubilità per radicali delle equazioni di grado superiore al quarto, che pone fine a problemi classici quali la costruibilità con riga e compasso di determinate figure e la quadratura del cerchio;
• il compimento del processo di aritmetizzazione della analisi e la sua separazione dalla geometria: sotto lo stimolo di C.G. Gauss, la più grande autorità matematica del periodo, si giunge a ritenere che alla base di tutti gli ambienti numerici ci siano i numeri naturali e che a partire da questi si possano costruire gli altri tipi di numeri, fino ai reali e ai complessi, e si possa precisare il concetto di → continuità. Con la rigorosa definizione di → limite di K. Weierstrass, posto alla base di tutto il calcolo differenziale e integrale, questo processo giunge a compimento e il calcolo infinitesimale si svincola dalle idee intuitive dalle quali era sorto, non facendo più riferimento a “punti in movimento”, a “grandezze evanescenti” o ad altri approssimativi concetti, ma avvalendosi di una variabilità esclusivamente logica e delle proprietà dei numeri reali.
Non vanno dimenticate, tra la fine del xix secolo e l’inizio del xx, le ricerche su campi specifici e, tra queste, l’enorme lavoro di studio e classificazione delle curve e delle superfici algebriche, operato soprattutto in Italia da quella che sarà chiamata la scuola italiana di geometria algebrica (→ geometria algebrica). Tuttavia, complessivamente, la matematica prende un’altra direzione: il lavoro di Galois, che stabilisce un legame tra la risolubilità di una equazione algebrica e particolari gruppi di permutazioni associati ai suoi coefficienti, conduce infatti allo studio di questi particolari gruppi e di altre strutture algebriche via via considerate, quali gli → anelli, i → campi e gli → spazi vettoriali. La matematica raggiunge così un livello di astrazione e generalità ancora più elevato: dal primitivo studio aritmetico sui numeri e le loro operazioni e da quello più astratto relativo alle equazioni si passa allo studio delle strutture in cui sono ambientate tali equazioni. Relazioni tra elementi di gruppi arbitrari, operazioni in spazi di funzioni, spazi di tutte le forme e tutte le dimensioni fanno ora parte della matematica.
In più diretta relazione con le ricerche in fisica si sviluppano anche altre branche quali il calcolo con i → tensori a dimensione infinita, l’analisi funzionale e un ulteriore approfondimento nello studio delle equazioni differenziali. Si verifica in sostanza una straordinaria espansione sia dei campi di applicazione della matematica sia del suo grado di astrazione, fino ad arrivare, con la teoria degli → insiemi di G. Cantor e la considerazione dell’→ infinito attuale, al grado più alto e perciò insidioso.
La matematica come insieme di teorie correlate ma indipendenti
All’inizio del Novecento la matematica presenta molti problemi aperti in più direzioni e il secolo si apre emblematicamente proprio con l’enunciazione da parte di D. Hilbert, al secondo Congresso internazionale dei matematici a Parigi (1900), dei problemi aperti più importanti (→ Hilbert, problemi di). Tra questi, essendosi persa con la nascita delle geometrie non euclidee l’idea che la matematica sia una costruzione ideale, nel senso platonico, in cui si riflette in modo univoco il mondo reale, Hilbert poneva quello di una fondazione rigorosa della matematica stessa che la rendesse immune da possibili contraddizioni e quello di una fondazione della fisica su basi matematiche. Pochi anni dopo, l’ambizione hilbertiana di una matematica che dia garanzie su sé stessa e sia a fondamento delle altre scienze (che in effetti assumono una forma sempre più matematizzata) si infrange. Nel 1902, infatti, B. Russell scopre una contraddizione nella teoria degli insiemi (→ Russell, antinomia di) aprendo così la cosiddetta crisi dei → fondamenti, da cui scaturirono differenti tentativi di reimpostare la matematica su basi diverse (→ formalismo, → logicismo, → intuizionismo). Ma il colpo mortale a ogni tentativo fondazionale generale della matematica viene inferto alcuni anni più tardi dai teoremi di → Gödel (1930-31), che rappresentano il più importante risultato della matematica e della logica del xx secolo: la dimostrazione che la matematica non può dimostrare con i propri mezzi la propria non contraddittorietà.
Nel corso del Novecento, la matematica diventa sempre più un insieme di teorie correlate, ma indipendenti e spesso largamente non comunicanti tra loro, nel senso che matematici di settori diversi spesso non comprendono gli uni gli studi degli altri e utilizzano linguaggi estremamente specialistici e non sempre coerenti nei diversi settori (tale frammentazione, che è conseguenza della specializzazione, rappresenta un problema comune a tutte le scienze). L’ultimo tentativo di riedificazione della matematica su basi comuni viene effettuato dal gruppo francese denominatosi Nicolas Bourbaki, la cui impostazione è anche detta strutturalismo perché erige la matematica a partire dagli insiemi, sistemati assiomaticamente (si vedano per esempio gli assiomi di → Zermelo-Fraenkel) e considerando strutture algebriche, d’ordine e topologiche e loro isomorfismi. Per altri versi, il xx secolo, proprio alla luce delle insidie presenti nelle astrazioni troppo disinvolte, ha visto emergere ricerche matematiche e logiche sui processi di calcolo, di carattere estremamente teorico, ma finemente connesse a una procedura così apparentemente elementare come il calcolo aritmetico. Queste ricerche hanno condotto, con A.M. Turing e J. von Neumann, alla costruzione di modelli teorici di calcolo automatico che, insieme agli sviluppi dell’elettronica, hanno dato come frutto gli odierni e sempre più potenti computer. Questo nuovo mezzo di calcolo ha aperto a sua volta nuovi settori di studio legati alla possibilità di computare e, incidentalmente, anche a una nuova visione di funzione, di cui si accentua l’aspetto della calcolabilità effettiva più che quello relazionale astratto. Contemporaneamente, il processo di digitalizzazione e informatizzazione della società ha condotto a ulteriori ricerche in teoria dei numeri (per le implicazioni enormi che si hanno in → crittografia) e nel campo della matematica discreta.
Lettere e numeri: lo sviluppo del linguaggio algebrico