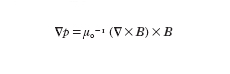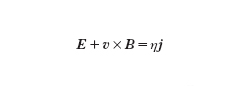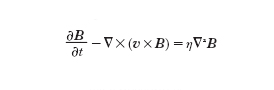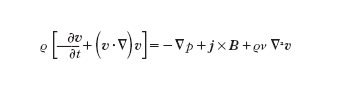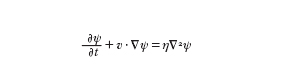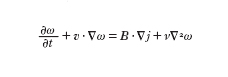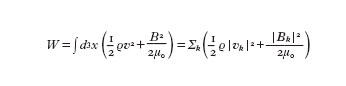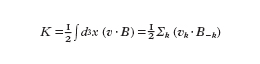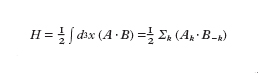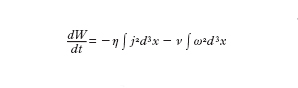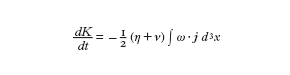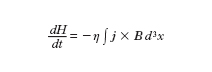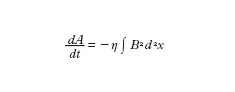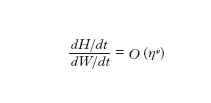Magnetofluidodinamica

Magnetofluidodinamica

(App. III, ii, p.10; IV, ii, p. 372; V, iii, p. 287)

Magnetofluidodinamica dei plasmi

Gli sviluppi più significativi della m. dei plasmi, detta anche magnetoidrodinamica (MHD) dei plasmi, avvenuti nell'ultimo decennio hanno portato un notevole avanzamento delle conoscenze nelle ricerche sulla fusione, sui plasmi spaziali e astrofisici, sui fenomeni di base in plasmi di laboratorio. I temi di ricerca dominanti riguardano l'osservazione e l'interpretazione di diversi processi MHD non lineari, quali per es. le oscillazioni a denti di sega e le disrupzioni nei tokamak, la dinamica dei reversed-field pinch, i brillamenti solari.

Tra i fattori determinanti in tale sviluppo si possono citare: l'uso di nuove tecniche diagnostiche per misurare la struttura del campo magnetico nella regione interna calda del plasma confinato nel tokamak (per es. mediante applicazione dell'effetto Stark su un fascio di atomi neutri iniettati nel plasma); la realizzazione di esperimenti di laboratorio per lo studio della formazione di strutture magnetiche singolari e della riconnessione magnetica (v. oltre); l'impiego crescente di satelliti e gruppi di satelliti per le misure del plasma e del campo magnetico nella coda magnetica della Terra; lo studio delle strutture localizzate di plasma nella cromosfera solare, nella regione di transizione e nella corona (per es. per mezzo di spettroscopia UV e visibile), lo studio del vento solare, lo studio delle magnetosfere dei pianeti; lo sviluppo di modelli teorici non lineari, unito a continui progressi nella simulazione numerica del comportamento del plasma. Nel seguito vengono trattati i processi MHD alla base dei più rilevanti fenomeni non lineari osservati nei plasmi, quali la riconnessione magnetica, lo sviluppo della turbolenza e la formazione di strutture coerenti nel plasma.

Riconnessione magnetica

La riconnessione magnetica consiste nel cambiamento topologico della configurazione magnetica mediante rottura e ricongiungimento delle linee di forza. Essa rappresenta uno dei mezzi principali con i quali l'energia del campo magnetico è convertita in energia termica ed energia cinetica macroscopica del plasma. Il processo di riconnessione non è previsto dalla MHD ideale ed è reso possibile dalle piccole deviazioni rispetto al caso ideale presenti nella legge di Ohm generalizzata, per es. quelle dovute alla resistività del plasma: tali deviazioni infatti introducono un parziale disaccoppiamento fra il moto del plasma e quello del campo magnetico altrimenti vincolati dalla legge di congelamento. Gli effetti sono trascurabili sul moto a grande scala e diventano essenziali nelle ristrette regioni dove la riconnessione avviene.

Per caratterizzare gli effetti dissipativi nel plasma si introducono il numero di Reynolds R_e=VL/ν, il numero di Reynolds magnetico R_m=VL/η, il numero di Lundquist S=v_AL/η. In queste espressioni V rappresenta la velocità media caratteristica del fluido, v_A la velocità di Alfvén, L una lunghezza caratteristica della configurazione, ν la viscosità ed η la resistività elettrica. R_m rappresenta il rapporto fra il tempo caratteristico di decadimento resistivo L2/η e il tempo convettivo L/V. Il numero di Reynolds magnetico per plasmi astrofisici è enorme: da 108 all'interno del Sole a 1021 nel mezzo galattico interstellare. Sulla base delle attuali conoscenze si ipotizza che a numeri di Reynolds così elevati la riconnessione avvenga in due parti: si creano dapprima forti gradienti spaziali per effetti MHD ideali; quindi nelle regioni a forti gradienti hanno luogo i processi di riconnessione.

La formazione nel plasma di regioni di riconnessione può essere compresa considerando la condizione di equilibrio magnetofluidodinamico ideale:

formula [

1]

dove p è la pressione, B l'induzione magnetica e μ₀ la permeabilità magnetica del vuoto.

Le soluzioni di questa equazione, a causa della non linearità del termine a secondo membro, prevedono in generale la presenza di discontinuità tangenziali nella configurazione magnetica, ovvero di superfici, caratterizzate dalla presenza di una corrente superficiale, attraverso le quali il campo presenta una variazione discontinua. Se ora si tiene conto della resistività finita del plasma, le superfici di discontinuità diventano in realtà strati di spessore finito, detti strati di corrente, all'interno dei quali avviene la riconnessione, con conseguente rilascio, o dissipazione, di energia magnetica. Nell'evoluzione di una configurazione magnetica a grande scala spaziale gli effetti non lineari danno origine a strutture a piccola scala, con formazione di strati di cοrrente. È da osservare che la diffusione resistiva del campo magnetico ha luogo ovunque nel plasma a causa della resistività finita, anche se estremamente piccola; la sua rapidità, tuttavia, dipende dalla scala di variazione spaziale del sistema ed è significativa solo negli strati di corrente.

Nel modello non ideale più semplice si introduce nella legge di Ohm ideale l'effetto della resistività:

formula [

2]

dove E è il campo elettrico, v la velocità e j la densità di corrente.

L'equazione per il campo magnetico diventa pertanto:

formula [

3]

Nell'equazione del moto gli effetti dissipativi sono essenzialmente dovuti alla viscosità ionica e possono essere introdotti mediante un termine diffusivo con coefficiente scalare:

formula [

4]

dove ϱ è la massa volumica.

fig. 1

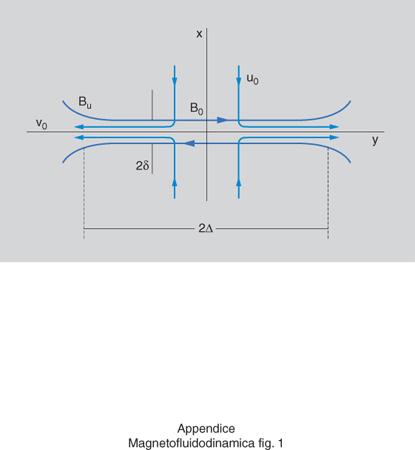
Il modello più semplice di riconnessione è quello stazionario bidimensionale, detto modello di Sweet-Parker. In esso le variabili sono indipendenti da una coordinata (z), la regione di riconnessione è caratterizzata dalla larghezza 2Δ e da uno spessore 2δ in direzione ortogonale (fig. 1); il plasma entrante nella regione di riconnessione è caratterizzato dalla velocità u₀ e dal campo di induzione magnetica B₀; il plasma uscente dai valori corrispondenti v₀, B_u. Si assume il plasma incomprimibile e con densità uniforme (per cui u₀Δ=v₀δ) e si ritiene che all'esterno della regione di riconnessione sia valida la legge di Ohm ideale e che all'interno il termine resistivo sia dominante: si ha la relazione u₀B₀≅ηj≅ηB₀/δ. Nella regione di riconnessione il plasma viene accelerato verso l'esterno dalla forza dovuta al gradiente di pressione (lungo±y). La condizione di equilibrio dello strato di corrente, tenendo presente che la velocità di entrata u₀ è usualmente molto minore della velocità di Alfvén v_A, dà la velocità di uscita v₀=v_A. Si ottengono le relazioni v_A/u₀=(v_AΔ/η)1/2=S₀1/2, Δ/δ=S₀1/2, dove è stato introdotto il numero di Lundquist S₀ dello strato di corrente. Il tasso di riconnessione risulta in questo caso ηj≅v_AB₀S₀⁻1/2. Queste stime danno tempi di riconnessione piuttosto lunghi. Per es., se si considerano valori di S₀ tipici della corona solare si ottengono tempi maggiori per diversi ordini di grandezza rispetto a quelli osservati nei brillamenti solari.

Un'analisi più dettagliata della riconnessione nel caso di geometria bidimensionale può essere effettuata mediante la simulazione numerica. Il campo di induzione magnetica e la velocità possono essere espressi tramite le funzioni potenziale ψ (componente z del potenziale vettore) e ϕ (funzione di corrente):

B=e_z×∇ψ, v=e_z×∇ϕ, dove e_z è il versore dell'asse z. La componente z della densità di corrente diventa j=∇²ψ e la componente z della vorticità ω=∇²ϕ. Il sistema magnetofluidodinamico bidimensionale può essere descritto dalle sole

formula [

5]

formula [

6]

fig. 2

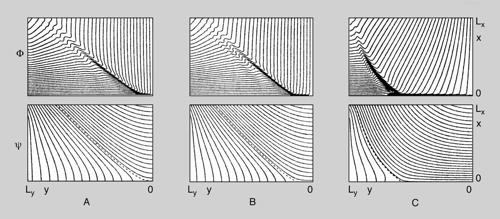
Lo studio numerico delle soluzioni del sistema in una regione rettangolare del piano x, y, di dimensioni lineari L_x ed L_y, associato a condizioni al contorno di flusso di plasma entrante (con velocità u_L) da due lati opposti, e uscente dagli altri due, permette di correlare alla resistività e al tasso di riconnessione M=∙ψ/∙t, assegnati esternamente, le caratteristiche dello strato di corrente, ovvero la sua larghezza 2Δ, lo spessore 2δ, la velocità u₀ e il campo di induzione magnetica B₀=M/u₀ al bordo dello strato. In condizioni di riconnessione stazionaria si trovano le seguenti leggi di scala: Δ∝(MR_m)²; δ∝M; u₀∝R_m⁻¹; B₀∝MR_m, con R_m=Lu_L/η. Si nota che a parità di tasso di riconnessione, la larghezza dello strato aumenta al diminuire di η, mentre lo spessore è indipendente da η. All'aumentare di R_m il campo al bordo dello strato di corrente aumenta. L'aumento di Δ al diminuire di η avviene fino a quando Δ≅L. Questo processo è mostrato dai risultati di una simulazione numerica presentati nella fig. 2. Le leggi di scala al variare della resistività diventano in questo caso δ∝(η² L/M)¹^/³; B₀∝Mδ/η; u₀∝η/δ.

Al diminuire di η il rapporto Δ/δ aumenta: se lo strato è sufficientemente sottile (Δ/δ≅100) la configurazione stazionaria diventa instabile rispetto ai modi tearing. Strati di corrente instabili danno origine alla formazione di isole magnetiche all'interno dello strato, che migrano verso l'esterno trasportate dal flusso di plasma uscente. Nelle osservazioni sperimentali strutture di questo tipo, dette plasmoidi, costituiscono oggetti in movimento, riconoscibili nel plasma di fondo. I dati da satelliti suggeriscono la presenza nella coda geomagnetica di plasmoidi, che si staccano e si allontanano dal Sole durante le tempeste magnetiche. La formazione e la dinamica di plasmoidi sono studiate anche in esperimenti di laboratorio.

I modelli di riconnessione riportati si applicano ai casi di riconnessione quasi stazionaria bidimensionale, quali per es. la coalescenza di isole magnetiche, l'evoluzione non lineare del modo tearing nel tokamak, la formazione di plasmoidi nella coda geomagnetica.

Quando la simmetria del sistema non è tale da giustificare l'uso di un modello bidimensionale si presentano nuove caratteristiche, dovute alla struttura tridimensionale della configurazione magnetica. L'indagine numerica dei vari aspetti della dinamica tridimensionale è in continuo progresso.

Nel sistema possono essere presenti punti singolari isolati a campo magnetico nullo. Queste singolarità, essenzialmente diverse da quelle bidimensionali, sono per es. i punti ellittici (O) e i punti iperbolici (X, Y) nel piano x, y, che corrispondono a linee singolari nello spazio 3D. Un'altra peculiarità è la comparsa di linee di forza stocastiche in configurazioni magnetiche chiuse. In questo caso una singola linea di forza non rimane localizzata su una superficie di flusso magnetico ma occupa un volume finito. Il flusso di plasma in tale regione può dare origine a turbolenza magnetoidrodinamica.

Turbolenza MHD

Fenomeni a carattere esplosivo, quali le disrupzioni nei tokamak e i brillamenti solari, avvengono su scale di tempo molto rapide, non giustificabili mediante un meccanismo di riconnessione stazionaria basato sulla dissipazione resistiva collisionale. Sembra infatti che i tempi caratteristici osservati siano indipendenti dalla resistività collisionale η e siano collegati invece al tempo di Alfvén τ_A=L/v_A. Modifiche alle leggi di scala si hanno introducendo nella legge di Ohm effetti generalmente trascurati, che diventano dominanti in regimi a bassa collisionalità, quali l'inerzia degli elettroni o la viscosità anomala. Modifiche più considerevoli della dinamica del processo di riconnessione per piccoli valori di η si ottengono considerando il comportamento non stazionario del plasma nella regione di riconnessione.

Per valori molto piccoli di η possono essere generati piccoli strati di corrente secondari, con tempi caratteristici inferiori alla scala di tempo globale, e si ha una transizione a un regime turbolento. In tali condizioni il processo di dissipazione di energia diventa molto efficiente. La simulazione numerica mostra che a elevati numeri di Reynolds il tasso di dissipazione diventa indipendente da η. La turbolenza non è distribuita uniformemente nel sistema, ma è localizzata in regioni di piccola dimensione fluttuanti nello spazio, caratterizzate da forti variazioni dei campi. Turbolenza MHD è presente nei plasmi spaziali e in molti plasmi di laboratorio. Il vento solare, in particolare, è diventato uno dei mezzi fondamentali per l'indagine dei processi di generazione, evoluzione e dissipazione della turbolenza.

Nella turbolenza ben sviluppata, a elevati numeri di Reynolds, è presente nel sistema una distribuzione continua di scale spaziali: dalla scala globale, dell'ordine delle dimensioni del sistema, alle scale molto piccole, sulle quali avviene la dissipazione. Nelle regioni lontane dai contorni, dove la turbolenza può essere considerata statisticamente uniforme, la generica quantità fluttuante nello spazio f(x) può essere rappresentata dalle sue componenti di Fourier (relative a una regione con dimensioni lineari L), chiamate modi spaziali: f(x)=Σ_k f_ke^ik∙x. Un'osservazione importante riguarda l'isotropia della turbolenza: in idrodinamica la turbolenza in un sistema di riferimento che si muove con la velocità media del fluido può essere considerata isotropa. In m. questa ipotesi non è generalmente valida. Se nel plasma è presente un campo di induzione magnetica a grande scala B₀ le variazioni spaziali nella direzione del campo sono continue. Il moto perpendicolare al campo può far nascere strutture a piccola scala, che danno origine a dissipazione turbolenta: l'isotropia potrà essere valida solo relativamente al piano perpendicolare al campo (turbolenza isotropa bidimensionale o 2D). Se invece il campo medio è nullo, la turbolenza sarà isotropa tridimensionale (3D).

La dinamica dei modi presenti nello stato turbolento del sistema può essere studiata a partire dalla distribuzione di equilibrio delle grandezze invarianti del sistema ideale. Nel sistema magnetofluidodinamico (3D) vi sono tre invarianti di interesse: l'energia totale W=W_V+W_B, somma dell'energia cinetica W_V e dell'energia magnetica W_B, l'elicità trasversale K, l'elicità magnetica H, definite dalle relazioni seguenti (si considera un plasma incomprimibile con densità uniforme):

formula [

7]

formula [

8]

formula [

9]

dove A è il potenziale vettore.

Nella MHD 2D gli invarianti sono l'energia, l'elicità trasversale e il valore quadratico medio del potenziale magnetico A=(1/2) Σ_k|ψ_k|².

Le distribuzioni spettrali degli invarianti all'equilibrio W_V,k, W_B,k, H_k, K_k, A_k, possono essere dedotte a partire dalla distribuzione di equilibrio nello spazio delle fasi ϱ_G della statistica classica, data dalla formula di Gibbs. Per il caso 3D risulta: ϱ_G=Z⁻¹ exp {−αW−βH−γK}; per il caso 2D: ϱ_G=Z⁻¹ exp {−αW−βA−γK}.

Per dedurre la dinamica degli invarianti nello spazio k bisogna osservare che gli invarianti ideali siano conservati nelle interazioni non lineari e che le loro componenti spettrali seguano le relazioni del bilancio dettagliato. Se una data grandezza viene iniettata nel sistema in un certo intervallo spettrale k≅k_in essa sarà diffusa in altre regioni dello spazio k. Il processo di trasferimento nello spazio k, detto comunemente cascata, avviene per intervalli Δk molto piccoli mediante interazioni a tre modi, che sono efficaci quando i numeri d'onda k dei modi interagenti sono dello stesso ordine di grandezza: |k_i−k_j |=Δk≤k; sono quindi necessari molti intervalli per passare dalla scala di iniezione k_in ⁻¹ alla scala di dissipazione k_d ^‒¹. In un sistema dissipativo possiamo considerare due casi estremi: un processo di cascata diretto (o normale), corrispondente a un flusso da k_in verso numeri d'onda maggiori, sino a k_d; un processo di cascata inverso, da k_in verso numeri d'onda più piccoli. Per un sistema limitato spazialmente quest'ultimo processo porta a un accumulo, o condensazione, verso i valori più piccoli possibili di k, impedendo al sistema di raggiungere uno stato stazionario, non essendovi dissipazione a grandi lunghezze d'onda. Gli stati di equilibrio ideale sono lontani dallo stato della turbolenza reale, corrispondente a un sistema di non equilibrio dissipativo forzato. Le dinamiche non lineari nei due sistemi sono tuttavia le stesse: pertanto, le distribuzioni ideali indicano la direzione dell'evoluzione del sistema dissipativo effettivo. Risulta che a grandi valori di k le energie all'equilibrio sono essenzialmente equiripartite, sia nel caso 3D, sia in quello 2D. Pertanto, vi sarà la tendenza dell'energia a fluire verso grandi k, cioè una cascata di energia diretta, così come avviene nella turbolenza idrodinamica descritta dalle equazioni di Navier-Stokes.

Gli invarianti puramente magnetici, l'elicità magnetica H per il caso tridimensionale e il potenziale quadratico medio A per il caso bidimensionale, hanno distribuzioni di equilibrio con un forte picco a piccoli valori di k. Queste grandezze, che sono conservate nelle interazioni non lineari, seguiranno quindi un processo di cascata inverso verso piccoli valori di k, a partire dall'intervallo di iniezione k_in. Questo meccanismo è confermato dalla prevalenza dell'energia magnetica a piccoli k. Poiché lo spettro di equilibrio dell'elicità trasversale è simile a quello dell'energia, essa seguirà un processo di cascata diretto.

Strutture coerenti ed effetto dinamo

Nell'idrodinamica classica tridimensionale non sono previsti processi di autorganizzazione, cioè la formazione di strutture coerenti a grande scala. Nell'idrodinamica bidimensionale, invece, l'autorganizzazione è un processo dominante e consiste nella formazione e nella crescita, per coalescenza, di vortici coerenti. Questo processo di aumento di energia a piccoli numeri d'onda è associato con la cascata inversa dell'energia. Poiché in m. vi sono grandezze invarianti che seguono un processo di cascata inversa, cioè l'elicità magnetica per il caso 3D e il potenziale quadratico medio nel caso 2D, sono previsti processi di autorganizzazione, che conducono alla formazione di strutture magnetiche a grande scala. In condizioni di decadimento non forzato tale processo è collegato al decadimento selettivo della turbolenza; nel caso di turbolenza forzata dà origine all'effetto dinamo turbolento. Poiché i campi magnetici a grande scala sembrano essere in condizioni di forza elettrodinamica nulla (force free), la formazione di tali strutture è associata a un crescente allineamento del campo magnetico con la densità di corrente, j×B=0. Un processo di autorganizzazione simile, vale a dire l'allineamento della velocità al campo magnetico, v×B=0, è connesso con la conservazione dell'elicità trasversale K. Poiché K non segue una cascata inversa, il meccanismo di questo allineamento è meno evidente.

L'autorganizzazione nella turbolenza è connessa ai tassi di dissipazione degli invarianti ideali. Nella MHD 3D sono dati dalle relazioni seguenti:

formula [

10]

formula [

11]

formula [

12]

Nella MHD 2D le prime due equazioni rimangono le stesse, la terza è sostituita da:

formula [

13]

Tassi di decadimenti diversi danno origine alla dissipazione selettiva. Nel caso 2D si ha dA/dt=O (η); dW/dt=O (η^α), dove O ( ) significa 'ordini di grandezza di' e α≈0 per una turbolenza completamente sviluppata.

fig. 3

Pertanto, per R_m≫1 si ha A≈cost: questo implica la crescita di A_k verso piccoli numeri d'onda, cioè una cascata inversa del potenziale magnetico. Questo processo è evidente dalla simulazione numerica riportata nella fig. 3. Lo stato finale in un sistema chiuso è determinato dal principio variazionale δ[W−μ²A]=0, che fornisce lo stato di minima energia per un valore fissato del potenziale quadratico medio. Al principio variazionale corrispondono le equazioni di Eulero ∇²ψ+μ²ψ=0 e ∇²ϕ=0, nelle quali μ² è determinato dal valore di A. La prima equazione caratterizza una configurazione a forza nulla, la seconda implica velocità nulla. Il sistema pertanto evolve verso uno stato con campo magnetico statico: W_V/W_B→0. Prima di raggiungere lo stato finale con energia W_min, le equazioni possono essere soddisfatte localmente in alcune regioni di coerenza, corrispondenti a vortici magnetici di forma circolare, generati durante il decadimento della turbolenza, visibili in fig. 3.

Nella turbolenza 2D le grandezze W e A sono fortemente correlate. Nella MHD 3D l'accoppiamento fra W e H è meno stringente. H_k segue un processo di cascata inversa, si concentra cioè verso piccoli numeri d'onda. Il sistema si rilassa verso uno stato di minima energia, mantenendo H costante, descritto dal principio variazionale δ [W−μ H]=0, che dà le equazioni ∇×B−μB=0 e v=0. Lo stato di minima energia è di nuovo un campo a forza nulla, con μ costante. Si trova quindi che a causa del decadimento selettivo il sistema turbolento tende a rilassarsi verso una configurazione statica a forza nulla a grande scala, corrispondente all'allineamento di j e B. La cascata inversa dell'elicità magnetica è correlata strettamente alla generazione di campi magnetici a grande scala per mezzo di moti fluidi turbolenti.

Effetto dinamo è detto il meccanismo attraverso il quale l'energia cinetica di un fluido conduttore è trasformata in energia del campo magnetico. In tale processo, un 'seme' di campo magnetico proveniente da una piccola fluttuazione di corrente può venire 'allungato' e riconnesso a causa del moto del fluido turbolento. L'effetto dinamo è cruciale per la comprensione di molti aspetti della fisica spaziale e dell'astrofisica. È ritenuto essere all'origine dei campi magnetici in diversi oggetti cosmici, quali i pianeti, il Sole, il disco di accrescimento delle stelle, le galassie, ed è fortemente collegato alla fisica delle novae e delle supernovae. Le condizioni per l'azione dinamo richiedono flussi a grande scala in mezzi a elevata conduttività elettrica. Recenti esperimenti di laboratorio hanno permesso di ottenere numeri di Reynolds magnetici dell'ordine di 100, adatti allo studio dell'effetto dinamo. Un possibile meccanismo dell'effetto dinamo è qui di seguito riportato. Esprimendo il campo di velocità v e il campo magnetico B come somma di una parte media, variabile solo su grandi scale spaziali, e di una piccola parte fluttuante (v=v₀+ ˜v, B=B₀+ B˜), il valore medio del campo elettrico prodotto dalla turbolenza a piccola scala sarà: E∝−〈˜v×B˜>. Esso risulta essere collegato al campo magnetico medio dalla relazione E=αB₀+β∇×B₀, nella quale α∝H_V (elicità cinetica, definita da H_V=∫ω∙v d³x) e β∝〈˜v2>. L'equazione per l'evoluzione di B₀ diventa allora: ∙B₀/∙t=−∇×(αB₀)+(η+β)∇2B₀. Il termine contenente α dà origine all'amplificazione del campo magnetico a grande scala. La condizione α∙0 richiede che il flusso turbolento, anche se isotropo, non sia simmetrico per riflessione. Questo flusso nasce naturalmente in sistemi ruotanti. Poiché la maggior parte degli oggetti astrofisici che trasportano campi magnetici a grande scala sono formati da fluidi conduttori in rotazione, il termine α è diventato il punto centrale della teoria dell'effetto dinamo. L'equazione riportata ha tuttavia validità limitata perché in essa sono stati trascurati alcuni termini non lineari nella dinamica delle fluttuazioni. A numeri di Reynolds molto elevati il campo B₀ agisce da campo guida per le fluttuazioni ˜v: esse diventano onde di Alfvén con v×B˜≈̳0. Questo fenomeno, detto effetto Alfvén, porta a una rapida equipartizione dell'energia cinetica e magnetica alle piccole scale. Come conseguenza, il termine α viene ridotto. D'altra parte, insieme all'energia magnetica a piccola scala si genera anche elicità magnetica, la quale, a causa del processo di cascata inversa, porta a una crescita del campo magnetico a grande scala. Si ha in questo caso un processo dinamo turbolento non lineare. Se nel sistema è presente un campo magnetico B₀ elevato, il processo dinamo è modificato, tenendo presente che la turbolenza a piccola scala non altera l'elicità magnetica, poiché

con ν〈1. In questo caso risulta E=(B₀/B²₀)∇∙h, dove h è il flusso di elicità, che contiene l'effetto della turbolenza a piccola scala. Dall'espressione di h si ottiene E=−(B₀/B²₀)∇∙D∇(j₀∙B₀/B²₀), con D positivo. Si deduce che in una configurazione con un campo magnetico statico molto elevato (v_A≫v₀) la resistività turbolenta β si annulla, perché un valore finito di β porterebbe a un rapido decadimento dell'elicità. L'effetto di turbolenza a piccola scala sui campi medi, sia nell'effetto dinamo non disruptivo, sia nella dirupzione turbolenta, è descritto nella legge di Ohm (2) da un termine −η₂∇⁽⁴⁾j (iperresistività).

In aggiunta all'autorganizzazione, che porta a un allineamento di j e B, collegato alla quasi costanza dell'elicità magnetica, vi è un ulteriore processo di autorganizzazione in un sistema MHD turbolento, che conduce all'allineamento di v e B. Le osservazioni effettuate dai satelliti sul vento solare, il solo sistema accessibile con una turbolenza MHD stazionaria completamente sviluppata, mostrano stati in cui le fluttuazioni della velocità e del campo magnetico sono fortemente correlate, v=±v_A. Confrontando il tasso di decadimento dell'energia W e dell'elicità trasversale K, quest'ultimo risulta essere più piccolo. Questo indica che lo stato di rilassamento è lo stato di minima energia, per un dato valore di K, determinato dal principio variazionale δ[W−2λK]=0. Questo porta all'equazione v=±v_A valida in ogni punto dello spazio. Lo stato di rilassamento corrisponde a un'onda di Alfvén polarizzata linearmente. Il processo di rilassamento avviene dinamicamente. La turbolenza a piccola scala può essere considerata un insieme di onde di Alfvén che si propagano lungo il campo medio, con interazione fra modi che si propagano in direzioni opposte.

bibliografia

D. Biskamp, Nonlinear magnetohydrodynamics, Cambridge 1993; E.N. Parker, Spontaneous current sheets in magnetic fields, Oxford 1994.