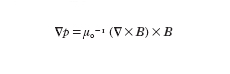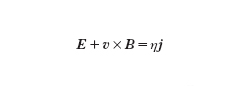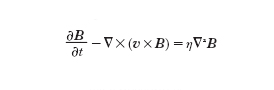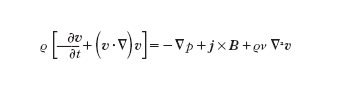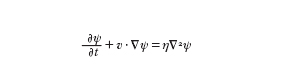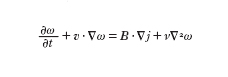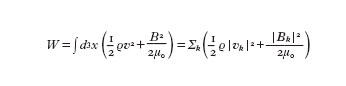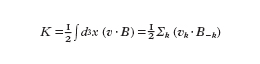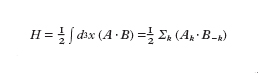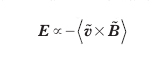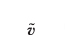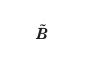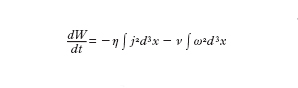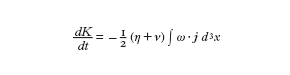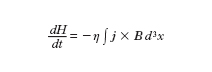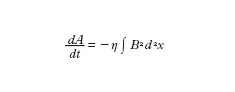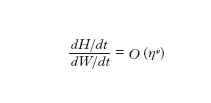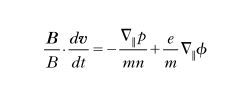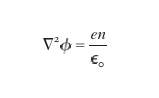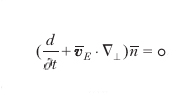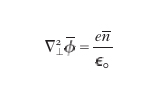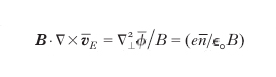Magnetofluidodinamica dei plasmi

Magnetofluidodinamica dei plasmi

Gli sviluppi più rilevanti della m. dei p. si devono al notevole incremento delle osservazioni sperimentali, riguardanti sia plasmi astrofisici e spaziali, in primo luogo il plasma solare, sia plasmi di laboratorio, in particolare quelli di interesse per la fusione controllata mediante sistemi di confinamento magnetico.

È anche da segnalare lo sviluppo di nuovi esperimenti per lo studio dei meccanismi di base della magnetofluidodinamica (MFD, Magneto Fluid Dynamics) e di quelli dedicati alla riproduzione in laboratorio dei fenomeni analoghi che avvengono in astrofisica. In particolare, è stata raggiunta una migliore caratterizzazione dei fenomeni di riconnessione magnetica in esperimenti di laboratorio; esperimenti con laser di alta potenza hanno permesso di riprodurre le caratteristiche essenziali dei flussi fluidodinamici e di instabilità rilevanti per diversi plasmi astrofisici. Tali esperimenti includono anche la formazione di getti supersonici magnetizzati e non, la produzione di onde d'urto, lo studio di plasmi in rotazione differenziale, nei quali possono nascere instabilità MFD. Sono anche aumentati in gran misura i campi di applicazione della MFD e in generale dei modelli fluidi dei plasmi. A ciò si aggiunge il miglioramento notevole della qualità dei dati, dovuto all'impiego di nuove tecniche diagnostiche e di nuove strumentazioni. L'aumento delle informazioni sul comportamento del plasma in una grande varietà di situazioni ha condotto a uno sviluppo notevolmente significativo di modelli teorici, nei quali vengono estesi i limiti di validità dello schema consueto MFD e sono inclusi anche alcuni effetti derivanti da modelli cinetici e a più fluidi.

Lo sviluppo di codici numerici che tengono conto della geometria effettiva, tridimensionale, del sistema fisico e che funzionano su computer paralleli, ha portato a una enorme crescita dell'impatto della simulazione numerica sui modelli teorici interpretativi; la complessità di fenomeni tipici della MFD, quali, per es., la riconnessione magnetica, lo sviluppo della turbolenza, la formazione di strutture, rende tuttavia le capacità di calcolo attuali non ancora completamente adeguate per una descrizione soddisfacente del comportamento del plasma. Per poter apprezzare i progressi recenti nei temi di ricerca sopra menzionati è opportuno tenere presenti le principali caratteristiche e i limiti dello schema MFD. Nella sua formulazione più semplice la m. descrive fenomeni nei quali un plasma si comporta come un unico fluido, elettricamente neutro, avente una conduttività elettrica molto elevata. Questo modello può essere usato in luogo di altri più complessi cinetici e a più fluidi quando sono soddisfatte alcune limitazioni alle scale temporali e spaziali caratteristiche dei fenomeni in considerazione.

Indicando con L,τ, V∼L/τ rispettivamente la lunghezza, l'intervallo di tempo e la velocità caratteristici di tali fenomeni, le principali limitazioni possono essere scritte: L≫r_D (ove r_D è la lunghezza di Debye), affinchè sulla scala L sia soddisfatta la condizione di neutralità; L≫r_L (ove r_L è raggio di Larmor delle particelle) e ω_ciτ ≫1 (ove ω_ci è la frequenza di ciclotrone degli ioni): ovvero le variazioni temporali avvengono su scale di tempo maggiori del periodo del moto di girazione delle particelle nel campo magnetico e le variazioni spaziali su scale di lunghezza maggiori del raggio di Larmor.

Queste condizioni permettono di poter considerare la dinamica del plasma nel modello MFD risultante da uno schema cinetico nel quale si effettua un procedimento di media sul moto di girazione delle particelle. Nella m. dei p. si considerano perturbazioni le quali si propagano con velocità piccola rispetto alla velocità della luce c; la corrente di spostamento èpertanto trascurata rispetto alla corrente di conduzione e la densità di corrente j è legata al campo magnetico B/μ₀ dalla legge di Ampère

formula. [

1]

Nel sistema MFD la dinamica del plasma viene descritta dalle equazioni di bilancio della massa (continuità), da quelle del momento e dell'energia del fluido (che viene di seguito scritta in forma adiabatica):

formula, [

2]

formula, [

3]

formula, [

4]

ove ρ, p e v sono densità, pressione e la velocità del fluido, ν è la viscosità e d/dt≡∂/∂t+v∙∇ è la derivata convettiva. Chiude il sistema l'equazione per l'evoluzione di B, che deriva dalla legge di Ohm generalizzata, trattata in seguito.

Nello schema MFD si possono trattare fenomeni estremamente vari, caratterizzati da ulteriori articolazioni delle scale di tempo e di lunghezza. Queste possono essere individuate, a grandi linee, a partire da un'analisi di scala della legge di Ohm generalizzata, che, in termini di variabili fluide assume la forma:

formula, [

5]

nella quale n≡ne è il numero di elettroni a unità di volume e si è usata la condizione di neutralià n≡ni (per una specie ionica di carica unitaria), Pe è il tensore delle pressioni elettronico, η è la resistività elettrica; nell'equazione si è trascurato me/mi≪1. Diverse caratteristiche nel comportamento del plasma al variare dei parametri del sistema si possono dedurre dalla stime dell'ordine di grandezza dei termini che compaiono nell'equazione [5].

Nelle stime il termine a sinistra è ritenuto ^O(I); il primo termine a destra (termine resistivo) è pesato da 1/R_m, ove R_m≡μ₀VL/η è il numero di Reynolds magnetico, e diventa trascurabile per R_m≫1; il secondo termine a destra, detto termine di Hall, è in ordine di grandezza (c/Lω_pi)(v_a/V), ove v_a=B/(μ₀nm_i)^1/2 è la velocità di Alfvén (c/ω_pi è detta lunghezza d'inerzia ionica); esso può essere trascurato se L≫(c/Lω_pi)(v_a/V); il terzo termine (termine di pressione) nella componente perpendicolare al campo è pesato da (r_Le/L)(v_te/V) e può essere trascurato rispetto ai termini a sinistra dell'equazione se L≫r_Le(v_te/V); è da notare che il rapporto fra queso termine e il termine di Hall è dato dal rapporto fra la densità di energia termica elettronica e la densità di energia magnetica; l'ultimo termine, dovuto all'inerzia degli elettroni è pesato da c/Lω_pe e diventa trascurabile per L≫c/ω_pe, detta lunghezza d'inerzia elettronica.

In queste espressioni ω_pe=e [n/(ε₀m_e)]^1/2, ω_pi=ω_pe(m_e/m_i)^1/2 sono rispettivamente la frequenza di plasma elettronica e la frequenza di plasma ionica, vte è la velocità termica degli elettroni, rLe il raggio di Larmor degli elettroni termici. Nello schema MFD ideale (R^m, Lω^pi /c, L/r^Li→∝) l'intero termine a destra dell'equazione [5] è considerato nullo: E+vxB=_°; la velocità del fluido perpendicolare al campo magnetico è quella della deriva elettrica v_E=x_B/B². In tal caso, tenendo presente la legge d'induzione, si ha

formula. [

6]

Da questa relazione si deduce che il campo magnetico è congelato nel plasma, ovvero le sue linee di forza si muovono solidalmente al plasma (legge del congelamento). Nella MFD detta resistiva si tiene conto nel membro a destra della legge di Ohm del solo termine di resistività, dominante rispetto agli altri termini. In questo caso nell'evoluzione del campo B al termine di congelamento si aggiunge un termine diffusivo; l'equazione (6) infatti diventa

formula, [

7]

ove, per semplicità, i termini dovuti alla variazione spaziale della resistività η sono stati ritenuti trascurabili. La diffusione resistiva del campo magnetico è caratterizzata da un coefficiente di diffusione η/μ₀ e da un tempo caratteristico di diffusione sulla lunghezza L dato da τ_r=μ₀L²/η. La validità della legge di Ohm resistiva è limitata a scale spaziali L molto maggiori del raggio di Larmor ionico e della lunghezza inerziale ionica L≫c/Lω_pi, L≫r_Li. Per fenomeni che si svolgono su scale spaziali inferiori alla lunghezza d'inerzia ionica c/ω_pe≪L〈c/ω_pi il termine di Hall diventa importante nella legge di Ohm generalizzata (5) e contribuisce a disaccoppiare il moto degli elettroni e quello degli ioni sulla scala della lunghezza inerziale ionica.

In questo schema, detto m. di Hall, la legge di Ohm generalizzata diventa E+vxB=ηj+jxB/(en), e l'equazione di evoluzione del campo magnetico pertanto si scrive:

formula [

8]

ove è stata introdotta la velocità vB=−j/(en) (velocità di Hall).

Una condizione limite notevole del sistema MFD di Hall si verifica quando la velocità v_B, rimanendo molto piccola rispetto alla velocità termica degli elettroni v_te, è molto maggiore della velocità di Alfven v_A e della velocità sonora c_s: c_s, v_A≪v_B≪v_te; in tal caso la velocità fluida v può essere trascurata rispetto alla velocità di Hall e l'equazione di induzione diviene

formula [

9]

Il modello teorico corrispondente al sistema di equazioni così modificato è detto elettro-magnetofluidodinamico (EMFD). Nel limite di conduttività infinita questa equazione rappresenta il congelamento del campo magnetico nella sola componente elettronica del plasma.

I modelli teorici sopra descritti hanno particolare applicazione allo studio della riconnessione magnetica, uno dei processi fondamentali che avvengono in un plasma o in fluido magnetizzato, fenomeno non ancora ben compreso e oggetto di continue indagini sperimentali e teoriche. La riconnessione produce un cambiamento della topologia delle linee del campo di induzione magnetica B, con conversione di energia magnetica in energia cinetica di moto medio (macroscopico) del fluido, energia termica ed energia delle particelle veloci accelerate durante il processo. Si verifica per elevati valori del numero di Reynolds magnetico in regioni ristrette dello spazio caratterizzate da intensa densità di corrente elettrica (singolare in assenza di diffusione magnetica).

Si noti infatti che il campo di induzione B varia nel tempo per il trasporto convettivo e la diffusione: il primo processo è dominante rispetto al secondo in quasi l'intero spazio, tranne in prossimità delle singolarità ove il gradiente del campo diventa molto grande, insieme alla densità di corrente: in queste regioni può generalmente avvenire la riconnessione, spontaneamente oppure indotta dal moto del plasma, poiché la condizione di congelamento non permette riconnessione. La riconnessione è responsabile di molti processi dinamici che avvengono in plasmi di laboratorio e in corpi astrofisici, in particolare nel Sole e nella magnetosfera. Nel Sole i brillamenti solari rappresentano una conversione esplosiva, mediante riconnessione, di energia magnetica immagazzinata in altre forme di energia. Così la riconnessione è probabilmente responsabile del riscaldamento della corona solare; il processo avverrebbe mediante la formazione di molti piccoli strati di corrente e sarebbe in grado di mantenere la corona solare alla temperatura di alcuni milioni di gradi, molto più elevata della temperatura della superficie del Sole, di circa 6000 K.

Nella magnetosfera il vento solare deforma il campo magnetico sino a dare origine a una coda geomagnetica. Occasionalmente il campo nella coda geomagnetica può riconnettersi in maniera esplosiva, producendo una tempesta geomagnetica.

Le osservazioni con satelliti e i risultati delle simulazioni numeriche mostrano che l'assottigliamento della coda geomagnetica a dimensioni inferiori della lunghezza d'inerzia ionica è una condizione necessaria al fine di produrre una rapida riconnessione. La riconnessione può anche avvenire sporadicamente in prossimità della faccia frontale della magnetopausa, collegando il campo geomagnetico al campo magnetico interplanetario e producendo i cosiddetti eventi di trasferimento di flusso. Come già osservato, questi fenomeni possono essere descritti nello schema della MFD di Hall, appropriato allo studio di processi che avvengono su scala di lunghezza inferiore alla lunghezza d'inerzia ionica c/ω_pi, in particolare allo studio della riconnessione in sottili strati di corrente e della penetrazione rapida di un campo magnetico impulsato nel plasma.

Nuove misure su plasmi di laboratorio in particolari configurazioni toroidali hanno infatti mostrato che nei processi di riconnessione tridimensionale il termine di Hall è dominante rispetto al termine resistivo e al termine inerziale; si è anche osservata la formazione di strutture sulla scala della lunghezza d'inerzia ionica, correlate con la presenza di particelle sopratermiche.

In generale il processo di riconnessione coinvolge la dipendenza delle grandezze fisiche dalle tre coordinate spaziali; tuttavia, in importanti casi la simmetria del sistema permette di considerare solo due coordinate spaziali. Mentre la dinamica della riconnessione magnetica a due dimensioni si basa su modelli teorici ben verificati ed è ben compresa; la riconnessione tridimensionale pone problemi non ancora risolti, che sono oggetto dei più recenti sviluppi della MFD. Il processo di riconnessione a due dimensioni è relativamente semplice e ha luogo solo nei punti singolari X, ove la densità di corrente è estremamente elevata e i meccanismi non ideali permettono alle linee di campo di spezzarsi e di cambiare connessione.

In questo caso è possibile individuare la velocità delle linee di campo e stabilire una corrispondenza uno a uno fra le linee che entrano nella regione di riconnnessione e le linee riconnesse uscenti. La riconnessione a tre dimensioni presenta nuove caratteristiche: la struttura dei punti a campo magnetico nullo nello spazio tridimensionale e la topologia delle linee di campo sono più complesse; nel caso più semplice, vi sono due diverse famiglie di linee di campo passanti per il punto nullo. La riconnessione tridimensionale può avvenire in prossimità di un punto nullo, ove si presentano tre diversi tipi di riconnessione; può avvenire anche in assenza di un punto nullo, in tal caso si ha la formazione di complesse strutture nelle linee di campo, simili a fili intrecciati e ritorti.

Nella regione di riconnessione e nel plasma uscente da tale zona non si individuano le velocità delle linee di campo, che cambiano continuamente le loro connessioni. La riconnessione magnetica è sovente correlata a una condizione di turbolenza nel plasma. Immagini ad alta risoluzione dei brillamenti solari mostrano spesso fenomeni di riconnessione e fluttuazioni di turbolenza; simili fluttuazioni si osservano anche nelle simulazioni numeriche se il numero di Reynolds magnetico è sufficientemente elevato. La rotazione del plasma induce facilmente turbolenza; le corrispondenti fluttuazioni magnetiche e di velocità del fluido possono dare origine a campi magnetici a grande scala. Questo fenomeno costituisce una possibile spiegazione dell'effetto dinamo, ossia il meccanismo attraverso il quale l'energia cinetica di un fluido conduttore viene trasformata in energia del campo magnetico; il citato effetto è ritenuto essere all'origine dei campi magnetici tanto delle stelle quanto dei pianeti.

In fluidi conduttori in rotazione è stata osservata la generazione di un campo magnetico toroidale a partire da un campo magnetico poloidale assisimmetrico (effetto ω); affinchè il campo poloidale sia mantenuto dalla rotazione del fluido è necessaria la presenza di una forza elettromotrice turbolenta che è caratterizzata dal campo elettrico

(ove le parentesi stanno a indicare la media sulle scale delle fluttuazioni) prodotto da fluttuazioni a piccola scala di velocità

e di campo magnetico

Queste fluttuazioni rompono la simmetria del sistema e interagiscono coerentemente per generare il campo magnetico a grande scala. Recenti risultati sperimentali ottenuti in un flusso assisimmetrico turbolento di sodio liquido in geometria sferica sembrano confermare il modello teorico. La turbolenza induce anche viscosità turbolenta nel plasma. Partendo da dati da satelliti di misure di vento solare, raccolti per alcuni decenni, lo studio della correlazione fra l'attività geomagnetica e la viscosità turbolenta del vento solare ha condotto a una conferma riguardo alla validità del concetto di viscosità MFD nell'accoppiamento fra vento solare e campo geomagnetico. La turbolenza ha inoltre un ruolo molto importante nei fenomeni di trasporto che avvengono nella regione del bordo dei plasmi confinati magneticamente in configurazioni di interesse per la fusione. Alcune misure hanno permesso di visualizzare la struttura turbolenta del plasma al bordo, che spesso contiene strutture localizzate (blobs) che si muovono radialmente e poloidalmente (∼1 km/s); la dinamica di queste strutture non lineari indica la presenza di un rapido trasporto convettivo al bordo del plasma.

Si è assistito così a un impatto crescente di potenti strumenti computazionali sulla comprensione di vari fenomeni astrofisica: allo scopo di studiare i flussi MFD in sistemi assisimmetrici e in sistemi completamente tridimensionali, per studiare l'origine dei getti astrofisici, le onde d'urto nel mezzo interstellare, la turbolenza, dai plasmi di interesse fusionistico ai dischi di accrescimento. La presenza nei plasmi magnetizzati di una gran varietà di scale spaziali e temporali rende un approccio computazionale allo studio di tali sistemi estremamente utile se non cruciale.

Si consideri che il modello di descrizione più dettagliato per un plasma magnetizzato è quello basato su equazioni cinetiche che descrivono l'evoluzione della funzione di distribuzione di ciascuna specie nello spazio delle fasi (a 6 dimensioni) delle particelle. L'alta dimensionalità rende questo approccio non praticabile sulle scale di tempo lunghe e per le geometrie di interesse sperimentale. I modelli fluidi costituiscono un'approssimazione al modello cinetico e la loro dimensionalità ridotta permette di esplorare un intervallo più ampio di scale spaziali e temporali.

Un problema di notevole importanza in tale riduzione riguarda la trattazione dell'accoppiamento fra processi cinetici a piccola scala e processi a grande scala, come introdurre correttamente nello schema fluido valido sulle grandi scale gli effetti cinetici e in generale gli effetti dei processi a piccola scala, per fare un esempio, la viscosità turbolenta e la resistività anomala, usata allo scopo di simulare nella MFD resistiva l'effetto di microinstabilità, senza peraltro eliminare i contributi di di qualche scala. Un campo di indagine a carattere interdisciplinare nel quale sono stati ottenuti risultati di rilievo, dalla dinamica dei fluidi non viscosi alla produzione e manipolazione di antimateria (positroni e/o antiprotoni), è quello dei plasmi non neutri, in particolare plasmi con cariche dello stesso segno. Tali plasmi vengono generalmente studiati utilizzando per il loro confinamento dispositivi, detti trappole di Penning cilindriche, caratterizzati dalla presenza di un intenso campo magnetico assiale e da campi elettrici statici prodotti da conduttori cilindrici coassiali posti a diversi potenziali, che contribuiscono a confinare assialmente il plasma. L'equilibrio fluido di tale sistema corrisponde a un plasma carico in rotazione nel quale le forze d'inerzia e la forza dovuta al campo elettrico autoconsistente sono bilanciate, trasversalmente all'asse, dalla forza di Lorentz. L'evoluzione del sistema nello schema fluido è retta dalle seguenti equazioni (scritte per un plasma di elettroni)

formula, [

10]

formula, [

11]

formula, [

12]

formula, [

13]

formula. [

14]

Nelle condizioni sperimentali più comuni il campo magnetico dal plasma è trascurabile rispetto a quello prodotto da sorgenti esterne e le scale di tempo e di lunghezza dell'evoluzione del sistema permettono una descrizione mediata sul periodo di ciclotrone delle particelle, in cui la deriva elettrica v_E=−∇_⊥ϕ×B/B² determina la velocità perpendicolare al campo v_⊥≅v_E; la dinamica assiale è descritta dall'equazione

formula, [

15]

e il potenziale soddisfa l'equazione di Poisson

formula, [

16]

Nel caso di campo magnetico uniforme e di simmetria cilindrica il plasma all'equilibrio ruota con velocità di rotazione dipendente dalla densità e dal campo magnetico. Se il periodo di oscillazione delle particelle nella buca di potenziale assiale è sufficientemente breve, il moto mediato su tale periodo è governato dalla dinamica trasversale incomprimibile

formula, [

17]

e dall'equazione di Poisson mediata

formula, [

18]

ove le quantità barrate sono mediate sul moto longitudinale.

Notando che

,

la vorticità del plasma risulta essere proporzionale alla densità; l'equazione (17) rappresenta quindi l'equazione di conservazione della vorticità per un fluido bidimensionale non viscoso. Questa analogia ha portato a interessanti risultati teorici e sperimentali sulla turbolenza e la formazione di strutture persistenti (cristalli di vortice) nel sistema e permette di effettuare esperimenti di dinamica dei fluidi non viscosi utilizzando plasmi non neutri.

bibliografia

Plasmas in the laboratory and in the universe. New insights and new challenges, AIP (American Institute of Physics) Conference Proceedings 703, Como 2003, a cura di G. Bertin, D. Farina, R. Pozzoli, Melville (NY) 2004; Program of the 47^th annual meeting of the division of plasma physics, Denver (Co) 2005, in Bulletin of the American physical society, 2005, 50, 8.