Pascal, lumaca di
Pascal, lumaca di
Pascal, lumaca di curva algebrica piana del quarto ordine, che prende il nome dal padre di B. Pascal, Étienne Pascal (1588-1651), magistrato e studioso di problemi fisici e matematici. È ottenuta come concoide della circonferenza, nel modo che segue. Siano O e P, rispettivamente, un punto fisso e un punto mobile su una circonferenza di raggio r. Fissata una lunghezza k > 0, siano A1 e A2 due punti distanti k da P e appartenenti alla retta OP. Il luogo descritto da A1 e A2 al variare di P sulla circonferenza è detto lumaca di Pascal. La forma della curva dipende dai valori dei parametri r e k. Si possono presentare i tre seguenti casi:
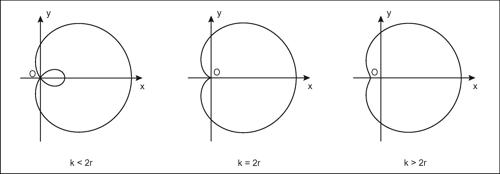
• se k < 2r la curva ha un nodo in O;
• se k = 2r la curva ha una cuspide in O e, in tal caso, è detta cardioide;
• se k > 2r la curva è priva di punti doppi.
In particolare se k = r la curva prende il nome di trisettrice. La lumaca di Pascal può essere definita anche
• come luogo descritto da un punto fisso su un cerchio che rotola, senza strisciare, esternamente a un altro cerchio fisso di uguale raggio;
• come podaria della circonferenza.
L’equazione della lumaca di Pascal in coordinate cartesiane è (x 2 + y 2 − 2rx)2 = k 2(x 2 + y 2), mentre in coordinate polari è ρ = k + 2rcos θ.