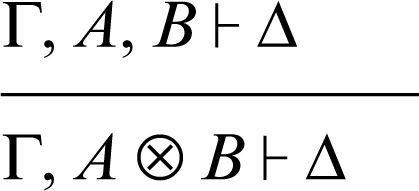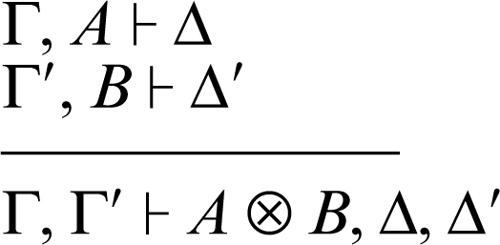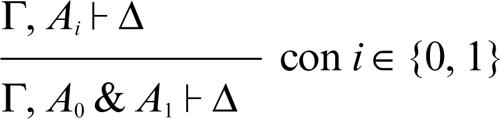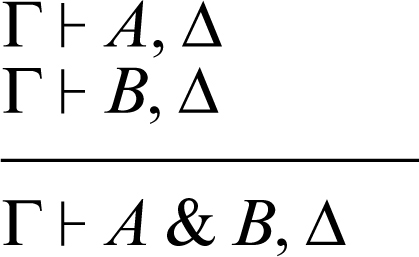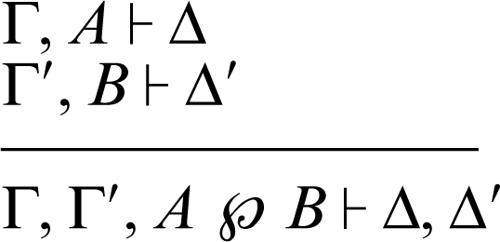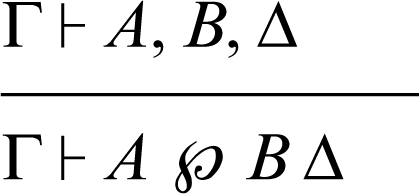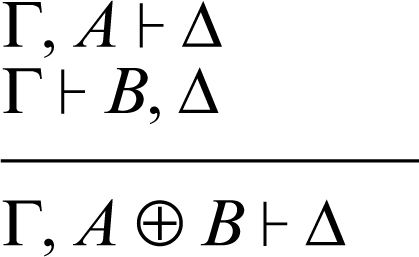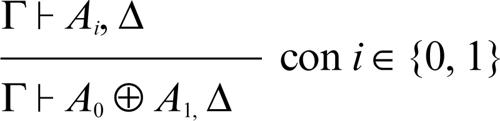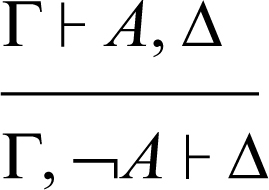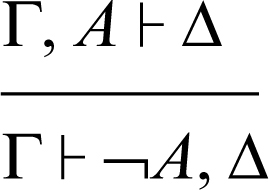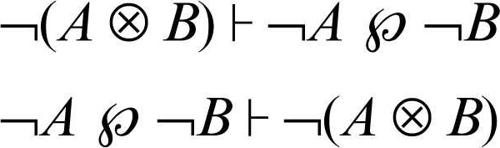logica lineare

logica lineare

logica lineare area di ricerca della logica matematica nata nel 1986 e diffusasi in seguito alla pubblicazione, nel 1987, dell’articolo Linear logic del logico francese Jean-Yves Girard (1947). Essa recupera l’aspetto “costruttivo” della → logica intuizionista unendolo ad alcune caratteristiche peculiari della logica classica, fra cui la presenza di una pervasiva simmetria strutturale. La logica lineare nasce nell’ambito della teoria della dimostrazione e in particolare il suo sviluppo è legato alla semantica della logica intuizionista, tuttavia si pone come strumento utile alla ricerca in vari settori fra cui il → lambda-calcolo, la → programmazione logica e la teoria della → complessità computazionale.

La logica lineare elimina le due regole strutturali della contrazione e dell’indebolimento che caratterizzano la logica classica nella sua formulazione nel calcolo dei → sequenti. L’eliminazione delle regole strutturali ha come conseguenza lo sdoppiamento dei connettivi classici: ognuno di questi ha infatti, nella logica lineare, due possibili caratterizzazioni, una moltiplicativa e una additiva. Il linguaggio della logica lineare presenta così, rispetto ai linguaggi logici precedenti, un numero maggiore di connettivi, che lo rendono più ricco. In particolare, la logica lineare prevede l’utilizzo di costanti moltiplicative, costanti additive, connettivi moltiplicativi, connettivi additivi e operatori esponenziali.

Le costanti moltiplicative sono:

• il vero moltiplicativo, indicato con il simbolo 1;

• il falso moltiplicativo, indicato con il simbolo ⊥.

Le costanti additive sono:

• il vero additivo, indicato con il simbolo ⊺;

• il falso additivo, indicato con il simbolo 0.

I connettivi moltiplicativi sono:

• la congiunzione moltiplicativa detta times e indicata con il simbolo ⊗;

• la disgiunzione moltiplicativa detta par e indicata con il simbolo ℘.

I connettivi additivi sono:

• la congiunzione additiva detta and o con e indicata con il simbolo &;

• la disgiunzione additiva detta più e indicata con il simbolo ⊕;

Anche l’implicazione lineare è duplice: una implicazione moltiplicativa indicata dal simbolo -o e una implicazione additiva indicata dal simbolo ‘⇀. Queste le regole che definiscono i connettivi:

congiunzione moltiplicativa ⊗ a sinistra:

congiunzione moltiplicativa ⊗ a destra:

congiunzione additiva & a sinistra:

congiunzione additiva & a destra:

disgiunzione moltiplicativa ℘ a sinistra:

disgiunzione moltiplicativa ℘ a destra:

disgiunzione additiva ⊕ a sinistra:

disgiunzione additiva ⊕ a destra:

negazione (lineare) a sinistra:

negazione (lineare) a destra:

Come emerge dalla simmetria delle regole, si ottengono le leggi di de Morgan: sia moltiplicative

sia additive

Inoltre si definisce l’implicazione moltiplicativa

e l’implicazione additiva

La disgiunzione additiva, soddisfa la proprietà della disgiunzione (ossia, se Γ ⊢ A ⊕ B allora vale almeno una delle due Γ ⊢ A o Γ ⊢ B); codifica così l’interpretazione costruttivista della disgiunzione («una prova di A o una prova di B»). La disgiunzione moltiplicativa invece non soddisfa la proprietà della disgiunzione e codifica il comportamento delle disgiunzioni dimostrabili, nella logica classica, a partire dalla legge del terzo escluso (in quanto (A ℘￢A) è un teorema, ma non lo è (A ⊕￢A)) oppure dalla regola di assurdo classico (in quanto ￢ è involutorio). Gli operatori esponenziali sono indicati dai simboli: ? e ! e sono così interpretabili: !A sta per «A è un teorema» e ?A sta per «A è soddisfacibile» o analogamente «non A non è un teorema»; l’analogia si ha perché ￢!A equivale a ? ￢A. Si definiscono inoltre i quantificatori in modo classico, anche se le loro proprietà risentono della differenza, rispetto alla logica classica, dovuta alla negazione lineare. Dall’elenco fornito si evince una simmetria nella definizione dei connettivi. Inoltre la differenza fra connettivi moltiplicativi e additivi rispecchia la differenza presente fra enunciati veri, che possono essere usati un numero arbitrario di volte nel ragionamento, ed enunciati che possono essere usati per un numero limitato di volte nel ragionamento perché il loro utilizzo può determinarne la perdita della verità; per esempio l’affermazione «ho 30 euro quindi pago il pranzo» può essere utilizzata una sola volta in quanto perde la sua validità dopo che i 30 euro sono stati spesi.

Una delle maggiori innovazioni introdotte dalla logica lineare è costituita dai proof-net o reti di prova; un proof-net è un grafo che rappresenta geometricamente una dimostrazione logica. È possibile dimostrare che ogni proof-net proviene da una deduzione formale del calcolo dei sequenti lineare, risultato noto come teorema di sequenzializzazione. Inoltre la rappresentazione geometrica delle dimostrazioni permette di visualizzare un passo di eliminazione del taglio (→ taglio, regola del) da una dimostrazione come la deformazione del grafo (proof-net) relativo alla dimostrazione stessa.

Il vantaggio maggiore della logica lineare è che le derivazioni, pur rispettando le simmetrie classiche, sono consistenti dal punto di vista computazionale: la perdita di questa proprietà, forse il maggior limite della logica classica, è infatti una conseguenza dell’uso delle regole strutturali, e non una conseguenza delle simmetrie interne (involutività della negazione e leggi di de Morgan) che la logica lineare mantiene.