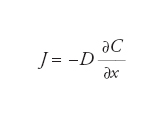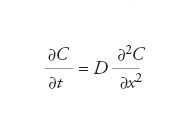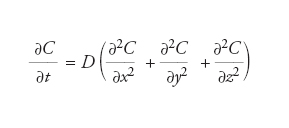legge di Fick
legge di Fick
Sta alla base dei processi di diffusione ed è stata originariamente formulata nell’Ottocento dal medico Adolf Eugen Fick studiando il flusso di un gas attraverso una membrana. Essa prevede che la quantità di gas che in un intervallo di tempo passa attraverso le membrane alveolari dipende da un coefficiente (detto coefficiente di diffusione), dall’estensione della superficie di scambio, dalla differenza della concentrazione fra i due ambienti e dal tratto lungo il quale ha luogo la diffusione stessa. Dal punto di vista matematico viene espressa come segue:
dove C è la concentrazione della specie diffondente, x è la direzione lungo la quale diffonde e J il flusso, espresso solitamente in moli per unità di tempo e di superficie perpendicolare alla direzione del flusso stesso. D è il coefficiente di diffusione o diffusività, che solitamente viene espresso in cm2 s−1. Esso dipende strettamente dall’ambiente in cui è immerso il fluido e riflette la rapidità di propagazione. Il segno negativo è giustificato dal fatto che il flusso va da una concentrazione più alta a una più bassa. La definizione precedente prende il nome di prima legge di Fick. Nel caso in cui si voglia considerare anche la variazione nel tempo della concentrazione C del componente che diffonde, il suo bilancio fornisce la seguente equazione differenziale:
la cui integrazione porta alla dipendenza della concentrazione dal tempo t e dalla coordinata x. Questa legge, definita seconda legge di Fick, riguarda la diffusione lungo un’unica direzione; in uno spazio tridimensionale, x, y, z, assume la forma:
Si tratta di un’equazione differenziale di secondo ordine alle derivate parziali la cui integrazione richiede la conoscenza delle condizioni iniziali e al contorno. Essa, nel corso degli anni, ha trovato un’applicazione generale, in chimica e in fisica nucleare, per il calcolo del moto dei neutroni in particolare nei reattori.