Legame chimico

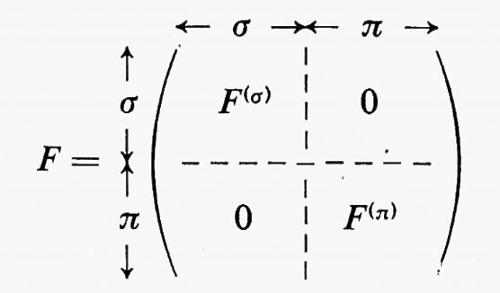
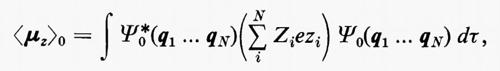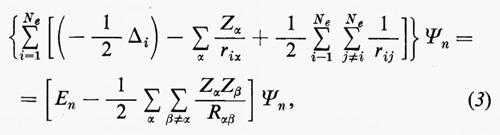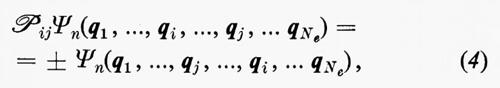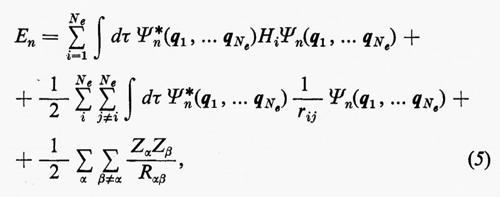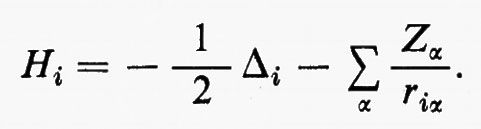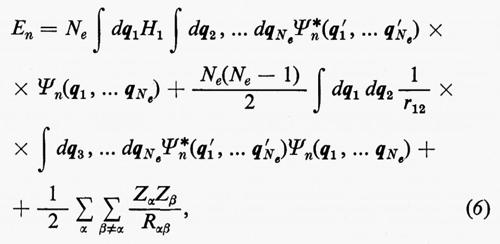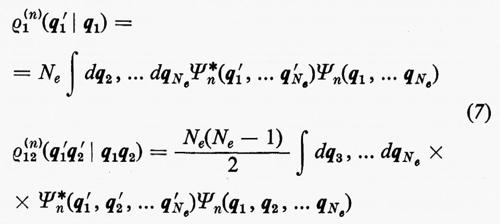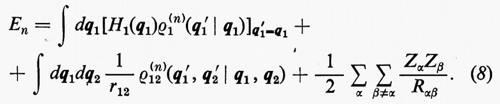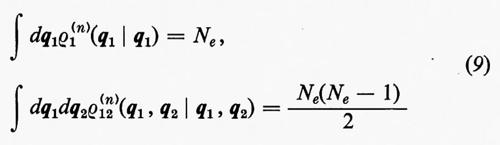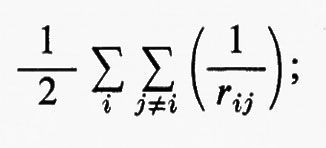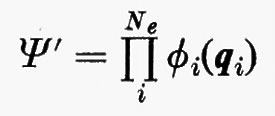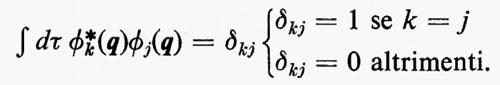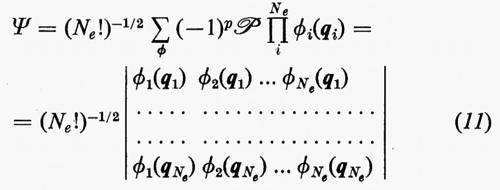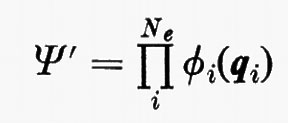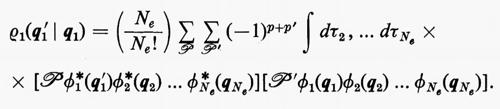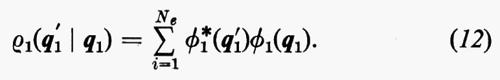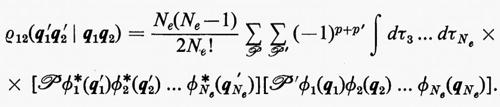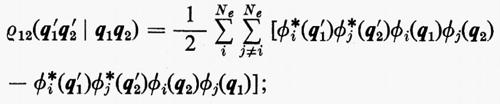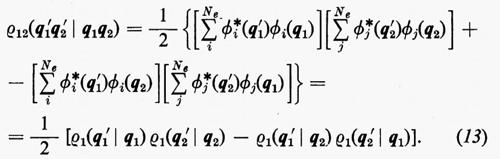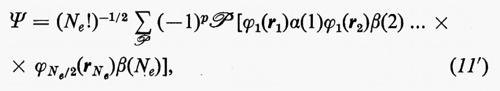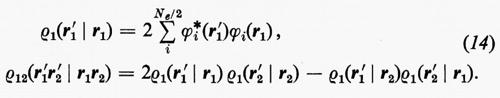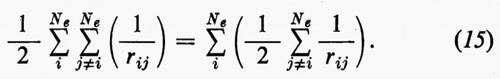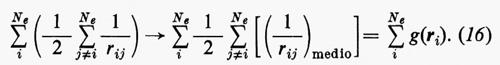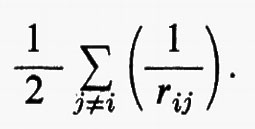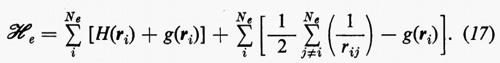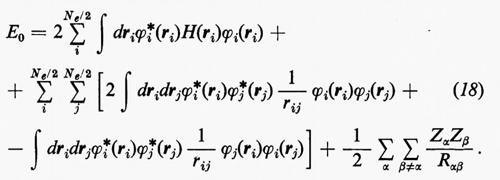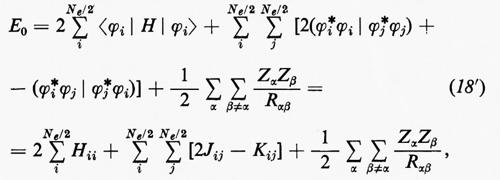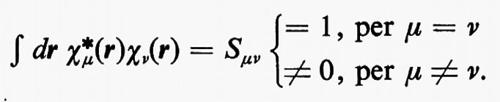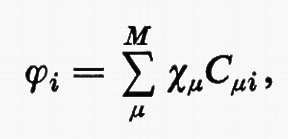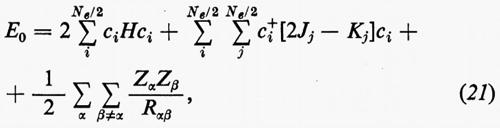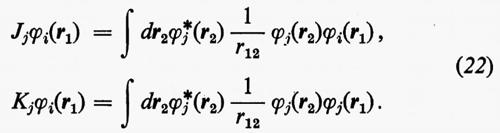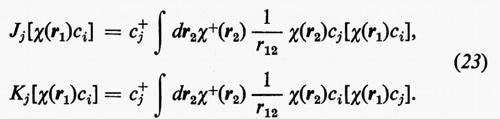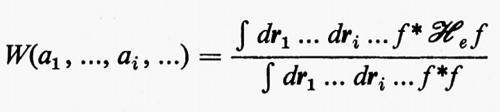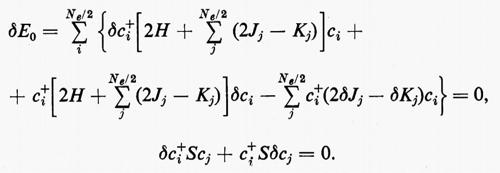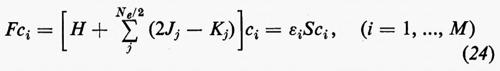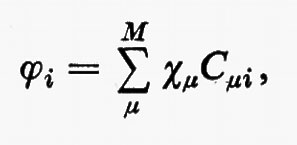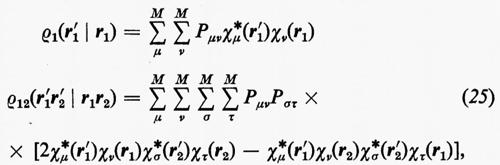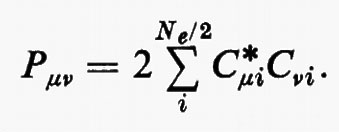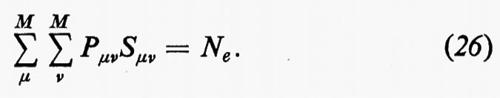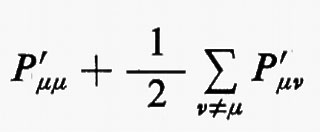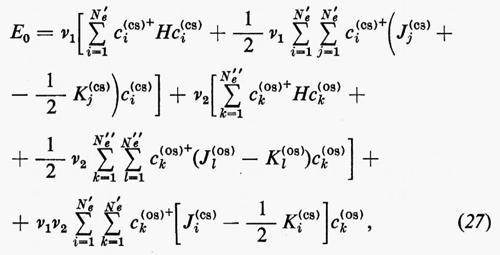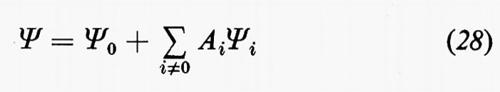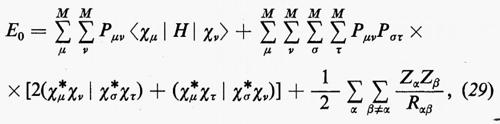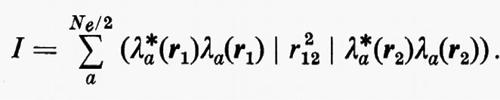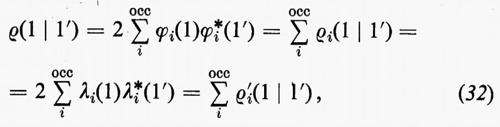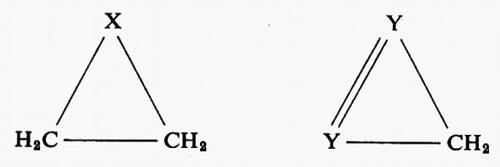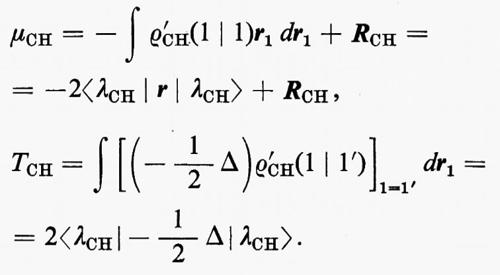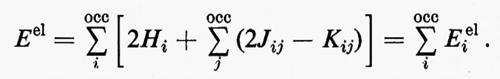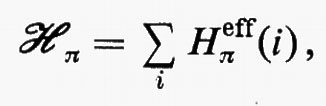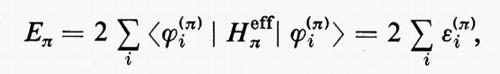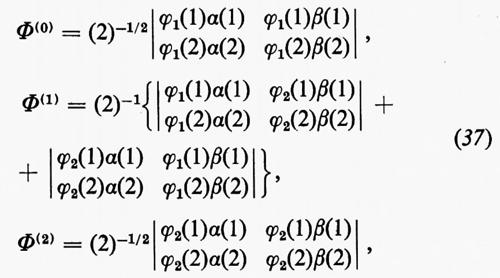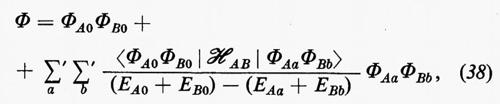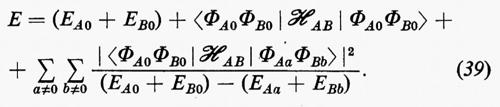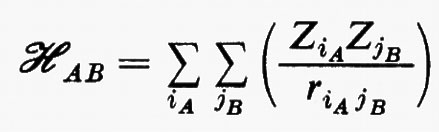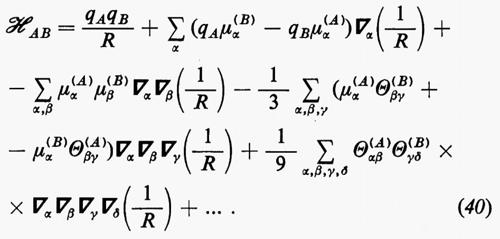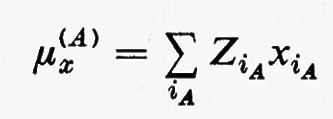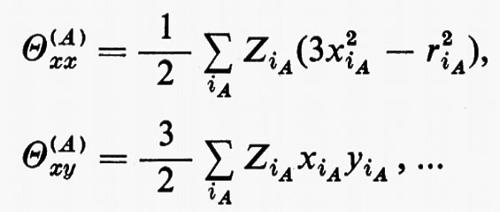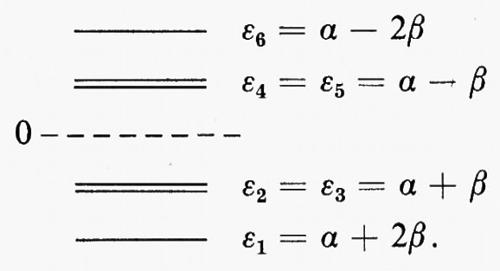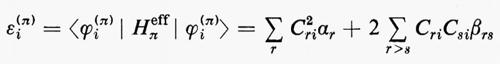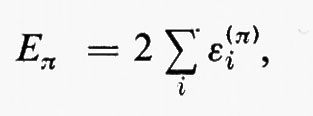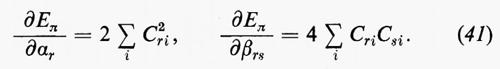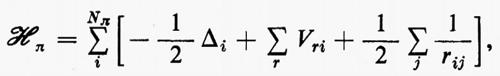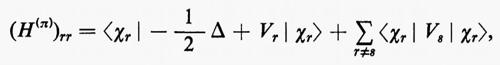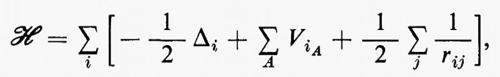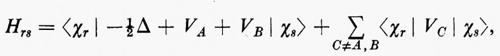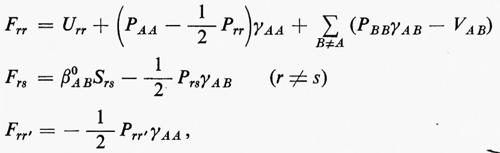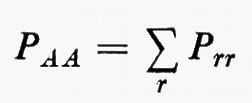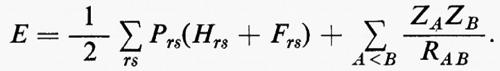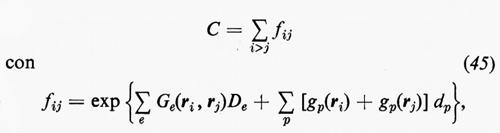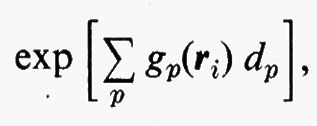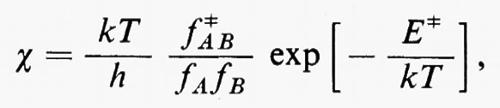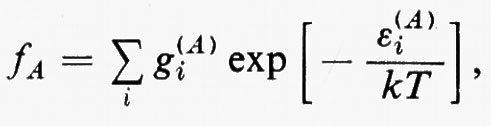Legame chimico

di Eolo Scrocco e Giovanni Paolo Arrighini

SOMMARIO: 1. Problemi della teoria del legame chimico. □ 2. Impostazione quanto-meccanica del problema di sistemi a molti elettroni: a) approssimazione di Born-Oppenheimer e suoi limiti di validità; b) equazione di Schrödinger (trascurando effetti relativistici e magnetici); c) antisimmetria della funzione d'onda elettronica; d) matrici densità del I e Il ordine: proprietà e significato. □ 3. Trattamento approssimato del problema di sistemi a molti elettroni: a) modello a particelle indipendenti: determinante di Slater e matrici densità associate; b) orbitali molecolari e doppia occupazione: stati a guscio chiuso e corrispondenti matrici densità; c) orbitali molecolari ottimali: metodo del ‛campo auto-compatibile' (SCF); d) orbitali molecolari espressi in termini di orbitali atomici (approssimazione MOLCAO); e) concetto di ‛popolazione' di Mulliken; f) stati a guscio aperto e stati eccitati; g) superamento del modello a particelle indipendenti: energia di correlazione; h) basi atomiche di corrente utilizzazione: orbitali tipo Slater e tipo gaussiano, integrali necessari in calcoli molecolari. □ 4. Applicazioni della teoria: a) alcuni esempi di calcoli molecolari accurati: molecole NH₃ e H₂O, previsione di loro proprietà fisiche; b) orbitali molecolari localizzati; c) proprietà di ‛quasi invarianza' di orbitali localizzati; grado di trasferibilità tra molecole chimicamente simili; d) gruppi di elettroni chimicamente distinti: funzione d'onda molecolare espressa come prodotto antisimmetrizzato di funzioni di gruppo; e) forze intermolecolari: forze a lunga e a media distanza; f) molecole di grandi dimensioni e problemi connessi: alcuni metodi semiempirici ampiamente utilizzati. □ 5. Problemi aperti e conclusioni. □ Bibliografia.

1. Problemi della teoria del legame chimico.

I compiti di una teoria completa del legame chimico sono numerosi, dovendo essa rendere conto di un gran numero di fatti sperimentali. In particolare, per esempio, deve giustificare perché alcuni atomi (quelli dei gas nobili più leggeri) non siano in grado di formare molecole stabili, a differenza di tutti gli altri elementi; perché le molecole siano degli aggregati atomici che nel loro stato fondamentale presentano una stabilità maggiore degli atomi costituenti; perché un elemento si combini soltanto con un numero relativamente piccolo di altri atomi; deve infine prevedere quali siano le configurazioni stabili degli atomi all'interno della molecola (problemi di stereochimica). Oltre a spiegare queste proprietà, che possiamo chiamare statiche, una teoria del legame chimico deve permettere di calcolare le forze che legano i vari atomi tra loro e la dinamica delle vibrazioni interne; deve spiegare le interazioni con la radiazione elettromagnetica responsabili delle transizioni a livelli eccitati (problemi della fotochimica); deve predire quali sono le trasformazioni che due o più molecole subiscono durante quelle collisioni che portano a una reazione chimica; deve contenere elementi sufficienti a valutare le forze residue che si esercitano tra molecole, forze che sono responsabili degli stati di aggregazione condensati della materia e che giocano anche un ruolo importante nella fenomenologia degli urti molecolari. A gran parte di questi interrogativi ha dato una risposta soddisfacente la teoria quantistica della valenza, come e stata sviluppata dopo i classici lavori di W. Heitler e F. London (v., 1927), F. Hund (v., 1928 e 1931), R. S. Mulliken (v., 1928 e 1932) e E. Hückel (v., 1931 e 1932). Certamente, allo stato attuale, la teoria ha raggiunto un sufficiente grado di perfezione, si da essere in grado di spiegare in maniera soddisfacente tutte le proprietà statiche della molecola e di fornire valori ragionevolmente accurati di molte proprietà caratteristiche (energia, distribuzione della carica elettronica, parametri geometrici, momenti di multipolo, ecc.) per molecole di piccole dimensioni, costituite da atomi delle prime due righe del sistema periodico.

Naturalmente la teoria quantistica del legame chimico ha in sé tutti gli elementi necessari per una comprensione completa di qualsiasi proprietà statica e dinamica, anche per molecole di grandi dimensioni e contenenti atomi di elevato peso atomico. Allo stato attuale, l'interpretazione e la previsione qualitativa di molti dei fatti sperimentali enumerati in precedenza hanno raggiunto un notevole grado di attendibilità, per cui, per una rassegna facilmente comprensibile dei risultati qualitativi della teoria, rimandiamo ai numerosi testi indicati nella bibliografia (v. Pauling, 1960³; v. Coulson, 1961²; v. Murrell e altri, 1965; v. Cartmell e Fowles, 1966). In questa sede ci proponiamo di riprendere l'impostazione generale del problema quanto-meccanico generale della struttura elettronica molecolare, con l'intento di mettere in luce lo stato attuale della teoria e prospettare i possibili sviluppi futuri.

2. Impostazione quanto-meccanica del problema di sistemi a molti elettroni.

a) Approssimazione di Born-Oppenheimer e suoi limiti di validità.

Ogni teoria rigorosa della struttura molecolare si basa sullo studio quanto-meccanico delle interazioni di un sistema di molte particelle elettricamente cariche (i vari nuclei e gli elettroni della molecola). Il problema matematico richiede la soluzione dell'equazione differenziale di Schrödinger:

ℋ Ψ_n=E_nΨ_n (1)

in modo da ottenere i possibili livelli energetici E_n e le corrispondenti autofunzioni Ψ_n (caratteristiche dei possibili stati molecolari) che descrivono completamente il sistema. (L'espressione esplicita dell'operatore hamiltoniano ℋ che compare nella (1) verrà fornita più avanti). Infatti, una volta note queste autofunzioni, si può calcolare, in via di principio, ogni proprietà fisica osservabile della molecola (per es., energia, ripartizione della densità di carica elettronica, distanze interatomiche di equilibrio, proprietà spettroscopiche, ecc.). Le proprietà medie di uno stato possono essere calcolate associando un operatore Ω alla grandezza fisica osservabile ω che si desidera conoscere, valutando l'integrale

in cui q_i rappresenta l'insieme delle coordinate di posizione r_i≡(x_i y_i z_i) e di spin σ_i della particella i-esima e dτ=dq₁ ... dq_N è l'elemento di volume dello spazio delle configurazioni per le N particelle del sistema. (Per es., la componente μ_z del momento di dipolo elettrico molecolare μ per lo stato fondamentale è data da

in cui Z_ie è la carica della i-esima particella, eguale a −e per un elettrone, a +8e per un nucleo di ossigeno). Una formula analoga alla (2), ma contenente le funzioni d'onda Ψ_n e Ψ_n′ di due stati differenti, permette di calcolare quelle proprietà connesse con le transizioni tra i due stati stessi, quali si incontrano, per esempio, in problemi di interazione tra molecola e radiazione elettromagnetica.

Sfortunatamente, come già nella meccanica classica, il problema di molte (N) particelle interagenti non è risolubile in termini esatti già per N〈2; è pertanto inevitabile il ricorso a metodi approssimati. Per il caso di sistemi molecolari, una prima semplificazione ragionevole è quella suggerita da M. Born e J. R. Oppenheimer, secondo la quale il moto degli elettroni viene studiato pensando i nuclei fermi, dato che la massa M di questi ultimi è molte migliaia di volte quella m degli elettroni (per es., per l'ossigeno, M/m〈29.000). In questa approssimazione, le distanze internucleari assumono il ruolo di parametri e il problema va risolto di volta in volta per una ben determinata configurazione dei nuclei. Una seconda approssimazione, anch'essa molto ragionevole per quel che concerne problemi di interesse chimico (nei quali si ritengono sufficientemente buoni valori dell'energia approssimati a i kcal/mole), consiste nel trascurare sia gli effetti relativistici sia le interazioni magnetiche. Anche se i contributi relativistici all'energia sono in generale tutt'altro che trascurabili, specialmente nel caso di atomi pesanti, tuttavia il loro valore rimane sostanzialmente invariato nel passaggio dallo stato di atomi separati a quello di atomi legati in molecola; e la chimica è interessata esclusivamente alla variazione di energia tra questi stati. Anche i termini di energia legati alle interazioni magnetiche tra gli elettroni sono quasi sempre trascurabili per tutte le molecole non lineari e nello stato fondamentale di quelle lineari con un numero pari di elettroni.

b) Equazione di Schrödinger (trascurando effetti relativistici e magnetici).

Se si introducono queste semplificazioni, l'equazione di Schrödinger (1) per gli N_e elettroni nel campo dei nuclei supposti fermi assume la seguente forma

dove la quantità entro parentesi graffa rappresenta la parte elettronica ℋ_e dell'operatore hamiltoniano ℋ nell'equazione (1); questo operatore contiene termini di energia cinetica (−½Δ_i), termini di energia potenziale di attrazione tra l'i-esimo elettrone e il generico nucleo di carica Z_α e termini di energia potenziale di repulsione tra l'i-esimo e il j-esimo elettrone. In fine la somma a secondo membro rappresenta l'energia di repulsione tra i nuclei, che per ogni configurazione degli atomi rimane costante. Tutti questi operatori sono espressi, per comodità, in unità atomiche (u.a.), in cui carica e massa dell'elettrone sono assunte unitarie e le distanze sono misurate in multipli del raggio della prima orbita dell'atomo di idrogeno di Bohr, a₀=0,529172 Å. In queste unità, l'unità di energia equivale a 627,5 kcal/ mole.

c) Antisimmetria della funzione d'onda elettronica.

Dal fatto che l'operatore hamiltoniano ℋ_e in (3) è simmetrico rispetto allo scambio delle coordinate di due qualsiasi elettroni, si deduce che le possibili autofunzioni Ψ_n possono essere classificate in due categorie, quelle simmetriche e quelle antisimmetriche rispetto a tale scambio. Matematicamente ciò si esprime nella forma

dove ℘_ij è un operatore che permuta le coordinate q_i e q_j. Il confronto di numerose proprietà previste dalla teoria con quelle ottenute sperimentalmente ha permesso di stabilire che per gli elettroni (e, più in generale, per le particelle a spin semintero) vale, a secondo membro della (4), il segno −. Come conseguenza di questa proprietà, la funzione d'onda si annulla nei punti dello spazio delle configurazioni elettroniche in cui q_i=q_j. Questo fatto porta a conseguenze molto importanti, sulle quali ci soffermeremo più avanti.

Se si moltiplicano ambo i membri della (3) a sinistra per la complessa coniugata Ψ^*_n di Ψ_n e s'integra su tutto lo spazio delle configurazioni, supponendo che le autofunzioni Ψ_n siano normalizzate, cioè che ∫ Ψ^*_n Ψ_ndτ=, si ottiene per l'autovalore E_n l'espressione:

dove tutti i termini contenenti le coordinate del solo elettrone i-esimo sono stati raggruppati nell'operatore

d) Matrici densità del I e II ordine: proprietà e significato.

In effetti, le informazioni contenute nella funzione d'onda Ψ_n(q₁ ... q_Ne), a causa dell'identità delle particelle, sono ridondanti se siamo interessati, come capita sempre nei problemi d'interesse chimico, al calcolo di proprietà rappresentate da operatori mono- e biparticellari (come per es. l'energia, v. formula 5). Conviene pertanto introdurre nuove quantità, chiamate ‛matrici densità', che contengano solo le variabili strettamente necessarie. Per introdurre queste funzioni in maniera intuitiva, riprendiamo in esame la (5). Se si tiene conto dell'identità degli elettroni, questa equazione può essere anche scritta, più semplicemente, nella forma

dove si è fatta la convenzione che gli operatori indicati nei due termini operino solo sulle coordinate non accentate e che, una volta effettuata l'operazione, prima d'integrare venga posto nuovamente q_1′=q₁, ecc. Se poniamo

l'espressione dell'energia (6) si scrive più semplicemente

Alle grandezze ρ1⁽ⁿ⁾ e ρ1⁽2ⁿ⁾ si dà rispettivamente il nome di matrici densità del primo e del secondo ordine per lo stato n-esimo. Dalla definizione loro data attraverso la (7) è facile vedere che gli elementi diagonali di queste matrici godono delle seguenti proprietà:

e pertanto il loro significato è il seguente:

(1/N_e)ρ1⁽ⁿ⁾(q₁ ∣ q₁)dq₁

è la probabilità di trovare un elettrone ‛qualsiasi' del sistema nell'elemento di volume dq₁ che caratterizza la sua posizione e il suo spin, a prescindere dalla posizione e dallo spin di tutti i rimanenti N_e−1 elettroni;

[2/N_e(N_e−1)]ρ1⁽2ⁿ⁾(q₁, q₂∣q₁, q₂)dq₁dq₂

rappresenta invece la probabilità di trovare contemporaneamente un elettrone ‛qualsiasi' in dq₁ e un altro ‛qualsiasi' in dq₂, indipendentemente dalla posizione e dallo spin di tutti i rimanenti N_e−2.

Le matrici densità del secondo ordine godono inoltre di un'altra importante proprietà, connessa con l'antisimmetria della funzione d'onda Ψ_n:

ρ(₁n₂)% (q1′, q2′∣q₁, q₂)=−ρ(₁n₂)%(q2′, q1′∣q₁, q₂)=

=−ρ(₁n₂)% (q1′, q2′∣q₂, q₁)

e pertanto ρ(₁n₂)% (q₁, q₂∣q₁, q₂)=0 per q₁=q₂, che è un modo di formulare il principio di esclusione di Pauli, secondo il quale è nulla la probabilità di trovare contemporaneamente due elettroni con lo stesso spin in uno stesso punto dello spazio. L'azzerarsi della matrice densità del secondo ordine nel punto r₁=r₂ per due particelle dello stesso spin introduce una drastica diminuzione della probabilità di presenza dei due elettroni nell'intorno di quel punto (buca di Fermi) e questo corrisponde a un forte effetto di correlazione tra i moti dei due elettroni, esclusivamente connesso con l'antisimmetria della funzione d'onda. Avremo modo di vedere più avanti che questo non è il solo effetto correlativo presente nei sistemi di più particelle cariche.

3. Trattamento approssimato del problema di sistemi a molti elettroni.

a) Modello a particelle indipendenti: determinante di Slater e matrici densità associate.

Come già si è accennato, la risoluzione in forma analitica esatta dell'equazione di Schrödinger già per molecole di piccole dimensioni è completamente preclusa a causa dell'elevato numero di elettroni (in una molecola chimicamente semplice, quale il cloruro di metile, il numero di elettroni è 26; questo numero per il toluolo è già salito a 50, ecc.). È pertanto indispensabile ricorrere a metodi di risoluzione approssimata, che possono essere suggeriti dalla forma dell'operatore hamiltoniano. A questo scopo prendiamo in considerazione l'equazione (3) e per il momento supponiamo assenti i termini di energia di repulsione elettronica

allora, nell'ambito dell'approssimazione di Born-Oppenheimer, l'hamiltoniano conterrebbe solamente una somma di operatori hamiltoniani H_i (v. anche eq. 5), ciascuno dei quali funzione delle coordinate di una sola particella. In questo caso è facile dimostrare che la funzione d'onda esatta per il sistema degli N_e elettroni può essere scritta come un prodotto

di funzioni d'onda ϕ_i monoparticellari, ciascuna delle quali è soluzione dell'equazione

H(q_k)ϕ_k(q_k)=W_kϕ_k(q_k) (10)

e membro di un insieme ortonormale, cioè tale che

Un siffatto prodotto non ha in generale alcuna proprietà di simmetria rispetto allo scambio delle coordinate di due particelle qualsiasi. A partire da questa soluzione, tuttavia, si può costruire una funzione avente le giuste proprietà di simmetria sopra ricordate e che rimane ancora autofunzione dell'equazione di Schrödinger non contenente i termini di repulsione elettronica. Una funzione di questo genere, normalizzata, è quella proposta da Slater

la quale è ottenuta facendo una combinazione lineare degli N_e! prodotti ottenibili dalla

permutando in tutti i modi possibili le variabili q_j tra le funzioni ϕ_j. Nella (11), ℘ è un operatore di permutazione di parità p. È facile verificare che la funzione (11) è antisimmetrica rispetto allo scambio di due particelle (il determinante cambia segno per lo scambio di due righe) e che soddisfa anche al principio di esclusione di Pauli (buca di Fermi), in quanto la funzione si annulla se q_i=q_j (due righe del determinante divengono eguali).

È utile vedere anche la forma esplicita che assumono le funzioni densità del primo e del secondo ordine nel caso in cui la funzione d'onda abbia la forma monodeterminantale (11). Dalla prima delle definizioni (7) si ha

Se si tiene conto dell'ortonormalità delle funzioni ϕ_j, si vede che tutti gli integrali nei quali ℘′≠℘ sono nulli e che quindi la funzione densità del primo ordine prende la forma

Per la matrice densità del secondo ordine, ancora dalla definizione (7), si può scrivere

In questo caso, per l'ortonormalità delle ϕ_j sono diversi da zero solo i termini delle somme per i quali la permutazione ℘′ è identica alla permutazione ℘ o differisce da questa solo per lo scambio delle coordinate q₁ e q₂ degli elettroni 1 e 2. Per ℘′=℘ i termini corrispondenti compaiono con il segno +; gli altri hanno il segno −. Si ha pertanto:

includendo nelle somme anche i termini con j=i il risultato non cambia, ma così facendo si può scrivere ρ₁₂ nella forma compatta seguente:

b) Orbitali molecolari e doppia occupazione: stati a guscio chiuso e corrispondenti matrici densità.

A causa del limitato spazio a disposizione, dovremo limitarci a considerare nelle applicazioni (che vedremo in seguito) solo gli stati fondamentali di molecole contenenti un numero pari di elettroni (che costituiscono la grande maggioranza), ossia molecole in stati di singoletto. In questo caso, in completa analogia con i problemi atomici, quando l'hamiltoniano non contiene espressamente termini d'interazione magnetica, ciascuna funzione monoelettronica ϕ(q), chiamata spin-orbitale, può essere fattorizzata in un prodotto di una funzione ϕ(r) chiamata ‛orbitale molecolare', dipendente dalle sole coordinate spaziali, e di una funzione η_σ delle coordinate di spin, che può assumere due forme α e β a seconda che l'autovalore σ dell'operatore di spin σ_z abbia il valore σ=+½ o σ=−½ u.a. Le due autofunzioni di spin sono ortonormali, cioè sono tali che ∫ dτ α*α=∫ dτ β*β=1, ∫ dτ α*β=∫ dτ β*α=0. Con queste restrizioni, la funzione polielettronica approssimata (11) diviene

nella quale, come si vede, in ciascun orbitale molecolare ϕ_i sono stati alloggiati due elettroni con spin antiparallelo. Vale forse la pena a questo punto di esplicitare la forma che assumono le funzioni densità del primo e secondo ordine associate a una funzione d'onda che abbia la forma (11′); se si tiene conto della doppia occupazione di ciascun orbitale molecolare ϕ_i, integrando rispetto alle variabili di spin e sfruttando la ortonormalità di α(i) e β(i), si ottiene

(1/N_e)ρ₁(r₁ ∣ r₁)dr₁ rappresenta ora la probabilità di trovare un qualsiasi elettrone del sistema nell'elemento di volume dr₁ indipendentemente dal valore della sua variabile di spin. Un'interpretazione analoga vale per la ρ₁₂.

c) Orbitali molecolari ottimali: metodo del ‛campo autocompatibile' (SCF).

Ritornando ora al problema concreto della determinazione di una buona funzione d'onda, notiamo che di fatto l'hamiltoniana reale (3) contiene termini di repulsione elettronica, che portano un contributo rilevante all'energia e modificano la (11) o la (11′) sia alterando la forma delle funzioni monoelettroniche ϕ_i in esse contenute, sia richiedendo, come vedremo più avanti, l'aggiunta di altre funzioni correttive. Per cercare di comprendere il primo tipo di modifica alla funzione (11) o (11′), si può notare che la parte bielettronica di ℋ_e può essere scritta

Sembra ragionevole pertanto il tentativo di sostituire la somma entro parentesi, nella (15), con un opportuno valor medio (che sarà precisato meglio tra poco):

Quest'approssimazione è chiamata del ‛campo autocompatibile' e fu suggerita da Hartree e Fock per problemi atomici; in questo modello gli operatori approssimati monoelettronici g(r_i) dipendono direttamente dalla distribuzione spaziale media degli altri elettroni, da cui a sua volta dipende il calcolo del valore medio della somma

Utilizzando questa osservazione si possono allora sommare e sottrarre all'hamiltoniano elettronico (3) i termini monoelettronici

e si ottiene

Come si vede, questo artificio permette di sostituire i termini di repulsione elettronica contenuti nella (3) e dati dalla seconda somma nella (17) con un potenziale di repulsione effettivo, certamente piuttosto piccolo ovunque, tranne che per r_ij ≃ 0, essendo costituito dalla differenza tra il potenziale ‛istantaneo' sentito dall'elettrone i-esimo (originato da tutti gli altri elettroni) e il suo valore medio g(r_i). A questo potenziale repulsivo effettivo, a breve raggio d'azione, è stato dato il nome di ‛potenziale residuo'.

Sulla base di queste considerazioni, ossia supponendo piccoli gli effetti dovuti al potenziale residuo, risulta abbastanza evidente che una funzione d'onda della forma monodeterminantale (11′) può essere considerata una ragionevole partenza per una teoria della struttura elettronica molecolare. Il problema pertanto si sposta in quello della ricerca di opportuni orbitali molecolari (M.O.), che rendano la forma monodeterminantale (11) la funzione d'onda più vicina possibile alla soluzione esatta dello stesso problema. Supposti per il momento noti questi orbitali molecolari ottimali, sotto la condizione ulteriore che essi formino un insieme ortonormale, cioè tale che ∫ϕ^*_i(r)ϕ_j(r)dτ=δ_ij, in accordo con la (5) l'energia totale E₀ dello stato fondamentale si scrive

Per semplificare le notazioni, porremo d'ora in poi la (18) nella forma

dove il significato dei simboli introdotti è immediato per confronto con la (18).

Il risultato (18′) deriva dalle (5) e (11) se si tiene conto: a) della ortonormalità sia delle funzioni di spin che degli orbitali molecolari ϕ_j; b) del fatto che l'hamiltoniano contiene solo termini monoelettronici H_i e bielettronici 1/r_ij; c) che in conseguenza di a) i contributi alla parte monoelettronica derivano solo dalla stessa permutazione nelle funzioni a destra e a sinistra dell'operatore, mentre i contributi alla parte bielettronica derivano anche dalle permutazioni nella funzione di destra (o di sinistra) che differiscono per un solo scambio da quelle della funzione di sinistra (destra).

Nell'espressione (18′) alcuni termini sono d'immediata interpretazione classica: H_ij rappresenta l'energia di un elettrone alloggiato nell'orbitale ϕ_i nel campo dei soli nuclei della molecola; la quantità 2J_ij+2J_ji+2J_ii+2J_jj+−K_ii−K_jj=4J_ij+J_ii+J_jj rappresenta l'energia elettrostatica di repulsione tra 4 elettroni, due dei quali alloggiati nell'orbitale molecolare ϕ_i e due in quello ϕ_j. I rimanenti termini K_ij(i≠j) non hanno un'interpretazione classica e derivano dall'antisimmetria della funzione d'onda.

d) Orbitali molecolari espressi in termini di orbitali atomici (approssimazione MOLCAO).

A questo punto forse conviene diminuire ulteriormente la generalità dell'impostazione e vedere quali forme comode possono concretamente essere usate per l'esplicitazione degli orbitali molecolari ϕ_j. Ci metteremo d'ora innanzi nella cosiddetta ‛approssimazione MOLCAO' (Molecular Orbitals costruiti in termini di Linear Combinations di Atomic Orbitals), nella quale gli orbitali molecolari vengono costruiti come combinazione lineare degli orbitali atomici χ degli atomi che costituiscono la molecola, centrati ciascuno sul proprio nucleo. La scelta di questa forma degli orbitali può essere giustificata dal fatto che, se le distanze interatomiche non sono troppo piccole (rispetto alle dimensioni atomiche), l'hamiltoniano nelle vicinanze di un nucleo è dominato dai termini relativi all'atomo in questione e pertanto l'orbitale molecolare in quell'intorno deve ragionevolmente essere approssimato dall'orbitale atomico corrispondente.

Indichiamo con {χ_A1, χ_A2, ..., χ_AMA, χ_B1, χ_B2, ..., χ_BMB, ...} l'insieme di M=M_A+M_B+... orbitali atomici centrati rispettivamente sugli atomi A, B, ..., che, per semplicità di notazione, indicheremo genericamente con {χ}={χ₁, χ₂, χ₃, ... χ_M} Va notato che la base {χ} è in generale normalizzata ma non ortogonale, cioè

All'integrale S_μν si dà il nome di integrale di ‛sovrapposizione' tra gli orbitali atomici χ;_μ e χ_ν. Questo insieme di orbitali rappresenta nel metodo MOLCAO la base per lo sviluppo di tutti gli orbitali molecolari ϕ_j; ciascuno di essi, infatti, può essere approssimato mediante una combinazione lineare.

ovvero, più compattamente, in forma matriciale,

ϕ=χC. (19)

Nella (19) ϕ e χ rappresentano rispettivamente le due matrici riga (ϕ₁ϕ₂ ... ϕ_Ne/2) e (χ₁χ₂ ... χ_M) degli orbitali molecolari e di quelli atomici, mentre C è una matrice rettangolare costituita dagli N_e/2 vettori colonna c_i di lunghezza M. (L'orbitale molecolare i-esimo, nella base χ_μ, è pertanto rappresentato dal vettore colonna c_i di C). L'ortonormalità dell'insieme di orbitali molecolari {ϕ} (19) è esprimibile come

∫dr ϕ⁺(r)ϕ(r)=∫dr C⁺χ⁺χC=C⁺SC=1, (20)

dove S è la matrice (quadrata) di ‛sovrapposizione' di elementi S_μν.

Con questa forma degli orbitali molecolari, l'espressione dell'energia (18′) può essere scritta

dove sono state introdotte, per comodità, le matrici H=∫χ⁺Hχ dr, J_j, K_j; nella (21) i termini c+_iJ_jc_i e c+_iK_jc_i rappresentano, nel metodo MOLCAO, i valori degli integrali di repulsione elettronica J_ij e K_ij che figurano nella relazione generale (18′).

Le matrici quadrate (M×M) J_j e K_j possono essere facilmente individuate se si definiscono i due operatori J_j, coulombiano, e K_j, di scambio, mediante le relazioni

Ricordando la (19), le relazioni operatoriali (22) assumono la forma

Dalle equazioni (23), moltiplicando a sinistra ambo i membri per [χ(r₁)c_i)⁺=c+_iχ⁺(r₁) e integrando rispetto a r₁, è facile vedere che si ritrovano le eguaglianze c+_iJ_jc_i=J_ij e c+_iK_jc_i=K_ij.

Una volta fissato l'insieme delle funzioni atomiche di base {χ}, l'energia E₀ resta funzione degli elementi della matrice C. Per la determinazione dei coefficienti ottimali C_μi viene utilizzato un teorema fondamentale della meccanica quantistica (teorema variazionale), secondo il quale, detta f(r₁, ..., r_i, ...; a₁, ..., a_i, ...) una funzione arbitraria che sia a quadrato sommabile e ‛regolare', dipendente dalle variabili r_i del sistema e da un certo numero di parametri a_i aggiustabili, l'espressione

rappresenta un limite superiore all'energia E₀ dello stato fondamentale del sistema, limite che coincide con il valore E0^esatto se la funzione f coincide con l'autofunzione esatta Ψ0^es. La migliore approssimazione W a E0^esatto è quella che si ottiene minimizzando la W rispetto a tutti i parametri a_i. Nel caso che stiamo esaminando, la minimizzazione dell'energia va eseguita rispetto ai parametri c_i, con il vincolo aggiuntivo che gli orbitali molecolari restino ortonormali (v. eq. 20); ciò comporta le seguenti condizioni:

Sviluppando in dettaglio il formalismo, si ottengono le seguenti equazioni non lineari (v. Roothaan, 1951) nelle c_i (J_j e K_j sono funzioni dei coefficienti c_i da determinare)

cui devono soddisfare i vettori c_i. La matrice F che compare nella (24) è nota come matrice di Fock. I numeri ε_i sono chiamati ‛energie orbitaliche' associate ai vari orbitali molecolari ϕ_i=χc_i e sono i possibili autovalori della matrice di Fock F. Le M equazioni (24), che sono accoppiate tra loro, possono essere risolte con tecniche iterative: prefissato un insieme di ‛vettori tentativo' ci⁽⁰⁾, si calcolano le corrispondenti matrici Jj⁽⁰⁾ e Kj⁽⁰⁾, si risolve il problema secolare (24) per ottenere delle ci⁽¹⁾ di approssimazione successiva e si ripete il processo iterativamente sino a convergenza. Delle M soluzioni c_i, le N_e/2 di energia ε_i più bassa vengono utilizzate per costruire la funzione d'onda approssimata autocompatibile Ψ (SCF wavefunction) dell'equazione (11); i rimanenti (M−N_e/2) orbitali (orbitali ‛virtuali') possono essere utilizzati per costruire funzioni d'onda approssimate per gli stati eccitati della molecola.

e) Concetto di ‛popolazione' di Mulliken.

Prima di passare a parlare dei miglioramenti che possono essere apportati alla funzione d'onda monodeterminantale SCF ottenuta nell'approssimazione MOLCAO, vediamo come, per questa forma della funzione d'onda, si esplicitano le matrici densità. Ricordando le equazioni (14) e che

si trova con facili passaggi

in cui si è posto

La matrice P, di elementi P_μν, è il doppio della matrice densità, nello spazio definito dagli orbitali di base {χ}. Per meglio visualizzare il significato fisico della matrice P, integriamo rispetto a r₁ l'elemento diagonale ρ₁(r₁ ∣ r₁); si ottiene:

La matrice di elementi P′_μν=P_μνS_μν, che chiameremo con Mulliken matrice di popolazione, è di notevole interesse chimico, perché descrive dettagliatamente la ripartizione della carica elettronica all'interno della molecola. Infatti, gli elementi P′_μν misurano (in unità di carica elettronica) le quantità di carica che si trovano sulle ‛distribuzioni' normalizzate χ^*_μχ_μ e χ^*_μχ_ν/S_μν (∫χ^*_μχ_μ dr=1, ∫χ^*_μχ_ν dr/S_μν=1). In particolare, gli elementi diagonali di questa matrice rappresentano le cosiddette ‛popolazioni orbitaliche nette', mentre quelli non diagonali rappresentano le ‛popolazioni di sovrapposizione'. Accanto alla popolazione orbitalica netta, ancora Mulliken ha proposto di definire ‛popolazione orbitalica lorda' la quantità

che si ottiene sommando alla popolazione netta dell'orbitale χ_μ la metà della popolazione di sovrapposizione tra χ_μ e tutti gli altri orbitali atomici della molecola (cioè sommando tutti gli elementi di una riga della matrice P′).

f) Stati a guscio aperto e stati eccitati.

In questa rassegna, che è e resta necessariamente incompleta, non possiamo tuttavia esimerci dal fare un breve accenno alla descrizione quanto-meccanica approssimata dello stato fondamentale di quelle molecole (nella maggior parte dei casi radicali) che contengono un numero dispari di elettroni e che quindi non possono essere descritte mediante una struttura a orbitali molecolari doppiamente occupati. Tanto per citare qualche esempio, basti pensare alle molecole di ossido e biossido di azoto (NO e NO₂), alle analoghe contenenti cloro ClO e ClO₂, ecc. e ai moltissimi radicali come OH, CN, CH₃, ecc. Inoltre molti stati eccitati di molecole che pure contengono un numero pari di elettroni (e quindi sono quasi sempre caratterizzate da uno stato fondamentale che può essere approssimativamente descritto come una struttura a gusci chiusi) derivano sempre, nella stessa approssimazione, da transizioni di un elettrone da un orbitale doppiamente riempito a un orbitale non occupato (virtuale); la struttura elettronica risultante è caratterizzata dalla presenza contemporanea di orbitali doppiamente e singolarmente occupati. Si dice che la funzione d'onda approssimata che descrive un tale stato elettronico rappresenta una situazione a gusci aperti (open shell). Ovviamente un tale stato è caratterizzato in generale da una risultante del momento angolare complessivo di spin diversa da zero. Dato che la teoria generale della rappresentazione quanto-meccanica di una struttura elettronica a gusci aperti è piuttosto complessa e richiede uno spazio non compatibile con la presente trattazione, ci limiteremo ad accennare brevemente al semplice caso di un sistema di N_e=2N_e′+N_e″ elettroni che possono essere raggruppati in un guscio chiuso di 2N_e′ e in uno aperto di N_e″ elettroni, quando questi ultimi occupino singoli orbitali con tutti gli spins paralleli tra loro. In questo caso la funzione d'onda complessiva può ancora essere approssimata da un singolo determinante di Slater contenente N_e′ orbitali doppiamente riempiti (a spins antiparalleli) e N_e″ orbitali singolarmente occupati da elettroni, tutti con spin α oppure β. Una situazione di questo genere è, per esempio, quella che caratterizza i numerosi radicali con un solo elettrone spaiato.

Se gli orbitali molecolari del guscio chiuso e di quello aperto sono indicati rispettivamente con ϕ^cs=χc^(cs) e ϕ^os=χc^(os), l'espressione dell'energia analoga alla (21) risulta, in armonia con la derivazione che se ne è data:

dove sono stati introdotti i numeri di occupazione ν₁=2 e ν₂=1 rispettivamente per il guscio chiuso e aperto. Nella (27) il primo termine rappresenta l'energia del gruppo di elettroni appartenenti al guscio chiuso come se fosse isolato; analogamente per il secondo termine, che si riferisce al guscio aperto. Infine l'ultimo termine rappresenta l'interazione tra gli elettroni dei due gusci. La minimizzazione dell'energia (27) rispetto ai vettori colonna c^(cs) e c^(os) (con il vincolo che essi rimangano un insieme di vettori ortonormali) conduce a due complicati sistemi di equazioni accoppiate nelle incognite c^(cs) e c^(os), che possono in generale essere risolti iterativamente sino a convergenza. In tal modo risultano definite le funzioni ϕ^(cs) e ϕ^(os) che definiscono la funzione d'onda dello stato.

La situazione in cui gli elettroni degli orbitali singolarmente occupati non abbiano tutti lo stesso spin è notevolmente più complessa e la ‛giusta' autofunzione, sia pure approssimata, dello stato non è rappresentabile da un singolo determinante di Slater.

g) Superamento del modello a particelle indipendenti: energia di correlazione.

Sinora ci siamo limitati a considerare l'approssimazione monodeterminantale della funzione d'onda e il metodo SCF per il calcolo degli orbitali. In particolare, si è cercato di mostrare come concretamente si possono approssimare gli orbitali molecolari, sviluppandoli su una base finita di orbitali atomici. I risultati che si ottengono con una funzione d'onda di questa forma, come vedremo più avanti in alcuni esempi, sono da considerare nettamente buoni per il caso di grandezze osservabili collegate a operatori monoelettronici (v. eq. 2), quali ad esempio momento di dipolo elettrico e di multipoli superiori, suscettività diamagnetica, costanti di accoppiamento di quadrupolo nucleare, ecc. Un po' meno soddisfacenti sono invece i risultati che si ottengono per grandezze osservabili associate con operatori bielettronici; tra queste, di estrema importanza è l'energia, l'operatore associato alla quale (hamiltoniano) contiene, come si è visto (3), sia termini monoelettronici che bielettronici. Questa insufficiente approssimazione dell'energia non può essere eliminata completamente anche se si aumenta indefinitamente il numero delle funzioni atomiche di base; si può dimostrare, infatti, che l'energia calcolata per mezzo di una funzione monodeterminantale non può superare un valore limite (che chiameremo d'ora in avanti limite Hartree-Fock). Tale limite differisce ancora dall'energia esatta (non relativistica) per un termine dipendente dal numero di elettroni del sistema ed è dell'ordine di grandezza di 20 kcal/mole per elettrone, scarto che certamente rende la precisione dell'energia calcolata molto lontana dalla precisione chimica richiesta.

Nel caso della molecola di acqua, per esempio, l'energia sperimentale totale è di 47.992 kcal/mole, mentre l'energia Hartree-Fock stimata è di 47.728 kcal/mole, con un divario di 264 kcal/mole. Questo divario è percentualmente molto piccolo (l'energia Hartree-Fock è pari al 99,4% dell'energia sperimentale), ma in assoluto tutt'altro che trascurabile, se si pensa che l'energia classica di dissociazione in atomi (cioè quella in cui non si tiene conto dell'energia di punto zero) è di 219 kcal/mole. (Per la previsione delle energie di dissociazione, tuttavia, la situazione è un po' meno sfavorevole di quanto potrebbe sembrare, poiché si tratta di calcolare una differenza tra l'energia degli atomi separati e quella della molecola e quest'operazione è accompagnata da una parziale cancellazione degli errori; per l'H₂O si calcola infatti un'energia di dissociazione SCF di 157 kcal/mole).

La differenza tra l'energia sperimentale (non relativistica) e il limite HF calcolato con la funzione (11′) è chiamata ‛energia di correlazione' ed è legata all'inadeguatezza della funzione d'onda SCF, che è scritta semplicemente come prodotto (antisimmetrizzato) di funzioni dipendenti ciascuna dalle coordinate di una singola particella; questa forma non esclude la presenza contemporanea di due elettroni con spins diversi in uno stesso punto dello spazio (r_i=r_j) che, chiaramente, a causa della forte repulsione coulombiana (1/r_ij→∞ quando r_i→r_j), è fisicamente interdetta (buca di Coulomb).

Sono stati suggeriti vari metodi per migliorare la forma della funzione d'onda. Un approccio abbastanza naturale è quello d'introdurre esplicitamente nella funzione d'onda una dipendenza diretta dalle distanze interelettroniche r_ij. Hylleraas (v., 1929) sviluppò per primo questo metodo nel suo ormai classico studio dell'atomo di elio mentre i primi tentativi d'includere esplicitamente le distanze interelettroniche nella funzione d'onda di una molecola sono dovuti a James e Coolidge (v., 1933); più recenti applicazioni sono dovute a Kolos e Wolniewicz (v., 1968). Tuttavia, sino a tempi molto recenti, tale metodo è stato ritenuto impraticabile per sistemi con più di due elettroni e solo recentemente, come vedremo nella parte conclusiva dell'articolo, è stato di nuovo preso in considerazione. Un secondo metodo, ampiamente usato, è quello di rappresentare la funzione d'onda come combinazione lineare

di determinanti di Slater, il cui primo termine sia direttamente la soluzione SCF (che è già un'approssimazione molto buona), mentre gli altri sono determinanti ottenuti da quello SCF per sostituzione singola o multipla di orbitali molecolari virtuali (che provengono anch'essi dalla soluzione delle equazioni di HF) a quelli dello stato fondamentale: metodo dell'interazione delle configurazioni (I.C.). I coefficienti A_i sono dei parametri da determinare in base al teorema variazionale. Vedremo più oltre alcuni risultati ottenuti con questo metodo, ma sin da ora possiamo dire che la convergenza del procedimento con l'aumentare del numero di determinanti Ψ_i è in generale molto lenta.

Riassumendo, possiamo dire che per un sistema di molti elettroni, nell'approssimazione di considerare i nuclei fissi, si ottiene una buona funzione d'onda come prodotto antisimmetrizzato di orbitali molecolari monoparticellari (11′), purché ciascuno di essi sia ottimizzato nel campo autocompatibile di HF. Un raffinamento della funzione d'onda può essere successivamente ottenuto per mezzo di un'interazione di configurazioni. In pratica ciascun orbitale molecolare viene scritto come combinazione lineare di orbitali atomici centrati sui nuclei della molecola e l'ottimizzazione è effettuata rispetto ai coefficienti delle combinazioni lineari.

h) Basi atomiche di corrente utilizzazione: orbitali tipo Slater e tipo gaussiano, integrali necessari in calcoli molecolari.

Prima di passare a una concisa rassegna di risultati, e a un'interpretazione chimica di essi, può essere utile a questo punto spendere qualche parola sulle difficoltà che in concreto si incontrano nell'applicazione dei metodi descritti. A questo scopo riprendiamo l'espressione generale (8) dell'energia e particolarizziamola al caso in cui le matrici densità siano espresse nella forma MOLCAO delle equazioni (25), per lo stato fondamentale della molecola; si ottiene facilmente:

dove si è posto

〈χ_μ ∣H∣ χ_ν>=∫dr₁ χ^*_μ(r₁)H(r₁)χ_ν(r₁)

e

(χ^*_μχ_ν ∣ χ^*_σχ_τ)=∫dr₁dr₂ χ^*_μ(r₁)χ_ν(r₁) χ^*_σ(r₂)χ_τ(r₂)/r₁₂.

Si vede così che una volta scelta la base {χ}, l'utilizzazione del metodo è legata al calcolo preliminare degli integrali mono- e bielettronici, tripli e sestupli rispettivamente, che compaiono nella (29). Una prima difficoltà è connessa al numero molto grande d'integrali che devono essere calcolati. Per esempio, per una molecola come l'acetaldeide CH₃CHO, se si impiega la meno estesa base possibile di 19 orbitali atomici χ, è necessario calcolare 570 integrali di tipo monoelettronico e 18.145 integrali bielettronici. Poiché i risultati che si ottengono con tale base sono ancora alquanto lontani dal limite HF, se si vuole effettuare un calcolo più accurato con una base di dimensioni raddoppiate (38), i numeri precedenti diverrebbero rispettivamente 2.223 e 274.911. Come si vede, la mole del calcolo, anche per una molecola di dimensioni abbastanza piccole, diviene presto imponente, essenzialmente per la crescita molto rapida (circa come M⁴/8, M essendo il numero di funzioni di base χ) del numero di integrali bielettronici. La seconda difficoltà è connessa con il calcolo numerico di ciascun integrale e dipende dal tipo di funzione di base impiegata. Per valutare meglio questo punto conviene specificare i due tipi di funzioni di base χ più correntemente adoperati. Il primo tipo di funzioni atomiche di base largamente utilizzato è qucilo di Slater (funzione STO, da Slater-Type Orbitals)

χ_nlm(r, ϑ, ϕ)=[(2ζ)²ⁿ⁺¹/(2n!)]^1/2r^n-1 e^-ςrS_lm(ϑ, ϕ), (30)

dove ζ è un parametro variazionale (esponente orbitale), S_lm(ϑ, ϕ) è un' armonica sferica reale individuata dai numeri quantici interi l e m, e n è il numero quantico principale (per il seguito, può essere utile ricordare che nella notazione della spettroscopia atomica le funzioni con l=0 sono chiamate di tipo s, quelle con l=1 di tipo p, con l=2 di tipo d, ecc. e che il numero quantico m, per un dato l, è ristretto ad assumere i 2l+1 valori compresi tra l e −l); queste funzioni χ_nlm non sono di tipo idrogenoide; tuttavia, per un'opportuna scelta di ζ s'identificano con alcune di esse, e precisamente con quelle aventi l=n−1: pertanto coincidono con gli orbitali idrogenoidi 1s, 2p, 3d, ecc. Il comportamento asintotico a grandi distanze di queste funzioni può essere reso identico a quello di una qualsiasi funzione idrogenoide; la loro caratteristica però è quella di essere funzioni senza nodi nella parte radiale e di non formare un insieme ortogonale. Opportune combinazioni lineari di funzioni del tipo (30) forniscono ottime rappresentazioni degli orbitali HF atomici. Una rappresentazione conveniente per mettere in risalto le proprietà direzionali degli orbitali di Slater è quella che fa uso dei cosiddetti diagrammi polari per rappresentare i fattori dipendenti dagli angoli S_lm(ϑ, ϕ). In questi diagrammi, il valore della funzione S_lm, per una data coppia di angoli ϑ e ϕ, è dato dalla lunghezza del vettore che parte dall'origine degli assi e la cui orientazione è individuata dagli angoli ϑ e ϕ; il luogo dei punti dell'estremo libero di questo vettore descrive una superficie continua, che racchiude lobi positivi e negativi (corrispondenti al segno della funzione). La fig. 1 rappresenta i diagrammi polari di alcune delle funzioni S^lm usate più frequentemente. Si vede chiaramente che mentre le funzioni s sono a simmetria sferica, quelle con l≠0 risultano notevolmente e variamente direzionate.

Il calcolo degli integrali corrispondenti (particolarmente quelli bielettronici) è molto complesso; tuttavia esistono oggi vari tipi di programmi per calcolatori elettronici che permettono, in tempi ragionevoli, di calcolare tutti gli integrali necessari.

Il secondo tipo di funzioni di base usate è quello proposto per primo da Boys e costituito da funzioni gaussiane (funzioni GTO, da Gaussian-Type Orbitals),

χ(x, y, z)=Nf(x, y, z) exp[−α(x²+y²+z²)], (31)

dove N è un coefficiente di normalizzazione, a un parametro variazionale, x, y e z coordinate cartesiane rispetto al punto in cui è centrata la funzione e dove il prefattore f(x, y, z) vale 1 per funzioni di tipo s, ed è uguale a x, y o z per funzioni di tipo p, ecc. Il vantaggio dato dall'impiego di questo tipo di basi è essenzialmente legato alla molto maggiore facilità di calcolo di tutti i tipi d'integrali, che infatti, per queste funzioni, possono essere espressi in termini di funzioni risolutive assai semplici. D'altra parte, i comportamenti asintotici a grandi distanze e sul centro di sviluppo non sono corretti, il che comporta la necessità di usare un maggior numero di funzioni gaussiane rispetto a quelle di tipo Slater per ottenere risultati di accuratezza comparabile (per ogni STO sono in genere necessarie da 2 a 5 GTO).

4. Applicazioni della teoria.

a) Alcuni esempi di calcoli molecolari accurati: molecole NH₃ e H₂O, previsione di loro proprietà fisiche.

Passiamo ora a esaminare qualche esempio di applicazione dei metodi esposti. Molti risultati di elevata accuratezza sono stati ottenuti, in questi ultimi anni, per molecole biatomiche e poliatomiche lineari, contenenti atomi della prima riga del sistema periodico. In questa sede ci limiteremo a esaminare qualche risultato molto recente relativo a molecole non lineari; abbiamo scelto come primo caso quello della molecola di ammoniaca NH₃ (v. Rauk e altri, 1970). Per questa molecola, la cui geometria nello stato fondamentale è una piramide trigonale con l'azoto al vertice, è stata usata una base di 91 funzioni di tipo gaussiano (per l'atomo di azoto: 13 di tipo s, 24 di tipo p e 12 di tipo d; per ogni atomo d'idrogeno: 8 di tipo s e 6 di tipo p), nel seguito parzialmente contratte in gruppi di combinazioni lineari, con coefficienti fissi, di più funzioni di base. La contrazione riduce il numero delle ‛effettive' funzioni (alcune singole, altre rappresentate dalle combinazioni lineari di cui sopra) da 91 a 56 (per l'atomo di N: 8 di tipo s, 15 di tipo p, 12 di tipo d; per ogni atomo di H: 4 di tipo s, 3 di tipo p). Per questa molecola gli autori riportano solo calcoli di tipo SCF, che però sono stati eseguiti per varie configurazioni geometriche, variando sia la distanza N-H, sia l'angolo della piramide. Il primo risultato interessante è che la geometria di equilibrio prevista teoricamente corrisponde molto bene a quella sperimentale (distanza N-H calcolata: 1,00 Å, contro 1,01 Å sperimentale; angolo HN̂H calcolato 107°2′ contro 106°7′). Per quanto riguarda l'energia totale, il calcolo SCF fornisce −35.279 kcal/mole rispetto al dato sperimentale (non relativistico) di −35.489 kcal/mole; la differenza di 210 kcal/mole (corrispondente a circa 21 kcal/mole per elettrone) rappresenta una stima dell'energia di correlazione per questa molecola. Come già visto in un esempio precedente e come si vedrà anche meglio più oltre, da un calcolo SCF non ci si possono attendere, in generale, buoni valori dell'energia di dissociazione: in questo caso il valore calcolato è di 202 kcal/mole rispetto al valore sperimentale 295 kcal/mole. Il momento di dipolo calcolato, 1,66 debye, si confronta abbastanza bene con quello sperimentale, 1,54 debye. Gli autori hanno anche cercato di prevedere le costanti di forza di stretching (K_R) del legame N-H e di bending (K_α) dell'angolo piramidale; i valori ottenuti, K_R=22,07 mdyne/Å e K_α=1,83 mdyne/Å, sono in discreto accordo con quelli sperimentali corrispondenti, 21,78 e 1,48. Questi ultimi risultati possono essere considerati soddisfacenti se si tiene conto dell'estrema sensibilità di queste grandezze alla forma della funzione d'onda. Un'altra grandezza molto delicata da calcolare è il valore della barriera d'inversione di questa molecola: come è noto, infatti, l'atomo di azoto nell'ammoniaca può passare da una parte all'altra del piano di base della piramide contenente i tre idrogeni, superando una piccola barriera, corrispondente alla configurazione planare, che sperimentalmente ammonta a 5,8 kcal/mole; il valore trovato con la funzione d'onda SCF è 5,1 kcal/mole.

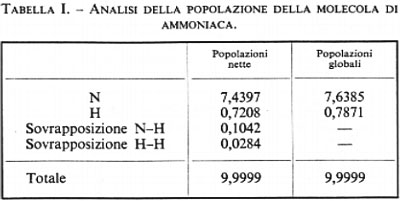
Un'analisi della funzione d'onda che ha un certo interesse chimico può essere fatta utilizzando la matrice di popolazione P′, di cui già abbiamo parlato; i risultati essenziali di tale analisi sono raccolti in tab. I, dove sono riportate le popolazioni totali atomiche e di sovrapposizione. Questi risultati mostrano che in seguito alla formazione dei legami si è avuto un trasferimento totale di 3(0,1042+0,0284)=0,3978 cariche elettroniche dagli atomi N e H alle zone internucleari, ove è prevalente la ‛sovrapposizione' delle densità di carica atomiche; inoltre si è avuto un trasferimento di 0,4397 elettroni dagli atomi d'idrogeno a quello di azoto; questo risultato non è inatteso, se si tiene conto della maggiore elettronegatività dell'azoto rispetto all'idrogeno.

I risultati di questo primo esempio mostrano che una teoria del legame chimico basata su una funzione d'onda abbastanza accurata di tipo SCF permette di prevedere adeguatamente molti dei fatti sperimentali elencati all'inizio di questo articolo: l'energia degli atomi legati in molecola risulta infatti inferiore a quella degli atomi separati (l'energia di legame calcolata è pari al 68% di quella sperimentale), la configurazione più stabile (di minima energia) è quella piramidale (la geometria è prevista con errori dell'ordine dell'1% sia per l'angolo che per le distanze), il momento di dipolo elettrico (che fornisce un'indicazione della variazione della distribuzione di carica elettronica nella molecola in seguito alla formazione dei legami chimici) è previsto con uno scarto inferiore all'8%. Le costanti di forza armoniche con cui gli atomi sono legati alle loro posizioni di equilibrio sono anch'esse previste in maniera ragionevole. La teoria inoltre prevede l'esistenza di due conformazioni di equilibrio, separate da una barriera, la cui altezza viene stimata con notevole accuratezza.

Anche se la teoria basata sull'uso di una funzione monodeterminantale SCF (11′) conduce a risultati che sono in generale semiquantitativamente corretti, tuttavia essa non appare adeguata per una determinazione precisa delle energie di dissociazione; la ragione di ciò va ricercata nella perdita di quella parte di energia che abbiamo chiamato energia di correlazione e che risulta differente per il sistema costituito dagli atomi separati rispetto a quello degli atomi legati in molecola. Un ulteriore esempio permetterà di apprezzare le difficoltà inerenti al miglioramento della funzione d'onda; a tal fine consideriamo il caso della molecola di acqua H₂O, uno dei pochi casi di molecole triatomiche non lineari per i quali siano disponibili al tempo stesso sia buone funzioni d'onda SCF sia funzioni d'onda di accuratezza superiore. Senza andare in dettaglio a esaminare per questa molecola i risultati ottenuti per la geometria di equilibrio, la ripartizione di carica, ecc., ci soffermeremo solamente sui risultati relativi all'energia. Un calcolo SCF molto accurato di Neumann e Moskowitz (v., 1968), fatto su una base di funzioni atomiche gaussiane, fornisce il valore di −47.727 kcal/mole, che è da confrontare con il dato ‛sperimentale' non relativistico di −47.992 kcal/mole (99,4%). Poiché si può stimare che l'energia corrispondente a tale funzione sia al più ~−20 kcal/mole distante dal limite HF, si può prevedere per tale limite un valore di circa −(47.727+20)=−47.747 kcal/mole, per cui l'energia di correlazione (−47.992+47.747) è dell'ordine delle −-245 kcal/mole (cioè, ancora vicina alle 20 kcal/mole per elettrone). Sfortunatamente gli stessi autori non forniscono una funzione d'onda di accuratezza superiore a quella SCF, per cui, per avere un'idea delle difficoltà inerenti a un miglioramento dell'energia SCF, dobbiamo utilizzare, per la stessa molecola di H₂O, i risultati ottenuti con un calcolo, solo di poco meno accurato, di altri autori (v. Arrighini e altri, 1970), che utilizza una base piuttosto estesa di 29 funzioni di Slater. L'energia SCF calcolata con questa funzione è −47.714 kcal/mole (che, in base alle stime precedenti, differisce ora di circa 34 kcal/mole dal limite HF). La differenza di −278 kcal/mole rispetto al dato sperimentale non relalivistico è quindi ancora dovuta per la maggior parte all'energia di correlazione. Questa funzione d'onda è stata migliorata usando il metodo dell'interazione delle configurazioni (28); la somma che compare nella (28) è estesa alle 2.064 funzioni Ψ_i corrispondenti a tutte le simultanee eccitazioni di due elettroni dai 5 orbitali occupati nello stato fondamentale SCF ai 24 orbitali virtuali disponibili. Si può dimostrare che le configurazioni eccitate, corrispondenti a singole eccitazioni, nel caso di orbitali HF non contribuiscono all'energia che a ordini superiori al secondo (teorema di Brilbuin). Date le eccessive dimensioni (2.065×2.065) della matrice da diagonalizzare per la determinazione dei coefficienti A_i della (28), il problema secolare relativo è stato risolto perturbativamente, arrestando il calcolo al secondo ordine per l'energia dello stato fondamentale. Il miglioramento dell'energia ottenuto, −160 kcal/mole, corrisponde al 74% dell'energia di correlazione stimata (−215 kcal/mole). È bene sottolineare che questa stima è approssimata sia perché è stato effettuato solo un calcolo perturbativo invece che un'esatta diagonalizzazione, sia perché sono stati impiegati orbitali SCF MOLCAO che sono approssimazioni buone, ma non perfette, ai veri orbitali HF. Tuttavia il valore ottenuto è da considerare largamente indicativo della porzione dell'energia di correlazione che può essere fornita da un calcolo di interazione di configurazioni molto esteso. Si può pertanto concludere che il metodo dell'interazione delle configurazioni, pur essendo potenzialmente idoneo a fornire funzioni d'onda molto accurate, ha tuttavia la caratteristica di essere molto lentamente convergente. Torneremo alla fine di questo articolo sul problema di come migliorare la funzione d'onda SCF.

b) Orbitali molecolari localizzati

Discuteremo ora alcuni metodi che permettono d'interpretare in maniera chimicamente più intuitiva la funzione d'onda SCF. Come appare dalla (11′), la funzione d'onda complessiva è costruita mediante orbitali molecolari monoelettronici ϕ_j che, a loro volta, sono espressi come combinazioni lineari di orbitali atomici appartenenti ai vari atomi della molecola; pertanto questi orbitali molecolari ϕ_j sono ‛delocalizzati', nel senso che si estendono su tutta la molecola e non permettono, di conseguenza, una visualizzazione intuitiva del loro contributo alla formazione dei singoli legami. Infatti, l'intuizione chimica, sostanziata da numerose osservazioni empiriche, quali l'additività dei contributi di particolari ‛gruppi' di elettroni (di core, di lone-pair, di legame) a molte proprietà molecolari (momento di dipolo elettrico, energia di legame, suscettività magnetica, rifrattività, ecc.), porta a dividere gli elettroni della molecola in vari gruppi: a) elettroni che, appartenendo ai gusci più interni dei vari atomi, non partecipano apprezzabilmente alla formazione dei legami (elettroni di core); b) elettroni che, pur appartenendo ai gusci esterni di valenza dei vari atomi, non partecipano anch'essi apprezzabilmente alla formazione dei legami (coppie di elettroni di lone-pair); c) elettroni, infine, che concorrono a formare legami chimici (una coppia per ciascun legame semplice) e la cui distribuzione di carica è notevolmente localizzata tra i due atomi legati (elettroni di legame). Per giungere a una rappresentazione più intuitiva della funzione d'onda in armonia con quanto sopra ricordato, è conveniente convertire gli orbitali molecolari delocalizzati (chiamati anche orbitali canonici) in orbitali chimicamente più significativi (orbitali ‛localizzati'). Questa conversione può essere eseguita utilizzando la proprietà di invarianza della matrice densità del primo ordine rispetto a una qualsiasi trasformazione unitaria degli orbitali canonici stessi, cioè una trasformazione che converta tutto il gruppo degli orbitali occupati ϕ della (19) in un nuovo gruppo di orbitali λ=ϕU, con U arbitraria matrice di trasformazione unitaria di dimensioni (N_e/2×N_e/2). È facile verificare tale proprietà di invarianza, riscrivendo la matrice densità ρ₁ sia in termini degli orbitali ϕ che in termini degli orbitali λ:

ρ₁(r₁ ∣ r₁′)=ϕ(r₁)ϕ*(r₁′),

ρ₁′ (r₁ ∣ r₁′)=λ(r₁)λ*(r₁′)=ϕ(r₁)UU*ϕ*(r₁′)=

=ϕ(r₁)ϕ*(r₁′)=ρ₁(r₁ ∣ r₁′),

in quanto, essendo U unitaria, UU*=U*U=1. Per una funzione d'onda monodeterminantale, quest'invarianza garantisce anche quella di ρ₁₂ e pertanto quella di tutte le grandezze osservabili d'interesse chimico. Vi sono, ovviamente, infinite trasformazioni U, tutte egualmente valide in linea di principio; tuttavia sono state proposte da vari autori (Boys, Ruedenberg, Magnasco ecc.) alcune forme particolari di U, adatte a trasformare gli orbitali canonici in orbitali localizzati. (Per una recente rassegna v. Weinstein e altri, 1971). Una scelta abbastanza semplice è quella di Boys, che propone di ricercare quella matrice U che rende minima la quantità

Questa condizione equivale a contrarre contemporaneamente al massimo ciascun orbitale o, come ancora dimostrato da Boys, a rendere massima la somma dei quadrati delle distanze reciproche dei centroidi di tutti gli orbitali occupati della molecola.

A titolo d'esempio, prendiamo ancora in considerazione la molecola di H₂O e riferiamola a un sistema di assi cartesiani, quale quello della fig. 2. Questa molecola contiene dieci elettroni che, nel modello SCF, sono sistemati, a coppie con spin antiparallelo, su 5 orbitali molecolari. Uno di questi orbitali coincide praticamente con l'orbitale atomico 1s del guscio K dell'atomo di ossigeno; tre dei restanti quattro orbitali canonici sono orbitali delocalizzati, simmetrici rispetto a una riflessione nel piano molecolare xz (orbitali σ), mentre il rimanente è un orbitale antisimmetrico rispetto allo stesso piano (orbitale π). In fig. 3, a sinistra, sono riportati i contorni di eguale densità di carica elettronica (ottenuti a partire da una funzione d'onda SCF-MOLCAO costruita su base minimale) nel piano xz per i tre orbitali canonici e nel piano xy per l'orbitale π; nella parte destra della stessa figura sono riportate le analoghe mappe (nel piano xz) per gli orbitali localizzati dei legami O-H (b₁ e b₂) e (nel piano yz) per i due orbitali di lone-pair l₁ e l₂. Va notato che questi orbitali di lone-pair sono prevalentemente localizzati nella zona degli z negativi, simmetricamente disposti uno al disopra e uno al disotto del piano xz. Complessivamente i quattro orbitali localizzati hanno orientazioni approssimativamente tetraedriche. Come si vede, le ripartizioni di carica dei due tipi di orbitali ottenuti per mezzo del processo di localizzazione presentano caratteristiche diverse, in quanto in ciascuno degli orbitali di legame b₁ e b₂ i due nuclei O e H sono immersi in una distribuzione di carica elettronica che si estende sostanzialmente nella zona di spazio a essi adiacente, mentre nell'altro tipo di orbitali l₁ e l₂ la distribuzione di carica tende a proiettarsi lontano dagli atomi d'idrogeno e pertanto non contribuisce sostanzialmente ai legami. Un'analisi conveniente che, anche se non rigorosa, ha il pregio di visualizzare il significato di questi orbitali, mostra come un lone-pair sia costituito ‛prevalentemente' da una combinazione lineare, con coefficienti opportuni, di un orbitale di tipo 2se uno di tipo 2p, entrambi appartenenti all'ossigeno (v. fig. 1); infatti, in tale orbitale, i coefficienti che pesano il contributo delle funzioni 1s centrate sui due atomi d'idrogeno H₁ e H₂ sono piccoli e possono essere trascurati in quest'analisi. Orbitali come questo, costituiti da un mescolamento di funzioni atomiche s e p appartenenti allo stesso atomo, prendono il nome di ‛ibridi' sp. A titolo d'esempio, nella fig. 4 viene riportata la mappa della densità di carica associata all'ibrido χ_sp=Aχ_2s+Bχ_2pz dell'ossigeno nel caso particolare A=B=1/√-2 (1/√-2 è il corretto coefficiente di normalizzazione per l'ibrido χ_sp quando A=B e le χ siano di per sè normalizzate). La somiglianza tra questo particolare orbitale ibrido e quelli di lone-pair l₁ e l₂ della fig. 3 è immediata: con un'opportuna scelta dei coefficienti di mescola- mento A e B le due mappe possono essere fatte praticamente coincidere. (Di fatto, l'orbitale 2p che interviene nell'orbitale di lone-pair l₁ è una risultante dei due orbitali atomici 2p_y e 2p_z dell'ossigeno; questo mescolamento ha l'effetto di orientare l'orbitale stesso nella direzione indicata dalla retta r₁ di fig. 3; una considerazione analoga vale per l'altro orbitale di lone-pair l₂). Un'analoga analisi approssimata eseguita su uno dei due orbitali di legame (per es., b₁) mostra che la ripartizione di carica a esso associata corrisponde con buona approssimazione a quella di un orbitale molecolare costruito come combinazione lineare ϕ_b1=C₁χ_sp(O)+C₂χ_1s(H₁) di due ‛sole' funzioni atomiche, una appartenente all'atomo di ossigeno e l'altra all'atomo di idrogeno H₁. (In questo caso viene trascurato il piccolo contributo dovuto alla funzione 1s centrata sul- l'altro idrogeno H₂). A sua volta, l'ibrido χ_sp(O) è del tipo mostrato in fig. 4 e orientato lungo il legame OH₁. È importante notare che la densità di carica ρ₁(1 ∣ 1)≡ρ₁(1) corrispondente all'orbitale ϕ_b1, ρ₁(1)=2{C²₁[χ_sp(O)]²+C²₂[χ_1s(H₁)]²+2C₁C₂[χ_sp(O)χ_1s(H₁)]}, non è costituita dalla semplice somma delle densità di carica [χ_sp(O)]² e (χ_1s(H₁)]², ma contiene anche un termine di ‛sovrapposizione' che è sensibilmente diverso da zero nella zona intermedia ai due atomi O e H₁; poiché questo termine, negli orbitali di legame, è positivo, esso descrive il fatto che nell'avvicinamento degli atomi per formare il legame si verifica una migrazione di carica dagli atomi verso la zona a loro intermedia. Inoltre, se ∣C₁∣≠∣C₂∣, contemporaneamente ha luogo, lungo il legame, un trasferimento di carica verso quello dei due atomi cui è associata la ∣C_i∣ maggiore.

L'esempio ora visto della molecola d'acqua dimostra l'utilità degli orbitali localizzati per estrarre dalla funzione d'onda informazioni intuitive e d'interesse chimico immediato, quali la forma degli orbitali di legame e di lone-pair, la loro direzionalità, i trasferimenti di carica nei singoli legami, ecc.

c) Proprietà di ‛quasi invarianza' di orbitali localizzati; grado di trasferibilità tra molecole chimicamente simili.

Vogliamo ora mostrare che un'analisi delle distribuzioni di carica, in termini di orbitali localizzati, per gruppi di molecole strutturalmente simili, è in grado di giustificare quelle regole empiriche di additività cui abbiamo fatto cenno in precedenza. Questa giustificazione si fonda sul fatto che nell'approssimazione SCF tutte le proprietà chimicamente interessanti della molecola sono determinate dalla matrice densità del primo ordine, che ha l'importante caratteristica di essere una funzione additiva di contributi associati ai singoli orbitali molecolari occupati e di essere invariante sotto una qualsiasi trasformazione unitaria:

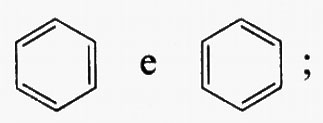
ove, per esempio, i ϕ_i sono orbitali canonici e i λ_i orbitali localizzati. Appare ovvio che per poter. parlare di trasferibilità del contributo a una proprietà molecolare, all'interno di una serie, è innanzi tutto indispensabile accertare il grado di conservazione (nel passaggio da una molecola all'altra) della forma del particolare orbitale coinvolto. Sembra anche evidente, dalle considerazioni fatte a proposito della molecola H₂O, che gli orbitali più adatti per una verifica di questo genere siano presumibilmente quelli localizzati. Per meglio chiarire i termini del problema, prendiamo in considerazione, a titolo d'esempio, la seguente serie di molecole organiche cicliche, ad anello triatomico,

(con X≡CH₂, NH, NH+₂, 0, S; e Y≡CH, N), per le quali sono state calcolate funzioni SCF su basi minimali di Slater (v. Bonaccorsi e altri, 1970). Tutte queste molecole hanno in comune il raggruppamento >CH₂, che è inserito in un contesto molecolare di volta in volta diverso, e pertanto si prestano a un confronto della forma e di alcune proprietà intrinseche, per esempio del legame localizzato C−H.

Per mancanza di spazio non possiamo mostrare le mappe delle distribuzioni di carica associate a ciascun legame C−H in tutta la serie; si nota tuttavia tra esse una notevole somiglianza, che induce ad approfondire in maniera più quantitativa il loro grado di conservazione. A questo scopo esamineremo l'andamento, nella serie, di grandezze caratteristiche di questo orbitale, quali il suo momento di dipolo elettrico, la sua energia cinetica intrinseca (molto sensibile alla forma dell'orbitale), ecc. Se nella (32) viene evidenziato il contributo ρ′_CH(1∣1′)=2λ_CH(1)λ*_CH(1′) corrispondente al legame che stiamo considerando, è facile ottenere il corrispondente contributo al momento di dipolo elettrico e all'energia cinetica intrinseci del legame:

Nella prima equazione, il primo contributo a secondo membro è quello della coppia elettronica, mentre il secondo rappresenta quello di due cariche positive unitarie, poste rispettivamente sui nuclei C e H, in modo da definire senza ambiguità il momento di dipolo elettrico di legame. Per ampliare l'analisi, è anche utile ricordare che per una funzione d'onda SCF relativa a una struttura a gusci chiusi, l'energia totale elettronica della molecola può scriversi nella forma

In questo caso però, a differenza dell'energia cinetica T_CH, il termine Ee_i¹ associato all'orbitale localizzato di legame λ_i è determinato, oltre che dalle interazioni con i nuclei C e H e dalla repulsione intrinseca della coppia elettronica, anche dalle interazioni con il ‛resto' molecolare. Per utilizzare l'energia Ee_i¹ come ‛test' di trasferibilità dell'orbitale localizzato λ_i essa dev'essere ripartita ulteriormente (seppure in modo non univoco) in due contributi, Ee_i¹=E0_i+U_i in cui E0_i rappresenta l'energia intrinseca dell'orbitale in esame e U_i l'energia di interazione con il ‛resto' molecolare; esplicitamente, per il caso che ci interessa:

E0_i=2[T_i+V_iC+V_iH]+J_ii, λ_i=λ_CH, (33)

in cuiV_iC eV_iH sono ora i termini di attrazione tra un elettrone della coppia e i nuclei C e H rispettivamente, e J_ii è l'energia di repulsione dei due elettroni della coppia stessa. È facile vedere da (32) e (33) che U_i ha la seguente forma

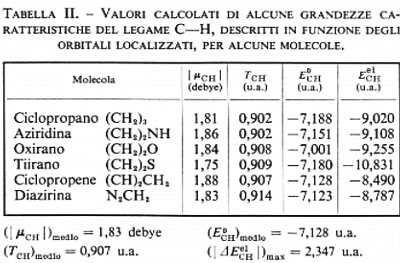
esso raccoglie, come si è detto, le energie di attrazione dei due elettroni di legame con tutti gli altri nuclei diversi da C e H, e tutte le energie repulsive con gli altri elettroni del ‛resto' molecolare. Ci si deve pertanto aspettare che se un particolare orbitale localizzato λ_i resta sensibilmente invariato nel passaggio da una molecola all'altra, anche il termine E0_i (33) subisca solo lievi variazioni, al contrario del valore dell'energia Ee_i¹, che è ampiamente distribuito su ampi intervalli di valori a causa del termine di interazione U_i che varia sensibilmente da un contesto molecolare a un altro. In tab. II sono riportati i valori calcolati di ∣μ_CH∣, T_CH, E0_CH e Ee_Cl_H per la serie di molecole ad anello triatomico cui avevamo fatto riferimento in precedenza. Come si vede, lo scarto massimo dalla media è per il momento elettrico del 4,4%, per l'energia cinetica del 7,7% e per E0_CH dell'1%, confermando un notevole grado d'invarianza e quindi di trasferibilità da molecola a molecola. Un maggior numero d'informazioni sul grado d'invarianza è contenuto nei grafici della fig. 5A e B, nella quale è riportato Ee_i¹=U_i+E0_i in funzione di U_i, per i≡CH, CC lone-pair di N, lone-pair di O, per una numerosa serie di molecole analizzate con i metodi sopra descritti. Se il grado d'invarianza fosse perfetto, i grafici per ogni i dovrebbero essere rette di pendenza uno: di fatto, lo sparpagliamento dei punti corrispondenti ai casi esaminati è sufficientemente ristretto, risultando per esempio per il lone-pair dell'O ΔE0_i/(ΔE_i)_max≃0,08.

d) Gruppi di elettroni chimicamente distinti: funzione d'onda molecolare espressa come prodotto antisimmetrizzato di funzioni di gruppo.

Le considerazioni finora fatte permettono di giustificare parzialmente la partizione di molte proprietà molecolari in contributi dovuti a singole coppie elettroniche; in realtà, l'esperienza chimica e chimico-fisica mette in evidenza l'esistenza di raggruppamenti funzionali anche più complessi (per es. CH₃, NH₂, NO₂, OH, ecc.), caratterizzati da una notevole costanza di proprietà nel passaggio da una molecola a un'altra analoga. Questa considerazione ha suggerito la possibilità di rappresentare la funzione d'onda complessiva della molecola sotto forma di un prodotto (opportunamente antisimmetrizzato) di funzioni d'onda caratteristiche di singoli gruppi: ovviamente questa approssimazione è tanto più valida quanto più debolmente interagenti tra loro sono i gruppi che la costituiscono. Se A, B, C, ... identificano i vari gruppi funzionali della molecola, contenenti rispettivamente N_A, N_B, N_C, ... elettroni, la funzione d'onda approssimata molecolare per lo stato k, Φ_k può essere scritta nella forma

Φ_k(q₁, ..., q_N)=MA[Φ A^(KA)(q₁, ..., q_NA)×

×Φ B^(KB)(q_NA+1 ..., q_NA+NB) ...], (35)

in cui Φ A^(KA), Φ B^(KB), ... sono ‛funzioni d'onda di gruppo', per gli stati K_A di A, K_B di B, ecc., singolarmente anfisimmetriche rispetto agli scambi interni delle coordinate elettroniche, A è un operatore di antisimmetrizzazione (che permuta le coordinate di elettroni di gruppi differenti) e M è un opportuno fattore di normalizzazione. Non è difficile rendersi conto che la funzione d'onda (35) contiene come caso particolare quello della funzione d'onda monodeterminantale (11) (fattorizzazione in gruppi di 1 elettrone).

Il problema matematico connesso con l'impiego variazionale di una funzione d'onda di questo tipo è molto complicato, a meno che le varie funzioni di gruppo non soddisfino la cosiddetta condizione di ‛ forte' (strong-orthogonality), per cui

∫dq₁Φ A^(KA)*(q₁, q_k, q_l, ...)Φ B^(KB)(q₁, q_r, q_s, ...)=0.

Per esempio, nel caso di uno stato molecolare rappresentato da una funzione d'onda del tipo Φ=MA[Φ_AΦ_B], corrispondente a una partizione degli elettroni in due soli gruppi A e B, la condizione di ‛ortogonalità forte' permette di scrivere l'energia nella forma molto semplice

E^e1=E_A+E_B+J_AB−K_AB, (36)

in cui E_A(E_B) è l'energia del gruppo A(B) di elettroni nel campo di tutti i nuclei della molecola, mentre i termini J_AB e K_AB rappresentano le energie di interazione coulombiane e di scambio dei due gruppi di elettroni. La minimizzazione dell'energia E^e1 può essere condotta per approssimazioni successive, a partire da funzioni d'onda approssimate per i due gruppi di elettroni A e B, rispettivamente. Come primo passo, manteniamo fissa la funzione d'onda Φ_B del gruppo B (di conseguenza anche E_B resta costante); questo permette di scrivere l'energia E^e1 (36) nella forma E^e1=E_B+EA^(eff), in cui EA^(eff)=E_A+J_AB−K_AB rappresenta l'energia del gruppo A nel campo ‛efficace' di tutti i nuclei e di tutti gli elettroni (tale energia naturalmente dipende dalla funzione d'onda approssimata scelta per rappresentare il gruppo B). Come secondo passo, mediante il teorema variazionale si cerca di ottimizzare la funzione di gruppo Φ_A minimizzando EA^(eff); il procedimento viene poi ripetuto, mantenendo fissa la funzione Φ_A così trovata e variando Φ_B. Questo procedimento alterno viene arrestato quando i valori dell'energia E, relativi a due passi successivi, differiscano di una quantità sufficientemente piccola prefissata. Un raffinamento alla semplice funzione d'onda (35) può essere ottenuto considerando una combinazione lineare Φ=Σ_kC_kΦ_k di funzioni Φ_k del tipo (35), anziché una sola di esse. In questa nuova funzione ciascuna Φ_k corrisponde a uno ‛stato' particolare della molecola ed è ottenuta, a sua volta, da funzioni di gruppo corrispondenti a particolari ‛stati' dei due gruppi stessi. L'applicazione forse più immediata del metodo di partizione della funzione d'onda in funzioni di gruppo, che siano ortogonali in senso forte, si ha in quelle molecole in cui siano presenti raggruppamenti di elettroni descritti da funzioni di gruppo di simmetria diversa. Un caso tipico è per esempio quello delle molecole organiche contenenti doppi legami coniugati (polieni, benzene e derivati aromatici, ecc.), nelle quali la metà degli elettroni dei doppi legami sono alloggiati in orbitali simmetrici rispetto al piano molecolare (orbitali σ) e l'altra metà in orbitali antisimmetrici rispetto allo stesso piano (orbitali π) : in questo caso la suddivisione degli elettroni in gruppi σ e π assicura automaticamente la condizione di ortogonalità forte per ragioni di simmetria. Possiamo notare che una tale suddivisione è profondamente radicata nel pensiero chimico fin dai primordi della chimica organica dei composti aromatici, e ha trovato numerosissime applicazioni nel campo della chimica quantistica sotto forma di metodologie approssimate per il calcolo di funzioni d'onda e di proprietà di questa classe di molecole (metodi semiempirici). Un altro esempio, abbastanza evidente, in cui la partizione in gruppi può trovare utili applicazioni, è fornito dalla suddivisione degli elettroni di una molecola in elettroni dei gusci interni dei vari atomi ed elettroni dei gusci di valenza. Come ulteriore esempio si può citare l'utilizzazione delle funzioni di gruppo per lo studio delle interazioni tra una o più molecole, che siano abbastanza lontane da avere ‛sovrapposizioni' sufficientemente piccole. Facendo riferimento a quanto è stato detto a proposito del sensibile grado d'invarianza delle proprietà associate alle coppie elettroniche di legame, core, lone-pair, quando sono descritte in termini di orbitali localizzati, si intuisce che un miglioramento rispetto alla semplice funzione d'onda monodeterminantale può essere ottenuto pensando la funzione d'onda complessiva come costituita da ‛funzioni d'onda di coppia' (‛geminali'). Ciascuna di queste ‛funzioni di coppia' può essere descritta, secondo il metodo dell'interazione delle configurazioni, come combinazione lineare di determinanti di Slater (2×2), il primo dei quali è costruito con l'orbitale molecolare localizzato corrispondente. Per fare un esempio, supponiamo che un orbitale localizzato di legame tra due atomi A e B di una molecola sia approssimativamente descritto da ϕ₁=N₁[χ_A+χ_B] (χ_A+χ_B essendo orbitali atomici di A e B rispettivamente) e supponiamo inoltre che ϕ₂=N₂[χ_A−χ_B] sia il primo orbitale eccitato corrispondente; allora è facile vedere che da tale base possono essere costruite tre ‛funzioni di coppia', alloggiando gli elettroni a) entrambi in ϕ₁; b) uno in ϕ₁ e uno in ϕ₂; c) entrambi in ϕ₂. Chiamando Φ⁽⁰⁾, Φ⁽¹⁾ e Φ⁽²⁾ le ‛funzioni di coppia' costruite sulla base dei determinanti di Slater corrispondenti,

la combinazione lineare Λ=A⁽⁰⁾Φ⁽⁰⁾+A⁽¹⁾Φ⁽¹⁾+A⁽²⁾Φ⁽²⁾ è una buona approssimazione alla funzione di gruppo della coppia di elettroni del legame AB. (La combinazione lineare dei due determinanti di Slater nella Φ⁽¹⁾ è necessaria per assicurare che la funzione stessa descriva uno stato di singoletto). Se la funzione d'onda molecolare complessiva viene fattorizzata in funzioni geminali di questo tipo, il problema della minimizzazione dell'energia si riconduce a un calcolo iterativo analogo a quello illustrato per il caso generale. L'impiego di questo metodo conduce a un miglioramento dell'energia rispetto a un semplice calcolo SCF, in quanto si tiene parzialmente conto della correlazione elettronica interna della coppia.

e) Forze intermolecolari: forze a lunga e a media distanza.

Nella parte introduttiva di questo articolo, elencando i problemi connessi con la teoria del legame chimico, si è accennato alla necessità d'interpretare quelle forze residue che si esercitano tra le molecole e che sono responsabili, da una parte, della fenomenologia relativa alla dinamica delle reazioni chimiche e, dall'altra, dell'esistenza delle fasi condensate della materia. In linea di principio, questo problema non è assolutamente diverso da quello affrontato per lo studio delle proprietà di una singola molecola. Da un punto di vista metodologico, tuttavia, è opportuno classificare le interazioni tra molecole in almeno due categorie: quelle che si esplicano a distanze intermolecolari dello stesso ordine di grandezza di quelle tra gli atomi delle due molecole (interazioni a breve raggio e a raggio intermedio) e quelle che si riferiscono a distanze sufficientemente grandi (interazioni a lungo raggio), tali cioè che possano far trascurare la sovrapposizione tra le funzioni d'onda delle due molecole. Il primo caso (di particolare interesse per tutti i processi che conducono a reazioni chimiche), sebbene sia oggetto d'intense ricerche da parte di numerosi ricercatori con metodologie sia perturbative sia variazionali, non sembra sfortunatamente suscettibile di una trattazione semplice ed efficace al tempo stesso, se non forse in termini di una fattorizzazione della funzione d'onda complessiva in funzioni di gruppo. Per mettere in evidenza le difficoltà connesse con lo studio di questo genere d'interazioni, possiamo sottolineare il fatto che a tutt'oggi non esistono calcoli veramente accurati e completi neppure per la semplice reazione di scambio H₂+H→H+H₂. Per questa reazione sono stati effettuati calcoli entro l'accuratezza chimica (tra 0,2 e 0,8 kcal/mole) per le sole configurazioni lineari H−H−H da B. Liu (1973). L'altro tipo d'interazione, quello a lungo raggio, presenta certamente difficoltà inferiori in quanto, a causa della grande separazione, è sostanzialmente trascurabile la sovrapposizione tra le funzioni d'onda Φ_A e Φ_B delle molecole separate; questo comporta, a sua volta, che la funzione d'onda complessiva sia ben rappresentata da un semplice prodotto Φ_AΦ_B, dato che i termini di scambio K_AB sono trascurabili.

Il problema, che può essere affrontato sia per via perturbativa sia per via variazionale, verrà qui esaminato brevemente in entrambe le approssimazioni. Indichiamo con ℋ=ℋ_A+ℋ_B+ℋ_AB l'operatore hamiltoniano complessivo del sistema, costituito dalla somma degli hamiltoniani ℋ_A e ℋ_B rispettivi delle molecole A e B imperturbate, e dal termine d'interazione ℋ_AB (la cui forma verrà specificata tra breve). Nell'approccio perturbativo, detta Φ_Aa la funzione d'onda imperturbata dello stato generico a della molecola A e Φ_Bb l'analoga per uno stato b di B, si può dimostrare che la funzione d'onda complessiva perturbata al primo ordine ha la forma:

in cui E_Aa e E_Bb sono le energie imperturbate degli stati a e b generici delle due molecole A e B, rispettivamente. La notazione Σ_a′ Σ_b′ sta a indicare che i due indici a e b non possono essere contemporaneamente zero; pertanto nelle somme saranno contenuti prodotti del tipo 1) Φ_A0Φ_Bb, 2) Φ_AaΦ_B0 e 3) Φ_AaΦ_Bb.

L'energia corrispondente alla (38) risulta allora, sino a termini del secondo ordine:

In questa espressione, l'energia complessiva E è decomposta nella somma di vari contributi: il primo, (E_A0+E_B0), rappresenta l'energia delle molecole imperturbate, il secondo rappresenta l'energia d'interazione elettrostatica tra le distribuzioni di carica, pensate rigide, delle due molecole; infine si può dimostrare che nell'ultimo termine sono contenuti due differenti contributi: quello relativo all'energia di polarizzazione di una molecola nel campo dell'altra (contributo induttivo dovuto ai termini 1) e 2) di cui sopra) e quello dovuto alle interazioni tra distribuzioni di carica fluttuanti nelle due molecole (contributo dispersivo legato ai termini di tipo 3). Per l'utilizzazione concreta di questo approccio perturbativo, l'hamiltoniano d'interazione

(in cui, in unità atomiche Z_iA=−1 per un elettrone e Z_iA=Z_α per il nucleo α di A) viene solitamente rappresentato nella forma di una somma di termini corrispondenti alle interazioni tra i vari multipoli elettrici che descrivono le distribuzioni di carica delle due molecole. Detta R la distanza di separazione tra i baricentri di queste, l'hamiltoniano d'interazione ℋ_AB scrive

In questa espressione α, β, γ, δ, ...=x, ψ, z e ∇ è l'operatore gradiente; inoltre, per esempio

rappresenta la carica risultante della molecola A (zero per una molecola neutra),

rappresenta la componente x dell'operatore momento di dipolo elettrico di A; infine

rappresentano le componenti diagonale e fuori diagonale dell'operatore momento di quadrupolo di A. Lo sviluppo (40) contiene interazioni di tipo monopolo-monopolo, monopolo-dipolo, dipolo-dipolo, ecc. Per due molecole neutre (q_A=q_B=0) il termine d'interazione più basso diverso da zero è, in principio, quello dipolo-dipolo. Ovviamente lo sviluppo multipolare (40) deve essere limitato, per ragioni pratiche, a un numero piuttosto piccolo di termini, per cui questo tipo di approssimazione sarà valido per molecole di piccole dimensioni e a separazioni piuttosto grandi. Infatti, per esempio, per una molecola abbastanza complessa quale l'adenina, che è una delle basi coniugate che entrano nella struttura a doppia elica della molecola DNA, il potenziale elettrostatico nel piano molecolare è rappresentato dalle linee equipotenziali di fig. 6; come si vede, la forma di questo potenziale è piuttosto complessa, presentando varie zone di minimo e superfici nodali, per cui una sua rappresentazione per mezzo di uno sviluppo multipolare limitato appare chiaramente insufficiente.

Passando all'approccio variazionale, la funzione d'onda complessiva che dev'essere ottimizzata può essere ancora rappresentata come prodotto delle funzioni d'onda Φ_A e Φ_B delle due molecole interagenti, Φ=Φ_AΦ_B e l'hamiltoniano d'interazione ℋ_AB non viene solitamente sviluppato in serie di multipoli. Anche in questo caso, a causa della grande distanza tra le molecole, si potrà trascurare il termine di scambio K_AB, e poichè l'energia totale E può essere scritta nella forma E=E_B+EA^eff (si veda il seguito dell'equazione (36), tenendo presente che, nel caso attuale, l'energia E include anche i contributi di repulsione nucleare), il calcolo di minimizzazione potrà essere condotto secondo il seguente schema: in un primo tempo si riottimizza l'energia della molecola A nel campo efficace prodotto dalla molecola B (campo dovuto all'effetto puramente coulombiano della distribuzione di carica elettronica-nucleare in B), successivamente si ottimizza l'energia E_B della molecola B nel campo efficace corrispondente alla nuova distribuzione di carica trovata per la molecola A; il procedimento viene proseguito alternativamente, sino a convergenza. Se le funzioni d'onda di partenza, sia per A che per B, sono monodeterminantali, questo procedimento di ottimizzazione è di tipo SCF e si può dimostrare che l'energia risultante contiene termini d'interazione elettrostatica diretta e termini dovuti alla polarizzazione reciproca delle distribuzioni di carica delle due molecole. A questo livello di approssimazione della funzione d'onda non si ottengono i contributi dispersivi all'energia, corrispondenti a una parte del terzo termine nello sviluppo perturbativo (39). Se però si utilizzano gli orbitali virtuali di A e di B, ottenuti dal processo SCF di cui sopra, per condurre un calcolo d'interazione delle configurazioni interno a ciascuna delle due molecole sotto l'effetto del campo dell'altra, si può ottenere un ulteriore contributo all'energia che, in questo schema variazionale, è interpretabile come energia di correlazione interna di A e di B e che corrisponde al contributo dispersivo cui si è accennato nell'approccio perturbativo. Se poi nel campo efficace viene inclusa anche la parte dovuta al termine di scambio K^AB, e quindi per la funzione d'onda si assume la forma MA[Φ_AΦ_B], questo stesso approccio conduce a risultati sufficientemente accurati anche per distanze intermolecolari alle quali la sovrapposizione non è più trascurabile, purché abbastanza piccola.

f) Molecole di grandi dimensioni e problemi connessi: alcuni metodi semiempirici ampiamente utilizzati.

I metodi discussi sinora e le possibilità effettive degli attuali calcolatori elettronici permettono lo studio accurato di sistemi molecolari di complessità non molto elevata. D'altronde, la massima parte dei problemi chimicamente interessanti richiede la conoscenza della struttura elettronica di molecole di medie e grandi dimensioni. Per questo motivo si è necessariamente proceduto allo studio di numerosi approcci al problema e di numerose metodologie di calcolo (che vanno sotto il nome di metodi semiempirici) che, benché non portino a valori accurati dell'energia e di altre proprietà molecolari, sono tuttavia di notevole utilità al fine di una valutazione semiquantitativa globale delle grandezze strutturali e d'interesse chimico della molecola e, specialmente, sono efficaci per uno studio comparativo di proprietà in serie omologhe.

Un primo metodo molto efficace e ampiamente utilizzato per lo studio di molecole contenenti gruppi di elettroni π, quali molecole aromatiche e polieni, è quello originariamente suggerito da E. Hückel (v., 1931). In tale metodo viene sfruttata la diversa simmetria degli orbitali molecolari corrispondenti agli elettroni σ e agli elettroni π, per cui è automaticamente assicurata la ortogonalità in senso forte (strong-orthogonality) tra le funzioni d'onda relative ai due gruppi di elettroni. La funzione d'onda complessiva può pertanto essere scritta Φ=MA[Φ_σΦ_π] e l'energia, come si è visto, E=E_σ+Eπ^eff. Per esempio, nella molecola di benzene appartengono al gruppo σ i 36 elettroni che costituiscono i gusci interni K degli atomi di C e i legami semplici C−H e C−C, mentre appartengono al gruppo π i rimanenti 6 elettroni: i primi sono descritti da orbitali molecolari simmetrici rispetto al piano dell'anello, i secondi da orbitali antisimmetrici rispetto allo stesso piano. Pertanto, nell'approssimazione monodeterminantale per entrambe le funzioni Φ_σ e Φ_π la matrice di Fock F del problema si fattorizza rigorosamente in una parte σ e in una parte π, come è mostrato nello schema sottostante:

Nel metodo di Hückel, la base di orbitali atomici scelta è di tipo minimale, cioè include un solo orbitale π per atomo di carbonio. La prima ipotesi del metodo consiste nel supporre nota la funzione Φ_σ; a questo punto viene fatta l'ulteriore approssimazione di assumere per l'hamiltoniano relativo agli elettroni π la forma molto semplice

nella quale Eπ^eff (i) è un operatore monoelettronico effettivo che incorpora sia gli effetti medi della repulsione con gli elettroni del gruppo σ, sia quelli con gli altri elettroni del gruppo π. In questa approssimazione, detti ϕ⁽i^π) gli orbitali molecolari soluzioni della parte F^(π) della matrice di Fock, l'energia totale degli elettroni π si scrive semplicemente

in cui ε⁽i^π) sono gli autovalori della matrice F^(π) e la somma è estesa a tutti i livelli occupati. Inoltre, affinché il metodo possa essere facilmente utilizzabile, si fanno le seguenti ulteriori ipotesi: a) che gli orbitali atomici π utilizzati (uno per ciascun atomo di C) costituiscano una base orto-normale; b) che gli elementi diagonali F r⁽_r^π) della matrice F^(π) siano tutti eguali tra loro, F r⁽_r^π)=α (si noti che mentre per il benzene, data l'alta simmetria, questa non è una condizione restrittiva, nel naftalene, per esempio, questa ipotesi introduce un'ulteriore approssimazione, in quanto in questa molecola sono eguali tra loro gli elementi corrispondenti alle posizioni 1, 4, 5, 8 ed eguali tra loro - ma leggermente differenti dai precedenti - quelli relativi alle posizioni 2, 3, 6, 7 o alle posizioni 9 e 10); c) che gli elementi fuori diagonale F r⁽_r^π) siano tutti nulli, tranne quelli corrispondenti ad atomi di C adiacenti, per i quali si assume un valore comune F r⁽_r^π)_±1=β (anche qui, per posizioni non simmetricamente analoghe, a rigore questi elementi di matrice sarebbero leggermente differenti; l'approssimazione di trascurare gli elementi di matrice tra atomi di C non adiacenti è parzialmente giustificata dal fatto che F r⁽_s^π) (r≠s) decresce molto rapidamente col crescere della distanza interatomica). Con queste approssimazioni, la matrice di Fock F^(π) per il gruppo di elettroni π viene drasticamente semplificata; per il benzene, per esempio, essa acquista la forma:

La sua diagonalizzazione porta alle energie orbitali indicate nello schema che segue (i livelli ε₂, ε₄ sono doppiamente degeneri):

Pertanto l'energia totale degli elettroni π risulta eguale a (6α+8β) dove, indicando con χ_r il generico orbitale atomico π dell'atomo r, α=〈χ_r∣Eπ^eff∣χ_r>, β=〈χ_r∣Eπ^eff∣χ_r±1>. Nel metodo di Hückel, a causa della forma non esplicitamente determinata dell'operatore Eπ^eff, questi integrali non vengono calcolati e vengono invece considerati come parametri semiempirici. Per la previsione di molte proprietà relative agli elettroni π (energia di risonanza, transizioni elettroniche, indici di legame, lunghezze di legame, costanti di forza, ecc.) la conoscenza del parametro α non è indispensabile. Come primo esempio di applicazione del metodo di Hückel a molecole aromatiche, prendiamo in considerazione il calcolo dell'energia di risonanza. Come si ricorderà, l'energia totale di legame di una molecola può essere ottenuta, empiricamente, come somma delle energie di tutti i legami in essa contenuti; così, per esempio, l'energia di legame dell'etano CH₃−CH₃ è E=6E_CH+E_CC. Se ora si va a calcolare con questa regola l'energia di legame di una molecola aromatica (per es., il benzene) si trova che il valore ottenuto è inferiore a quello effettivo della molecola, cioè che la molecola è in realtà più stabile di quanto sarebbe se ad essa fosse associata una singola struttura tra quelle che è possibile scrivere usando la grafia classica della chimica organica. Per esempio, per il benzene, le due strutture canoniche di Kekulé che è possibile scrivere sono

esse sono caratterizzate da differenti disposizioni dei doppi legami π, pur avendo nell'approssimazione additiva la stessa energia, E=6E_CH+6E⁽_Cσ_C⁾+3E⁽_Cπ_C⁾. Una stima di questo genere porta a un errore per difetto di circa 40 kcal/mole: questo scarto è da attribuire a un effetto puramente quantistico, legato fondamentalmente alla risonanza tra le due strutture estreme di Kekulé. Con riferimento a questo esempio, si definisce in generale energia di risonanza di un composto aromatico la differenza tra l'energia effettiva della molecola e l'energia di una delle strutture canoniche equivalenti che possono essere formulate con la grafia classica della chimica organica. Per il benzene, per esempio, nell'approssimazione di Hückel questa energia puo essere calcolata come differenza dell'energia totale π, (6α+8β), e l'energia di tre doppi legami π separati (come quelli di tre molecole di etilene CH₂=CH₂ isolate), per ognuno dei quali è E⁽_Cπ_C⁾=2(α+β). (La matrice di Fock F^(π) per un doppio legame π isolato è

la cui diagonalizzazione fornisce i livelli (α+β) e (α−β), il primo dei quali è doppiamente occupato). Pertanto l'energia di risonanza ammonta a (6α+8β)−3×2(α+β)=+2β e, come si vede, dipende solo dal parametro β. Risultati analoghi per un certo numero di molecole aromatiche sono raccolti nella tab. III: nella seconda colonna è riportata l'energia di risonanza calcolata (in unità β), nella terza l'energia di risonanza determinata sperimentalmente (in kcal/mole) e nella quarta i corrispondenti valori calcolati assumendo per il parametro β il valore empirico di −20 kcal/mole. Come si vede, l'accordo è abbastanza soddisfacente e giustifica in parte, a posteriori, le approssimazioni fatte.

A causa del suo carattere semiempirico, ci si può attendere che la teoria di Hückel si presti a essere utilizzata anche per lo studio di molecole aromatiche contenenti eteroatomi (N, O, S). Per questo basta assegnare degli opportuni valori ai parametri α e β per caratterizzare gli elementi della matrice approssimata di Fock relativi agli orbitali atomici π degli eteroatomi. Questa generalizzazione è stata ampiamente applicata da numerosi ricercatori; tuttavia i risultati non sono da considerarsi altrettanto buoni come quelli che la teoria fornisce per le molecole aromatiche normali.

La teoria di Hückel si presta a essere sfruttata a fondo per ricavare numerose altre informazioni sulle proprietà molecolari. Per mancanza di spazio non possiamo soffermarci molto su questi aspetti della teoria; tuttavia non è possibile non menzionarne alcuni. Ricordando che l'energia orbitalica dell'i-esimo orbitale π è data da:

e che

si vede facilmente che:

Ora è facile mostrare, analizzando la funzione densità 2Σ_iϕ^*_iϕ_i, che 2Σ_iC²_ri rappresenta (in unità e) la quantità di elettroni localizzati nell'orbitale atomico π dell'atomo r; inoltre, dalla (41), risulta evidente che 4Σ_iC_riC_si rappresenta, in unità β, quella parte dell'energia totale π che è, per così dire, localizzata nella zona compresa tra gli atomi r e s. Pertanto, alla q_r=∂E_π/∂α_r si dà il nome di ‛carica orbitalica', mentre alla grandezza P_rs=½(∂E_π/∂β_rs) si dà il nome di ‛ordine di legame π'. Nei sistemi di doppi legami coniugati, quali quelli presenti nei sistemi aromatici, dove i legami tra atomi di carbonio hanno carattere intermedio tra semplice e doppio, tale indice (che varia nell'intervallo tra zero e uno) fornisce una misura del grado di doppio legame presente tra gli atomi r e s. L'ordine di legame pertanto può essere utilizzato per prevedere le distanze di legame e le costanti di forza. Infatti, se indichiamo con R_s la lunghezza propria di un legame semplice carbonio-carbonio (come, per es., quello dell'etano, uguale a 1,54 Å) e R_d la lunghezza propria di un doppio legame C=C (come quello dell'etilene, R_d=1,33 Å), è possibile dimostrare la seguente semplice relazione che fornisce la lunghezza di un legame, avente caratteristiche intermedie tra quello semplice puro e quello doppio puro, in funzione del suo ordine di doppio legame

R_r=R_s−P_rs(R_s−R_d). (42)

Una relazione del tutto analoga vale per la previsione della costante di forza relativa a un legame carbonio-carbonio avente caratteristiche intermedie tra quelle di un legame semplice e quelle di un legame doppio:

K=K_s+P_rs(K_d−K_s).

A titolo di esempio, in tab. IV sono riportate per la molecola di naftalina le distanze di legame sperimentali e quelle calcolate in base alla (42). Come si vede l'accordo è abbastanza soddisfacente, tenuto conto della tesi che sono alla base della teoria.

Come si è già accennato, la grandezza q_r=∂E_π/∂α_r fornisce una misura della porzione di carica elettronica π localizzata sull'atomo r; i valori di questa grandezza si prestano pertanto a una previsione qualitativa delle zone in cui preferenzialmente dovrebbe verificarsi un attacco da parte di reagenti elettrofili o nucleofili nelle reazioni a meccanismo ionico. Per esempio, per la molecola di Piridina è stata calcolata la seguente ripartizione della carica π.

per cui si può prevedere che un attacco elettrofilo per la reazione di sostituzione di un atomo di idrogeno (per es. nitrazione) avvenga preferenzialmente in posizione 3; l'esperienza conferma questa e altre numerosissime previsioni fondate su questo metodo.

Collegata strettamente con il concetto di ordine di legame, nella teoria di Hückel viene definita un'altra grandezza, chiamata ‛indice di valenza libera', la quale svolge per le reazioni a meccanismo radicalico un ruolo analogo a quello che la carica q_r svolge nel caso di reazioni a meccanismo ionico. Per comprendere il significato di questa grandezza, prendiamo in considerazione la molecola di butadiene, per la quale è stata calcolata la seguente ripartizione degli indici di doppio legame

Come si vede, gli atomi di carbonio C₁ e C₂ sono impegnati in misura diversa nella formazione di legami con gli atomi circostanti, in quanto C₁ forma due legami (σ) interi con gli idrogeni, un legame intero (σ) con C₂ e solo 0,894 legami π con C₂, per un totale di N₁=3,894 legami. Analogamente, è facile verificare che l'atomo C₂ è invece impegnato nella misura di N₂=4,341. Poichè si può dimostrare che per un atomo di carbonio (escludendo i legami tripli) il valore più grande possibile di N è N_max=4,731, si vede che la valenza ancora non saturata (valenza libera) per l'atomo C₁ è F₁=4,731−3,894=0,837; analogamente per l'atomo C₂ essa è 0,390. Questo fa presumere che l'atomo di carbonio C₁ sia il più reattivo nei confronti di un attacco radicalico.

Un'altra metodologia ampiamente utilizzata per lo studio di sistemi di elettroni π, e più raffinata della teoria di Hückel, è quella dovuta a Pariser-Pople-Parr (PPP). A differenza della teoria di Hückel, nella quale l'hamiltoniano totale π, ℋ_π, era approssimato come somma di hamiltoniani π effettivi monoelettronici, Hπ^eff (i), e l'energia totale degli elettroni π era quindi la semplice somma delle energie orbitaliche ε_iπ in questo caso l'hamiltoniano contiene esplicitamente anche termini bielettronici ed è scritto nella forma

in cui V_ri è un potenziale di core che rappresenta l'energia potenziale dell'i-esimo elettrone π nel campo efficace dell'r-esimo atomo di carbonio. Nello schema SCF MOLCAO il processo di minimizzazione dell'energia richiede la conoscenza della matrice di Fock F^(π)=H^(π)+G^(π) (v. 24), per cui è necessario valutare gli integrali monoelettronici 〈χ_r∣χ_s> e 〈χ_r∣−½∆+V_t∣χ_s> e bielettronici (χ^*_rχ_s∣χ^*_tχ_v). Per ridurre drasticamente la mole dei calcoli necessari, nel metodo PPP viene usata ancora una base minimale di orbitali atomici π e vengono fatte varie approssimazioni. Una prima approssimazione concerne la valutazione degli elementi di matrice di H^(π). Per i termini diagonali,

il primo termine a secondo membro rappresenta l'energia di un elettrone π sull'atomo r e viene ragionevolmente approssimato con −I, I essendo il potenziale di ionizzazione dell'atomo di carbonio nello stato di valenza (trigonale) caratteristico di questo elemento nelle molecole a doppi legami coniugati; ciascun termine della somma a secondo membro, che rappresenta l'energia elettrostatica di interazione tra un elettrone π sull'atomo r con il campo efficace dovuto al core dell'atomo s, è approssimato semplicemente come −Zs^eff/R_rs, Zs^eff essendo un'opportuna carica puntiforme effettiva su s, e R_rs la distanza tra i nuclei degli atomi r e s. Gli elementi di matrice fuori diagonale, se si trascurano gli integrali tricentrici del tipo 〈χ_r∣V_t∣χ_s>, si riducono semplicemente a (H^(π))_rs=〈χ_r∣−½∆+V_r+V_s∣χ_s> e vengono spesso presi come parametri empirici, o anche come proporzionali alla sovrapposizione S_rs, cioè Hr⁽sπ%$⁾≃KS_rs. Resta da vedere come nel metodo PPP vengano stimati gli integrali bielettronici. A questo proposito, viene fatta un'ulteriore semplificazione che consiste nel considerare nulli tutti gli integrali bielettronici in cui compaia la distribuzione χ_r(1)χ_s(1), con r e s appartenenti ad atomi diversi (neglect of differential overlap). Ne consegue che gli integrali (χ^*_rχ_s∣χ^*_t χ_v) sono tutti trascurati, a meno che non sia χ_r=χ_s e χ_t=χ_v, e pertanto si riducono ai due tipi (χ^*_rχ_r∣χ^*_tχ_t) (bicentrico) e (χ^*_rχ_r∣χ^*_rχ_r) (monocentrico). Il primo di questi viene approssimato sostituendo l'interazione effettiva con quella 1/R_rt di due cariche unitarie puntiformi poste sui due nuclei (Pople) oppure, ricordando il diagramma polare di un orbitale π (v. fig. 1), con l'interazione di due distribuzioni di carica, una sull'atomo r e una sull'atomo t, ciascuna delle quali è rappresentata da lobi sferici, uniformemente carichi, posti uno al disopra e uno al disotto del piano molecolare (Pariser-Parr). Per l'integrale monocentrico viene preso il valore (χ^*_rχ_r∣χ^*_rχ_r)=I−A, I essendo ancora il potenziale di ionizzazione e A l'affinità elettronica dell'atomo di carbonio nello stato di valenza trigonale. Questa approssimazione è basata sulle seguenti considerazioni relative all'ipotetica reazione tra atomi separati: C•+C•→C⁺+C^-, per la quale, ovviamente, ΔE=I−A. Infatti, se si tiene conto che l'energia dei due elettroni sul C^- è 2〈χ_r∣−½∆+V_r∣χ_r>+(χ^*_rχ_r∣χ^*_rχ_r) e quella degli stessi due elettroni, ciascuno sul proprio atomo C•, è 2〈χ_r∣−½∆+V_r∣χ_r>, la variazione di energia è anche data da ΔE=(χ^*_rχ_r∣χ^*_rχ_r), per cui appare ragionevole assumere (χ^*_rχ_r∣χ^*_rχ_r)=I−A.

Il metodo PPP è stato ampiamente utilizzato per la previsione di proprietà di molecole a doppi legami coniugati nel loro stato fondamentale (momento elettrico, distanze di legame, ripartizioni di carica, ecc.); inoltre, quando è stato accoppiato al metodo dell'interazione delle configurazioni, ha trovato utili applicazioni anche per lo studio delle transizioni elettroniche tra lo stato fondamentale e i primi stati eccitati.

Tra i numerosi altri metodi approssimati proposti da vari autori, ci limiteremo infine a ricordarne uno solo, molto recente, dovuto a Pople e noto con la sigla CNDO (Complete Neglect of Differential Overlap). Questo metodo, che è utilizzabile anche per molecole sature, può considerarsi un'estensione del metodo PPP e si basa ancora sull'uso dell'hamiltoniano completo

in cui però la somma su A corre su tutti gli atomi della molecola e V_iA rappresenta il potenziale efficace dovuto al nucleo dell'atomo A e agli elettroni di core dello stesso atomo. Anche in questo metodo, per valutare gli integrali necessari, vengono introdotte numerose approssimazioni che elenchiamo brevemente (per semplificare le notazioni, in quanto segue faremo la convenzione che gli orbitali con indice r appartengano all'atomo A e quelli con indice s a un atomo diverso, per es. B): 1) si sostituisce la matrice di sovrapposizione S con la matrice unità nelle equazioni di Roothaan (24); 2) si trascura la sovrapposizione differenziale in tutti gli integrali bielettronici, per cui (χ^*_rχ_s∣χ^*_tχ_v)=(χ^*_rχ_r∣χ^*_sχ_s)δ_rsδ_tv (sono considerati diversi da zero solo integrali bicentrici e monocentrici); 3) tutti gli integrali bicentrici tra due atomi A e B sono presi uguali tra loro, cioè (χ^*_rχ_r∣χ^*_sχ_s)=γ_AB, per ogni r appartenente ad A e per ogni s appartenente a B; 4) gli integrali di tipo 〈χ_r∣V_B∣χ_r′> sono approssimati con un valore unico V_AB dipendente solo dagli atomi A e B: 〈χ_r∣V_B∣χ_r′>=V_ABδ_rr′; 5) negli elementi della parte monoelettronica H della matrice di Fock F,

si trascura la somma poiché contiene integrali tricentrici; il termine rimanente invece viene assunto proporzionale alla sovrapposizione, con una costante di proporzionalità dipendente solo dalla coppia di atomi A e B, coè

H_rs≃〈χ_r∣−½∆+V_A+V_B∣χ_s>=β⁰_ABS_rs.

Utilizzando tutte queste approssimazioni, gli elementi della matrice di Fock assumono la seguente forma:

dove

U_rr=〈χ_r∣−½∆+V_A∣χ_r>,

mentre

rappresenta la popolazione elettronica totale associata con l'atomo A. Una volta fissati i valori dei parametri γ, β⁰ e V, il calcolo viene portato avanti iterativamente, partendo da una matrice approssimata C⁽⁰⁾ per i coefficienti MOLCAO (necessari per il calcolo delle popolazioni atomiche e orbitaliche) fino a raggiungere la convergenza. L'energia totale viene infine calcolata mediante l'espressione

Con questo metodo sono state ottenute funzioni d'onda approssimate per un numero notevole di molecole di piccole e medie dimensioni con risultati che, vista la crudezza delle approssimazioni introdotte, possono essere considerati ragionevolmente soddisfacenti. Il metodo si è dimostrato discretamente valido per un primo approccio al problema della previsione della geometria molecolare più stabile.

5. Problemi aperti e conclusioni.

Quanto è stato sin qui esposto sinteticamente mostra come la teoria del legame chimico abbia raggiunto, in via di principio, gli scopi cui si era accennato nelle prime pagine, anche se la sua applicazione si è dimostrata efficace sinora (per ragioni tecniche di calcolo) solo per molecole di piccole dimensioni. Molti problemi, tuttavia, restano aperti; tra questi, per esempio: a) miglioramento delle funzioni d'onda molecolari oltre il limite HF; b) previsione degli stati eccitati molecolari, che sono coinvolti in tutta la spettroscopia del visibile e dell'UV e sono inoltre di particolare importanza nelle reazioni fotochimiche; c) studio delle forze intermolecolari che intervengono nel corso delle collisioni non reattive tra molecole (studiate sperimentalmente con tecniche di raggi molecolari) e che sono importanti per le proprietà dei gas sotto alte pressioni; d) interazioni molecolari reattive; e) sistemazione coerente e rigorosa della teoria dei legami nei composti di coordinazione e metallorganici; f) adsorbimento fisico e chimico alle interfacce solido-liquido e solido-gas, importante in particolare per l'attività catalitica; ecc. In mancanza di spazio per un esame esauriente di tutti questi argomenti, accenneremo solo a due dei problemi su elencati, quelli relativi ai punti a) e d).

Come si è visto, il metodo più usato nello studio del legame chimico è quello SCF che, pur fornendo una messe grandissima d'informazioni di ottima precisione per le osservabili associate a operatori monoelettronici, tuttavia fornisce valori non sufficientemente accurati per l'energia. Abbiamo visto che questo difetto è legato all'inadeguatezza delle funzioni d'onda monodeterminantali, che non permettono di tenere conto dell'energia di correlazione elettronica; tale difetto non è molto grave quando si vogliano confrontare grandezze energetiche in serie di molecole simili, ma diventa tale quando sia necessario conoscere (con la precisione chimica di almeno 1 kcal/mole) proprietà quali le energie di dissociazione dei legami o le energie di attivazione nei problemi di reattività chimica. Pertanto, un capitolo ancora completamente aperto è quello della ricerca di un'adeguata metodologia per lo studio dell'energia di correlazione.

Negli ultimi anni sono stati fatti molti tentativi in questa direzione, ma i risultati ottenuti sino a oggi non sono molto incoraggianti in vista della loro applicazione a problemi molecolari di qualche complessità. Molto recentemente, tuttavia, Boys e Handy hanno proposto una tecnica matematica certamente interessante e che apre nuove prospettive alla soluzione del problema (v., per es., la recente rassegna di Handy, 1975). Questi autori partono dall'idea che la funzione d'onda SCF, Ψ^SCF, possa essere considerata una buona approssimazione della vera funzione d'onda molecolare Ψ, e propongono come migliore approssimazione la

Ψ=CΦ, (43)

in cui C=C(r_ij, r_i, r_j) è una funzione correlativa, esplicitamente dipendente dalle distanze interelettroniche, da scegliere in maniera tale che la funzione Φ risulti la più vicina possibile alla Ψ^SCF. Questo metodo, che si ricollega ai classici lavori di Hylleraas per l'atomo di He, di James e Coolidge e, più recentemente, di Kolos e Roothaan per la molecola H₂, non aveva trovato finora utilizzazioni per sistemi contenenti un numero di elettroni n〈2, a causa dell'enorme difficoltà del calcolo di integrali con un numero molto grande di dimensioni che s'incontrano nella più generale funzione di questo tipo.

La (43), sostituita nell'equazione di Schrödinger ℋΨ=EΨ, fornisce ℋCΦ=ECΦ che, moltiplicata a sinistra per C^-1, può essere scritta [C^-1ℋC−E]Φ=0. Quest'ultima equazione, che possiamo chiamare equazione di Schrödinger modificata poiché sostituisce all'operatore hamiltoniano il nuovo operatore C^-1ℋC−, costituisce la base del metodo. È facile vedere che l'energia fornita da questa equazione è espressa da

E=〈Φ∣C^-1ℋC∣Φ>=〈ΦC^-1∣ℋ∣CΦ> (44)

e pertanto il calcolo approssimato di E comporta l'impiego di due differenti funzioni, C^-1Φ e CΦ, a sinistra e a destra rispettivamente dell'operatore hamiltoniano. Per la minimizzazione di questa forma dell'energia è necessario l'uso di una speciale tecnica di calcolo, che dagli autori è stata chiamata ‛bivariazionale'. Ovviamente, se la funzione CΦ soddisfacesse esattamente all'equazione di Schrödinger normale, la C^-1Φ non potrebbe essere una soluzione esatta, in quanto ciò comporterebbe C=C^-1=1; tuttavia Boys e Handy hanno dimostrato che, se la funzione CΦ è sufficientemente accurata, il valore che si ottiene per l'energia dalla (44) è molto buono, anche se la funzione di sinistra C^-1Φ non rappresenta un'altrettanto buona approssimazione di Ψ. La forma scelta da Boys e Handy per la funzione di correlazione è del tipo

in cui D_e e d_p sono coefficienti variazionali. Si può dimostrare che l'ottimizzazione dei fattori monoelettronici

attraverso i parametri d_p, serve a compensare parzialmente le variazioni che altrimenti sarebbe necessario apportare agli orbitali monoelettronici quando la funzione d'onda monodeterminantale Φ è accoppiata con il fattore di correlazione C. Pertanto tali parametri possono essere utilizzati per lasciare il più possibile invariato e vicino alla Ψ^SCF il fattore Φ; infine, la completa ottimizzazione della funzione di correlazione C, attraverso tutti i parametri, assicura che C e C^-1 differiscono tra loro il meno possibile. Possiamo notare che un aspetto molto interessante del metodo ora esaminato è quello di lasciare il più possibile invariata e vicina alla Ψ^SCF la funzione Φ, il che è particolarmente comodo per tutti gli aspetti interpretativi della funzione d'onda, che così restano sostanzi4mente quelli della Ψ^SCF di partenza. Un ulteriore vantaggio del metodo, come dimostrato dagli autori, è che gli integrali necessari per il calcolo non hanno dimensioni superiori a sei. Un elemento negativo del criterio bivariazionale di Boys e Handy è che, contrariamente al metodo variazionale normale, esso non permette di prevedere la banda di errore in cui è contenuta l'energia calcolata rispetto a quella vera. Le prime applicazioni di questo metodo all'atomo di neon (10 elettroni) e alla molecola di LiH (4 elettroni) hanno dimostrato la possibilità concreta di ottenere l'energia entro i limiti della precisione chimica.

Un altro problema di fondo (e forse il problema ‛chiave' della chimica), che è strettamente collegato con la disponibilità di funzioni d'onda accurate, è quello della previsione dei meccanismi e della cinetica delle reazioni chimiche. Si tratta, anche in questo caso, di un capitolo in gran parte aperto, benché le basi teoriche per l'interpretazione della complessa fenomenologia della dinamica delle reazioni chimiche siano da tempo ben note. Per esempio, secondo la teoria del complesso attivato (v. Glasstone e altri, 1941) dovuta a Eyring, Polanyi e altri, la costante di velocità per una reazione bimolecolare in fase gassosa è ricavata da considerazioni termodinamico-statistiche sul sistema costituito dalle due molecole coinvolte nell'atto elementare di reazione. In questa teoria, per la caratterizzazione del processo cinetico che porta da reagenti a prodotti è sufficiente la conoscenza: a) dello ‛stato' delle molecole separate; b) dello ‛stato' del ‛complesso attivato' (di quello ‛stato', cioè, nel quale le due molecole al momento dell'urto si trovano in intimo contatto e costituiscono una specie di supermolecola). Si dimostra infatti che la costante di velocità χ è data dalla relazione

in cui k e h sono rispettivamente le costanti di Boltzmann e di Planck, T la temperatura assoluta, E^???30??? l'energia di attivazione, cioè la differenza di energia tra lo ‛stato' a) e lo ‛stato' b), mentre f_A, f_B e f_A^???30???_B sono le funzioni di partizione relative rispettivamente alle molecole A e B e alla supermolecola labile AB che si forma al momento dell'urto. Come è noto, la funzione di partizione f_A di una specie molecolare A è data da

in cui εi^(A) sono le energie dei suoi livelli energetici e gi^(A) le corrispondenti degenerazioni. Pertanto, per una previsione a priori delle costanti di velocità è indispensabile una conoscenza dettagliata della ipersuperficie dell'energia E(Q₁, Q₂, ..., Q_k, ...) nell'iperspazio definito da tutti i parametri conformazionali, indipendenti, Q_k, dell'insieme delle due molecole. Particolare cura dev'essere rivolta allo studio della zona che caratterizza lo ‛stato' di complesso attivato; infatti, l'ubicazione del punto rappresentativo di tale complesso sulla ipersuperficie fornisce tutti i parametri Q_k^???30??? che caratterizzano la sua geometria (e quindi i momenti d'inerzia, che permettono il calcolo del contributo rotazionale a f_A^???30???_B), mentre le curvature nei piani (E, Q_k), nell'intorno di questo punto, forniscono le costanti di forza che permettono il calcolo dei modi normali di vibrazione del complesso attivato e pertanto del contributo vibrazionale alla funzione di partizione f_A^???30???_B. Contemporaneamente, l'energia di attivazione viene calcolata come differenza tra l'energia del complesso attivato e quella di reagenti a distanza infinita uno dall'altro. Appare abbastanza evidente come il problema di queste interazioni a breve raggio vada affrontato con notevole cura, poiché le costanti di velocità dipendono in modo assai critico dai risultati di un calcolo di questo genere e, in maniera particolarmente sensibile, dalla stima che si può fare dell'energia di attivazione E^???30???.

Bibliografia.

Arrighini, G. P., Guidotti, C., Salvetti, O., SCF Mo's and molecular properties of H₂O, in ‟Journal of chemical physics", 1970, LII, pp. 1037-1041.

Bonaccorsi, R., Scrocco, E., Tomasi, J., Molecular SCF calculations for the ground-state of some three-membered ring molecules, in ‟Journal of chemical physics", 1970, LII, pp. 5270-5284.

Cartmell, E., Fowles, G. W. A., Valency and molecular structure, London 1966.

Coulson, C. A., Valence, Oxford 1961² (tr. it.: La valenza, Bologna 1955).

Glasstone, S., Laidler, K., Eyring, H., The theory of rate processes, New York 1941.

Handy, N. C., Correlated wavefunctions obtained by the variational method and the method of moments, in ‟International Review of Science" (Physical Chemistry series two), 1975, I, pp. 79-106.

Heitler, W., London, F., Wechselwirkung neutraler Atome homöopolare Bindung nach der Quantenmechanik, in ‟Zeitschrift für Physik", 1927, LIV, pp. 455-472.

Hückel, E., Quantentheoretische Beiträge zum Benzolproblem. I. Die Elektronenkonfiguration des Benzols und verwandter Verbindungen, in ‟Zeitschrift für Physik", 1931, LXX, pp. 204-286.

Hückel, E., Quantentheoretische Beiträge zum Benzolproblem. II. Quantentheorie der induzierten Polaritäten, in ‟Zeitschrift für Physik", 1931, LXXII, pp. 310-337.

Hückel, E., Quantentheoretische Beiträge zum Problem der aromatischen und ungesättigten Verbindungen. III, in ‟Zeitschrift für Physik", 1932, LXXVI, pp. 628-648.

Hund, F., Zur Deutung der Molekelspektren. IV, in ‟Zeitschrift für Physik", 1928, LI, pp. 759-795.

Hund, F., Zur Frage der chemischen Bindung, in ‟Zeitschrift für Physik", 1931, LXXIII, pp. 1-30.

Hylleraas, E. A., Neue Berechnung der Energie des Heliums in Grundzustande, sowie des tiefsten Terms von Ortho-Helium, in ‟Zeitschrift für Physik", 1929, LIV, pp. 347-366.

James, H. M., Coolidge, A. S., The ground-state of the hydrogen molecule, in ‟Journal of chemical physics", 1933, I, pp. 825-835.

Kolos, W., Wolniewicz, L., Improved theoretical ground-state energy of the hydrogen molecule, in ‟Journal of chemical physics", 1968, XLIX, pp. 404-410.

Mulliken, R. S., The assignment of quantum numbers for electrons in molecules. I, II, in ‟Physical review", 1928, XXXII, pp. 186-222, 761-772.

Mulliken, R. S., Electronic structures of polyatomic molecules and valence. II. General considerations, in ‟Physical review", 1932, XLI, pp. 49-71.

Murrell, J. N., Kettle, S. F. A., Tedder, J. M., Valence theory, London 1965.

Neumann, D., Moskowitz, J. W., One-electron properties of near-Hartree-Foch wavefunctions. I. Water, in ‟Journal of chemical physics", 1968, IL, pp. 2056-2070.

Pauling, L., The nature of the chemical bond, New York 1960³ (tr. it.: La natura del legame chimico, Roma 1961).

Rauk, A., Allen, L. C., Clementi, E., Electronic structure and inversion barrier of ammonia, in ‟Journal of chemical physics", 1970, LII, pp. 4133-4144.

Roothaan, C. C. J., New developments in molecular orbital theory, in ‟Reviews of modern physics", 1951, XXIII, pp. 69-89.

Weinstein, H., Pauncz, R., Cohen, M., Localized molecular orbitals, in ‟Atomic and molecular physics", 1971, VII, pp. 96-140.