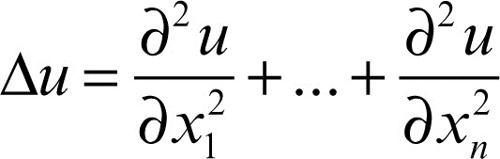laplaciano

laplaciano

laplaciano o operatore di Laplace, denotato solitamente con Δ (o anche con ∇²), associa a una funzione u di n variabili la somma delle sue derivate seconde pure

Per esempio, in tre variabili Δu = u_xx + u_yy + u_zz. Tale operatore corrisponde alla divergenza del gradiente di u: Δu = ∇ ⋅ ∇u, dove ∇ è l’operatore differenziale → nabla; quindi, ∇u indica il gradiente di u ed è un vettore, la cui divergenza è ∇ ⋅ ∇u (si giustifica così la notazione ∇² utilizzata a volte per il laplaciano; → derivata parziale).