La seconda rivoluzione scientifica: matematica e logica. Teoria dei sistemi e controllo

La seconda rivoluzione scientifica: matematica e logica. Teoria dei sistemi e controllo

Teoria dei sistemi e controllo

La teoria del controllo si è formata, come campo di ricerca indipendente, nel corso del XX secolo. Il suo grande sviluppo internazionale è soprattutto un prodotto della seconda metà del Novecento; infatti l'esplosione dell'attività della comunità scientifica internazionale in questo campo si verificò nei due decenni successivi alla guerra, quando, in seguito agli sforzi comuni dei ricercatori e delle istituzioni di vari paesi, furono poste le basi di quella che ora si chiama teoria classica del controllo automatico. Per capire tutto ciò che è stato creato in quegli anni e nei successivi è necessario conoscere la preistoria della teoria del controllo, che risale all'Ottocento, e lo sviluppo di questi studi agli inizi del XX secolo.

Lo sviluppo della teoria del controllo automatico nell'Ottocento

Il primo lavoro scientifico nel quale si usò un metodo matematico per analizzare l'interazione di un controllore e di un oggetto controllato (in termini moderni, un sistema chiuso da un feedback) fu l'articolo di George B. Airy (1801-1892) On the regulator of the clock-work for the effecting uniform movements of equatoriales (1840, 1850-51). Lavorando con un telescopio che seguiva automaticamente una stella sotto osservazione, Airy aveva notato che il regolatore centrifugo accoppiato con il tubo, che ruotava per mezzo di un peso attaccato, qualche volta assicurava una rotazione uniforme ma spesso generava oscillazioni che rendevano impossibile seguire la stella. Cercando la causa dell'instabilità del meccanismo, Airy dedusse le equazioni del moto del tubo e del regolatore ma, avendo ottenuto complicate equazioni non lineari, invece di linearizzarle, determinò una soluzione approssimata per mezzo di lunghi calcoli, simili a quelli della teoria delle perturbazioni in astronomia. Airy fu, tuttavia, il primo a capire il ruolo dell'attrito in un processo di controllo e inventò uno speciale dispositivo di freno, uno smorzatore idraulico, che svolse un ruolo importante nella successiva elaborazione della teoria del controllo automatico.

Durante la seconda metà del XIX sec. soltanto in Inghilterra furono usate più di 75.000 macchine a vapore, controllate dai semplici controllori centrifughi di Watt, e spesso si verificarono disturbi della stabilità del sistema 'macchina a vapore-controllore'. Le riviste di quegli anni erano ricche di descrizioni di questi casi e di appelli a investigare la natura di tale fenomeno, che ostacolava il progresso dell'industria. Nel 1868 il grande fisico inglese James C. Maxwell (1831-1879) pubblicò un articolo intitolato On governors nel quale per la prima volta formulava le equazioni del moto; inoltre Maxwell le linearizzò considerando piccole oscillazioni dalla posizione di equilibrio. Egli mostrò che i problemi connessi con la stabilità del sistema 'macchina a vapore-controllore' si riducono all'analisi di equazioni differenziali ordinarie del terzo ordine a coefficienti costanti, mentre per la stabilità del moto occorre analizzare la posizione rispetto all'asse immaginario delle radici delle corrispondenti equazioni caratteristiche. Per le equazioni del terzo ordine Maxwell risolse facilmente il problema, scoprì le condizioni di stabilità e, prevedendo in modo geniale gli sviluppi scientifici in questo campo, notò di non essere in grado di determinare le condizioni per equazioni di grado superiore al terzo auspicando che questi problemi attraessero i matematici. Il 23 gennaio del 1868 egli sollevò tale questione in una seduta della London Mathematical Society. Il problema fu risolto nel 1877 da Edward J. Routh (1831-1907) in Advanced part of the dinamics of the sistems of rigid bodies e il suo criterio, detto di Routh, è ancora largamente utilizzato nella letteratura sulla teoria del controllo automatico. Il lavoro di Maxwell non diede però una soluzione al problema ingegneristico e non risolse le difficoltà che sorgevano nell'industria perché, avendo preso in considerazione controllori che ora si definiscono astatici (laddove in pratica erano usati dappertutto controllori statici), nella deduzione delle equazioni delle macchine Maxwell aveva trattato quella che oggi è chiamata regolazione intrinseca, trascurabile nei dispositivi di quei tempi. Questo problema fu di nuovo formulato da Ivan Aleksandrovič Wyšnegradskij (1831-1895) partendo da equazioni più adeguate alle condizioni reali (Wyšnegradskij 1876, 1877).

L'effetto della regolazione intrinseca fu eliminato dall'analisi di Wyšnegradskij e nell'equazione del controllore (statico invece che astatico) venne preso in considerazione l'effetto di attrito viscoso. Le equazioni risultanti descrivevano più precisamente la situazione dei controllori industriali di quel periodo. In seguito, dopo aver letto e citato il lavoro di Maxwell, Wyšnegradskij linearizzò le equazioni per mezzo di una transizione alle piccole oscillazioni, ottenendo così un'equazione caratteristica di terzo grado e stabilendo facilmente le condizioni per le quali tutte le radici sono situate sulla sinistra dell'asse immaginario, in modo tale da assicurare la stabilità. Queste condizioni fornivano indicazioni concrete (introduzione di un regolatore, impiego di meccanismi statici nel controllo diretto, ecc.) che permettevano agli ingegneri di risolvere il problema del controllo automatico e dei dispositivi di potenza nell'industria.

I brillanti risultati scientifici di Aurel Stodola (1859-1942) alla fine del XIX sec. portarono a compimento questo indirizzo di ricerca (Stodola 1893, 1899). Partendo dal lavoro di Wyšnegradskij, Stodola studiò la stabilità di un sistema complesso che includeva varie turbine, controllori e tubature intermedie. Questi problemi erano già stati affrontati da Henri Léauté (1885), ma Stodola fu il primo a pensare di linearizzare le loro equazioni e mostrò la validità delle previsioni di Maxwell; il problema generale del controllo automatico fu per la prima volta ridotto a quello di studiare le radici delle equazioni non di terzo grado ma di grado arbitrario. Non avendo informazioni sul lavoro di Routh, Stodola si rivolse al suo collega Adolf Hurwitz (1859-1919), chiedendogli di individuare le condizioni in base alle quali le radici di equazioni algebriche di grado arbitrario sono situate, nel piano complesso, sulla sinistra dell'asse immaginario (Hurwitz 1895). Applicando un teorema di Charles Hermite, Hurwitz trovò un elegante criterio, ancora oggi in uso nella teoria del controllo automatico, chiamato qualche volta, con onestà storica, criterio di Routh-Hurwitz. Il nome di Stodola è connesso con una scoperta più importante: studiando i controllori degli aerei americani di quel periodo, nei quali la posizione del manicotto era influenzata sia dalle forze di inerzia centrifughe, dipendenti dalla velocità angolare controllata, sia dalle forze di inerzia tangenti, dipendenti dalla accelerazione angolare, Stodola scoprì l'effetto dell'azione della compensazione derivativa, che avrebbe svolto un ruolo importante nei successivi sviluppi della teoria del controllo automatico.

All'inizio del XX sec. si era compreso che le equazioni differenziali costituiscono uno strumento adeguato per l'analisi di controllo. Era stato dimostrato che il problema della stabilità di un sistema si riduce allo studio dell'equazione dell'approssimazione lineare e quindi, in definitiva, all'analisi delle posizioni sul piano complesso delle radici dell'equazione caratteristica ed erano stati formulati anche criteri di stabilità tuttora usati.

Teoria del controllo automatico nei primi decenni del Novecento

La possibilità di usare un modello matematico nei problemi tecnici di controllo dei motori, apparentemente assai complicata e di difficile formalizzazione, colpiva l'immaginazione. Nei primi decenni del XX sec. non si ebbero ulteriori sviluppi della teoria matematica del controllo automatico, piuttosto chiarimenti e perfezionamenti dei risultati ottenuti.

Dal 1920 al 1940 la teoria del controllo si sviluppò non tanto 'in profondità', quanto, piuttosto, 'in ampiezza'. I risultati e i metodi utilizzati per il controllo dei motori furono gradualmente applicati ad altri settori. Negli anni Venti furono pubblicati lavori riguardanti il controllo di processi di calore e fu riscoperto il fenomeno della regolazione intrinseca che, già noto a Maxwell e non particolarmente importante nei problemi di controllo delle macchine, divenne centrale nei problemi di controllo del calore. La teoria del controllo di motori elettrici e la teoria delle navi autopilotate e dei piloti automatici ebbero uno sviluppo graduale, tuttavia ognuno di questi problemi fu considerato come nuovo, non connesso con gli altri e studiato da zero, conservando in tal modo lo schema elaborato nel XIX sec.: si ricavavano le equazioni differenziali dell'oggetto controllato e del controllore, le si linearizzava e si studiavano le radici dell'equazione caratteristica. Tuttavia, in contrasto con gli studi del XIX sec., l'attenzione degli scienziati si rivolse sempre di più non soltanto alla stabilità ma anche all'analisi del processo di controllo per l'approssimazione lineare, ossia alla stima della deviazione massima possibile delle coordinate del sistema durante il processo transiente, del tempo necessario per lo stabilirsi dell'equilibrio e di altri parametri che caratterizzano il processo transiente nel sistema connesso oggetto-controllore. La comprensione da parte della comunità scientifica dei problemi di controllo in altri settori è un frutto del periodo successivo alla guerra.

Un solo problema dovrebbe essere messo particolarmente in evidenza: la valutazione delle pure forze di attrito, governate dalla legge di Coulomb, nelle equazioni del moto del controllore centrifugo. La forza di questo attrito è una funzione discontinua a tratti e tenerne conto era in quegli anni un difficile problema non lineare. Nei primi decenni del XX sec. apparvero articoli nei quali si tentava di considerare l'effetto dell'attrito di Coulomb conservando lo schema di Maxwell-Wyšnegradskij-Stodola. Un modello matematico opportuno non era ancora disponibile e pertanto gli autori ottennero risultati estremamente parziali oppure ridussero il problema a un complesso calcolo numerico. Tuttavia il valore di questi lavori è grande, in quanto per la prima volta venivano messe in luce l'importanza e la difficoltà dei problemi di controllo non lineari.

Con l'avvento dei metodi di frequenza furono raggiunte negli anni Trenta nuove frontiere nella teoria del controllo automatico. I fondamenti di questi metodi furono stabiliti nel 1932 nella Regeneration theory di Harry Nyquist (1889-1976). In questi anni prebellici venne pubblicato un lavoro di Aleksandr Vasil′evič Michailov (Michailov 1938), non adeguatamente apprezzato dai contemporanei, che successivamente svolse un ruolo considerevole nello sviluppo della teoria del controllo. In esso Michailov suggeriva nuove idee nell'applicazione dei metodi di frequenza alla teoria del controllo e ai circuiti logici e, ancora più importante, per la prima volta considerava il 'controllo in generale' come un nuovo ramo della scienza e non come teoria del controllo di qualche oggetto concreto.

Le basi della teoria classica del controllo automatico

fig. 2

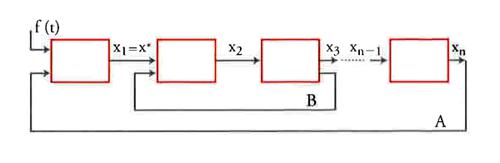
La grande esperienza accumulata nel XIX sec. e nei decenni iniziali del XX nell'analisi di sistemi di controllo specifici (di macchine a vapore, di turbine idrauliche e a vapore, di generatori elettrici e motori, di piloti automatici, ecc.) permise di individuare alcune caratteristiche comuni derivanti dalla struttura delle equazioni dell'approssimazione lineare. Si comprese che lo studio di tutti questi sistemi si riduce all'analisi di uno schema che può essere rappresentato come in fig. 2. In questo schema ogni grado di libertà del sistema è associato a uno specifico blocco ed è descritto, in accordo con le equazioni di Lagrange e la loro analisi elettrodinamica, da un'equazione differenziale lineare di grado non superiore al secondo. Ogni elemento dello schema agisce sul successivo praticamente senza azione inversa, in analogia con le servo-connessioni di Winfried Oppelet (Oppelet 1949), e l'ultimo elemento agisce sul primo, realizzando così il principale dei feedback (indicato con A nella fig. 2); ci possono essere anche uno o più feedback interni (indicati con B nella fig. 2). Deve essere considerato fondamentale il fatto che la trasformata di Laplace e la trasformata di Fourier sono strumenti adeguati per l'analisi di questi schemi, ossia per l'analisi dei corrispondenti sistemi di equazioni lineari.

Il passaggio dalle variabili alle loro trasformate di Laplace permette di definire la nozione di funzione di trasferimento di un elemento come il rapporto tra la trasformata di Laplace dell'azione in ingresso e la trasformata di Laplace dell'azione in uscita dall'elemento. Per analogia si può introdurre la nozione di funzione di trasferimento di un sistema aperto (come il sistema nella fig. 2 con il feedback A disconnesso) e di funzione di trasferimento di un sistema chiuso sul quale agiscano forze esterne. Come risultato si ha che la funzione di trasferimento del sistema può essere facilmente individuata mediante un'operazione algebrica a partire dalla funzione di trasferimento degli elementi, e che la conoscenza della funzione di trasferimento è sufficiente per valutare tanto la stabilità del sistema quanto le più importanti proprietà specifiche del processo che avviene in esso.

In modo simile, l'uso della trasformata di Fourier permette di convertire le equazioni differenziali linearizzate del sistema nelle corrispondenti equazioni definite nel dominio spettrale e di introdurre la nozione di frequenza caratteristica sia di ogni elemento del sistema, sia del sistema chiuso e aperto considerato come un tutto unico. Fu così possibile definire una specifica algebra di circuito le cui basi furono poste nell'articolo di Michailov.

Di conseguenza, alla fine degli anni Quaranta del XX sec. la teoria del controllo automatico non era più soltanto una collezione di esempi per l'analisi di problemi pratici ed era stato delineato chiaramente l'oggetto del suo studio, ossia lo schema strutturale del tipo mostrato nella fig. 2, indipendentemente dallo specifico ambito di applicazione. Furono inoltre definiti il modello matematico e il linguaggio idonei allo studio di questi sistemi, e quest'ultimo fu denominato linguaggio delle funzioni di trasferimento e delle frequenze caratteristiche di un sistema.

Tutti i successivi sviluppi, negli anni Cinquanta e Sessanta del XX sec., della teoria del controllo automatico e della teoria dei sistemi linearizzati furono connessi con l'uso di questo apparato matematico. Lo scopo delle ricerche fu quello di determinare le condizioni di stabilità e le caratteristiche del processo transiente importanti per le applicazioni tecniche, senza risolvere le equazioni differenziali. L'insieme di queste caratteristiche fu denominato qualità del controllo. Le ricerche di quegli anni furono così condotte in tre direzioni: valutazione della stabilità, stima della qualità del controllo e analisi di alcuni problemi specifici dei sistemi di controllo linearizzati.

Valutazione della stabilità del sistema

Nel lavoro già citato, Michailov propose, in alternativa ai criteri di Routh-Hurwitz, l'uso di una curva appositamente costruita nel piano complesso sulla base della funzione di trasferimento del sistema: l'odografo di Michailov.

Risultò che tramite la forma dell'odografo è possibile determinare le condizioni necessarie e sufficienti per la stabilità del sistema di controllo linearizzato. Quasi indipendentemente i metodi di frequenza vennero sviluppati da Nyquist, e giustamente il criterio di stabilità basato sulla forma dell'odografo, ossia il criterio fase-ampiezza, è chiamato criterio di Nyquist-Michailov.

Sviluppando questa idea, Jurij Isaakovič Neimark (Neimark 1947, 1948) formulò la teoria delle cosiddette D-partizioni, le quali rappresentano la trasformazione conforme dell'asse immaginario che sta nel piano dei poli della funzione di trasferimento (o, equivalentemente, nel piano delle radici della equazione caratteristica del sistema linearizzato di equazioni differenziali) nel piano di uno o due parametri complessi, i quali entrano in modo lineare nell'equazione differenziale.

Il metodo della D-partizione venne elaborato nel dettaglio e quindi largamente adottato. Tuttavia, i suoi successivi sviluppi hanno incontrato una difficoltà fondamentale: i parametri di un sistema reale sono quelli che caratterizzano i suoi elementi e i suoi stati (fig. 2), come per esempio le costanti temporali, i coefficienti di amplificazione degli stati e così via, mentre i coefficienti dell'equazione caratteristica sono funzioni lineari complicate di tali parametri. Questo è il motivo per cui, in un sistema, non è sempre possibile scegliere due parametri indipendenti e, inoltre, i coefficienti dell'equazione caratteristica di norma non sono mutuamente indipendenti.

Sorse anche il problema della stabilità strutturale del sistema di controllo linearizzato, ossia dell'individuazione di condizioni necessarie e sufficienti per un sistema con una struttura definita (del tipo della fig. 2) affinché sia reso stabile da una scelta dei parametri dei suoi elementi. Questo problema fu formulato e completamente risolto da Mark Aronovič Aizerman (Aizerman 1948) per i sistemi con ciclo singolo, ossia per i sistemi, mostrati in fig. 2, senza feedback interno del tipo B e con un numero arbitrario di elementi. Per i sistemi di questo tipo fu dimostrato un teorema importante sul valore critico del coefficiente di amplificazione: si trovò che per ogni sistema con ciclo singolo esiste un valore critico K_cr del coefficiente di amplificazione tale che il sistema è stabile per ogni K⟨K_cr positivo e non lo è per ogni K>K_cr. Venne alla luce tuttavia che più è piccolo K, più è grande l'errore statico del sistema (ossia la deviazione da zero delle coordinate controllate); fu così individuata una incompatibilità tra l'errore statico del controllo e la stabilità.

Qualità del processo di controllo

La nozione di qualità del processo di controllo riguarda l'insieme di certi parametri caratteristici delle corrispondenti equazioni differenziali lineari (per es., lo schema in fig. 2) nel caso in cui su alcuni elementi dello schema stia agendo una forza esterna, espressa da una funzione nota del tempo, per esempio la funzione di Heaviside unitaria. Questi parametri sono: l'errore statico, il tempo t_s necessario per fissare l'errore statico, la deviazione massima delle coordinate controllate durante il processo transiente, la monotonicità del processo transiente e così via. Per stimare questi parametri senza ricorrere all'integrazione delle equazioni differenziali del processo vengono utilizzati i tre metodi già citati, consistenti nella valutazione della stabilità a partire, rispettivamente, dall'esame della posizione nel piano complesso degli zeri e dei poli della funzione di trasferimento, dalla considerazione della forma delle frequenze caratteristiche del sistema e dalle cosiddette stime integrali.

In caso di stabilità, tutti i poli della funzione di trasferimento sono sulla sinistra dell'asse immaginario. La distanza del primo polo dall'asse immaginario, chiamata 'grado di stabilità', permette di stimare indirettamente il tempo di stabilizzazione del processo transiente. Il valore del minimo angolo nel piano complesso con vertice nell'origine delle coordinate e bisettrice il semiasse reale negativo, comprendente nella sua area tutti i poli della funzione di trasferimento, permette di stimare la deviazione massima del processo transiente, detta overshoot nelle applicazioni tecniche. L'analisi di questi metodi indiretti di stima ha consentito la messa a punto del metodo dell'odografo delle radici, secondo il quale non viene studiata la posizione nel piano complesso dei poli e degli zeri della funzione di trasferimento per assegnati valori dei parametri, bensì gli odografi delle radici, ossia le curve che queste descrivono al variare di alcuni parametri, dai quali si deduce il coefficiente di amplificazione all'interno di limiti assegnati.

Un altro indirizzo è connesso con la stima dei parametri del processo transiente a partire dalla forma delle frequenze caratteristiche del sistema, la quale permette di valutare molte proprietà del processo transiente. Inoltre applicando l'idea fondamentale dell'integrale di Fourier, si può costruire il processo transiente in un sistema linearizzato di ordine arbitrario per mezzo di un'integrazione sull'asse reale.

Il metodo delle stime integrali è correlato con il fatto che in un sistema linearizzato arbitrario l'integrale rispetto al tempo del processo transiente della variabile controllata, o della sua deviazione quadratica, o anche di alcune variabili connesse con la forma quadratica del processo, può esser calcolato per mezzo delle frequenze caratteristiche senza conoscere i parametri del processo transiente stesso. Contemporaneamente stime integrali dettagliate forniscono importanti informazioni sulle deviazioni della variabile controllata nel corso del processo transiente.

A parte tutte queste idee, ma strettamente in connessione con l'analisi delle equazioni, rimane il problema dell'invarianza del sistema di controllo automatico.

Si supponga che la variabile controllata sia l'output del primo stato del circuito (indicato da x* in fig. 2) e che allo stesso sia applicata, oltre al feedback A, un'azione esterna f(t) funzione del tempo t. Dopo aver eliminato nel modo usuale tutte le altre variabili (passando alla trasformata di Laplace questa eliminazione diviene una semplice operazione algebrica), si ottiene un'equazione differenziale ordinaria:

[1] D(p)x*=K(p)f(t),

dove p=d/dt è l'operatore di derivazione rispetto a t e D(p) e K(p) sono polinomi con coefficienti costanti; il grado del polinomio K(p) è inferiore a quello del polinomio D(p).

Georgij Vladimirovič Šipanov già negli anni Trenta aveva dimostrato che i parametri del feedback del sistema possono essere scelti in modo che tutti i coefficienti del polinomio K(p) siano rappresentati da differenze di valori indipendenti dal tempo, e quindi siano tutti nulli; ciò riduce l'equazione [1] a:

[2] D(p)x*=0.

Nella [2], che rappresenta il caso di oscillazioni forzate, x* è uguale a zero indipendentemente da f(t). Tale risultato causò un acceso dibattito negli anni successivi alla guerra, e i sistemi costruiti su questo principio ricevettero il nome di sistemi invarianti. La paradossalità della situazione consiste nel fatto che x*=0 è possibile solo se la deviazione da zero della funzione f(t) è compensata dal feedback che però, a sua volta, entra in azione solo quando x*½0.

La soluzione di questo paradosso fu rinviata di molti anni e soltanto alla fine del XX sec. è stato chiarito che i sistemi invarianti di tale tipo non sono 'robusti' dal momento che perdono stabilità in corrispondenza di una qualunque piccola alterazione dei loro parametri.

Un altro approccio al problema dell'invarianza è stato suggerito da Viktor Sergeevič Kulebakin (1891-1970) (Kulebakin 1949). Considerata l'equazione

[3] K(p)Z=0

si può vedere che se nella [1] si assume f(t) uguale alla soluzione z(t) della [3], allora il secondo membro della stessa equazione diviene zero e sorge una nuova equazione invariante. È evidente che se le radici dell'equazione caratteristica K(p)=0 differiscono in modo sensibile le une dalle altre, la classe delle funzioni z(t) che sono soluzioni della [3] è sufficientemente ampia, e fornisce una classe di equazioni per la quale questo metodo assicura l'invarianza.

Problemi non lineari di controllo automatico

L'elaborazione della teoria dei sistemi di controllo linearizzati fu facilitata sia perché la soluzione generale può essere facilmente scritta esplicitamente sia perché esiste un'adeguata analisi mediante le trasformate di Laplace e di Fourier. Piuttosto diversa è la situazione con i problemi non lineari nei quali le equazioni differenziali degli stati (fig. 2), e perciò dell'intero sistema, non possono essere linearizzate mediante transizione a piccole oscillazioni intorno allo stato di equilibrio considerato. Determinare non soltanto la soluzione generale, ma anche soluzioni periodiche o altri attrattori, risulta un problema complesso che non sempre si è in grado di risolvere. La teoria dei problemi lineari di controllo automatico si è affermata sulla base di un graduale superamento di queste difficoltà.

Gli scienziati hanno incontrato problemi non lineari fin dal XIX sec., quando, studiando i controllori centrifughi di motori a vapore e turbine, sorse la necessità di prendere in considerazione l'attrito secco. La caratteristica fisica di questo attrito è la discontinuità e tale proprietà causa arresti ('zone di insensibilità') del manicotto del controllore in alcune fasi del moto. Wyšnegradskij trascurò l'attrito secco cosicché il suo lavoro è stato oggetto di critiche. L'influenza di tale attrito sui processi di controllo fu ulteriormente analizzata da diversi ricercatori, ma ha comportato per lungo tempo complessi calcoli numerici. Aleksandr Aleksandrovič Andronov (1901-1952) insieme ai suoi collaboratori, elaborò un significato del termine 'soluzione generale' di un problema non lineare. Per Andronov ciò significava individuare nei problemi studiati ogni possibile struttura topologica dello spazio delle fasi, considerando tutti i possibili attrattori, le superfici separatrici, la loro mutua posizione e così via, nonché la partizione dello spazio dei parametri del sistema in domini, ognuno dei quali corrisponde a una concreta struttura topologica dello spazio delle fasi. Per problemi classici sull'attrito secco e per altri più complessi problemi lineari a tratti, tali soluzioni generali furono ottenute con l'invenzione del 'metodo della mappa puntuale' (Andronov 1956). Secondo questo metodo in ogni dominio dello spazio delle fasi nel quale la caratteristica non lineare non abbia discontinuità, le traiettorie di fase realizzano una mappa puntuale di un iperpiano in un altro che diviene l'oggetto da studiare.

Un modo del tutto diverso di analizzare i sistemi non lineari è connesso con l'applicazione di vari metodi, per i quali, nel caso dei problemi di controllo, Lev Semenovič Gol′dfarb (Gol′dfarb 1940) ottenne una forma semplice di costruzione grafica usando la frequenza caratteristica della parte lineare del sistema e una caratteristica speciale disegnata per l'elemento non lineare. Il metodo di Gol′dfarb fu ripreso ampiamente nella letteratura perché permetteva di trovare facilmente gli stati periodici (i cicli limite di Poincaré) e in certi casi di valutare la loro stabilità. L'applicazione di tutti questi metodi alla teoria del controllo automatico si fonda in una certa misura sull'ipotesi che il sistema considerato differisca in maniera trascurabile dal sistema che ha una soluzione periodica nota. Tale ipotesi, spesso adeguata per problemi di meccanica ed elettronica, in generale non è verificata nei problemi di controllo. Il fatto che il metodo di Gol′dfarb porti a risultati ragionevoli si deve a un'altra ipotesi per il controllo dei sistemi, la cosiddetta 'ipotesi di filtro'.

Le difficoltà connesse con la ricerca della soluzione generale di problemi non lineari portò in maniera naturale a individuare una classe di problemi per i quali l'enunciato stesso del problema sembrava più semplice e completamente ragionevole.

fig. 3

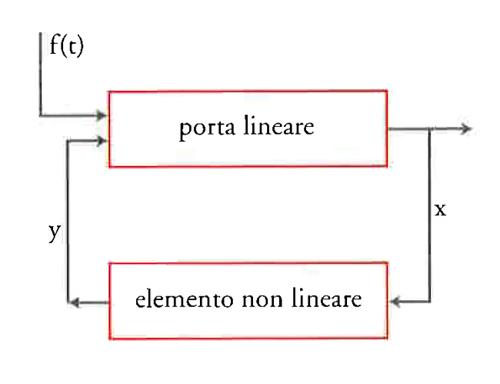
Nella fig. 3 è mostrato un sistema che consiste di una parte lineare arbitraria, descritta dall'equazione

[4] D(p)x=K(p)y

e chiusa da un feedback non lineare stazionario

[5] y=f(x),

o non stazionario

[6] y=f(t,x).

Sotto la semplice ipotesi y=kx, nei sistemi di questo tipo si può tracciare un raggio che parte dall'origine delle coordinate, tale che per ogni k all'interno dell'angolo delimitato dal raggio e dall'asse delle ascisse, il corrispondente sistema lineare sia stabile. Sorse la domanda: è vero che mediante la sostituzione di y=kx con y=f(x) o con y=f(t,x), sotto l'ipotesi che tale feedback non lineare, stazionario o no, si mantenga all'interno dell'angolo suddetto, lo spazio delle fasi del corrispondente sistema non lineare è topologicamente equivalente allo spazio delle fasi di un sistema lineare stabile, contenente soltanto un attrattore all'origine delle coordinate (un punto singolare) e che da ogni punto dello spazio delle fasi, preso come punto iniziale, la traiettoria tende a questo attrattore? Tali sistemi sono stati detti assolutamente stabili.

Apparve chiaro che per i sistemi del secondo ordine questo è vero con la sola eccezione delle traiettorie che tendono asintoticamente al raggio, tuttavia per i sistemi di ordine superiore sono stati trovati controesempi. Un progresso fu ottenuto in quest'area con l'uso delle funzioni di Aleksandr Michajlovič Ljapunov (1857-1918). Si è dimostrato che le forme quadratiche delle funzioni di Ljapunov determinano un angolo sufficientemente ampio tale da assicurare stabilità assoluta.

Nel 1951 Anatolij Isakovič Lur′e suggerì l'uso della funzione di Ljapunov alla cui forma quadratica si doveva sommare l'integrale del feedback non lineare f(x) o f(t,x). Ciò non di meno in questo modo fu soltanto ottenuto un ampliamento dell'angolo che garantisce la stabilità assoluta. Nel 1960, al I Congresso IFAC lo scienziato rumeno Viktor Nikolaevič Popov (Popov 1966) riportò un risultato inaspettato: si può determinare una funzione analoga alla frequenza caratteristica della parte lineare del sistema, la conoscenza della quale è sufficiente a individuare l'angolo che garantisce la stabilità assoluta. Inoltre, Popov dimostrò che in tal modo si può determinare l'angolo entro il quale la stabilità è assicurata dalla funzione di Ljapunov espressa in una forma quadratica arbitraria oppure anche nella forma di Lur′e.

Approccio variazionale ai problemi di controllo

In tutti i lavori appena descritti l'azione esterna f(t) sul 'primo elemento' del sistema, cioè sull'oggetto da controllare (fig. 2), è considerata come un carico o un 'rumore' e lo scopo del controllore (cioè della chiusura del sistema mediante un feedback) come un modo per compensare questa azione o, in altre parole, per mantenere, per quanto possibile, la deviazione della variabile di controllo nell'intorno del valore zero.

Una formulazione diversa del problema sorse nei primi anni del dopoguerra principalmente in connessione con problemi di ingegneria militare (controllo dei primi missili a reazione, radar, sistemi di rilevamento e puntamento in artiglieria, e così via.).

L'azione f(t) nello schema in fig. 2 viene considerata adesso non come un carico o un rumore, ma come un'azione di controllo nel senso stretto del termine. Il suo scopo è portare la coordinata x^* da un valore a un altro in un modo in qualche maniera ottimale. Le equazioni differenziali del sistema, sia non lineari sia lineari, vengono considerate come vincoli ed è soltanto tra le loro soluzioni che bisogna ricercare la curva estremale del problema. Oltre a ciò si possono aggiungere ulteriori vincoli espressi da uguaglianze o disuguaglianze sui valori delle coordinate x (un tipico esempio è costituito dai vincoli sulle coordinate di fase). Come funzionale che raggiunge il massimo o minimo valore sulla curva estremale si usa l'integrale rispetto al tempo di funzioni del tipo F[x(t),f(t)]. All'inizio problemi come questi furono enunciati non nei casi generali di controllo, ma per alcune situazioni particolari descritte da funzionali di forma ovvia. Così, per esempio, Aleksandr Jakovlevič Lerner enunciò il problema di trasporto di un sistema da uno stato a un altro nel minor tempo possibile (Lerner 1954). Questo problema fu per molti aspetti esteso da Hsue-Shen Tsien (Tsien 1954) ma soltanto Aleksandr Aronovič Fel′dbaum (1948a e b, 1953) ne colse tutta la generalità, tentando di risolverlo prima che alcuni matematici riuscissero a ottenere l'elegante soluzione che in tutto il mondo è nota come principio del massimo di Pontrjagin (1961).

Indipendentemente da questi risultati della scuola russa Richard E. Bellmann (che lavorava alla Rand Corporation) aveva proposto già da qualche tempo l'uso del metodo variazionale per un problema di allocazione di risorse leggermente diverso. Ben presto Bellmann comprese che era in gioco l'enunciazione del problema del controllo in termini variazionali generali; egli riuscì a elaborare un suo metodo per la soluzione di problemi impostati in questo modo, metodo che fu poi chiamato 'di programmazione dinamica'. Il lavoro di Bellmann stimolò la pubblicazione di un gran numero di articoli da parte di molti autori di diversi paesi e procurò grande popolarità sia al metodo di programmazione dinamica, sia all'enunciato variazionale del problema del controllo.

Lev Il′ič Rozoner, che era stato il primo a pubblicare una dimostrazione del principio del massimo di Pontrjagin, si accorse della profonda analogia tra tale principio e il metodo di programmazione dinamica di Bellmann, da un lato, e le equazioni di Hamilton-Jacobi dall'altro. Dopo il suo lavoro molti aspetti del problema furono definitivamente chiariti e i successivi sviluppi della teoria del controllo ottimale si sono intimamente legati con le tecniche del calcolo delle variazioni e con la ricerca di nuove e diverse aree di applicazione dei problemi di ottimizzazione.