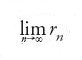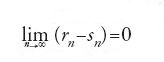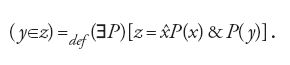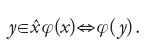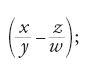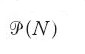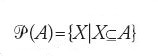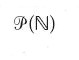La seconda rivoluzione scientifica: matematica e logica. Le scuole di filosofia della matematica
La seconda rivoluzione scientifica: matematica e logica. Le scuole di filosofia della matematica
Le scuole di filosofia della matematica
I più importanti programmi di fondazione della matematica che si affermarono nella prima parte del Novecento emersero come risposta agli sviluppi della matematica e della logica nell'ultima parte del secolo precedente. Il primo di questi programmi, il cosiddetto logicismo, intendeva ridurre la matematica a principî puramente logici.
In seguito alla notevole fioritura della matematica nei secc. XVII e XVIII, l'attenzione verso le questioni di rigore, di chiarificazione concettuale e di esposizione e organizzazione sistematiche si era molto accresciuta. In particolare, l'uso problematico degli infinitesimi e delle somme e prodotti infiniti nell'analisi venne eliminato a favore di un'utilizzazione rigorosa del concetto di limite per i numeri reali e per i numeri complessi. Inoltre, a quest'ultimo sistema fu dato un solido fondamento con la riduzione al sistema dei numeri reali, rappresentando x+yi, dove x e y sono reali, mediante la coppia (x,y), con adeguate definizioni di 'addizione' e 'moltiplicazione' di tali coppie.
Il processo di riduzione fece un sostanziale passo in avanti, indipendentemente, con Georg Cantor (1845-1918) e con Richard Dedekind (1831-1916), mediante la costruzione dei numeri reali a partire dal sistema dei numeri razionali. Cantor rappresentò i numeri reali come limiti di successioni di numeri razionali, e Dedekind li interpretò in termini di estremo superiore (oppure di estremo inferiore) di sottoinsiemi di razionali. Infine, Leopold Kronecker (1823-1891) definì i numeri razionali partendo dal sistema degli interi positivi (1,2,3,…) oppure, alternativamente, dal sistema dei numeri naturali (0,1,2,…).
Il processo generale di riduzione: i contributi di Dedekind, Peano e Cantor
Ciascun passo nel processo riduttivo consisteva nel rimpiazzare gli oggetti di un sistema numerico S con rappresentazioni di essi costruite a partire da oggetti di un sistema più basilare S0, in cui queste combinazioni vengono considerate identiche quando rappresentano lo stesso oggetto appartenente a S. Per esempio, la definizione di Kronecker dei numeri razionali positivi con le coppie ordinate (n,m), dove n,m sono interi positivi, rappresenta n/m, e identifica (n,m) con (p,q) se e solo se n/m=p/q, ossia nq=mp. La rappresentazione di Cantor dei numeri reali prende una successione di numeri razionali r=(r0,…,rn,…) per rappresentare
quando r soddisfa il criterio (interno) di convergenza di Cauchy; allora r=(r0,…,rn,…) è 'identificata' con s=(s0,…,sn,…) quando
dove quest'ultimo limite viene definito usando soltanto i numeri razionali.
Se si guardano le riduzioni successive dai numeri complessi passando per i reali fino ai numeri naturali, si vede che certe nozioni generali quali quelle di coppia, insieme (o classe), successione, relazione, operazione (o funzione), e così via, costituiscono i componenti principali nella costruzione di ciascun sistema a partire da uno più basilare. Queste nozioni sono fondamentali per tutta la matematica e, a seconda del punto di vista, possono essere considerate di natura insiemistica o logica. Con l'opera di Cantor, Dedekind e Giuseppe Peano (1858-1932), verso la fine del XIX sec. risultò chiaro che poteva essere compiuta una riduzione 'finale', definendo il sistema dei numeri naturali esclusivamente mediante tali nozioni più basilari. Il contributo di Dedekind e Peano in questa direzione fu quello di fornire una caratterizzazione assiomatica del sistema dei numeri naturali (rispettivamente, nel 1888 e nel 1889). Nella concezione di Peano, l'insieme ℕ è dato (I) da un elemento 'speciale' 0 e (II) da una operazione di successore, sc, dove sc(x) è interpretato come x+1 per ogni x (benché tale operazione preceda la definizione di '+' e di '1', e non sia scritta in questa forma). Gli assiomi inoltre stabiliscono che (III) 0 non è successore di alcun numero naturale, (IV) sc è un'operazione iniettiva da ℕ a ℕ, e (V) ℕ è il più piccolo insieme che contiene 0 ed è chiuso rispetto al successore. Un po' più formalmente, usando i simboli '∈' per 'è membro di' e '⇒' per 'implica', gli assiomi di Peano sono:
I 0∈ℕ
II x∈ℕ⇒sc(x)∈ℕ
III x∈ℕ⇒sc(x)≠0
IV x∈ℕ∧y∈ℕ & sc(x)=sc(y)⇒x=y
V Se X è un qualsiasi sottoinsieme di ℕ tale che 0∈X e (x∈X⇒sc(x)∈X) per ogni x, allora X contiene tutti gli elementi di ℕ.
L'ultimo assioma, il V, è alla base delle dimostrazioni per induzione su ℕ: per mostrare che una proprietà P(x) vale per ogni x∈ℕ, è sufficiente mostrare che vale P(0) e che P(x)⇒P(sc(x)) per ogni x (si prenda X come l'insieme di tutti gli x∈ℕ per i quali valga P(x)). Dedekind applicò l'induzione per giustificare le definizioni ricorsive in ℕ, con le quali viene determinata una funzione F su ℕ fissando F(0) e dicendo come F(sc(x)) è definito in termini di F(x) per ogni x. La utilizzò inoltre per mostrare che gli assiomi per ℕ sono categorici, cioè che se ℕ,0,sc e ℕ′,0′,sc′, sono due qualsiasi realizzazioni di I-V, allora esse sono isomorfe: si ottiene la richiesta corrispondenza biunivoca x→x′ prendendo F(0)=0′ e F(sc(x))=sc′(F(x)), così che x′=F(x) per ogni x∈ℕ.
Ciò che gli assiomi di Peano (o di Dedekind) non garantiscono è l'esistenza di qualche loro realizzazione (o 'modello'). Dedekind argomentò a sostegno di questa esistenza considerando l'infinità (potenziale) degli oggetti del (suo) pensiero, dove il successore di un oggetto x è il pensiero che x può essere un oggetto del (suo) pensiero. Tuttavia, questa bizzarra interpretazione psicologica non venne accettata da altri matematici. Di fatto, una costruzione più matematica era già disponibile grazie alla teoria degli insiemi di Cantor, elaborata in una notevole serie di scritti che vanno dal 1874 al 1897.
Il principale contributo di Cantor consiste nella coerente estensione a insiemi arbitrari (finiti o infiniti) delle nozioni di numero ordinale e di numero cardinale. La prima di queste nozioni è usata per rispondere a questioni del tipo: "come sono disposti gli elementi di un insieme in un suo dato (buon) ordinamento?". La seconda nozione è usata per rispondere alla domanda: "quanti elementi ha un insieme X?", che a sua volta è strettamente correlata alla questione: "quando due insiemi X e Y hanno lo stesso numero di elementi?". La risposta che dà Cantor è in termini della relazione di equivalenza insiemistica '∼', dove si definisce che X∼Y quando esiste una corrispondenza biunivoca tra gli elementi di X e quelli di Y. Cantor afferma allora che a ciascun insieme X è associato il suo numero cardinale, card(X), in modo tale che due insiemi hanno lo stesso cardinale proprio quando essi sono equivalenti in questo senso, cioè card(X)=card(Y) se e solo se X∼Y. Egli concepiva card(X) come ottenuto da un doppio processo di astrazione da X, astraendo prima dalla natura dei singoli elementi mentre stanno in un dato ordine, e poi da qualsiasi ordine; per questo motivo, usava
per denotare card(X). Tuttavia, questi processi di astrazione erano spiegati soltanto vagamente, e non specificò niente di più su come card(X) potesse essere rappresentato in termini di oggetti o nozioni più basilari.
Se si accetta l'associazione di un numero cardinale card(X) a ciascun insieme X in una qualche maniera che soddisfi la condizione sopra esposta per l'uguaglianza di cardinali, si presentano varie strade per poter definire insiemisticamente un modello degli assiomi di Peano. In uno di questi si definisce 0 come il cardinale dell'insieme vuoto. Poi, per il successore, dato x=card(X), si prende sc(x)=card(X′) dove X′ è ottenuto da X aggiungendo esattamente un nuovo elemento (questa definizione è problematica se viene ammesso un insieme 'universale' X che consiste di tutti gli oggetti; ma, in tal caso, si può rimpiazzare X con un insieme Y tale che X∼Y, dove Y non è universale). Infine, ℕ può essere definito come il più piccolo insieme che contiene 0 e che è chiuso per l'operazione di successore, cioè
[1] x∈ℕ=def∀X[0∈X&∀y(y∈X⇒sc(y)∈X)⇒x∈X].
Questa definizione soddisfa immediatamente l'assioma di induzione V, e gli altri assiomi I-IV per 0 e sc sono facilmente verificati.
Il programma logicista di Frege
Per completare la riduzione 'finale' del sistema dei numeri naturali, bisognava ancora dare una definizione di numero cardinale in termini di più basilari nozioni insiemistiche o logiche. Gottlob Frege (1848-1925) e Bertrand Russell (1872-1970) la fornirono entro un più vasto programma 'logicista' di riduzione della matematica a principî logici (per Frege, tale riduzione doveva includere l'aritmetica e l'analisi, ma non la geometria; per Russell doveva comprendere tutta la matematica pura). Entrambi condividevano l'idea di definire card(X) come la classe di equivalenza [X] di X nella relazione ∼ fra insiemi, cioè
[2] card(X)=def la classe di tutti gli insiemi Y tali che X∼Y.
Si deve notare che qui le nozioni di 'insieme' e 'classe' sono usate in maniera intercambiabile (mentre esse vengono distinte nelle teorie moderne degli insiemi e delle classi).
Per procurarsi l'opportuno quadro concettuale e per eseguire rigorosamente il suo programma, Frege cominciò sviluppando un nuovo sistema di logica simbolica che presentò nella sua monografia Begriffsschrift, eine der arithmetischen nachgebildete Formelsprache des reinen Denkens (Notazione concettuale, un linguaggio formale del pensiero puro modellato su quello dell'aritmetica, 1879). Esso andava molto al di là della sillogistica aristotelica e della logica delle classi e delle relazioni (dovuta a Boole, DeMorgan, Peirce e Schröder). In termini tecnici moderni, la logica di Frege era un calcolo dei predicati del secondo ordine, che utilizzava negazione, implicazione e quantificatore universale come operatori logici di base, e conteneva un sistema completo per il calcolo proposizionale e dei predicati del primo ordine. Questi divennero contributi permanenti per la logica moderna, benché in un simbolismo differente da quello proposto da Frege, il quale usava uno scomodo sistema ideografico di notazione. Il moderno simbolismo logico discende invece dall'opera di Russell che a sua volta sviluppò quella di Peano.
Le variabili del primo ordine, o individuali, nel sistema di Frege variano su tutti gli oggetti dell'universo, siano essi concreti o astratti, e quindi anche su tutti gli oggetti della matematica. Le variabili del secondo ordine variano invece su arbitrari predicati o proprietà (o 'concetti', nella terminologia di Frege) così come su arbitrarie relazioni (predicati con più di un argomento).
Frege assume che ciascuna funzione proposizionale φ(x) del suo sistema determina una proprietà P che vale per qualunque x proprio quando φ(x) è vera. Questo è ciò che oggi viene chiamato 'assioma di comprensione per le proprietà'
[3] ∃P∀x[P(x)⇔φ(x)],
dove '∃' sta per 'esiste', '∀' per 'per ogni', '⇔' per 'se e solo se', e dove la variabile predicativa 'P' non compare in φ. In secondo luogo, ciascuna funzione proposizionale φ(x) determina una classe
(scritta {x∣φ(x)} in un simbolismo più moderno), che è la sua estensione (o Wertverlauf, nella terminologia di Frege), e due funzioni φ(x) e ψ(x) determinano la stessa classe proprio nel caso in cui esse sono coestensive, ossia, l'assioma di estensionalità è assunto per le classi nella forma
Infine, si suppone che le classi siano oggetti matematici e quindi appartenenti all'universo degli individui. La teoria delle classi può essere interpretata nel sistema di Frege, introducendo la relazione di appartenenza tra individui e classi esplicitamente con la seguente definizione:
Segue da tali principî che si ha un assioma di comprensione per classi, nella forma
Frege portò a termine il suo programma di fondazione logica dell'aritmetica nelle opere Die Grundlagen der Arithmetik (I fondamenti dell'aritmetica, 1884) e Grundgesetze der Arithmetik (Leggi fondamentali dell'aritmetica, 1893-1903). La sua definizione di equinumerosità dei predicati, P∼Q, è equivalente alla definizione di Cantor per le classi a essi associate,
Allora, il 'numero degli x tali che P(x)', in simboli NxP(x), viene definito come la classe delle estensioni delle Q tali che P∼Q; che nel sistema di Frege svolge il ruolo di card(X) per
Su questa base, si può procedere a definire 0, sc e ℕ proprio come si è fatto per gli insiemi.
Nonostante la grande cura che Frege dedicò al proprio quadro concettuale, la precisione con cui eseguì le sue deduzioni, e nonostante l'apparente plausibilità del suo programma, il sistema era viziato nei suoi fondamenti. Russell, nel 1901, dimostrò infatti che era contraddittorio e comunicò la scoperta in una lettera a Frege nel 1902. Il paradosso di Russell è ottenuto semplicemente formando la classe
Così, per l'assioma di comprensione per le classi, abbiamo
[8] ∀x[x∈r⇔x∉x]
e, in particolare,
[9] r∈r⇔r∉r,
che dà luogo immediatamente a una contraddizione.
Frege ricevette la lettera di Russell mentre il secondo volume dei Grundgesetze era in stampa, e fece in tempo ad aggiungere un'appendice che conteneva il paradosso di Russell. Egli suggerì anche, frettolosamente, che una restrizione dell'assioma di estensionalità potesse servire a evitarlo; ma, successivamente, la 'via di uscita' di Frege si rivelò inefficace. In ogni caso, il piano di Frege per il suo programma logicista venne totalmente sconvolto; egli non scrisse mai il terzo volume dei Grundgesetze finendo con l'abbandonare il suo progetto.
Il programma logicista di Russell
Nell'elaborazione del programma logicista, Russell fu influenzato principalmente dalle opere di Cantor e di Peano: dal primo attraverso la sua teoria delle classi; dal secondo mediante la sua logica simbolica. Russell aveva incontrato Peano nel 1900 e fu colpito dalla precisione del suo approccio. Russell elaborò la propria sintesi delle idee di Cantor e di Peano, che apparve nel 1903 nel libro The principles of mathematics. Egli intendeva dimostrare che tutta la matematica pura tratta concetti definibili a partire da un numero molto piccolo di concetti logici fondamentali, e che tutte le sue verità sono deducibili da un numero molto piccolo di principî logici fondamentali, un programma successivamente riassunto nella tesi secondo la quale 'la matematica e la logica sono identiche'. Tuttavia, l'opera del 1903 non è presentata in un simbolismo logico, nonostante il carattere tecnico di concetti, principî e argomenti adoperati, è invece esposta nel linguaggio ordinario per un pubblico generale filosofico e matematico. Il piano di Russell era quello di portare a termine un secondo volume nel quale sarebbero stati elaborati tutti i dettagli del programma; esso doveva avere come coautore il suo maestro, il matematico e filosofo Alfred North Whitehead (1861-1947) e doveva essere 'rivolto esclusivamente ai matematici'. Nel corso della preparazione della pubblicazione dei Principles Russell venne a conoscenza dell'opera di Frege e riconobbe che questi aveva largamente anticipato la sua; di fatto, egli aveva preso visione dei Grundlagen der Arithmetik, ma affermò che "[...] a causa della grande difficoltà del simbolismo [di Frege], non ero riuscito a coglierne l'importanza o a comprenderne il contenuto". Russell aggiunse quindi un'appendice A al suo volume, intitolata The logical and arithmetical doctrines of Frege.
Fu così che mentre stava ultimando i Principles Russell si dedicò ai problemi sollevati dai paradossi o antinomie della teoria delle classi. Non era il primo: fra gli altri, Cesare Burali-Forti (1861-1931) aveva pubblicato nel 1897 il paradosso del massimo numero ordinale e Cantor aveva scritto a Dedekind nel 1899 sul paradosso del massimo numero cardinale. Russell era a conoscenza di entrambi, e proprio durante il processo di analisi del paradosso di Cantor al fine di isolarne la difficoltà cruciale giunse al suo paradosso della classe di tutte le classi che non appartengono a sé stesse. Infatti, rispetto alle precedenti antinomie, il paradosso di Russell era decisamente più semplice e più incisivo, privo come è di nozioni o argomentazioni speciali.
Considerando il proprio paradosso, Russell riconobbe ‒ in contrasto con Frege ‒ che il punto cruciale del problema riguardava l'uso incondizionato dell'assioma di comprensione, in base al quale ciascuna proprietà φ(x) determina una classe
di tutti gli oggetti x che soddisfano φ. Nell'appendice B a The principles of mathematics Russell fece il suo primo tentativo di soluzione delle contraddizioni, sotto il titolo The doctrine of types. Questa impone che ogni funzione proposizionale φ(x) abbia in anticipo un campo di significato, il 'tipo' della sua variabile x, e che le questioni della sua verità o falsità abbiano senso solo all'interno di tale 'tipo'. In un adeguato ordinamento dei tipi, poi, il tipo di una classe è maggiore del tipo di ogni argomento x, e per questa ragione non avrebbe senso domandarsi se x∈x. Così, in accordo con questa linea di ragionamento, non hanno senso né la proprietà φ(x)=(x∈x) né la sua negazione (x∉x).
Russell introdusse poi il termine 'predicativo' per distinguere le proprietà φ(x) che determinano classi da quelle ‒ chiamate impredicative ‒ che non le determinano, ma non ebbe un atteggiamento costante riguardo ai criteri opportuni per distinguere in ciascun caso tra proprietà predicative e proprietà impredicative. Fra il 1903 e il 1908 affrontò questo problema e considerò seriamente una varietà di soluzioni oltre a quella dell'uso delle distinzioni di tipo, e fra esse la cosiddetta teoria 'senza classi'. Nello stesso periodo, egli stava anche parando gli attacchi che Jules-Henri Poincaré (1854-1912) portava all'intero programma logicista. Ironicamente, fu combinando il principio del circolo vizioso di Poincaré per l'analisi e la soluzione delle antinomie con la dottrina dei tipi e la teoria senza classi che Russell alla fine optò per il proprio approccio nell'articolo Mathematical logic as based on the theory of types (1908), vero punto di riferimento.
L'attenzione di Poincaré si indirizzava al cosiddetto 'paradosso di Richard' del 1905 (dovuto a Jules Richard), che riguardava non le classi ma una nozione incondizionata di definibilità. Nei suoi scritti sul tema dei paradossi nel 1906 e negli anni successivi, Poincaré vedeva la fonte della difficoltà sempre nella presenza di un circolo vizioso. In base alla sua analisi, in ciascuno di quei casi c'è una presunta definizione di un oggetto in termini che fanno implicitamente riferimento all'oggetto stesso; per esempio, nel caso del paradosso di Richard la definizione è quella di un certo numero reale in termini della totalità di tutti i numeri reali definibili, mentre nel paradosso di Burali-Forti essa è quella del massimo ordinale in termini della totalità di tutti gli ordinali. Adottando la terminologia di Russell per questa analisi più specifica, Poincaré chiamava 'predicative' quelle definizioni che non comportano un circolo vizioso e 'impredicative' quelle che lo comportano e che devono dunque essere bandite. Russell, nel suo articolo del 1908, bandì come Poincaré le definizioni impredicative dalla sua formulazione del principio del circolo vizioso: "Nessuna totalità può contenere membri definiti [soltanto] in termini di essa" elaborando una versione modificata della dottrina dei tipi (tipi ramificati), più complicata di quella originariamente concepita e orientata a includere la teoria senza classi.
Russell dovette avanzare altre ipotesi problematiche, e cioè il cosiddetto 'assioma dell'infinito' e l'assioma della scelta. Il primo, per il quale esistono infiniti individui, è necessario per assicurarsi che ciascun numero cardinale finito abbia un successore. Il secondo era emerso nell'ambito della teoria degli insiemi come necessario al fine di stabilire molti risultati nell'aritmetica dei cardinali transfiniti; esso asserisce la possibilità di scelte simultanee da una collezione arbitraria di insiemi non vuoti, anche quando non viene precisato alcun modo di definire tali scelte.
L'elaborazione dettagliata di questo programma logicista ampiamente modificato, delineato nell'articolo di Russell del 1908, venne svolta nell'opera monumentale di Whitehead e Russell, Principia mathematica, pubblicata in tre volumi nel periodo 1910-1913. Il nome di Whitehead fu messo per primo, come autore più anziano, ed egli di certo contribuì molto alla sua stesura, ma il piano complessivo e la maggior parte dello scritto furono di Russell. Questo lavoro è ciò che era stato inizialmente previsto come secondo volume dei Principles of mathematics. Benché il passaggio dai Principles ai Principia avesse richiesto l'esplicita introduzione di ipotesi (quali l'assioma di riducibilità, l'assioma dell'infinito e l'assioma di scelta) il cui statuto logico era dubbio, Russell asseriva ancora, molti anni dopo, nella sua introduzione alla seconda edizione dei Principles: "Non ho mai trovato ragione di modificare la tesi fondamentale delle pagine seguenti, e cioè che matematica e logica siano identiche". Tuttavia, in questo campo Russell non ha trovato quasi nessun seguace, e il suo straordinario sforzo di salvare il programma logicista viene generalmente ritenuto un fallimento.
Sebbene molti dei dettagli concreti del lavoro svolto nei Principia mathematica e la sua risposta alla questione ‒ cos'è la matematica? ‒ non abbiano conservato il loro valore, tale opera ebbe un impatto enorme. Ciò che i Principia mostrarono fu la possibilità di definire molte nozioni matematiche in precisi termini simbolici basandosi su un numero assai esiguo di nozioni basilari e di svolgere ampie argomentazioni matematiche in una forma completamente rigorosa, passo dopo passo, a partire da pochissimi principî e regole deduttive fondamentali. Che sia o no giustificata la tesi che la matematica è logica, l'esercizio dei Principia mathematica penetrava certamente fino alle radici logiche della matematica ed estendeva a tutte le sue parti l'ideale di rigore formale il cui precedente esemplare era stato quello della geometria euclidea, due millenni prima.
Predicativismo: Poincaré e Weyl
Poincaré, uno dei principali matematici del suo tempo, è generalmente considerato il precursore sia del programma predicativista sia di quello intuizionista sui fondamenti della matematica. Famoso per i suoi prolifici contributi in tutte le branche della matematica, ma specialmente in analisi e in fisica matematica, Poincaré scrisse anche molti libri e saggi divulgativi sulla filosofia della scienza e della matematica in uno stile brillante e vivace. Nei suoi scritti sulla filosofia della matematica ‒ dal 1893 fino alla morte ‒ Poincaré si interessò più del ruolo dell'intuizione che di quello della logica. In particolare, egli riteneva che il sistema dei numeri naturali fosse direttamente comprensibile e che il principio di dimostrazione per induzione fosse sanzionato dall'intuizione e non richiedesse una riduzione a qualcosa di più basilare. A partire dal 1905, avviò un attacco incessante ai programmi insiemistici e logici per la fondazione della matematica, e specialmente al programma logicista, non vedendo alcun bisogno di ridurre la nozione di numero naturale a concetti logici.
L'attacco di Poincaré alla teoria degli insiemi poggiava su una concezione della natura della matematica fondamentalmente opposta a quella di Cantor. Secondo Poincaré tutte le nozioni matematiche hanno la loro fonte nell'intuizione o sono ottenute da essa mediante definizione esplicita. Gli oggetti matematici non hanno un'esistenza platonica indipendente, come sembra si debba richiedere per giustificare i principî insiemistici, e in particolare non ci sono totalità infinite. Con questa filosofia 'definizionista' della matematica, Poincaré arrivò alla sua analisi dei paradossi e alla proscrizione delle definizioni impredicative: bisogna fare attenzione a distinguere definizioni apparenti da quelle che lo sono realmente. Le definizioni impredicative si caratterizzano per il fatto che pretendono di isolare un oggetto da una totalità facendo riferimento in modo essenziale (o esplicitamente o implicitamente) a quella totalità. Se questo procedimento è concepito come la 'creazione' di un tale oggetto mediante una definizione, si viola il requisito che il definiens debba, in tutti i suoi aspetti, essere precedente al definiendum.
Poincaré non elaborò le sue idee in maniera sistematica; in particolare, egli non scrisse niente sulla scelta di un simbolismo o della logica del ragionamento matematico. Il programma predicativista sviluppò la sua filosofia definizionista senza farsi problemi sulla logica coinvolta, assumendo cioè il classico calcolo dei predicati. Il programma intuizionista sostenne con più forza le sue tesi sull'origine soggettiva della matematica e abbandonò la logica della verità e della falsità in favore di una logica di ciò che può essere stabilito con metodi costruttivi, intuitivamente evidenti.
Il successivo progresso sostanziale nel programma predicativista venne compiuto da Hermann Weyl (1885-1955) nel 1918 con la monografia Das Kontinuum (Il continuo). Matematico della scuola di Hilbert, Weyl coltivò anche un durevole interesse per la filosofia della scienza e della matematica, ma l'opera del 1918 fu la sua unica incursione 'tecnica' nel campo dei fondamenti. Sembra che egli fosse arrivato a una posizione predicativista indipendentemente da Poincaré e da Russell. Come Poincaré e diversamente da Russell, Weyl accettava come basilari il sistema dei numeri naturali e i principî a esso associati di dimostrazione per induzione e di definizione ricorsiva. Attribuiva a Russell la formulazione del principio del circolo vizioso, mentre citava le 'osservazioni molto incerte' di Poincaré al riguardo delle definizioni impredicative. D'altro canto, Weyl affermava che un 'vero abisso' lo separava da Russell e dal suo tentativo di definire i numeri naturali come classi di equivalenza tramite la relazione di equinumerosità e la sua assunzione dell'assioma di riducibilità.
Secondo Weyl, il primo compito essenziale era quello di capire quanta analisi matematica si potesse sviluppare su una base strettamente predicativa, dati i numeri naturali. Poiché il sistema dei numeri razionali può essere ridotto al sistema dei numeri naturali, e poiché il 'continuo' dei numeri reali può essere identificato con successioni o insiemi di numeri razionali (secondo il metodo di Cantor o di Dedekind), i principî appropriati da considerare sono quelli che governano gli insiemi o le successioni di numeri naturali. Così, Weyl edificò in Das Kontinuum un sistema assiomatico del secondo ordine le cui variabili di tipo 0 vengono interpretate come varianti sui numeri naturali, e quelle di tipo 1 come varianti su insiemi (relazioni, funzioni), definibili predicativamente, di numeri naturali. Tuttavia, diversamente da Russell, egli non ramificò gli oggetti di tipo 1 in livelli, poiché si rese conto che ciò l'avrebbe portato a difficoltà simili a quelle con cui Russell si era precedentemente scontrato.
Di fatto, il sistema assiomatico di Weyl non è conforme ai moderni requisiti di formalizzazione ed emergono varie ambiguità quando si tenta di ricostruirlo in questi termini.
Poiché Weyl assume nel suo sistema la logica classica, la quantificazione sui numeri naturali è considerata come determinata in maniera vero-funzionale. Ciò potrebbe essere considerata un'accettazione implicita dell'insieme ℕ dei numeri naturali come una totalità infinita completa (contrariamente a Poincaré). Tuttavia nel sistema di Weyl non c'è nessuna ammissione, implicita o esplicita, di una totalità completa dei sottoinsiemi di ℕ, contrariamente alla teoria cantoriana degli insiemi.
I numeri razionali sono introdotti nel sistema di Weyl come 4-ple di numeri naturali (x,y,z,w), con y≠0 e w≠0, che rappresentano
ed esse sono dette 'uguali' sotto la relazione di equivalenza che ci si aspetta. Per i numeri reali si considerano le sezioni di Dedekind nei numeri razionali ℚ, cioè particolari insiemi di tali 4-ple. Grazie alla corrispondenza biunivoca tra ℚ e ℕ, i numeri reali corrispondono a certi sottoinsiemi di ℕ. Allora, un insieme S di numeri reali è dato da una proprietà che corrisponde a una proprietà φ(Y) di sottoinsiemi Y di ℕ. Ora, l'estremo superiore di S (quando è superiormente limitato) è nel modello di Dedekind semplicemente l'unione delle sezioni inferiori che sono membri di S. L'appartenenza in questa unione corrisponde all'appartenenza nell'unione degli insiemi Y che soddisfano φ(Y), cioè deve esistere un insieme X che soddisfa
[11] ∀x[x∈X⇔∃Y(φ(Y) & x∈Y].
Tuttavia, l'esistenza di un tale X non è garantita; e questa è prima facie una definizione del sottoinsieme X di ℕ a partire dalla totalità dei sottoinsiemi di ℕ, quindi è impredicativa, e il suo uso non può essere in generale giustificato nel sistema di Weyl. Poiché l'assioma dell'estremo superiore per i numeri reali è il principio fondamentale dell'analisi, la sua mancanza sembrerebbe costituire un ostacolo insuperabile per il programma predicativista di Weyl riferito all'analisi. Tuttavia, nel suo sistema può essere derivato il principio dell'estremo superiore per le successioni di reali, e ciò risulta sufficiente per molte applicazioni. Infatti, una successione di numeri reali corrisponde a una successione ⟨X0,…,Xn,…⟩ di sottoinsiemi di N, ed è data da un'unica relazione binaria R tale che x∈Xn⇔R(x,n). Allora, l'unione degli insiemi Xn in questa successione è definita da
[12] ∀x[x∈X⇔∃nR(x,n)].
Sulla base di questo principio ristretto dell'estremo superiore, Weyl fu capace di mostrare in Das Kontinuum che l'intera teoria classica delle funzioni continue di numeri reali (che sono determinate interamente dai loro valori sui numeri razionali) può essere sviluppata in una maniera semplice e naturale sulla base del suo sistema. Weyl non mostrò però come sviluppare predicativamente le più moderne teorie dell'integrazione (come quella di Lebesgue) che si applicano a classi molto più ampie di funzioni. Weyl stesso modificò le sue concezioni due anni dopo la pubblicazione di Das Kontinuum, nella direzione dell'approccio, ancora più radicale, dell'intuizionista Luitzen Egbertus Jan Brouwer (1881-1966); ma negli anni successivi divenne pessimista sulle prospettive della rivoluzione di Brouwer, pur mantenendo la sua simpatia verso la filosofia a essa soggiacente. D'altra parte, Weyl non ripudiò mai completamente il suo programma di fondazione predicativista, che continuò a menzionare durante gli anni successivi nei suoi articoli sulla filosofia della matematica.
Gli assiomi di Zermelo per la teoria degli insiemi
Secondo Cantor, due insiemi qualsiasi A e B possono essere confrontati rispetto alla loro cardinalità, cioè card(A)≤card(B) oppure card(B)≤card(A). La sua argomentazione a sostegno di questa proprietà faceva uso del cosiddetto principio del buon ordinamento (BO), per il quale gli elementi di un insieme qualsiasi possono essere disposti in una successione transfinita ⟨X0,X1,…,Xw,Xw+1, ⟩ in cui ciascun sottoinsieme non vuoto ha un primo elemento. Cantor dimostrò anche che per ciascun insieme A c'è un insieme B la cui cardinalità è maggiore di quella di A, cioè card(A)⟨card(B), ed esso è l'insieme di tutti i sottoinsiemi X di A, {X∣X⊆A}. Questo insieme è anche chiamato insieme potenza di A, ed è denotato
Ora, per BO, si ha una successione transfinita completa di cardinali infiniti, per i quali Cantor usava la lettera ebraica ℵ (aleph) con indici 0,1,…,ω,ω+1,…; ℵ0=card(ℕ) è il cardinale di ogni insieme numerabilmente infinito (per es., anche l'insieme dei numeri razionali), e ℵ1 è il più piccolo cardinale non numerabile. Poiché ℵ0<2ℵ0, segue che ℵ1≤2ℵ0. Il numero 2ℵ0 non è soltanto la cardinalità di
ma è anche la cardinalità dell'insieme di tutti i numeri reali (per la loro corrispondenza con i sottoinsiemi dedekindiani dei numeri razionali); così 2ℵ0 è anche detto cardinalità del continuo. Un'immediata questione è se 2ℵ0=ℵ1 è vera; la congettura di Cantor, che così fosse, è detta ipotesi del continuo:
[13] 2ℵ0=ℵ1.
Essa rimane ancor oggi la fondamentale questione irrisolta della teoria cantoriana dei numeri cardinali.
Evidentemente, Cantor dava per scontato che per ogni insieme infinito A l'insieme potenza
sia una totalità definita, con un suo numero cardinale. Inoltre, in base al suo principio del buon ordinamento, ci deve essere qualche maniera di stabilire un buon ordinamento di
compiendo una successione transfinita di scelte arbitrarie di sottoinsiemi di A fino a che non si esaurisce
Non si conosce alcuna procedura per bene ordinare
per non parlare di
quando A è un qualsiasi altro insieme infinito (per es., Formula
o Formula
ecc.). Nonostante molti matematici trovassero intuitive le nozioni e le argomentazioni di Cantor, anche quelli più vicini alle sue idee trovarono problematico il principio del buon ordinamento.
L'apparire dei paradossi insiemistici accrebbe le preoccupazioni intorno alla sicurezza del soggetto, benché si potessero respingere gli insiemi interessati in questi casi (quello di 'tutti gli insiemi', o di 'tutti i cardinali', o di 'tutti gli ordinali'), perché in qualche modo marginali piuttosto che centrali come il continuo. Inoltre, ci fu un gruppo di matematici influenti, a cominciare da Kronecker, che erano estremamente critici verso la teoria cantoriana a causa della sua base 'metafisica', cioè a motivo della filosofia platonica della matematica che essa sottintendeva: si supponeva infatti che gli insiemi fossero entità esistenti indipendentemente dalle costruzioni e definizioni dell'uomo.
Nessuna meraviglia, allora, che nella lista dei ventitré principali problemi non risolti, presentata da David Hilbert (1862-1943) nella sua famosa conferenza al Congresso internazionale dei matematici del 1900, i primi due riguardassero i fondamenti della matematica: precisamente, il problema del continuo e la coerenza di un sistema assiomatico per i numeri reali. Nella sua discussione del I problema, Hilbert affermò di non essere convinto dell'argomentazione sostenuta da Cantor a sostegno del principio del buon ordinamento, e riformulò l'ipotesi del continuo in una maniera che non dipendeva da esso, e precisamente: se S⊆ℝ, e S è infinito, allora S∼ℕ oppure S∼ℝ. Hilbert pensava anche che dovesse esistere una dimostrazione diretta di questo enunciato così importante (il buon ordinamento), dimostrazione che si sarebbe potuta forse ottenere dando effettivamente un buon ordinamento su ℝ.
Nel 1904 Ernst Zermelo (1871-1953) pubblicava un articolo in cui introduceva un nuovo principio chiamato assioma della scelta (AS), dal quale egli dedusse il principio del buon ordinamento. La formulazione che Zermelo diede di AS fu che per ogni insieme A esiste una funzione f sulla collezione di tutti i sottoinsiemi non vuoti di A, che sceglie un elemento di ciascuno di quei sottoinsiemi, cioè f(X)∈X per ciascun sottoinsieme non vuoto di A. In effetti, AS postulava l'esistenza di scelte simultanee che potevano essere usate per le scelte successive richieste al fine di formare un buon ordinamento di A. Un passo, questo, che potrebbe essere giudicato come un progresso soltanto se AS fosse ritenuto più evidente di BO.
L'articolo di Zermelo del 1904 provocò forti critiche, sia perché postulava AS sia perché usava altri concetti e principî insiemistici. Alcuni critici, erroneamente, pensarono che nell'argomentazione di Zermelo fosse presente una forma del paradosso di Burali-Forti. Ma la critica principale ad AS fu questa: si afferma che esiste una funzione f senza alcun metodo disponibile per definirla o costruirla esplicitamente (eccetto per quegli A che sono già ben ordinati). Infatti, si vede facilmente che BO implica AS, dunque si tratta di principî equivalenti. Più tardi, Zermelo trovò una forma modificata, ma equivalente, di AS che appare intuitivamente più chiara. Essa afferma che, se S è una collezione di insiemi disgiunti e non vuoti, allora esiste una funzione f su S che assegna a ciascun X in S un elemento di X; questa forma di AS viene visualizzata più facilmente rispetto a quella originaria, ed è considerata da molti come intuitivamente evidente, nonostante il fatto che non sia costruttiva.
Per rispondere alle varie obiezioni mosse contro AS e per chiarire a quali altri principî insiemistici si facesse riferimento, Zermelo pubblicò nel 1908 il primo sistema assiomatico di teoria degli insiemi. Intuitivamente parlando, l'universo della sua teoria consiste in alcuni oggetti basilari, e in insiemi 'costruiti' a partire da quegli oggetti. Si suppone che gli insiemi esistano indipendentemente dai modi di definirli, e dunque viene assunto l'assioma di estensionalità, cioè ∀A∀B[∀x(x ∈ A⇔x ∈B)⇒A=B]. Gli assiomi di Zermelo asseriscono anche l'esistenza di vari insiemi, quali l'insieme vuoto, e permettono di formare l'unione di due qualsiasi insiemi, A∪B, e l'insieme potenza di ogni insieme,
Viene postulata l'esistenza di un insieme infinito, un A che contiene 0 e che soddisfa ∀ x (x ∈A⇔{x}∈ A); prendendo sc(x)={x}, si può identificare l'insieme ℕ dei numeri naturali con il più piccolo sottoinsieme di A che contiene 0 ed è chiuso rispetto a questa operazione di successore. Più in generale, Zermelo postulò una forma ristretta dell'assioma di comprensione, detta assioma di separazione (Aussonderungsaxiom), il quale dice che, per ogni insieme A e ogni 'proprietà ben definita' P(x) di elementi di A, si può formare il sottoinsieme B di A che consiste esattamente di quegli x∈A che soddisfano P(x); in simboli, B={x∈A∣P(x)}. Un modello informale di questi assiomi fu presentato per la prima volta da Zermelo nel 1930.
Il sistema di Zermelo è 'senza tipi' nel senso che è ragionevole considerare x∈y per oggetti qualsiasi x e y; in particolare, si può porre la questione se x∈x vale. Tuttavia, non c'è una maniera (evidente) di derivare il paradosso di Russell nel suo sistema data la natura ristretta del suo assioma di comprensione, l'assioma di separazione. Da esso si può concludere soltanto che, per ogni insieme A, si può formare l'insieme B={x∈A∣x∉x}; ma in questo caso si deduce soltanto la conclusione perfettamente coerente che B∉A (poiché se B∈A, allora B∈B⇔B∉B). Ne segue che non esiste l'insieme di tutti gli insiemi, nel sistema di Zermelo. In modo simile, non esiste l'insieme di tutti gli ordinali o di tutti i cardinali, e dunque esso è anche al riparo dai paradossi di Burali-Forti e di Cantor. Naturalmente, è pur sempre immaginabile che il sistema assiomatico di Zermelo sia incoerente; quanto abbiamo detto assicura soltanto che le antinomie 'usuali' non producono qui nessuna contraddizione. D'altro canto, non c'è modo nel sistema di Zermelo di trattare i numeri cardinali come classi di equivalenza rispetto a ∼, poiché non si può stabilire l'esistenza dell'insieme di tutti gli insiemi equivalenti a un dato insieme. Nei sistemi assiomatici secondo lo stile di Zermelo si devono quindi prevedere definizioni alternative dei numeri cardinali (e, similmente, dei numeri ordinali).
Successivi miglioramenti e ampliamenti della teoria degli insiemi di Zermelo furono forniti da Thoralf Skolem e Abraham Fraenkel, Paul Bernays e Kurt Gödel. Oggi si parla dunque dei sistemi assiomatici ZF (Zermelo-Fraenkel) e BG (Bernays-Gödel). Con l'aggiunta dell'assioma di scelta, essi forniscono sistemi estremamente flessibili in cui tutta la teoria cantoriana degli insiemi può essere rappresentata senza apparenti contraddizioni. Sotto questo aspetto, essi sono molto superiori alle teorie dei tipi e hanno preso il loro posto come fondamento di quella parte della moderna pratica matematica che fa uso essenziale dei concetti e principî insiemistici.
L'assiomatizzazione di Zermelo e di coloro che l'hanno proseguita mostrò, con una chiarezza mai raggiunta prima, che le fondamenta della teoria degli insiemi erano radicate in una concezione platonista della matematica. I componenti costitutivi di tale teoria incorporano infatti la concezione per cui: (1) gli insiemi sono entità che esistono indipendentemente dai pensieri e costrutti umani, e benché astratti, sono ritenuti parte di una realtà oggettiva, esterna; (2) gli insiemi infiniti quali quelli dei numeri naturali e dei numeri reali sono ritenuti esistenti come oggetti completi, in atto; (3) per ciascun insieme, la totalità dei sottoinsiemi arbitrari di quell'insieme esiste come insieme completo, ben definito; (4) ogni proposizione intorno agli insiemi ha un valore di verità definito (vero o falso), indipendente dai modi con cui noi possiamo verificarlo.
Deve essere notato che l'accettazione della concezione platonista in generale, in base alla quale gli oggetti matematici sono considerati come entità (astratte) esistenti indipendentemente, non è necessariamente legata a qualcuna o a tutte le quattro tesi. È per questa ragione che la loro accettazione è detta platonismo insiemistico. Fra le asserzioni facilmente ammesse da questa posizione, ci sono gli assiomi di estensionalità, dell'infinito, dell'insieme potenza, di separazione e di scelta; inoltre, si accetta in logica la legge del terzo escluso, in base alla quale per qualsiasi proposizione φ o vale φ o vale ¬φ, in simboli φ⋁¬φ. Come abbiamo visto l'uso dell'assioma dell'insieme potenza applicato a ℕ, e l'assioma di separazione per proprietà arbitrarie formulate nel linguaggio della teoria degli insiemi, conducono a conclusioni impredicative. L'accettazione della logica classica incorporata nella legge del terzo escluso porta direttamente a risultati non-costruttivi di esistenza, mediante il metodo di dimostrazione per assurdo. Ciò fu una delle ragioni della critica costruttivista al platonismo insiemistico che portò allo sviluppo di un programma fondazionale che a esso si oppose: l'intuizionismo.
L'intuizionismo di Brouwer
Il primo critico della teoria cantoriana degli insiemi, da un punto di vista costruttivista, fu Kronecker, già maestro di Cantor. Oltre agli insiemi finiti, egli era disposto ad ammettere nella matematica soltanto insiemi infiniti 'in potenza' e, fra essi, soltanto quelli riducibili alla successione dei numeri naturali 0,1,2,…; inoltre, accettava dimostrazioni di esistenza unicamente se costruttive. I suoi durissimi attacchi all'opera di Cantor durante gli ultimi anni del XIX sec. ebbero su questi un effetto personale deleterio. Poincaré fu, come abbiamo già ricordato, un altro critico della teoria degli insiemi e del logicismo, ed è considerato per certi aspetti un precursore dell'intuizionismo, benché non in maniera troppo coerente e sistematica. Più o meno suoi contemporanei furono i cosiddetti 'semiintuizionisti' che, fra gli altri, comprendevano i matematici francesi Émile Borel, René-Louis Baire e Henri-Léon Lebesgue. Essi accettavano insiemi numerabilmente infiniti e l'iterazione transfinita di costruzioni fino al minimo ordinale non numerabile. I semiintuizionisti non accettavano l'assioma di scelta, che era però inevitabilmente presente nella loro matematica in forma più o meno mascherata, e pur pensando che tutte le dimostrazioni di esistenza dovessero essere ottenute con costruzioni o definizioni esplicite, non adottarono restrizioni sulla logica da usare.
Fu il matematico olandese Brouwer che per primo puntò l'attenzione sulla questione della giustificabilità della legge del terzo escluso (LTE) secondo una concezione costruttivista della matematica. Nell'articolo del 1908 The unreliability of logical principles Brouwer sosteneva che la LTE per insiemi infiniti è basata su un'estensione ingiustificata di quel principio valido per insiemi finiti. Nella sua tesi di dottorato del 1907 aveva già insistito sull'origine soggettiva della matematica nell'intuizione umana e sulla necessità di restringere le questioni della verità in matematica a quelle asserzioni che possono essere verificate o confutate. Ovviamente, per un insieme finito A e per una proprietà P decidibile possiamo verificare ∃xP(x)⋁∀x¬P(x) controllando volta per volta ciascun x∈A per vedere se vale o no P(x). In generale non c'è alcuna maniera di eseguire una tale verifica quando A è infinito, anche se P è decidibile.
Dal 1908 al 1913 Brouwer lasciò da parte le questioni fondazionali per dedicarsi alla topologia, nella quale ottenne profondi e importanti risultati. In seguito, dal 1918, Brouwer si impegnò a ricostruire la matematica interamente su basi intuizioniste (termine che egli usava per la sua forma di costruttivismo). Non soltanto la legge del terzo escluso doveva essere rigettata, ma anche tutte le forme di infinito attuale. Per verificare ∃xP(x) quando x varia su un insieme infinito S, si deve davvero produrre qualche a∈S per il quale P(a) è dimostrata; d'altro canto, per verificare ∀xP(x) si deve avere una dimostrazione grazie alla quale, dato un qualsiasi a∈S, si possa fornire una dimostrazione di P(a). Ciò giustifica la dimostrazione per induzione sui numeri naturali: dati P(0) e ∀x(P(x)⇒Psc(x)) ci si rende conto di avere una procedura che, dato un qualsiasi n∈ℕ, stabilisce P(n), dapprima da P(0)⇒P(1), poi da P(1)⇒P(2),…, fino a raggiungere P(n−1)⇒P(n).
Il primo ostacolo per una ricostruzione semplice e lineare della matematica in conformità ai principî intuizionisti si presenta nella teoria dei numeri reali. I numeri reali potrebbero essere identificati con le successioni di Cauchy potenzialmente infinite di numeri razionali; ma che senso avrebbe trattare con successioni 'arbitrarie'? Risulta che, se si restringe l'attenzione proprio a quelle successioni che sono determinate da leggi effettive, appaiono anomalie di ogni genere. Brouwer introdusse invece una nuova concezione, quella delle 'successioni a (libera) scelta', le quali potrebbero essere determinate mediante una serie di libere scelte o di atti casuali, e delle quali si potrebbe avere in ogni stadio soltanto un'informazione parziale e finita (Brouwer era stato anticipato in questa concezione del continuo da Borel). Con i numeri reali concepiti come successioni di Cauchy a scelta, una funzione reale a valori reali può essere determinata usando soltanto una quantità finita di informazioni sul suo argomento, definendo il suo valore con un grado di precisione a piacere. Seguendo questa linea di ragionamento, Brouwer arrivò alla conclusione che ogni siffatta funzione deve essere continua, in contraddizione con l'esistenza classica di funzioni discontinue. Inoltre, Brouwer si trovò costretto a introdurre nozioni non convenzionali e a raggiungere strane conclusioni che, nonostante la sua statura di matematico, furono accolte dalla stragrande maggioranza della comunità matematica con incomprensione e/o rifiuto. Ciononostante, lo studio metamatematico dell'intuizionismo, iniziato dal suo studente e discepolo Arend Heyting (1898-1980), suscitò un successivo sviluppo di altre forme sistematiche di costruttivismo.
Il programma finitista di Hilbert
Quando Hilbert pronunciò il suo intervento dal titolo Mathematische Probleme al Congresso internazionale del 1900, era riconosciuto come uno dei più grandi matematici del suo tempo. Era solo a metà della sua carriera scientifica, eppure aveva già ottenuto fondamentali risultati in algebra, teoria dei numeri, geometria e analisi; negli anni successivi avrebbe dato ulteriori importanti contributi all'analisi, alla fisica matematica e ai fondamenti della matematica.
Come è stato già ricordato, i primi due fra i problemi di Hilbert riguardavano direttamente i fondamenti della matematica. Il programma di Hilbert per stabilire la coerenza dei sistemi assiomatici venne espresso per la prima volta in termini più specifici nel II problema, in cui richiedeva una dimostrazione della coerenza di un sistema d'assiomi per i numeri reali. Ciò aveva la sua origine nel lavoro che Hilbert aveva compiuto negli anni precedenti sui fondamenti assiomatici della geometria. In quel progetto, Hilbert era ritornato agli assiomi di Euclide, dapprima per migliorarli al fine di adeguarli agli standard moderni di rigore, e poi per sollevare nuove questioni metateoriche quali la loro indipendenza e la loro coerenza. Egli dimostrò la coerenza della geometria piana euclidea con la sua interpretazione nel piano cartesiano, data mediante coppie di numeri reali, e della geometria euclidea dello spazio, nel sistema delle coordinate di numeri reali a tre dimensioni.
La richiesta di Hilbert di una dimostrazione della coerenza del sistema dei numeri reali arrivò così come passo successivo a quella per la geometria. La sua formulazione del II problema mostra perché egli la ritenesse necessaria: per lui, la fondazione di una qualsiasi scienza deve fornire un sistema esatto e completo di assiomi; inoltre, un concetto matematico esiste se, e soltanto se, un tale sistema di assiomi può essere mostrato come non contraddittorio. In particolare, "la dimostrazione della compatibilità degli assiomi [per i numeri reali] è al tempo stesso la dimostrazione dell'esistenza matematica del sistema completo dei numeri reali". Ciò che Hilbert in quel momento non forniva era un qualche suggerimento su come si potesse eseguire una tale dimostrazione di non contraddittorietà. Evidentemente, egli credeva che essa sarebbe stata semplice e naturale, e che poi si sarebbe passati a dimostrare l'esistenza delle classi numeriche transfinite di Cantor mediante una dimostrazione di non contraddittorietà, 'proprio come quella del continuo'. Ma in un articolo del 1904 presentò una visione meno ottimistica per questa estensione, in considerazione dei paradossi insiemistici.
Nel corso degli anni successivi, e durante la Prima guerra mondiale, l'attenzione di Hilbert verso questi temi fu in parte distolta dal suo lavoro sulle equazioni integrali e sulla fisica matematica. Egli, tuttavia, ritornò a pubblicare sulle questioni fondazionali con la sua conferenza del 1918 intitolata Axiomatisches Denken (Pensiero assiomatico), dove cominciò a esporre il suo programma, ormai maturo, relativo ai fondamenti della matematica, poi elaborato in una serie di pubblicazioni fino al 1931. Lo scopo ultimo di Hilbert era quello di giustificare l'uso dei concetti e dei metodi cantoriani nella matematica fornendo una dimostrazione della coerenza di un sistema di assiomi per la teoria degli insiemi, secondo lo stile di Zermelo. Hilbert tuttavia era sensibile alle critiche di Kronecker e di Brouwer e si rendeva conto che una vera e propria giustificazione dell'infinito attuale avrebbe dovuto essere basata su metodi dai quali dovevano essere eliminati tutti gli elementi infinitari.
Più in dettaglio, il programma di Hilbert era concepito come segue. Una data parte informale della matematica va rappresentata formalmente in una teoria assiomatica T, specificata con precisione entro un linguaggio formale L. Questo linguaggio deve essere dato mediante alcuni simboli basilari e attraverso regole per costruire da essi le formule ben formate di L come successioni finite di simboli. Alcune di queste formule dovranno poi essere assunte come assiomi, distinguendo quelli che hanno un carattere logico generale e quelli che riguardano il contenuto di T; inoltre, dovranno essere date regole di inferenza per costruire dimostrazioni (o derivazioni) formali dagli assiomi sotto forma di successioni finite di formule. In queste ipotesi, può essere deciso in maniera effettiva, per ciascuna successione finita σ di successioni finite di simboli basilari, e per ciascuna formula φ se σ è o no una dimostrazione di φ. Una volta che una teoria assiomatica formale T è presentata in tale maniera, l'insieme delle formule dimostrabili di T è determinato come quello dei risultati finali di tali dimostrazioni, e T è coerente se nessuna contraddizione formale φ&¬φ è dimostrabile da T. L'asserzione della coerenza di T è puramente 'finitaria', nel senso che si riferisce soltanto a possibili configurazioni finite σ date come successioni finite di termini, ciascuno dei quali è una successione finita di simboli di L. Il programma di Hilbert di ottenere una giustificazione incontrovertibile di una T siffatta richiedeva che la dimostrazione di coerenza di T dovesse essere condotta con metodi esclusivamente finitari.
Oltre a questo programma generale, Hilbert propose anche alcune specifiche tecniche di teoria della dimostrazione per realizzarlo. Nella sua concezione, l'infinito attuale sorge già, nell'aritmetica classica, in formule come ∃xR(x)⋁∀x¬R(x), dove R è decidibile, poiché ciò comporta implicitamente la possibilità di passare in rassegna la totalità dei numeri naturali (proprio come aveva sostenuto Brouwer). Asserzioni puramente finitarie sarebbero quelle della forma R(x) con R decidibile e x variabile aperta (libera), che potrebbero essere verificate per ciascuna istanza R(n) in un dominio di oggetti finiti quali i numeri naturali. L'idea di Hilbert era che una dimostrazione δ di una tale R(x) dovesse in qualche modo essere trasformabile mediante una successiva eliminazione delle asserzioni quantificate in δ, in una dimostrazione δ′ di R(x) in cui tutte le asserzioni sono in questa forma finitaria. L'Ansatz di Hilbert mostrava come ciò poteva essere compiuto in casi relativamente semplici; ma egli lasciò ai suoi assistenti e collaboratori di Gottinga ‒ specialmente a Bernays, Wilhelm Ackermann e John von Neumann ‒ il compito di portare a compimento la Beweistheorie, o teoria della dimostrazione, per il suo programma. L'obiettivo iniziale doveva essere una dimostrazione di coerenza per una versione del primo ordine (PA) dell'aritmetica di Peano. Tuttavia, dopo alcuni passi falsi di Ackermann (che pensò di aver ottenuto una dimostrazione di coerenza non soltanto per PA ma anche per una teoria dell'analisi), von Neumann mostrò che era stata davvero stabilita, con metodi chiaramente finitari, soltanto la coerenza di un frammento di PA.
Non si trattava di una sconfitta temporanea. Ciò emerse nel 1931 dagli sbalorditivi risultati di Gödel in base ai quali se T è una qualsiasi teoria formale, presentata finitariamente e che contiene PA, la consistenza di T non può essere dimostrata con metodi che possano essere formalizzati in T, a meno che T non sia già essa stessa incoerente. Inoltre, sembrava che tutti i metodi finitari, del genere di quelli impiegati nella scuola di Hilbert, potessero facilmente essere formalizzati in PA. Così, senza far intervenire metodi finitari sostanzialmente nuovi che vanno al di là di PA, non si poteva sperare di fornire una dimostrazione finitaria della coerenza di PA (assumendo che PA sia davvero coerente ‒ ciò di cui difficilmente si potrebbe dubitare). Proprio tali metodi furono poi proposti da Gerhard Gentzen (1909-1945) nel 1936, con l'uso dell'induzione transfinita fino a certi ordinali numerabili finitamente descritti, applicata ad asserzioni di forma puramente finitaria. Tuttavia, l'estensione dei metodi finitari operata da Gentzen è controversa e non c'è affatto un accordo generale sul fatto che la sua dimostrazione di coerenza di PA sia conforme ai criteri di Hilbert. A ogni modo, è difficile dubitare della possibilità di formalizzare tutti i metodi finitari in una parte T (relativamente debole) della teoria degli insiemi di Zermelo, e per tale T il teorema di Gödel sulla indimostrabilità della coerenza costituisce un ostacolo definitivo al programma di Hilbert.
Hilbert stesso si rifiutò di ammettere ‒ nella prefazione all'opera Grundlagen der Mathematik (Fondamenti della matematica, 1934) ‒ che i teoremi di Gödel segnassero il fallimento del suo programma. Ma egli doveva già aver preso visione di un altro risultato che sconvolgeva la sua concezione complessiva. Il teorema di Löwenheim-Skolem, stabilito nel 1920, mostrava infatti come ogni teoria T formulata nella logica del primo ordine che ha un modello infinito deve avere un modello numerabile. In tal modo nessuna tale T potrebbe essere un sistema categorico di assiomi per i numeri reali, cioè determinare univocamente il concetto di numero reale a meno di isomorfismo. Per ottenere un sistema categorico di assiomi per i reali si dovrebbero usare assiomi di ordine superiore, essenzialmente infinitari, quali l'asserzione della completezza; ma ciò ci farebbe uscire dal campo dei sistemi assiomatici formali finitari, contrariamente ai requisiti del programma di Hilbert.
Ciò che Hilbert compì con il suo insegnamento sulla logica e sui fondamenti fu la trasformazione finale di questa problematica ‒ il cui scopo iniziale, nelle concezioni di Frege e di Russell, era stato quello di costituire un sistema universale e globale di logica che incorporasse tutta la matematica ‒ in un campo di ricerca in cui gli oggetti di interesse sarebbero stati varie particolari teorie assiomatiche 'locali' T per parti differenti della matematica, da trattare con i metodi matematicamente rigorosi nell'ambito della emergente disciplina chiamata logica matematica o metamatematica. La teoria della dimostrazione iniziata da Hilbert si è sviluppata fino a essere una parte sostanziale e tecnicamente sofisticata della logica matematica, in cui sono state perseguite con successo forme relativizzate del programma di Hilbert.