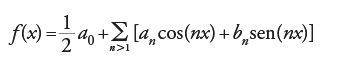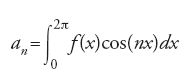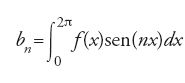La seconda rivoluzione scientifica: matematica e logica. La teoria della misura

La seconda rivoluzione scientifica: matematica e logica. La teoria della misura

La teoria della misura

Con la nozione matematica di misura si vogliono analizzare concetti che si riferiscono al mondo fisico quali la lunghezza, l'area, il volume, la massa, la carica elettrica, e così via. Gli oggetti da misurare sono rappresentati da insiemi e con il termine 'misura' si intende una funzione additiva di insiemi, ossia una funzione che assegna all'unione di due insiemi disgiunti la somma dei valori che essa assegna a ciascuno dei due.

Esempi concreti di misura e di metodi per calcolare la misura di insiemi particolari sono antichi quanto la storia stessa. Una prima teoria fu introdotta dagli antichi greci nell'ambito dello sviluppo del sistema numerico. Nella seconda metà del XVII sec., con il calcolo integrale di Isaac Newton (1643-1727) e Gottfried Wilhelm Leibniz (1646-1716), venne formulata una teoria più sistematica e completa. In tale teoria il grafico di una funzione f è usato per descrivere la frontiera di un insieme la cui misura è l'integrale di f. Il teorema fondamentale del calcolo, che stabilisce una relazione tra l'integrale e la derivata, cioè tra l'area e il tasso di variazione, fornì un nuovo potente strumento per definire e studiare le proprietà della misura.

Nel XIX sec. fu intrapreso da parte di alcuni dei maggiori matematici del tempo un programma di revisione delle nozioni di funzione, continuità, integrale e derivata. Tale programma fu in gran parte motivato dal lavoro di Jean-Baptiste-Joseph Fourier (1768-1830) Théorie analytique de la chaleur, del 1822, in cui si rendeva necessaria l'integrazione di espressioni più complesse rispetto a quelle fino ad allora considerate. Esso condusse, intorno alla metà del secolo, a una definizione generale di integrale da parte di Georg Friedrich Bernhard Riemann (1826-1866), ma anche alla consapevolezza che il teorema fondamentale del calcolo (così come altri teoremi, frequentemente applicati, concernenti lo scambio dell'ordine tra integrazione e passaggio al limite sotto il segno di integrale) non è valido se non sono verificate opportune ipotesi. Tutto ciò condusse anche alla considerazione di insiemi molto più complicati di quelli trattati in precedenza, insiemi che sono descritti non da qualche condizione geometrica intuitiva o fisica, ma, più indirettamente, da alcune espressioni analitiche, come per esempio l'insieme di tutti i punti dove una data funzione non è continua. Di conseguenza, e a causa delle nuove funzioni o dei nuovi insiemi che era necessario trattare, la teoria della misura o dell'integrazione non aveva più la semplicità e la facilità di applicazione dell'impostazione elementare del passato. Il lavoro in quest'area nella seconda metà del XIX sec. ebbe come scopo principale la ricerca di una più adeguata nozione di misura e di integrale al fine di ottenere teoremi più semplici e più potenti.

Solo negli ultimi anni del XIX sec. émile Borel (1871-1956) giunse infine all'introduzione di una nozione di misura sulla retta reale, la quale era destinata a condurre a una teoria fra le più belle e più largamente usate in matematica. Lo sviluppo di questa teoria, dovuto nei suoi stati iniziali principalmente a Henri-Léon Lebesgue (1875-1941), e le sue successive applicazioni a quasi ogni settore dell'analisi e alle maggiori aree della fisica, costituiscono una delle parti più significative della storia della matematica del XX secolo.

La misura e l'integrale di Lebesgue

La misura di Borel

Nel 1898 Borel estese il concetto di lunghezza di un intervallo a quello di una misura definita su una vasta classe di insiemi della retta reale; tale misura possiede proprietà particolarmente utili e per definirla utilizziamo in questo caso le locuzioni 'misura di Borel' e 'insiemi di Borel'. La sua innovativa idea chiave è la nozione di 'additività numerabile'. Una funzione definita su una famiglia di insiemi è 'numerabilmente additiva' se il valore che essa assegna all'unione di una successione infinita di insiemi disgiunti è uguale alla somma dei valori che assegna a ciascuno degli elementi della successione.

Partendo dalla famiglia degli intervalli e dalla funzione che assegna a ogni intervallo la sua lunghezza, Borel procedette ricorsivamente allo scopo di ampliare, passo dopo passo, il dominio di definizione della funzione aggiungendo a ogni stadio insiemi i cui complementari erano già definiti o che erano l'unione di una successione disgiunta di insiemi già definiti. In questo modo si ottiene una famiglia chiusa rispetto alle operazioni di complementazione e di unione numerabile e la misura risultante è numerabilmente additiva. Una qualsiasi famiglia di insiemi in un qualsiasi spazio la quale goda di queste proprietà viene chiamata attualmente 'famiglia di Borel' o 'σ-algebra'.

La misura e l'integrazione di Lebesgue

Nella sua famosa tesi di dottorato Intégrale, longueur, aire, discussa alla Facoltà di Scienze della Sorbona nel 1902, Lebesgue semplificò ed estese la definizione di misura di Borel sviluppando una teoria dell'integrazione e della derivazione sulla quale si basa gran parte dell'analisi contemporanea.

Lebesgue, limitandosi inizialmente a considerare i sottoinsiemi di un intervallo di lunghezza unitaria, dato che un insieme aperto è l'unione di una successione disgiunta di intervalli, definì la misura di un tale insieme come la somma delle lunghezze di questi intervalli. Poiché un insieme chiuso è il complementare di un insieme aperto, egli definì inoltre la misura di un chiuso come uno meno la misura del suo complementare. Quindi passò a definire la misura esterna di un qualsiasi insieme come l'estremo inferiore delle misure degli aperti che lo contengono e la misura interna come l'estremo superiore delle misure dei chiusi contenuti nell'insieme. Se la misura esterna e interna di un insieme coincidono, l'insieme si dice 'misurabile' e la sua misura è il suddetto valore comune. Lebesgue mostrò che la famiglia degli insiemi misurabili contiene gli insiemi di Borel e che, inoltre, su tali insiemi la sua misura coincide con quella di Borel. Anche la nuova misura è numerabilmente additiva e la famiglia degli insiemi misurabili è una σ-algebra. Quindi Lebesgue estese questa misura all'intera retta reale e, per analogia, introdusse misure simili negli spazi euclidei di dimensioni superiori per rappresentare l'area nel piano, il volume nello spazio tridimensionale e così via.

Quanto all'integrazione, egli definì innanzi tutto l'integrale di una funzione positiva definita sui reali come la misura bidimensionale della regione sotto il suo grafico, quindi l'integrale di una qualsiasi funzione come la differenza fra gli integrali delle sue parti positiva e negativa. Lebesgue chiamò una funzione 'misurabile' se l'immagine inversa di un intervallo è un insieme misurabile e dimostrò che esiste l'integrale di una funzione misurabile limitata su un intervallo limitato. L'integrale di Riemann veniva così esteso a una classe più vasta di funzioni. Dopo aver verificato la validità delle proprietà algebriche elementari dell'integrale, egli dimostrò uno dei più importanti teoremi di analisi, il teorema della convergenza dominata di Lebesgue: se ogni elemento di una successione convergente di funzioni misurabili è limitato in modulo da una funzione integrabile, allora l'integrale del limite della successione è il limite degli integrali dei suoi elementi. L'integrazione in dimensioni superiori segue linee analoghe.

Nel 1904, volgendo la sua attenzione alla derivazione, Lebesgue ritrovò il teorema fondamentale del calcolo in una forma particolarmente semplice. Un'asserzione si dice valida 'quasi ovunque' se l'insieme dei punti dove non è verificata ha misura nulla. Lebesgue dimostrò innanzi tutto che una funzione monotona ‒ e anche la somma o la differenza di due funzioni monotone ‒ è differenziabile quasi ovunque. Quindi dimostrò che l'integrale indefinito di una funzione è differenziabile quasi ovunque e che la sua derivata è uguale quasi ovunque alla funzione integranda. Infine, caratterizzò tutte le funzioni che possono essere espresse come integrali indefiniti: tale classe di funzioni coincide con la classe delle funzioni 'assolutamente continue'. La nozione di continuità assoluta era stata introdotta precedentemente da Giuseppe Vitali (1875-1932). Una funzione è assolutamente continua se la sua variazione totale su un insieme aperto tende a zero quando la misura dell'aperto tende a zero.

Ora, una funzione a variazione totale limitata si può esprimere come differenza di due funzioni monotone e quindi è differenziabile quasi ovunque. Tuttavia, l'integrale indefinito della sua derivata non è necessariamente uguale alla funzione stessa. La loro differenza è caratterizzata dal fatto di avere derivata quasi ovunque nulla. Funzioni che godono di questa proprietà si dicono 'singolari': non sono necessariamente costanti, anzi possono assumere qualsiasi valore su un intervallo. Lebesgue mostrò che una funzione a variazione limitata può essere decomposta nella somma di una funzione assolutamente continua e di una funzione singolare. Questo è il famoso teorema di decomposizione di Lebesgue. Perciò le funzioni assolutamente continue sono precisamente quelle funzioni a variazione limitata che sono uguali all'integrale indefinito della loro derivata.

Nei primissimi anni del XX sec., Lebesgue aveva dunque già posto le fondamenta di una teoria della misura e dell'integrazione sulla retta reale che estendeva l'ambito di applicazione del calcolo integrale e differenziale in modo inimmaginabile prima di lui. Tale teoria inoltre consentiva di operare con gli integrali, le derivate e i limiti con un minimo di semplici e naturali restrizioni. I decenni successivi furono testimoni della crescita straordinaria di tale settore, delle applicazioni sempre più vaste di queste idee ad altri campi e della nascita, infine, di nuove importanti aree della matematica a partire dalle nozioni e dai risultati della teoria della misura.

Le linee di sviluppo da questo punto in poi si muovono simultaneamente in così tante direzioni e sono talmente intrecciate, specialmente con quelle di altri campi, che un resoconto puramente cronologico dei fatti non permetterebbe di apprezzarne adeguatamente i risultati. Elencheremo perciò alcune delle principali aree nelle quali la teoria della misura ha prodotto contributi significativi e seguiremo cronologicamente tali sviluppi solo all'interno di ciascuna area.

Funzioni di insiemi

Proprio come il calcolo integrale aveva condotto allo studio di funzioni il cui dominio consiste di punti nello spazio euclideo, l'integrazione secondo Lebesgue condusse allo studio sistematico di funzioni il cui dominio consiste di sottoinsiemi di uno spazio. Queste sono chiamate funzioni di insiemi per sottolinearne la differenza dalle funzioni di punti. Come vedremo, l'integrazione secondo Lebesgue stimolò anche lo studio dei 'funzionali' cioè di funzioni che hanno come argomento altre funzioni. La motivazione per studiare in ambito generale le funzioni di insiemi venne dapprima dalla considerazione degli integrali indefiniti ma, poco dopo, anche dall'esigenza di definire misure che consentissero di risolvere problemi tipici di numerosi campi interni ed esterni alla matematica.

Gli integrali indefiniti sono funzioni della forma

[1] F(x)=∫^x_af(s)ds,  F(x,y)=∫^y_b∫^x_af(s,t)ds dt, ecc.

Nel 1910, nel tentativo di estendere i risultati che connettono gli integrali con le derivate dalla retta reale agli spazi euclidei di dimensione superiore, Lebesgue sostituì gli estremi di integrazione nelle espressioni [1] con intervalli, rettangoli, ecc. e infine con insiemi misurabili. Questo gli permise di formulare le condizioni di variazione limitata e di continuità assoluta nelle dimensioni superiori in un modo semplice e naturale e lo condusse a considerare le funzioni di insiemi negli spazi euclidei. Lebesgue definì una misura su tali spazi come una funzione di insiemi numerabilmente additiva e a variazione limitata. Nel 1913 Johann Radon (1887-1956) lasciò cadere la condizione di variazione limitata e nel 1915 Maurice-René Fréchet (1878-1973) sostituì lo spazio euclideo con uno spazio astratto qualsiasi. La misura divenne quindi una funzione numerabilmente additiva definita su una σ-algebra di sottoinsiemi di un qualsiasi spazio.

Con l'introduzione delle misure astratte, il problema fondamentale della teoria divenne (e in gran parte è tuttora) la costruzione di una misura adatta a uno scopo specifico; frequentemente tale scopo è esterno alla teoria della misura propriamente detta. I metodi per costruire misure sono perciò di grande importanza e hanno ricevuto un'attenzione considerevole. Il metodo più comune consiste nel definire la nuova misura tramite l'integrale indefinito di una funzione rispetto alla misura di Lebesgue in uno spazio euclideo. Per esempio, interpretando l'integrando come la densità di massa di un materiale, l'integrale rappresenta la quantità di massa contenuta in una regione. L'idea si estende facilmente all'integrale rispetto a una qualsiasi misura definita su uno spazio. Tuttavia le misure che si ottengono con tale procedura sono tutte assolutamente continue rispetto alla misura iniziale, il che è una restrizione significativa.

Un altro approccio segue un'idea suggerita nel 1894 da Thomas Jan Stieltjes (1856-1894) in un lavoro concernente non la teoria della misura ma un problema sulle frazioni continue. Egli fece notare che una funzione f monotona sulla retta reale può essere interpretata come una distribuzione di massa ponendo che f(b)−f(a) rappresenti la quantità di massa nell'intervallo (a,b). Posto ciò, i momenti di massa intorno all'origine sono rappresentati da integrali della forma

[2] ∫^x_ndf (x),

integrali che Stieltjes definì 'alla Riemann' sostituendo la lunghezza b−a di un intervallo con la differenza f(b)−f(a). Non è difficile effettuare la costruzione di Lebesgue al posto di quella di Riemann per ottenere una misura associata a f. Tali misure, chiamate 'misure di Lebesgue-Stieltjes', non sono necessariamente assolutamente continue e sono particolarmente adatte per essere utilizzate nelle scienze fisiche così come in probabilità e in statistica. Utilizzando il metodo già descritto, se f è la differenza di due funzioni monotone si ottengono tutte le misure a variazione limitata sulla retta. Questo approccio può essere esteso alle funzioni definite su spazi euclidei di dimensione superiore, ma si rivela tecnicamente piuttosto macchinoso.

Nel 1914, allo scopo di estendere la nozione di lunghezza di una curva, di area di una superficie, e così via, Constantin Carathéodory (1873-1950) introdusse due procedure estremamente generali per la costruzione di misure. La prima, valida per uno spazio qualsiasi, consiste di due passi: (1) data una qualsiasi funzione non negativa su una famiglia di sottoinsiemi di un insieme dato, si costruisce una funzione definita per tutti i sottoinsiemi dello spazio, chiamata misura esterna, la quale è numerabilmente 'subadditiva' (ossia la misura di un insieme ricoperto da una successione di insiemi è minore o uguale alla somma delle misure degli insiemi della successione); (2) per ogni misura esterna si ottiene, attraverso una semplice condizione algebrica, una σ-algebra sulla quale la misura esterna è numerabilmente additiva. La famiglia degli insiemi misurabili secondo Carathéodory è per definizione la suddetta σ-algebra. Questa costruzione, basata su formule concrete, si rivela estremamente potente in quanto produce una misura a partire da dati e condizioni assolutamente generici. Essa risolve il problema fondamentale di estendere una funzione numerabilmente additiva su una famiglia ristretta, come la famiglia degli intervalli, a una funzione (sempre numerabilmente additiva) su una σ-algebra. Quasi ogni misura nota può essere ottenuta direttamente o indirettamente con questa costruzione.

La seconda procedura di Carathéodory, applicabile solamente agli spazi metrici, specializza le misure ottenute attraverso la prima procedura pervenendo a misure connesse alla metrica dello spazio. Utilizzando le sfere come elementi della famiglia primitiva e i diametri alla potenza k-esima come funzioni primitive, Carathéodory applica il primo procedimento per ottenere misure k-dimensionali su uno spazio metrico. Poco dopo, sostituendo le sfere con arbitrari insiemi limitati, Felix Hausdorff (1868-1942) sviluppò considerevolmente la teoria di tali misure, note oggi come 'misure di Hausdorff'. Esse svolgono un ruolo rilevante nella geometria differenziale, dove si usano largamente gli integrali di linea e di superficie.

La costruzione di alcune fra le più importanti misure, basate su questi e su altri metodi, sarà discussa nel contesto dei particolari campi di applicazione.

Integrazione

Nel suo lavoro originale del 1902, per la definizione dell'integrale Lebesgue adottò il classico punto di vista geometrico dell'integrale come 'area al di sotto della curva': una funzione f di n variabili determina, tramite il suo grafico, una regione nello spazio (n+1)-dimensionale e l'integrale di f è la misura di questa regione. Negli anni successivi, dato che le nozioni di misura e di integrale venivano estese a situazioni sempre più generali, furono introdotte altre definizioni basate su punti di vista differenti. Le differenze sono principalmente tecniche e mentre la metodologia varia caso per caso, a causa delle diverse esigenze, le proprietà essenziali dell'integrale di Lebesgue vengono comunque mantenute. Generalmente tali costruzioni tendono a seguire uno fra questi due punti di vista generali, vale a dire: quello geometrico, che mette in evidenza l'uso degli insiemi, e quello dell'analisi funzionale, che rimarca l'uso delle funzioni. Menzioniamo esclusivamente i prototipi più comuni di ognuno dei due punti di vista.

Limite di una somma. Assegnata una misura m e una funzione f, l'integrale di f rispetto a m si ottiene facendo una partizione del dominio, effettuando una somma per ogni partizione e quindi passando al limite rendendo le partizioni sempre più raffinate. Una partizione è una successione finita o infinita di insiemi misurabili disgiunti A_n la quale ricopre l'intero spazio e la somma è della forma

dove x_n è un elemento di A_n. Secondo l'interpretazione geometrica il prodotto che compare negli addendi della [3] è uguale all''altezza per la misura della base', cioè all''area del rettangolo' la cui base è l'insieme A_n e la cui altezza è f(x_n). Questo punto di vista è particolarmente adatto per i metodi usati in fisica, dove l''area' può essere reinterpretata come massa o energia.

Funzionali lineari. Questo approccio si basa sul fatto che l'integrale della somma di due funzioni è la somma dei loro integrali e considera perciò l'integrale come una funzione che assegna un valore a ogni integrando, cioè come funzione di una funzione: da ciò nasce l'idea di 'funzionale lineare'. Si parte con una famiglia primitiva di funzioni (per es., quelle a gradini o quelle continue e limitate) per le quali il valore dell'integrale sia noto e quindi si estende il funzionale lineare a una classe più vasta di funzioni usando come strumento alcune delle proprietà fondamentali richieste all'integrale. Per l'integrale di Lebesgue si usa la proprietà che per una successione monotona di funzioni positive l'integrale del limite è il limite degli integrali. Il primo a usare questa costruzione fu Percy J. Daniell (1889-1946) nel 1918 e ci si riferisce a essa come all''integrale di Daniell'.

Il legame tra i due punti di vista si basa sul fatto che la misura di un insieme A è l'integrale di una funzione, chiamata 'funzione caratteristica' di A; tale funzione assegna il valore 1 a ogni punto di A e il valore 0 a tutti gli altri punti.

Dopo i primi anni Venti del XX sec. la teoria dell'integrazione secondo Lebesgue era essenzialmente completata e la sua relazione con gli altri integrali (specialmente con gli integrali impropri secondo Riemann) completamente esplorata. I maggiori teoremi del calcolo integrale erano stati riottenuti con modifiche naturali, prima per la misura di Lebesgue sugli spazi euclidei e poi per misure più generali su altri spazi. Accenniamo in particolare alla rappresentazione dell'integrale di una funzione sul piano tramite due integrali iterati sulla retta. Secondo Lebesgue questo risultato fu dimostrato per funzioni integrabili da Guido Fubini (1879-1943) nel lavoro Sugli integrali multipli del 1907 e fu esteso più tardi al prodotto cartesiano di una qualsiasi coppia di spazi di misure: ci si riferisce a esso come al teorema di Fubini.

Derivazione

L'estensione della teoria della derivazione dalla retta reale agli spazi euclidei di dimensioni superiori presentò difficoltà inaspettate. Nel contesto delle funzioni di insiemi la derivata di una funzione F in un punto x è definita come il limite dei rapporti della forma F(A)/m(A), dove l'insieme A si contrae al solo punto x e m indica la misura di Lebesgue. Nella teoria classica sulla retta, gli insiemi A sono intervalli contenenti x. Se nelle dimensioni superiori si sostituiscono gli intervalli con i rettangoli questa teoria non è più valida. La fonte delle difficoltà si trova nell'esistenza di rettangoli molto sottili, per i quali il rapporto tra il lato più lungo e quello più corto tende all'infinito. Questo problema non emerge in dimensione uno. Nel 1905 Vitali dimostrò un teorema fondamentale sul quale si basa la maggior parte della teoria della derivazione, il teorema di ricoprimento di Vitali: se una famiglia H consiste soltanto di sfere e ogni punto di un insieme E può essere ricoperto da sfere di H aventi un diametro arbitrariamente piccolo allora si può estrarre da H una successione di sfere disgiunte che ricopre quasi tutto E. Usando questo risultato, Lebesgue fu in grado di estendere nel 1910 la sua versione del teorema fondamentale del calcolo dalla retta reale agli spazi euclidei di dimensione superiore. Questo stesso teorema fu esteso nel 1913 da Radon ad altre misure definite sugli spazi euclidei, diverse dalla misura di Lebesgue.

Nel teorema di Vitali si possono sostituire le sfere con 'rettangoli pieni'. Anche la nozione di 'pienezza' può essere definita per altri insiemi e rispetto ad altre misure oltre a quella di Lebesgue. Si dice che una famiglia di insiemi H possiede la 'proprietà di Vitali' se per tale famiglia è valida la conclusione del teorema di ricoprimento di Vitali. Anche la nozione di continuità assoluta si estende facilmente: una funzione di insiemi è 'assolutamente continua' rispetto a una misura positiva assegnata m se F(A)=0 quando m(A)=0. Estendendo i concetti in questo modo, la teoria di Lebesgue, che mette in relazione integrazione e derivazione, può formularsi, in un ambito generale, come segue: se la derivata di F rispetto a m è definita usando una famiglia H che ha la proprietà di Vitali, allora F è assolutamente continua rispetto a m se e solo se la derivata f di F rispetto a m esiste quasi ovunque e F è l'integrale indefinito di f rispetto a m.

La necessità per la derivabilità di una funzione di trovare un'appropriata famiglia H con la proprietà di Vitali ha dato origine a una letteratura considerevole su questo argomento. Tale problema, tuttavia, fu aggirato nel 1930 da Otton Martin Nikodym (1887-1974), il quale dimostrò che se m è una misura positiva e F una funzione limitata assolutamente continua rispetto a m, allora esiste sempre una funzione f tale che F sia l'integrale indefinito di f rispetto a m. Ci si riferisce a questa funzione f come alla 'derivata di Radon-Nikodym' di F rispetto a m. Nel 1960 fu dimostrato infine che, per una qualsiasi misura positiva e limitata m, esiste sempre una famiglia di Vitali per la derivabilità rispetto a m.

La teoria delle funzioni

Analisi funzionale

La nozione di spazio topologico cominciò a emergere verso la fine del XIX sec. e si affermò definitivamente nella prima metà del XX secolo. Uno spazio topologico è un insieme su cui è definita una struttura con la quale si possono definire i limiti, e a questo scopo si introducono certi insiemi che svolgono un ruolo fondamentale: gli 'aperti', i 'chiusi' e i 'compatti'. Oltre agli spazi euclidei, gli esempi più comuni sono le famiglie di funzioni, come lo spazio delle funzioni continue sull'intervallo [0,1]. Gli spazi metrici, gli spazi localmente compatti, gli spazi di Hilbert e di Banach sono tutti esempi di spazi topologici. L'analisi funzionale si occupa principalmente dello studio degli spazi di funzioni e utilizza sia nozioni di algebra lineare sia di analisi. La sua relazione con la teoria della misura è così forte che esiste la tendenza a identificare i due campi. Menzioneremo solo alcuni dei principali punti di contatto.

Il legame fondamentale tra le due teorie fu stabilito nel 1909 da Frigyes Riesz (1880-1956), il quale dimostrò nel lavoro Sur les opérations fonctionnelles linéaires che ogni funzionale lineare L continuo sullo spazio delle funzioni g continue su [0,1] può essere rappresentato come l'integrale rispetto a una funzione f a variazione limitata, più precisamente

[4]  L(g)=∫g(x)df(x).

Poiché f dà origine a una misura m su [0,1], il teorema stabilisce, tramite l'integrazione, una corrispondenza biunivoca tra funzionali lineari continui e misure. Nei trent'anni successivi questo teorema è stato esteso sotto ipotesi più generali, sostituendo l'intervallo [0,1] con uno spazio localmente compatto. Ci si riferisce a tale risultato come al 'teorema di rappresentazione' di Riesz. Le misure considerate, note come 'misure di Radon', hanno proprietà particolarmente utili in relazione ad alcune classi di insiemi interessanti da un punto di vista topologico. Questa corrispondenza tra funzionali lineari e misure fa sì che idee e metodi dell'analisi funzionale siano applicabili alla teoria della misura e viceversa.

Un altro punto di contatto è lo studio degli spazi delle funzioni 'sommabili' (chiamate anche 'integrabili') o a 'quadrato sommabile', spazi denotati con L₁ e L₂. Nel 1907 Ernst Sigismund Fischer (1875-1954) e Riesz mostrarono indipendentemente che, quando i limiti sono definiti in termini di integrali, questi spazi sono 'completi', una proprietà di convergenza particolarmente desiderabile. Questo risultato cruciale, valido per l'integrale di Lebesgue ma non per quello di Riemann, è la pietra angolare per qualsiasi ambito applicativo, dalla fisica alla statistica, dalle equazioni differenziali all'analisi armonica. La completezza consente di individuare gli esempi più importanti ‒ in realtà i prototipi ‒ di spazi di Banach e di Hilbert in analisi funzionale. Essa è stata estesa a integrali rispetto a una misura qualsiasi su uno spazio qualsiasi e a una vasta classe di funzioni, generando quelli che sono noti come gli spazi L_p.

Un terzo punto di contatto è dato dalle misure a valori vettoriali. Nel 1933 Salomon Bochner (1899-1982) iniziò lo studio di misure che assegnano a ogni insieme un vettore definito in uno spazio di Banach, anziché un numero. Tali misure erano state studiate da molto tempo in fisica, nelle equazioni differenziali e in geometria differenziale nel caso in cui lo spazio di Banach ha dimensione finita, cioè è uno spazio euclideo. Queste misure sorgono, per esempio, nel contesto del moto di una particella sotto l'influenza di un campo di forze. Supponendo lo spazio del moto di dimensione infinita e usando l'approccio di Lebesgue si aprirono nuove e vaste aree di applicazione. Nei dieci anni successivi la teoria fu estesa ad altri spazi vettoriali, particolarmente da Billy J. Pettis, Nelson Dunford, Israil Moiseevič Gel′fand e Ralph S. Phillips. Negli anni Sessanta fu estesa ulteriormente ai gruppi e ai semigruppi. Di particolare interesse è stata la teoria della derivazione delle misure a valori vettoriali, teoria che viene usata per studiare la geometria degli spazi di Banach.

Analisi armonica

Il lavoro di Fourier del 1822 sulla teoria del calore menzionato all'inizio richiedeva la rappresentazione di una funzione come serie di seni e coseni, serie note oggi come 'serie di Fourier'. Più precisamente, egli affermò che tutte le funzioni f possono esprimersi nella forma

dove

e

Per le applicazioni che Fourier aveva in mente, era effettivamente importante che la parola 'tutte' fosse presa sul serio e che si includessero anche le funzioni discontinue. La sua dimostrazione era basata sullo scambio delle due operazioni: l'integrale e la somma infinita. L'affermazione di Fourier sollevò serie obiezioni, ma l'uso che egli fece della rappresentazione [5] fu così ricco di conseguenze, e le applicazioni così importanti, da impedire che fosse respinta senza appello; un riesame delle nozioni fondamentali utilizzate fu intrapreso subito dopo la pubblicazione del suo scritto del 1822. Il lavoro sull'integrale di Riemann, pubblicato postumo nel 1866, fornì una solida base per la definizione dei coefficienti a_n e b_n. Esso non poteva tuttavia permettere lo scambio tra l'integrazione e la somma infinita in tutti i casi interessanti. Quindi la teoria delle serie di Fourier nel XIX sec. era costituita essenzialmente da una collezione di teoremi difficili con ipotesi complicate. La sostituzione dell'integrale di Riemann con quello di Lebesgue trasformò tale disciplina matematica in una teoria elegante e sistematica, nota come 'analisi armonica', con vaste applicazioni, in special modo in fisica e nelle equazioni differenziali. In essa un ruolo cruciale è svolto dagli spazi L₁ e L₂ e dal teorema di Fischer-Riesz già menzionato. L'analisi armonica motivò gran parte dello sviluppo dell'analisi funzionale, in particolare lo studio degli spazi di Hilbert.

Un nuovo e fondamentale strumento che estese notevolmente la portata della teoria fu la costruzione, da parte di Alfréd Haar (1885-1933) nel 1933, di una misura invariante per traslazioni su un gruppo metrico, misura che può svolgere lo stesso ruolo della misura di Lebesgue. Negli anni Quaranta questa costruzione fu successivamente estesa a ogni gruppo localmente compatto. Tale misura, nota come 'misura di Haar', costituisce oggi le fondamenta della teoria. I coefficienti di Fourier di una funzione hanno dato origine nella teoria moderna alla trasformata di Fourier di una misura ottenuta sostituendo i seni e i coseni con una funzione esponenziale complessa (o, in un ambito più generale, con una funzione che viene detta 'carattere'). Più precisamente la trasformata di Fourier F di una misura m è definita dalla formula

[8] F(t)=∫e^itxdm(x).

Nel 1933 Bochner dimostrò che in ogni spazio euclideo la trasformata di Fourier stabilisce una corrispondenza biunivoca tra le misure positive limitate e certe funzioni continue note come 'funzioni definite positive'. La trasformata di Fourier è diventata uno degli strumenti principali per costruire e analizzare le proprietà delle misure, in particolare la convergenza di successioni di misure; inoltre essa è usata in altri campi, come la probabilità e la fisica matematica. L'analisi armonica oggi è una vasta area di importanti ricerche matematiche, le quali occupano una posizione centrale e si muovono in ogni direzione, ben oltre rispetto a quanto Fourier aveva immaginato.

Le applicazioni e gli sviluppi moderni

Probabilità

Prima dello sviluppo della teoria della misura il settore della probabilità era anch'esso essenzialmente una collezione di problemi sul gioco di azzardo e di metodi ad hoc per risolverli. L'interesse dei matematici per questi problemi risale almeno ai lavori di Blaise Pascal (1623-1662) e Pierre de Fermat (1601-1665) nel XVII secolo. Tuttavia, non esisteva alcuna teoria generale né definizioni fondamentali adeguate su cui basare una tale teoria. La soluzione di questo problema è uno dei maggiori risultati del XX sec. ed è interamente dovuta allo sviluppo della teoria della misura.

L'uso di una misura per descrivere una probabilità fu introdotto da Borel stesso intorno alla fine del XIX sec. lavorando sulla retta reale. Negli anni 1920-1923 Norbert Wiener (1894-1964) costruì una misura sullo spazio delle curve continue per definire la probabilità che descrive il moto di una particella sospesa in un fluido, il cosiddetto 'moto browniano'. Questo fenomeno era stato per qualche tempo oggetto di studio per i fisici ed era stato trattato matematicamente da Albert Einstein (1879-1955) e da Marian Smoluchowski (1872-1917) intorno al 1905. L'idea di utilizzare una misura su uno spazio così complicato per descrivere un fenomeno fisico aprì prospettive totalmente nuove. Nei due decenni che seguirono lo studio di questa misura, a cui ora ci si riferisce come alla 'misura di Wiener', condusse alla costruzione di una teoria generale della probabilità e dei processi stocastici.

Negli anni 1930-1933 Andrej Nikolaevič Kolmogorov (1903-1987) pose le fondamenta formali per la teoria della probabilità. Lo spazio di base è un insieme che rappresenta tutte le possibilità dei fenomeni che si vogliono studiare. Un 'evento' è un sottoinsieme di questo spazio e una 'probabilità' è una misura positiva su una σ-algebra di eventi, la quale assegna il valore uno all'intero spazio. Una 'variabile aleatoria' è una funzione misurabile su questo spazio e il suo 'valore atteso' o 'media' è l'integrale di tale funzione. In questo modo la teoria della probabilità diventò parte della teoria della misura inserendosi così nella corrente principale della matematica. Da un lato ciò mise tale disciplina in condizione di crescere e di ampliare le sue possibilità applicative nelle direzioni più disparate, dalla statistica alla teoria del potenziale alla fisica matematica; dall'altro lato stimolò nei matematici l'interesse per lo studio di problemi e per l'uso di metodi totalmente nuovi e differenti.

La misura di Wiener e il lavoro pioneristico, su quest'argomento, svolto da Paul Lévy (1886-1971) negli anni Venti e Trenta, condussero alla nascita di quel settore della probabilità che è lo studio dei processi stocastici, sviluppato nel suo stato iniziale principalmente da Joseph L. Doob. Questa teoria necessita di misure di probabilità su spazi di dimensione infinita come gli spazi di curve. Tale disciplina ha avuto una crescita rilevante nella seconda metà del secolo e le sue tecniche sono state applicate per la soluzione di problemi appartenenti a ogni settore dell'analisi, delle scienze sociali così come delle scienze fisiche. La teoria dei processi stocastici si occupa principalmente dell'evoluzione di un sistema nel tempo. Il sistema è rappresentato da un punto in uno spazio S, che può dipendere, in modo abbastanza complesso, dal fenomeno da studiare. L'evoluzione del sistema nel tempo è rappresentata da una curva nello spazio S. La legge che governa questa evoluzione è rappresentata da una misura sullo spazio delle curve. Di solito il problema principale è la costruzione di una tale misura a partire da alcune osservazioni iniziali o assunzioni. Una volta ottenuta, questa misura diventa uno degli strumenti più efficaci per studiare il fenomeno.

Fisica matematica

La matematica ha occupato un evidente ruolo di sostegno teorico alla fisica fin dalla nascita di questa scienza. La scoperta di un nuovo importante fenomeno fisico è stata sempre accompagnata da una nuova significativa attività matematica. Le scoperte della fisica atomica nel XX sec. non hanno fatto eccezione. La teoria della misura e l'analisi funzionale, essendosi sviluppate pressapoco nello stesso periodo, hanno svolto un importante ruolo nella teoria atomica. A loro volta i problemi della fisica hanno esercitato una enorme influenza su queste due discipline.

Negli anni Trenta John von Neumann (1903-1957) costruì un modello matematico per la meccanica quantistica che presto divenne quello standard nel settore. In questo modello lo spazio fondamentale è quello delle funzioni a quadrato sommabile, secondo Lebesgue, definite sullo spazio tridimensionale, cioè L₂, il quale come abbiamo visto è uno spazio di Hilbert. Le nozioni fisiche di posizione, momento, energia, ecc. sono rappresentate da trasformazioni lineari (chiamate operatori) di questo spazio in sé stesso. Gran parte della teoria si basa sul fatto che gli stessi operatori possono essere espressi come integrali rispetto a una misura a valori vettoriali, detta misura spettrale. Questo fatto, noto come 'teorema spettrale', fu dimostrato da Marshall H. Stone (1903-1989) nel 1929 per gli operatori illimitati che si presentano nella meccanica quantistica. Lo studio di questi operatori e quindi delle corrispondenti nozioni fisiche fa un uso essenziale delle loro misure spettrali. Dunque la teoria della misura è utilizzata sia nella descrizione soggiacente al modello sia nei metodi usati nel modello per comprendere i fenomeni osservati in laboratorio. Inoltre, l'interpretazione di molte espressioni che nascono nel corso di questo lavoro si basa sulla nozione moderna di probabilità.

Negli anni Quaranta Richard P. Feynman (1918-1988) introdusse un nuovo punto di vista nello studio dei fenomeni atomici. All'interno di questo approccio un ruolo cruciale è svolto da certe espressioni integrali che attirarono molto rapidamente l'attenzione dei matematici. Mark Kac (1914-1984) stabilì che casi speciali di questi integrali sono in relazione con la misura e l'integrale di Wiener. La formula di Feynman-Kac che ne risultò e i problemi relativi sono stati fonte di ricerca matematica in un'area a cui ci si riferisce in generale con il nome di 'integrazione funzionale'; questo settore ha a che fare con la misura e l'integrazione su spazi di funzioni, cioè sugli spazi che compaiono nell'analisi funzionale. In tale campo sono stati ottenuti due importanti risultati nel 1958. Il primo, dovuto a Robert Adolfovič Minlos, mostra come costruire una misura di probabilità gaussiana su un nuovo tipo di spazio, noto come spazio nucleare. Tale spazio era stato introdotto nel 1953 da Alexander Grothendieck nel lavoro Sur les applications linéaires faiblement compact d'espaces du type C(K). Il secondo, dovuto a Vladimir Sazonov, estende il teorema di Bochner (il quale collega le misure con le funzioni definite positive tramite la trasformata di Fourier) dagli spazi euclidei a quelli di Hilbert. Tali risultati hanno dato origine a una vasta letteratura in questo settore, tanto da produrre una teoria matematica parallela a quella dei processi stocastici.

Teoria geometrica della misura

Lo studio delle curve e delle superfici negli spazi euclidei ha una storia molto lunga. Esso è il fine principale della geometria differenziale ed è in gran parte motivato da problemi derivanti dalla fisica e dallo studio delle equazioni differenziali. Le sue connessioni con la teoria della misura tendono a essere più tecniche di quelle con la probabilità e l'analisi funzionale.

Come abbiamo visto, la costruzione delle misure di Carathéodory mirava a risolvere problemi in questo settore e condusse direttamente alle misure di Hausdorff. Esse, a loro volta, hanno dato origine a una raffinata nozione di dimensione che permette una sottile analisi di insiemi 'patologici', cioè di insiemi apparentemente molto complicati, in spazi euclidei o in spazi metrici più generali. Come esempio, si può pensare agli insiemi che rappresentano la traiettoria seguita da una particella in un moto browniano. Inoltre, la necessità di considerare integrali lungo curve e, più in generale, su superfici k-dimensionali in spazi di dimensione n ha condotto a una grande quantità di lavori che mettono in relazione le proprietà geometriche di queste superfici con il comportamento degli integrali. Le condizioni per l'esistenza di tali integrali dipendono frequentemente dalla dimensione di Hausdorff. Il lavoro pioneristico di Hassler Whitney (1907-1989) negli anni Quaranta e Cinquanta e quello di Ennio De Giorgi (1928-1996) e di Herbert Federer, tra gli altri, hanno dato origine alla 'teoria geometrica della misura'. I suoi metodi sono in stretta relazione con le idee della geometria differenziale come le nozioni di forma, direzione, orientazione e così via. In questo contesto, il teorema fondamentale del calcolo prende la forma di relazione tra l'integrazione su una regione e l'integrazione lungo la sua frontiera. Le versioni classiche, note come teoremi di Stokes e Gauss, largamente usate in aree quali l'idrodinamica e l'elettromagnetismo, sono state estese a situazioni molto generali così da ampliare in modo significativo la portata delle loro applicazioni.