La seconda rivoluzione scientifica: matematica e logica. Il calcolo geometrico
La seconda rivoluzione scientifica: matematica e logica. Il calcolo geometrico
Il calcolo geometrico
Quando pubblicò il trattato Die lineale Ausdehnungslehre (La teoria lineare dell'estensione, 1844) Hermann Günter Grassmann (1809-1877) aveva in mente un'ampia revisione della matematica. Non solo la sua teoria dell'estensione doveva costituirne un "nuovo ramo", ma anche l''intero tronco' della matematica doveva venir rifondato sulla base di una nuova disciplina, la teoria delle forme (Formenlehre). Per la sua grande originalità, quell'opera non ebbe facile accoglienza presso il mondo matematico tedesco. Né valse a migliorare le cose la versione pubblicata nel 1862, che Grassmann riteneva più aderente alla mentalità dei matematici. Occorrerà attendere la fine degli anni Sessanta del XIX sec., quando tematiche affini si stavano ormai affermando, per cogliere sensibili influenze della sua opera.
Grassmanniani e quaternionisti
Gli allievi e i successori immediati persero di vista il contesto generale in cui Grassmann collocava la sua teoria e non furono in grado di andare oltre una specializzazione relativamente ristretta, rimanendo confinati alla geometria (sintetica) oppure cercando di elaborare ulteriormente quello che per loro era il suo 'sistema'. Per esempio, l'obiettivo principale di Hermann Ernst Grassmann (1857-1922), uno dei suoi figli attivi in campo matematico, professore di matematica all'Università di Giessen, fu di trovare altri seguaci del sistema del padre e far loro pubblicare ulteriori applicazioni di questa forma di calcolo (Schubring 1996a). Egli stesso fu autore di vari trattati sulla teoria generale delle curve nello spazio, presentata senza alcun collegamento, per esempio, con gli sviluppi della teoria delle varietà che si riallacciava a Riemann. Ecco perché Felix Christian Klein (1849-1925) ha parlato dei 'grassmanniani' come di una 'setta', dedita soltanto a perfezionare i concetti del maestro (Schubring 1996b), e nel corso di una controversia con Victor Schlegel, uno dei più stretti seguaci di Grassmann, li accusò di coltivare i loro studi in maniera isolata e unilaterale, senza preoccuparsi di collegarli e integrarli con le contemporanee tendenze della matematica (Rowe 1996).
Un analogo sviluppo di tipo settario aveva conosciuto anche la concezione concorrente dei numeri ipercomplessi, quella dei quaternioni. "Tutte queste caratteristiche proprie dei settari convinti si riscontrano ora tra i quaternionisti, gli allievi di Hamilton", osservava Klein. "Non c'è neppure bisogno di dire che grassmanniani e quaternionisti si combattono strenuamente, e che ciascuna delle scuole si è separata in campi ferocemente avversi tra loro" (Klein 1979, pp. 169-170).
Tali aspre contrapposizioni divennero manifeste quando, a partire dalle teorie di Grassmann e di Hamilton si arrivò allo sviluppo del calcolo vettoriale vero e proprio. Mentre nel campo della matematica pura, al di fuori della geometria, entrambe le teorie a tutta prima non produssero effetti profondi, nelle applicazioni, per esempio in meccanica, ottennero invece grandi successi. Infatti, alla luce delle nuove teorie molte grandezze meccaniche erano rappresentabili come vettori, diventando così notevolmente più facili da manipolare.
Una decisiva funzione di battistrada fu svolta da Peter Guthrie Tait (1831-1901), professore di filosofia naturale all'Università di Edimburgo. Tait divenne una figura di primo piano tra i quaternionisti subito dopo la morte di William R. Hamilton, vegliando in veste sacerdotale sulla purezza delle dottrine hamiltoniane. Egli non soltanto pubblicò otto libri sui quaternioni, ampliandone la teoria, ma nel far ciò sviluppò anche molte nuove teorie suscettibili in seguito di trasposizione in termini di calcolo vettoriale. In particolare, il suo Elementary treatise on quaternions (1873) preparò il passaggio dalla teoria dei numeri ipercomplessi alla meccanica. Il primo capitolo si occupava esclusivamente del calcolo vettoriale: uguaglianza di vettori, addizione e sottrazione di vettori, moltiplicazione di vettori per scalari. Anche il secondo capitolo trattava in modo prevalente la parte vettoriale dei quaternioni; non vi comparivano soltanto il prodotto vettoriale e l'algebra vettoriale, ma anche l'operatore nabla ∠, poi diventato fondamentale.
L'opera di Benjamin Peirce (1809-1880), professore di astronomia e fisica alla Harvard University, costituisce un ulteriore esempio del superamento dell'angusta teoria dei quaternioni. Nel suo importante volume Linear associative algebra (1870, 1881) egli si serviva dei quaternioni per studiare strutture algebriche generali. Vale la pena di menzionare il fatto poco noto che l'espressione 'algebra lineare' compare per la prima volta nel 1882 nel titolo di un libro di un autore periferico, Hüseyin Tevfik Paşa (1832-1901). Formatosi all'accademia militare di Istanbul, dopo aver ricoperto l'incarico di addetto militare ottomano in Francia, Hüseyin Tevfik soggiornò dal 1872 al 1880 negli Stati Uniti, dove si dedicò a studi e ricerche matematiche. Venne a conoscenza dei lavori di Tait e Peirce e, partendo dai quaternioni, nel suo libro (ristampato nel 1988) studiò le algebre associative e non associative (Schubring 1996b).
Infine, fu Josiah W. Gibbs (1839-1903), professore di fisica matematica a Yale, a lasciare l'ambito ristretto dell'ortodossia dei quaternioni e a porre le basi del moderno calcolo vettoriale con il manuale Elements of vector analysis (1881, 1884). Gibbs si rese conto del fatto che i quaternioni sono inutili per il calcolo vettoriale, perché entrambi i prodotti essenziali, il prodotto scalare e il prodotto esterno o vettoriale, si possono ottenere anche indipendentemente dal prodotto di quaternioni (Crowe 1967). Gibbs non volle mai aderire ad alcuna scuola. Aveva studiato tre anni in Francia e in Germania per conto proprio, familiarizzando con le opere di Möbius e di Grassmann, e collocava i propri metodi tra quelli di Hamilton e quelli di Grassmann, a suo dire "pressappoco quelli di Hamilton", "quasi esattamente quelli di Grassmann". Considerava il suo manuale più strettamente aderente al sistema di Grassmann che a quello di Hamilton, anche se le sue notazioni seguivano le stesse della tradizione quaternionista. In effetti Gibbs ha introdotto i vettori come elementi essenziali, definendo per essi le operazioni, in particolare il prodotto scalare (direct product) e il prodotto esterno (skew product). Egli era interessato non solo alle applicazioni in fisica matematica, ma anche allo sviluppo della matematica pura e in particolare dell'algebra, e perciò sottolineò ripetutamente l'estrema importanza del sistema di Grassmann.
Volendo indagare le origini delle sue singolari e innovative idee, Gibbs si imbatté nel primo scritto di Grassmann, la sua tesi sul flusso e il riflusso (Theorie der Ebbe und Flut). Egli cercò invano di convincere i figli del matematico tedesco a dare alle stampe questo scritto; prima di prendere in considerazione gli aspetti storici, essi volevano il pieno riconoscimento dell'opera del padre da parte del mondo matematico. Riscosse invece successo l'appello rivolto a Klein, che ebbe l'idea di pubblicare le opere complete di Grassmann, vincendo così la resistenza dei figli. Apparse tra il 1894 e il 1911 a cura di Friedrich Engel, esse contribuirono notevolmente a rendere più accessibili le concezioni di Grassmann. Purtroppo l'originario promotore del progetto non riuscì a vedere realizzato il suo desiderio: Gibbs morì otto anni prima che Theorie der Ebbe und Flut apparisse a stampa nel 1911.
Il calcolo geometrico secondo Peano e la sua scuola
Grazie a una serie di articoli apparsi sul "Journal" di Crelle, che avevano mostrato la fecondità dell'Ausdehnungslehre nei più diversi rami della matematica, le idee di Grassmann non erano sfuggite a qualche studioso più attento a tematiche geometriche. In Italia vennero particolarmente apprezzate da Barnaba Tortolini, da Giusto Bellavitis e soprattutto da Luigi Cremona. Tuttavia, alla diffusione delle teorie di Grassmann in Italia contribuì più di ogni altro Giuseppe Peano (1858-1932), che dal 1885 aveva sostituito Angelo Genocchi (1817-1889) nell'insegnamento delle 'Applicazioni geometriche del calcolo infinitesimale' presso l'Università di Torino. Nell'omonimo volume, che nel 1887 raccoglie le sue lezioni, Peano presenta gli elementi del calcolo geometrico, le cui origini riconosce nei lavori di Möbius, Hamilton e Grassmann. Nell'esposizione egli privilegia tuttavia il linguaggio di Bellavitis, forse per l'influenza di Genocchi, legato al matematico padovano da sincera amicizia e stima.
L'anno seguente, 1888, Peano pubblica il Calcolo geometrico secondo l'Ausdehnungslehre di H.Grassmann preceduto dalle operazioni della logica deduttiva, un'opera di cruciale importanza anche per la storia della logica. In questo fondamentale lavoro, Peano presenta con elementi di originalità e grande chiarezza espositiva le concezioni di Grassmann, traducendone i concetti astratti nel linguaggio della geometria elementare. Inoltre, ogni capitolo del volume contiene una parte dedicata alle applicazioni, soprattutto in geometria, elementare e proiettiva, e in meccanica. La nozione di forma (o formazione) geometrica è la base di tutto l'impianto teorico. Siano m,n,p,…,q numeri reali, una forma geometrica è un'espressione del tipo:
[1] mα+nβ+pγ+…+qτ.
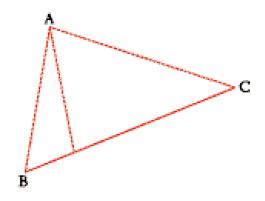
Se α,β,γ,… e τ denotano 'punti', la forma si dirà di prima specie (o primo grado), se denotano 'linee', di seconda specie, se denotano 'superfici', di terza specie e se, infine, individuano 'volumi', di quarta specie (Peano non considera forme di specie superiore alla quarta). Il 'prodotto progressivo' tra una forma di specie i e una forma di specie j, supponendo i+j≤4 (nel caso del piano, i+j≤3), è la somma dei prodotti di ogni termine della prima per ogni termine della seconda. Risulterà allora che un punto A è la forma di prima specie più semplice e che un segmento (orientato) AB è il prodotto progressivo di due punti, come pure che un triangolo ABC lo è di tre punti oppure di un segmento BC per il punto A. D'altro canto la forma di prima specie B−A rappresenta anch'essa un segmento orientato. Si ha inoltre che AB=−BA e quindi AA=0. Il prodotto progressivo interpreta l'operazione di 'proiezione', come si può constatare sia nel caso del prodotto AB (proiezione dal punto A al punto B) sia nel caso del prodotto ABC (fig. 2, proiezioni dal punto A ai punti del segmento BC).
In questo contesto, alcuni semplici fatti geometrici si lasciano tradurre in particolari prodotti progressivi uguagliati a zero. Così per esempio:
Un'altra fondamentale operazione del calcolo geometrico è il prodotto regressivo, corrispondente all'operazione geometrica di intersezione o sezione. Nel caso piano, esso viene così definito da Peano: "Alla scrittura ABCD attribuiremo il significato:
[2] ABCD=(ACD)B−(BCD)A
perciò la scrittura ABCD rappresenta una formazione di prima specie che è collineare con AB [...]. A essa daremo il nome 'intersezione' o 'prodotto regressivo'". Analogamente si potrà estendere la definizione allo spazio. La condizione per avere il prodotto regressivo è che, se i e j indicano rispettivamente la specie (o il grado) di due formazioni, nel caso spaziale sia i+j>4 e, nel piano i+j>3. A ragione Peano utilizza la stessa notazione sia per il prodotto progressivo sia per quello regressivo, essendo la discriminante tra i due prodotti costituita solo dal valore della somma i+j.
In particolare, nel Calcolo geometrico Peano mostra anche come si possano con facilità introdurre le coordinate. Tuttavia, a suo parere, il loro uso costituisce una sorta di intermediazione numerica per lo studio degli enti geometrici e delle loro proprietà, mentre il calcolo geometrico offre un approccio immediato e diretto alle questioni geometriche. Come scriverà nel 1926 Cesare Burali-Forti (1861-1931), il quale tra gli allievi di Peano fu quello che maggiormente si dedicò a ricerche sull'argomento
Le coordinate stesse, nessuna specie eccettuata, derivano come casi particolari, dal calcolo geometrico assoluto. L'opinione di taluni per cui il calcolo geometrico escluda le coordinate è dunque inesatta; il calcolo geometrico può non fare uso delle coordinate, ma è pronto a darle di qualsiasi specie. L'opinione inversa che il calcolo geometrico richieda necessariamente le coordinate cartesiane e sia un semplice e insignificante tachigrafo delle coordinate è dunque del tutto erronea. (Burali-Forti 1926, p. viii)
Discussioni e polemiche
Lo sviluppo dell'algebra vettoriale proposto da Gibbs ottenne infine un notevole successo grazie ai lavori di Oliver Heaviside (1850-1925), un autodidatta inglese che aveva apportato importanti contributi agli aspetti matematici dell'elettrodinamica. Come molti fisici dell'epoca, Heaviside notò che la teoria ortodossa dei quaternioni costituiva più che altro un intralcio, e sviluppò quindi un autonomo calcolo vettoriale, concettualmente analogo a quello di Gibbs. Pur conservandone qualche notazione, il sistema proposto da Heaviside era del tutto indipendente dalla tradizione hamiltoniana. Tra le sue principali innovazioni, vanno menzionati soprattutto gli operatori curl (rotazione) e div (divergenza). Nel primo volume della Electromagnetic theory (1893) egli descrisse questo nuovo calcolo in un capitolo di oltre 170 pagine, che costituiva il testo più ampio sull'argomento. Heaviside vi perfezionava notevolmente il calcolo vettoriale, facendone uno strumento matematico flessibile, che sotto il nome di sistema Gibbs-Heaviside metteva a disposizione i necessari fondamenti matematici non solo per l'elettrodinamica, ma anche per altri settori della fisica matematica.
Gibbs e Heaviside avevano usato i quaternioni soltanto come punto di partenza, costruendo per il resto una teoria ampiamente autonoma, come ribadivano anche in modo aggressivo nelle loro pubblicazioni. Essi furono coinvolti in un'aspra e feroce polemica durata per anni con Tait e i suoi seguaci, che continuavano a sostenere la priorità e l'utilità dei quaternioni in matematica e in fisica. Nella polemica non soltanto gli hamiltoniani si contrapponevano ai grassmanniani, ma anche, e forse in modo più accentuato, i vettorialisti in senso stretto ai sostenitori di sistemi generali (come quelli di Hamilton e di Grassmann). In particolare la disputa si sviluppò tra gli hamiltoniani ortodossi capeggiati da Tait e i vettorialisti che si rifacevano alle idee di Gibbs. I primi sostenevano che costruire un calcolo geometrico trascurando i quaternioni e in particolare i prodotti completi e i quozienti tra vettori voleva dire tornare indietro, significava rinunciare a una teoria e ai relativi algoritmi generali che permettevano di esprimere in modo matematicamente significativo questioni inerenti il calcolo vettoriale (un quaternione è la somma del prodotto scalare di due vettori, cambiato di segno, con il loro prodotto vettoriale). Anche il sistema grassmanniano presentava un unico tipo di prodotto che, come aveva spiegato Peano, nello spazio tridimensionale si distingueva a seconda che i+j fosse minore, uguale, o maggiore di 4. Il rischio di essere un semplice strumento tachigrafico era la critica più ricorrente che gli hamiltoniani (e non solo loro) facevano alle posizioni dei vettorialisti. Questi ultimi, per contro, ritenevano eccessivo e poco funzionale nelle applicazioni l'uso dei quaternioni o delle forme geometriche, ed ebbero partita vinta nel campo delle applicazioni alla fisica, in particolare alla meccanica.
Un altro punto di questa polemica che vale la pena di sottolineare era il ruolo delle coordinate. Mentre Hamilton intendeva i quaternioni come un metodo di calcolo diretto con grandezze geometriche, Gibbs e Heaviside accusavano la 'quaternionistica' di essere un metodo cartesiano, richiamandosi con ciò all'intento fondamentale di Grassmann di sviluppare un calcolo che operasse con grandezze geometriche senza l'ausilio di coordinate. A rendere le cose più complicate c'erano poi le differenti notazioni, anche all'interno delle correnti rivali. Lo scontro divenne manifesto nel 1908, al III Congresso internazionale dei matematici a Roma, quando fu istituita finalmente una commissione internazionale per l'unificazione delle notazioni del calcolo vettoriale. Quando nel 1909 i suoi membri Burali-Forti e Roberto Marcolongo (1862-1943) pubblicarono una proposta di unificazione, si levò un coro di indignate proteste e ci fu un dilagare sterminato di soluzioni alternative. La commissione non fu in grado di portare a conclusione il suo incarico fino al Congresso seguente, tenutosi nel 1912.
Secondo Michael Crowe, che ha analizzato dettagliatamente questa polemica, essa riguardava essenzialmente l'Inghilterra e gli Stati Uniti. Per quanto concerne gli sviluppi nell'Europa continentale egli si è limitato a constatare l'affermarsi del calcolo vettoriale di Gibbs e Heaviside, da lui definito come quello moderno. Indubbiamente il sistema di Hamilton si trovava avvantaggiato nell'area anglosassone, dove praticamente non esisteva alcuna traduzione dei lavori di Grassmann, anche se era presente una serie di lavori sulla sua opera, a cominciare da quelli di William K. Clifford (1878). Con l'intenso sviluppo dell'elettrodinamica, fu in questa disciplina che si impose a tutta prima il sistema dell'algebra vettoriale di Gibbs e Heaviside, che comportava il ripudio dell'ortodossia dei quaternioni e l'integrazione al suo interno di elementi del sistema di Grassmann. Finalmente, dopo che Klein e Sommerfeld lo adottarono nel 1897 per le loro ricerche sul giroscopio, sulla scia del manuale di August Föppl Einführung in die Maxwellsche Theorie der Elektrizität (Introduzione alla teoria maxwelliana dell'elettricità,1894), quel sistema fu recepito e in larga misura accettato in elettrodinamica anche nell'area di lingua tedesca. Tra il 1900 e il 1920 questa forma di calcolo vettoriale fu sempre più usata anche in meccanica, sicché i 'bi-vettoriani'puri, come erano stati definiti da Peano i seguaci di Grassmann, finirono per trovarsi in minoranza rispetto ai 'mono-vettoriani'.
Epilogo
La problematica relativa al calcolo geometrico trova sistemazione definitiva nel corpus matematico negli anni successivi alla Prima guerra mondiale con la definizione di alcune tematiche fondamentali e la contemporanea perdita di interesse per l'argomento. Quest'ultima tuttavia non dipese soltanto dalla comparsa di impostazioni alternative, in particolare dagli sviluppi dell'algebra delle matrici. Infatti, la rilevanza del calcolo geometrico nel panorama delle ricerche geometriche del periodo è davvero alquanto relativa. D'altro canto, alcune generalizzazioni delle idee originarie di Grassmann e Hamilton, come i biquaternioni dello stesso Hamilton (1853) e di Clifford (1870), gli ottetti di John Graves (1843) e di Arthur Cayley (1845, 1847), gli stessi lavori di Peirce sembravano essere poco fecondi. Inoltre, un fondamentale teorema di Ferdinand Georg Frobenius (1849-1917) stabiliva che i numeri reali, i numeri complessi, i quaternioni a coefficienti reali sono gli unici corpi associativi che da un punto di vista additivo costituiscono spazi vettoriali di dimensione finita rispettivamente 1, 2, 4 sui numeri reali.
Anche se il calcolo vettoriale si era affermato con tanto successo in fisica matematica, in generale i matematici non ritenevano che quel calcolo fosse molto utile, neppure in geometria. Anche le sue applicazioni alla geometria differenziale rimanevano marginali rispetto alle correnti dominanti, rappresentate per lungo tempo da Luigi Bianchi (1856-1928) e Jean-Gaston Darboux (1842-1917), che non ne facevano il minimo uso. Soltanto in seguito all'affermarsi della teoria della relatività di Einstein il calcolo vettoriale e tensoriale divenne strumento irrinunciabile della geometria differenziale, e i lavori di Wilhelm Blaschke (1885-1962) e Dirk J. Struik (1894-2000) negli anni Venti del XX sec. ne fondarono i metodi nella loro forma classica. Negli stessi anni élie Cartan (1869-1951), che aveva presentato al pubblico francese il 'prodotto estensivo' di Grassmann in un ampio capitolo sui 'numeri complessi d'ordine superiore' dell'Encyclopédie des sciences mathématiques di Jules Molk, si ispirava alla teoria delle forme lineari e dei multivettori di Grassmann per elaborare la propria teoria delle forme differenziali, a cui si riallaccia il moderno sviluppo dell'algebra multilineare nell'opera di Bourbaki.