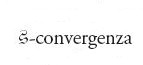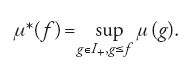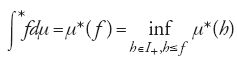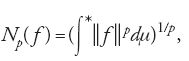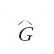La seconda rivoluzione scientifica: matematica e logica. Il Bourbakismo

La seconda rivoluzione scientifica: matematica e logica. Il Bourbakismo

Il Bourbakismo

L'avvento e l'influenza di Bourbaki costituiscono uno dei fenomeni più sorprendenti nella matematica del XX secolo. All'inizio del Novecento si stava preparando una rivoluzione in matematica e si sviluppava una tendenza verso l'assiomatizzazione e la formalizzazione. David Hilbert (1862-1943), la grande figura del momento, riteneva che in un enunciato matematico, la struttura logica fosse più importante del significato dei termini, e che quindi alle parole punto, retta, piani della geometria si potessero sostituire senza inconvenienti i termini tavolo, sedia, boccale di birra. La Francia non aveva protetto il proprio capitale intellettuale nel corso della Prima guerra mondiale; la sua scuola matematica era regredita e non occupava più una posizione d'avanguardia. Questa sfida fu raccolta da alcuni giovani della École Normale Supérieure di Parigi nel 1934. Il loro obiettivo iniziale era scrivere un manuale aggiornato, destinato a presentare un'esposizione coerente e completa dell'analisi matematica. Il nucleo del gruppo era formato da Henri Cartan, Claude Chevalley, Jean Delsarte, Jean Dieudonné, André Weil. All'inizio comprendeva anche René de Possell, Charles Ehresmann, Szolem Mandelbrojt e il fisico Jean Coulomb. Prendeva così forma un matematico policefalo che adottava il nome di un generale dell'esercito di Napoleone III, Bourbaki. Più tardi aggiunse l'iniziale N, come Nicolas. All'indomani della Seconda guerra mondiale alcuni dei rappresentanti tra i più attivi del gruppo occuparono cattedre di matematica all'Università di Nancy e Weil si stabilì a Chicago; da allora le pubblicazioni saranno edite nella città immaginaria di Nancago.

Mentre il riferimento storico del loro progetto è rappresentato dagli Elementi di Euclide, le opere di Richard Dedekind (1831-1916) e Giuseppe Peano (1858-1932) per la teoria dei numeri e di Hilbert per la geometria sono considerate dei modelli di riferimento, come successivamente quelle di Jean Leray (Leray 1949), Cartan, Samuel Eilenberg (Cartan 1956) per l'algebra omologica; Andrej Nikolaevič Kolmogorov (Kolmogorov 1933) per il calcolo delle probabilità. Bourbaki vuole essere l'Euclide dei tempi moderni, l'autore di un'opera di riferimento indispensabile per la comprensione dell'insieme delle matematiche contemporanee. La famosa esclamazione di Dieudonné, che richiedeva l'introduzione delle matematiche più recenti nell'insegnamento, "Abbasso Euclide!", non costituisce una contradictio in terminis.

Bourbaki e i suoi metodi

La concezione generale dell'opera, messa a punto all'inizio quasi esclusivamente da francesi, si viene a collocare nella linea di Hilbert piuttosto che in quella di Jules-Henri Poincaré (1854-1912): una costruzione rigorosa sottesa dalle strutture matematiche, mentre Poincaré aveva della matematica una visione più empirica, meno preoccupata delle riflessioni strettamente astratte. La prima riunione di lavoro intenso, il primo congresso Bourbaki, ebbe luogo a Besse-en-Chandesse (Auvergne) nel 1935. Nel corso di quest'anno Bourbaki pubblicò anche il suo primo articolo relativo alla teoria della misura di Constantin Carathéodory (1873-1950).

La preparazione del trattato è laboriosa. Un membro del gruppo è incaricato di redigere un'esposizione globale su un certo campo delle matematiche contemporanee. Questo lavoro di sintesi viene esaminato collettivamente e una persona è incaricata della redazione 'bourbakista'. Il manoscritto è poi criticato senza pietà. Si succedono diversi redattori e di conseguenza si esige uno spirito di corpo. Ciononostante, alcuni manoscritti quasi terminati resteranno nel cassetto: per esempio, un lavoro annunciato sulla teoria delle categorie.

L'intera opera si intitolerà Eléments de mathématique. Il termine Eléments si intende riferito a Euclide e non nel senso di elementare. Si tratta di realizzare uno sviluppo sistematico, strutturato, comprensivo dell'assiomatica necessaria che dovrà servire come strumento di base per un matematico. È un'impresa di codifica ma a carattere creativo, destinata a far progredire le matematiche. Al tempo stesso si tratta degli elementi di matematica (mathématique) e non delle matematiche (mathématiques), come vorrebbe la lingua francese: si vuole sottolineare l'unitarietà di questa scienza. Per i bourbakisti la giustificazione del metodo adottato s'imporrà a mano a mano che usciranno le pubblicazioni, così come per Diogene il movimento si dimostra camminando.

Gli assiomi devono enunciare correttamente le regole del gioco, il contesto in cui si opera. Il punto di partenza è costituito dalla logica formale e dalla teoria degli insiemi. Le strutture sono classificate in ordine di complessità crescente. È così che all'inizio sono esaminate le strutture algebriche e topologiche, in seguito collegate. La retta dei numeri reali, munita di una struttura molto ricca, appare abbastanza tardi; bisogna passare dall'insieme dei numeri razionali a quello dei reali poiché la gerarchia delle strutture deve andare dal semplice al complesso, dal generale al particolare. Le regole generali del metodo sono suggerite dalle idee esposte da Hilbert in Axiomatisches Denken (Pensiero assiomatico, 1918).

Tav. I

L'apparizione cronologica dei diversi fascicoli dell'opera (Tav. I) non è assolutamente conforme all'organigramma strutturale e le edizioni successive di uno stesso argomento subiscono riarrangiamenti molto importanti.

L'utilizzazione concomitante di differenti edizioni relative a uno stesso soggetto può rivelarsi difficile. È appunto il caso degli spazi vettoriali topologici e dell'integrazione. Le istruzioni per l'uso dell'opera, con cui si apre ogni fascicolo, indicano la direzione nella quale si muove l'autore:

Il trattato prende le matematiche al loro inizio e dà dimostrazioni complete. La sua lettura non presuppone dunque, in linea di principio, alcuna conoscenza matematica particolare, ma solamente una certa abitudine al ragionamento matematico e una certa capacità di astrazione. Ciò nondimeno il trattato è destinato di preferenza a lettori con una buona conoscenza delle materie insegnate nel primo o nei primi due anni di università.

La presentazione, molto esigente per il lettore, non subisce modifiche a mano a mano che le pubblicazioni escono. Il corpo del testo comprende le parti giudicate fondamentali, più generali o più utili. Negli Exercices vengono proposti molti punti importanti o difficili ma non vengono fornite dimostrazioni.

Bisogna riconoscere a Bourbaki il merito di aver operato una scelta felice e accurata dei nuovi termini. La decisione è spesso presa in funzione della comodità, dell'eleganza dei suoni o può anche essere dettata da un gioco di parole, se non si tratta di una burla (spesso presente nella tradizione degli allievi dell'École Normale Supérieure). Bourbaki introduce lo spazio tonnelé (imbottigliato) nella teoria degli spazi vettoriali topologici; definisce gli encombrements (ingombri) e i concassages (sminuzzamenti) nella teoria dell'integrazione. Il suo linguaggio si imporrà rapidamente. Il senso attribuito ai termini immagine inversa, compatto, ricoprimento, palla, sfera e filtro si diffonde; i nuovi simboli matematici proposti, come quello per designare l'insieme complementare (C), conosceranno fortune alterne.

La numerazione adottata nell'opera è stata giudicata complicata, se non addirittura scheletrica. L'esempio tipo dato da Bourbaki stesso è: 'AC. III. 4 N° 5 Cor. de la prop. 6'.

Bourbaki è stato accusato di dogmatismo, dimenticando senza dubbio il fatto che l'obiettivo perseguito è la messa a punto di una sintesi piuttosto che di una enciclopedia.

Tav. II

Il piano dell'opera (Tav. II) comprende una prima parte consacrata alle strutture inserita in una piattaforma comune costruita secondo un programma coerente e in ordine di complessità crescente, e una seconda parte dove le teorie sono affiancate e non meramente classificate.

Insiemi

Il I Libro, intitolato Théorie des ensembles (E), servirà da fondamento a tutta l'opera. L'edizione del 1970 comprende essenzialmente un'esposizione rigorosa dei fondamenti ed è completato da un Fascicule de résultats destinato ai potenziali utenti matematici, all'inizio del quale si legge: "Un insieme è formato da elementi suscettibili di possedere certe proprietà e di avere tra loro, o con elementi di altri insiemi, certe relazioni" (1951, E, p. 2).

La prima parte consta di quattro capitoli. Il primo ha come obiettivo quello di fornire una descrizione della matematica formale. Dopo aver introdotto i segni che costituiscono il linguaggio delle relazioni, il saggio formalizza le nozioni di assioma implicito ed esplicito, di teorema e di dimostrazione. Si definiscono i quantificatori e si stabiliscono le loro proprietà. Si introducono le relazioni e i simboli funzionali.

Il secondo capitolo dal titolo Théorie des ensembles fornisce effettivamente il quadro organico della strumentazione di base. Qui sono descritte le nozioni di inclusione, di complementare di un insieme e di insieme vuoto. La definizione di coppia ordinata conduce a quella di prodotto di due insiemi, mentre quella di grafico permette di studiare le corrispondenze. Una specificità bourbakista consiste nell'insistere sulla nozione di funzione, distinta da quella di applicazione, secondo le seguenti precise definizioni.

Si dice che un grafico F è un grafico funzionale se per ogni x esiste al più un oggetto corrispondente a x tramite F. Si dice che una corrispondenza f=(F, A, B) è una funzione se il suo grafico F è funzionale e se il suo insieme di partenza è uguale al suo insieme di definizione. Se A e B sono due insiemi, un'applicazione da A in B è una funzione f il cui insieme di partenza (uguale all'insieme di definizione) è uguale ad A e il cui insieme di arrivo è uguale a B.

Bourbaki si autorizza a usare frasi come: "Sia una applicazione f:A→B" o anche "Sia f:A→B". Si spiegano le restrizioni, le estensioni di una funzione, la composizione di due funzioni e la funzione inversa; si definiscono inoltre le funzioni iniettive, suriettive e biiettive.

Si passa poi allo studio delle proprietà dell'unione e dell'intersezione di una famiglia di insiemi, nonché dei ricoprimenti e delle partizioni di insiemi. Si introducono i prodotti di una famiglia di insiemi e i prodotti parziali; si spiega la relazione d'equivalenza e anche la nozione correlativa di compatibilità.

Il terzo capitolo costituisce una presentazione sistematica degli insiemi ordinati, della cardinalità e della teoria dei numeri interi. Le definizioni di ordine e di preordine permettono di introdurre le nozioni di applicazione crescente, elemento massimale ed elemento minimale, massimo e minimo, maggiorante e minorante, estremo superiore e inferiore, insieme filtrante e reticolo. Il concetto di insieme totalmente ordinato conduce alla nozione generale di intervallo, mentre l'introduzione dell'equipotenza di insiemi porta alla definizione e alle proprietà dei cardinali. Si dice che il cardinale a è finito o intero se a≠a+1. Si presentano i calcoli sugli interi naturali. Si espongono la divisione euclidea e le proprietà fondamentali dell'analisi combinatoria. Seguono considerazioni precise sugli insiemi infiniti, gli insiemi numerabili e calcoli con cardinali infiniti; infine si studiano i limiti proiettivi e induttivi.

Il quarto capitolo presenta la nozione matematica di struttura: "Lo scopo di questo capitolo è descrivere una volta per tutte un certo numero di costruzioni e di dimostrazioni che intervengono molto frequentemente in matematica" (1970, E, cap. IV, p. 1).

Si esaminano l'isomorfismo e il trasporto di strutture in un contesto generale. Si esplicitano le nozioni di morfismo, struttura più fine, struttura iniziale e finale. Lo studio si chiude presentando gli insiemi e le applicazioni universali.

Il punto di vista bourbakista relativo alla logica matematica è quello del matematico attivo non particolarmente interessato alle questioni dei logici puri, come emerge dall'introduzione al Fascicule des résultats:

Il lettore troverà nel presente fascicolo la maggior parte delle definizioni e dei risultati di teoria degli insiemi che saranno utilizzati nel proseguimento di quest'opera; non vi troverà alcuna dimostrazione. Per quanto riguarda le nozioni e i termini introdotti nel seguito, dei quali non è stata data una definizione, egli potrà limitarsi ad attribuire loro il senso usuale; ciò non porrà alcun inconveniente per la lettura di questo trattato e renderà quasi immediata la maggior parte delle proposizioni enunciate in tale fascicolo. La lettura del libro sulla teoria degli insiemi è indispensabile per i lettori desiderosi di sapere come si possano superare le difficoltà logiche create dalla presenza di tali termini non definiti [...]. Il lettore non mancherà di osservare che il punto di vista 'naïf' che è adottato in questo volume per esporre i principî della teoria degli insiemi è in opposizione diretta con quello 'formale' adottato nel libro di teoria degli insiemi di cui tale fascicolo è il riassunto; ci si intenda: questo contrasto è voluto e corrisponde agli scopi diversi in vista dei quali sono scritte queste due parti della nostra opera. (1970, E, R, p. 1)

Algebra

La prima versione del libro Algèbre (A) si limita a presentare le strutture algebriche; introduce le nozioni di gruppo, gruppo con operatori, gruppo di trasformazioni, anello e anello con operatori, corpo. Il libro, al susseguirsi delle uscite delle edizioni successive si è arricchito nella forma e nei contenuti ed è diventato molto esaustivo. Il trattato di algebra costituisce la parte dell'opera che ha subito il maggior numero di rifacimenti successivi.

Il primo capitolo presenta le strutture algebriche fondamentali. Dopo aver introdotto le nozioni di 'magma' e di legge di composizione descrive l'associatività, la stabilità di una parte, gli elementi permutabili, le leggi commutative, le leggi quoziente. Spiega inoltre le nozioni di elemento neutro, elemento semplificabile, elemento invertibile, l'insieme degli interi razionali e le potenze. Introduce il concetto generale di azione di un insieme su un altro; in questo contesto spiega anche la distributività. La definizione di gruppo è seguita da quella di gruppo di operatori G nell'insieme Ω, cioè di gruppo G munito di un'azione su Ω, distributiva rispetto alla legge del gruppo. Si discutono i sottogruppi, i gruppi quozienti, la decomposizione di un omomorfismo di gruppi e il teorema di Jordan-Holder; si studiano i gruppi monogeni. A proposito di gruppi operanti su un insieme si introducono le nozioni di stabilizzatore, di automorfismo interno, di orbita, di insieme omogeneo e si descrive il gruppo di permutazioni di un insieme finito. La teoria dei gruppi fa poi intervenire le nozioni di estensione, commutatore, successione centrale discendente, gruppo nilpotente, successione derivata, gruppo risolubile, p-gruppo, sottogruppo di Sylow. Appaiono in seguito il magma libero, il monoide libero, il gruppo libero e la presentazione di un gruppo. Lo studio degli anelli comprende gli omomorfismi di anelli, i sottoanelli, gli ideali, gli anelli quoziente, i prodotti di anelli e lo studio della decomposizione diretta di un anello; si definisce l'anello delle frazioni. Si arriva così ai corpi, ai domini di integrità, agli ideali primi e finalmente al campo dei numeri razionali; infine si definiscono i limiti proiettivi e induttivi.

Il secondo capitolo tratta l'algebra lineare. Introduce innanzi tutto i concetti di modulo, spazio vettoriale, combinazione lineare, applicazione lineare, sottomodulo, modulo quoziente, successione esatta, prodotto di moduli, somma diretta di moduli, sottomodulo supplementare, famiglia libera, base, annullatore, forma lineare, duale, ortogonalità, trasposta di un'applicazione lineare, base duale, biduale ed equazione lineare. Si studiano i prodotti tensoriali di moduli e di applicazioni lineari. Segue l'esame delle relazioni tra prodotti tensoriali e moduli d'omomorfismo, della traccia di un endomorfismo, dei limiti proiettivi e induttivi di moduli. Si approfondisce lo studio degli spazi vettoriali considerando in particolare dimensione, codimensione e rango di una applicazione lineare, e il prodotto tensoriale di spazi vettoriali.

Si introducono gli spazi affini e gli spazi proiettivi; si descrive inoltre il calcolo baricentrico e si esaminano le varietà lineari affini e le applicazioni lineari affini. Si arriva quindi allo studio delle matrici, considerate in particolare su un gruppo commutativo o su un anello e in relazione alle applicazioni lineari. Si discutono le matrici quadrate, diagonali, monomiali e triangolari. Si spiega il cambiamento di base e si definiscono le matrici equivalenti e quelle simili. Si prende in esame il prodotto tensoriale di matrici equivalenti e simili. Si introducono i gruppi commutativi graduati, gli anelli graduati e i moduli graduati.

Il terzo capitolo costituisce uno studio approfondito dell'importante classe delle algebre. In esso si definiscono i concetti di sottoalgebra, di ideale di un'algebra, di algebra quoziente, dei limiti proiettivi e induttivi di algebre e infine di base di un'algebra. Si esaminano in dettaglio numerosi esempi: algebre di endomorfismi, di matrici, algebre quadratiche, di Cayley (legate ai quaternioni), algebre di polinomi e anche algebre libere.

Il capitolo prosegue con lo studio delle algebre graduate, dei prodotti tensoriali di algebre, delle algebre tensoriali e dei tensori, delle algebre simmetriche. Si descrivono le algebre esterne; si stabiliscono le loro proprietà funtoriali e si mette in rilievo l'anticommutatività.

Si introducono il determinante di un endomorfismo e di una matrice quadrata e se ne esplicita il calcolo. La teoria dei determinanti dà luogo a un trattato completo e si studia la traccia relativa a un modulo. Si sviluppa inoltre la nozione di derivazione e si descrivono la composizione delle derivazioni, le derivazioni di algebre e le proprietà funtoriali corrispondenti. Il capitolo termina con l'esame di due nozioni complementari: le algebre e le coalgebre.

Il quarto capitolo introduce lo studio sistematico dei polinomi. Si considerano i polinomi su un dominio d'integrità, la divisione euclidea, le funzioni polinomiali su un anello commutativo e su un dominio d'integrità infinito. Intervengono in seguito le frazioni razionali e le funzioni razionali. Il differenziale e la derivata sono studiati per polinomi e frazioni razionali in un numero finito di variabili su un anello commutativo con identità; si precisa qui la derivazione di un'algebra. Si prendono infine in considerazione le serie formali; Bourbaki fa osservare che la maggior parte di tali risultati si esprime in maniera più suggestiva nel linguaggio della topologia, non ancora disponibile nel contesto adottato.

Il quinto capitolo è relativo ai corpi commutativi. Vi sono definiti i campi primi e la caratteristica. Si sviluppa la teoria delle estensioni e si espone il teorema di Dedekind, la derivazione nei campi e la teoria di Galois. Il capitolo termina con lo studio delle radici dell'unità, dei campi finiti e delle estensioni cicliche.

Il sesto capitolo inizia presentando le proprietà generali dei gruppi ordinati per esporre successivamente la positività, il teorema di decomposizione e gli elementi estremali. Nel seguito si passa agli anelli ordinati, ai corpi ordinati e alle estensioni di corpi ordinati.

Il settimo capitolo introduce gli anelli a ideali principali e spiega la divisibilità, la scomposizione in fattori estremali, la divisibilità degli interi razionali e quella dei polinomi in una variabile su un campo. Vi si espone la teoria dei moduli sugli anelli a ideali principali. L'ultima parte è relativa agli endomorfismi degli spazi vettoriali; essa studia i moduli associati, i valori e i vettori propri e la riduzione alla forma diagonale. Per il polinomio caratteristico si considerano la traccia e il determinante; si determina il polinomio caratteristico del prodotto tensoriale di due endomorfismi.

L'ottavo capitolo tratta i moduli e gli anelli semisemplici spiegando il ruolo delle nozioni di commutatore, bicommutatore, fattori e radicali. Si espone la rappresentazione lineare delle algebre ed è trattato in appendice il problema dell'aggiunta di una unità a un'algebra senza unità.

Il nono capitolo è una presentazione rigorosa di temi algebrici che esprimono alcune proprietà geometriche. Si parte da uno studio delle applicazioni bilineari e sesquilineari, dell'ortogonalità e dell'aggiunto di un omomorfismo. Si sviluppano in dettaglio il teorema di Witt e le algebre di Clifford. L'ultimo paragrafo tratta la nozione di angolo; le similitudini nel piano e la trigonometria piana ricevono una formulazione algebrica. A questo proposito Bourbaki conclude i suoi commenti storici nei termini seguenti: "Superata in quanto scienza autonoma e vivente, la geometria classica si è così trasfigurata in un linguaggio universale della matematica contemporanea, di una duttilità e di una comodità incomparabili" (1959, A, cap. IX, p. 199).

Il decimo capitolo, pubblicato solamente nel 1980, costituisce una monografia molto elaborata sull'algebra omologica.

Topologia generale

Nell'introduzione al libro Topologie générale (TG) Bourbaki giustifica le sue scelte. Benché le nozioni di limite e di continuità siano meno tardive di quella di intorno, quest'ultima è la prima nozione a essere presentata; si arriva così a un'ampia generalizzazione della geometria euclidea. Bourbaki può passare al concetto generale di spazio topologico prima dello studio dei numeri reali. Per quanto riguarda la scelta fatta per la definizione degli intorni, che ha dato luogo a lunghe esitazioni soprattutto da parte di Felix Hausdorff (1914) e di Maurice-René Fréchet (1928), Bourbaki scrive: "Il sistema di assiomi sul quale ci siamo finalmente fermati copre sensibilmente i bisogni attuali dell'analisi, senza cadere in una generalità eccessiva e priva di oggetto" (1971, TG, p. xii).

Bourbaki giudica d'altronde poco espressivo il termine di topologia (etimologicamente 'scienza del luogo'), preferito attualmente a quello di analysis situs.

Il libro sulla topologia, considerata come una delle basi dell'edificio matematico, non ha subito modifiche importanti nella sua concezione via via che apparivano le nuove edizioni, ma numerosi complementi vi sono stati aggiunti. Si tratta in effetti di dare un solido senso matematico alle nozioni fondamentali di limite, continuità e intorno.

Il primo capitolo presenta le strutture topologiche. Si definiscono gli insiemi aperti, chiusi, il concetto di spazio topologico e di omeomorfismo. Bourbaki insiste nel chiamare intorno d'una parte A ogni insieme che contiene un aperto contenente A. Si introduce il sistema fondamentale di intorni e la base di una topologia. Sono spiegate in questo capitolo le nozioni usuali di parte interna, chiusura e parte densa; in seguito si passano in rassegna le nozioni di sottospazio topologico, spazio topologico quoziente, la decomposizione canonica di un'applicazione continua, i prodotti di spazi topologici, i limiti proiettivi di spazi topologici nonché le applicazioni aperte o chiuse. Una specificità bourbakista consiste nel parlare dei filtri introdotti da Cartan. Un filtro su un insieme X è un insieme F di parti di X che soddisfa le seguenti proprietà: una qualsiasi parte di X contenente un insieme di F appartiene a F; qualsiasi intersezione finita di insiemi di F appartiene a F; l'insieme vuoto non appartiene a F. Si chiama ultrafiltro su X un filtro tale che non esiste alcun filtro strettamente più fine di esso. Il punto x di X è limite del filtro F se F è più fine del filtro degli intorni di x; si dice allora che F converge verso x.

Uno spazio topologico che soddisfi l'assioma di separazione di Hausdorff è detto separato. Si definisce lo spazio regolare. Bourbaki può formulare definizioni equivalenti della quasicompattezza di uno spazio topologico X: qualsiasi ultrafiltro è convergente; qualsiasi ricoprimento aperto di X ammette un sottoricoprimento finito (proprietà detta di Borel-Lebesgue). Uno spazio quasicompatto separato è detto compatto. La nozione della quasicompattezza non è studiata nelle prime edizioni. L'immagine di uno spazio quasicompatto attraverso un'applicazione continua è quasicompatta. Si stabilisce il teorema di Tychonov relativo al prodotto di spazi compatti. Si dirà che uno spazio topologico è localmente compatto se è separato e ogni punto possiede un intorno compatto. Il teorema di Alexandrov permette di associarvi uno spazio compatto X′ e un omeomorfismo sul complementare di un punto di X′. Uno spazio localmente compatto è detto numerabile all'infinito se è unione numerabile di insiemi compatti. La nozione di spazio paracompatto risalente a Dieudonné generalizza quella di spazio compatto. Si definiscono gli insiemi e gli spazi connessi; l'immagine di una parte connessa attraverso un'applicazione continua è connessa. Si studia il concetto di componente connessa di uno spazio topologico.

A seguito delle ricerche dell'eminente bourbakista Weil, il capitolo II è consacrato allo studio degli spazi uniformi. Una struttura uniforme su un insieme X è data attraverso un insieme U di parti di X×X che soddisfano gli assiomi seguenti: qualsiasi insieme di U contiene la diagonale di X×X; se V∈U, allora {(x,y)∈X×X; (y,x)∈V}∈U per qualunque V∈U, esiste W∈U tale che W°W⊂V, dove W°W è l'insieme dei (x,y)∈W×W per i quali esiste z∈X tale che (x,z)∈W e (z,y)∈W. Gli insiemi di U sono gli intorni della struttura uniforme. Una struttura di spazio topologico può esservi associata canonicamente. Si dice che un'applicazione f di uno spazio uniforme X in uno spazio uniforme X′ è uniformemente continua se per ogni intorno V′ di X′ esiste un intorno V di X tale che la relazione (x,y)∈V implica (f(x), f(y))∈V′. Le strutture uniformi possono essere confrontate. Dato uno spazio uniforme X e un intorno V di X, si dice che una parte A di X è un insieme piccolo di ordine V se A×A⊂V. Un filtro F su uno spazio uniforme X è un filtro di Cauchy se per ogni intorno V di X esiste un insieme piccolo d'ordine V appartenente a F. Uno spazio uniforme per il quale ogni filtro di Cauchy è convergente è detto spazio completo. In questo senso ogni spazio uniforme può essere completato.

Il terzo capitolo permette allora di esporre l'importante teoria dei gruppi topologici. Si esplicitano le nozioni e le proprietà relative ai sottogruppi topologici, ai gruppi topologici quozienti, agli spazi omogenei topologici, ai prodotti di gruppi topologici. Ogni gruppo topologico può essere munito di una struttura uniforme sinistra o destra. Si presentano anche gli anelli topologici e i corpi topologici. Si studiano infine i limiti proiettivi associati.

È in questo contesto che si colloca il quarto capitolo, dedicato ai numeri reali. Partendo dal gruppo ordinato dei numeri razionali, ℝ si ottiene come completamento di ℚ. L'addizione corrisponde a una struttura uniforme. Si indicano le proprietà topologiche della retta numerica e in particolare l'assioma di Archimede e il teorema di Borel-Lebesgue; le parti connesse si identificano con gli intervalli. Si può ora considerare il corpo topologico ℝ; si trascrivono le proprietà della retta reale ampliata

Segue uno studio delle funzioni numeriche, più specificamente di quelle che sono continue o semicontinue. Si esaminano infine le somme e prodotti infiniti di numeri reali e si spiegano gli sviluppi di numeri reali relativi a una base.

Il quinto capitolo presenta lo studio dei sottogruppi, dei gruppi quozienti di ℝ, del toro T, e quello delle funzioni esponenziali e logaritmiche.

Il sesto capitolo studia più in generale lo spazio numerico ℝn, la sua topologia, la distanza euclidea, e prosegue con lo spazio proiettivo reale ℙ_n.

Il settimo capitolo tratta i sottogruppi e i gruppi quozienti di ℝn nonché gli omomorfismi continui associati.

L'ottavo capitolo espone la teoria dei numeri complessi e dei quaternioni, la misura degli angoli, le funzioni trigonometriche, le somme e i prodotti infiniti di numeri complessi e gli spazi proiettivi complessi.

Il nono capitolo mostra l'utilizzazione dei numeri reali in topologia generale. Dato un insieme X si chiama scarto su X una qualsiasi applicazione

che soddisfi le seguenti condizioni: comunque si prenda x∈X, f(x,x)=0; comunque si prendano x∈X, y∈X, z∈X, si ha che f(x,y)≤f(x,z)+f(z,y). Vi si può associare una struttura uniforme. La compattificazione di Stone-Cech è qui spiegata. La distanza è uno scarto finito d per il quale d(x,y)=0 implica x=y; X costituisce allora uno spazio metrico. Lo spazio topologico X è detto metrizzabile se ammette una distanza compatibile con la topologia. Si studiano nello stesso contesto i gruppi metrizzabili, i corpi valutati, gli spazi normati su un corpo valutato e le algebre normate su un corpo valutato. Il seguito del trattato concerne gli spazi normali e il teorema di Urysohn. Si studiano diversi tipi di spazi topologici particolari; gli spazi rari, magri, di Baire, polacchi, di Souslin, sparsi, di Lusin. Si descrive la tribù dei boreliani e si presentano gli spazi di Lindelöf.

Il decimo e ultimo capitolo presenta gli spazi funzionali. Introduce la nozione generale di

,

studia la convergenza compatta, l'equicontinuità e dimostra il teorema di Ascoli. Spiega l'approssimazione delle funzioni continue numeriche con funzioni di un reticolo e con polinomi e stabilisce il teorema di Stone-Weierstrass.

Funzioni di variabile reale

Il libro sulle Fonctions de variables réelles (FVR) costituisce il volume più classico dell'opera. È una monografia di analisi matematica che viene introdotta in questi termini:

L'oggetto di questo libro è lo studio elementare delle proprietà infinitesimali delle funzioni di una variabile reale; l'estensione di tali proprietà alle funzioni di più variabili reali o, a maggior ragione, alle funzioni definite in spazi più generali potrà essere trattata solamente in libri futuri.

Le proprietà che dimostreremo sono utilizzate quando si riferiscono a funzioni numeriche (finite) di una variabile reale; ma la maggior parte si estende senza ulteriore ragionamento alle funzioni di una variabile reale definite in uno spazio vettoriale di dimensione finita sul campo ℝ: anzi, più generalmente, alle funzioni che prendono valori in uno spazio vettoriale topologico su ℝ. Tutte queste funzioni intervengono frequentemente in analisi ed è per esse che enunceremo tutte le proprietà che non sono specifiche delle funzioni numeriche. (1976, FVR, cap. I, p. 9)

Il primo capitolo studia la derivata di una funzione vettoriale definita su un sottoinsieme di ℝ. Le definizioni sono espresse nel linguaggio dei limiti, disponibile nel quadro degli spazi vettoriali topologici. La trattazione presenta la linearità della derivazione, la derivata di un prodotto, di una funzione inversa, di una funzione composta, di una funzione reciproca.

Si dimostra il teorema di Rolle per le funzioni numeriche; e il teorema degli incrementi finiti per queste funzioni e quindi per quelle a valori vettoriali. La considerazione delle derivate d'ordine superiore conduce alla formula di Taylor. Si espongono la continuità e la derivabilità delle funzioni convesse e i criteri di convessità.

Il secondo capitolo presenta la teoria delle primitive e degli integrali per le funzioni di una variabile reale a valori in uno spazio normato completo su ℝ. In assenza della nozione di misura, se f:I→ℝ per una parte I di ℝ, la funzione g definita su I è detta primitiva di f se è continua e g′(x)=f(x) in ogni punto x del complementare rispetto a I di una parte numerabile. Si introducono le funzioni a gradino e le funzioni regolate. Si ottiene l'integrale definito a partire dalle somme di Riemann. Si stabiliscono le proprietà generali dell'integrale e la forma del resto nella formula di Taylor.

Il seguito tratta la definizione dell'integrale in un intervallo non compatto. Si mostra l'utilità della nozione di convergenza assoluta di un integrale e si spiega l'integrale di un limite di funzioni in un intervallo compatto. Inoltre si studia la formula di derivazione di un integrale rispetto a un parametro e si stabilisce la formula di inversione dell'ordine delle integrazioni in un integrale doppio di una funzione continua.

Il terzo capitolo fornisce una descrizione completa della derivazione delle funzioni dette elementari e cioè le esponenziali, le logaritmiche, le circolari e le circolari inverse. Si introducono l'esponenziale complesso e il logaritmo complesso e si determinano le primitive delle funzioni razionali; si spiegano quindi le funzioni circolari complesse e le funzioni iperboliche. Seguono poi gli sviluppi delle funzioni esponenziali, delle funzioni circolari e delle funzioni a queste collegate.

Ripercorrendo la storia della matematica relativa ai temi dei primi tre capitoli del volume, Bourbaki scrive:

Abbiamo così raggiunto la tappa finale del calcolo infinitesimale classico, quella cioè che è rappresentata dai grandi trattati di analisi della fine del XIX sec.; dal nostro punto di vista, quello di Jordan occupa tra tutti un posto di riguardo, da una parte per ragioni estetiche, ma dall'altra perché, costituendo un'ammirevole messa a punto dei risultati dell'analisi classica, annuncia a più riprese l'analisi moderna e le prepara la via. Dopo Jordan viene Lebesgue e si entra nel campo di un altro libro della presente opera. (1976, FVR, cap. III, p. 66)

Il quarto capitolo presenta la teoria delle equazioni differenziali per le funzioni vettoriali. Si stabiliscono i teoremi di esistenza e di unicità; sono studiate in modo particolare le equazioni e i sistemi di equazioni differenziali lineari.

Il quinto capitolo sviluppa lo studio locale di una funzione. Si spiegano le relazioni di confronto e si considerano gli sviluppi asintotici di una funzione. Un'appendice riguarda le funzioni (H) di Hardy.

Il sesto capitolo studia gli sviluppi di Taylor generalizzati relativamente alle algebre K[X] dei polinomi a una variabile su un corpo commutativo K di caratteristica 0. Si presentano gli sviluppi euleriani delle funzioni trigonometriche.

Il settimo capitolo spiega la funzione gamma nel dominio dei reali e in quello dei complessi, gli integrali euleriani e la formula di Stirling.

Spazi vettoriali topologici

I primi due fascicoli sugli Espaces vectoriels topologiques (EVT) hanno fatto sì che si sovrapponessero le formulazioni di alcune definizioni di base, per esempio quella di insieme polare. Questa difficoltà è superata nel libro edito nel 1981.

Il primo capitolo inizia illustrando l'idea generale di spazio vettoriale topologico su un campo valutato. La completezza conduce agli spazi di Banach. Si studiano i sottospazi, le parti equilibrate, le parti assorbenti. Intervengono poi le varietà lineari, gli iperpiani chiusi e gli spazi vettoriali topologici localmente compatti. Si sviluppano in seguito le proprietà degli spazi vettoriali topologici metrizzabili.

Il secondo capitolo introduce innanzitutto la nozione di seminorma. Espone la convessità, descrive i coni convessi e le funzioni convesse. Si dimostra la forma analitica del teorema di Hahn-Banach. Si studia lo spazio vettoriale topologico localmente convesso; si introduce lo spazio di Fréchet come spazio localmente convesso metrizzabile completo. Si dimostra la forma geometrica del teorema di Hahn-Banach nel quadro del problema della separazione degli insiemi convessi. La definizione di spazi vettoriali topologici in dualità autorizza il linguaggio delle topologie deboli e degli insiemi polari; si dimostra il teorema dei bipolari. Si considerano in seguito i punti estremali degli insiemi convessi compatti e si stabilisce il teorema di Krein-Milman. Si enuncia infine la forma generale del teorema di Hahn-Banach per gli spazi vettoriali topologici.

Il terzo capitolo studia, in un quadro del tutto generale, gli spazi di applicazioni lineari continue; in particolare, il problema dei limiti, il teorema di Banach-Seinhaus e il teorema del grafico boreliano.

Il quarto capitolo costituisce un trattato completo della dualità degli spazi vettoriali topologici su ℝ o su ℂ. Si descrivono la topologia compatibile con la dualità e il linguaggio della topologia indebolita sullo spazio vettoriale dato. Si considerano ancora il biduale, gli spazi riflessivi e, in particolare, gli spazi normati. Si introduce lo spazio di Montel; segue lo studio del duale di uno spazio di Fréchet e anche quello di morfismi specifici di tali spazi. Diversi criteri di compattezza sono esplicitati.

Il quinto capitolo espone la teoria elementare degli spazi di Hilbert, presentando tutte le nozioni essenziali: le forme hermitiane positive, le forme di Hilbert, le famiglie ortogonali, il procedimento di ortonormalizzazione, il prodotto tensoriale di spazi di Hilbert. Si studiano classi di operatori negli spazi di Hilbert nonché applicazioni parzialmente isometriche, endomorfismi positivi e le applicazioni dette di Hilbert-Schmidt.

Integrazione

Nel 1952 appare il primo volume sull'integrazione (INT), suddiviso in quattro capitoli.

Il capitolo introduttivo discute le disuguaglianze di convessità, quelle di Hölder e di Minkovski, e le seminorme associate. Il secondo capitolo definisce gli spazi di Riesz, studia le forme lineari in questi spazi e considera, più precisamente, gli spazi completamente reticolati.

Nel terzo capitolo Bourbaki introduce la sua teoria della misura e dell'integrazione. Il risultato di Frigyes Riesz (1880-1956), che caratterizza il duale dello spazio vettoriale delle funzioni continue in un intervallo compatto, diventa adesso definizione. Se E è uno spazio compatto, una misura (di Radon) μ in E è una qualunque forma lineare continua nello spazio C(E) delle funzioni numeriche continue definite in E; per f∈C(E), μ(f) è l'integrale di f rispetto a μ. Si considerano le misure positive e la norma di una misura. Se E è uno spazio localmente compatto, K(E) indica lo spazio vettoriale delle funzioni numeriche continue in E, a supporto compatto; la misura (di Radon) μ è una forma lineare in K(E) tale che, per qualunque compatto K di E, la restrizione di μ alle funzioni di K(E) a supporto in K è una forma lineare continua. Si studiano le misure limitate, la topologia vaga sullo spazio delle misure, il supporto di una misura e le misure a supporto compatto. Queste definizioni sono estese alle funzioni vettoriali continue; si introduce il centro di gravità. Si descrivono il prodotto di misure e il limite proiettivo di misure.

Il quarto capitolo riguarda il prolungamento delle misure. Sia E uno spazio localmente compatto; si indica con I₊ l'insieme delle funzioni positive, non necessariamente finite, semicontinue inferiormente in E. L'integrale superiore di f∈I₊ rispetto alla misura positiva μ è definito da

Se G è un aperto di E e φ_G è la funzione caratteristica associata, si pone μ*(G)=μ*(φ_G); la misura esterna μ* è così definita. Se f è una funzione positiva di E si pone

S'introduce anche la misura esterna d'una parte qualunque di E. La funzione f è detta trascurabile per μ se μ*(f)=0; si spiega il linguaggio di Lebesgue del 'quasi ovunque'. La parte A è detta trascurabile se μ*(A)=0.

Si considerano ora funzioni di E in uno spazio di Banach F. È stabilita la disuguaglianza di Minkowski; si pone

,

con 1≤p⟨∞. Con

si designa la chiusura dello spazio delle funzioni continue di E in F, a supporto compatto, relativo alla topologia definita dalla seminorma N_p; L^p_F(E,μ) è lo spazio di Banach quoziente associato.

Si stabiliscono le proprietà delle funzioni con potenza p-esima integrabile; si dimostra il teorema di Lebesgue. Una parte A di E è detta integrabile se, essendo φ_A la funzione caratteristica di A, risulta φ_A∈L¹; μ(A)=∫φ_Adu è la misura di A. Sono qui forniti i criteri dell'integrabilità di A. Si introducono anche la nozione di clan e le funzioni additive d'insieme.

L'applicazione f:E→F si dice misurabile rispetto a μ se per ogni compatto K di E esiste un insieme μ-trascurabile N in K e una partizione di K∩⊂N formata da una successione (K_n) di insiemi compatti tali che la restrizione di f a ogni K_n sia continua. La parte A è detta misurabile se lo è la funzione φ_A. Si trascrivono quindi le proprietà delle funzioni misurabili e delle parti misurabili. Infine, il capitolo ritorna sulle disuguaglianze di convessità e illustra le disuguaglianze di Hölder per gli spazi Lp.

Il quinto capitolo è intitolato Intégration des mesures. Vi si fissano alcuni concetti importanti sulle misure di Radon, come quello delle misure indotte. Se f è una funzione positiva su E, si chiama integrale superiore essenziale di f rispetto alla misura positiva μ il limite superiore degli ∫*fφ_kdu, dove k varia nell'insieme delle parti compatte di E; si definiscono le funzioni essenzialmente integrabili. Si studiano le misure definite attraverso le densità numeriche, le misure equivalenti, le misure esterne legate alla dualità degli spazi Lp, le misure diffuse e le misure atomiche. Si considera l'immagine di una misura attraverso una trasformazione di spazi localmente compatti. Si studia poi l'integrazione rispetto a una misura indotta, si definisce il prodotto di misure e si dimostra il teorema di Lebesgue-Fubini.

Il sesto capitolo tratta le funzioni vettoriali. Si definiscono le misure vettoriali e si dimostra una forma del teorema di Dunford-Pettis. La disintegrazione delle misure è la soluzione astratta di un problema che risale intuitivamente al metodo degli indivisibili di Bonaventura Cavalieri (1598-1647).

Il settimo capitolo introduce le definizioni di misura invariante, relativamente invariante e quasi invariante. Si dimostrano l'esistenza e l'unicità (a meno di un fattore moltiplicativo) di una misura (di Haar) invariante a sinistra μ, nel gruppo localmente compatto G. Si studiano le proprietà della funzione modulo Δ determinata da ∫_G f(xa)Δ(a)dμ(x)= =∫_G f(x)dx, con a∈G, f∈L¹(G,μ). D'altra parte si esamina l'esistenza di misure quasi invarianti e di misure invarianti in uno spazio omogeneo. Si esplicita la misura di Haar su uno spazio quoziente; vengono trattati numerosi esempi e applicazioni.

L'ottavo capitolo tratta la teoria generale della legge associativa costituita dal prodotto di convoluzione, in particolare per le misure limitate. La teoria in questione permette di considerare l'algebra delle misure su un gruppo localmente compatto e la convoluzione di una misura con una funzione. Si determinano unità approssimate limitate in questa algebra.

Il nono capitolo costituisce un lavoro originale. La trattazione molto generale riprende gli argomenti del quarto capitolo, concedendo però una parte più ampia all'aspetto riguardante le funzioni d'insieme delle misure previsto dai probabilisti. Questa nuova impostazione è così descritta:

Questo capitolo è consacrato all'integrazione negli spazi topologici separabili non necessariamente localmente compatti, e in particolare negli spazi vettoriali localmente convessi; l'integrazione permette di estendere a questi ultimi la teoria della trasformata di Fourier. Il tipo di esposizione scelto nei primi paragrafi consiste nel riportarsi, per quanto possibile, al caso degli spazi compatti trattato nei capitoli precedenti. (1969, INT)

Dopo l'introduzione di una nozione di encombrement, si definiscono le premisure e le misure per uno spazio topologico qualsiasi. Si studiano le funzioni localmente trascurabili e le funzioni misurabili, nonché il supporto di una misura. Si introduce una nozione di concassage sullo spazio topologico. Si definisce l'integrale superiore e si sviluppa una teoria dell'integrazione.

Nel seguito si considerano le operazioni sulle misure. Si studia la misura indotta, la misura definita da una densità, l'immagine di una misura, il sollevamento e il prodotto di misure, una forma del teorema di Fubini e un risultato della disintegrazione di una misura.

Un importante sviluppo precisa il legame tra le misure e le funzioni additive d'insieme. Si studiano i limiti proiettivi e i sistemi proiettivi di misure; la teoria della misura è approfondita per gli spazi completamente regolari.

L'ultima parte introduce il concetto di promisura, un sistema proiettivo di misure su uno spazio localmente convesso. Si può considerare l'immagine di una promisura e definire la trasformata di Fourier su una promisura. Segue un calcolo di integrali gaussiani con esempi di promisure gaussiane. Si descrive la misura di Wiener ed è verificata la continuità della trasformata di Fourier. Si studiano le misure sul duale di uno spazio nucleare e su uno spazio di Hilbert. Infine si presenta una versione del teorema di Bochner relativo alle funzioni di tipo positivo.

Algebra commutativa

Dal XIX sec. si è evidenziata una certa analogia tra teoria dei numeri algebrici e geometria algebrica; più precisamente, tra l'anello dei numeri algebrici e quello delle funzioni algebriche. Il libro Algèbre commutative (AC) si propone di sviluppare concetti fondamentali applicabili tanto agli anelli commutativi quanto ai moduli su tali anelli. Si legge nell'introduzione: "Se l'algebra commutativa è uno strumento essenziale per sviluppare la geometria algebrica in tutta la sua generalità, dal canto suo [...] il linguaggio della geometria risulta essere estremamente adatto per esprimere i teoremi di algebra commutativa e suggerirne una certa intuizione, naturalmente abbastanza assente nell'algebra astratta" (1961, AC, cap. I, p. 11).

Il primo capitolo introduce la nozione di diagramma con la seguente osservazione restrittiva: "Un diagramma non è un oggetto matematico ma solamente una figura" (ibidem, p. 14).

È qui che si definisce il diagramma commutativo, il diagramma del serpente. Il capitolo costituisce una descrizione precisa e dettagliata della teoria dei moduli piatti con i prodotti tensoriali come punto di partenza. Quest'indagine è precedente all'edizione del fascicolo sull'algebra omologica. Nell'attesa il lettore è rimandato alla consultazione delle opere di Cartan ed Eilenberg (1956) e di Roger Godement (1958).

Il secondo capitolo tratta il passaggio dalla localizzazione alla globalizzazione. Dopo aver formulato la definizione di ideale primo, il capitolo descrive gli anelli e i moduli di frazioni. L'introduzione degli anelli locali e dei moduli su un anello locale permette il passaggio dal locale al globale; si studiano inoltre gli spazi irriducibili, gli spazi topologici noetheriani, lo spettro primo di un anello e la topologia di Zariski.

Il terzo capitolo è dedicato alle algebre graduate di tipo finito e agli anelli e moduli filtrati. Il quarto capitolo esamina gli ideali primi associati a un modulo e la decomposizione primaria. Il quinto capitolo discute gli elementi interi, il problema del sollevamento degli ideali primi e gli anelli di Jacobson. Il sesto capitolo studia le valutazioni su un anello o su un corpo, la topologia definita da una valutazione e il valore assoluto. Il settimo capitolo tratta il problema dei divisori. Vi si presentano gli anelli di Krull, di Dedekind e gli anelli fattoriali. L'ottavo capitolo riguarda la nozione generale di dimensione di un anello e di un'algebra. Il nono capitolo studia gli anelli locali noetheriani completi.

Varietà

Il fascicolo di risultati sulle Variétés différentielles et analitiques (VAR) espone le nozioni fondamentali e i risultati principali della teoria delle varietà differenziali e delle varietà analitiche su un corpo valutato completo non discreto.

Le funzioni differenziabili, la composizione di funzioni derivabili, le derivate parziali sono presentate dapprima in un quadro generale; nel seguito sono esaminate più specificamente le funzioni differenziabili reali e le funzioni analitiche reali o complesse.

Si fornisce il linguaggio di base delle varietà: mappe, atlanti, spazi tangenti, immersione, submersione e subimmersione. Vengono introdotti i concetti di fibrazione e di spazio fibrato, mentre la definizione di fibrato vettoriale permette di parlare di prodotti tensoriali, di spazi tensoriali e anche di algebra esterna.

Alcune versioni del teorema di Stokes sono soltanto enunciate, sebbene la ricerca di una dimostrazione appropriata di questo celebre teorema sia stata una delle spinte propulsive per l'impresa Bourbaki. Nel parlare dei programmi di calcolo infinitesimale nel primo ciclo universitario, Dieudonné passa sotto silenzio lo studio degli integrali multipli e delle forme differenziali, schierandosi contro una presentazione eccessivamente dettagliata di tali argomenti.

Gruppi e algebre di Lie

Il libro su Groupes et algèbres de Lie (LIE) è costituito da quattro volumi.

Il primo capitolo è una presentazione dettagliata della teoria delle algebre di Lie. Vi si fissano in partenza le nozioni fondamentali, come quelle di ideale, di serie derivata, di serie centrali discendenti e ascendenti, per poi passare allo studio dell'algebra inviluppante di un'algebra di Lie, alla dimostrazione del teorema di Poincaré-Birkoff-Witt e al problema delle rappresentazioni di un'algebra di Lie. Un'attenzione particolare è rivolta alle algebre di Lie nilpotenti, alle algebre di Lie risolubili e al radicale di un'algebra, segue poi lo studio delle algebre di Lie semisemplici e la dimostrazione del teorema di Levi-Malcev. Il capitolo si conclude con lo studio del teorema di Ado.

Il secondo capitolo riguarda le algebre di Lie libere: si tratta di un resoconto specialistico di risultati le cui radici risalgono a Philip Hall (1904-1982), Wilhelm Magnus (1907-1990) ed Ernst Witt (1911-1991) e in cui viene presentata la serie di Hausdorff.

Il terza capitolo getta le basi della teoria dei gruppi di Lie. Si inizia con la spiegazione delle nozioni fondamentali (compresa la definizione locale di un gruppo di Lie) e con l'introduzione del gruppo dei vettori tangenti a un gruppo di Lie. Di seguito troviamo illustrato il dizionario che stabilisce la corrispondenza tra i gruppi di Lie e le algebre di Lie. Per garantire il passaggio dai gruppi alle algebre si sviluppano le proprietà funtoriali e la rappresentazione aggiunta. Il passaggio inverso si ottiene tramite l'applicazione esponenziale. Dopo aver presentato i calcoli formali nei gruppi di Lie, si passa allo studio dei gruppi di Lie reali e complessi, dei gruppi di Lie su un corpo ultrametrico, dei gruppi di Lie su ℝ, del gruppo ℚ_p dei numeri p-adici, nonché dei relativi sottogruppi. Più avanti i concetti di commutatore, centralizzatore, normalizzatore permettono di introdurre i gruppi di Lie nilpotenti, quelli risolubili, lo studio del radicale di un gruppo di Lie e i gruppi di Lie semisemplici. Infine è presentato il gruppo degli automorfismi di un gruppo di Lie. Lo studio dei gruppi semisemplici analitici e algebrici conduce a strutture più complesse che, con le loro algebre di Lie, sono l'oggetto del lavoro dei capitoli successivi. Bourbaki ci segnala che "nella stesura di questi tre capitoli un aiuto prezioso è stato apportato dalle numerose conversazioni con Jacques Tits […]" (1968, A, capp. 4-6, p. 8). Vengono qui discussi i gruppi di Coxeter, i sistemi di Tits, i gruppi generati dalle riflessioni, i sistemi di radici, il gruppo affine di Weyl, e in appendice, i grafi e le loro componenti connesse: alberi e foreste.

Il settimo capitolo descrive le sottoalgebre di Cartan, gli elementi regolari di un gruppo di Lie, gli automorfismi elementari di un'algebra di Lie, gli elementi regolari di un'algebra di Lie, nonché le algebre di Lie scindibili.

L'ottavo capitolo comincia con lo studio dell'algebra di Lie SL(2,k) per un corpo commutativo k di caratteristica zero e le sue rappresentazioni, per passare poi all'algebra di Lie semisemplice dispiegata. Vi si descrivono gli automorfismi di un'algebra di Lie semisemplice e la sottoalgebra massimale di un'algebra di Lie semisemplice.

Teorie spettrali

Il libro intitolato Théories spectrales (TS) è un trattato che si occupa delle algebre di Banach e dell'analisi armonica commutativa astratta.

La prima parte presenta le algebre normate. Si comincia con l'introdurre le nozioni di algebra unitaria, spettro, carattere, ideale primo, nonché la topologia di Jacobson. Per le algebre normate si studiano il raggio spettrale, il radicale e lo spettro di un elemento. La teoria di Gelfand permette di caratterizzare l'algebra di Banach commutativa e di esplicitare il corrispondente calcolo funzionale olomorfo. Lo studio delle algebre di Banach commutative regolari introduce il problema della sintesi armonica. Le algebre normate involutive danno luogo a una teoria elaborata: è il caso, per esempio, delle C*-algebre commutative, caratterizzate assieme al calcolo funzionale a esse associato. In particolare sono studiati gli oggetti fondamentali che costituiscono l'algebra del gruppo localmente compatto e l'algebra delle funzioni numeriche continue su uno spazio compatto.

Il secondo capitolo discute i gruppi localmente compatti commutativi. Dopo aver introdotto il gruppo duale

dei caratteri continui, si studiano la trasformata di Fourier, il teorema di Plancherel e l'algebra di gruppo A(G). La formula di inversione di Fourier porta alla regolarità dell'algebra di gruppo L¹(G) e alla teoria della dualità di Pontrjagin, e si stabilisce la formula di Poisson. Il capitolo espone inoltre la struttura dei gruppi localmente compatti commutativi G e la sintesi armonica in L¹(G), L^∞(G), L²(G).

In contrasto con l'aridità del carattere generale dell'opera, Bourbaki aggiunge alle varie parti le Notes historiques, che dal 1960 saranno tra l'altro raccolte in un loro specifico volume. Nell'illustrare lo stato attuale della matematica, egli cambia finanche lo stile del suo testo, che diventa quasi narrativo, allo scopo di porre in chiara evidenza il percorso delle idee.

Alcuni matematici del gruppo Bourbaki hanno inoltre pubblicato opere di riferimento per proprio conto, come per esempio la Theory of Lie groups I (1946) e la Théorie des groupes de Lie II, III, (1951, 1955) di Claude Chevalley; l'opera di Henri Cartan e di Samuel Eilenberg; gli Eléments de géometrie algebrique (1971) di Alexander Grothendieck e di Jean Dieudonné. Poiché numerosi testi preparati da Bourbaki e prossimi alla versione definitiva non sono stati pubblicati ci si deve domandare se l'impresa possa ancora sperare in un avvenire. Nonostante l'indelebile influenza che essa ha avuto sul metodo matematico così come sullo stile delle pubblicazioni matematiche per almeno un terzo del XX sec., tale impresa non potrà probabilmente essere proseguita nella stessa forma a causa dei grandi cambiamenti avvenuti nella matematica che hanno notevolmente ridotto l'importanza del concetto di struttura.