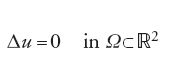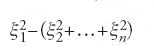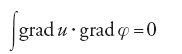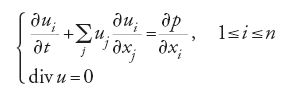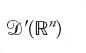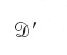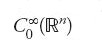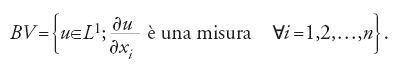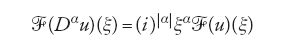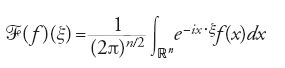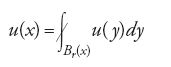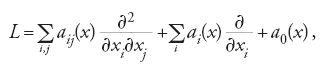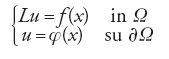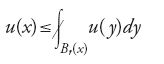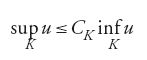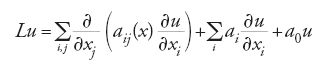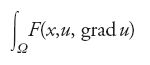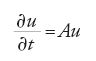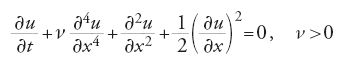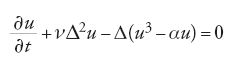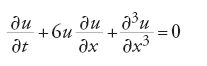La seconda rivoluzione scientifica: matematica e logica. Equazioni differenziali alle derivate parziali

La seconda rivoluzione scientifica: matematica e logica. Equazioni differenziali alle derivate parziali

Equazioni differenziali alle derivate parziali

Lo studio delle equazioni differenziali alle derivate parziali (EDP) comincia nel XVIII sec. a opera di Euler, Jean Le Rond d'Alembert, Joseph-Louis Lagrange e Pierre-Simon de Laplace come strumento decisivo per la descrizione della meccanica dei continui e più in generale come il principale metodo per lo studio analitico dei modelli delle scienze fisiche. L'analisi dei modelli fisici è ancor oggi fondamentale per lo sviluppo delle EDP. A partire dalla metà del XIX sec., in particolare con i lavori di Georg Friedrich Bernhard Riemann, esse sono divenute uno strumento essenziale anche in altre branche della matematica. Questo duplice punto di vista è stato cruciale per lo studio delle EDP nel XIX e XX secolo. Da un lato è mantenuto il rapporto con i modelli della fisica, dell'ingegneria e di altre discipline applicate; dall'altro vi sono potenziali applicazioni delle EDP, spesso rivelatesi rivoluzionarie, come strumento di sviluppo di altre branche della matematica. Questa duplice prospettiva fu espressa esplicitamente per la prima volta da Jules-Henri Poincaré in un articolo del 1890 che doveva rivelarsi profetico. Poincaré sottolineava come una grande varietà di problemi significativi di fisica che nascono in campi molto diversi tra loro (elettricità, idrodinamica, teoria del calore, magnetismo, ottica, elasticità, ecc.) si somigliano tutti, hanno un air de famille, e vanno quindi trattati con metodi comuni. Poincaré evidenziava inoltre l'interesse di avere a disposizione dimostrazioni rigorose, anche se i modelli sono soltanto un'approssimazione della realtà fisica. Ciò perché i matematici desiderano che le loro ricerche si concludano in una forma precisa e convincente, e perché la teoria che ne risulta è uno strumento che viene usato in aree della matematica di grande rilievo, come per esempio l'analisi di Riemann delle funzioni abeliane.

In quello stesso lavoro si trova inoltre un'intuizione, anch'essa profetica, e precisamente che varie equazioni della fisica matematica avrebbero avuto un ruolo significativo all'interno della stessa matematica. Ciò ha in effetti caratterizzato per tutto il XX sec. il ruolo fondamentale delle EDP come principale collegamento tra argomenti centrali della matematica applicata e delle scienze fisiche e lo sviluppo di idee matematiche in aree attive di ricerca della matematica pura.

Le origini della teoria moderna delle equazioni alle derivate parziali e l'opera di Poincaré

Fin verso il 1870 lo studio delle EDP riguardava soprattutto i metodi euristici per determinare soluzioni di problemi al contorno e soluzioni esplicite di problemi particolari. Sotto l'influenza del programma, sostenuto da Karl Theodor Wilhelm Weierstrass intorno al 1870, che mirava a rendere rigorosa l'analisi, cominciò a crescere un'attenzione sistematica verso dimostrazioni rigorose di fondamentali risultati di esistenza. Il caso più evidente fu il problema di Dirichlet, introdotto da Riemann nel 1851, che richiede di risolvere l'equazione:

con la condizione al contorno

[2] u=φ su ∂Ω.

Riemann aveva ricondotto la risolubilità di questo problema a quello dell'esistenza di una funzione minimizzante per l'integrale di Dirichlet

nella classe di funzioni che soddisfano la condizione v=φ su ∂Ω. Nonostante Riemann avesse fornito un modello elettrostatico per il principio di Dirichlet, i metodi con i quali egli aveva dimostrato l'esistenza di una funzione minimizzante non erano però matematicamente soddisfacenti, come sottolinearono Weierstass e la sua scuola.

Contro l'argomentazione di Riemann si sollevarono due tipi di critiche. Innanzitutto, per funzionali simili all'integrale di Dirichlet era stato dimostrato che non esistono minimizzanti. Inoltre, Friedrich Prym, nel 1871, aveva fornito un esempio di un dato continuo al contorno, definito sul cerchio, per il quale nessuna estensione al cerchio ha energia finita. Così, per molti decenni, la legittimità del principio di Dirichlet secondo Riemann, come mezzo per dimostrare l'esistenza di funzioni armoniche, fu messa seriamente in dubbio. Questo programma fu ristabilito come fondamentale tema di ricerca da David Hilbert nel 1900, e diede luogo allo sviluppo di numerosi metodi.

Uno dei risultati dell'attenzione richiamata da Riemann sull'importanza dello studio delle funzioni armoniche (teoria del potenziale) nella teoria geometrica delle funzioni fu che, negli ultimi tre decenni del XIX sec., si svilupparono metodi diversi per la risoluzione del problema di Dirichlet. Il metodo di Hermann Amandus Schwarz, elaborato intorno al 1870, consiste nel dividere il dominio W in due parti e risolvere quindi alternativamente il problema in ognuna delle due parti. Nel 1877 Carl Neumann introdusse il metodo delle equazioni integrali per il problema di Dirichlet in un dominio convesso, rappresentando le possibili soluzioni mediante potenziali a doppio strato. Questo approccio venne sviluppato più sistematicamente nel corso del decennio successivo da Poincaré e più tardi da Erik Ivar Fredholm (1866-1927) e da Hilbert.

Nel 1890 Poincaré fornì la prima dimostrazione completa, in domini abbastanza generali, dell'esistenza e unicità di una soluzione dell'equazione di Laplace con condizioni continue al contorno di Dirichlet. Egli introdusse il cosiddetto metodo del balayage, un metodo iterativo che si basa sulla soluzione del problema di Dirichlet per sfere del dominio, e fa ampio uso del principio del massimo e della disuguaglianza di Harnack per le funzioni armoniche. Un'esposizione sistematica di questo metodo fu data nelle lezioni che Poincaré tenne nel 1894-1895 alla Sorbona. Assieme ai testi di Adolf von Harnack e Johann Conrad Korn, esse rappresentano l'origine del grande sviluppo della teoria del potenziale dei decenni seguenti. Il principio di massimo per equazioni paraboliche ed ellittiche del secondo ordine ha avuto un ruolo centrale in tutto il XX secolo.

Un ulteriore contributo di Poincaré risale al 1894, anno di pubblicazione di un articolo fondamentale in cui egli stabilì l'esistenza di una successione infinita di autovalori e delle corrispondenti autofunzioni. Questo risultato segna l'inizio della teoria spettrale, uno degli argomenti più importanti non solo per l'analisi funzionale, ma anche per il ruolo che ebbe in fisica teorica e in geometria differenziale nel XX secolo.

Tav. I

Charles-Émile Picard (1856-1941) e la sua scuola, a cominciare dai primi anni Ottanta del XIX sec., applicarono il metodo delle 'approssimazioni successive' per risolvere problemi non lineari ottenuti perturbando leggermente problemi lineari che ammettono una soluzione unica (Tav. I). Con questo metodo Poincaré dimostrò nel 1898 l'esistenza di una soluzione dell'equazione non lineare:

[4] ∆u=eu

che compare nella teoria della funzioni fuchsiane. Motivato da questo problema e da molti altri, non lineari, della fisica matematica, Poincaré formulò il principio del metodo della continuità, con il quale si cerca di ottenere soluzioni di equazioni non lineari immergendole in una famiglia di problemi dipendente da un parametro, cominciando da un problema semplice e cercando di estendere la risolubiltà modificando gradualmente il parametro stesso. Esso diventò uno strumento molto importante nella teoria della biforcazione di Aleksandr Michajloviã Ljapunov, Erhard Schmidt e altri, come pure per la teoria dell'esistenza per equazioni ellittiche non lineari sviluppata da Sergej Natanoviã Bernètejn, Jean Leray e Juliusz Pawel Schauder.

Il programma di Hilbert

Nel famoso discorso tenuto al Congresso internazionale dei matematici di Parigi del 1900, Hilbert presentò ventitré problemi (che saranno poi noti come problemi di Hilbert), due dei quali riguardano la teoria delle EDP ellittiche non lineari. Anche se ristretti inizialmente a un quadro variazionale, i problemi XIX e XX stabilirono quello che sarebbe stato il vasto programma di ricerca per il Novecento in questo campo.

Il problema XIX riguarda la questione della 'regolarità' delle soluzioni (in particolare l'analiticità delle soluzioni), il XX quella dell'esistenza di soluzioni di problemi al contorno, e in particolare l'esistenza di soluzioni che minimizzano principî variazionali. In relazione al problema XX, Hilbert ravvivò l'interesse per l'approccio di Riemann al principio di Dirichlet. I metodi che egli originariamente propose nel periodo 1900-1905 per il principio di Dirichlet sono complessi e difficili da seguire, ma diedero origine a vari tentativi di soluzione del problema da parte di numerosi autori, quali Beppo Levi, Henri-Léon Lebesgue, Stanislaw Zaremba, Leonida Tonelli e Richard Courant, che si rivelarono fruttuosi nella creazione di molti nuovi strumenti. Il suggerimento iniziale di Hilbert consisteva nel considerare una successione minimizzante per l'integrale di Dirichlet e dimostrare che un'opportuna successione modificata converge uniformemente a una funzione minimizzante.

Tav. II

Una variante di questo approccio fu ottenuta qualche anno dopo da Zaremba utilizzando una forma 'ammorbidita' dell'originale successione minimizzante. Un'altra versione fu presentata da Courant. Tutti questi metodi seguono il suggerimento originale di Hilbert e si basano su un criterio di compattezza nella topologia uniforme, fornito dal teorema di Ascoli. Occorre ricordare che nel 1900 la teoria degli spazi L^p in termini dell'integrale di Lebesgue, e la loro completezza, non erano ancora stati formulati. Fu Levi il primo a osservare nel 1906 che una successione minimizzante per l'integrale di Dirichlet è una successione di Cauchy nella norma di Dirichlet, e quindi converge in un opportuno spazio di completamento (rispetto alla norma di Dirichlet) a una funzione generalizzata. Con questa osservazione egli diede inizio allo studio degli spazi di funzioni associati al metodo diretto del calcolo delle variazioni, e che sono oggi noti come spazi di Sobolev (Tav. II).

Una soluzione del problema XIX fu ottenuta per le equazioni ellittiche non lineari del secondo ordine in due dimensioni da Bernètejn a partire dal 1904. I suoi metodi diedero origine a tecniche fondamentali per stabilire stime a priori per le soluzioni e le loro derivate, utilizzando in particolare la linearizzazione di equazioni non lineari nell'intorno di una soluzione.

A seguito dei risultati di Poincaré e Fredholm (1903), Hilbert, nei suoi lavori sulle equazioni integrali lineari formulò un programma generale per stabilire l'esistenza e la completezza di autofunzioni per operatori integrali lineari autoaggiunti e per l'applicazione di questi risultati alle EDP.

Bernètejn e l'inzio delle stime 'a priori'

A partire dal 1906, nei suoi lavori sulla risolubilità del problema di Dirichlet per le equazioni ellittiche non lineari, Bernètejn osservò che per poter applicare il metodo della continuità è necessario che, durante il procedimento di modifica graduale dei parametri, l'ampiezza del loro intervallo di variazione non si riduca a zero. Ciò si ottiene se le soluzioni ricavate con tale procedimento appartengono a un sottoinsieme compatto di un opportuno spazio di funzioni. Questa proprietà viene di solito stabilita dimostrando che le potenziali soluzioni e le loro derivate di vari ordini soddisfano 'limitazioni a priori'. Nel caso da lui studiato (equazioni ellittiche non lineari del secondo ordine nel piano) Bernètejn sviluppò il primo metodo sistematico per la determinazione delle stime a priori. Tali tecniche furono ampiamente affinate nel corso dei decenni successivi.

Nell'applicare il metodo a dimostrazioni di esistenza, Bernètejn si limitò ai casi in cui il problema perturbato si può risolvere per approssimazioni successive. Trent'anni dopo, Leray e Schauder combinarono le tecniche di stima a priori alla Bernètejn con concetti topologici come quello di grado di un'applicazione. Eliminando la restrizione della soluzione unica del problema linearizzato, si allargò in modo considerevole la classe delle equazioni alle quali il metodo si poteva applicare. Bernètejn nel 1904 risolse in senso positivo il problema XIX di Hilbert, dimostrando che una soluzione C³ di quella che oggi viene detta equazione ellittica completamente non lineare del secondo ordine nel piano:

[5]  F(x,y,u,Du,D²u)=0

è analitica ogniqualvolta lo è F. Per dimostrarlo, Bernètejn stabilì stime per le derivate delle soluzioni date in forma di serie di potenze. Al termine della sua argomentazione egli osservò che sarebbe stato possibile usare tali metodi per ottenere una soluzione positiva del problema XX di Hilbert sull'esistenza di soluzioni del problema di Dirichlet. In una serie di lavori che si svolsero per vari decenni, Bernètejn sviluppò tale programma stabilendo il primo metodo sistematico per dimostrare l'esistenza di soluzioni mediante stime a priori.

Schauder ritornò su questo problema nel 1934, separando la questione dell'analiticità da quella dell'esistenza. Egli osservò che le opportune stime per l'esistenza nel caso quasi lineare sono stime C^2,a, le stesse applicate da Leray-Schauder. L'ipotesi di regolarità iniziale in base alla quale l'esistenza viene stabilita tramite il metodo diretto del calcolo delle variazioni è molto più debole di C³: la soluzione appartiene a un certo spazio di Sobolev W^1,p, e nasce il problema di sapere se queste soluzioni deboli siano lisce. Tale problema fu risolto con successo da Charles B. Morrey nel 1943 in due dimensioni e il caso generale fu finalmente risolto da Ennio De Giorgi e John F. Nash nel 1957.

Risolubilità delle equazioni ellittiche lineari del secondo ordine

A seguito dei lavori di Neumann e dello sviluppo di una teoria sistematica delle equazioni integrali a opera di Poincaré, Fredholm, Hilbert e altri, fu sferrato un generale attacco al problema dello studio delle soluzioni delle equazioni ellittiche lineari del secondo ordine ottenute mediante rappresentazioni integrali. Nel caso analitico, Eugenio Elia Levi costruì nel 1907 soluzioni elementari e funzioni di Green per operatori generali lineari ellittici di ordine superiore. Il metodo parametrico fu applicato anche da Hilbert e la sua scuola allo studio di particolari problemi al contorno.

Un importante strumento in questa teoria è stata l'introduzione nel 1882 della condizione di Hölder, a opera appunto di Otto Ludwig Hölder, in un libro sulla teoria del potenziale. Lo studio di potenziali a uno e due strati, a densità appartenente a spazi di Hölder, diventò oggetto di intense ricerche con i lavori di Ljapunov (1898) e Arthur Korn (1907), in relazione alle equazioni dell'elasticità, di Leon Lichtenstein a partire dal 1912 e di Paul Lévy (1920).

Seguendo nel suo libro sulla teoria del potenziale (1929), la trattazione, data da Oliver D. Kellogg, delle funzioni armoniche, Schauder, e poco dopo Renato Caccioppoli, applicarono queste tecniche per ottenere stime a priori in spazi C^2,a per le soluzioni del problema di Dirichlet per equazioni ellittiche del secondo ordine a coefficienti C^0,a.

Schauder affronta esplicitamente il programma di stabilire risultati di esistenza per questi problemi lineari, combinando il metodo delle stime a priori con la teoria di Riesz sugli operatori lineari compatti negli spazi di Banach. Si trattò di un ponte importante tra l'analisi funzionale e la teoria delle EDP. Questo punto di vista di Schauder, unito alla topologia algebrica, fu applicato alle equazioni non lineari da Leray e Schauder.

La teoria di Leray-Schauder

Nel lavoro di Bernètejn, i risultati di esistenza, ottenuti con tecniche di prolungamento, si basano su condizioni di unicità per la soluzione di problemi linearizzati. Ciò restringe notevolmente la classe delle equazioni che possono essere trattate con quel metodo. Il contributo di Leray e Schauder nel famoso lavoro del 1934 fu quello di liberarsi della condizione di unicità per basarsi unicamente su stime a priori e metodi topologici.

Lo strumento principale che essi applicarono fu l'estensione a spazi di dimensione infinita del grado delle applicazioni, un importante passo avanti dell'analisi funzionale non lineare. Sulla base di precedenti risultati parziali di Birkhoff-Kellogg sulle estensioni del teorema del punto fisso di Brouwer a dimensioni infinite, Schauder nel 1930 aveva stabilito il fondamentale teorema del punto fisso, secondo il quale un'applicazione compatta di una palla in sé ha un punto fisso (un'applicazione si dice compatta se è continua e ha un'immagine relativamente compatta). Nel 1929-1932 Schauder generalizzò il principio di Brouwer dell'invarianza dei domini per applicazioni della forma (I-C), dove C è compatta e I denota l'applicazione identica. Nel 1934 Leray e Schauder estesero il grado delle applicazioni di Brouwer alla classe delle applicazioni della forma (I-C) e utilizzarono questa teoria, assieme alle stime a priori, per dimostrare teoremi di esistenza per equazioni quasi lineari del secondo ordine nel piano. Ciò diede luogo a un nuovo e vasto programma per ottenere ulteriori risultati di esistenza stabilendo opportune stime a priori.

Il nocciolo di questo metodo sta nell'importante proprietà del grado. Il grado, deg(I-C,G,p) si ottiene dal calcolo algebrico del numero di soluzioni dell'equazione:

[6] (I-C)u=p, u∈G

dove G è un aperto limitato in uno spazio di Banach X. Il grado è definito soltanto se non vi sono soluzioni dell'equazione sul bordo di G. Il grado è invariante per deformazioni continue C_t dell'applicazione purché resti definito durante una deformazione compatta continua, vale a dire non devono comparire soluzioni dell'equazione sul bordo durante la deformazione.

Per applicare questo principio, per esempio quando G è una palla, occorre dimostrare che non compaiono soluzioni sul bordo della palla. In pratica si dimostra per mezzo di stime a priori che le soluzioni si trovano tutte all'interno di una palla fissata. Si costruisce la deformazione C_t per collegare il dato problema C=C₁ con un problema semplice per il quale il grado si può calcolare facilmente, per esempio C₀=0. La dimostrazione delle stime a priori necessarie ha spesso posto problemi difficili, alcuni dei quali sono stati risolti solo dopo decenni di intenso lavoro. L'esempio più clamoroso è l'equazione di Monge-Ampère:

[7]  det(D²u)=f (x)

per la quale le stime furono completate soltanto nel 1980.

Hadamard e la classificazione delle EDP e loro problemi al contorno

Nello studio delle EDP classiche (equazioni di Laplace, del calore, delle onde), a ogni equazione sono di solito associate condizioni al contorno di tipo molto particolare. Per l'equazione di Laplace si ha la condizione di Dirichlet (u=φ su ∂Ω) o la condizione di Neumann (nella quale si prescrive la derivata normale ∂u/∂n su ∂Ω). Per l'equazione del calore la classica condizione al contorno consiste nel prescrivere il valore iniziale della soluzione (e nel caso di un dominio limitato la condizione di Dirichlet sul bordo del dominio per valori positivi della variabile tempo). Nel caso dell'equazione delle onde il più classico problema al contorno è il problema di Cauchy, che prescrive sia la posizione iniziale sia la velocità iniziale (al tempo t=0).

È spesso oscuro, dal punto di vista fisico, il motivo per il quale si stabilisce se una condizione al contorno è adeguata per una data equazione; è un punto che deve essere chiarito grazie a una comprensione profonda della matematica coinvolta. Fu Hadamard, nel suo libro del 1923 sul problema di Cauchy, a formulare chiaramente il principio con cui distinguere i problemi 'legittimi' o ben posti: la soluzione deve esistere in un dominio per tutti gli opportuni dati al contorno, deve essere univocamente determinata da questi dati ed essere 'stabile' rispetto alle norme appropriate.

In tal modo, per esempio, per il problema di Cauchy, il teorema di Cauchy-Kovalevskaja, dimostrato nel XIX sec. per equazioni con dati analitici, stabilisce l'esistenza di soluzioni in serie di potenze per equazioni che non sono caratteristiche rispetto alla superficie iniziale. Ciò comprende, per esempio, l'equazione di Laplace, ma in quest'ultimo caso il dominio di esistenza della soluzione varia drasticamente con i dati e le soluzioni risultano fortemente instabili rispetto ai dati al contorno. Il problema è quindi 'mal posto' nel senso di Hadamard.

Egli propose anche di determinare classi di equazioni le cui soluzioni abbiano particolari proprietà in termini di polinomi caratteristici. Questi sono i polinomi che si ottengono sostituendo ciascuna derivata parziale ∂/∂x_j con la variabile algebrica ξ_j e mantenendo il massimo ordine per ciascuna variabile. Si ottengono in particolare tre classi fondamentali di operatori del secondo ordine, detti ellittici, iperbolici e parabolici che sono, rispettivamente, generalizzazioni dell'operatore di Laplace, delle onde e del calore. Gli operatori ellittici sono definiti da polinomi quadratici che si annullano solo per ξ=0. Quelli iperbolici corrispondono, dopo un cambiamento di variabile, a

,

mentre il caso parabolico corrisponde, dopo un cambiamento di variabile, a

Questa classificazione fu in seguito estesa a EDP di ordine qualunque, a equazioni non lineari e ai sistemi. Essa fornisce il quadro fondamentale con il quale la teoria delle EDP è stata studiata sistematicamente. Vi sono in effetti diverse teorie corrispondenti a questo sistema di classificazione, che comprendono la teoria delle equazioni ellittiche, iperboliche, paraboliche e molti casi limite.

Continuando l'opera di Vito Volterra (1860-1940) sull'equazione delle onde, Hadamard sviluppò negli anni Venti del XX sec. una teoria sistematica della soluzione del problema di Cauchy per equazioni iperboliche lineari del secondo ordine in un numero qualunque di dimensioni, compresa la famosa proprietà di Huygens per l'equazione delle onde in uno spazio a un numero dispari di dimensioni. In generale, le soluzioni delle equazioni iperboliche dipendono soltanto dai dati di Cauchy in un dominio finito, il cono di dipendenza. Nel caso dell'equazione delle onde in dimensione dispari la soluzione dipende solo dai dati di Cauchy sul bordo del cono. La ben nota congettura di Hadamard afferma che l'equazione delle onde in dimensione dispari è l'unica EDP che ha questa proprietà.

La proprietà della dipendenza finita per l'equazione delle onde è strettamente legata alla velocità finita di propagazione nei segnali governati da equazioni di questo tipo. L'equazione del calore non gode di tale proprietà e ha velocità di propagazione infinita. Queste considerazioni sono fondamentali nelle applicazioni delle equazioni iperboliche alla teoria elettromagnetica, nella quale le soluzioni dell'equazione di Maxwell si propagano alla velocità della luce, come pure nelle equazioni della relatività dove, in base ai principî fondamentali, i segnali non si possono propagare a velocità superiori a quella della luce.

Il lavoro di Hadamard sulle equazioni iperboliche del secondo ordine fu generalizzato da Frigyes Riesz alla fine degli anni Quaranta del Novecento. Teorie sistematiche delle equazioni iperboliche e di sistemi di ordine qualunque furono sviluppate da vari matematici, in particolare da Ivan Georgieviã Petrovskij e Leray.

Soluzioni deboli

Fino agli anni Venti del XX sec. le soluzioni delle EDP erano generalmente intese nel senso di soluzioni classiche, cioè di classe C^k per un operatore differenziale di ordine k. La nozione di soluzione 'generalizzata' o 'debole' venne alla luce per diverse ragioni.

La prima e più semplice si ebbe in relazione al metodo diretto del calcolo delle variazioni. Nel caso di un problema variazionale, per esempio l'integrale di Dirichlet E con una successione minimizzante (u_n) di funzioni lisce per E, B. Levi e Zaremba osservarono che (u_n) è una successione di Cauchy nella norma di Dirichlet e, grazie a una semplice disuguaglianza, nella norma L². Era quindi naturale introdurre il 'completamento H' nella norma di Dirichlet dello spazio delle funzioni lisce che soddisfano una data condizione al contorno. Si tratta di una variante del processo iniziato un decennio prima nel caso degli spazi L². Lo spazio H è un sottospazio lineare di L² dotato di una norma diversa. Per definizione, per ogni elemento u di H esiste una successione di funzioni lisce (u_n) tali che grad u_n converge a un limite in L². Questo limite si può considerare come grad u, interpretato in un senso generalizzato. Tutto ciò si trova nei lavori di Levi e Leonida Tonelli; dell'argomento si occuparono anche Kurt Otto Friedrichs, Morrey e molti altri.

Il secondo punto di vista si presenta in problemi nei quali la soluzione viene costruita come limite di un processo di approssimazione. Le stime sulle soluzioni possono non essere sufficientemente forti per garantire che il limite sia una soluzione nel senso classico.

D'altra parte può essere ancora possibile dimostrare che questo limite possiede alcune proprietà che potrebbero avere le soluzioni classiche, e in particolare le relazioni che si ottengono moltiplicando l'equazione per una funzione di test liscia e integrando per parti. Ciò è ben noto nel caso di un'equazione lineare; per esempio, una soluzione classica u dell'equazione di Laplace:

[8] ∆u=0 in Ω

soddisfa:

per ogni

lo spazio delle funzioni definite in Ω, 'lisce' e a supporto compatto; e deve soddisfare anche

L'osservazione principale è che la [9] ha senso per tutte le funzioni u∈C¹ (e anche per quelle u∈H appena viste). La relazione [10] ha senso se u∈L² (o anche soltanto per u∈L¹_loc).

Nel caso di problemi lineari, in particolare per equazioni ellittiche e paraboliche, è spesso possibile dimostrare che le soluzioni, anche nel senso più debole [10], sono classiche. Il primo esempio esplicito è il celebre lemma di Weyl, dimostrato nel 1940 per l'equazione di Laplace. Questo punto di vista è stato molto sviluppato e condiviso negli anni Sessanta del XX secolo.

L'esistenza di 'soluzioni deboli' è una conseguenza immediata del processo di completamento descritto sopra. L'introduzione della nozione di soluzione debole rappresenta una svolta metodologica cruciale nello studio delle EDP e i loro problemi al contorno poiché offre la possibilità di spezzare la ricerca in due passi: (1) 'esistenza' di soluzioni deboli; (2) 'regolarità' delle soluzioni deboli.

In molti casi il secondo passo si rivela tecnicamente difficile, o addirittura impossibile. A volte la regolarità che si può ottenere è soltanto parziale, e ciò accade in particolare nel caso di equazioni non lineari. Tra i primi e più noti esempi vi sono l'equazione di Navier-Stokes:

e l'equazione di Euler:

che descrivono entrambe il flusso di fluidi incompressibili. L'equazione di Euler è il limite non viscoso della [11].

L'esistenza e unicità locale (cioè per piccoli intervalli di tempo) di una soluzione classica per l'equazione di Euler fu stabilita a cominciare dal lavoro di Lichenstein nel 1925 e più recentemente con i lavori di V. Arnold (1966), David G. Ebin e Jerrold E. Marsden (1970), Jean-Pierre Bourguignon e Haïm Brezis (1974), e Roger Temam (1975). In due dimensioni, l'esistenza di una soluzione classica globale (cioè per qualunque valore della variabile tempo) è stata considerata da W. Wolibner nel 1933 e completata da Tosio Kato nel 1967. L'esistenza di soluzioni globali classiche in tre dimensioni è a tutt'oggi un problema aperto.

Per l'equazione di Navier-Stokes l'esistenza di soluzioni 'globali deboli' (con date condizioni iniziali) fu ottenuta dapprima da Leray nel 1933, e quindi, in una forma leggermente diversa, da Eberhard Hopf nel 1950. Si è dimostrato che in due dimensioni queste soluzioni sono regolari, mentre in tre dimensioni la regolarità e l'unicità delle soluzioni deboli costituiscono uno dei più noti problemi aperti delle EDP.

Per altri ben noti modelli fisici, come la teoria delle leggi di conservazione iperboliche non lineari, per esempio l'equazione di Burger:

si possono definire soluzioni deboli che sono non regolari, vale a dire si possono avere discontinuità in un tempo finito anche se la condizione iniziale è liscia. Esse danno luogo al fenomeno delle onde d'urto con importanti applicazioni in fisica.

La teoria delle distribuzioni di Schwartz

Laurent Schwartz, nella celebre opera Théorie des distributions (1950-51) presentò le soluzioni generalizzate delle equazioni alle derivate parziali in una nuova prospettiva. Schwartz creò un calcolo, basato sull'estensione della classe delle funzioni ordinarie a una nuova classe di oggetti, le distribuzioni appunto, conservando però molte operazioni fondamentali dell'analisi, compresa l'addizione, la moltiplicazione per funzioni C^∞, la differenziazione, come pure, sotto certe condizioni, la convoluzione e la trasformata di Fourier. La classe

delle distribuzioni (su Rⁿ) comprende tutte le funzioni di

,

e ogni distribuzione T ha derivate ben definite di tutti gli ordini entro quella classe. In particolare, ogni funzione continua (non necessariamente differenziabile nel senso usuale) ammette derivata in

Se

è un operatore differenziale lineare a coefficienti lisci, allora L(T) è ben definita per ogni distribuzione T ed è ancora una distribuzione.

La definizione di distribuzione data da Schwartz si basa sulla nozione di dualità degli spazi vettoriali topologici.

è lo spazio dei funzionali lineari continui su

,

è cioè il duale dello spazio delle funzioni test a supporto compatto

,

dotato di un'opportuna topologia che comporta la convergenza delle derivate di ogni ordine. Questa definizione implica che ogni distribuzione T si può rappresentare localmente come una somma (finita) di derivate (nel senso delle distribuzioni) di funzioni continue, cioè:

per qualche funzione continua f_a e per qualche m.

Questa teoria permise di sistemare, rendendole al tempo stesso più trasparenti, precedenti definizioni di funzioni generalizzate sviluppate da Oliver Heaviside, Hadamard, Leray e Sergej L´voviã Sobolev nell'ambito della teoria delle EDP, e da Norbert Wiener, Salomon Bochner e Torsten Carleman in analisi di Fourier.

Altre significative motivazioni per la teoria delle distribuzioni erano:

a) dare un significato più trasparente alla nozione di soluzioni elementari (o fondamentali) E di un operatore ellittico L, che nel linguaggio della teoria delle distribuzioni è

[16] L(E) = δ₀

dove δ₀ è la misura di Dirac in 0, cioè δ₀(φ)=φ(0);

b) la soluzione di d'Alembert dell'equazione delle onde 1-dimensionale è u(x,t)=f(x+t)+g(x-t). La u è una soluzione classica se f e g sono lisce, e u è una soluzione nel senso delle distribuzioni se f e g sono soltanto continue (o anche soltanto L¹loc).

In termini di teoria delle distribuzioni, gli spazi di Sobolev si possono definire come:

Molte applicazioni della teoria delle distribuzioni si sono avute in problemi formulati in termini di spazi di Sobolev. Altre classi significative hanno però un ruolo importante. Un esempio è lo spazio delle 'funzioni a variazione limitata'

Questa definizione ha permesso di fare chiarezza in un campo complicato di nozioni tra loro in contrasto (in particolare nei lavori di Tonelli e Lamberto Cesari). Lo spazio BV è molto utile nel calcolo delle variazioni (per es., nella teoria geometrica della misura, nella meccanica delle fratture e nel trattamento delle immagini) come pure nello studio delle onde d'urto per le leggi di conservazione iperbolica non lineare.

Per una particolare sottoclasse

di distribuzioni, le distribuzioni temperate

Schwartz definì una trasformata di Fourier che porta

in

La classe

è definita anch'essa come lo spazio duale di una più ampia classe di funzioni test C^∞:

Con la classe

si può utilizzare il fatto molto importante che la trasformata di Fourier di D^αu è

dove

e ξ^α₁=ξ^α...ξ^α_n.

Per un operatore differenziale lineare a coefficienti costanti:

[22] L=Σa_αD^α

lo studio della soluzione dell'equazione Lu=f, dopo una trasformata di Fourier, si riduce allo studio di un'equazione algebrica:

dove

Questo problema è quindi equivalente allo studio della divisione per polinomi in vari spazi di distribuzioni. Tale punto di vista, e l'introduzione della trasformata di Fourier nel campo complesso (come fu suggerito la prima volta da Leray), è stato oggetto di intense ricerche che cominciarono nella metà degli anni Cinquanta del XX sec. nel lavori di Leon Ehrenpreis, Bernard Malgrange e Lars Hörmander.

Ciò ha dato luogo a una 'teoria della risolubilità locale' per EDP a coefficienti costanti, poi generalizzata in una teoria della risolubilità locale per equazioni a coefficienti variabili.

Nei decenni successivi la teoria delle distribuzioni fornì un linguaggio unificante per la trattazione generale delle soluzioni delle EDP. Oltre all'uso universale in analisi, essa è infatti stata largamente adottata in numerose aree dell'ingegneria e della fisica. Un'importante estensione delle tecniche della teoria delle distribuzioni è la teoria dei funzionali analitici di Sato e della sua scuola e altre teorie di iperfunzioni a essa collegate.

Metodi negli spazi di Hilbert

Uno dei grandi progressi degli anni Trenta del Novecento è stato lo sviluppo, in una forma concettualmente chiara e comprensibile, della teoria degli operatori lineari autoaggiunti e il contesto più generale per l'analisi funzionale dato dai lavori di Stefan Banach (1892-1945) e della sua scuola. La prima si basava su lavori precedenti di Fredholm, Hilbert e Riesz sulle equazioni integrali, ma la nuova formulazione dei principî fondamentali della meccanica quantistica in termini di teoria degli operatori diede un enorme impulso a uno sviluppo più sofisticato della teoria degli operatori negli spazi di Hilbert, in forma geometrica e analitica. Allo stesso tempo, a eccezione di lavori isolati di Friedrichs e Hermann Weyl, poche applicazioni di tali idee furono fatte alle EDP. Questa situazione cambiò molto rapidamente alla fine degli anni Quaranta, specialmente grazie ai primi lavori di M.I. Visik (1951) sotto l'influenza di Israil Moiseeviã Gel9fand. Visik considerò la formulazione del problema di Dirichlet per un operatore lineare uniformemente ellittico non autoaggiunto (non necessariamente del secondo ordine). I suoi risultati furono migliorati da Lars Gårding (1953) e in lavori dello stesso genere da Felix E. Browder, Friedrichs, Peter D. Lax, A. Milgram e Jacques-Louis Lions. Il contributo più importante di Gårding fu l'introduzione in questo campo dell'uso esplicito dell'analisi di Fourier e in particolare del ruolo centrale del teorema di Plancherel (1910), il quale afferma che la trasformata di Fourier è una trasformazione unitaria di L²(Rⁿ) in sé. Per ottenere una soluzione classica, a questi risultati di esistenza (e unicità) delle soluzioni del problema generalizzato di Dirichlet occorre aggiungere, quando tutti i dati siano lisci, risultati sulla regolarità di tali soluzioni generalizzate. Questi ultimi fanno intervenire sia la regolarità all'interno sia quella sulla frontiera. I risultati del primo tipo furono ottenuti con i seguenti metodi: (1) uso delle soluzioni fondamentali per operatori ellittici di ordine superiore, stabilite da Fritz John generalizzando risultati classici di Eugenio Elia Levi nel caso analitico; (2) uso del metodo di Friedrichs 'dei mollificatori' che comporta convoluzioni della funzione u con una successione di nuclei smoothing; (3) uso del metodo di Lichtenstein delle differenze finite rivisto da Morrey.

I primi due metodi si applicano a un problema più ampio, e cioè alla dimostrazione che tutte le soluzioni con distribuzioni dell'equazione Lu=f, con u∈D'(Ω) sono C^∞ quando L è ellittico, u∈L² a coefficienti lisci e f è C^∞. Quando L è il laplaciano e u∈L², tale risultato era stato stabilito da Weyl nel 1940 e questo 'lemma di Weyl' ha spinto allo studio della regolarità delle soluzioni con distribuzioni delle equazioni ellittiche. Si tratta dell'esempio più importante di una situazione nella quale ogni soluzione con distribuzioni u dell'equazione Lu=f con f∈C^∞ deve essere C^∞. Questa proprietà è stata studiata a fondo per operatori generali sotto il nome di 'ipoellitticità'.

Tali risultati sono stati applicati anche per ottenere soluzioni di equazioni di evoluzione che coinvolgono L, che siano del tipo dell'equazione delle onde parabolica generalizzata.

Uno sviluppo legato a questo e di grande importanza è dovuto all'applicazione dei 'metodi dell'energia' allo studio del problema di Cauchy per EDP e per i sistemi di EDP lineari e strettamente iperbolici. Dopo i lavori iniziali di Friedrichs sui sistemi iperbolici simmetrici, la piena generalità dei risultati anteguerra di Petrovskij fu ritrovata e ampliata da Leray, che utilizzò stime di energia globale. Queste stime furono più tardi localizzate da Gårding.

Il principio del massimo e applicazioni; le stime di De Giorgi-Nash

Un principio che caratterizza le funzioni armoniche in un dominio Ω di Rⁿ è che, per ogni x,

per ogni palla B_r(x) di Ω, dove

denota la media. Di conseguenza u non può assumere un valore massimo in un punto interno, a meno che non sia costante. A cominciare dall'opera di Paraf nel 1892, continuata da Picard e Lichtenstein, questa conclusione fu estesa a operatori lineari uniformemente ellittici del secondo ordine:

a coefficienti lisci purché a₀≤0. Un miglioramento di questo risultato fu stabilito da Hopf nel 1927 senza ipotesi di continuità sui coefficienti (purché limitati). I suoi risultati affermano che se u∈C² soddisfa:

con f≥0 in Ω, e se u raggiunge un massimo non negativo M in un punto interno di Ω, allora u≡M. In particolare, se u soddisfa la [26] con f≥0 in Ω e φ≤0 su ∂Ω, allora u≤0 ovunque in Ω. Così l'applicazione (f,φ)→u conserva l'ordine, cioè f₁≤f₂ e φ₁$φ₂ implicano u₁≥u₂. Una conseguenza di ciò è l'unicità della soluzione della [26]. Le deboli ipotesi nel risultato di Hopf implicano che esso si estenda a soluzioni molto generali di equazioni non lineari. A cominciare da Bernètejn il principio di massimo ha fornito uno strumento decisivo per dimostrare stime a priori e risultati di esistenza. Il procedimento ha sempre comportato una scelta ingegnosa di funzioni ausiliarie che soddisfino disuguaglianze alle derivate parziali ellittiche. Una delle prime importanti applicazioni del principio di massimo è stato l'uso nella teoria del potenziale delle funzioni subarmoniche:

per tutte le B_r(x)⊂Ω (o, ciò che è equivalente, ∆u≥0 nel senso della teoria delle distribuzioni). Per esempio, la soluzione di ∆u=0 in Ω con u=φ su ∂Ω coincide con sup_i∈I u_i, dove (u_i)_i∈_I denota la famiglia delle funzioni subarmoniche su Ω tali che u_i≤φ su ∂Ω. L'approccio prende il nome da Oskar Perron, che lo iniziò nel 1923. Wiener generalizzò tale risultato nel 1924 per ottenere una condizione necessaria e sufficiente affinché in un dato x₀ di ∂Ω, la suddetta u soddisfi u=φ. Da queste considerazioni si può ricavare un metodo costruttivo per risolvere una classe di equazioni ellittiche non lineari tramite un'iterazione monotona, in presenza di una coppia ordinata di sub e supersoluzioni.

Un risultato dello stesso tipo, ma più profondo, è la disuguaglianza di Harnack (1887), che afferma che se u è armonica in Ω, u≥0 in Ω, allora per ogni dominio compatto K⊂Ω

dove C_K dipende soltanto da K. Questo principio fornisce un'utile proprietà di compattezza per le funzioni armoniche.

Importanti progressi in questa direzione furono fatti da De Giorgi nel 1957, e successivamente migliorati da J. Moser e Guido Stampacchia. Il punto è che il principio del massimo, come pure la disuguaglianza di Harnack, sussistono per operatori ellittici del secondo ordine in forma di divergenza:

con a_0,≤0 sotto l'ipotesi che i coefficienti a_ij siano limitati e misurabili e soddisfino una condizione di ellitticità uniforme:

Si suppone che le soluzioni appartengano a H¹(Ω)=W^1,2(Ω). Un risultato fondamentale, la cui dimostrazione si basa su una sofisticata applicazione dei suddetti principî, afferma che ogni soluzione u∈H¹(Ω) di Lu=0 è continua, e più precisamente appartiene a qualche C^0,a. Un'analoga conclusione fu ottenuta indipendentemente da Nash per la corrispondente equazione parabolica. Come già detto queste stime costituiscono i primi passi fondamentali per risolvere il problema XIX di Hilbert, cioè per dimostrare che il problema variazionale assiociato al funzionale F:

con u=φ su ∂Ω ha un minimo liscio purché F sia liscia e la corrispondente equazione di Euler-Lagrange sia uniformemente ellittica. Questo risultato completò il lungo sforzo per stabilire la regolarità delle soluzioni deboli per problemi 'scalari', cioè quando u è una funzione a valori reali.

In molte importanti situazioni fisiche e geometriche u non è uno scalare, ma è un vettore e la corrispondente equazione di Euler-Lagrange è un sistema. Fu naturale chiedersi se la teoria si estendesse ai sistemi. Nel 1968 De Giorgi costruì un controesempio sorprendente, in cui la soluzione ha la forma x/uxu e non è continua. Un altro esempio, nel quale interviene una F liscia, si deve a Enrico Giusti e Mario Miranda. Ciò escluse la possibilità di una teoria della regolarità per le soluzioni dei sistemi. In due dimensioni questa regolarità sussiste, come dimostrò Morrey negli anni Quaranta. In dimensioni superiori una regolarità parziale fu stabilita a partire dai lavori di Frederick J. Almgren jr, De Giorgi, Herbert Federer, Giusti, Miranda e Morrey alla fine degli anni Sessanta, con la dimostrazione che l'insieme singolare di una soluzione è piccolo rispetto a un'opportuna misura di Hausdorff.

Equazioni di evoluzione non lineari, flussi di fluidi e dinamica dei gas

Numerosi problemi di grande importanza in fisica e in ingegneria sono formulati in termini di equazioni di evoluzione non lineari. La forma più generale di queste equazioni è:

dove l'operatore non lineare A e lo spazio delle funzioni su cui agisce dipendono dalla natura del problema.

Storicamente, le equazioni maggiormente studiate, in particolare dal punto di vista della costruzione di una teoria matematica rigorosa, nacquero per descrivere i flussi dei liquidi incomprimibili: l'equazione di Navier-Stokes [11] e l'equazione di Euler [12]. In questo caso la possibilità di un blow-up della soluzione, cioè un tempo T* nel quale la soluzione o una delle sue derivate diventino infinite in qualche punto è stata associata da Leray e da altri al problema fisico della turbolenza, uno dei più significativi problemi macroscopici della fisica. Lo studio di possibili singolarità per l'equazione di Navier-Stokes in tre dimensioni, iniziato nel 1933 da Leray è stato proseguito da Ludwig Scheeffer (1977) e Luis Caffarelli, Robin Kohn e L. Nirenberg nel 1982 per escludere, per esempio, tutta una retta di singolarità nello spazio-tempo. Stabilire se nelle equazioni di Navier-Stokes e di Euler tridimensionali vi siano punti singolari è ancora oggi uno dei maggiori problemi aperti. In due dimensioni esistenza e regolarità locali sono state dimostrate e il problema della descrizione del comportamento della soluzione per t→∞ si è concentrato su concetti provenienti dalla teoria dei sistemi dinamici, in particolare sullo studio degli 'attrattori'. Nel 1971 è stato suggerito da David Ruelle e Floris Takens, in un articolo che ha sollevato molte discussioni, che il fenomeno della turbolenza possa dipendere dall'esistenza di un attrattore complicato. Questi attrattori e il loro comportamento caotico sono stati studiati in tutti i particolari per alcuni sistemi di dimensione finita da Stephen Smale e dalla sua scuola. Nel 1963 il meteorologo Edward Lorenz scoprì un semplice sistema di tre equazioni differenziali ordinarie per il quale i calcoli numerici indicavano una complicata struttura asintotica per t→∞. La ricerca recente sulle equazioni dissipative non lineari di evoluzione che ammettono soluzioni globali si è occupata particolarmente della riduzione dello studio della soluzione per t→∞ al caso della dimensione finita, con i lavori degli anni Ottanta di Babin e Visik, C. Foias e Temam, e della Olga Ladyzhenskaya. Uno stimolo a queste ricerche venne dalla scoperta delle cascate di Feigenbaum che descrivono alcuni fenomeni universali nell'iterazione di applicazioni. Queste cascate sono state scoperte anche sperimentalmente in ricerche sui flussi dei fluidi.

Oltre quella di Navier-Stokes, altre equazioni sono state studiate dal punto di vista dei loro attrattori, come l'equazione di Kuramoto-Sivashinski:

nata in teoria della combustione, o quella di Cahn-Hilliard:

con ν>0, che nasce nelle transizioni di fase. Sempre nello stesso contesto, un diverso fenomeno compare nell'equazione di Korteweg-De Vries (KdV):

che descrive le onde nei canali poco profondi. Qui si ha il fenomeno dei 'solitoni', osservato per la prima volta da John S. Russell nel 1834. Sono soluzioni che conservano indefinitamente la propria forma, e possono interagire con altre soluzioni dello stesso tipo senza perdere la propria individualità. Una teoria dei solitoni per la KdV fu iniziata nella metà degli anni Sessanta da M. Kruskal e dai suoi collaboratori.

Un'altra direzione di ricerca che ha origine nella dinamica dei gas e dei fluidi compressibili è la teoria delle leggi di conservazione non lineari e delle onde d'urto. Per un'equazione scalare queste leggi hanno la forma:

dove le funzioni φ_i sono lisce. Un caso particolare è l'equazione di Burger già menzionata. Soluzioni corrispondenti a particolari condizioni iniziali erano state costruite da Riemann (1858). La teoria generale di queste equazioni è stata iniziata nel 1950 da Hopf e continuata nel 1957 da Olga Arsen9evna Oleinik e Lax.

EDP non lineari e analisi funzionale non lineare

Il metodo delle approssimazioni successive, studiato fin da Picard negli anni Ottanta del XIX sec., fu enunciato in un elegante quadro generale da Banach nel 1922: in uno spazio metrico completo X, un'applicazione f:X→X che soddisfa

ha un unico punto fisso x₀ dato da x₀=lim_n→∞fⁿ(a) per ogni punto iniziale a∈X. Una conseguenza è il teorema delle funzioni inverse, che afferma che se F applica un intorno U di u₀∈X in Y, dove X e Y sono spazi di Banach e F è C¹ su U con L=F'(u₀) biunivoca su Y, allora l'equazione F(u)=f ha un'unica soluzione in un intorno di u₀, per ogni f in un intorno di f₀=F(u₀).

Un programma tendente a estendere questo risultato quando F'(u₀) non è invertibile, detto 'teoria della biforcazione', ebbe origine dai lavori di Ljapunov (1906) e Schmidt (1908) per trattare problemi posti per la prima volta nel 1885 da Poincaré nel quadro dell'astrofisica. La situazione tipica è quella di una famiglia di funzioni F_λ(u) dipendenti da un parametro λ, con λ reale e F_λ(0)=0 per ogni λ, e con F₀(u) che ammette derivata in 0, F9₀(0)=L con uno spazio nullo di dimensione 1 e un codominio chiuso di codimensione 1. Sotto semplici ipotesi si stabilisce l'esistenza per λ vicino a 0 di un ramo di soluzioni non nulle u(λ) dell'equazione F_λ (u(λ))=0. Tali risultati si sono dimostrati utili in una grande varietà di applicazioni in fisica e in ingegneria, come i problemi di rottura in elasticità, la convezione del calore e i fluidi rotanti. L'estensione al caso in cui la dimensione dello spazio nullo di L è maggiore di 1 fu ottenuta nei primi anni Cinquanta da Mark Aleksandroviã Krasnoselskij e la sua scuola con metodi variazionali e topologici. Il risultato definitivo sull'esistenza di rami globali, cioè con l che varia in R, si ebbe nel 1971 a opera di Paul Rabinowitz, che applicò la teoria del grado di Leray-Schauder. Esso afferma che nell'ipotesi di compattezza ogni ramo o si estende all'infinito (in XxR), o finisce in un altro punto di biforcazione.

Tutto ciò illustra una persistente divisione di risultati tra locale e globale. Spesso i risultati locali si ottengono mediante un argomento di perturbazione da una situazione di linearità, con alcune varianti di approssimazioni successive, mentre i risultati globali richiedono di solito strumenti sofisticati, quali argomenti variazionali o topologici, spesso in combinazione con stime a priori.

La forma più generale e sofisticata dell'argomento della perturbazione fu trovata nel 1956 da Nash, nella dimostrazione dell'esistenza di immersioni isometriche C^∞ di varietà riemanniane in spazi euclidei. Nash considera un'applicazione F dello spazio X=C^∞(M) in un altro spazio Y=C^∞(N) tale che F'(u₀) ha un'inversa continua L che non recupera completamente la regolarità perduta sotto l'azione dell'operatore differenziale F. Poiché X e Y non sono spazi normati completi, il teorema delle funzioni inverse non si applica. Nash ideò un argomento per ottenere un'inversa locale per F combinando iterazioni di L, di F e di operatori di smoothing. Questo argomento fu modificato nel 1966 da Moser e applicato al problema di stabilire l'analogo C^∞ dei risultati di Kolmogorov e Arnold nel caso analitico sull'esistenza di orbite quasi periodiche, come perturbazioni di orbite periodiche in sistemi hamiltoniani (come quelli della meccanica celeste)

Riguardo ai risultati globali uno dei progressi chiave è stata la teoria del grado di Leray-Schauder. Un altro potente approccio è stata l'introduzione di strumenti topologici nello studio di problemi variazionali. Anche se questo approccio era stato prefigurato da Poincaré e Georg D. Birkhoff, la forza di tali idee fu effettivamente riconosciuta a cavallo tra gli anni Venti e Trenta del Novecento nel lavoro di Ljusternik e Schnirelmann e Morse. In particolare, Ljusternik e Schnirelmann, nel caso di problemi variazionali su varietà di dimensione finita, trovarono una minorazione per il numero dei punti critici in termini di invarianti topologici, per esempio in termini della categoria di Ljusternik e Schnirelmann. La teoria di Morse per funzioni non degeneri Φ dà una classificazaione più fine dei punti critici in termini di forme quadratiche associate a Φ"(u₀). Morse applicò questo metodo allo studio di un classico problema posto da Poincaré: l'esistenza di infinite geodetiche su una superficie di energia ellittica.

Calcolo delle soluzioni di EDP, analisi numerica e informatica

Uno dei fenomeni più notevoli e importanti delle applicazioni delle EDP, nelle scienze fisiche e nell'ingegneria, a partire dalla Seconda guerra mondiale, è stato l'impatto dei calcoli ottenuti con i computer ad alta velocità. Anche se non si è trattato di una panacea, malgrado le previsioni estremamente ottimistiche di alcuni profeti e pionieri in questo campo, compreso John von Neumann, i computer hanno tuttavia drasticamente cambiato la pratica della matematica applicata, dando luogo a nuovi problemi e indicando nuove prospettive. In meteorologia, per esempio, (un settore che secondo von Neumann avrebbe comportato le maggiori conseguenze teoriche per i computer), la pratica universale delle previsioni meteorologiche si è divisa nei compiti, tra loro duali, della raccolta dei dati atmosferici su base planetaria e della loro analisi mediante i supercomputer più complessi. D'altra parte è diventato sempre più chiaro, per via della struttura intrinsecamente caotica della situazione (come nella 'teoria del caos', applicata per la prima volta in questo campo da Lorenz) che vi sono limitazioni intrinseche, che non possono essere superate semplicemente da calcoli massicci.

Nella pratica, quasi tutte le EDP si studiano con mezzi computazionali. Sono studi che prendono due forme, tra loro discordanti. La prima, più limitata, è quella dell'analisi numerica classica, una branca della matematica applicata che ottiene risultati che comprendono limitazioni sugli errori e mediante argomenti relativamente rigorosi. Fa uso di spazi funzionali di dimensione finita e si basa sulla risoluzione di problemi approssimati in un contesto finito-dimensionale. L'altra forma, utilizzata su scala più grande, riguarda l'approccio spesso definito 'computazionale'. In questo approccio si preparano modelli computazionali semplificati per le equazioni da risolvere, e si calcola la soluzione nella situazione semplificata, senza peraltro preoccuparsi di controllare la validità matematica del procedimento. La giustificazione si ottiene in termini di fenomenologia dei risultati, anche se ciò è fonte di ambiguità e di controversie sulla validità del processo computazionale, in particolare in situazioni difficili da analizzare da un punto di vista teorico, come la turbolenza.

Si assiste così allo sviluppo di uno strumento estremamente potente per ottenere risultati concreti sulle EDP che provengono da contesti applicativi, uno strumento che però crea problemi molto difficili che dovranno essere risolti in futuro. Un aspetto della nuova situazione è l'uso dei calcoli sia come 'strumento sperimentale per produrre congetture' su argomenti di carattere analitico sia per lo studio di simulazioni numeriche quale fonte di suggerimenti per trattazioni rigorose. Come in tutti i campi della scienza, le metodologie teorica, sperimentale e computazionale devono integrarsi per rendere possibile un attacco adeguato ai problemi più difficili e più importanti.