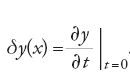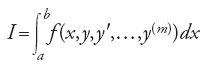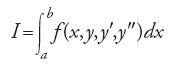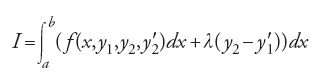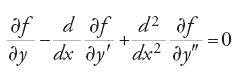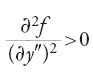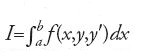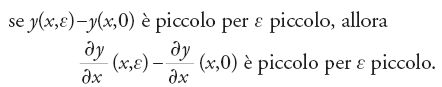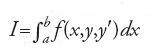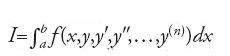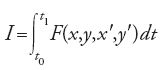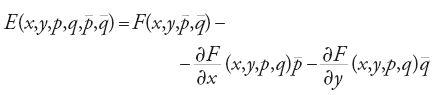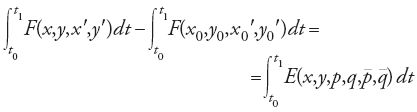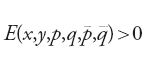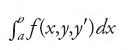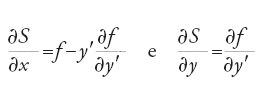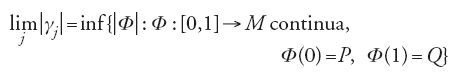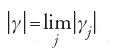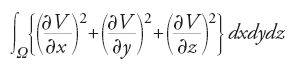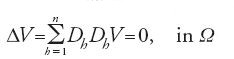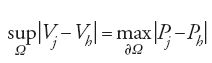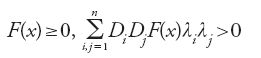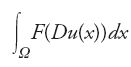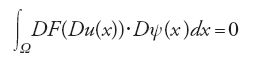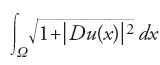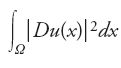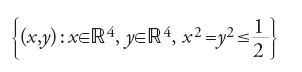La seconda rivoluzione scientifica: matematica e logica. Calcolo delle variazioni

La seconda rivoluzione scientifica: matematica e logica. Calcolo delle variazioni

Calcolo delle variazioni

Tra il 1870 e il 1920 si assiste al consolidamento degli argomenti classici. Sempre maggiore importanza viene data al rigore, ai teoremi di esistenza e allo sviluppo dei metodi di Weierstrass per la ricerca di condizioni sufficienti. Inizia inoltre a imporsi un punto di vista che richiede di formulare i problemi più importanti di questo settore come esempi, molto generali, di ottimizzazione vincolata. Un'attiva area di ricerca, creata da Constantin Carathéodory (1873-1950) nel 1925, ma con radici in precedenti lavori, riguardava lo sviluppo dei metodi della teoria dei campi e la teoria di Hamilton-Jacobi. Il calcolo delle variazioni ebbe un ruolo rilevante nella nascita dell'analisi funzionale moderna. Matematici come Jacques-Salomon Hadamard (1865-1963) consideravano questa materia dal punto di vista dell'analisi funzionale: il problema principale comportava la scelta di un funzionale minimizzante in un insieme di funzionali, e quindi presupponeva uno spazio di funzioni con proprietà ben definite. All'interno del calcolo delle variazioni vi furono anche sviluppi che appartenevano piuttosto ad altri settori della matematica e alle scienze applicate: negli anni Trenta del XX sec., il calcolo delle variazioni in grande e la teoria di Morse e, negli anni Cinquanta, la teoria del controllo ottimo e della programmazione dinamica.

Il problema della condizione sufficiente

di Craig Fraser

La variazione seconda da Legendre a Mayer

Prima degli studi di Adrien-Marie Legendre del 1786 i matematici supponevano che l'equazione variazionale per un dato problema ne desse la soluzione. Essi ragionavano nel seguente modo: se una funzione, o curva, è ottimizzante, allora soddisfa questa equazione, e quindi una soluzione di tale equazione è una soluzione del problema variazionale. Nei primi sviluppi della disciplina, contenuti nelle opere dei Bernoulli e di Leonhard Euler fino al 1755, la curva veniva alterata in un punto o in un numero finito di punti; l'equazione differenziale risultante si otteneva dall'ipotesi che la curva fosse minimizzante o massimizzante. Nella terminologia moderna, l'equazione rappresenta una condizione necessaria, ma i matematici di quel periodo non pensavano in questi termini. Si concludeva tuttavia che se si trovava una funzione che soddisfaceva l'equazione data il problema era risolto. L'introduzione del 'procedimento δ῝ di Lagrange specificò per la prima volta un insieme ben delimitato di curve di confronto date in termini analitici. Se l'equazione della curva era y=y(x), la classe delle curve di confronto era della forma y(x)+δy(x). Nel 1772 Euler fornì quella che doveva diventare l'espressione analitica standard di δy: data una classe di confronto di curve della forma y(x,t), si prenda per δy(x) il primo termine dello sviluppo di Taylor di y(x+t)−y(x):

Legendre per primo si accorse che per trovare il minimo di

oltre alla variazione prima δI occorreva considerare anche la variazione seconda. La teoria della variazione seconda fu poi formulata in forma pressoché definitiva da Christian Gustav Adolph Mayer (1839-1907) in un articolo pubblicato nel 1868 sulla rivista di Crelle. Mayer riduceva un problema variazionale generale a un problema di moltiplicatori di Lagrange. Già Rudolf Friedrich Alfred Clebsch (1833-1872) aveva osservato nel 1858 che il classico problema variazionale di minimizzare l'integrale I poteva essere riformulato come un problema di moltiplicatori. Per esempio, se m=2, introducendo un'equazione ausiliaria y₂−y′₁=0, l'integrale

diventa

dove λ è un'opportuna funzione moltiplicatrice.

Combinando le equazioni di Euler per l'integrale [4] con y₂ −y′₁=0 si ottiene

cioè l'equazione di Euler per l'integrale [3], equazione che deve essere soddisfatta da una funzione y(x) che minimizzi I.

Nel caso in esame, la condizione per la realizzazione di un minimo che Legendre aveva introdotto nel 1786 si riduce ‒ mediante una certa trasformazione della variazione seconda di I ‒ a:

Nel 1837 Carl Gustav Jacob Jacobi (1804-1851) introdusse poi il concetto di punto coniugato. Supponiamo di muoverci lungo l'intervallo [a,b] partendo dal punto iniziale finché non troviamo un secondo punto tale che la variazione seconda dell'integrale fra tali estremi sia zero. Allora il punto in questione si chiama punto coniugato e l'esistenza di un valore minimo per l'integrale non può più essere assicurata. Da qui deriva la 'condizione di Jacobi', secondo la quale l'esistenza di un minimo è garantita se l'intervallo non contiene punti coniugati.

Mayer fu il primo a identificare il principale aspetto teorico legato alla variazione seconda, dimostrando che, se la condizione di Jacobi era soddisfatta, allora si poteva ottenere un'opportuna trasformazione della variazione seconda e ritrovare la condizione di Legendre. Il lavoro di Mayer ebbe un'importanza teorica fondamentale. Le ricerche successive apportarono solo alcuni raffinamenti e precisazioni e sarebbero state riassunte da Oskar Bolza (1857-1942) in un libro pubblicato in inglese nel 1904.

Weierstrass

La teoria classica della variazione seconda per il problema

dagli inizi nei lavori di Lagrange fino alla forma finale in quelli di Mayer, si basava sull'ipotesi che sia δy sia δy′ fossero piccoli. Quando y(x,ε) è una famiglia ammissibile di curve tali che y(x)=y(x,0), deve valere la seguente implicazione:

Per famiglie della forma y(x,ε)=y(x)+εζ(x), il tipo considerato da Euler, tale ipotesi è soddisfatta, e potrebbe sembrare che valga anche per famiglie del tipo utilizzato da Jacobi, nelle quali y(x,ε) è una soluzione dell'equazione di Euler. Tuttavia, come osservò Karl Theodor WilhelmWeierstrass (1815-1897), l'implicazione [7] non vale in generale, per esempio non vale se y(x,ε)=y(x)+εsen(x/ε). Sebbene gli studiosi precedenti, come Legendre, fossero consapevoli che per la famiglia delle curve di confronto erano necessarie restrizioni, Weierstrass per primo le enunciò in termini analitici chiari ed espliciti.

Weierstrass affrontò la questione della condizione sufficiente con una sensibilità logica più profonda dei suoi predecessori e introdusse esplicitamente la distinzione moderna tra condizione necessaria e condizione sufficiente. Inoltre, portò nella disciplina la consapevolezza della necessità di esprimere in termini analitici precisi la natura delle funzioni e delle variazioni in questione. Entrambi gli aspetti lo aiutarono a cogliere i limiti della teoria classica, e lo spinsero a sviluppare una teoria alternativa.

In letteratura si suggerisce talvolta che Weierstrass fosse in qualche modo arrivato alla formulazione giusta, o naturale, del problema variazionale: è quanto sostenne molto chiaramente Oskar Bolza nel suo libro del 1904. In realtà, anche il metodo di Weierstrass imponeva restrizioni alle variazioni che dipendevano da necessità tecniche. Nel caso del problema variazionale

nel quale la derivata seconda compare nella f, sia l'ordinata y sia la sua derivata y′ per la curva di confronto devono differire soltanto per piccole quantità dai corrispondenti valori per la curva estremante, proprio come accadeva nella teoria classica per il problema

Inoltre, la teoria di Weierstrass fornisce risultati per una classe di funzioni più ampia di quella considerata nel caso classico soltanto usando un criterio più forte (e probabilmente più artificioso): vi sono vantaggi ma anche un prezzo da pagare. In effetti, la teoria classica e quella di Weierstrass sono differenti, ciascuna con proprie caratteristiche, propri interessi e pregi, e non è corretto affermare che una è superiore o più naturale dell'altra. Si consideri il problema variazionale generale di massimizzare o minimizzare

Nella teoria classica vi sono restrizioni su δy^(k), per k=1,2,…,n, mentre nella teoria di Weierstrass le restrizioni su δy^(k) sono presenti per k=1,2,…,n−1; per k>n nessuna delle due teorie impone restrizioni sulle variazioni δy^(k). Il metodo di Weierstrass fornisce certamente risultati 'più forti', ma soltanto grazie a un criterio più complesso ed esigente della classica condizione di Legendre.

La funzione eccesso e la condizione di Weierstrass

I metodi di Weierstrass furono esposti in lezioni tenute all'Università di Berlino nel 1879 e nel 1882. Nell'impostazione parametrica di Weierstrass un dato punto su una curva è specificato dalle funzioni coordinate x(t), y(t). Siano A=(x(t₀),y(t₀)) e B=(x(t₁),y(t₁)) i punti iniziale e finale. Si voglia, per esempio, minimizzare l'integrale variazionale:

Sia (x₀(t),y₀(t)) la curva che unisce A e B, cioè la soluzione dell'equazione differenziale di Euler per il problema. Se nell'intervallo [t₀,t₁] non vi sono punti coniugati a t₀ c'è una regione, o 'campo' del piano xy che contiene la curva (x₀(t),y₀(t)), con la seguente proprietà: per ogni punto C=(x,y) della regione passa una sola curva soluzione, nel senso di Euler, che unisce A e C. Denotiamo con p(x,y) e q(x,y) il valore della derivata di questa curva in un generico punto C. Consideriamo ora una qualunque curva (x(t),y(t)) che unisca A e B e passi per C. Siano

le derivate di questa curva nel punto C. La funzione eccesso E è definita in C come segue:

Weierstrass dimostrò che la differenza tra gli integrali calcolati lungo (x(t),y(t)) e lungo(x₀(t),y₀(t)) è

un risultato che diventò noto come 'teorema di Weierstrass'. Dalla [10] segue che se

allora l'arco ((x₀(t),y₀(t)) minimizza I. Così la [11] è una condizione sufficiente affinché I sia un minimo. È la condizione fondamentale nella teoria di Weierstrass.

È importante osservare che le lezioni di Weierstrass rimasero inedite fino al 1927, quando il suo lavoro originale aveva ormai un interesse essenzialmente storico. Alla fine del XIX sec. le sue idee furono sviluppate e diffuse da altri ricercatori. La tesi di Ernst Zermelo (1871-1953), discussa a Berlino nel 1895, era dedicata all'estensione dei metodi del campo a integrali variazionali nei quali la funzione integranda F contiene derivate di ordine superiore di x e y. L'analisi di Zermelo mostrava molto chiaramente come certe restrizioni sulle curve di confronto fossero necessarie: per esempio, che la pendenza della curva in ciascun punto debba essere molto vicina a quella della curva estremante. Nel 1900 David Hilbert riformulò il risultato di Weierstrass usando l'integrale noto come integrale invariante. Servendosi del metodo dei moltiplicatori Mayer estese l'analisi di Hilbert a un insieme molto generale di problemi, con più variabili e vincoli. Sui metodi di Weierstrass, Hilbert e Mayer, basati sulla nozione di campo, si concentrò una gran quantità di lavori di calcolo delle variazioni. Fu l'ultima importante area di sviluppo della teoria classica.

Ottimizzazione vincolata

Problemi di ottimizzazione vincolata erano sorti molto presto nella storia del calcolo delle variazioni. Uno di questi è il classico problema isoperimetrico: trovare una curva chiusa di dato perimetro e area massima, come pure problemi dello stesso genere; per esempio quello di determinare la forma di una catena appesa di data lunghezza nella quale il baricentro si trovi nel punto più basso possibile. Euler e Lagrange studiarono problemi nei quali era presente un vincolo accessorio, espresso analiticamente con un'equazione differenziale. Uno di questi era il problema della brachistocrona in un mezzo resistente: la resistenza veniva appunto trattata come un vincolo espresso analiticamente con un'equazione differenziale.

Euler e Lagrange svilupparono vari metodi per trattare problemi con vincoli. Un svolta si ebbe con i lavori di Lagrange del periodo 1797-1804, nei quali egli introduceva per questi problemi il metodo dei moltiplicatori. Negli sviluppi moderni della materia il problema più generale si esprime in termini di ottimizzazione di un dato integrale soggetto a verificare condizioni espresse con equazioni differenziali.

Il metodo dei moltiplicatori di Lagrange si sviluppò ampiamente nel corso del XIX sec., fino ad arrivare a maturità nei già citati lavori di Mayer. Questi, a partire da alcune idee di Paul du Bois-Reymond (1831-1889) e Ludwig Scheeffer (1859-1885), elaborò un approccio originale e coronato da successo che lo portò a pubblicare nel 1886 una nuova formulazione del metodo.

La complessità del metodo dei moltiplicatori è evidenziata dal fatto che nei trenta anni successivi al lavoro di Mayer del 1886 sarebbero state pubblicate altre tre dimostrazioni, la prima nel 1896 dall'olandese Barend Turksma, la seconda nel 1906 da Hilbert, e la terza dall'americano Gilbert A. Bliss (1876-1951) nel 1918. Le impostazioni di Mayer, Turksma, Hilbert e Bliss erano diverse sia nel procedimento sia nel punto di vista, e davano pertanto luogo a quattro diverse prospettive riguardo al metodo in questione. Il lavoro degli ultimi due matematici necessitava di teoremi di immersione per spazi funzionali, un argomento che dopo il 1900 fu strettamente associato a ricerche sul metodo dei moltiplicatori e che era fondamentale nell'impostazione di Bliss.

Tra i vari autori del periodo, Hadamard fornì nel 1910 una discussione particolarmente chiara dei risultati di immersione.

La teoria di Carathéodory

di Craig Fraser

In un importante articolo del 1925 Constantin Carathéodory approfondì i legami tra il calcolo delle variazioni e la teoria delle equazioni differenziali ordinarie e alle derivate parziali, un argomento che rientrava nella classica teoria di Hamilton-Jacobi e del quale Carathéodory tratta diffusamente nel suo libro del 1935. Sia dato il problema variazionale di massimizzare o minimizzare

Consideriamo la curva y=y₀(x) che unisce i punti estremi A e B, soluzione dell'equazione di Euler per il problema. Supponiamo che y=y₀(x) sia immersa in un campo di estremali, cioè in una famiglia di soluzioni dell'equazione di Euler nella quale esista una sola curva estremale che unisce A e un qualunque altro punto della regione. La funzione caratteristica è

dove l'integrazione ha luogo lungo l'unica estremale y=y(x) che unisce (a,y(a)) e (x,y(x)). Dalle proprietà della variazione abbiamo

Tuttavia

e quindi

Dall'ultima equazione possiamo esprimere y′ in termini di x,y e ∂S/∂y. Posto H=−(f−y′∂f/∂y) si ottiene in definitiva ∂S/∂x+H(x,y,∂S/∂y)=0. Si può dimostrare che le soluzioni di questa equazione differenziale alle derivate parziali corrispondono alle soluzioni dell'equazione di Euler per il problema variazionale.

Carathéodory voleva sviluppare queste idee nell'ambito della teoria di Weierstrass. Il suo lavoro fu proseguito da numerosi ricercatori in Belgio e in Germania negli anni Trenta e Quaranta del Novecento, tra i quali Théophile de Donder, Théophile Lepage e Hermann Boerner. Quest'ultimo affermò nel 1952 che Carathéodory aveva conquistato per il calcolo delle variazioni ciò che Euclide non riteneva possibile per la geometria, e cioè una 'via regia' verso la verità in quella disciplina. Negli anni Cinquanta e Sessanta, alcuni autori collegarono le idee di Carathéodory al controllo ottimo, un argomento proprio dell'ingegneria.

Il metodo 'diretto' di Hilbert

di Mario Miranda

Nel 1899 Hilbert pubblica una breve nota Über das Dirichletsche Prinzip (Sul principio di Dirichlet) che si può considerare come l'atto di nascita del metodo diretto. In una pagina di questa nota si incontra la dimostrazione dell'esistenza della linea di minima lunghezza o geodetica, fra le linee congiungenti due punti fissati. Le difficoltà nella risoluzione di tale problema dipendono dall'ambiente in cui i punti e le corrispondenti linee di collegamento sono contenuti.

Il metodo presentato da Hilbert è, come ogni frutto di genio, elementare e al tempo stesso applicabile con successo in un contesto molto generale: cioè uno spazio metrico di natura qualunque, vale a dire un insieme di punti nel quale sia definita una distanza d(x,y). Lo strumento funzionale che Hilbert utilizzò per trattare il problema delle geodetiche, e subito dopo quello dell'elettrostatica, è il concetto di funzione lipschitziana, introdotto da Rudolf Otto Sigismund Lipschitz (1832-1903): cioè una funzione f fra due spazi metrici tale che esista una costante C per cui valga sempre d(f(x),f(y))≤Cd(x,y). La lipschitzianità è una proprietà più forte della continuità, duttile quanto questa e molto vicina alla differenziabilità, un concetto che non è definito in qualunque spazio metrico, ma verso il quale coduce l'analisi delle soluzioni di ogni problema di minimo, come quello delle geodetiche.

Illustriamo il metodo di Hilbert. Siano P e Q due punti fissati di un dato spazio metrico M. In M si può definire il concetto di 'lunghezza' di una curva senza fare ricorso a nozioni proprie del calcolo differenziale. Supponiamo dunque che esistano curve di lunghezza finita Φ colleganti P con Q. La lunghezza di Φ verrà indicata con ∣Φ∣. Per risolvere il problema della geodetica si consideri una successione minimizzante {γ_j} di curve congiungenti P con Q, tale che, cioè

Le curve γ_j possono essere scelte in modo che la successione {γ_j} sia costituita da funzioni lipschitziane con la medesima costante, ovvero che sia una famiglia equilipschitziana. Quindi, se lo spazio M è localmente compatto (cioè se da ogni successione limitata può estrarsi una successione convergente) avremo, come Hilbert mostrò, che dalla successione {γ_j} potrà estrarsi una successione di funzioni convergenti in ogni punto di [0,1] verso una funzione lipschitziana γ, la cui lunghezza verifica l'uguaglianza

La curva γ sarà perciò soluzione del problema.

Più complesso è il discorso riguardante il problema dell'elettrostatica, metodologicamente accostato da Hilbert al problema delle geodetiche utilizzando la lipschitzianità. Il problema è quello del calcolo della funzione potenziale di un dato campo elettrico. I fisici sapevano che tale funzione ha un'importante proprietà, matematicamente dimostrabile, che ne facilita il calcolo: la conoscenza dei valori della funzione potenziale sul bordo di una regione limitata dello spazio, all'interno della quale non vi siano cariche elettriche, determina univocamente i valori della stessa funzione in tutti i punti interni della regione. Il problema, detto appunto dell'elettrostatica, era di formulare procedimenti per il calcolo di tali valori, partendo dalla conoscenza della geometria della regione e della funzione potenziale sul bordo.

Negli anni Trenta del XIX sec. Carl Friedrich Gauss (1777-1855) aveva osservato che la funzione potenziale

ha la proprietà di minimizzare l'integrale

nella classe delle funzioni che assumono i suoi stessi valori sul bordo di una regione Ω, che indicheremo con ∂Ω.

L'osservazione di Gauss trasse in inganno matematici di valore per molti anni. Essi la interpretarono come una risoluzione del problema, mentre si trattava, come avrebbe finalmente osservato Weierstrass, di una formulazione variazionale dello stesso problema. Questa aspettava un adeguato metodo di dimostrazione per diventare teorema.

Fra i matematici entusiasti dell'osservazione di Gauss si distinse Peter Gustav Lejeune Dirichlet (1805-1859) il quale, nelle sue lezioni, la presentava come un'affermazione di esistenza ‒ un principio ‒ che diverrà noto come principio di Dirichlet e sarà poi utilizzato da matematici di grande valore, tra i quali Georg Friedrich Bernhard Riemann (1826-1866). Hilbert fu il primo a fornire una dimostrazione del principio di Dirichlet o se si vuole, della congettura di Gauss: il problema dell'elettrostatica può risolversi dimostrando l'esistenza del minimo di un opportuno integrale.

Immediatamente prima del successo di Hilbert vi era stato un tentativo di Cesare Arzelà (1847-1912) che dimostrava l'esistenza del minimo in classi di funzioni dotate di derivate seconde equilipschitziane. Un tale vincolo, dettato dall'esigenza di ottenere soluzioni dotate di derivate seconde continue, non avrebbe precluso la via verso la soluzione del problema, ove fosse stato possibile garantire per questa il carattere lipschitziano delle derivate seconde. Lungimirante fu l'atteggiamento di Hilbert che si accontentò di provare l'esistenza del minimo in classi di funzioni equilipschitziane. Questo approccio risulterà vincente in molti casi non banali, nei quali i dati del problema permettono di dimostrare a priori il carattere lipschitziano delle soluzioni.

Hilbert seppe poi dimostrare che le soluzioni lipschitziane del problema di minimo avevano l'ulteriore regolarità necessaria per poter scrivere per esse la proprietà differenziale

dove D_h è la derivazione parziale rispetto alla variabile x_h.

Le soluzioni trovate da Hilbert erano dunque funzioni armoniche. Per provare questa proprietà si può ragionare per approssimazione. Se abbiamo un dato al bordo polinomiale, sappiamo infatti risolvere il problema dell'elettrostatica, e trovare una soluzione armonica. Grazie poi al cosiddetto 'principio del massimo', la risolubilità può essere estesa a ogni dato continuo.

Infatti, da un noto teorema di approssimazione di Weierstrass, per ogni funzione continua Φ:∂Ω→ℝ esiste una successione di polinomi {P_j} con lim_j max_∂Ω∣Φ−P_j∣=0. Dette V_j le funzioni armoniche su Ω, eguali a P_j su ∂Ω, avremo che le V_j convergeranno uniformemente su Ω, essendo

Poniamo dunque V=lim_jV_j . Si può dimostrare che tale V è come le V_j armonica in Ω, oltre a essere uguale a Φ su ∂Ω.

Il teorema di Hilbert-Haar e di De Giorgi

di Mario Miranda

Il metodo suggerito da Hilbert per la risoluzione del problema dell'elettrostatica è di fatto applicabile alla risoluzione di una larga classe di problemi variazionali. Ciò fu esplicitamente osservato dal matematico ungherese Alfréd Haar (1885-1933), in una nota del 1927. Haar considerò una qualunque funzione F di n variabili, non negativa e strettamente convessa, cioè

per ogni x∈ℝⁿ e per ogni λ=(λ₁,...λ_ν)∈ℝⁿ−{0}.

Per ogni aperto limitato Ω di ℝⁿ e per ogni funzione lipschitziana u, si può calcolare l'integrale

e considerare il problema di minimizzarne il valore sotto la condizione u=φ su ∂Ω, dove φ è un'assegnata funzione lipschitziana.

Le ipotesi su F assicurano che se φ è costante o è un polinomio di primo grado, l'unica soluzione del problema è data dalla funzione φ stessa. Questa proprietà permette di ripercorrere il cammino di Hilbert per arrivare a dimostrare l'esistenza del minimo sotto opportune condizioni. L'ulteriore regolarità delle soluzioni lipschitziane di Hilbert-Haar non è, in generale, un quesito di facile risposta.

In generale la questione della regolarità rientra, come caso particolare, nel XIX dei famosi ventitré problemi elencati da Hilbert nella storica conferenza al Congresso internazionale dei matematici, tenutosi a Parigi nel 1900. La dimostrazione della continuità delle derivate prime delle soluzioni lipschitziane di Hilbert-Haar è conseguenza di un notevole contributo di Ennio De Giorgi (1928-1996), pubblicato nel 1957. Il problema sta nel trasferire alle 'soluzioni continue' ottenute come limiti uniformi di soluzioni regolari, la proprietà di essere soluzioni; occorre quindi dimostrare l'esistenza delle derivate prime delle 'soluzioni continue' e lavorare poi sulla relazione

valida per ogni funzione lipschitziana ψ nulla su ∂Ω.

Questa strada è stata percorsa nel caso dell'equazione delle superfici minime, caso corrispondente all'integrale

Strumento fondamentale per il trattamento delle 'soluzioni continue' dell'equazione delle superfici minime è la proprietà, dimostrata nel 1968 da Enrico Bombieri, De Giorgi e Mario Miranda: le soluzioni regolari equilimitate dell'equazione delle superfici minime sono localmente equilipschitziane.

Il problema di Plateau-De Giorgi

di Mario Miranda

Joseph Plateau (1801-1883), negli anni Quaranta del XIX sec. evidenziò, con semplici esperimenti realizzati utilizzando fili di ferro e acqua saponata, interessanti proprietà delle superfici. Immergendo in acqua saponata un filo di ferro chiuso su sé stesso, Plateau otteneva una pellicola appesa al bordo metallico, realizzando materialmente la superficie di area minima fra quelle aventi il filo come bordo. Le superfici esibite da Plateau e facilmente riproducibili eccitarono la fantasia dei geometri e dei fisici matematici. I tempi però non erano maturi perché una soddisfacente teoria delle superfici minime fosse sviluppata con strumenti puramente matematici. Ciò non stupisce, quando si ricordi che fino alla fine del XIX sec. non era stato ancora dimostrato un teorema di esistenza del minimo dell'integrale di Dirichlet

,

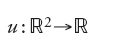
e si tenga presente che l'area della superficie che è grafico della funzione u è data dall'integrale

,

più ostico di quello di Dirichlet. Le maggiori difficoltà sono ancor più evidenti quando si guardi alle equazioni differenziali associate ai due integrali

L'equazione delle superfici minime non ha un buon elenco di soluzioni elementari, mentre l'equazione di Laplace lo ha già ricchissimo nell'ambito dei polinomi. Esistono polinomi omogenei armonici di ogni grado, con i quali si può localmente approssimare ogni altra funzione armonica.

Anche nel caso bidimensionale le idee standard per trovare soluzioni elementari danno scarsi risultati. In questo caso ci si imbatte però in un fenomeno ancor più stupefacente: oltre ai polinomi di grado zero o uno, nessun'altra funzione

è soluzione dell'equazione delle superfici minime.

Questo è l'enunciato di un teorema del 1910 di Sergej Natanovič Bernštejn. Quella iniziata con tale teorema è una vicenda matematica affascinante e ancora attuale. La sfida che gli esperimenti di Plateau lanciarono ai matematici fu di dimostrare l'esistenza e la regolarità delle superfici minime di assegnato contorno. Questa sfida fu raccolta nella prima metà del Novecento, limitatamente alle superfici contenute nello spazio ℝ³. Verso il 1930 teoremi significativi furono ottenuti indipendentemente da Jesse Douglas e da Tibor Radó. Nella seconda metà del secolo il problema di Plateau fu generalizzato in ogni dimensione e in ogni codimensione. Per la codimensione uno, in ogni dimensione, la teoria più semplice ed efficace è quella dovuta a De Giorgi. Si tratta della teoria degli insiemi di perimetro finito, presentata negli anni 1954-1955 e applicata subito dopo con successo dallo stesso De Giorgi al problema di Plateau, anticipando i risultati trovati indipendentemente da John F. Nash.

Le superfici di De Giorgi (n−1) dimensionali nello spazio ℝⁿ sono le frontiere degli insiemi di perimetro finito e la loro misura è data dal perimetro. De Giorgi diede nel 1960 un teorema di esistenza per la sua formulazione del problema di Plateau e dimostrò la regolarità, con possibili eccezioni, delle sue soluzioni; tali eccezioni si verificano solo per dimensioni alte. Il primo esempio di soluzione singolare del problema di Plateau-De Giorgi fu dato da James Simons nel 1968 e la sua singolarità fu dimostrata da Bombieri, De Giorgi ed Enrico Giusti nel 1969. è il cono:

il cui bordo è una varietà compatta analitica contenuta nella sfera unitaria di ℝ⁸.