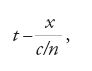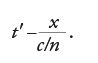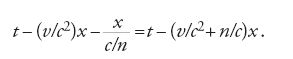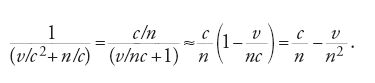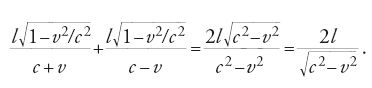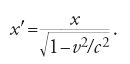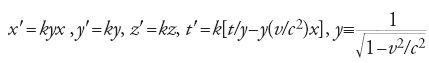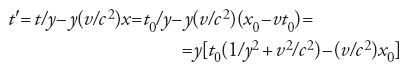La seconda rivoluzione scientifica: fisica e chimica. L'ottica e l'elettrodinamica dei corpi in movimento
La seconda rivoluzione scientifica: fisica e chimica. L'ottica e l'elettrodinamica dei corpi in movimento
L'ottica e l'elettrodinamica dei corpi in movimento
Il moto dell'etere
Il problema dello stato di moto dell'etere, il mezzo ipotetico attraverso il quale si riteneva che si propagassero le onde luminose o in generale, come si giunse a ritenere nella seconda metà dell'Ottocento, i campi elettromagnetici, sottintendeva la seguente questione: l'etere rimane immobile e completamente imperturbato dalla materia che si muove attraverso esso oppure quest'ultima trascina, in tutto o in parte, l'etere che le è intorno o che si trova al suo interno? Il fenomeno dell'aberrazione stellare sembrava fornire una valida prova a favore della prima ipotesi ‒ o, meglio, di una sua variante introdotta da Augustin-Jean Fresnel (1788-1827) nel 1818, secondo la quale la maggior parte dell'etere rimane immobile, mentre la materia trasparente ne trascina un po'.
Anche se rimanevano poco chiari i meccanismi sottesi all'effetto di trascinamento dell'etere, si giunse generalmente ad accettare l'idea che, per giustificare l'inosservabilità del presunto movimento della Terra attraverso l'etere immobile si doveva ipotizzare che tutta la materia trasparente trascinasse qualsiasi luce che si propagava attraverso essa, con una frazione della propria velocità. Tale frazione, che risultava dipendere dall'indice di rifrazione, venne chiamata coefficiente di trascinamento di Fresnel (Tav. IIa, IIb, IIc).
Questo effetto assicurava che, entro i limiti di precisione ottenibili all'epoca, l'ottica terrestre seguisse le stesse leggi valide per un sistema di riferimento in cui l'etere è a riposo e in tal modo spiegava i risultati sempre negativi degli esperimenti ottici cosiddetti 'del primo ordine' sul presunto movimento della Terra attraverso l'etere (precisi al primo ordine rispetto alla costante di aberrazione, cioè al rapporto tra la velocità media della Terra nella sua orbita intorno al Sole e la velocità della luce). L'assenza di questi effetti del primo ordine fu confermata da numerosi esperimenti e si produssero dimostrazioni sempre più generali del fatto che tutti questi risultati si potessero spiegare con la sola aggiunta del coefficiente di Fresnel all'ipotesi dell'etere immobile. D'altra parte, malgrado il successo della formula di Fresnel, la sua interpretazione in termini di trascinamento parziale dell'etere restava problematica e molti studiosi, che accettavano apertamente l'una, prendevano le distanze dall'altra.
Problematica era la necessità di far ricorso al coefficiente di Fresnel per spiegare i fenomeni della dispersione e della doppia rifrazione. Poiché l'indice di rifrazione dipende dalla frequenza della luce rifratta, la materia trasparente avrebbe dovuto, secondo l'interpretazione di Fresnel, trascinare una diversa quantità di etere per ciascun colore; analogamente, avrebbe dovuto trascinare quantità diverse per il raggio ordinario e per quello straordinario nella doppia rifrazione.
C'era, naturalmente, una spiegazione differente e più semplice di questi risultati sperimentali, che non richiedeva l'ipotesi del trascinamento parziale nella materia trasparente. Infatti, se tutto l'etere all'interno della materia fosse stato trascinato da questa, l'etere alla superficie della Terra sarebbe stato in quiete rispetto a essa, e ciò avrebbe spiegato automaticamente il motivo della mancata osservazione della deriva dell'etere. Il concetto di un etere trascinato era inoltre molto più naturale rispetto a quello di un etere immobile. I fenomeni di polarizzazione avevano chiarito che le onde luminose sono trasversali e non longitudinali, e ciò implicava che l'etere, qualora fosse stato possibile descriverlo come un sistema meccanico, non avrebbe potuto essere un gas o un fluido ma avrebbe dovuto essere un solido elastico, con un alto grado di rigidità per spiegare il valore elevato della velocità della luce. La maggior parte dei teorici che studiavano modelli meccanici di questo solido elastico non sembrava preoccuparsi del problema, nonostante fosse implausibile che la Terra e tutta la materia dell'Universo si muovessero all'interno di un mezzo solido senza minimamente perturbarlo.
Fu principalmente questo aspetto inverosimile che spinse George G. Stokes (1819-1903), negli anni Quaranta dell'Ottocento, a sviluppare un modello in cui la Terra trascinava l'etere. L'aberrazione stellare continuava a rappresentare il più solido argomento contro un modello come questo e molti degli sforzi di Stokes furono dedicati a tentare di dimostrare come si potesse spiegare l'aberrazione in base sia a un etere trascinato sia a un etere immobile.
Nel 1851 Armand-Hippolyte-Louis Fizeau (1819-1896) riuscì a determinare con un metodo diretto il coefficiente di Fresnel nell'acqua in movimento. Negli esperimenti precedenti, questo coefficiente era sempre stato chiamato in causa per compensare qualche altro effetto della deriva dell'etere che ci si sarebbe aspettato di osservare e che si era dimostrato invece inosservabile. Un vantaggio notevole dell'ipotesi del trascinamento dell'etere era stata la possibilità di giustificare i risultati negativi degli esperimenti sulla deriva dell'etere senza alcun bisogno del coefficiente di Fresnel, necessario invece per poter interpretare i risultati dell'esperimento di Fizeau; questo esperimento forniva in tale modo un notevole supporto all'ipotesi di un etere immobile, come pure al coef ficiente di Fresnel.
Nel 1881, però, Albert A. Michelson (1853-1931) effettuò un esperimento di deriva dell'etere del secondo ordine il cui risultato negativo, a suo parere, confutava l'ipotesi di Fresnel di un etere immobile ed era nettamente in favore dell'ipotesi di Stokes, di un trascinamento dell'etere. Si trattava di una conclusione molto azzardata, se non altro perché l'errore sperimentale era pari a circa la metà dell'effetto atteso sulla base dell'ipotesi dell'etere immobile. Nel 1886, nel prepararsi a ripetere l'esperimento del 1881, Michelson realizzò nuovamente e con maggiore precisione, insieme al suo nuovo collaboratore Edward W. Morley (1838-1923), l'esperienza di Fizeau, confermando la previsione di Fresnel e dando torto a Stokes. Il famoso esperimento di Michelson e Morley del 1887 diede però lo stesso risultato negativo del primo tentativo di Michelson del 1881, con errori sperimentali minori.
Questo lasciò gli sperimentatori nell'imbarazzo: l'ipotesi di Fresnel e quella di Stokes sembravano entrambe insostenibili. Nel frattempo però l'ipotesi di Stokes era entrata in crisi per altri motivi. In primo luogo, in un importante articolo di rassegna del 1886 sugli esperimenti di deriva dell'etere, Hendrik Antoon Lorentz (1853-1928) sostenne che Stokes aveva formulato ipotesi contraddittorie sul comportamento dell'etere per interpretare il fenomeno dell'aberrazione. In secondo luogo, risultò molto difficile trovare una risposta a tutti i fenomeni ottici incorporando qualsiasi forma di trasci na mento dell'ete re nella teoria dell'elettrodinamica di Maxwell. Discutendo l'ottica indipendentemente dall'elettrodinamica, Lorentz aveva sostenuto nel suo articolo che si potevano spiegare tutti gli esperimenti in base a una teoria intermedia tra quelle di Fresnel e di Stokes, in cui compariva il coefficiente di Fresnel e nella quale tutta la materia in movimento trascinava in parte l'etere. D'altra parte lo stesso Lorentz, negli anni Novanta dell'Ottocento, aveva rielaborato la teoria di Maxwell basandosi su una netta separazione dell'etere e della materia, e negando qualsiasi trascinamento dell'etere.
Uno dei primi successi della teoria di Lorentz fu comunque, nel 1892, la derivazione teorica del coefficiente di Fresnel, attribuito come dovuto all'interazione esistente tra materia ed etere, senza alcun bisogno di ricorrere al trascinamento dell'etere.
Nel 1895 Lorentz fornì una derivazione più generale del coefficiente di Fresnel, servendosi di un parametro ausiliario che chiamò 'tempo locale'. Formalmente la sua dimostrazione è molto vicina a quella del coefficiente di trascinamento nella relatività ristretta, basata sulla somma relativistica delle velocità relative. Il tempo locale era una delle variabili ausiliarie utilizzate da Lorentz per il suo cosiddetto 'teorema degli stati corrispondenti'. Nello stesso anno egli dimostrò una versione del primo ordine di questo teorema e la utilizzò per fornire una spiegazione molto generale dei risultati negativi di un'ampia classe di esperimenti ottici del primo ordine sulla deriva dell'etere. Il teorema di Lorentz mette in relazione due configurazioni di campo elettromagnetico, una in un sistema di riferimento a riposo rispetto all'etere e l'altra in un sistema in moto uniforme attraverso l'etere, e afferma che, se una configurazione è ammessa dalle leggi dell'elettrodinamica, lo è anche l'altra.
Più precisamente in questo teorema la descrizione matematica della configurazione nel sistema di riferimento in moto, in termini delle quantità ausiliarie introdotte da Lorentz (come il tempo locale al posto del tempo reale), coincide con quella dello stato corrispondente nel sistema in quiete espressa in termini delle quantità reali. Le quantità ausiliarie per il sistema in moto sono scelte in modo tale che, trascurando quantità del secondo ordine, esse soddisfano le stesse leggi soddisfatte dalle quantità reali nel sistema in quiete. Lorentz dimostrò che due configurazioni del campo legate reciprocamente dal teorema degli stati corrispondenti sono concordi in molte delle loro proprietà osservabili e, in particolare, danno luogo a distribuzioni identiche di luminosità. Gli esperimenti sulla deriva dell'etere, che alla fine si riducono all'osservazione di tali distribuzioni di luminosità come la maggior parte degli esperimenti di ottica, forniranno per tale motivo risultati negativi. Per giungere a questa conclusione deve essere soddisfatta un'ulteriore condizione e cioè che in un esperimento ottico i sistemi materiali, come le configurazioni delle sorgenti di luce, delle lenti, degli specchi, e così via, che generano una certa configurazione di campo in una condizione di quiete rispetto all'etere, produrranno, una volta messe in movimento, lo stato corrispondente di quella configurazione di campo nel sistema in moto. Nell'ambito della versione del primo ordine del teorema di Lorentz, e degli esperimenti cui Lorentz voleva applicare il teorema, la condizione di cui sopra varrà a patto che valga il principio di relatività galileiana della meccanica newtoniana per i sistemi macroscopici, come Lorentz in effetti ipotizzava che fosse.
Con la versione esatta del teorema degli stati corrispondenti, che Lorentz ricavò nel 1899, la situazione divenne più complicata. Le distribuzioni di luminosità determinate da una configurazione di campo in un sistema in moto attraverso l'etere si contraevano leggermente nella direzione del movimento, rispetto a quelle dello stato corrispondente relativo alla stessa configurazione nel sistema in quiete. La teoria di Lorentz prediceva quindi un risultato negativo per gli esperimenti di deriva dell'etere del secondo ordine (analogamente al caso degli esperimenti del primo ordine), soltanto a condizione che (contrariamente a quanto ci si sarebbe aspettato in base al principio galileiano di relatività) i sistemi macroscopici fossero soggetti alla stessa contrazione che il teorema esatto degli stati corrispondenti prevedeva per le configurazioni di campo, ossia a quelle che sarebbero state chiamate 'trasformazioni di Lorentz'.
Questa ipotesi della contrazione era stata in effetti già proposta nel 1889 da George F. Fitzgerald (1851-1901) e dallo stesso Lorentz nel 1892, allo scopo specifico di riconciliare l'ipotesi dell'etere immobile con il risultato negativo dell'esperimento di Michelson e Morley. All'inizio l'ipotesi della contrazione sollevò perplessità, ma ciononostante nel corso degli anni Novanta dell'Ottocento si affermò l'opinione generale che qualsiasi teoria basata su un etere immobile dovesse incorporarla, così come l'inclusione del coefficiente di Fresnel garantiva la compatibilità con la mancanza di qualsiasi prova del movimento rispetto all'etere.
Quando Lorentz prese a considerare dal punto di vista microscopico le configurazioni di materia che dessero luogo a configurazioni di campo legate reciprocamente dal teorema degli stati corrispondenti scoprì che, se voleva che la sua teoria prevedesse risultati negativi per una vasta categoria di esperimenti del secondo ordine sulla deriva dell'etere, doveva introdurre ulteriori e impreviste ipotesi. Egli doveva cioè assumere che le forze, le masse e i tempi in un sistema in movimento dipendessero tutti dalla velocità del sistema rispetto all'etere. Formalmente, la dipendenza dalla velocità assoluta in tutti questi casi è proprio la stessa che la relatività ristretta prevede per la velocità relativa. Per la massa, Walter Kaufmann (1871-1947) e altri sottoposero a verifica sperimentale questa dipendenza dalla velocità per mezzo di esperimenti sugli elettroni veloci prodotti dal decadimento beta. Simili esperimenti vennero effettuati inizialmente al volgere del secolo e, prima che si raggiungesse un consenso sul fatto che i migliori risultati sperimentali fossero in accordo con le previsioni di Lorentz e Einstein, continuarono negli anni Dieci del Novecento.
L'origine delle complicazioni di cui sopra, mediante le quali la teoria di Lorentz diviene compatibile con tutti i risultati sperimentali, sta nel fatto che la teoria utilizza la meccanica newtoniana, che è invariante rispetto alle trasformazioni di Galilei, insieme con la versione ‒ rielaborata dallo stesso Lorentz ‒ dell'elettrodinamica di Maxwell, che è intrinsecamente invariante rispetto alle trasformazioni di Lorentz. La grande svolta della relatività ristretta fu il riconoscimento che l'invarianza delle leggi dinamiche della fisica rispetto alle trasformazioni di Lorentz, che nella teoria di Lorentz rappresenta soltanto una peculiarità matematica delle leggi dell'elettrodinamica, riflette in realtà una nuova struttura cinematica spaziotemporale, proprio come l'invarianza rispetto alle trasformazioni di Galilei riflette la vecchia struttura spaziotemporale intrinseca alla teoria newtoniana. Ciò implicava, tra l'altro, che la meccanica newtoniana invariante in senso galileiano si dovesse sostituire con una nuova meccanica invariante in senso lorentziano, ossia con la meccanica relativistica.
La dipendenza dalla velocità di lunghezze, tempi, masse e forze, che Lorentz aveva introdotto come eccezione alle regole della meccanica newtoniana, è semplicemente la norma per le velocità relative in questa nuova meccanica relativistica.
La scelta tra Stokes e Fresnel: gli esperimenti di Michelson e Morley
James C. Maxwell, poco tempo dopo aver pubblicato l'articolo fondamentale in cui per la prima volta identificava la luce come onda elettromagnetica, progettò ed effettuò esperimenti volti a rilevare l'effetto sulla rifrazione del presunto movimento della Terra attraverso l'etere (il movimento inverso, dell'etere rispetto alla Terra, è la deriva dell'etere). Maxwell scrisse il resoconto dei risultati negativi dell'esperimento in un articolo che sottopose a Stokes nel 1864 per la pubblicazione nei "Proceedings of the Royal Society". Quando Stokes lo informò che François Arago aveva effettuato esperimenti simili molto tempo prima e che Fresnel era stato in grado di spiegarne i risultati negativi per mezzo del coefficiente di trascinamento, Maxwell ritirò l'articolo.
Poco prima di morire ritornò sul problema del movimento della Terra rispetto all'etere. Nella voce 'etere' per la nona edizione della Encyclopaedia Britannica egli sostenne che il solo modo per misurare la velocità della Terra rispetto all'etere in un esperimento di laboratorio consisteva nel cercare variazioni di velocità della luce riflessa tra due specchi. Si può dimostrare con un semplice calcolo che l'effetto dovuto all'etere in un esperimento di questo tipo è dell'ordine di v2/c2, troppo piccolo, secondo Maxwell, per poter essere misurato. D'altra parte, lo studioso aveva ideato una determinazione astronomica della velocità del Sistema solare rispetto alla Terra, nella quale l'ordine di grandezza dell'effetto da misurare era v/c e in cui occorreva effettuare misurazioni precise degli intervalli tra eclissi successive dei satelliti di Giove che, come aveva dimostrato Ole Christensen Römer, permettevano di ricavare la velocità della luce. L'idea di Maxwell consisteva nell'analizzare i dati relativi a tali eclissi lungo un periodo di dodici anni, cioè il periodo dell'orbita di Giove intorno al Sole. Supponendo che la velocità rispetto all'etere del Sistema solare nel suo insieme rimanesse essenzialmente costante in tale intervallo di tempo, la velocità della luce determinata attraverso il metodo di Römer avrebbe dovuto variare tra c−v, quando la luce proveniente da Giove si propagava in senso contrario alla deriva dell'etere attraverso il Sistema solare, e c+v sei anni dopo, quando la direzione di propagazione della luce e la deriva dell'etere erano concordi.
Maxwell scrisse all'astronomo americano David P. Todd (1855-1939) chiedendogli se esistessero dati abbastanza precisi su Giove e sui suoi satelliti tali da consentire di misurare la velocità del Sistema solare attraverso l'etere. Maxwell però morì poco tempo dopo e su "Nature" fu pubblicata la sua lettera, nella quale ripeteva che il metodo da lui proposto implicava soltanto effetti del primo ordine, mentre gli esperimenti di laboratorio implicavano effetti del secondo ordine, che riteneva non misurabili. La lettera attrasse l'attenzione di Michelson, un giovane ufficiale della Marina militare americana, che si era già guadagnato una certa fama per aver misurato con elevata precisione la velocità della luce e che raccolse la sfida di misurare gli effetti di laboratorio ritenuti da Maxwell non rilevabili.
L'esperimento di Michelson (Tav. IIIa, IIIb) inizialmente non suscitò grande interesse, ed egli tornò alle sue misure della velocità della luce, non curandosi neanche di pubblicare la correzione di un risultato, errato per un fattore 2 dovuto all'effetto di deriva dell'etere.
Il suo interesse per gli esperimenti sulla deriva dell'etere si riaccese solamente nel 1884, quando a Baltimora si trovò ad ascoltare una serie di lezioni di William Thomson (1824-1907), meglio noto come lord Kelvin. Michelson era stato nel frattempo congedato dalla Marina e nominato professore di fisica presso la Case School of Applied Science a Cleveland, fondata di recente. Lo accompagnò nel suo viaggio a Baltimora Morley, professore di chimica, uno dei suoi colleghi della Case School. Fu questo l'inizio di alcuni anni di stretta collaborazione tra i due, che si interruppe piuttosto bruscamente quando Michelson accettò nel 1889 un incarico presso la Clark University a Worcester.
Thomson e John W. Strutt (1842-1919), meglio noto come lord Rayleigh, recatosi anche lui a Baltimora e con il quale Michelson aveva per qualche tempo intrattenuto una corrispondenza, esortarono vivamente Michelson a ripetere l'esperimento del 1881 sulla deriva dell'etere. Come passo preliminare essi suggerirono di ripetere l'esperimento di Fizeau del 1851, per verificare con maggiore accuratezza il valore del coefficiente di Fresnel. Utilizzando una tecnica molto simile a quella usata nell'esperimento sulla deriva dell'etere del 1881, Michelson e Morley poterono confermare la validità della formula di Fresnel con precisione maggiore di quella ottenuta da Fizeau.
Nel pubblicare i loro risultati nel 1886, Michelson e Morley audacemente trassero conclusioni esattamente opposte a quelle esposte da Michelson nel 1881: "La conclusione di questo lavoro è dunque che il risultato annunciato da Fizeau è essenzialmente giusto e che l'etere luminifero non è assolutamente influenzato dal moto della materia che esso permea" (Michelson 1886, p. 386).
Replicare l'esperimento di Michelson del 1881 con precisione superiore rappresentava il passo successivo.
Il perfezionamento più notevole nel nuovo progetto consisteva nella possibilità di ruotare l'interferometro con una precisione di gran lunga migliore che non nel 1881. Un altro miglioramento consisteva nel fatto che la luce veniva riflessa più volte nei bracci dell'interferometro, prima che i due fasci fossero riuniti per produrre la figura di interferenza, e perciò ci si attendeva un incremento di un fattore dieci dell'effetto dovuto alla deriva dell'etere: lo spostamento di fase previsto era di 0,4 ca. e, con questo nuovo strumento, Michelson e Morley erano convinti di poter misurare spostamenti di fase fino a 0,01; quando però iniziarono le misure, essi non trovarono alcuno spostamento di fase al di sopra di questa soglia.
Michelson e Morley furono questa volta più prudenti nel trarre le loro conclusioni: "Sembra, alla luce di quanto abbiamo detto, ragionevolmente certo che se c'è un movimento relativo tra la Terra e l'etere luminifero, questo deve essere molto piccolo" (Michelson 1887, p. 341). Essi inoltre, con maggior sicurezza, affermarono che il nuovo risultato confutava "la spiegazione di Fresnel dell'aberrazione", cioè l'ipotesi di un etere immobile, e menzionarono la dimostrazione di Lorentz secondo cui la proposta di Stokes di un etere completamente trascinato era incompatibile con l'aberrazione stellare osservata, lasciando come unica alternativa una teoria ibrida di Lorentz. Michelson e Morley, tuttavia, avanzarono perplessità sulla capacità di questa teoria di spiegare il loro risultato: "Se ora fosse legittimo concludere da questo lavoro che l'etere è in quiete rispetto alla superficie della Terra [...] anche la teoria [di Lorentz] fallirebbe". Poiché, per ammissione degli stessi Michelson e Morley, i loro risultati dimostravano soltanto che la velocità della Terra rispetto all'etere era "probabilmente meno di un sesto della sua velocità orbitale, e certamente meno di un quarto" (ibidem), non è chiaro se le prospettive, per una teoria basata su un trascinamento parziale dell'etere, fossero così cupe come il loro commento sembra suggerire.
L'elettrodinamica di Maxwell e la relazione tra l'etere e la materia
Nel XIX sec. furono sviluppati due tipi di teorie per lo studio dei fenomeni elettrodinamici: teorie fenomenologiche macroscopiche, come quella di Franz Neumann (1798-1895), che tentò di inquadrare i fenomeni di induzione in un insieme di principî strettamente connessi alla fenomenologia osservata, e teorie microscopiche, come quella di Wilhelm Weber (1804-1891), che provò a spiegare tali fenomeni sulla base di un modello microscopico delle forze elettriche e magnetiche agenti tra particelle cariche.
Entrambe le teorie si basavano sul concetto di interazioni dirette e istantanee, del tipo 'azione a distanza': nel caso di Neumann tra le cariche macroscopiche e gli elementi di corrente o i circuiti, per Weber tra le particelle cariche a riposo o in moto; un altro elemento comune era la conclusione a cui giunsero riguardo ai fenomeni di induzione, ossia che essi dipendevano soltanto dallo stato di moto relativo dei conduttori, dei magneti e così via.
Non è facile caratterizzare il lavoro di Maxwell nei termini della dicotomia tra teorie fenomenologiche e descrittive da un lato e teorie microscopiche ed esplicative dall'altro, che caratterizzò lo sviluppo dell'elettrodinamica dei corpi in movimento durante tutto il XIX secolo. In origine Maxwell si riferì a un modello teorico meccanico, del campo elettromagnetico basato sull'etere; all'epoca della pubblicazione del suo A treatise on electricity and magnetism (1873), però, questo modello passò in secondo piano, lasciando il posto a una descrizione dei fenomeni elettrici e magnetici, e della materia, in termini di campi vettoriali nello spazio, cui l'etere poteva anche fare da supporto, ma che non erano associati ad alcun modello meccanico esplicito. Il fatto che fosse possibile ricavare da una funzione lagrangiana le equazioni che governano questi campi fu considerato sufficiente per caratterizzare la teoria come modello dinamico, presupponendo che in ultima analisi si sarebbe dovuto specificare il modello meccanico sotteso. Come Maxwell riconobbe, e come aveva sottolineato Jules-Henri Poincaré, esisteva un'infinità di modelli meccanici compatibili con la lagrangiana del campo, circostanza che contribuì molto a scoraggiare ulteriori speculazioni meccaniche. Poiché Maxwell postulò l'esistenza dei quattro campi vettoriali D, B, E e H (D e B sono le 'quantità' elettriche e magnetiche, mentre E e H le 'intensità' corrispondenti) e dovette includere relazioni macroscopiche costitutive tra le intensità e le quantità, la sua teoria si può considerare una teoria macroscopica e fenomenologica. Queste relazioni venivano semplicemente postulate, una per ogni mezzo, incluso l'etere, senza tentarne una derivazione a partire dalla struttura del mezzo stesso.
Maxwell non sviluppò una teoria completa dell'elettrodinamica dei corpi in movimento, probabilmente perché ciò avrebbe richiesto sul moto relativo dell'etere e della materia ipotesi dettagliate che dovevano sembrargli premature. Tuttavia, egli dimostrò che il suo modello dei fenomeni induttivi, basato sulla teoria dei campi, prevedeva che tali effetti dipendessero soltanto dallo stato di moto relativo dei sistemi coinvolti, e non dal loro stato di moto rispetto all'etere.
Oliver Heaviside (1850-1925) e Heinrich Rudolf Hertz (1857-1894) fornirono l'elemento mancante che serviva a sviluppare un'elettrodinamica completa dei corpi in movimento. Essi ipotizzarono che, all'interno della materia, lo stato di moto dell'etere coincidesse con lo stato di moto della materia stessa, rispetto al mare immenso dell'etere lontano da qualsiasi materia (lo stato di moto dell'etere in prossimità della materia non viene chiarito nelle trattazioni di Hertz e Heaviside). Da tale ipotesi consegue che le equazioni del campo elettromagnetico, e quindi tutti i fenomeni che da queste si deducono, assumono la stessa forma se riferiti a qualsiasi sistema rigido, indipendentemente dal suo stato di moto rettilineo o rotatorio: "Ne segue che il moto assoluto di un sistema rigido di corpi non influenza in alcun modo i processi elettrodinamici interni, purché i corpi considerati, incluso l'etere, partecipino al movimento" (Hertz 1890, p. 373).
Questo spiega certamente perché nel considerare i fenomeni elettrici o magnetici non fosse necessario tener conto del moto della Terra; tuttavia, poiché la teoria di Maxwell include pure l'ottica, si poneva in aggiunta il problema di spiegare il risultato dell'esperimento di Fizeau (appena confermato, con maggiore precisione, da Michelson e Morley), che allora si pensava dovuto a un trascinamento parziale dell'etere all'interno di un mezzo trasparente in movimento.
Hertz e Heaviside erano consapevoli del conflitto che esisteva tra le loro teorie e i risultati relativi all'ottica dei corpi in movimento: "Le poche indicazioni di cui disponiamo su questo moto [dell'etere] ‒ scrisse Hertz ‒ suggeriscono che [...] l'etere si muova in modo indipendente dalla materia, anche all'interno della materia stessa" (ibidem). Come Maxwell, però, Hertz riteneva prematura la formulazione di ipotesi dettagliate sul loro moto relativo e preferiva accontentarsi della possibilità di sviluppare un'elettrodinamica completa dei corpi in movimento, anche se incapace di dar conto di tutti gli effetti ottici.
L'esperimento di Michelson e Morley rese la situazione ancor più confusa, dal momento che i loro risultati si potevano spiegare facilmente nell'ipotesi che l'etere fosse trascinato completamente dalla materia, mentre quelli ottenuti da Fizeau sembravano precludere tale possibilità.
La teoria di Lorentz dell'etere immobile: il teorema degli stati corrispondenti e l'ipotesi della contrazione
Nell'articolo del 1886 sull'ottica dei corpi in movimento, Lorentz aveva lasciata aperta la possibilità di un trascinamento parziale dell'etere. La sua famosa teoria dell'elettrone, però, sviluppata negli anni Novanta dell'Ottocento, si basava sull'ipotesi di un etere completamente immobile. Al contrario di Hertz e di Heaviside, Lorentz costruì la sua teoria sulla base di una separazione netta tra etere e materia: nella sua visione, il solo modo nel quale i due potevano interagire era attraverso minuscole particelle cariche (chiamate inizialmente 'ioni' e in seguito 'elettroni', che si pensavano presenti in gran quantità in tutta la materia) le quali generavano i campi elettrici e magnetici nell'etere, governati dalle equazioni di Maxwell; a loro volta, su queste particelle cariche tali campi agivano attraverso la forza di Lorentz F=q(E+v×B). Lorentz postulò, nella sua teoria microscopica, l'esistenza di due soli campi fondamentali: in termini dei quattro campi della teoria di Maxwell che abbiamo sopra menzionato, per l'etere si identificavano semplicemente E con D e B con H. Era compito della teoria macroscopica ricavare le relazioni costitutive per i mezzi materiali, a partire dalle equazioni di campo valide nel vuoto e dal modello microscopico che descriveva la struttura atomistica di ciascun mezzo materiale. Per esempio, il campo elettrico di un'onda elettromagnetica incidente sulle particelle cariche di un mezzo trasparente avrebbe posto le particelle in moto armonico intorno alle loro posizioni di equilibrio. Il momento di dipolo dipendente dal tempo che ne risultava per ogni carica creava un'onda secondaria, emergente dalla carica stessa. L'effet to netto risultante dall'interferenza coerente dell'onda primaria, che si propaga a velocità c, con tutte le onde secondarie emanate dalle cariche nel mezzo è un'onda che si propaga a velocità c/n, dove n è l'indice di rifrazione del mezzo (il quale risulta così legato alle costanti caratteristiche degli oscillatori armonici elementari carichi e al loro numero per unità di volume).
Lorentz affrontò il formidabile compito di spiegare, sulla base della sua teoria dell'elettrone, il motivo per cui gli esperimenti ottici fallivano sistematicamente nel rilevare il moto della Terra rispetto all'etere immobile postulato dalla teoria. Non era soltanto il risultato dell'esperimento del secondo ordine di Michelson e Morley che sembrava contraddire i principî fondamentali della sua teoria; era anche tutt'altro che banale giustificare i risultati negativi di tutti gli esperimenti di primo ordine effettuati nel corso del secolo, la cui spiegazione necessitava del coefficiente di Fresnel. Lorentz doveva in qualche modo ricavare questo coefficiente dalla sua versione della teoria elettromagnetica, senza introdurre alcun trascinamento dell'etere. Nel 1892 egli riu scì nell'intento, nella sua prima trattazione esauriente dell'elettrodinamica dei corpi in movimento (Lorentz 1892), ricavando le equazioni per la propagazione delle onde elettromagnetiche in un dielettrico in moto attraverso l'etere, riferite al sistema solidale con il dielettrico e scoprendo che un'onda che si propaghi, per esempio, lungo la direzione del moto di un sistema di riferimento che si muove a velocità v deve possedere una velocità c/n−v/n2 in quello stesso sistema di riferimento.
La velocità dell'onda rispetto all'etere è dunque (c/n−v/n2)++v=c/n+(1−1/n2)v, in accordo con il coefficiente di Fresnel. È quindi l'onda a essere parzialmente trascinata dal mezzo e non l'etere. Dal punto di vista microscopico, possiamo descrivere ciò che accade quando un'onda elettromagnetica incide su un mezzo trasparente in movimento nel modo seguente: (1) il campo elettrico dell'onda ha l'effetto di spostare le particelle cariche, nel caso in cui siano a riposo, dalle loro posizioni di equilibrio, come accadrebbe se il mezzo non fosse in moto; (2) a causa del loro moto collettivo, però, le particelle sono anche soggette a una forza di Lorentz aggiuntiva qv×B da parte del campo magnetico dell'onda. Tenendo conto di entrambi gli effetti sulle onde secondarie prodotte dalle particelle cariche, la velocità netta di propagazione dell'onda nel mezzo in movimento si riduce di un termine v/n2 rispetto al valore c/n che assume quando il mezzo è in quiete rispetto all'etere. L'onda è soltanto in parte trascinata dal mezzo in cui si propaga.
Il risultato ottenuto da Lorentz rendeva più facile sbarazzarsi dell'etere. Come è stato scritto: "Un etere totalmente trascinato, come quello di Stokes e di Hertz, doveva essere una realtà materiale; così anche un etere parzialmente trascinato, nella misura della sua condensazione, come quello di Fresnel; soltanto un etere assolutamente immobile e che sfuggiva sempre e completamente ai movimenti della materia poteva essere considerato privo di ogni realtà fisica" (Sesmat 1937, p. 525).
Nel trattato del 1892 Lorentz si servì di quantità ausiliarie, mediante le quali semplificare la forma di equazioni valide per alcuni problemi, riguardanti sistemi in moto attraverso l'etere. In un libro che pubblicò tre anni dopo, egli seguì questo approccio più sistematicamente, introducendo quantità ausiliarie grazie alle quali poté dare alle equazioni per la propagazione della luce nei mezzi in movimento la stessa forma (al primo ordine in v/c) valida per i mezzi in quiete rispetto all'etere. La più importante di tali quantità era una nuova variabile temporale t′ che, in un sistema in moto attraverso l'etere a velocità v nella direzione x, era legata al tempo t usuale dalla relazione:
[1] t′=t−(v/c2)x.
A causa della sua dipendenza dalla posizione, Lorentz chiamò questa variabile ausiliaria 'tempo locale'. Sostituì anche nel sistema in movimento i campi elettrici e magnetici reali con campi ausiliari, le cui componenti erano combinazioni lineari di quelle dei campi reali, con coefficienti dipendenti da v. Trascurando quantità di ordine superiore in v/c questi campi ausiliari, come funzioni delle coordinate spaziali e del tempo locale nel sistema in movimento, soddisfano le stesse equazioni valide per i campi reali ‒ che sono funzioni delle coordinate spaziali e del tempo reale in un sistema in quiete rispetto all'etere. A ogni configurazione di campo che sia soluzione delle equazioni nel sistema in quiete rispetto all'etere corrisponde quindi una configurazione di campo che, con buona approssimazione, è soluzione delle equazioni nel sistema in movimento: la descrizione della prima configurazione in termini delle quantità reali permette di descrivere la seconda in termini delle corrispondenti quantità ausiliarie. Tale coppia di configurazioni di campo, una nel sistema in quiete e l'altra in un sistema in moto attraverso l'etere, identificava due 'stati corrispondenti'. Il teorema degli stati corrispondenti afferma che, se una delle due configurazioni è compatibile con le equazioni del campo elettromagnetico, lo è anche l'altra.
Servendosi di questo teorema Lorentz dimostrò che nessun esperimento ottico del primo ordine ‒ consistente nell'osservazione di un'alternanza di zone luminose e zone oscure, come avviene nella maggior parte degli esperimenti di ottica ‒ potrà mai rilevare il moto della Terra rispetto all'etere. L'argomentazione di Lorentz era molto semplice: ciò che percepiamo come oscurità è l'annullarsi del campo elettrico e del campo magnetico che formano l'onda luminosa, mediando su un tempo lungo rispetto al periodo della luce, mentre una luminosità elevata rappresenta un valore elevato di questa media; per descrivere una certa distribuzione di luminosità in un sistema in quiete rispetto all'etere è quindi sufficiente specificare i punti in cui il campo elettrico e il campo magnetico si annullano in media e i punti dove la media è diversa da zero. Nello stato corrispondente che è riferito al sistema in movimento i campi ausiliari assumono gli stessi valori che, nei corrispondenti punti nel sistema in quiete, assumono i campi reali e, poiché le componenti dei campi reali sono combinazioni lineari di quelle dei campi ausiliari, i campi reali si annullano ogni qualvolta ciò accada per quelli ausiliari. Questo spiega i risultati negativi di una vasta classe di esperimenti ottici del primo ordine, se si suppone ulteriormente, come fece implicitamente Lorentz, che la configurazione di campo elettromagnetico prodotta dall'apparato ottico nel sistema in movimento sia lo stato corrispondente della configurazione di campo prodotta dallo stesso apparato ottico in un sistema in quiete rispetto all'etere. Tale ipotesi è valida se si assume che sia soddisfatto il principio di relatività galileiana per i sistemi coinvolti.
Si noti che, perché l'argomentazione di Lorentz sia valida, è essenziale che le distribuzioni di luminosità siano per loro natura stazionarie. Se ciò non fosse, la dipendenza del tempo locale dalla coordinata x comporterebbe complicazioni: se due punti distinti sono simultaneamente oscuri nel tempo ordinario in un sistema in quiete rispetto all'etere, i punti corrispondenti saranno simultaneamente oscuri, nel tempo locale, in un sistema in movimento, ma è soltanto grazie al fatto che l'oscurità persiste in entrambi i punti abbastanza a lungo che ci sarà oscurità simultaneamente nel tempo ordinario.
Servendosi della nozione di tempo locale, Lorentz fu in grado di ricavare in modo molto semplice il coefficiente di Fresnel. Supponiamo che un'onda piana si propaghi in un mezzo in quiete rispetto all'etere con velocità c/n lungo l'asse x di un sistema cartesiano di coordinate, anch'esso in quiete rispetto all'etere. Le componenti del campo elettrico e del campo magnetico che descrivono quest'onda dipendono da x e t esclusivamente attraverso la combinazione
da cui dipende la fase dell'onda. Nello stato corrispondente in un sistema in moto attraverso l'etere con velocità v in
direzione x, sia le componenti dei campi ausiliari sia quelle dei campi reali dipenderanno quindi da x e dal tempo locale t′ soltanto attraverso la quantità
Ciò significa che la dipendenza da x e dal tempo t si manifesta solamente attraverso
Da questa formula si può vedere che la velocità dell'onda rispetto al mezzo in movimento è
La velocità dell'onda rispetto all'etere è quindi c/n++(1−1/n2)v, in accordo con il coefficiente di Fresnel.
Si noti che in questa nuova dimostrazione non entra in gioco esplicitamente la teoria elettromagnetica: l'elemento essenziale è semplicemente l'espressione del tempo locale che, prima dell'avvento della teoria della relatività di Einstein, per Lorentz non era altro che una variabile ausiliaria, senza alcun significato fisico. Nel 1900 però, se non prima, Poincaré concluse che orologi in moto attraverso l'etere, se sincronizzati da un osservatore solidale con il moto per mezzo di segnali luminosi, avrebbero segnato il tempo locale. Può darsi che Poincaré nell'attribuire un significato fisico al tempo locale sia stato influenzato dal lavoro di uno dei suoi maestri, Potier. In genere questa condizione viene formulata in termini di una 'velocità' aggiuntiva da sommare a quella della luce che si propaga attraverso il mezzo in movimento. Nel 1874 Potier formulò la condizione sufficiente affinché le leggi dell'ottica siano le stesse (al primo ordine in v/c) in sistemi in quiete e in sistemi in moto attraverso l'etere, in termini di un 'tempo' da sommare a quello impiegato dalla luce a transitare attraverso il mezzo in movimento. Questa differente formulazione appare molto naturale se si ricava il coefficiente di Fresnel utilizzando il principio di tempo minimo di Fermat, come fecero lo stesso Fresnel, Wilhelm Veltmann ed Éleuthère-Élie-Nicolas Mascart. In effetti, queste derivazioni dimostrano che tutte le leggi dell'ottica in un mezzo in movimento rimangono invariate in confronto a quelle valide in un sistema in quiete rispetto all'etere, purché tutti i cammini ottici siano calcolati in termini del tempo locale. La natura cinematica fondamentalmente relativistica del coefficiente di Fresnel, che all'inizio non fu colta neanche da Einstein, si sarebbe infine compresa, comunque, senza bisogno di riformulazioni come quella di Potier. Nel 1907 Max von Laue (1879-1960) dimostrò che il coefficiente di Fresnel deriva da un'applicazione diretta del teorema relativistico di somma delle velocità. La dimostrazione di Laue è matematicamente equivalente a quella di Lorentz del 1895.
Nel capitolo conclusivo del suo libro del 1895, Lorentz prese in esame diversi esperimenti che non poteva spiegare in base al teorema del primo ordine degli stati corrispondenti. Il più importante tra questi è l'esperimento di Michelson e Morley. Lorentz ripeté in quella sede la spiegazione da lui proposta tre anni prima che, come aveva nel frattempo scoperto, era già stata suggerita da Fitzgerald. Entrambi avanzarono l'ipotesi che il risultato negativo dell'esperimento si potesse spiegare supponendo che i corpi in moto attraverso l'etere subissero una contrazione nella direzione del moto, di un fattore pari a (1−v2/c2)1/2. Nel calcolo quindi, se il braccio è parallelo alla deriva dell'etere, si deve sostituire la lunghezza l del braccio con l(1−v2/c2)1/2:
Questa quantità è esattamente pari al tempo di percorrenza della luce nel caso in cui il braccio è perpendicolare alla deriva dell'etere. Lorentz in effetti previde altre possibili variazioni di dimensione dei corpi, conseguenti al moto di questi attraverso l'etere, mantenendo pari a (1−v2/c2)1/2 il rapporto tra la variazione nella direzione del moto e quella nella direzione perpendicolare al moto.
Lorentz si sforzò di rendere plausibile l'ipotesi della contrazione, servendosi di un risultato che aveva dimostrato in elettrostatica: se una distribuzione di carica è in equilibrio in un sistema in quiete rispetto all'etere, essa si trova in equilibrio statico in un sistema in moto attraverso l'etere se è contratta di un fattore (1−v2/c2)1/2 nella direzione del moto, lo stesso fattore necessario a giustificare l'esperimento di Michelson e Morley. Lorentz ricavò questo risultato con un metodo, che ricorda la sua trattazione dell'ottica nei corpi in movimento, basato sul teorema degli stati corrispondenti. Egli introdusse diverse quantità ausiliarie per far sì che le equazioni dell'elettrostatica nei sistemi in movimento (cioè le equazioni che descrivevano distribuzioni di carica in cui non si aveva moto relativo, ma soltanto un moto globale con velocità costante rispetto all'etere) assumessero la stessa forma di quelle valide per i sistemi in quiete rispetto all'etere. Le più importanti di queste quantità ausiliarie sono nuove coordinate spaziali, che dipendono dalla velocità del sistema attraverso l'etere. Per un sistema in moto con velocità v nella direzione x, soltanto la coordinata x viene sostituita da una nuova coordinata ausiliaria:
Per qualsiasi distribuzione di carica in un sistema in quiete rispetto all'etere, ci sarà una distribuzione corrispondente di carica nel sistema in movimento, la cui descrizione in termini delle variabili ausiliarie sarà identica a quella valida per il sistema in quiete in termini delle quantità reali. Per esempio, le distanze tra le cariche nel sistema in moto, in termini delle coordinate ausiliarie, saranno uguali alle distanze tra le corrispondenti cariche nel sistema in quiete, in termini delle coordinate reali. Dal momento che una distanza Δx′=l in termini delle coordinate ausiliarie corrisponde a una distanza reale Δx=l (1−v2/c2)1/2, la distribuzione di carica nel sistema in moto risulterà accorciata di un fattore (1−v2/c2)1/2 nella direzione del moto, in confronto alla corrispondente dist ribuzione di carica nel sistema in quiete rispetto all'etere. Se questa fosse stata in equilibrio statico, lo sarebbe stata anche la configurazione contratta in movimento attraverso l'etere.
Lorentz mise in chiaro nel titolo del suo libro del 1895 che la teoria ottica ed elettrodinamica dei corpi in movimento che aveva sviluppato era da considerarsi soltanto provvisoria. Egli era in grado di fornire una giustificazione assai generale di molti esperimenti del primo ordine, basandosi sul teorema degli stati corrispondenti, tuttavia doveva ricorrere a ipotesi ad hoc per trattare un piccolo numero di esperimenti del secondo ordine. Pochi anni dopo, Lorentz formulò una versione esatta del teorema degli stati corrispondenti; servendosi di essa poté fornire una trattazione unificata di un ampio ventaglio di esperimenti del primo e del secondo ordine. Nel 1899 Lorentz pubblicò la prima formulazione di questo teorema esatto e della teoria costruita a partire da esso. Il teorema esatto degli stati corrispondenti si ottiene attraverso un uso combinato sia delle quantità ausiliarie utilizzate nella versione del primo ordine del teorema sia di quelle usate nella trattazione dell'elettrostatica nei mezzi in movimento. In un sistema in moto attraverso l'etere con velocità v in direzione x, le coordinate ausiliarie e il tempo locale si possono scrivere come:
k è un fattore globale di scala, che differisce da 1 solamente per un termine dell'ordine di v2/c2 e che porremo uguale a 1, come fece Lorentz, in ultimo, nel 1904. Le equazioni precedenti diventano allora essenzialmente equivalenti a una trasformazione di Lorentz dalle coordinate (x0,y0,z0,t0), valide per un osservatore in un sistema che nella trattazione di Lorentz si troverebbe in quiete rispetto all'etere, alle coordinate (x′,y′,z′,t′), valide per un osservatore nel sistema in moto. Si tenga presente che le coordinate (x,y,z,t) sono legate alle (x0,y0,z0,t0) dalla trasformazione di Galilei:
Combinando la trasformazione da (x0,y0,z0,t0) a (x,y,z,t) con quella da (x,y,z,t) a (x′,y′,z′,t′), ritroviamo le trasformazioni di Lorentz nella forma che ci è familiare:
L'ultima di queste formule si ricava come segue:
dove (1/y2+v2/c2) è uguale a 1.
Dal punto di vista del teorema esatto di Lorentz degli stati corrispondenti, ciò che interessava era la trasformazione dalle coordinate (x,y,z,t) alle coordinate ausiliarie (x′,y′,z′,t′) del sistema in movimento. Come aveva fatto nel 1895 al primo ordine in v/c, Lorentz fu in grado di dimostrare in modo esatto che i campi ausiliari, in quanto funzioni delle coordinate ausiliarie e del tempo locale nel sistema in movimento, soddisfano le stesse equazioni dei campi reali, intesi come funzioni delle coordinate reali e del tempo reale, nel sistema in quiete rispetto all'etere. Tale risultato permette di giustificare i risultati negativi degli esperimenti ottici di deriva dell'etere considerando, come abbiamo fatto già per la versione del primo ordine, la relazione tra le distribuzioni di luminosità associate a determinate configurazioni di campo in un sistema in quiete rispetto all'etere e quelle associate agli stati corrispondenti in un sistema in moto; se nella distribuzione di luminosità per il primo sistema la luminosità è bassa (o alta) in un punto P con coordinate reali (a,b,c), sarà bassa (o alta) anche nel punto P′della distribuzione corrispondente per il secondo sistema, con le stesse coordinate ausiliarie, e cioè con coordinate reali (a/y,b,c).
Come nel caso delle distribuzioni di cariche elettrostatiche, ciò significa che la distribuzione di luminosità nel sistema in moto è accorciata di un fattore (1−v2/c2)1/2 nella direzione del moto rispetto alla distribuzione corrispondente nel sistema in quiete. La teoria di Lorentz prevede che la deriva dell'etere non sia rilevabile dalle distribuzioni di luminosità se, indipendentemente dall'accuratezza degli esperimenti, gli elementi ottici strumentali che producono tali distribuzioni subiscono, a causa del loro movimento, una contrazione uguale a quella delle distribuzioni stesse. L'ipotesi della contrazione proposta da Lorentz e Fitzgerald, congiuntamente al teorema esatto degli stati corrispondenti, spiega perché nessun esperimento simile sarà mai in grado di rilevare la deriva dell'etere. A stimolare la nuova e più generale teoria di Lorentz fu in effetti una variante dell'esperimento di Michelson e Morley proposta nel 1898 da Alfred Liénard (1869-1958) ma mai realizzata: egli aveva suggerito di porre un mezzo trasparente all'interno dei bracci dell'interferometro, così che la contrazione di Lorentz-Fitzgerald non avrebbe più assicurato che il tempo di percorrenza fosse indipendente dall'orientazione dei bracci. Sia Liénard sia Lorentz sospettavano fortemente che il risultato, come quello di tanti esperimenti precedenti, sarebbe stato negativo e nell'articolo del 1899 Lorentz specificò che la sua nuova teoria era in grado di spiegare il motivo.
L'ipotesi fisica che si deve affiancare alla formulazione puramente matematica del teorema degli stati corrispondenti e che conduce a prevedere un risultato negativo per un'intera categoria di esperimenti sulla deriva dell'etere comporta in realtà molto di più del solo effetto di contrazione proposto originariamente da Lorentz e da Fitzgerald. Formulata con più precisione, l'ipotesi è che gli elementi della strumentazione ottica che producono una certa distribuzione di luminosità in un sistema in quiete rispetto all'etere si trasformino, se messi in movimento, nella configurazione strumentale che produce la corrispondente distribuzione di luminosità nel sistema in moto. La stessa ipotesi, nel 1895, era stata tacitamente ammessa nella versione del primo ordine del teorema degli stati corrispondenti e, in quel contesto, era verificata a patto che i sistemi macroscopici si comportassero in accordo con il principio di relatività galileiana. Ciò non vale più nel contesto della versione esatta del teorema, poiché l'ipotesi comporta che, contrariamente al principio galileiano, i sistemi materiali si contraggano muovendosi attraverso l'etere; essa comporta anche, come Lorentz notò esplicitamente nell'articolo del 1899, che la frequenza degli elettroni oscillanti che generano le onde luminose sia minore nei sistemi in moto, piuttosto che in quelli in quiete rispetto all'etere. Secondo il teorema degli stati corrispondenti, infatti, il periodo di oscillazione delle onde luminose in un sistema in quiete rispetto all'etere, espresso in termini del tempo reale, sarà uguale al periodo delle onde corrispondenti nel sistema in moto, nel tempo locale: un periodo T in tempo locale implica un periodo (più lungo) yT in tempo reale. In altre parole, la frequenza della luce nel sistema in moto è minore della frequenza corrispondente nel sistema in quiete di un fattore (1−v2/c2)1/2 e, se il sistema in quiete rispetto all'etere deve trasformarsi nel sistema che genera lo stato corrispondente nel sistema in moto, anche la frequenza degli elettroni deve cambiare. Lorentz fece soltanto un accenno a questo importante risultato, che fu poi ricavato in modo indipendente e presentato con maggiore enfasi da Joseph Larmor (1857-1942) nel 1900.
Di questo effetto si deve tener conto nell'analisi dell'esperimento di Michelson e Morley, nel quale la differenza di fase tra la luce che proviene dai due bracci dell'interferometro si ottiene moltiplicando la differenza nei tempi di percorrenza per la frequenza della luce: il tempo di percorrenza del braccio di un interferometro in moto è di un fattore y più lungo del tempo corrispondente per un interferometro in quiete ‒ e l'ipotesi della contrazione assicura che ciò è vero indipendentemente dal fatto che il braccio si muova parallelamente o perpendicolarmente alla deriva dell'etere ‒ tuttavia la frequenza della luce nell'interferometro in moto è più bassa di un fattore y, da cui segue che le differenze di fase nell'interferometro in moto sono esattamente le stesse dell'interferometro in quiete.
Lorentz si rese conto che l'ipotesi generale che aveva affiancato al teorema esatto degli stati corrispondenti aveva implicazioni inaspettate. Scoprì che le oscillazioni degli elettroni che generano la luce nel sistema in movimento soddisfano le leggi del moto di Newton soltanto se si suppone che le forze agenti, e perfino la massa degli elettroni, dipendano in un modo specifico dalla velocità di quest'ultimi rispetto all'etere. L'ipotesi che la massa di un corpo carico dipendesse dalla velocità era stata già avanzata in precedenza e Lorentz era quindi preparato ad accettare le conseguenze della sua nuova teoria. Alcuni anni più tardi fu possibile verificare sperimentalmente la dipendenza della massa dell'elettrone dalla velocità, studiando la deflessione dei raggi beta in un campo elettromagnetico.
Nell'articolo del 1899 Lorentz espose la nuova teoria per grandi linee, principalmente per dimostrare che l'approccio basato sugli stati corrispondenti poteva fornire gli elementi necessari a giustificare i risultati negativi di esperimenti come quello proposto da Liénard. Nel 1904 Lorentz pubblicò un'esposizione sistematica e completa della teoria in un articolo, Electromagnetische verschijnselen in een stelsel, dat zich met willekeurige snelheid, kleiner den die van het licht, beweegt (Fenomeni elettromagnetici in un sistema in movimento con velocità più piccola di quella della luce), che fu stimolato sia dalla critica tagliente di Poincaré riguardante l'ipotesi della contrazione, sia da recenti esperimenti del secondo ordine sulla deriva dell'etere, volti esplicitamente a verificare l'ipotesi della contrazione.
In primo luogo, Morley aveva trovato un nuovo colla boratore in Dayton C. Miller (1866-1941). Nel 1904 i due ripeterono l'esperimento di Michelson e Morley con un interferometro i cui bracci erano realizzati in legno, volendo verificare se la contrazione dipendeva o meno dal materiale utilizzato; essi non rilevarono alcuno spostamento di fase sistematico, nemmeno quando, nel 1905, trasportarono l'interferometro in montagna. Si può affermare che, a questo punto, Morley e Miller avessero perso i contatti con gli sviluppi teorici, poiché, a seguito del successo della teoria di Lorentz, nella comunità dei fisici la nozione di trascinamento dell'etere era stata quasi completamente abbandonata a favore di un etere immobile; ciononostante, Miller continuò nella sua ricerca sulla deriva dell'etere ed effettuò un'altra serie di prove negli anni Venti.
Più importanti degli esperimenti di Morley e Miller furono quelli effettuati nel 1902 da lord Rayleigh e nel 1904 da De Witt Bristol Brace (1859-1905), per verificare se la contrazione di Lorentz-Fitzgerald avrebbe reso birifrangenti alcuni cristalli, e una prova compiuta nel 1903 da Frederick T. Trouton (1863-1922) e dal suo studente Henry R. Noble con cui si era tentato di rilevare l'esistenza di una coppia di forze agente su un condensatore in movimento e tendente ad allinearne le armature con la direzione del moto. Quest'ultima verifica traeva origine da quella sulla deriva dell'etere suggerita da Fitzgerald poco prima della sua morte, che prevedeva un condensatore in un pendolo a torsione (Trouton 1902). Prima ancora che l'esperimento di Trouton-Noble fosse effettuato, Larmor aveva già sostenuto che si sarebbe potuto spiegarne il risultato negativo mediante l'ipotesi della contrazione. Tale esperimento sulla deriva dell'etere è particolarmente interessante in quanto si tratta di un esperimento non ottico e del secondo ordine.
Nel 1899 Lorentz aveva già esteso il teorema degli stati corrispondenti dalla sola ottica all'ottica associata all'elettrostatica e, nel 1904, elaborò la teoria in modo da poterla applicare, almeno in linea di principio, all'intera elettrodinamica. Fin dal 1895 egli aveva formulato il teorema degli stati corrispondenti per le equazioni macroscopiche che governano la propagazione della luce nei mezzi trasparenti; nel 1899, e più sistematicamente nel 1904, elaborò il teorema per le equazioni microscopiche di Maxwell-Lorentz. In questa nuova versione del teorema, Lorentz sostituì anche le densità di corrente e di carica con alcune quantità ausiliarie. In pratica, l'applicabilità della teoria di Lorentz era limitata alle situazioni statiche e stazionarie che si incontravano in ottica, in elettrostatica e in magnetostatica, principalmente a causa del fatto che Lorentz non considerava ancora che il tempo locale e la maggior parte delle altre quantità ausiliarie definite per i sistemi in movimento fossero le quantità realmente misurate da un osservatore solidale con un sistema in moto.
Nel 1904 Lorentz non cambiò soltanto la formulazione del teorema degli stati corrispondenti ma anche il modo di affiancare al teorema le ipotesi fisiche che lo trasformavano in una teoria in grado di prevedere risultati negativi per molti esperimenti di deriva dell'etere. Invece di aggiungere l'ipotesi generale secondo la quale i sistemi materiali, in diversi stati di moto, cambiano in maniera tale che le configurazioni di campo che essi producono siano sempre i membri appropriati di una famiglia di stati corrispondenti, aggiunse ipotesi fisiche più specifiche, dalle quali l'ipotesi generale poteva essere ricavata. La più importante tra queste era l'ipotesi che tutte le forze e tutte le masse dovessero essere soggette alla stessa dipendenza dalla velocità che Lorentz aveva proposto nel 1899. Oltre a postulare questa proprietà, egli presentò un modello concreto dell'elettrone, la cui massa esibiva la dipendenza dalla velocità voluta, a patto che si ponesse uguale a 1 il fattore indeterminato k, che compare nella formula per le quantità ausiliarie.
L'elettrone di Lorentz era una distribuzione superficiale sferica di carica, soggetta a una versione microscopica della contrazione di Lorentz-Fitzgerald e la cui massa era interamente dovuta all'interazione dell'elettrone con il suo stesso campo. Max Abraham fece notare subito che il modello era incoerente, in quanto Lorentz non aveva suggerito alcun meccanismo che rendesse stabile l'elettrone puramente elettromagnetico. Poincaré, essendosi imbattuto nello stesso problema che Abraham aveva riconosciuto nel modello di Lorentz, escogitò poco tempo dopo tale meccanismo. Soltanto dopo un decennio circa si chiarì che la dipendenza della massa dalla velocità, della quale Lorentz cercava di fornire una spiegazione dettagliata con il modello di elettrone proposto nel 1904, è in effetti una proprietà generale che riguarda tutte le particelle descritte dalla nuova meccanica relativistica.
Nello stesso articolo in cui propose la correzione del modello di elettrone di Lorentz, Poincaré perfezionò anche la dimostrazione del teorema degli stati corrispondenti, sostituendo le quantità ausiliarie che il fisico olandese aveva introdotto per le densità di carica e di corrente con altre leggermente diverse. Poincaré si era reso conto che le quantità ausiliarie erano le quantità misurate dall'osservatore in moto, il che semplificava notevolmente il compito di giustificare il risultato negativo degli esperimenti sulla deriva dell'etere sulla base del teorema degli stati corrispondenti. Fu proprio Poincaré a coniare il termine 'trasformazioni di Lorentz' per le trasformazioni dalle quantità misurate in un sistema a quelle misurate in un altro; quindi completò la dimostrazione del fatto che le equazioni di Maxwell-Lorentz sono invarianti rispetto alle trasformazioni di Lorentz (per fare uso del nuovo modo di enunciare il teorema degli stati corrispondenti).
Poincaré dimostrò anche che le trasformazioni di Lorentz formano ciò che i matematici chiamano un 'gruppo'. Questo vuol dire, grosso modo, che la trasformazione inversa di una trasformazione di Lorentz e la composizione di due trasformazioni di Lorentz sono a loro volta trasformazioni di Lorentz. L'ipotesi fisica che Lorentz aveva aggiunto nel 1899 al teorema degli stati corrispondenti per rendere la teoria capace di prevedere i risultati negativi degli esperimenti sulla deriva dell'etere si può ora esprimere come la richiesta che le leggi che governano la parte non elettromagnetica dei sistemi studiati siano invarianti di Lorentz, proprio come le equazioni valide per la parte elettromagnetica. Una tale teoria è del tutto equivalente, dal punto di vista empirico, alla relatività ristretta.
Lorentz utilizzò per la prima volta l'interpretazione delle quantità ausiliarie come quantità misurate nel sistema in moto in una serie di lezioni che tenne nel 1906 presso la Columbia University, pubblicate nel 1909. Egli attribuì in quella occasione tutto il merito di questa reinterpretazione a Einstein ma, stranamente, non menzionò Poincaré. Lorentz comunque non accettò l'interpretazione dell'invarianza quale riflesso di una nuova struttura dello spazio-tempo e si attenne sempre alle nozioni prerelativistiche di spazio e di tempo, riguardando la sua invarianza come una proprietà che accidentalmente concerneva tutte le leggi che governavano i sistemi nello spazio-tempo newtoniano. Lorentz trovò particolarmente difficile abbandonare le nozioni di simultaneità assoluta e di etere come substrato per il campo elettromagnetico.
Oltre alla teoria di Lorentz erano in voga verso la fine del secolo anche le teorie dell'elettrodinamica dei corpi in movimento di Emil Cohn, Larmor e Johann E. Wiechert. I primi due autori dovevano molto al lavoro di Lorentz, mentre Wiechert giunse in modo indipendente ad alcuni dei risultati ottenuti dal fisico canadese. Cohn si era proposto di costruire una teoria in grado di spiegare sia l'esperimento di Fizeau sia quello di Michelson e Morley. Da seguace della filosofia di Ernst Mach (1838-1916), che propugnava lo scetticismo verso tutti i concetti non direttamente accessibili all'esperienza, fu probabilmente più facile per Cohn compiere un passo che dovette apparirgli necessario: se una teoria elettromagnetica che utilizza il concetto di etere deve formulare ipotesi contraddittorie sul movimento dell'etere all'interno della materia per spiegare esperimenti differenti, bisogna rinunciare al concetto di etere. Cohn era ben consapevole che la teoria macroscopica, che Lorentz aveva ricavato da un modello microscopico, era in grado di spiegare tutti i fenomeni elettrodinamici del primo ordine e gli effetti ottici senza necessità di introdurre l'ipotesi della contrazione; da buon seguace di Mach, egli si sforzò di eliminare anche tutte le ipotesi atomistiche.
Cohn nel 1900 giunse a una modifica del secondo ordine delle equazioni macroscopiche di Lorentz, che è esattamente invariante rispetto alla versione del 1895 delle trasformazioni di Lorentz per le coordinate spaziotemporali e per i campi. Sempre nello spirito dell'insegnamento di Mach, egli interpretò la velocità v della materia come riferita al moto non rispetto all'etere, ma alle stelle fisse; la teoria di Cohn utilizzava ancora, quindi, uno stato preferenziale di quiete, anche se si trattava di uno stato osservabile empiricamente. Utilizzando tali equazioni Cohn fu in grado di spiegare il risultato dell'esperimento di Fizeau, in modo formalmente molto simile a Lorentz (senza alcun riferimento all'etere, naturalmente).
La dimostrazione effettuata da Lorentz del fatto che il moto attraverso l'etere non aveva alcun effetto del primo ordine sugli esperimenti ottici sulla Terra poteva, tuttavia, essere adesso trasformata in una dimostrazione esatta del fatto che il moto rispetto alle stelle fisse non produceva effetti; da questo seguiva il risultato negativo dell'esperimento di Michelson e Morley.
In uno sviluppo successivo risalente al 1904, Cohn interpretò il tempo locale come il tempo fornito da orologi sulla Terra sincronizzati da segnali ottici, ma suggerì che metodi meccanici di sincronizzazione avrebbero dato ancora il tempo assoluto. La teoria di Cohn suscitò molte critiche, tra le quali alcune legate alla previsione paradossale per cui, in certe condizioni, la velocità della luce in un mezzo in movimento avrebbe potuto essere maggiore di c sia in una direzione sia in quella opposta. Con la soluzione di Einstein ai problemi dell'elettrodinamica e dell'ottica dei corpi in movimento, mediante una reinterpretazione della teoria di Lorentz, la teoria di Cohn scomparve presto dall'orizzonte della fisica.