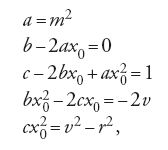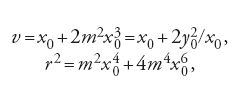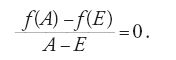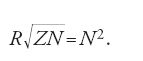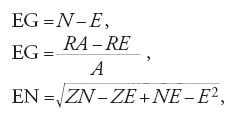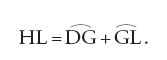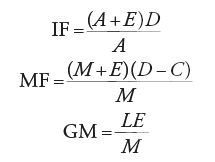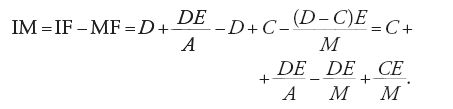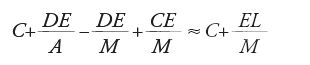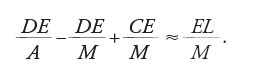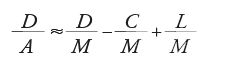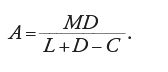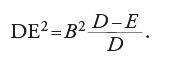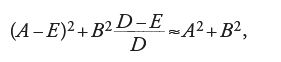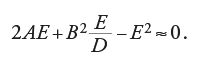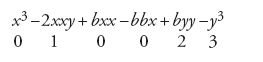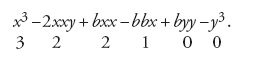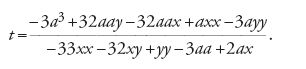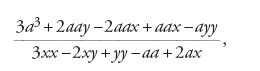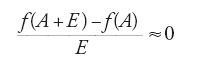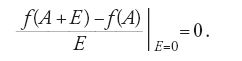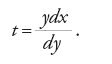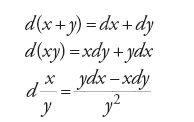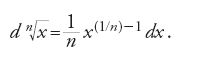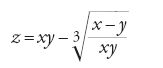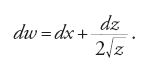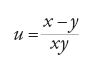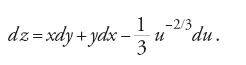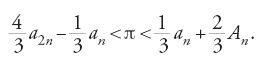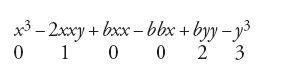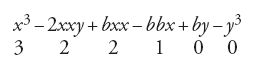La Rivoluzione scientifica: i domini della conoscenza. Dalla Geometrie al calcolo: il problema delle tangenti...

La Rivoluzione scientifica: i domini della conoscenza. Dalla Geometrie al calcolo: il problema delle tangenti...

Dalla Géométrie al calcolo: il problema delle tangenti e le origini del calcolo infinitesimale

La geometria delle curve

La pubblicazione nel 1637 del Discours de la méthode, di cui la Géométrie è l'ultimo dei saggi, segna un punto di svolta nella matematica moderna. Descartes aveva innovato radicalmente l'impianto classico della geometria delle curve, introducendo un nuovo oggetto, la curva-equazione. Anche se non mancavano nella Géométrie metodi tradizionali di considerare le curve, tra cui una serie di macchine per il loro tracciamento, per la verità più ideali che pratiche, il posto principale spettava alla rappresentazione delle curve mediante equazioni, una tecnica totalmente innovativa che gli aveva permesso, tra le altre cose, di risolvere completamente il problema di Pappo e di dare un metodo universale per la soluzione geometrica delle equazioni.

In ambedue i casi, il ruolo dell'equazione è essenziale: senza la corrispondenza, quasi un'identificazione, tra le curve e le loro equazioni, il problema di Pappo sarebbe stato risolto solo in un numero estremamente limitato di casi, poco al di là di quelli noti fin dall'Antichità. Similmente, la teoria geometrica delle equazioni sviluppata nel Libro III, e in particolare la costruzione delle soluzioni di un'equazione algebrica ottenuta mediante l'intersezione di una curva opportuna con una circonferenza, può essere condotta a termine solo utilizzando in maniera essenziale le equazioni dell'una e dell'altra, equazioni che simmetricamente rendono possibile costruire per punti le singole curve risolvendo successivamente equazioni di grado inferiore.

Ma, soprattutto, l'introduzione delle curve-equazioni permetteva di porre in maniera generale e poi di risolvere il problema delle tangenti, "il problema più utile e generale, non solo tra tutti quelli che conosco, ma anche tra tutti quelli che in Geometria ho sempre desiderato conoscere" (OS, II, p. 600).

A differenza degli altri temi affrontati nella Géométrie, fu questo problema ‒ e la soluzione che Descartes ne aveva proposto ‒ a essere, fin dall'apparire dell'opera cartesiana, oggetto di studi intensi che coinvolsero via via tutta la comunità scientifica e che portarono verso la fine del secolo alla scoperta del calcolo infinitesimale.

fig. 1

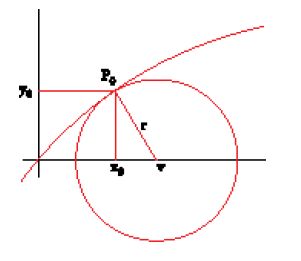
Come è noto, la soluzione di Descartes passa attraverso la considerazione della circonferenza tangente alla curva in un punto dato P₀=(x₀,y₀) (fig. 1). Una volta trovata quest'ultima, infatti, il suo raggio per P₀ sarà normale alla curva, e per ricavare la tangente non si dovrà far altro che prendere la perpendicolare al raggio. Descartes considera la circonferenza con centro nel punto v sull'asse delle ascisse e raggio r, dunque di equazione

[1] (x−v)²+y²=r²

e impone che essa abbia un'intersezione doppia in P₀ con la curva. Analiticamente, se la curva ha equazione P(x,y)=0 (con P polinomio di grado arbitrario), si elimina una delle variabili, per esempio la y, dal sistema formato dalle equazioni della curva e della circonferenza, e si richiede che il polinomio Q(x) così ottenuto abbia una radice doppia in x₀, ovvero che sia della forma

[2] Q(x)=(x−x₀)² R(x)

con R(x) da determinare. Se il polinomio P(x,y) è di grado n, Q(x) è di grado 2n, e R(x) di grado 2n−2. Uguagliando nella relazione precedente i coefficienti dei termini dello stesso grado si ottengono allora 2n+1 equazioni in 2n+1 incognite: i 2n−1 coefficienti di R(x) e i due parametri v e r, che determinano la circonferenza tangente, e che si ricavano risolvendo il sistema. Una volta trovata questa circonferenza, il raggio che passa per il punto P₀ è normale alle curve, e la retta tangente è la perpendicolare al raggio.

Il problema delle tangenti è dunque risolto nella sua generalità, almeno in linea di principio. In realtà il metodo conduce a calcoli piuttosto intricati, anche nei casi più semplici. A titolo di esempio, vediamo cosa avviene nella parabola, di equazione y=mx². Scrivendo questo valore di y nell'equazione della circonferenza, si ottiene (x−v)²+m²x⁴=r², ossia

[3] m²x⁴+x²−2vx+v²−r²=0.

Il polinomio a primo membro deve avere una radice doppia per x=x₀, e dunque deve essere della forma

[4] (x−x₀)² (ax²+bx+c),

che sviluppando diventa

Confrontando quest'ultima espressione con il primo membro della [3], e uguagliando i coefficienti delle differenti potenze della x, si ottiene

dalle quali si possono ricavare una a una le cinque incognite a, b, c, v e r. Si ha

e infine

che danno il centro e il raggio della circonferenza tangente.

La soluzione ottenuta in questo modo è piuttosto formale e per ritrovare la soluzione 'classica' occorre ancora un po' di geometria.

fig. 2

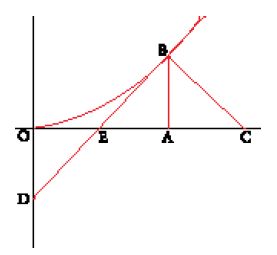
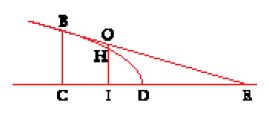
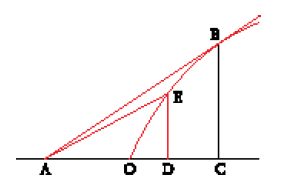
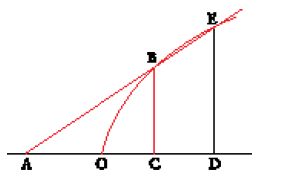
Nel disegno (fig. 2) si ha OA=x₀, AB=y₀, OC=v e BC=r. Si ha inoltre AC=v−x₀, e se si pone EA=z, risulta OE=x₀−z.

I triangoli ABC e AEB sono simili perché sono rettangoli, e gli angoli ACB e ABE sono uguali perché hanno i lati perpendicolari. Si ha allora AC:AB= =AB:AE, e quindi (v−x₀):y₀=y₀:z. Di qui si può ricavare z=y²₀/(v−x₀) e, ricordando che v=x₀+2y²₀/x₀, si trova infine z=x₀/2. Ma allora OE=EA, e i due triangoli EBA ed EDO sono uguali, per cui OD=AB=y₀. Si ritrova allora il risultato classico, secondo cui per trovare la tangente alla parabola in un punto B si riporta sull'asse un segmento OD uguale all'ordinata AB; la retta che congiunge D con B è tangente alla parabola.

In conclusione, se il metodo cartesiano permette di tracciare la tangente a ogni curva che si può esprimere con un'equazione (o, come diceva Descartes, a ogni curva 'geometrica'), il risultato coinvolge calcoli che sono lunghi anche nei casi più semplici e che lo diventano sempre più con l'aumentare del grado della curva. Inoltre, la soluzione viene data in termini analitici e non sempre ha l'immediatezza e l'eleganza di una soluzione geometrica.

Non mancavano quindi gli stimoli per ulteriori ricerche, che in effetti iniziarono negli ambienti cartesiani, in particolare olandesi, già nel periodo immediatamente seguente la pubblicazione della Géométrie. Tuttavia, prima di seguire questo percorso, lasciamo per un momento il metodo di Descartes per esaminare quello che negli stessi anni veniva proposto più privatamente da un altro grande matematico francese, Pierre de Fermat.

Il metodo dei massimi e minimi di Fermat

Quando nel 1637 Descartes pubblicava la Géométrie, Fermat già da qualche anno aveva elaborato un suo metodo per le tangenti, anche questo basato sulla rappresentazione analitica delle curve. Lungi dal renderle pubbliche, il matematico tolosano aveva preferito comunicare le proprie scoperte solo a una ristretta cerchia di amici, e con ogni probabilità furono proprio la notizia della prossima pubblicazione della Géométrie e le anticipazioni sul suo contenuto che lo spinsero a dare al metodo da lui elaborato una diffusione maggiore, al fine di evitare che venisse messa in dubbio non solo la priorità, ma anche l'indipendenza dei risultati che aveva conseguito. Pur in queste circostanze, Fermat non pensò a una pubblicazione a stampa dei suoi risultati, ma si limitò a diffonderli in un certo numero di opuscoli, che circolarono manoscritti in Francia e più tardi in Italia, grazie soprattutto alle cure di Marin Mersenne, che ne fece pervenire copia allo stesso Descartes. Le reazioni di quest'ultimo furono risentite e diedero luogo a una controversia che si protrasse per alcuni mesi e della quale ci occuperemo dopo aver descritto brevemente le idee di Fermat.

In realtà, più che di metodo si dovrebbe parlare di metodi, o quanto meno di un'evoluzione delle tecniche di Fermat. Un'evoluzione d'altra parte tutta da ricostruire, dato che le idee di Fermat furono poste su carta solo molto tempo dopo il loro apparire, e con ogni probabilità non nell'ordine nel quale esse si erano presentate.

fig. 4

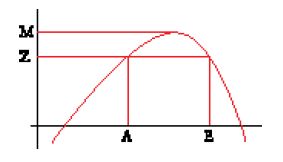
Il metodo prende origine dalle ricerche di Fermat sui massimi e i minimi di una funzione (o meglio di una grandezza variabile, dato che il concetto di funzione si preciserà solo molti decenni più tardi), che a loro volta si sviluppano a partire dallo studio dell'opera di François Viète, da cui Fermat trae anche le sue notazioni. Consideriamo dunque una funzione f, di cui vogliamo trovare, per esempio, il massimo che chiamiamo M (fig. 4). Se prendiamo un valore Z minore di M ‒ afferma Fermat ‒, l'equazione f(X)=Z avrà due soluzioni, A ed E, che si troveranno da una parte e dall'altra del punto di massimo. Poiché f(A)=Z e f(E)=Z, si avrà f(A)=f(E), ossia f(A)−f(E)=0, e dividendo per A−E:

Se ora aumentiamo il valore di Z, sempre però restando al di sotto del massimo M, i due punti A ed E si avvicineranno sempre più tra loro, finché verranno a coincidere quando Z raggiungerà il valore massimo M. Se dunque, dopo aver fatto le dovute semplificazioni, si pone E=A nell'equazione precedente, si troverà un'equazione dalla quale si potrà ricavare il punto di massimo A, e dunque il valore massimo M.

Per esempio, supponiamo di voler trovare, tra tutti i rettangoli di perimetro dato, quello che ha area massima. Se chiamiamo 2B il perimetro, e A la base del rettangolo, l'altezza sarà B−A, e l'area del rettangolo (B−A)A=BA−A². Si tratta allora di trovare il massimo della funzione f(A)=BA−A².

Seguendo il metodo precedente, avremo f(A)−f(E)=0, cioè BA−A²−BE+E²=0, ovvero

[10] B(A−E)−(A²−E²)=0.

Dividiamo ora per A−E e semplifichiamo. Ricordando che A²−E²=(A−E)(A+E), avremo

[11] B−(A+E)=0.

Per trovare il punto di massimo, si deve porre E=A nella relazione precedente; si ha allora B−2A=0, e dunque A=B/2. Di conseguenza, il rettangolo di area massima è il quadrato.

Le tangenti e l'adequazione

fig. 5

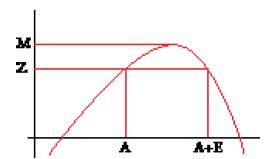
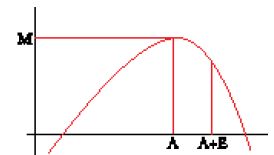
Prima che il metodo dei massimi e minimi fosse applicabile al problema delle tangenti, occorreva una piccola modifica. Come abbiamo visto, uno dei passaggi del metodo precedente consisteva nel dividere per A−E e semplificare. Ora questa semplificazione, che nell'esempio richiedeva solo la conoscenza della formula della differenza dei quadrati o, se si vuole, di eseguire la divisione di A²−E² per A−E, quando entrano in gioco potenze di grado più alto ha bisogno di divisioni più complicate, e dunque di calcoli molto più lunghi e difficili. Di qui una piccola variante che evita queste divisioni complesse. L'idea, afferma Fermat, consiste nell'indicare le due soluzioni (incognite) dell'equazione f(X)=Z, non già con A ed E come in precedenza, ma con A ed A+E (fig. 5); infatti, "poiché E (allo stesso modo di A) è una quantità variabile, niente vieta di chiamarla A+E" (Oeuvres, I, p. 150).

Le differenze con il metodo precedente sono minime. In questo caso bisognerà scrivere f(A+E)−f(A)=0, poi dividere per E, e infine porre E=0. Riprendendo l'esempio precedente, in cui f(X)=BX−X², avremo

[12] f(A)=BA−A², f(A+E)=B(A+E)−(A+E)²=BA+BE−A²−E²−2AE,

e quindi

[13] f(A+E)−f(A)=BE−E²−2AE.

Dividendo per E, otteniamo B−E−2A=0, e ponendo E=0, arriviamo come prima alla relazione B−2A=0 che risolve il problema. Da un punto di vista tecnico, la sola differenza è stata quella di sostituire la divisione per A−E, che in questo caso non comporta difficoltà ma che in generale può essere piuttosto lunga, con la divisione più semplice per la sola E. Si tratta di una semplificazione reale, perché se è vero che così facendo bisogna calcolare f(A+E), più complicata di f(E), è vero anche che questo calcolo comporta solo quello di potenze di A+E, più facili da eseguire che non le divisioni per A−E necessarie con l'altro metodo.

fig. 6

Il secondo metodo dei massimi e minimi può dunque sembrare un puro e semplice miglioramento tecnico del primo, che non ne cambia la struttura concettuale. In realtà le cose non stanno precisamente così. Se infatti esaminiamo la natura delle quantità A ed E che entrano nei due metodi, vediamo che si è prodotto un cambiamento che, per quanto piccolo, sarà importante per gli sviluppi successivi. Nel primo metodo, le quantità A ed E entravano in maniera simmetrica, rappresentando le due soluzioni dell'equazione f(X)=Z. Al variare di quest'ultima grandezza, anche A ed E variavano di conseguenza, fino a coincidere quando al posto di Z si prendeva il valore massimo M. In altre parole, A ed E erano ambedue incognite e variabili. Solo quando Z=M, cioè quando le due soluzioni A ed E si fondevano in una sola, una di esse, quella che avevamo indicato con E, spariva e l'altra perdeva il suo carattere di variabile per conservare solo quello di incognita, che veniva determinata risolvendo l'equazione risultante. Nel secondo metodo, invece, la situazione è molto più ambigua. È vero che in definitiva non si è fatto altro che cambiare il nome di una delle variabili, indicando con A+E quella che prima si era chiamata E; ma è anche vero che così facendo la simmetria formale tra le due variabili si è spezzata, e che ora la variabile A porta fin dall'inizio il segno di quello che diventerà ponendo E=0 (fig. 6). In breve, mentre nel primo metodo A ed E erano ambedue allo stesso tempo variabili e incognite, nel secondo le due caratteristiche precedentemente condivise si spezzano: A diventa fin dall'inizio la posizione, incognita ma non variabile, del punto di massimo, mentre E rappresenta la variazione, variabile ma non incognita, che facciamo subire al punto di massimo al fine di paragonare i valori relativi. Di conseguenza, la relazione f(A)=f(E), che nel primo metodo era una vera equazione, quando nel secondo si scrive A+E al posto di E diventa un'adequazione (adaequatio), un'equazione approssimata che sarà vera soltanto nello stadio finale, quando cioè si sarà posto E=0. "Questo confronto per adequazione produce due termini disuguali, che alla fine producono l'equazione (secondo il mio metodo) che ci dà la soluzione del problema" (Fermat a Mersenne, 1° aprile 1640, in Oeuvres, II, pp. 187-188).

fig. 7

In quest'ultima formulazione, il metodo è particolarmente adatto per affrontare il problema delle tangenti. Per comprenderne il meccanismo, seguiamo Fermat nel suo calcolo della tangente alla parabola. Sia dunque BHD una parabola, con asse EC, e sia B un punto nel quale si vuole trovare la tangente BE (fig. 7). È evidente che questa tangente sarà determinata quando si conoscerà la lunghezza del segmento DE.

La proprietà caratteristica della parabola è che le ordinate ID, CD stanno tra loro come i quadrati delle ascisse corrispondenti IH, CB:

[14] ID:CD=IH²:CB².

Se ora al posto del segmento IH con un estremo sulla curva si mette il segmento IO con l'estremo sulla tangente, essendo IH⟨IO sarà anche ID:CD⟨IO²:CB². D'altra parte, poiché IO:CB=IE:CE, avremo ID:CD⟨IE²:CE².

A questo punto Fermat sostituisce la disuguaglianza trovata con un'adequazione, scrivendo

[15] ID:CD IE²:CE².

Si può esprimere quest'ultima adequazione in termini algebrici, ponendo CD=B, DE=A, e CI=E. Si ha allora ID=B−E, CE=B+A, IE=B+A−E, e dunque

[16] (B−E):B ≈ (B+A−E)²:(B+A)²

ossia

[17] (B−E) (B+A)² ≈ B(B+A−E)².

A questo punto non resta che sviluppare i quadrati e semplificare. Si giunge così all'adequazione

[18] −E(B+A)² ≈ −2BE(B+A)+BE²

e dividendo per E dopo aver cambiato il segno ad ambedue i membri:

[19] (B+A)² ≈ 2B(B+A)−BE.

Se ora si pone E=0, l'adequazione diventa un'equazione. Si ha allora (B+A)²=2B(B+A), e dividendo per (B+A) si ottiene B+A=2B e quindi in conclusione A=B.

Per trovare la tangente alla parabola nel punto B basta allora prendere sull'asse un punto E in modo che DE=CD. La retta EB sarà tangente alla parabola, ritrovando così il risultato classico.

Naturalmente è possibile rileggere il metodo delle tangenti di Fermat come un'applicazione di quello dei massimi e minimi. È sufficiente infatti osservare che, essendo CE²:IE²==CB²:IO², se si pone CB=D, il rapporto

è sempre minore del rapporto CD:CB², a cui è uguale solo per E=0. Di conseguenza la funzione

ha un massimo per E=0. In questo modo, il problema delle tangenti è ricondotto al metodo dei massimi e minimi. Ci sono però due punti da precisare. Il primo, più tecnico, è che mentre in precedenza l'incognita A denotava la posizione del massimo o del minimo, nel problema delle tangenti questa posizione è nota fin dall'inizio (si sa a priori che il massimo della funzione f(E) deve cadere nel punto E=0), e proprio su questo fatto si fa leva per trovare la distanza incognita A=DE. In secondo luogo, e qui è posta la chiave dei possibili sviluppi del metodo, Fermat non applica mai il metodo precedente all'espressione [21], ma utilizza direttamente l'adequazione [16], ottenuta scrivendo sulla tangente la proprietà caratteristica della curva. E d'altra parte la riduzione della tangente alla parabola a un problema di massimo passa attraverso la considerazione del rapporto ID:IO² tra grandezze non omogenee, che Fermat, in omaggio al principio di omogeneità della teoria delle proporzioni, si guarda bene dall'introdurre, utilizzando invece i rapporti ID:CD e IH²:CB² tra grandezze omogenee.

fig. 9

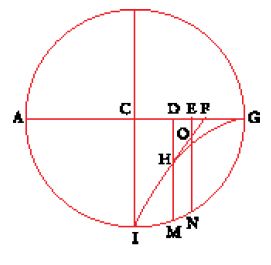
Possiamo vedere lo stesso metodo applicato ad un altro esempio, quello della tangente alla cissoide di Nicomede. Per trovare la tangente a questa curva in un dato punto H, Fermat chiama A la sottotangente DF, e pone AD=Z, DG=N, DH=R, e DE=E (fig. 9).

La proprietà caratteristica della cissoide IHG è espressa dalla proporzione

[22] MD:DG=DG:DH,

cioè, tenendo conto che per le proprietà della circonferenza si ha DM²=ZN,

Ciò posto, "si deve considerare la proprietà specifica non più sulla curva, ma sulla tangente" (Oeuvres, I, p. 160); si dovrà dunque scrivere

[24] NE:EG ≈ EG:EO.

Ora

e dunque

Elevando al quadrato e semplificando, si ottiene

[27] (N−E)⁴ A² ≈ (ZN−ZE+NE−E²)(RA−RE)².

I termini che non contengono E si eliminano grazie alla relazione caratteristica

Se ora si divide per E e si pone E=0, si giunge all'equazione

[28] 3ZA+NA=2ZN

che dà la sottotangente A.

Già da questi esempi possiamo vedere che il metodo di Fermat per le tangenti è sì basato su quello dei massimi e minimi, ma questa dipendenza non è diretta, passando essenzialmente per l'assunzione che la proprietà caratteristica della curva in esame si tramuti in un'adequazione quando la si scriva sulla tangente invece che sulla curva. Questa 'proprietà caratteristica della tangente', di rappresentare localmente la curva, è ancora più evidente quando Fermat, estende il suo metodo alle curve trascendenti, o più precisamente a quelle la cui proprietà caratteristica si esprima in termini della lunghezza di una curva data. In questo caso, secondo Fermat, "se si vuole si possono prendere le ordinate sulle tangenti trovate col metodo precedente al posto di quelle sulle curve; e inoltre (che è il pregio del metodo) si possono prendere porzioni delle tangenti già trovate al posto delle porzioni corrispondenti delle curve, in modo da trovare l'adequazione" (ibidem, p. 162).

fig. 10

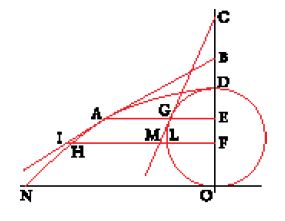
Possiamo vedere applicato quest'ultimo precetto nella ricerca della tangente alla cicloide, la sola che Fermat sviluppi nei dettagli. La cicloide è la curva disegnata da una circonferenza OLDO che ruota sulla retta NO (fig. 10). La sua proprietà caratteristica è che tagliandola con una retta orizzontale come AE, il segmento AG tra la cicloide e il cerchio generatore è uguale all'arco di circonferenza GD.

Per trovare la tangente alla cicloide in un suo punto A, si traccia la retta orizzontale AE, e nel punto G la tangente GC alla circonferenza. Quest'ultima è nota dalla geometria elementare; in particolare si possono considerare noti i segmenti GC e CE. Se scriviamo la proprietà caratteristica della cicloide relativamente alla retta IF, avremo che il segmento HL è uguale all'arco LD, e dunque alla somma dei due archi DG e GL:

Mettiamo ora in pratica il procedimento di Fermat. In primo luogo "si possono prendere le ordinate sulle tangenti trovate col metodo precedente al posto di quelle sulle curve"; nel nostro caso ciò significa che invece del segmento HL (con gli estremi sulle curve) si può prendere il segmento IM con gli estremi sulle tangenti. Inoltre, per Fermat, "si possono prendere porzioni delle tangenti già trovate al posto delle porzioni corrispondenti delle curve", ossia invece dell'arco GL si può prendere la porzione di tangente GM. Ciò facendo, l'equazione precedente diventa un'adequazione. Ricordando che l'arco DG è uguale al segmento GA, si ottiene allora

[30] IM≈AG+GM.

Introduciamo ora alcune notazioni algebriche, ponendo DE=B, FE=E, BE=A, AG=C, AE=D, GC=L, CE=M.

Avremo allora BF=A+E, e applicando il teorema di Talete ai triangoli IFB e MFC:

da cui

L'adequazione diventa allora

e dunque

Dividendo per E si ottiene

da cui in conclusione

Descartes contro Fermat

Come si è detto, uno dei motivi che indussero Fermat a mettere su carta il suo metodo dei massimi e minimi e delle tangenti fu l'annunciata pubblicazione della Géométrie di Descartes. Verso la fine del 1637, poco dopo la pubblicazione della Géométrie, Fermat mandò un breve trattato a Mersenne, che si affrettò a comunicarlo a Descartes. Lo scritto di Fermat non conteneva la prima versione della sua teoria dei massimi e minimi, né alcun tentativo di spiegazione di un metodo che veniva enunciato apoditticamente, e applicato ad alcuni problemi di massimo o di minimo e alla determinazione delle tangenti ad alcune curve, molte delle quali, come per esempio la parabola, note fin dall'Antichità.

Occorreva dunque una buona disposizione per accettare l'efficacia di un metodo appena abbozzato e, come si sa, la pazienza non era tra le principali doti di Descartes. D'altra parte quest'ultimo non aveva tutti i torti a diffidare delle intenzioni di Fermat, che pochi mesi prima aveva criticato la sua Dioptrique prima ancora che venisse pubblicata, sulla base di una copia che Jean de Beaugrand, incaricato di rivedere il Discours de la méthode, gli aveva mandato senza nemmeno avvertire l'autore.

è dunque giustificabile che Descartes considerasse l'opuscolo di Fermat come un'opera proveniente da un ambiente ostile e mirante a sminuire la sua Géométrie, come pure è comprensibile che il suo esame del metodo delle tangenti fosse particolarmente severo e tendesse, più che a impadronirsi di un algoritmo che vedeva come diretto concorrente del suo, a trovarne i punti deboli ed eventualmente a ricondurlo nell'ambito della sua trattazione.

Descartes porta il suo attacco in due direzioni. In primo luogo, attenendosi strettamente al testo di Fermat, in particolare al calcolo della tangente alla parabola, egli obietta che il metodo impiegato possa condurre a risultati erronei. Come abbiamo visto, Fermat basava il suo metodo sul fatto che la proprietà caratteristica della parabola ID:CD=IH²:CB² (fig. 7), scritta sulla tangente diventa una disuguaglianza ID:CD⟨IO²:CB², e così dà luogo all'adequazione (B−E):B (B+A−E)²:(B+A)², da cui si ricava la quantità A, e quindi la tangente. Ora, benché nella figura il punto I sia preso a destra di C, e quindi la quantità E sia positiva, è evidente dal metodo che la disuguaglianza ID:CD⟨IO²:CB² debba valere sia quando I è a destra di C, come nella figura, sia quando è a sinistra, o in altre parole che l'adequazione (B−E):B (B+A−E)²:(B+A)² debba valere sia per E positivo che per E negativo. Descartes invece prende alla lettera la figura e il calcolo di Fermat, come se fosse necessario assumere la disuguaglianza solo per E positivo, e può allora facilmente applicarne l'argomento sostituendo 'ellisse' a 'parabola'. Infatti se la curva è un'ellisse, la disuguaglianza ID:CD⟨IO²:CB² resta valida, ma soltanto per i punti I a destra di C, come nella figura. Dove Fermat aveva affermato nec unquam fallit methodus, Descartes può concludere semperque fallit methodus.

fig. 11

è evidente che si tratta di una lettura particolarmente pretestuosa e malevola: qualsiasi lettore non prevenuto non avrebbe mancato di convenire sul fatto che, quando al posto di una parabola si prendeva un'ellisse, si sarebbe dovuto anche sostituire al posto della proprietà caratteristica della parabola la corrispondente proprietà dell'ellisse. Più giustificata è invece la seconda obiezione mossa contro il 'metodo' di Fermat. Come si è detto, questi aveva asserito il legame tra il metodo delle tangenti e quello dei massimi e minimi, senza tuttavia spiegare come i due metodi fossero connessi. Descartes interpreta questa relazione nel senso che la tangente AB a una curva OEB è la retta più lunga tra tutte quelle che da A vengono tirate verso la curva, come AE (fig. 11). Prendendo una parabola e ponendo OC=D, BC=B, AC=A, DC=E, si ha AD=A−E, OD=D−E, e tenendo conto della proprietà caratteristica della parabola, DE²:BC²=OD:OC, si ricava

Risulta dunque

Si può allora scrivere l'adequazione

che semplificata dà

Se ora si applica il metodo di Fermat, dividendo per E e ponendo E=0, si perviene alla relazione

che dà un risultato assurdo, perché A deve ovviamente essere positivo.

In questo caso la critica di Descartes coglie effettivamente un punto delicato del metodo di Fermat, che né il suo autore né i seguaci né i critici hanno chiarito. In effetti, la risposta di Fermat fu che la retta AB non dà veramente un massimo, perché se si prende il punto D a destra di C la corrispondente retta AE ha lunghezza maggiore di AB. A questo argomento Descartes replicò che in tale caso non si sarebbe trattato di una retta tirata fino alla parabola, perché la retta AE avrebbe incontrato la parabola prima di E. In altre parole, Fermat prendeva in considerazione anche i punti al di là di C, e quindi sosteneva che la retta AB non dava un massimo, mentre Descartes si limitava ai punti compresi tra O e C, e in questo caso la retta AB dava sì un massimo, ma questo cadeva in un estremo, e il metodo di Fermat non era applicabile. Quest'ultima limitazione non emerse però dalla discussione, che si concentrò invece sulla legittimità di considerare anche i punti al di là di C.

Infine, Descartes sospettava che il metodo di Fermat si applicasse solo a casi particolari, forse addirittura che fosse stato costruito ad hoc per la parabola, e sfidò il suo antagonista a trovare la tangente alla curva che più tardi fu chiamata 'folium di Descartes', di equazione x³+y³=pxy. Fu forse proprio il successo di Fermat nel trovare la soluzione a questo problema, e anche la buona disposizione del matematico di Tolosa, sempre incline a smorzare i toni contrariamente a quanto facevano i suoi fautori, Roberval ed étienne Pascal, che indusse Descartes a porre fine alla disputa e a riconoscere la bontà del metodo di Fermat. A parte questa conclusione positiva, ognuno dei contendenti rimase persuaso della sostanziale preminenza della sua impostazione e la disputa si chiuse senza portare un reale progresso, né una chiarificazione della portata e dei limiti dei due metodi rivali.

Il problema delle tangenti tra la 'Géométrie' e il calcolo

Come si è già accennato, durante la sua vita, Fermat non pubblicò praticamente nulla. Il suo metodo delle tangenti, benché non del tutto ignorato, venne diffuso solo in una cerchia piuttosto ristretta di scienziati, praticamente limitata ai circoli parigini ‒ dove però si trovava in concorrenza con l'altrettanto inedito metodo cinematico di Roberval ‒ e ad alcuni ambienti galileiani, nei quali Mersenne lo aveva introdotto in occasione del suo viaggio in Italia nel 1644, ambienti però largamente digiuni delle tecniche dell'algebra letterale e dunque impreparati a raccogliere le novità in questo campo.

Al contrario, la Géométrie di Descartes ebbe una rilevante diffusione, sia come parte del Discours de la méthode, con il quale era apparsa originariamente nel 1637, sia soprattutto grazie alle numerose edizioni della traduzione latina, arricchite da commenti e spiegazioni che ne facilitavano la comprensione. Anche se la Géométrie continuò a essere stampata ancora nel Settecento, furono soprattutto le edizioni curate da Frans van Schooten nel 1649 e poi nel 1659-1661, che oltre alla traduzione contenevano commenti dello stesso van Schooten, di van Heuraet, di de Beaune, di Bartholin, a determinarne la fortuna tra gli scienziati europei.

I primi contributi di rilievo vennero ovviamente dagli studiosi più vicini a Descartes, in particolare dagli ambienti olandesi e parigini. Si trattava essenzialmente di ricerche che miravano a semplificare gli aspetti tecnici del metodo cartesiano e a eliminarne i punti deboli.

In primo luogo, la considerazione della circonferenza al posto della retta tangente elevava artificialmente il grado del polinomio risultante da n a 2n. Inoltre, la soluzione richiedeva l'eliminazione di una delle due variabili e la soluzione di un sistema in molte incognite, delle quali però solo due (i parametri v e r della circonferenza) erano essenziali per la soluzione. Infine il metodo cartesiano era applicabile solo alle curve che avevano un'equazione, cioè a quelle che oggi chiamiamo algebriche, e quindi escludeva a priori tutte quelle, come la cicloide, la quadratrice o la spirale, che ne erano prive e che venivano descritte mediante la loro costruzione o qualche altra proprietà caratteristica. Di qui la distinzione cartesiana tra curve geometriche e meccaniche, e l'esclusione di queste ultime dalla geometria, un'esclusione non di principio (lo stesso Descartes prenderà in esame la cicloide e ne troverà la tangente, introducendo en passant il centro istantaneo di rotazione) ma di metodo: per le curve meccaniche non si dà un calcolo generale. Su questi tre punti si concentrerà gran parte della ricerca postcartesiana.

Il primo punto affrontato riguarda la circonferenza tangente. Già nella prima edizione latina della Géométrie, pubblicata nel 1649, Florimond de Beaune aveva osservato come la considerazione della retta tangente, di equazione y=y₀+m(x−x₀), permettesse di evitare l'innalzamento del grado del polinomio risultante, che così risultava di grado n. Nella seconda edizione di dieci anni successiva, una nota di Jan Hudde insegnava come evitare l'introduzione del polinomio ausiliario R(x), in modo da ridurre le incognite alle sole v e r nella formulazione cartesiana, o meglio alla sola m in quella di de Beaune. Il metodo di Hudde consiste nell'osservare che un polinomio

[42] Q(x)=a₀+a₁x+a₂x²+a₃x³+…+a_nxⁿ

ha una radice doppia in un punto x₀ se e solo se, oltre a Q(x₀)=0, è anche verificata l'equazione Q₁(x₀)=0, dove Q₁(x) è il polinomio che si ottiene da Q moltiplicando i singoli termini per una qualsiasi progressione aritmetica k₀, k₁,…, k_n:

[43] Q₁(x)=k₀a₀+k₁a₁x+k₂a₂x²+…+k_na_nxⁿ.

In particolare si può prendere la progressione 0,1,2,…, n, e quindi in definitiva si giunge al sistema di due equazioni

di cui la prima è automaticamente verificata in quanto il punto P₀ giace sulla curva, e la seconda dà il valore del parametro m.

Vediamo per esempio il caso semplice della parabola di equazione py=x². Sostituendo y₀+m(x−x₀) al posto di y, si ottiene

[45] Q(x)=x²−py₀−pm(x−x₀)=x²−pmx +p(mx₀−y₀)

e

[46] Q₁(x)=2x²−pmx,

da cui si ricava m=2x₀/p. L'equazione della retta tangente alla parabola nel punto (x₀, y₀) è dunque

[47] y=y₀+2x₀(x−x₀)/p.

Il metodo di Hudde, come si è detto, ha il gran vantaggio di evitare l'introduzione del polinomio ausiliario e quindi di limitare i calcoli alla soluzione di una sola equazione. D'altra parte, esso richiede ancora in via preliminare l'eliminazione di una delle variabili tramite l'equazione della retta tangente, e quindi una manipolazione a volte laboriosa dell'equazione della curva; in sintesi, si tratta di un metodo e non ancora di un algoritmo.

La definitiva automatizzazione del procedimento è ancora opera di Hudde che, come aveva fatto per il metodo precedente, si limita a scrivere una lettera a van Schooten, stavolta però con la raccomandazione "che ciò che vi mando resti segreto, e che non diciate a chicchessia che si sia trovato qualcosa di simile". La regola, che Hudde enuncia solamente, è:

Ordinate tutti i termini dell'equazione che esprime la natura della curva in modo che risultino =0. […] Moltiplicate il termine in cui y figura alla massima potenza per un numero preso ad arbitrio, o anche per 0, moltiplicate il termine in cui y ha una dimensione in meno per lo stesso numero diminuito di un'unità, e continuate allo stesso modo con gli altri termini dell'equazione. Similmente moltiplicate per un numero ad arbitrio o per 0 il termine in cui x compare con l'esponente massimo: il termine nel quale x ha una dimensione in meno deve essere moltiplicato per lo stesso numero meno l'unità, e così via. Quando si divide il primo di questi prodotti per il secondo, il quoziente moltiplicato per −x è AC. ("Journal litéraire de la Haye", 1713)

All'incirca negli stessi anni, una regola simile era nota a René-François de Sluse, che nel 1662 ne parlava a Christiaan Huygens come di qualcosa che aveva trovato anni prima. Né Hudde né Sluse davano un cenno della dimostrazione, che invece troviamo in una memoria di Huygens, presentata all'Académie des Sciences nel 1667, ma pubblicata solo nel 1693 (Regula ad inveniendas tangentes linearum curvarum). Per condurla a termine, Huygens inserisce nel contesto cartesiano considerazioni di carattere infinitesimale.

fig. 13

Nella fig. 13, sia F(x,y)=0 l'equazione della curva OBE, e sia AE una retta che passa, oltre che per il punto B in cui si vuole tracciare la tangente, anche per un secondo punto E sulla curva. Se si pone OC=x, BC=y, AC=t e CD=e, si ha ED=y(1+e/t). Dato che il punto E sta sulla curva, si ha allora

[48] F[x+e,y(1+e/t)]=0.

Se in questa relazione si sviluppano le potenze, i termini che non contengono e si annullano a causa dell'equazione F(x,y)=0; divisi allora gli altri per e, e posto e=0, si ottiene una relazione dalla quale si ricava la sottotangente t. Infatti, "se si considera BE già come la tangente, e cioè si prende CD, ovvero e, infinitamente piccola, i termini in cui resta ancora e conterranno delle quantità infinitamente piccole, ovvero del tutto evanescenti" (Regula ad inveniendas tangentes linearum curvarum, in Oeuvres, XX, p. 243).

Si possono dunque trascurare fin dall'inizio i termini che contengono e² o potenze superiori di e, tenendo conto solo di quelli che contengono e alla prima potenza. Di conseguenza, della potenza (x+e)^k sopravviverà solo il termine kx^k−1e, mentre i fattori [y(1+e/t)]^m daranno luogo al termine my^m e/t. Di qui la conclusione: i termini dell'equazione finale "si costruiscono con una regola precisa a partire dalle date potenze delle x ed y; e cioè da una qualsiasi potenza della x, come x³, cambiando una delle x in e, e moltiplicando per l'esponente della x: nel nostro caso si ottiene 3exx. Dalle potenze della y invece moltiplicandola per e/t ed anteponendovi similmente l'esponente della y: così da y³ si ottiene 3y³e/t" (ibidem, p. 247).

Si ottiene così la regola delle tangenti: "Portati tutti i termini dell'equazione da una stessa parte, che dunque risulterà uguale a zero, si moltiplichino dapprima i termini nei quali compare la y per il numero di dimensioni che negli stessi ha y, e questa sarà la quantità dividenda. Quindi similmente si moltiplichino i termini che contengono x per l'esponente della x, e da ognuno si tolga una x; questa quantità si dovrà porre come divisore della quantità dividenda trovata sopra. Ciò fatto, si otterrà una quantità uguale a t ossia AD" (ibidem, p. 245).

In questo modo il passaggio dal metodo all'algoritmo è compiuto: la regola di Hudde-Sluse fa passare direttamente dall'equazione della curva all'equazione della tangente grazie a un procedimento meccanico di sostituzione dei termini. Ciò è ancora più evidente nella formulazione di Sluse, nella quale i passaggi intermedi sono puramente formali, non esprimendo nessuna relazione tra le grandezze geometriche coinvolte. Scrive Sluse:

Per trovare AD ovvero t, questa sarà la Regola Generale:

1) Espunte dall'equazione le parti nelle quali non compaiono né x né y, si pongano da un lato tutte quelle in cui c'è x, e dall'altro quelle in cui appare la y, con i loro segni + o −. Per semplicità chiameremo quest'ultimo lato destro, e l'altro lato sinistro.

2) Nel lato destro, si apponga ad ogni termine l'esponente della potenza che in esso ha la y; o, che è lo stesso, si moltiplichi per questo esponente.

3) Si faccia lo stesso per il lato sinistro, apponendo cioè ad ogni termine l'esponente della potenza che in esso ha la x. Ma inoltre, in ogni termine si cambi una x in t. Dico, che l'equazione così rimaneggiata fornisce il modo di condurre la tangente in un punto B dato.

La regola di Sluse appare in una lettera al segretario della Royal Society, e viene pubblicata nel gennaio 1673 sulle "Philosophical Transactions" con il titolo An extract of a letter from the excellent Renatus Franciscus Slusius. Nel contempo, Oldenburg trasmette a Sluse una lettera di Isaac Newton, nella quale viene formulato un metodo delle tangenti che lo stesso Sluse dirà essere identico al suo:

Nel frattempo non ti sarà ingrato ricevere quello che il nostro dottissimo Newton ha scritto recentemente sull'argomento al nostro Sig. Collins, con queste parole: "Non poco mi fa piacere sentire che matematici stranieri hanno trovato lo stesso mio metodo per condurre le tangenti. Di quale a mio parere esso sia, ti renderai conto con questo esempio. […] Si esprima con una qualsiasi equazione, ad esempio x³−2xxy+bxx−bbx+byy−y³=0, la relazione tra x ed y che determina la curva. La regola per condurre le tangenti è la seguente: si moltiplichino i termini dell'equazione per un'arbitraria progressione aritmetica secondo le potenze della y, come per esempio

e secondo le potenze della x, come

Il primo prodotto sarà il Numeratore, e il secondo diviso per x il Denominatore della frazione, che esprime la lunghezza AD". (The correspondence of Henry Oldenburg, IX, p. 427)

In effetti, a cavallo degli anni Settanta molti matematici in Inghilterra e sul Continente sono in possesso di metodi per le tangenti più o meno simili tra loro. A parte quello di Newton appena ricordato, i metodi sviluppati dai matematici inglesi hanno molte affinità, e a volte sostanziali parti comuni, con le tecniche di Fermat. Per esempio nelle Lectiones geometricae (1670), Isaac Barrow afferma: "Se nel calcolo entrerà un elemento infinitesimo di una qualsiasi curva; si sostituirà al suo posto una particella della tangente opportunamente presa; e cioè una qualsivoglia retta ad essa equipollente (per l'indefinita piccolezza della curva)" (ed. Godbid, p. 81).

Naturalmente, Barrow non si limita a ripetere la strada percorsa da Fermat, ma amplia molto la portata del metodo, specie per quanto riguarda le curve trascendenti. Se Fermat, grazie alla sostituzione di una porzione di tangente al posto dell'analoga porzione di curva, era riuscito a sottomettere al calcolo alcune curve trascendenti, tra cui la cicloide, Barrow considera intere classi di curve trascendenti, dipendenti sia dalla rettificazione sia dalla quadratura di altre curve; un metodo in cui alcuni storici nel passato hanno preteso di vedere un'anticipazione del teorema fondamentale del calcolo integrale.

Infine, è da registrare un singolare metodo per le tangenti dovuto al matematico tedesco Ehrenfried Walter von Tschirnhaus, forse su un'idea di Leibniz ‒ che alcuni anni più tardi scriverà a Huygens che "è successo più di una volta che [Tschirnhaus] ha dimenticato di aver visto da me degli esempi di cose che poi ha pubblicato come sue" (Die Briefwechsel, p. 602). Pubblicato sul "Journal des Sçavans" dell'8 giugno 1682 e sugli "Acta Eruditorum" del dicembre dello stesso anno, in un articolo dal titolo Nova methodus tangentes curvarum expedite determinandi, il metodo rimase praticamente sconosciuto ai contemporanei, sia perché immediatamente superato dal calcolo leibniziano che doveva apparire meno di due anni dopo, sia perché le regole enunciate, delle quali l'autore non dà alcuna giustificazione, a prima vista appaiono piuttosto bizzarre. Del pari esso è stato trascurato dagli storici, che hanno preferito per lo più soffermarsi su altre scoperte di Tschirnhaus, come la caustica per riflessione e, soprattutto, sui suoi contributi alla teoria delle equazioni algebriche. Non mi pare dunque inutile segnalare il metodo di Tschirnhaus, sia perché a dispetto della sua apparente incongruità esso conduce alla corretta determinazione della tangente nei casi considerati, sia perché esso è di gran lunga più generale di quelli allora noti, estendendosi a una larga classe di curve trascendenti.

Sia […] BDE una qualsiasi curva geometrica, come le chiama Cartesio; l'ascissa BO sia uguale ad x, l'ordinata CD uguale ad y, la retta AB che determina la tangente sia t: sia data inoltre la natura della curva, che ad es. sia tale che y³+x³+xxy sia uguale a xyy−a³+aay−aax+axx−ayy. Ciò posto, si ordinino tutti i termini di questa equazione in modo che la massima potenza dell'ordinata CD, ovvero y, sia da una parte dell'equazione: nel nostro caso sarà y³=−x³−xxy+xyy−a³+aay−aax+axx−ayy. […] Si formi una frazione il cui numeratore è costruito come segue: i termini che contengono la quantità nota a si assumano con i loro segni, e se questa è elevata alla prima potenza, si preponga a quel termine l'unità, se alla seconda il due, se alla terza il tre, e così via: nel presente esempio il numeratore sarà −3a³+2aay−2aax+axx−ayy. Si costruisca il denominatore con questo metodo: presi quei termini, nei quali compare l'ascissa x, e conservati i segni, se la quantità x compare alla prima potenza si preponga come sopra l'unità, se alla seconda il due; e avremo −3x³−2xxy+xyy−aax+2axx: diminuiti poi questi termini di una x il denominatore sarà −3xx−2xy+yy−aa+2ax. Dico che questa frazione è uguale alla quantità AB, e dunque nel presente esempio

E così in modo facile e universale si troveranno le tangenti a tutte le curve geometriche. (Nova methodus tangentes curvarum expedite determinandi, p. 392)

Per comprendere la formazione del numeratore, occorre ricordare che Tschirnhaus si muove nell'ambito della formulazione cartesiana, e che la a che appare nell'equazione della curva non è una qualsiasi costante, ma l'unità per la quale bisogna opportunamente moltiplicare o dividere in modo da rendere omogenea l'equazione. Nella Geómétrie Descartes afferma che, quando "l'unità non è determinata, tutte le parti di una stessa e singola linea debbono essere ordinariamente espresse da uno stesso numero di dimensioni; […] non si tratta però della stessa cosa quando l'unità è determinata, poiché essa può essere sottintesa laddove vi sono troppe dimensioni o troppo poche" (OS, II, p. 533). In realtà il metodo di Tschirnhaus non è limitato alle curve geometriche, ma si applica anche alle curve trascendenti nelle quali x rappresenta l'ascissa curvilinea, cioè la lunghezza d'arco di una curva data:

Sia dunque BDE una curva qualsiasi, e si ponga uguale a x una sua porzione BD, DF inoltre sia uguale ad y; e si formi una qualsiasi curva BF, ad esempio secondo la precedente equazione y³+x³+xxy=xyy−a^s+aay−aax+axx−ayy: per determinare la tangente AF alla curva BFG procedo così. Si prenda la frazione, secondo quanto detto sopra, e ad essa si aggiunga la quantità x; il risultato darà la porzione AD della tangente alla curva BDE. […] Nel caso presente, se si conduce AD tangente alla curva BDE in D, e si prende t uguale a

la retta AF è tangente alla curva BFG nel punto F. (Nova methodus, p. 393)

In conclusione, alla fine degli anni Settanta circolavano una gran varietà di metodi per le tangenti, alcuni derivati in linea diretta dalla Géométrie di Descartes, altri più vicini alle idee di Fermat. Tali metodi si distinguevano per la loro applicabilità anche a curve trascendenti, specie a quelle, come la cicloide, dipendenti dalla lunghezza di altre curve note. Si può dunque affermare che il problema delle tangenti era stato risolto per tutte le curve allora note, mediante un algoritmo uniforme nel caso delle curve algebriche, mentre le trascendenti dovevano essere trattate caso per caso o quanto meno per famiglie a seconda della loro generazione. Nondimeno, la soluzione non era del tutto soddisfacente, in quanto rimanevano ancora fuori della portata dei metodi nuovi le curve la cui equazione comprendeva un numero rilevante di radicali.

La situazione è per molti versi paradossale. Infatti queste curve sono in tutto e per tutto delle curve algebriche, e Fermat aveva insegnato come sbarazzarsi dei radicali e ridurne l'equazione a forma polinomiale, dunque tale da essere abbordabile con i metodi standard. Ma se in linea di principio il metodo di eliminazione di Fermat poteva essere applicato a una qualsiasi curva, indipendentemente dal numero e dall'indice delle radici che comparivano nella sua equazione, di fatto il polinomio che risultava da questa eliminazione era spesso di grado così elevato e coinvolgeva un tale numero di termini da non poter essere scritto materialmente. Abbiamo dunque un metodo che insegna come trattare queste curve, ma che non si può utilizzare a causa dell'enorme numero di calcoli che richiede; in breve, non è tanto il carattere algebrico, irrazionale o trascendente della curva a determinare l'applicabilità del metodo, quanto la maggiore o minore complessità dell'equazione.

La ragione di questa limitazione sta nel carattere globale comune a tutti i metodi delle tangenti conosciuti. Per capire meglio di cosa si tratta, torniamo per un momento all'origine della teoria di Fermat: il metodo dei massimi e dei minimi. Per trovare il massimo o il minimo di una funzione f(x), Fermat scriveva l'adequazione

[53] f(A+E)−f(A) ≈ 0,

che poi divideva per E:

e infine poneva E=0 per ottenere una vera equazione

In questa operazione, o meglio sequenza di operazioni, non pochi storici e matematici, a cominciare da Joseph-Louis Lagrange, hanno visto la prima apparizione della derivata. Per allettante che possa sembrare, questa interpretazione non coglie un punto centrale, rilevante soprattutto per comprendere la ragione profonda dei limiti dei vari metodi delle tangenti, non ultimo di quello dello stesso Fermat. In realtà si può affermare con migliori argomenti che nel metodo di Fermat si trova tutto, tranne la derivata.

Per comprendere meglio cosa si intenda, pensiamo un momento al modo in cui oggi si calcola il minimo o il massimo di una funzione f(x). Si calcola prima la derivata f′(x), e poi si considera l'equazione f′(x)=0, le soluzioni della quale daranno i possibili punti di massimo o di minimo. Abbiamo dunque un procedimento che si svolge in due passaggi: il calcolo della derivata e la soluzione dell'equazione f′(x)=0. Al contrario, se esaminiamo il procedimento di Fermat (ma lo stesso si può dire per gli altri metodi, a cominciare da quello cartesiano), vediamo che questi due passaggi sono fusi in uno, e che esso consiste nello scrivere l'adequazione f(A+E)−f(A) 0 e nel manipolarla fino a giungere all'equazione finale che dà i punti di massimo e di minimo.

A prima vista, la differenza può sembrare di poco conto; in realtà le conseguenze sono di non piccola portata, e il superamento delle difficoltà connesse col metodo di Fermat sarà uno dei caratteri principali del nuovo calcolo. La derivazione, o meglio la differenziazione, è infatti un'operazione che fa passare da una funzione f(x) alla sua derivata f′(x). Come tutte le operazioni, essa è soggetta a una serie di regole che permettono di separare le difficoltà; per esempio, se la funzione f(x) è somma di due funzioni: f(x)=g(x)+h(x), anche la sua derivata sarà la somma delle derivate corrispondenti: f′(x)=g′(x)+h′(x). Analogamente la derivata del prodotto può essere calcolata con opportune regole, così come esistono algoritmi che permettono di calcolare la derivata del quoziente, delle potenze e delle radici di ogni grado delle funzioni composte. È l'uso sistematico di queste regole che permette di derivare anche funzioni molto complesse, automatizzando un calcolo che senza di esse risulterebbe laboriosissimo, quando non impossibile.

Contrariamente alla derivata, l'equazione è sempre globale; se la funzione f è somma di due funzioni, f(x)=g(x)+h(x), l'equazione f(x)=0 non ha nulla a che vedere con le due g(x)=0 e h(x)=0. Non è pertanto possibile separare le difficoltà, che devono sempre essere affrontate tutte insieme. Da qui derivano i limiti dei metodi delle tangenti, messi in crisi non dal carattere trascendente delle curve in esame ‒ trattate senza problema con i metodi di Fermat, di Barrow e di Tschirnhaus ‒, ma dalla presenza di un cospicuo numero di radicali, che rendeva inapplicabili anche i metodi più sofisticati.

Questo punto è colto con precisione da Leibniz (nella lettera a Oldenburg, 21 giugno 1677, Die Briefwechsel, p. 242), che più volte proporrà come esempio della potenza del suo metodo il calcolo della tangente a curve molto complesse, come per esempio quella di equazione

Strettamente legato al precedente è un altro fattore bloccante, anch'esso proprio di tutti i metodi delle tangenti: la scelta della sottotangente come parametro per la descrizione della retta tangente. Da un punto di vista geometrico la scelta è la più naturale: posto che la tangente deve passare per il punto dato sulla curva, per individuarla basterà trovare un secondo punto, e quale sarà più semplice dell'intersezione con l'asse delle ascisse? Nondimeno, dal punto di vista analitico essa presenta l'inconveniente essenziale di una completa rigidità rispetto alle relazioni algebriche: quando l'ordinata di una curva si scrive come somma di quelle di due o più curve, non c'è nessuna relazione semplice che permetta di risalire dalle sottotangenti di queste a quella della curva di partenza. Ambedue questi problemi verranno risolti con l'invenzione del calcolo.

Il calcolo differenziale

Il calcolo vede ufficialmente la luce nel 1684, quando sugli "Acta Eruditorum" di Lipsia appare una memoria di Leibniz dal titolo Nova methodus pro maximis et minimis, itemque tangentibus, quae nec fractas nec irrationales quantitates moratur, et singulare pro illis calculi genus. In essa ambedue le difficoltà a cui avevamo accennato, la mancanza di un'operazione che consentisse di smontare la complessità dell'equazione di una curva e la scelta di un parametro più adatto a essere trattato algebricamente ‒ cioè che si comportasse in maniera semplice rispetto alle operazioni algebriche ‒, sono risolte contemporaneamente grazie all'introduzione del differenziale. Si è già detto del carattere operazionale della derivata, la cui assenza nella formulazione di Fermat era all'origine dei limiti di questo come degli altri metodi. Un tale concetto peraltro non poteva emergere, mancando completamente la nozione di funzione, che si affermerà solo nel secolo successivo. Al suo posto, Leibniz introduce un'operazione, la 'differenziazione', che agisce non sulle funzioni (per l'appunto ancora inesistenti), ma sulle variabili e sulle loro combinazioni, e che consiste nel considerare la differenza tra due valori infinitamente vicini delle variabili. Sono le proprietà formali della differenza, e insieme il carattere infinitesimo delle differenze in gioco, evidente anche se sempre sottinteso, che permettono di trovare le regole di differenziazione che Leibniz pone all'inizio della sua memoria sul calcolo.

fig. 17

Leibniz introduce il differenziale in un contesto che ricorda da vicino quello di Pierre de Fermat: come in quest'ultimo la variabile E che determinava l'adequazione era generica ma non esplicitamente infinitesima, e la sua caratterizzazione in questo senso veniva non dalla sua definizione ma dal fatto che si poteva sostituire l'ordinata sulla tangente a quella sulla curva e dal suo destino ultimo di annullarsi, così nella formulazione di Leibniz i differenziali dx e dy non sono a priori infinitesimi, ma acquistano questo carattere dalle regole di differenziazione. Preso arbitrariamente uno dei differenziali, per esempio dx, Leibniz nella Nova methodus ricava l'altro direttamente per mezzo della tangente (fig. 17): "Detta dx una retta presa ad arbitrio, una seconda retta che stia a dx come y sta ad AC la si chiamerà dy, ossia differenza delle y" (GM, V, p. 220).

In questo modo la determinazione della sottotangente t segue immediatamente dal calcolo del rapporto dx/dy, dato che per la similitudine dei triangoli ABC e BEG risulta AC:BC=BG:EG, ossia t:y=dx:dy, da cui

Quanto poi al calcolo del rapporto dx/dy, Leibniz si serve dell'equazione della curva, operando su di essa con le regole della differenziazione da lui stesso stabilite all'inizio della memoria:

e di quelle che ne derivano, in particolare il differenziale delle potenze

[59] dxⁿ=nxⁿ⁻¹dx

e delle radici

Una volta trovate le regole di differenziazione di somme, potenze e radici, si possono calcolare i differenziali di espressioni composte. Per esempio, il differenziale di

si potrà calcolare per passi successivi, ponendo dapprima

per cui

Se ora si pone

risulta

Infine

e quindi

Quanto poi al rapporto dx/dy, questo si otterrà differenziando secondo le regole viste l'equazione della curva, che può essere anche molto complessa, come per esempio

che Leibniz riporta "solo perché appaia il modo di usare le regole precedenti anche in un calcolo più difficile". In questo modo è possibile trovare la tangente a tutte le curve, indipendentemente dal grado di complicazione della loro equazione, dato che l'introduzione dei differenziali permette di separare le difficoltà in una serie di passi successivi.

L'introduzione dei differenziali ‒ o delle differenze, come erano chiamate originariamente ‒ ha permesso dunque di risolvere completamente il problema delle tangenti nel caso algebrico e di ricondurlo al problema di calcolare il differenziale nel caso delle curve trascendenti: la logaritmica e l'esponenziale, la cicloide, la spirale, la quadratrice e quelle che via via si presentavano ai matematici come soluzioni di problemi. Sono queste differenze che Leibniz prende come parametri principali al posto della sottotangente, che da questo momento conserverà solo il suo carattere di parametro geometrico, mentre sarà totalmente espunta dall'analisi. Si tratta evidentemente di una scelta non facile, non tanto per l'intervento di quantità infinitesime (inassegnabili), che erano ormai entrate da tempo nel linguaggio matematico, quanto perché queste quantità perdono il loro carattere ausiliario e di artifici tecnici, destinati a sparire nella formulazione finale, per assumere invece il ruolo di parametri fondamentali per la descrizione delle curve.

Una scelta non facile, si può aggiungere, soprattutto per Leibniz, che a queste quantità infinitesime aveva sempre negato una reale esistenza, considerandole piuttosto 'finzioni', anche se ben fondate, alla stregua degli immaginari e delle quantità negative. Le difficoltà concettuali di questa formulazione sono evidenti, al punto che Leibniz cerca di mascherarle nascondendo il carattere infinitesimo dei differenziali ‒ peraltro implicito nelle regole di differenziazione che non potrebbero sussistere altrimenti ‒ e introducendo questi ultimi per mezzo della tangente, definita più avanti come quella retta che congiunge punti infinitamente vicini della curva. Nondimeno, Leibniz è ben cosciente della superiorità del suo metodo rispetto a quelli precedenti, e ne individua le ragioni esattamente nell'introduzione della differenziazione come operazione sulle variabili e nella conseguente separazione delle difficoltà che invece con i metodi precedenti dovevano essere affrontate contemporaneamente. Già nella Nova methodus, dopo aver descritto il calcolo della tangente mediante quello del differenziale, commenta: "I metodi finora pubblicati non hanno un tale gradino intermedio, e infatti usano per lo più rette come la AC [la sottotangente, fig. 17] o altre simili, ma non il segmento dy […] il che scombina tutto; di qui deriva che si debbano in primo luogo eliminare le quantità fratte e irrazionali che contengono le variabili" (GM, V, p. 223).

Il passaggio dall'equazione algebrica di una curva alla sua 'equazione differenziale' risolve dunque il problema delle tangenti. Viceversa, la maggior parte dei problemi di geometria o di meccanica conduce a un'equazione differenziale, dalla quale bisogna risalire all'equazione 'finita' della curva che dà la soluzione. In questo caso si ha il 'problema inverso delle tangenti' ‒ o, in termini moderni, l'integrazione di un'equazione differenziale ‒ che si affermerà come il più importante risultato del nuovo calcolo. Se poi l'integrazione in termini finiti non è possibile, allora l'equazione differenziale prenderà il posto dell'equazione algebrica per caratterizzare la curva in questione. Così, per esempio, quando l'elaborazione del problema della curva brachistocrona condurrà alla relazione

Johann I Bernoulli concluderà direttamente che la soluzione è una cicloide, di cui la precedente è l'equazione differenziale.

Questi due problemi delle tangenti ‒ quello diretto risolto da Leibniz e quello inverso dell'integrazione delle equazioni differenziali ‒ sono ciò che caratterizza il calcolo differenziale, e non il cosiddetto 'teorema fondamentale del calcolo' (così battezzato un secolo più tardi), che asserisce il carattere inverso delle operazioni di derivazione e di integrazione. Quest'ultimo problema, benché più semplice del problema inverso delle tangenti, richiedeva l'introduzione del concetto di funzione, un concetto totalmente assente, o tutt'al più presente solo in forma larvata, nella matematica del Seicento. Non si tratta dunque, come più volte è stato affermato, di riconoscere il carattere inverso delle operazioni di derivazione e di integrazione, ma di affrontare i due problemi inversi: il calcolo delle tangenti e la soluzione delle equazioni differenziali. Quest'ultimo in particolare rappresenterà il problema principale, attorno al quale ruoteranno la geometria delle curve e delle superfici, la meccanica, l'idrodinamica, l'astronomia, l'acustica; in breve, l'intero universo delle scienze fisiche.

Le quadrature dopo Cavalieri

Accanto al calcolo differenziale si era affermato e sviluppato anche il calcolo integrale, come strumento indispensabile per affrontare il problema inverso delle tangenti. Anch'esso ha, ovviamente, una sua storia nel XVII secolo. Per delinearla brevemente, saremo ora costretti a compiere un salto all'indietro nel tempo.

Contemporaneamente alla geometria algebrica cartesiana, anche la teoria degli indivisibili attraversava una stagione di importanti successi. Cavalieri aveva pubblicato la Geometria indivisibilibus continuorum nova quadam ratione promota, o più semplicemente Geometria indivisibilium, come egli stesso la chiamava, quasi contemporaneamente alla Géométrie di Descartes, e con essa era riuscito a estendere molto al di là dei limiti della geometria classica il calcolo di aree e volumi di figure piane e solide. Nonostante le critiche provenienti per lo più da ambienti gesuitici, alle quali il matematico milanese si era trovato a dover far fronte negli anni seguenti la pubblicazione della Geometria, il metodo degli indivisibili, e in particolare il principio di Cavalieri, era diventato uno strumento chiave per il progresso dei metodi di quadratura.

In Italia, in particolar modo nell'ambito della 'scuola galileiana', hanno soprattutto corso i metodi 'geometrici' degli indivisibili che, seguendo l'impostazione originale di Cavalieri, coniugavano le nuove tecniche dimostrative con un linguaggio geometrico classico, al quale attingevano per rendere la teoria degli indivisibili partecipe di un rigore spesso contestato. E se è vero che in alcuni casi, specie in alcuni scritti mai pubblicati di Torricelli, gli indivisibili di Cavalieri acquistano un differente 'spessore' a seconda della loro posizione, e vengono in questa veste utilizzati per la costruzione delle tangenti ad alcune semplici curve, è anche vero che questi metodi non arrivano mai ad acquistare quel livello di generalità necessario per poter condurre a un reale progresso.

In realtà, quando si parla dell'uso torricelliano degli indivisibili, si deve sempre distinguere tra le Opere geometriche, il solo scritto pubblicato in vita dal faentino, e la massa dei manoscritti di Torricelli, che sono stati pubblicati in una criticatissima edizione delle Opere solo all'inizio di questo secolo. Nella prima, a parte un uso virtuosistico della dottrina di Cavalieri (si pensi solo alle venti diverse quadrature della parabola), gli indivisibili sono usati nella loro formulazione originale per trovare risultati di rilievo, come il calcolo del volume del 'solido acuto iperbolico', ottenuto ruotando un'iperbole attorno a un asintoto, in cui per la prima volta viene esibito un solido infinito con volume finito. Mancano invece del tutto le ricerche sui fondamenti della teoria, che dovevano portare Torricelli molto vicino a un punto di vista 'differenziale', in cui gli indivisibili vengono considerati come dotati se non di uno spessore, quanto meno di una 'quantità' distinta dalla loro lunghezza e variabile a seconda della loro posizione.

Si tratta per molti versi dello stesso ordine di idee in cui si muovono Roberval e Pascal con la teoria dei 'seni' delle curve, e che poi troverà la sua espressione definitiva nei differenziali leibniziani. D'altra parte, pur se dotati di una 'quantità' diversa dalla loro lunghezza, gli indivisibili di Torricelli non perdono mai il loro carattere di elementi unidimensionali e non acquistano quella dimensione infinitesima necessaria per un allargamento di orizzonte.

In ogni caso, dopo la morte quasi simultanea di Cavalieri, il 30 novembre 1647, e di Torricelli, il 25 ottobre dello stesso anno, gli indivisibili geometrici continueranno a essere utilizzati dal solo Stefano degli Angeli, allievo e confratello di Cavalieri, che tra il 1654 e il 1667 pubblicherà con cadenza quasi annuale un volume dedicato agli sviluppi del metodo degli indivisibili. Angeli abbandonerà queste ricerche solo per entrare in una polemica con Riccioli e Borelli sulla caduta dei gravi in relazione al moto della Terra, disputa in cui sosterrà la lettera del dettato galileiano.

Con gli studi di Angeli, gli indivisibili di Cavalieri giungono al limite estremo delle loro potenzialità. Perché si potesse progredire in questo campo, sarebbe stata necessaria un'indagine molto più approfondita sui fondamenti teorici del metodo, indagine che, nonostante le esortazioni di Cavalieri, Torricelli non volle mai intraprendere, e Angeli non seppe fare. Inoltre, anche se una tale ricerca fosse stata affrontata, probabilmente non avrebbe dato i frutti che Cavalieri sperava, visto che per ottenerli ci si doveva muovere non verso una rilettura dei fondamenti della teoria con il linguaggio della geometria classica, mantenendone inalterato il livello di generalità ‒ come il gesuato indicava quando invitava Torricelli ad indagare sui fondamenti del metodo degli indivisibili curvi ‒ ma al contrario verso lo sganciamento definitivo dai canoni classici e una corrispondente diminuzione di generalità.

Quest'ultima affermazione merita qualche spiegazione. Uno dei meriti della teoria degli indivisibili era per l'appunto il superamento dello studio dei singoli casi particolari, proprio della geometria classica, che veniva rimpiazzato da dimostrazioni generali, valide per grandi classi di figure, alle quali poi rinviare in ogni singolo caso. In ciò Cavalieri si muoveva sullo stesso cammino già intrapreso da Luca Valerio nel suo De centro gravitatis solidorum, e che due anni più tardi Descartes avrebbe percorso fino in fondo nella Géométrie. Tuttavia, uno dei problemi in questo passaggio dal particolare al generale è di scegliere la più opportuna classe di figure nelle quali operare, poiché essa deve essere abbastanza estesa da contenere i vari casi che si possono presentare al geometra, ma allo stesso tempo abbastanza circoscritta da conservare quelle proprietà fondamentali che permettono la dimostrazione dei risultati essenziali.

Valerio aveva operato nella classe delle figure monotone, dimostrando i suoi risultati sui centri di gravità di queste figure; Cavalieri si sarebbe in seguito convinto di poter includere nella sua teoria degli indivisibili tutte le figure geometriche, senza limitazione alcuna. Una convinzione illusoria, perché non si dimostra senza avere punti di partenza; infatti chi scorra le dimostrazioni della Geometria indivisibilium si accorgerà che in esse è implicita l'ipotesi che ogni figura sia composta da un numero finito di figure monotone. E non si tratta di una convinzione innocua, in quanto essa produrrà una tale complicazione nelle dimostrazioni da rendere praticamente impossibile ogni progresso in altre direzioni. Per esempio, l'emergere di paradossi, ben noti a Cavalieri prima ancora della pubblicazione della Geometria, costringerà il gesuato a cautelarsi con prescrizioni efficienti ma per molti versi arbitrarie, come quella del retto transito, secondo la quale le figure che si confrontano debbono trovarsi tra le stesse parallele in questo modo, tuttavia, egli non riuscì a trovare una giustificazione al fatto che figure diverse in grandezza possano avere i loro indivisibili in corrispondenza biunivoca. In un contesto molto più ristretto, Pascal riuscirà non solo a dar conto di questo fenomeno, ma anche a volgerlo a suo favore, ricavandone una serie di risultati che lo porteranno a un passo dal calcolo integrale.

fig. 19

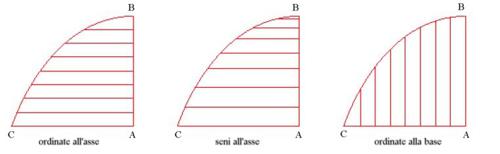
L'idea fondamentale è di Roberval, ma solo con Pascal essa giunge a un livello di elaborazione che va al di là del caso particolare e che permette di delineare un quadro complessivo nel quale i singoli risultati trovano il loro posto e la loro giustificazione. Entrambi riconoscono che nel calcolare con gli indivisibili non è sufficiente dire in quale direzione (la regula di Cavalieri) si debbano considerare gli indivisibili di una figura, ma è anche necessario che questi siano ugualmente densi, ovvero che traggano origine da una divisione della linea corrispondente in un numero indefinito di parti uguali. Così, per esempio, preso il trilineo rettangolo ABC (fig. 19), a seconda che si divida in parti uguali l'asse AB o la curva BC, tirando le rette orizzontali si hanno in un caso le ordinate all'asse, nell'altro i 'seni all'asse'. Se invece si divide in parti uguali la base CA, e si tirano le verticali dai punti di divisione, si ottengono le 'ordinate alla base'. In modo analogo, si possono definire anche i 'seni alla base', dividendo la curva in parti uguali e tirando le verticali. Ciò posto, Pascal può enunciare e dimostrare una serie di risultati, il più semplice dei quali dice che "la somma delle ordinate alla base è uguale alla somma delle ordinate all'asse", in quanto "ambedue sono uguali allo spazio del trilineo" (Traité des trilignes rectangles et de leur onglets, p. 143). O anche: "La somma degli archi della curva compresi tra il vertice e ognuna delle ordinate all'asse è uguale alla somma dei seni alla base". Infine enuncia un risultato generale che collega gli indivisibili con la grandezza delle figure e i loro centri di gravità:

Se di un trilineo si conoscono le cose seguenti:

1. La somma delle ordinate all'asse,

2. La somma dei quadrati di queste ordinate,

3. La somma dei cubi di queste ordinate,

4. La somma triangolare di queste ordinate,

5. La somma triangolare dei quadrati di queste ordinate,

6. La somma piramidale di queste ordinate,

si conosceranno anche la misura e i centri di gravità, sia del trilineo sia delle sue doppie ungule; in altre parole si conosceranno le cose seguenti:

1. La misura dello spazio del trilineo,

2. Il braccio del trilineo sull'asse,

3. Il braccio del trilineo sulla base,

4. La misura della doppia unghia della base,

5. Il braccio di questa unghia sulla base,

6. Il braccio di questa unghia sull'asse,

7. La misura della doppia unghia dell'asse,

8. Il braccio di questa unghia sulla base,

9. Il braccio di questa unghia sull'asse. (ibidem, p. 147)

D'altra parte, nonostante questi importanti risultati teorici, la mancanza più volte rilevata di una nozione abbastanza elaborata di funzione impedisce che si sviluppi per le quadrature un calcolo analogo a quello per le tangenti. A differenza di quanto avviene con la geometria cartesiana, il metodo degli indivisibili di Cavalieri e Torricelli, anche nella versione algebrizzata di Roberval e Wallis o in quella di tipo infinitesimale di Fermat e di Pascal, non fa che stabilire un quadro generale, geometrico in Cavalieri e Torricelli, algebrico negli altri, nell'ambito del quale il geometra potrà operare per affrontare le singole quadrature senza dover ricorrere all'ingombrante metodo di esaustione. Il problema delle quadrature assume dunque una forma sostanzialmente differente da quello delle tangenti: non si tratta di trovare una regola generale ‒ un calcolo ‒ per dare le quadrature di figure arbitrarie, ma piuttosto, approfittando della maggior duttilità della teoria degli indivisibili rispetto al metodo di esaustione, di trovare la quadratura di un maggior numero di figure, o al più di classi di figure, come le infinite parabole di Torricelli e di Fermat e le infinite spirali di Angeli. Una ricerca, questa, che via via che si esaurivano le classi più semplici e più interessanti di figure richiedeva sforzi sempre maggiori per dare risultati sempre più simili a esercitazioni accademiche.

Per questo motivo, nel quarto di secolo successivo alla scoperta degli indivisibili, la loro forza propulsiva va progressivamente esaurendosi, mentre riprendono corpo quei problemi classici, come la quadratura del cerchio e dell'iperbole, che il successo degli indivisibili era riuscito se non a risolvere, certo a far passare in secondo piano. Terminata con la sfortunata Quadratura circuli (1647) di Grégoire de Saint-Vincent la stagione della quadratura esatta del cerchio, si sviluppano le ricerche volte a trovare dei metodi di approssimazione eleganti ed efficaci sia per l'area del cerchio sia per quella dell'iperbole, e dunque per il calcolo dei logaritmi. Già Willebrord Snell aveva dato nel 1621, nel Cyclometricus, una formula di approssimazione per la lunghezza della circonferenza di raggio unitario. Egli, infatti, indicando con p_n e P_n i perimetri, e con a_n e A_n le aree dei poligoni regolari di n lati inscritti e circoscritti al cerchio di raggio 1, dimostrava le disuguaglianze:

È però solo dopo il 1650 che tali ricerche prendono vigore, dando luogo a risultati importanti. Così nel 1655 Wallis trova il suo prodotto infinito:

una formula riscoperta più tardi da Pietro Mengoli (1625-1686), e Huygens nel suo De circuli magnitudine inventa dimostra le disuguaglianze:

Poco più tardi, James Gregory (Vera circuli et hyperbole quadratura, 1667) otterrà per le successioni a_n ed A_n le formule di ricorrenza:

Infine nel 1682 Leibniz pubblica, nella De vera proportione circuli ad quadratum circumscriptum, il suo sviluppo in serie:

uno sviluppo peraltro noto sia a Gregory sia a Newton, il quale a quell'epoca aveva già ottenuto gli sviluppi di tutte le funzioni trigonometriche e delle loro inverse. Una sorte simile trovano le ricerche sulla quadratura dell'iperbole: dopo un certo numero di approssimazioni di vario tipo, l'area dell'iperbole e dunque i logaritmi vengono espressi da Niccolò Mercatore mediante uno sviluppo in serie, anche questo ben noto a Newton.

Lo studio delle serie, nel corso del Seicento, aveva dunque conosciuto un notevole sviluppo, restando però pur sempre nell'ambito dei metodi di approssimazione aritmetico-analitici. Newton, al contrario, ne farà una delle basi per affrontare e risolvere il problema delle tangenti e delle quadrature.

8. Il calcolo newtoniano

I problemi delle tangenti e delle quadrature si ritrovano all'origine del calcolo newtoniano, ma la loro posizione relativa è sostanzialmente differente. Nell'ambito di una concezione 'meccanica' della geometria, Newton considera le variabili come grandezze il cui valore aumenta o diminuisce con continuità, e l'equazione P(x,y)=0 di una curva come una relazione che regola le loro variazioni relative, e quindi come la traiettoria di un punto mobile. In altre parole, Newton immagina le variabili x e y come delle quantità 'fluenti' correlate dall'equazione data. Egli introduce quindi due nuove grandezze

che sono le velocità istantanee, o 'flussioni', delle variabili; i loro rapporti, che determinano la tangente alla curva data, poiché la velocità è tangente alla traiettoria, si potranno ricavare operando secondo opportune regole sulla funzione P(x,y). Come in Leibniz, il ruolo centrale è giocato dall'algoritmo che consente di trovare la flussione di un prodotto dalla quale si deducono quelle per le potenze, le radici, e quindi, con opportuni artifici, quelle per combinazioni più o meno complesse di varie funzioni. Siano dunque x e y due grandezze fluenti, e siano

le rispettive velocità. Per trovare la velocità del prodotto xy, Newton considera un tempuscolo (infinitesimo) o, dopo il quale x e y saranno divenute rispettivamente

Otteniamo quindi

e dunque, dato che l'ultimo termine è infinitesimo:

Le analogie matematiche con la formulazione leibniziana sono evidenti: sarà sufficiente sostituire le flussioni

(o meglio, i 'momenti

'),

con i differenziali dx e dy per ottenere il metodo di Leibniz per le tangenti, dato che nei due casi le regole di differenziazione sono identiche. Altrettanto evidenti sono d'altra parte le differenze fondazionali: nella formulazione leibniziana il calcolo richiede una vera e propria rivoluzione epistemologica con l'introduzione essenziale di quantità evanescenti; con Newton restiamo invece nell'ambito delle quantità finite ‒ le velocità ‒ la cui definizione rigorosa avrebbe certo condotto verso difficoltà analoghe a quelle insite nella teoria di Leibniz, ma che potevano essere ignorate a causa della familiarità del concetto.

Naturalmente anche il calcolo newtoniano deve far uso di quantità infinitesime, in particolare quando si vogliano ricavare le regole di differenziazione del prodotto e delle espressioni composte; ma, a differenza di Leibniz, Newton può confinare queste quantità minime ma ingombranti nel retrobottega degli artifici di calcolo, e presentare una vetrina di sole quantità finite e familiari. In definitiva, la soluzione del problema delle tangenti, che aveva richiesto a Leibniz una certa dose di coraggio intellettuale, si presentava per Newton come una naturale conseguenza dell'interazione dei suoi punti di vista sulla cinematica e sul moto con la geometria algebrica di Descartes, e dunque in un certo senso priva di un reale carattere di novità.

Quest'ultimo si potrà trovare piuttosto nell'uso continuo ed essenziale degli sviluppi in serie che, seppure introdotti in precedenza, o quanto meno indipendentemente, da altri geometri, in particolare da Mercatore e Gregory, trovano nell'analisi newtoniana un'estensione senza pari. Utilizzando un gran numero di metodi diversi, quali l'interpolazione, la divisione, l'estrazione di radice, il metodo dei coefficienti indeterminati e l'integrazione termine a termine, Newton riesce a dare gli sviluppi di tutte le funzioni conosciute: di qui la possibilità di assumere le serie come parte integrante della sua teoria.

Nelle mani di Newton, gli sviluppi in serie subiscono una sostanziale metamorfosi. Per i geometri che lo avevano preceduto, ma anche per i suoi contemporanei ‒ Leibniz in primo luogo ‒ essi erano uno tra i vari metodi di approssimazione, e dunque si situavano nel dominio del calcolo aritmetico ed analitico, un terreno contiguo ma distinto dal nuovo calcolo differenziale. Al contrario, per Newton essi sono la chiave per affrontare e risolvere nella loro massima generalità i principali problemi del calcolo.

Nell'analisi newtoniana le serie hanno un duplice aspetto. Come abbiamo visto, Newton era riuscito a trovare gli sviluppi in serie di tutte le funzioni conosciute: le potenze e le radici, le funzioni circolari e le loro inverse, i logaritmi e gli esponenziali. In realtà, a voler essere precisi, non essendo ancora stato introdotto il concetto di funzione, il seno, la tangente, il logaritmo, ecc., venivano piuttosto considerati come quantità variabili in relazione le une con le altre. Il fatto che tutte queste quantità potessero essere espresse con delle serie rendeva queste ultime un sostituto delle funzioni di cui, per così dire, assumevano la rappresentanza. Di più, le serie sono per definizione una naturale estensione dei polinomi, dei quali conservano la semplicità algoritmica e strutturale. Così, per mezzo delle serie Newton risolve, per esempio, il problema generale delle quadrature, riducendolo essenzialmente all'integrazione delle potenze: una volta trovato lo sviluppo in serie dell'ordinata della curva in questione, si può integrare termine a termine ottenendo una serie che ce ne dà la quadratura. Nella Recensio libri, una sorta di prefazione al Commercium epistolicum D. Johannis Collins, et aliorum, de analisi promota, scritta all'epoca della sua disputa con Leibniz, il metodo newtoniano è brevemente riassunto:

Wallis pubblicò la sua Arithmetica infinitorum nel 1655; dalla proposizione 59 di questo libro risulta che se x è l'ascissa di una curva, se m e n sono due numeri, e se x^m/n sono le ordinate innalzate ad angolo retto, allora l'area della figura sarà n/(n+m)x^(m+n)/n. Questo risultato è accolto da Newton come prima regola su cui fondare la sua quadratura delle curve. [...] Inoltre per la proposizione 108 dell'Arithmetica infinitorum di Wallis, e per molte altre proposizioni ad essa seguenti: se l'ordinata è costituita da due o più ordinate unite insieme dai segni + e −, anche l'area sarà allora costituita da due o più aree congiunte insieme rispettivamente dai segni + e −. Anche questa proposizione è stata assunta da Newton come seconda regola su cui fondare il suo metodo delle quadrature. La terza regola consiste nel ridurre le frazioni, i radicali, le radici affette da esponente in serie convergenti, quando non è possibile trovare altrimenti la quadratura; e nel quadrare, secondo le regole prima e seconda, le figure le cui ordinate sono i singoli termini della serie. (La disputa di Leibniz-Newton sull'analisi, p. 22)

Così il metodo usato da Gregory per ottenere i logaritmi, che equivaleva essenzialmente allo sviluppo in serie dell'ordinata dell'iperbole

e alla successiva integrazione termine a termine

viene esteso a tutte le curve conosciute, diventando un metodo generale di quadratura.

Peraltro quello delle quadrature è solo un caso particolare del problema dell'integrazione delle equazioni differenziali, di cui Newton dà una soluzione generale in termini di una serie di potenze. Per illustrare il metodo, riportiamo dalla Methodus fluxionum et serierum infinitarum l'integrazione dell'equazione

di cui Newton cerca la soluzione y(x) con y(0)=0. Se nell'equazione si prendono solo i termini di grado zero, si ha

e dunque il primo termine dello sviluppo sarà y=x. Introducendo questo valore nell'equazione, e conservando solo i termini di primo grado, avremo

da cui y=x−x². Di nuovo, si può inserire questo valore nell'equazione, e conservare i termini di secondo grado, poi quelli di terzo e così via. Per facilitare i calcoli, Newton disponeva i vari termini come nella seguente

Il cerchio è dunque chiuso: l'uso delle serie infinite permette di andare molto al di là dei risultati della Nova methodus leibniziana, e addirittura si propone come il metodo capace di dare la soluzione definitiva dei problemi più importanti dell'analisi. Questo punto di vista rende ancora più marginale il problema delle tangenti, centrale invece nell'elaborazione leibniziana, dato che la possibilità di sviluppare in serie ogni funzione rende applicabili al caso generale i metodi di Sluse, Hudde e in genere dei matematici del periodo che aveva preceduto il calcolo, e che, come abbiamo visto, erano limitati ai soli polinomi. La differenza tra i due punti di vista è particolarmente netta nella scelta degli esempi che i due scienziati portano a illustrazione dei rispettivi metodi: mentre Leibniz tende a marcare la differenza tra le sue tecniche differenziali e quelle precedenti, suggerendo esempi complicatissimi, Newton si limiterà sempre ai polinomi, al punto che Sluse, ricevendo da Oldenburg (a cui aveva inviato il suo metodo per le tangenti perché fosse pubblicato nelle "Philosophical Transactions") una copia di una lettera di Newton sullo stesso argomento, non può fare a meno di replicare seccamente rivendicando la sua priorità rispetto a un metodo che a ragione ritiene equivalente al suo.

Abbiamo così messo in luce, a dispetto di evidenti similitudini matematiche, una profonda divergenza di punti di vista riguardo all'importanza relativa delle varie dottrine che compongono il calcolo. Per Leibniz il punto cruciale è la differenziazione, che risolve il problema delle tangenti e consente di impostare quello generale delle equazioni differenziali. Di quest'ultimo si richiede peraltro la soluzione in termini finiti, dato che gli sviluppi in serie rientrano nel campo delle approssimazioni. Al contrario, per Newton il nucleo del calcolo risiede negli sviluppi in serie, e le flussioni assumono un ruolo tutto sommato marginale, essendo applicate a situazioni nelle quali già funzionavano bene i metodi precedenti. Inoltre, al contrario dei differenziali di Leibniz, la cui introduzione, come si è detto, rappresentava un'innovazione considerevole e richiedeva una notevole dose di coraggio intellettuale, le flussioni newtoniane si presentano talmente naturali da sfiorare la banalità, dunque di molto minor peso in rapporto agli sviluppi in serie, questi sì realmente innovativi. Questa valutazione, o meglio svalutazione, delle flussioni sarà una costante del punto di vista newtoniano. Il passo che già nel 1676 Newton scriveva nell'Epistola posterior ‒ "Poiché non posso dare qui il fondamento di queste operazioni, peraltro piuttosto ovvio, preferisco nasconderlo: 6a cc d ae 13e ff 7i 31 9n 4o 4q rr 4s 9t 12v x" (Newton a Oldenburg per Leibniz, 24 ottobre 1676, The correspondence of Isaac Newton, II, p. 115) ‒ viene ribadito quasi immutato nel 1718, senza che egli senta il bisogno di sfumarne i termini: "Ho detto in una di quelle lettere (quella del 24 ottobre 1676) che i fondamenti del Metodo erano ovvi" (The mathematical papers of Isaac Newton, VIII, p. 605).

Naturalmente ciò non vuol dire che delle flussioni si potesse fare a meno, e Newton ha ragione quando afferma che queste sono tanto essenziali per il suo metodo quanto lo sono le serie: senza le flussioni alcuni problemi, come quello inverso delle tangenti, non si potrebbero nemmeno formulare analiticamente. È chiaro però che le serie sono la chiave principale, se non l'unica, per la soluzione generale dei problemi del calcolo. Questa differenza di prospettiva ricorre più volte nella corrispondenza di Leibniz, che insiste sulla necessità di dare soluzioni in termini finiti, o quanto meno di perfezionare il metodo delle serie con criteri che permettano di stabilire quando una serie può essere espressa in termini finiti. Come scriverà a Oldenburg, ma con il pensiero rivolto a Newton: "se un uomo versatissimo in questa materia arriverà a un simile risultato, insegnandoci a trasformare una serie infinita in una finita quando ciò sia possibile, o quanto meno a riconoscere da quale serie finita sia stata dedotta, allora nel metodo delle serie infinite che si ottengono per divisione o estrazione difficilmente resterebbe ancora qualcosa a desiderare" (Leibniz a Oldenburg, in GM, I, p. 157).

Al di là dei diversi punti di vista, resta comunque il fatto che con l'uso combinato del calcolo flussionale e degli sviluppi in serie Newton era riuscito a impostare e a risolvere i principali problemi del nuovo calcolo, e in particolare il problema inverso delle tangenti, vale a dire l'integrazione delle equazioni differenziali. Dove Leibniz pone dei problemi, Newton fornisce dunque delle soluzioni. Paradossalmente, sarà proprio questa superiorità iniziale la causa principale della sconfitta del metodo newtoniano e del prevalere del programma leibniziano.

Il metodo delle flussioni e delle serie chiude i problemi, in primo luogo quello dell'integrazione delle equazioni differenziali, ma non li esaurisce. Esso opera come una macchina frantumatrice: da una parte si introduce l'equazione differenziale da integrare e dall'altra viene fuori pezzo a pezzo la soluzione sotto forma dei successivi termini della serie. Ma la serie non dà tutta la soluzione; infatti, anche a prescindere da questioni di convergenza, il carattere delle serie è eminentemente locale: esse possono essere usate per operazioni che riguardino il comportamento della soluzione nell'intorno di un punto, ma non sono di nessun aiuto quando se ne vogliano studiare le proprietà qualitative e globali.

Con evidenza molto maggiore tale divergenza di opinioni verrà alla luce in occasione della grande contesa.

9. La controversia sulla priorità

Newton aveva trovato i fondamenti del suo calcolo delle flussioni e delle serie fin dal 1666, dunque molti anni prima della pubblicazione della memoria di Leibniz. Non aveva però pubblicato nulla in proposito, affidando la diffusione dei suoi metodi, ma soprattutto di quello delle serie, alle lettere scambiate con i suoi corrispondenti: Collins, Barrow, Oldenburg. Da questi le lettere erano poi fatte pervenire ad altri studiosi, e in particolare a Leibniz, che ne aveva ricevuta una scritta a Collins nel 1672 e due scritte a Oldenburg nel 1676.

Nella prima lettera Newton descrive un metodo delle tangenti che nella sostanza è uguale a quello di Hudde e di Sluse, e afferma: "Talvolta ho unito questo metodo all'altro mediante il quale risolvo le equazioni riducendole a serie infinite" (La disputa, p. 83).

Il metodo delle serie è poi l'argomento principe delle due lettere a Oldenburg, nelle quali il metodo delle flussioni è sempre celato dietro anagrammi, che comunque contengono più gli enunciati di problemi che la loro soluzione. Di uno di questi abbiamo già parlato; dell'altro, Newton si serve solo per fissare la sua priorità "qualora altri ottenessero lo stesso risultato"; dopo averlo risolto commenta: "Il primo metodo consiste nell'estrazione di una quantità fluente dall'equazione che contiene la sua flussione; il secondo invece consiste nella semplice assunzione di una serie al posto di una qualsiasi delle quantità incognite, da cui possono facilmente ricavarsi le altre, e in un confronto dei termini omologhi dell'equazione risultante per determinare i termini della serie assunta" (ibidem, p. 128).

Non è chiaro quanta parte queste lettere di Newton abbiano avuto nell'invenzione del calcolo differenziale da parte di Leibniz, avvenuta proprio in quegli anni. Certo le differenze sono molto grandi, e ancora nel 1687, in uno scolio al lemma 2 del secondo libro dei Principia, nel quale trovava la flussione di una potenza, Newton asseriva che "il fondamento di entrambi [i metodi] è contenuto nel lemma precedente". In ogni caso, sempre nello stesso scolio, Newton riconosceva, o quanto meno non metteva in dubbio, l'indipendenza della scoperta leibniziana. Pochi anni più tardi, John Wallis pubblicava nell'Algebra un sunto del metodo newtoniano, e osservava che "analogo a questo metodo è il metodo differenziale di Leibniz, e quell'altro metodo, anteriore ad entrambi, che Barrow espose nelle sue Lectiones geometricae" (Opera matematica, II, p. 396), confondendo ancora il metodo di Leibniz con quello di Barrow, che come abbiamo visto non è che una variazione sul tema di Fermat. In conclusione, sia dalle parole dello stesso Newton sia da quelle di autori a lui vicini si può inferire che essi ritenessero sufficienti i metodi delle tangenti del periodo precedente al calcolo, ai quali assimilavano non solo il metodo newtoniano, ma anche quello di Leibniz, non trovandovi che differenze di notazioni. Che Leibniz non concordasse con loro, era evidente ed è provato dagli esempi che manda a Oldenburg in risposta alle lettere di Newton. Mentre questi non fa che riproporre curve algebriche mettendo in primo piano gli sviluppi in serie, Leibniz propone le sue curve dalle equazioni impossibili, come

Indipendentemente da queste divergenze di punti di vista, non mancano in questo periodo reciproche attestazioni di stima e riconoscimenti di originalità.

Questa atmosfera idilliaca viene turbata per un momento da un opuscolo di Nicolas Fatio de Duillier, Lineae brevissimi descensus investigatio geometrica duplex, dedicato al problema della brachistocrona, in cui accusa apertamente Leibniz di aver preso il suo calcolo da Newton: "Newton è stato il primo a scoprire, molti anni fa, questo calcolo. Se Leibniz, suo secondo inventore, abbia tratto alcunché da Newton, è una cosa su cui preferisco non dare alcun giudizio, ma voglio lasciarla stabilire da quelli che ebbero modo di vedere le lettere e gli altri manoscritti di Newton" (La disputa, p. 168).

Di questo attacco inopinato Leibniz si duole con Sloane, all'epoca segretario della Royal Society, che sconfessa l'operato di Fatio. L'anno successivo, nella recensione allo scritto di Fatio, Leibniz scrive: "Quando nel 1684 pubblicai gli elementi del mio calcolo, delle sue scoperte in questo campo sapevo solo ciò che egli stesso una volta mi aveva comunicato per lettera, cioè che poteva trovare le tangenti senza essere costretto a togliere gli irrazionali. […] Quando però vidi i Principia mi resi conto che Newton era pervenuto a cose ben maggiori. Che tuttavia si servisse di un calcolo tanto simile al mio calcolo differenziale non lo appresi prima che uscissero i volumi I e II delle Opere di Wallis" ("Acta Eruditorum", maggio 1700).

Per il momento Newton tace, e il momento di crisi sembra completamente superato. Così passa anche sotto silenzio l'attacco mosso da George Cheyne, che nel 1703 scrive a conclusione della Methodus fluxionum inversa: "Quando rifletto su tutte queste scoperte del grande Newton, non posso fare a meno di dichiarare che tutto ciò che è stato pubblicato da altri negli ultimi ventiquattro anni relativamente a questo o a metodi simili, non è che una ripetizione o un facile corollario di quanto Newton molto tempo fa ha comunicato ai suoi amici e al pubblico".

Lo stesso anno, Newton è nominato presidente della Royal Society; l'anno successivo esce l'Opticks, e unito a questa il Tractatus de quadratura curvarum, il primo scritto a stampa di Newton sul calcolo. In una recensione anonima, ma di Leibniz, apparsa immediatamente sugli "Acta Eruditorum", troviamo scritto: "Ora Newton, in luogo delle differenze di Leibniz, si serve, come d'altronde si è sempre servito [adhibet semperque adhibuit] delle flussioni […]. E ne ha fatto un uso molto elegante nei suoi Principia mathematica, e in altri scritti pubblicati dopo, allo stesso modo che [quemadmodum] Onorato Fabri, nella sua Synopsis geometrica ha sostituito [substituit] al metodo di Cavalieri il progresso dei moti" ("Acta Eruditorum", gennaio 1705).

Abbiamo riportato i precisi termini latini perché più tardi, sulla base delle parole "quemadmodum […] substituit", Leibniz verrà accusato di aver tacciato Newton di plagio, e si difenderà citando: "adhibet semperque adhibuit". Ma lo scontro è ancora una volta rimandato di qualche anno, ed esplode solo nel 1710 con la pubblicazione sulle "Philosophical Transactions" di un articolo di John Keill sulle forze centripete, alla fine del quale, senza evidenti connessioni con quanto precedeva, l'autore scrive: "Tutto ciò consegue dall'aritmetica delle flussioni, ormai divenuta famosa in questi ultimi tempi. Newton è senza alcun dubbio colui che l'ha scoperta per primo, come può accertare chiunque legga le sue lettere pubblicate da Wallis. In seguito questo stesso calcolo venne pubblicato da Leibniz negli "Acta Eruditorum", sotto diverso nome e con diversa notazione" ("Philosophical Transactions", 1708).

Davanti a una così esplicita accusa di plagio, Leibniz pensa di poter ripercorrere la strada di dieci anni prima, e scrive al segretario della Royal Society chiedendogli di invitare Keill a scrivere una rettifica. Di fronte a una risposta ambigua di quest'ultimo, Leibniz si rivolge al presidente, cioè allo stesso Newton, chiedendogli di pronunciarsi in merito. Per tutta risposta, viene nominata una commissione, incaricata di dirimere la disputa, composta da Halley, Jones, Burnet, Machin, de Moivre e Taylor, oltre ad altri personaggi estranei alla scienza. Nel 1713, la commissione pubblica il Commercium epistolicum, nel quale le affermazioni di Keill vengono riconosciute valide. Lo stesso Newton scrive una recensione a questo volume, pubblicata sulle "Philosophical Transactions" del gennaio 1715, e in versione francese nel tomo VII del "Journal litéraire" dell'Aia. Una versione rivista, dal titolo Recensio libri, verrà poi inserita in testa alla seconda edizione del Commercium, pubblicata nel 1722. Nel frattempo Leibniz, che probabilmente era stato colto di sorpresa dal succedersi degli eventi, comincia a scrivere una Historia et origo calculi differentialis, che però resterà inedita a causa della sua morte, avvenuta nel 1716.

Fin qui la cronaca degli avvenimenti. Quello che colpisce nell'atteggiamento dei principali attori di una delle più accese dispute scientifiche della storia è l'assoluta estraneità dei punti di vista dei due contendenti. Da una parte Leibniz, che continua a ripetere di non avere difficoltà ad accordare a Newton la priorità e il primato negli sviluppi in serie, ma che continua a rivendicare a sé stesso l'invenzione del calcolo dei differenziali, del quale non trova traccia negli scritti dell'avversario; dall'altra Newton, che insiste sull'unità del metodo delle flussioni e delle serie infinite, che invece Leibniz vorrebbe 'fare a pezzi' per attribuirsene una parte, lasciando a Newton solo il metodo delle serie. Ma a parlare più chiaramente di ogni commento sono i testi nella loro immediatezza.

L'oggetto del contendere

Recensio libri: "L'argomento ivi [nel Commercium epistolicum] discusso è il metodo generale per risolvere le equazioni finite in equazioni infinite e applicare tanto le une che le altre alla soluzione dei problemi secondo il metodo delle flussioni e dei momenti".

Leibniz a Conti: "Quando finalmente ebbi una copia del Commercium epistolicum, mi accorsi che si allontanava completamente dal suo scopo, e che le lettere in esso pubblicate non contenevano una sola parola capace di porre in dubbio la mia scoperta del calcolo delle differenze, su cui verteva la vera questione. Notai che invece si preferiva puntare tutto sulle serie, dove si accorda senza difficoltà la precedenza a Newton".

Newton a Conti: "Egli [Leibniz] si duole che il Comitato si sia allontanato dal suo scopo, gettandosi a esaminare le serie infinite; ma deve considerare che i due metodi di cui mi servo sono le due branche di un unico e identico metodo generale di analisi" (La disputa, pp. 17, 210, 229).

Leibniz a Newton: "Hanno addirittura cambiato lo stato della controversia; e infatti in quel loro scritto, che sotto il nome di Commercio epistolico di John Collins hanno pubblicato allo scopo di mettere in dubbio il primato di Leibniz, si trova a malapena qualche traccia del calcolo differenziale: ogni pagina è piena delle serie cosiddette infinite".

Leibniz a Newton: "E si son serviti dell'arte degli avvocaticchi, per stornare l'attenzione dei giudici dall'oggetto del contendere ad altro, e cioè alle serie infinite" (GM, V, pp. 393, 410).

La portata del metodo

Newton a Conti: "Nel 1684 Leibniz pubblicò soltanto gli elementi del calcolo differenziale, che applicò ad alcune questioni sulle tangenti e ad alcune altre riguardanti il metodo dei massimi e dei minimi, come Fermat e Gregory avevano fatto prima di lui; e fece vedere come si poteva procedere in questo genere di questioni, senza togliere le quantità irrazionali. Ma non passò ai problemi della più alta geometria" (La disputa, p. 234).

Leibniz a Newton: "Ma di tutto questo calcolo non si trovano nemmeno le tracce negli scritti dell'emulo precedenti i fondamenti del calcolo pubblicati dal nostro, né di alcunché che non avrebbero trovato allo stesso modo anche Huygens e Barrow, se avessero studiato gli stessi problemi" (GM, V, p. 409).

I metodi per le tangenti

Newton a Collins: "Sia AB l'ascissa e CB l'ordinata che forma con l'ascissa un angolo qualsiasi; si ponga AB=x e BC=y, e si esprima il rapporto fra x e y con una qualsiasi equazione, per esempio x³−2xxy+bxx−bbx+byy−y³=0 con cui si determina la curva AC. Allora la regola per condurre la tangente sarà: si moltiplichino tutti i termini di questa equazione per una qualsiasi progressione aritmetica, secondo le dimensioni di y, cioè

oppure secondo le dimensioni di x, cioè

Il primo prodotto sarà il numeratore e il secondo, diviso per x, il denominatore di una frazione che esprimerà la lunghezza di BD, dalla cui estremità D si deve condurre la tangente CD".

Leibniz a Oldenburg: "Questo stesso metodo può applicarsi anche quando si hanno radici sotto altre radici; per esempio, in un'equazione assai complessa come questa:

In una curva che abbia y come ascissa ed x come ordinata, l'equazione utile per trovare la tangente TC potrà subito essere scritta senza bisogno di nessun calcolo, e cioè

(La disputa, pp. 82, 134).

La priorità

Recensio libri: "In queste due lettere Newton aveva ricordato di essere in possesso di un'analisi generale, di cui una parte consisteva nel metodo delle serie convergenti, e un'altra in un metodo che permetteva di applicare quelle serie alla soluzione di quasi tutti i problemi".

Leibniz a Conti: "Non ho mai negato che nel mio secondo viaggio in Inghilterra abbia visto alcune lettere di Newton, ma non ho mai visto dove Newton abbia spiegato il suo metodo delle flussioni, e continuo a non trovarlo nel Commercium epistolicum".

Newton a Conti: "Nella mia lettera del 13 giugno 1676 ho detto che il mio metodo delle serie si estendeva a quasi tutti i problemi, ma che diveniva generale solo con l'aiuto di altri metodi, intendendo con ciò (come spiegavo nella lettera seguente) il Metodo delle flussioni ed il Metodo delle serie arbitrarie. Volermi ora carpire questi due altri metodi, è restringere il metodo delle serie, e limitarne la generalità. E se al sig. Leibniz è piaciuto di fare a pezzi questo mio metodo generale, e di sottrarmene prima una parte, poi un'altra, tralasciando il resto, ha offerto al Comitato una legittima occasione per esaminare il tutto nel suo complesso" (ibidem, pp. 41, 213, 229).

10. 'Unicuique suum'

Quest'ultimo brano di Newton, scritto nel 1716 a pochi mesi dalla morte del suo antagonista, è per molti aspetti rivelatore dei mutamenti che erano intervenuti tra la scoperta del calcolo nel XVII sec. e l'anno d'inizio della disputa: il 1711. Nel ventennio che va dal 1690 al 1710 è avvenuto esattamente ciò di cui Newton si lamenta. Il suo metodo generale, di cui egli più volte ha vantato l'evidente superiorità rispetto a quello di Leibniz, è stato fatto a pezzi, e una gran parte gli è stata sottratta, lasciandogli solo il merito di aver sviluppato e portato a perfezione la tecnica delle serie infinite. Contrariamente però a quanto egli pensa, questo non è stato il risultato di un subdolo piano messo in opera da Leibniz e dai suoi seguaci, ma il naturale svolgimento di un processo storico che aveva le sue radici nei due diversi punti di vista che abbiamo messo in evidenza.

Ricordiamo un momento i termini della questione. Con il suo calcolo differenziale Leibniz aveva risolto completamente il problema delle tangenti, e aveva posto su basi algebriche il problema delle quadrature, che peraltro era ridotto a un caso particolare del più generale problema dell'integrazione delle equazioni differenziali. Su tali problemi, e sulle loro applicazioni alla geometria e alla meccanica, Leibniz e i suoi lavoreranno a partire dal 1684 con crescente successo.

A quell'epoca Newton non solo aveva sviluppato il suo calcolo delle flussioni, equivalente, come abbiamo visto, al primo, ma era riuscito, con un abilissimo intreccio tra questo e il metodo degli sviluppi in serie ‒ un metodo che, sarà opportuno ricordarlo, si poteva proporre come universale solo una volta trovati gli sviluppi di tutte le funzioni note, cioè dopo la sistemazione newtoniana ‒ a risolvere in maniera del tutto generale il problema inverso delle tangenti.

Inoltre, a differenza del suo collega del Continente, il matematico newtoniano che avesse intrapreso lo studio di un'equazione differenziale, per esempio in connessione con un problema di meccanica o di geometria, sapeva benissimo che esisteva un metodo, per di più elaborato dalla più alta autorità in materia, che avrebbe immancabilmente condotto alla soluzione senza richiedere alcuno sforzo intellettuale. È vero che Newton aveva più volte ricordato l'opportunità di ricorrere alle serie solo quando fosse impossibile trovare la soluzione altrimenti; ma questa raccomandazione era ben poca cosa di fronte alla generalità e alla sicurezza delle tecniche di approssimazione, al punto che raramente i geometri inglesi si cimenteranno con questi importanti aspetti del calcolo, limitandosi a rinviare alla soluzione newtoniana. Quest'ultima poteva vantare un'indubbia superiorità nelle fasi iniziali del calcolo, quando i risultati del programma leibniziano erano ancora frammentari e dunque insufficienti a bilanciarne la generalità. A vent'anni di distanza, e cioè al momento del divampare della disputa, la situazione si è completamente rovesciata ed è ora il metodo di Newton a essere eclissato dal numero e dalla qualità dei risultati ottenuti sul Continente. Così a Newton, che riferendosi alla situazione quale era attorno al 1680 scrive nell'Account, poi rifuso nella Recensio libri: "Se l'operazione non arriva a dare equazioni finite, Newton ricorre alle serie convergenti; per cui il suo metodo risulta incomparabilmente più universale di quello di Leibniz, che è limitato alle sole equazioni finite dato che egli non ha accesso al metodo delle serie infinite" (La disputa, p. 58). Johann I Bernoulli può rispondere nel 1713:

ora un certo Cheyne se ne va in giro a dire che negli ultimi 20 o 30 anni non abbiamo pubblicato nulla, che non sia un'ennesima ripetizione o al più un corollario di poco peso di ciò che Newton aveva trovato prima; quasi che per noi non fosse rimasto nulla da fare, e che non siano di nessun pregio le cose che abbiamo pubblicato, e delle quali in Newton non si trovano nemmeno le tracce, come le Catenarie, le Velarie, le Isocrone paracentriche, le Brachistocrone, le nuove proprietà della Cicloide e i suoi innumerevoli segmenti quadrabili, il Calcolo degli esponenziali e il metodo di differenziarli, la misura delle Coevolute, il Moto trattorio e reptorio, la riduzione delle curve alle circolari, e innumerevoli altre che gli inglesi in parte tentarono, ma con tutto il loro calcolo delle flussioni hanno lasciato irrisolte, come si vede dal solo problema della Catenaria e della Trasformazione delle curve, sul quale hanno sudato per lungo tempo senza produrre altro che turpi paralogismi. (Johann I Bernoulli a Leibniz, in GM, III/2, p. 916)

L'elenco è impressionante e testimonia da solo del solco che si è aperto tra i due campi. Più ancora però impressiona il fatto che nessuno dei risultati menzionati da Bernoulli sia stato ottenuto da matematici inglesi o sia derivato da problemi da essi proposti o studiati. Si tratta infatti di problemi del tutto estranei al punto di vista newtoniano e con i quali Newton o altri si cimentarono solo se stimolati da sfide provenienti dal Continente.

Né probabilmente poteva essere altrimenti, perché, per entrare come parte attiva nell'attuazione di quello che oggi ci appare come un vero e proprio programma leibniziano di costruzione della nuova analisi, occorreva, se non compiere una scelta di campo, certo abbandonare il terreno della stretta ortodossia; e se non era necessario diventare leibniziani, di certo si doveva smettere di essere newtoniani.

Non occorreva abbracciare la notazione leibniziana, poiché l'uso delle notazioni newtoniane, senza dubbio meno eleganti e complete di quelle del calcolo differenziale, non costituiva una seria remora nell'affrontare problemi geometrici e meccanici e, anzi, in alcuni casi, come per esempio nei problemi di dinamica ‒ nei quali le notazioni newtoniane sono tuttora in uso ‒ queste erano altrettanto adatte delle altre.

Occorreva però prendere le distanze dall'opera newtoniana, dal momento che era essenziale separare in due parti la teoria di Newton, e di questa assumere solo il calcolo flussionale, relegando le serie tra i procedimenti di approssimazione numerica. In altre parole era necessario compiere quella separazione tra il metodo delle flussioni e quello delle serie che Newton aveva visto come una subdola manovra del suo antagonista per privarlo di quanto gli spettava. Che poi si assegnasse a Newton la paternità di uno solo o di ambedue questi metodi era tutto sommato secondario; quello che contava era la necessità di riconoscere che nel giudizio sulla loro importanza relativa Leibniz aveva visto più lontano di Newton.

Nessuno dei geometri inglesi se la sentirà di compiere un passo di questo genere per tutto il Settecento; al contrario, tutti continueranno a proclamare non solo l'indiscutibile priorità di Newton per quanto riguarda l'invenzione del metodo delle flussioni, ma anche la superiorità, altrettanto indiscutibilmente smentita dai fatti, del suo metodo generale delle serie. Così facendo, porteranno la matematica inglese, nella migliore delle ipotesi, a dedicarsi esclusivamente ai problemi degli sviluppi in serie, e altrimenti a estenuarsi su questioni fondazionali senza sbocchi. Nel momento in cui la sentenza della Royal Society sancisce la priorità newtoniana per quanto concerne la scoperta del calcolo, quella più duratura della storia riequilibra la bilancia stabilendo il primato del programma leibniziano. La matematica del XVIII sec. si svilupperà infatti seguendo la strada tracciata dallo scienziato tedesco.

Bibliografia

Galluzzi 1977: Galluzzi, Paolo, Galileo contro Copernico, "Annali dell'Istituto e Museo di storia della scienza di Firenze", 2, 1977, pp. 87-148.

Mahoney 1973: Mahoney, Michael S., The mathematical career of Pierre de Fermat 1601-1665, Princeton (N.J.), Princeton University Press, 1973 (2. ed.: 1994).