La Rivoluzione scientifica: i domini della conoscenza. Astronomia
La Rivoluzione scientifica: i domini della conoscenza. Astronomia
Astronomia
L'astronomia del Seicento è segnata da due eventi fondamentali, succedutisi a breve distanza l'uno dall'altro: la pubblicazione dell'Astronomia nova (1609) di Johannes Kepler e, quasi contemporaneamente, l'inizio delle osservazioni celesti di Galileo Galilei con il telescopio. L'elaborazione teorica e l'attività sperimentale dell'astronomia del XVII sec. saranno per gran parte lo sviluppo delle innovazioni kepleriane e delle scoperte empiriche galileiane.
A partire dal 1630, il miglioramento delle strumentazioni astronomiche condurrà a una nuova serie di scoperte e a una maggiore precisione delle osservazioni. La pratica e la professione dell'astronomia saranno ulteriormente trasformate a partire dagli anni Sessanta del Seicento, quando i governi di Francia e Inghilterra inizieranno a reclutare eminenti astronomi per sfruttare la loro competenza per il calcolo della latitudine e della longitudine terrestri e non nel ruolo di astrologi, come accadeva in passato. Con i Principia (1687) di Newton e le ulteriori scoperte empiriche negli anni Novanta del XVII sec., emergeranno nuove questioni e nuove sfide e si configurerà l'agenda dell'astronomia per il secolo successivo.
Johannes Kepler
Una delle principali novità della teoria planetaria di Kepler è l'attribuzione di un ruolo causale al Sole, che diventa in questo modo il principio fisico del moto planetario. In realtà, il sistema copernicano, con lo spostamento dell'astro al centro delle orbite planetarie, poteva far pensare che il Sole non avesse soltanto il ruolo di fornire luce e calore ai pianeti, ma anche quello di determinarne il moto: un'idea che si trova accennata nella Narratio prima (1540) di George Joachim Rhaeticus, un'esposizione introduttiva dell'astronomia di Copernico.
Sostenitore convinto del sistema eliocentrico sin dall'inizio della sua attività in campo astronomico ‒ fu infatti allievo di Michael Mästlin, uno tra i primi copernicani realisti ‒ Kepler tentò di trovare una spiegazione per il numero dei pianeti nel sistema copernicano, per la loro distanza dal Sole e per il loro moto. Egli era profondamente convinto che la struttura del Cosmo riflettesse un'armonia di origine divina: le parti immobili ‒ il Sole, le stelle fisse, gli spazi intermedi ‒ rispecchiavano le tre Persone della Trinità, mentre le distanze tra i pianeti corrispondevano alle relazioni tra i cinque solidi regolari (tetraedro, cubo, ottaedro, dodecaedro, icosaedro) della tradizione platonica. La Creazione del Cosmo poteva essere paragonata all'opera di un abile geometra.
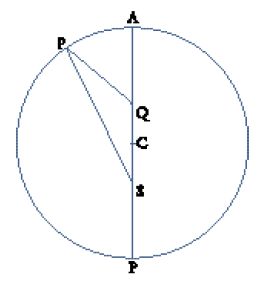
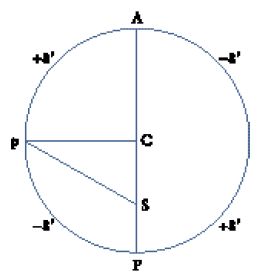
L'introduzione da parte di Kepler della speculazione fisica nello studio dei cieli si fonda, almeno inizialmente, su uno dei principî copernicani: i pianeti più distanti dal Sole si muovono più lentamente non solo nel loro moto angolare intorno al Sole, ma anche linearmente lungo le loro orbite; questo vuol dire che nel sistema planetario copernicano ogni singolo pianeta si muove tanto più lentamente quanto più è distante dal Sole. Ciò appariva più chiaro se per rappresentare i moti celesti si ricorreva allo strumento tolemaico del punto equante. In un cerchio, l'equante è un punto distinto dal centro, intorno al quale il moto circolare ha velocità angolare costante. Nella teoria tolemaica il punto equante e la Terra erano collocati simmetricamente a uguale distanza dal centro del cerchio (fig. 2); il moto 'lineare' lungo la circonferenza era più lento quando la distanza tra il punto equante e la circonferenza diminuiva. Nel sistema eliocentrico il Sole prendeva il posto della Terra e, in questo modo, a una maggiore distanza dal Sole corrispondeva un moto più lento del pianeta. Pur seguendo una dinamica di stampo aristotelico, Kepler concludeva che il Sole doveva essere l'origine del moto dei pianeti.
Nel 1600 Kepler fu chiamato a Praga da Tycho Brahe e ne divenne l'assistente. A Kepler fu assegnata la revisione di una teoria del moto di Marte elaborata dallo stesso Tycho e dal suo assistente Christen Sørensen (Longomontanus): la teoria si accordava con le osservazioni di Tycho sulle longitudini eliocentriche di Marte con un margine di errore contenuto entro i due minuti di arco, che era approssimativamente l'errore sistematico di Tycho. Tuttavia la stessa teoria si rivelò un totale insuccesso nel calcolo delle latitudini osservate di Marte.
In quasi cinque anni di calcoli laboriosi e di intenso lavoro teorico, Kepler mise finalmente a punto la teoria descritta nell'Astronomia nova, l'opera che racconta la storia della sua 'guerra contro Marte', della quale accentua i toni drammatici, per risultare più convincente. Fu stampata forse in mille copie e non fu più pubblicata fino al 1860 (quando apparve come terzo volume dell'Opera omnia di Kepler edita da Frisch). Negli anni che intercorsero, pochi lettori ebbero accesso all'opera e ancora meno riuscirono a interpretarne la complessità.
Le teorie cosmologiche precedenti, ivi compresa quella di Tycho, attribuivano un ruolo chiave al Sole medio, un punto in moto uniforme intorno alla Terra alla velocità media del Sole. Tycho assumeva che il piano dell'orbita del pianeta passasse attraverso il Sole medio, piuttosto che attraverso il Sole vero; per lui, le 'opposizioni' erano opposizioni al Sole medio piuttosto che a quello vero. Procedimenti simili erano stati seguiti da Tolomeo e da Copernico.
Al contrario, Kepler considerava il Sole reale come causa dinamica del moto eliocentrico del pianeta e pertanto cercò di sostituire il Sole vero a quello medio. Da alcune osservazioni effettuate da Tycho, riuscì a dedurre l'inclinazione dell'orbita di Marte rispetto all'eclittica e assunse che il piano di quest'orbita passava attraverso il Sole vero. L'inclinazione si dimostrò costante a circa 1°50′: era la conferma che Kepler cercava. Le oscillazioni periodiche attribuite al piano planetario nelle precedenti teorie furono eliminate.
Successivamente Kepler, sulla base delle osservazioni effettuate da Tycho, determinò nuovamente le dieci opposizioni di Marte che si erano verificate tra il 1580 e il 1600, in modo che fossero opposizioni al Sole vero e non a quello medio. Ottenne così dieci posizioni di Marte lungo l'eclittica, come fossero state osservate dal Sole vero, ciascuna corredata della collocazione temporale, vale a dire del momento in cui si era verificata. Questi erano i dati con i quali la sua teoria doveva concordare. Inoltre, addentrandosi nell'inesplorata regione della fisica celeste, Kepler si trovò di fronte una strada tortuosa e irta di ostacoli; gli mancavano gli strumenti analitici che noi oggi utilizzeremmo, e le sue idee sono talvolta ardue da seguire. Tenteremo pertanto di fornire soltanto una descrizione generale dei suoi metodi.
Nel suo primo tentativo di elaborazione teorica, Kepler prese in considerazione un'orbita circolare e, in accordo con Tolomeo, l'esistenza di un punto equante. Diversamente da quest'ultimo, però, tenne conto che il rapporto SC:SQ (fig. 2) potesse essere diverso da 1:2; né Tolomeo né Copernico avevano dimostrato in modo esplicito che tale valore fosse quello corretto e Kepler propose di sottoporlo a prova empirica.
Kepler prese in considerazione le osservazioni fatte da Tycho con Marte in opposizione, in modo tale che Marte apparisse a un osservatore sulla Terra nella stessa direzione in cui sarebbe apparso a un ipotetico osservatore sul Sole. Riuscì così a elaborare un modello per il moto in longitudine di Marte utilizzando un circolo eccentrico. Tuttavia, tale modello forniva risultati errati di circa 8′ agli ottanti (Tav. I).
Kepler risolveva il moto di un pianeta in una componente circumsolare, o 'trasversale', e in una componente 'radiale' da e verso il Sole. Quale causa del moto circumsolare, egli immaginò una virtus immateriale proveniente dal Sole e rotante insieme a esso (ipotizzando così la rotazione del Sole prima ancora che fosse scoperta per mezzo del telescopio).
Dalla bisezione dell'eccentricità, a questo punto verificata in modo empirico, Kepler sapeva che il Sole e il punto equante erano collocati simmetricamente su ciascun lato del punto medio C della linea degli apsidi AP (fig. 2). Ne conseguiva che il moto del pianeta all'afelio era, rispetto al suo moto al perielio, in rapporto inverso alle due distanze dal Sole (rispettivamente SA e SP). Nel formulare questo concetto egli non utilizzò il termine velocitas, ma disse che i 'ritardi' (morae, ossia i tempi trascorsi) del pianeta su piccoli archi uguali erano, all'afelio e al perielio, nello stesso rapporto delle distanze dei predetti archi dal Sole, cioè come SA sta a SP. Questa proporzionalità si applicava presumibilmente a tutta l'orbita. Kepler cercò di dedurre da essa il rapporto tra l'anomalia vera (l'angolo eliocentrico misurato dall'afelio) e l'anomalia media (il tempo trascorso dal passaggio all'afelio, espresso in gradi come una frazione di 360°).
In un primo tentativo, considerando l'orbita come un cerchio eccentrico rispetto al Sole, Kepler divise la semicirconferenza, a partire dall'afelio, in 180 archi da un grado ciascuno e nel punto medio di ogni arco tracciò il raggio vettore dal Sole. In tal modo il rapporto tra il tempo impiegato dal pianeta per attraversare un angolo misurato a partire dall'afelio e la metà del periodo dovrebbe essere, con buona approssimazione, uguale al rapporto fra la somma di tutti i raggi vettori contenuti nell'angolo e la somma di tutti i raggi vettori contenuti nel semicerchio. Kepler portò a termine questo lungo e laborioso calcolo considerando ogni grado di anomalia vera, ma non fu rigorosamente accurato: gli archi avrebbero dovuto essere infinitesimi. Ciononostante egli giunse a quella che è conosciuta come la 'legge delle aree': le aree descritte dal raggio vettore che unisce il Sole a un pianeta sono proporzionali ai tempi impiegati a percorrerle (Tav. II).
Soltanto alcuni anni più tardi, mentre stava scrivendo il Libro IV dell'Epitome astronomiae copernicanae (1620), Kepler si rese conto che questa legge esprimeva la sua ipotesi fondamentale: ciò che sarebbe dovuto variare in modo inversamente proporzionale alla distanza solare era la componente del moto ad angoli retti rispetto al braccio radiale dal Sole. La legge delle aree era pertanto un'esatta espressione di quanto Kepler aveva da sempre sostenuto. Quando scriveva l'Astronomia nova, egli non ne era consapevole, e pertanto considerò la legge delle aree approssimativa, fintanto che non la applicò, infine, alla sua ellisse; ciononostante, la utilizzò per verificare se particolari orbite fornissero longitudini più o meno corrette.
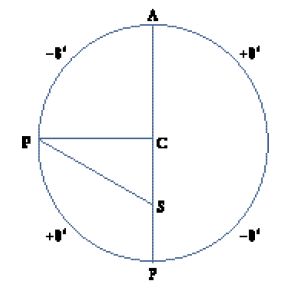
Esaminando l'orbita circolare, egli scoprì che il pianeta si sarebbe mosso troppo rapidamente negli apsidi (A e P) e troppo lentamente nelle longitudini intermedie. Gli errori massimi erano in corrispondenza degli ottanti, +8′ a 45° e −8′ a 135° dall'afelio, con errori simmetrici nel secondo semicerchio. Se si fosse dovuto tenere conto della legge delle aree, sarebbe stato necessario spostare una porzione di area dalle longitudini medie agli apsidi. L'orbita era quindi ovale? Calcolando le distanze Marte-Sole nelle longitudini medie per mezzo della triangolazione, Kepler scoprì che in realtà l'orbita in queste longitudini veniva a trovarsi all'interno del cerchio. È opportuno osservare che queste triangolazioni erano soggette a un errore notevolmente superiore rispetto a quello che si commetteva nella determinazione della longitudine eliocentrica attraverso osservazioni.
Nel frattempo, Kepler aveva cercato di immaginare una causa per il moto radiale del pianeta. Tolomeo aveva ottenuto un moto circolare eccentrico per mezzo di un epiciclo su un deferente. Poteva il pianeta essere messo in movimento intorno a un epiciclo da un motore interno? Supponendo che ciò fosse possibile, si sarebbe potuta ottenere un'orbita circolare soltanto se il moto dell'epiciclo fosse stato non uniforme, così come non uniforme era il moto sul deferente; se invece il moto dell'epiciclo fosse stato uniforme ‒ cosa più probabile ‒ l'orbita sarebbe stata ovale. Per verificare questa idea, Kepler approssimò l'orbita ovale con una ellisse e calcolò le aree per trovare la relazione tra le anomalie medie e quelle vere. Ancora una volta ci furono alcuni errori i cui margini massimi furono raggiunti nuovamente negli ottanti.
Casualmente, gli errori della nuova teoria erano esattamente gli opposti di quelli verificatisi per il cerchio. Essi potevano essere eliminati con un'orbita ellittica collocata a metà strada nella lunula compresa tra il cerchio della fig. 3 e l'ovale della fig. 4; ma perché il pianeta si sarebbe mosso secondo una tale ellisse? Kepler ritornò così al problema del moto radiale, immaginando che il pianeta fosse alternativamente attratto e respinto dal Sole, in modo tale da muoversi in una oscillazione sinusoidale, per una certa distanza, lungo il raggio vettore; pensò che la superficie del Sole potesse essere un polo di una specie di magnete, e che il pianeta potesse avere lati 'amichevoli' e 'non amichevoli'.
Come scoprì alla fine, le distanze diametrali (=1+ecosE) davano distanze Marte-Sole che concordavano in modo soddisfacente con le triangolazioni. Nella fig. 5, consideriamo Sr come la distanza diametrale. Una delle sue estremità dovrebbe essere situata sul Sole; ma dove si dovrebbe situare ‒ entro i margini consentiti dalle osservazioni ‒ l'altra estremità? Kepler inizialmente la situò sul raggio CM, ossia in q: il risultato fu un'orbita imperfetta, definita via buccosa. Cercando di calcolare le aree e le somme delle distanze in questa orbita, e confrontando i risultati con la hypothesis vicaria, egli trovò alcuni errori, negli ottanti, superiori a 4′ e ne dedusse che la teoria era errata. In realtà i suoi calcoli erano viziati: per la legge delle aree, le longitudini erano corrette fino a 1′. Se l'arco rq è protratto fino a p su MN (la perpendicolare ad AP che passsa per M), l'orbita attraverso p è la stessa ellisse che aveva fornito longitudini corrette per mezzo della legge delle aree.
Scoprendo così che i suoi ragionamenti di ordine fisico 'convergevano' con le osservazioni, Kepler giunse alla conclusione che nessun'altra figura poteva essere presa in considerazione per il pianeta se non un'ellisse perfetta, stabilendo in tal modo la 'prima legge di Kepler' (scoperta, in realtà, dopo la legge delle aree), secondo la quale le orbite dei pianeti sono ellissi in cui il Sole occupa uno dei fuochi. Altre orbite erano compatibili con questi dati, ma le osservazioni di Tycho, combinate con l'ipotesi di due 'forze' solari (in senso aristotelico) ‒ e cioè una spinta circumsolare, che variava in ragione inversa alla distanza solare, e un'attrazione e una repulsione, alternate nella direzione radiale ‒, avevano portato ai principî di cui aveva bisogno l'astronomia e che più tardi Newton avrebbe nuovamente dedotto dalla gravitazione universale e da una dinamica appropriata.
Negli anni successivi al 1609 Kepler applicò questi principî a tutti i pianeti, come pure alla prima anomalia della Luna (l'anomalia indipendente dalla perturbazione solare). Nel 1617 iniziò a pubblicare effemeridi annuali, dando le posizioni del Sole, della Luna e dei pianeti durante tutto l'anno, e la serie di pubblicazioni continuò fino a tutto il 1637. La responsabilità della collana passò quindi agli astronomi di Danzica, Lorenz Eichstädt, fino a tutto il 1665, e a Johannes Hecker, fino al 1680. In seguito, l'Académie des Sciences di Parigi fece propria la pubblicazione con il titolo di Connaissance des temps. In questo modo, nel corso degli anni, i calcoli di Kepler poterono essere ripetutamente confrontati con le osservazioni.
La teoria lunare, più complessa, presentava particolari difficoltà. Tycho aveva tenuto conto di nuove irregolarità, sconosciute sino a quel momento. La sua teoria della Luna servì da guida a Kepler, nonostante questi volesse ricondurre tutte le irregolarità a cause fisiche e a 'ragioni archetipe', ossia alle armonie che secondo lui il Divino Architetto aveva imposto al Cosmo. Rielaborò più di una volta la sua teoria dal punto di vista concettuale e geometrico, cercando di spiegare tanto la prima quanto la seconda anomalia per mezzo della legge delle aree. Combinando le due aree così ottenute approdò nel 1618 a una teoria nella quale la linea degli apsidi e l'eccentricità oscillavano l'una con l'altra sincronicamente, una teoria identica a quella più tardi sviluppata autonomamente, e con lo stesso metodo, da Jeremiah Horrocks, di cui parleremo più avanti. Tale teoria fu però abbandonata da Kepler, che temeva ‒ erroneamente ‒ che essa rendesse le distanze Terra-Luna troppo variabili.
La 'terza legge di Kepler' fu formulata, a dieci anni di distanza dalle prime due, negli Harmonices mundi (1619). Kepler scoprì la relazione che lega tra loro le distanze tra i pianeti: i quadrati dei periodi di rivoluzione dei pianeti sono proporzionali ai cubi dei semiassi maggiori delle loro orbite. Nell'Epitome astronomiae copernicanae Kepler fornì una deduzione dinamica di questa legge, adducendo una variazione ad hoc delle dimensioni e densità dei pianeti con la distanza dal Sole, una delle armonie imposte da Dio. Egli affermò che un'analoga proporzione fosse valida anche per i quattro satelliti galileiani di Giove.
Galileo Galilei
In contrasto con le complicate speculazioni matematiche di Kepler, le scoperte realizzate da Galilei grazie al telescopio avevano implicazioni la cui comprensione era alla portata di tutti: la Luna, con le sue montagne simili a quelle terrestri, non poteva essere il lucente gioiello sferico dei filosofi peripatetici; i minuscoli punti luminosi che circondavano Giove dimostravano che la Terra non era l'unico corpo celeste con un satellite; le macchie solari che si muovevano attraverso la superficie del Sole erano la prova della rotazione dell'astro e mostravano, contrariamente a quanto sostenuto da Aristotele, cambiamenti qualitativi in un corpo celeste; le fasi di Venere, analoghe a quelle lunari, dimostravano in modo evidente il suo moto orbitale intorno al Sole, un fatto incompatibile con il sistema planetario di Tolomeo. Per coloro che non potevano accettare l'idea del moto terrestre, rimaneva in alternativa il sistema geo-eliocentrico di Tycho, in cui il Sole orbita intorno alla Terra e gli altri pianeti intorno al Sole. Questo sistema sarà generalmente accolto nei paesi cattolici, anche a seguito degli eventi in cui Galilei fu tra i protagonisti.
Sostenitore del sistema copernicano sin dagli anni Novanta del Cinquecento, Galilei evitò di discuterne pubblicamente o di difenderlo fino al 1613, temendo che la Chiesa avrebbe condannato la teoria copernicana e impedito ogni ulteriore discussione. A quella data, infatti, gli interpreti più rigorosi della Bibbia, forse preoccupati delle inquietanti conseguenze delle nuove scoperte dovute al telescopio sugli uomini di fede, protestarono contro l'eliocentrismo. In una lettera a Benedetto Castelli (1578-1643), che circolò manoscritta a Firenze e Roma, Galilei seguiva Agostino nell'argomentare l'insostenibilità dell'interpretazione letterale della Bibbia. Nel dicembre del 1615 si recò a Roma nel tentativo di difendere la teoria copernicana dall'accusa di eresia.
La macchina della Chiesa era ormai in moto. Il 24 febbraio 1616 i consulenti teologici designati dal Sant'Uffizio diedero il loro parere, sostenendo che le dottrine del moto diurno della Terra intorno al proprio asse e annuale intorno al Sole immobile erano contrarie alla Scrittura, e dunque non valide né difendibili. Galilei, convocato in udienza davanti al cardinale Roberto Bellarmino il 26 febbraio, fu informato della decisione. Non potendo fare altro che accettarla, Galilei richiese e ottenne da Bellarmino un certificato che stabiliva che non aveva dovuto abiurare né gli era stata inflitta alcuna penitenza riparatrice.
Sette anni dopo, nell'agosto del 1623, Maffeo Barberini, amico di Galilei, ascese al trono papale con il nome di Urbano VIII. Galilei fu da lui ricevuto nel marzo del 1624 e propose la composizione di un dialogo che avrebbe confrontato il sistema copernicano con quello tolemaico, senza prendere in considerazione l'alternativa del sistema ticonico. La discussione avrebbe incluso un argomento a favore del moto terrestre per spiegare le maree.
Tale idea era nella mente di Galilei sin dagli anni Novanta del Cinquecento. Egli aveva elaborato una teoria con cui cercava di spiegare il fenomeno delle maree attraverso la combinazione dei moti di rotazione e di rivoluzione terrestre. Nonostante tale teoria presentasse molte difficoltà (il fenomeno delle maree sarà infatti spiegato completamente solo da Newton), Galilei vi credeva fermamente e, inoltre, riteneva che ogni altra spiegazione sarebbe stata respinta. Nella sua visione la scienza escludeva l'ipotetico: essa consisteva solamente di risultati sperimentali e di proposizioni derivate da principî primi non soggetti al dubbio.
Il dialogo di Galilei fu completato nel 1630 e, una volta ricevuto l'imprimatur dalla Chiesa, fu pubblicato nel 1632 con il titolo di Dialogo sopra i due massimi sistemi del mondo. Il libro scatenò una tempesta che si ritorse su Galilei, il quale aveva dato libero sfogo alla sua vena ironica, assegnando la difesa della posizione anticopernicana all'ingenuità di un personaggio chiamato Simplicio. Già nel 1624 Urbano VIII aveva osservato che, anche se l'argomento delle maree avesse trovato il generale consenso umano, Dio avrebbe potuto causare lo stesso fenomeno in modo diverso. Sostenuto da Simplicio, l'argomento apparve insignificante, se non addirittura offensivo per il papa.
Inoltre, il copernicanesimo di Galilei, per quanto mai apertamente sostenuto nel Dialogo, era evidente anche a un lettore poco avveduto. Dai registri del Sant'Uffizio, poi, fu reso noto un documento anonimo del 1616, dal quale risultava che a Galilei, alla presenza del cardinale Bellarmino, era stato intimato di abbandonare l'opinione copernicana della mobilità della Terra e della fissità del Sole e, di conseguenza, anche di non sostenerla, insegnarla o difenderla in alcun modo, a voce o per iscritto. L'autenticità del documento è ora considerata discutibile, ma all'epoca una commissione costituita appositamente concluse che Galilei, con il suo Dialogo, aveva trasgredito questa ingiunzione. Processato di fronte al tribunale dell'Inquisizione, fu invitato ad abiurare il copernicanesimo e condannato alla detenzione a vita, da scontare nella sua villa di Arcetri. Questo significava che egli poteva essere portato nuovamente di fronte all'Inquisizione in ogni momento e riesaminato per le sue posizioni eretiche.
Negli Stati cattolici, e in particolare in Italia, la libera speculazione cosmologica subì così una grave battuta d'arresto e la Chiesa incoraggiò quella ricerca scientifica che non metteva in discussione l'immobilità della Terra. Un'opera di valore che emerse da questo contesto fu l'Almagestum novum (1651) del gesuita bolognese Giovanni Battista Riccioli; nei suoi due consistenti volumi forniva una dettagliata storia tecnica dell'astronomia, riportando in modo abbastanza equilibrato gli argomenti a favore e contro l'eliocentrismo. Un altro astronomo gesuita, Christoph Scheiner (1573-1650), fu l'autore della Rosa Ursina, considerata per un intero secolo il più autorevole lavoro sulle macchie solari.
In Francia, le 'libertà gallicane' concesse alla chiesa francese consentirono a ecclesiastici cattolici come Ismaël Boulliau (1605-1694) e Pierre Gassendi (1592-1655) di dichiarare apertamente il loro copernicanesimo. In Inghilterra, verso la metà del secolo, gli astronomi protestanti erano tutti copernicani e giudicavano il trattamento riservato a Galilei dal Sant'Uffizio come un'ulteriore prova della perfidia papale.
Nel 1610 Galilei aveva osservato un singolare aspetto di Saturno: le ombre a entrambi i lati del disco centrale apparivano simili ad ansae (manici). Nel 1612, dopo aver scoperto le eclissi dei satelliti di Giove, si impegnò nella formulazione di tavole predittive di queste eclissi, con cui sperava di poter risolvere il problema della determinazione della longitudine. Il tempo locale di un'eclissi osservata da qualsiasi luogo nel globo terrestre meno il tempo desunto dalle tavole ‒ per Roma, per esempio ‒ avrebbe fornito la differenza in longitudine tra il luogo in cui si trovava l'osservatore e Roma. Galilei tornò su questo progetto ripetutamente, fino agli ultimi anni della sua vita, ma non disponeva dei presupposti necessari, dal momento che non possedeva una teoria abbastanza accurata né dei moti di Giove né di quelli dei suoi satelliti. Dopo il 1612 si assiste a una netta diminuzione delle scoperte dovuta all'esaurimento delle potenzialità del telescopio galileiano, la cui capacità massima di ingrandimento era di venti volte.
Da Kepler a Horrocks
Nel 1629 Kepler pubblicò una Admonitio ad astronomos in cui prevedeva i transiti di Mercurio e di Venere davanti al disco solare verso la fine del 1631. Tali transiti, mai individuati prima di allora, avrebbero consentito l'osservazione delle longitudini eliocentriche dei pianeti interni. Il transito di Venere nel 1631 non era visibile dall'Europa, ma quello di Mercurio fu osservato da Pierre Gassendi utilizzando un telescopio per proiettare l'immagine del Sole su una pergamena. Egli trovò che le previsioni di Kepler presentavano un errore di soltanto 13′ nella longitudine ‒ 5h 49m 30s in termini di tempo ‒ mentre le tavole di Tolomeo, Copernico e Christen Sørensen (Longomontanus, 1562-1647) si discostavano rispettivamente di 4°, 5° e 7°, errori esprimibili in giorni invece che in ore. Il diametro di Mercurio sul Sole appariva di dimensioni pari a soltanto un novantesimo di quello solare, assai più ridotte di quelle risultanti dalla speculazione 'armonica' di Kepler. L'osservazione rafforzò lo scetticismo già dimostrato da Gassendi nei confronti della speculazione armonica, come pure dell'astrologia (potevano corpi così piccoli influenzare le vicende umane?).
La relazione di Gassendi fu pubblicata nel 1632. Fra le varie repliche, vi fu quella di Martinus Hortensius (Maarten van den Hove), allievo di Philip van Lansberge: sia Hortensius sia Lansberge erano copernicani convinti, certi, come Copernico, che tutte le osservazioni effettuate nell'Antichità dovessero essere ritenute indiscutibilmente corrette. Entrambi respingevano le innovazioni dei 'tychonici': per esempio, non accettavano che Tycho avesse trascurato le osservazioni presumibilmente fatte da Tolomeo, per ottenere, da quelle di altri astronomi, una velocità costante di precessione degli equinozi; oppure non accettavano la riduzione della parallasse solare dall'antico valore di circa 3′ a 1′, fatta per conciliare le osservazioni con la nuova teoria delle latitudini di Marte.
Lansberge, nelle Tabulae motuum coelestium perpetuae (1632), aveva orgogliosamente rivendicato l'esatta concordanza tra le sue tavole e tutte le osservazioni disponibili. Hortensius, nella replica alle dichiarazioni di Gassendi, ammise che le tavole di Lansberge non erano del tutto esatte: malgrado l'impegno dell'autore, la teoria sul moto di Mercurio richiedeva alcune correzioni. Nel transito di Mercurio, le tavole di Lansberge presentavano un errore di 1°8′ nella longitudine e di 17′ nella latitudine. Hortensius si dilungò anche sull'assenza di valore delle speculazioni armoniche di Kepler. Sostenne, infatti, che i posteri avrebbero riso del lavoro sprecato su questi sogni inutili e che soltanto le osservazioni e le dimostrazioni geometriche erano attendibili.
Nel 1635 Noël Durrett, cosmografo al servizio del re di Francia e astrologo praticante, pubblicò la Nouvelle théorie des planètes [...] avec les tables Richeliennes. Sia le parti teoriche sia le tavole contenute nell'opera erano in gran parte una traduzione da Lansberge, benché Durrett fosse contrario al suo eliocentrismo e sostenesse con convinzione l'immobilità della Terra. Verso il 1639 era arrivato a riconoscere la maggior precisione delle Tavole rudolfine di Kepler, di cui si stava avvalendo per le previsioni. L'astrologo anticopernicano Jean-Baptiste Morin pubblicò nel 1650 una versione semplificata delle tavole di Kepler.
Nel 1640 Johannes Phocylides Holwarda pubblicò il suo Examen astronomiae Lansbergianae, una critica dei metodi di Lansberge. Calcolo dopo calcolo, Holwarda dimostrò che questi aveva contraffatto la propria teoria ‒ alterando, per esempio, un risultato delle osservazioni o consentendo che un errore di calcolo passasse inosservato ‒ al fine di farla concordare con le osservazioni. Holwarda contrappose la laboriosità, la sincerità e il sapere di Kepler alla disonestà e alla millanteria di Lansberge. In molti degli argomenti sui quali Lansberge dissentiva da Kepler ‒ la costanza della velocità del moto di precessione, la bisezione dell'eccentricità nella teoria solare, la riduzione della parallasse solare a 1′ ‒, Holwarda si schierò con Kepler contro Lansberge. Tuttavia, la reputazione di Lansberge non fu del tutto rovinata: le sue tavole furono nuovamente pubblicate nel 1653 e nel 1663. Basandosi su di esse, Francesco Montebruni e il marchese Cornelis Malvasia pubblicarono le effemeridi per gli anni 1645-1667.
Particolarmente dispiaciuto delle falsificazioni di Lansberge fu Jeremiah Horrocks. Nel 1633 aveva intrapreso, giovanissimo, lo studio dell'astronomia all'Università di Cambridge formandosi sulle opere di Lansberge. Al ritorno a Toxeth, suo paese di origine vicino Liverpool, iniziò una corrispondenza con William Crabtree di Manchester, che gli illustrò gli inganni di Lansberge e lo iniziò alle opere di Kepler.
Horrocks diventò un osservatore esperto, inizialmente senza avvalersi dell'uso del telescopio. Egli sottopose le costanti astronomiche di Lansberge e Kepler a prove di osservazione. Scrisse pagine di polemica contro Lansberge, ma molto più importanti per gli sviluppi dell'astronomia negli anni seguenti furono le correzioni da lui apportate ai parametri planetari e la revisione della teoria lunare di Kepler.
Le correzioni effettuate da Horrocks sulle costanti planetarie derivavano da una riduzione della parallasse solare. La parallasse di un corpo celeste in altezza è lo spostamento verso il basso, che dipende dal fatto che l'osservatore si trova sulla superficie terrestre e non sulla linea che unisce il centro della Terra al corpo celeste. Lo spostamento è massimo per un oggetto all'orizzonte, diminuisce fino a zero allo zenit e varia in proporzione inversa alla distanza dell'oggetto dalla Terra. Dall'Antichità fino a Tycho, gli astronomi supposero che la parallasse orizzontale del Sole fosse di circa 3′; ciò comportava che il Sole fosse distante circa. 1160 raggi terrestri. Kepler, al fine di inquadrare i moti di Marte in una teoria coerente, fu indotto a limitare le sue parallassi e, di conseguenza, a ridurre la parallasse solare a 1′. Nel condurre un'analoga ricerca sui moti di Venere, Horrocks fu portato a ridurre ulteriormente la parallasse solare, giungendo alla conclusione che essa non poteva superare i 14″.
Questa riduzione portò a un miglioramento della teoria solare. Fino al tardo XVII sec. i parametri della teoria solare erano determinati in base alle altezze del Sole osservate a mezzogiorno oppure in prossimità dei solstizi e degli equinozi. Le altezze rilevate necessitavano però di correzioni verso l'alto per la parallasse e verso il basso per la rifrazione. Horrocks non effettuò correzioni per la rifrazione, ma la sua riduzione della parallasse significava che il Sole doveva salire più in alto nel cielo in primavera e scendere meno in autunno, per poter essere all'equatore celeste. Dato che l'apogeo del Sole è a nord dell'equatore ne conseguì un'orbita del Sole relativa alla Terra meno eccentrica di quanto precedentemente ritenuto. Horrocks ridusse l'eccentricità dal valore kepleriano di 0,018 a 0,01730, diminuendo così la massima equazione del centro da 2°4′ a 1°59′ (il valore corretto nel 1640 era pari a 1°55′55″).
Poiché la Terra è il punto da cui si osservano gli altri pianeti, qualsiasi errore nella teoria solare si ripercuote nelle teorie relative a questi pianeti. Le correzioni effettuate da Horrocks sulla teoria solare di Kepler portarono al miglioramento dei valori relativi all'eccentricità e alle longitudini degli afeli di Mercurio, Venere e Marte. Horrocks previde con precisione il transito di Venere davanti al Sole il 24 novembre 1639 e, insieme a Crabtree, quel giorno osservò Venere nel Sole verso l'ora del tramonto, ottenendo così la prima misura diretta della longitudine eliocentrica di Venere.
Una conseguenza importante dei progressi conseguiti nelle teorie planetarie fu che la terza legge di Kepler si dimostrò molto precisa. Horrocks diede inizio alla pratica di calcolare le distanze solari medie dei pianeti ‒ difficili da determinare per mezzo dell'osservazione ‒ a partire dai loro periodi che per Mercurio, Venere, Terra e Marte possono essere determinati con grande precisione. Per Mercurio e Venere ciò portò a correzioni nelle longitudini previste fino a 3′ o 4′.
La principale realizzazione di Horrocks fu senza dubbio la teoria lunare che, come indicato, fu una naturale derivazione dell'uso che Kepler fece dell'area come misura del tempo, e della combinazione della prima anomalia (dovuta all'eccentricità dell'orbita lunare) con la seconda, o evezione (dovuta alla perturbazione esercitata dal sole), in un'unica anomalia. Il risultato fu un'ellisse con eccentricità e apside oscillanti. Horrocks confrontò questa teoria con le eclissi riportate nella letteratura astronomica, controllando le distanze radiali della Luna dalla Terra per mezzo della durata di queste eclissi. Non ebbe la possibilità di avvalersi del micrometro inventato da William Gascoigne (1612 ca.-1644), il quale, insieme a Crabtree, dopo la morte di Horrocks utilizzò questo strumento per misurare i diametri lunari e verificare con maggiore esattezza la teoria di Horrocks.
Dopo la guerra civile in Inghilterra e l'interregno, Thomas Streete, nell'Astronomia Carolina (1661), riprese le innovazioni apportate da Horrocks, alla teoria planetaria. L'opera di Horrocks Venus in sole visa fu pubblicata da Hevelius a Danzica nel 1662; la sua Opera posthuma fu stampata nel 1672 e pubblicata nel 1673 e, in una nuova edizione, nel 1678: includeva, in appendice, la versione di John Flamsteed della teoria lunare di Horrocks di cui si parlerà diffusamente in seguito.
Il dibattito sulle orbite ellittiche
L'Astronomia Philolaica (1645) dell'astrologo e sostenitore dell'eliocentrismo Ismaël Boulliau (Bullialdus) fu la prima opera, dopo quelle di Kepler, a sostenere la tesi del moto ellittico dei pianeti. Boulliau fu spinto ad adottare orbite ellittiche dai risultati delle osservazioni su Mercurio, compiute da Gassendi. Tuttavia, egli respinse con decisione l'ipotesi kepleriana del'esistenza di forze di attrazione e repulsione: ogni pianeta era mosso da una forma interna a sé stesso.
Seguendo Copernico, Boulliau riteneva che i moti dei pianeti fossero composti da moti circolari rigorosamente uniformi. Per ottenere l'ellisse da un moto circolare, egli supponeva che un pianeta in un dato momento si muovesse uniformemente lungo un circolo, ma in momenti successivi si spostasse da un circolo all'altro, poiché i circoli successivi sarebbero stati situati in un cono obliquo. Nella fig. 9, AI è l'asse del cono; BC è un diametro della base circolare del cono, ortogonale rispetto al piano contenente il triangolo ABC. Tutte le sezioni del cono parallele alla base (per es. KRW) sono cerchi, ma una sezione che incontri l'asse AI e il triangolo ABC con un angolo diverso sarà un'ellisse. Boulliau sceglie l'ellisse ottenuta tagliando il cono con un piano perpendicolare al triangolo ABC in modo che l'angolo AMK sia uguale all'angolo KRI; ne risulta che il triangolo MKR è isoscele. Il punto M sull'asse è un fuoco di questa ellisse.
Ipotesi essenziale per la teoria di Boulliau era quella del moto uniforme su cerchi paralleli alla base del cono. Tuttavia, quando egli giunse alla deduzione del moto dei pianeti, ignorò tale assunto sostituendolo con una complicata procedura. Più tardi, quando l'Astronomia Philolaica era già stata data alle stampe, scoprì che questo nuovo metodo forniva longitudini discordi dalle equazioni di Kepler per Marte, aumentando il divario nella longitudine eliocentrica a circa 2′. A questo punto, fece stampare le equazioni di Kepler per Marte su nuove pagine numerate 49-50 e le aggiunse al libro come supplemento.
Nonostante questo errore corretto tardivamente, le tavole di Boulliau ebbero una certa popolarità; in Inghilterra furono pubblicate due volte, con le 'epoche' ricalcolate per il meridiano di Londra: una prima volta nel 1653 nelle Tabulae Britannicae di Jeremy Shakerley, che ne apprezzò l'esattezza, e successivamente nel 1657 nell'Astronomia Britannica di John Newton.
Nel 1653, Seth Ward, professore saviliano di astronomia a Oxford, pubblicò l'Inquisitio brevis in Ismaelis Bullialdi Astronomiae Philolaicae fundamenta. Ward dimostrò che quanto inizialmente stabilito da Boulliau in merito al moto uniforme su tutti i cerchi paralleli alla base del cono comportava un moto costante sul piano dell'ellisse intorno al fuoco vuoto M (nella fig. 9, la linea da N a un punto x dell'ellisse è uguale a Mx, e Nx e Mx formano angoli uguali con l'asse AI; da ciò deriva che il moto angolare di x intorno a M è uguale al suo moto angolare intorno a N). Nella Inquisitio brevis come nella successiva Astronomia geometrica (1656), Ward sosteneva che il moto di un pianeta è esattamente uniforme intorno al fuoco superiore, e dimostrò come, partendo da questo presupposto, l'afelio e l'eccentricità potevano essere determinati dalle osservazioni e l'anomalia vera poteva essere dedotta dall'anomalia media.
Le affermazioni di Ward delinearono quella teoria che fu denominata 'ipotesi ellittica semplice'. Nel 1657 il conte Blaise-François Pagan pubblicò a Parigi la Theorie des planètes […] ou tous les orbes celestes sont géométriquement ordonnés; contre le sentiment des astronomes, nella quale fece proprio il principio dell'ipotesi ellittica semplice. Egli elencò gli errori delle tavole kepleriane, che arrivavano a un massimo di 8′ o 9′ di longitudine eliocentrica per Marte e a 30′ o 40′ per Mercurio. In realtà questi errori, con i segni invertiti, sono relativi all'ipotesi ellittica semplice. Pagan, che aveva perduto la vista da entrambi gli occhi, non aveva ritenuto necessario verificare le sue teorie per mezzo dell'osservazione.
Boulliau, neanche lui osservatore accurato ed esperto, confrontò la sua teoria con le osservazioni di Tycho e Gassendi e nell'Astronomiae Philolaicae fundamenta clarius explicata, del 1657, presentò un nuovo e più accurato metodo per ricavare l'anomalia vera da quella media: se nella fig. 10, l'orbita planetaria è l'ellisse AuvP, S è il Sole in un fuoco e Q è l'altro fuoco, dato l'angolo AQu come anomalia media, Boulliau tracciò una linea perpendicolare da u all'asse maggiore prolungandola dalla parte opposta fino al punto M. Tracciata MQ, il pianeta doveva trovarsi nel punto v, dove MQ incontra l'ellisse. Le anomalie vere ASv, ottenute in questo modo per Marte, differiscono dai valori di Kepler per meno di un minuto d'arco. Boulliau affermò che questa correzione era giustificata a priori dallo spostamento dal cerchio all'ellisse. Sull'altra sponda della Manica, Streete adottò lo stesso metodo nella citata Astronomia Carolina, attribuendolo all'amico Robert Anderson e motivandone l'utilizzo semplicemente perché necessario ai fini di una precisione empirica.
Un altro inglese che mirava a elaborare teorie planetarie empiricamente accurate fu l'astrologo Vincent Wing. Nello Harmonicon coeleste del 1651, egli suppose un punto equante mobile, oscillante lungo l'asse maggiore per un'ampiezza uguale a e2/4 e un periodo uguale alla metà di quello del pianeta. Quando scrisse l'Astronomia instaurata (1656), confrontò questa teoria con le osservazioni di Tycho e si rese conto che era necessaria un'ulteriore correzione empirica. Le sue teorie per i cinque pianeti, che furono nuovamente presentate nella sua ultima opera, l'Astronomia Britannica del 1669, erano esatte entro un margine inferiore al minuto d'arco.
Mentre nello Harmonicon coeleste Wing aveva sostenuto che il moto dei pianeti è essenziale e conferito da Dio, nell'Astronomia Britannica affermò che il Sole, ruotando sul suo asse, causava la rotazione di tutta la materia celeste in un vortice, trasportando i pianeti intorno a sé stesso. Anche Streete, nell'Astronomia Carolina, accettò l'ipotesi di vortici di questo tipo. La teoria dei vortici era piuttosto diffusa tra gli astronomi del periodo, ma nessuno aveva idea di come poterne derivare conseguenze sul piano quantitativo.
Verso la fine degli anni Cinquanta del Seicento, Christopher Wren tenne alcune lezioni al Gresham College di Londra sulla filosofia magnetica di William Gilbert (1544-1603) e sull'astronomia di Kepler, e nel 1659 rese pubblica una soluzione meccanica al 'problema di Kepler': come ottenere la longitudine eliocentrica dall'anomalia media, utilizzando la legge delle aree per mezzo della cicloide. Insieme a Robert Hooke (1635-1703) lavorò ad alcune ipotesi sul ruolo delle forze di attrazione nel moto dei pianeti e delle comete, seguendo una linea di pensiero che avrebbe dato i suoi frutti nell'opera di Isaac Newton.
Gli astronomi, generalmente, non si concentravano sulla ricerca di spiegazioni fisiche alle loro teorie planetarie. Negli anni Sessanta, Streete e Wing discussero animatamente nelle loro pubblicazioni la riduzione della parallasse solare proposta da Horrocks e la derivazione delle distanze solari medie dalla terza legge di Kepler. Streete sostenne l'immobilità degli afeli planetari rispetto alle stelle fisse, mentre Wing la negò (a ragione, benché gli afeli siano quasi immobili).
Niccolò Mercatore, un danese che viveva a Londra, presentò nel 1664 un'ipotesi planetaria che sovrapponeva un'orbita ellittica alla hypothesis vicaria di Kepler, con i fuochi dell'ellisse nel Sole e nel punto equante del diagramma kepleriano. Nella fig. 11 il pianeta è nel punto e; il centro M del cerchio di Kepler deve dividere la distanza focale SQ secondo la sezione aurea. Nei punti S, M e Q Mercatore vide il segno della Trinità. A imitazione di Leonardo da Vinci, immaginò una figura umana inscritta nell'ellisse, con la testa al perielio e i piedi all'afelio, ginocchia e cuore nei fuochi, braccia e mani tese verso gli estremi dell'asse minore: in questa figura vedeva l'immagine del Creatore.
Alcuni anni più tardi, Mercatore pubblicò una clamorosa confutazione dell'ipotesi ellittica semplice. Gian Domenico Cassini, nel numero di settembre 1669 del "Journal des Sçavans", aveva pubblicato un nuovo metodo, diretto e geometrico, per determinare gli apogei, le eccentricità e le anomalie del moto dei pianeti; si trattava, a quanto pare, della sua prima pubblicazione in Francia dopo l'arrivo dall'Italia. Il metodo considera il fuoco superiore dell'ellisse come punto equante. Nelle "Philosophical Transactions" del mese di marzo 1670, Mercatore rilevò che ‒ come Kepler e Boulliau avevano già scoperto in precedenza ‒ il fuoco superiore come punto equante è incompatibile con le osservazioni di Marte effettuate da Tycho. John Collins scrisse a James Gregory che Cassini era fortemente contrariato e che intendeva replicare; la replica di Cassini, tuttavia, non apparve fino al 1690.
Nuove scoperte telescopiche
Una seconda fase dell'astronomia telescopica si aprì verso la fine degli anni Trenta del Seicento con l'adozione di un nuovo progetto di telescopio, detto 'telescopio astronomico', descritto da Kepler nella Dioptrice (1611). Mentre nel telescopio di Galilei l'oculare concavo era situato tra l'obiettivo e il suo fuoco, qui l'oculare era una lente convessa a fuoco corto (in seguito sostituita da un oculare composto) e il fuoco dell'obiettivo veniva a trovarsi tra l'obiettivo e l'oculare; il campo visivo era più ampio di quello del telescopio di Galilei. Ingrandimenti di 50 volte (dati dal quoziente f1/f2 delle lunghezze focali delle due lenti) furono ottenuti in poco tempo; potevano inoltre essere collocati sul fuoco, dei reticoli e un micrometro filare. Per valori di f1 molto elevati furono adottati telescopi senza tubo, con le lenti dell'obiettivo collocate all'estremità superiore di un'asta manovrata da tiranti a fune metallica.
Il nuovo telescopio rese possibile la cartografia accurata della Luna. Il cartografo fiammingo Michael Florent van Langren elaborò nel 1645 la prima mappa lunare veramente accurata, allo scopo di determinare la longitudine terrestre: i momenti del sorgere e del calare di determinati picchi lunari sarebbero stati rilevati in diversi luoghi terrestri, mentre la differenza in ore locali avrebbe fornito la differenza in longitudine. Purtroppo, la mappa di van Langren non era abbastanza precisa per ottenere un tale risultato.
Un altro selenografo fu Johannes Hevelius, ricco produttore di birra di Danzica, il quale costruì quello che per un certo periodo di tempo fu il più avanzato osservatorio in Europa. Pubblicò molti trattati riguardanti le sue osservazioni astronomiche, tra i quali Mercurius in Sole visus (1662), una Cometographia (1668) e un catalogo delle stelle, Prodromus astronomiae (1690). La Selenographia (1647) era un ponderoso volume in cui descriveva i suoi strumenti e illustrava le osservazioni di vari corpi celesti, oltre che della Luna. Le quaranta incisioni di diverse fasi lunari e le tre grandi mappe della Luna, contenute nel volume, ne fecero il più autorevole trattato sulla Luna per circa un secolo. In due delle sue mappe, Hevelius descrisse la misura della librazione lunare così come l'aveva osservata.
Van Langren aveva designato le varie zone della superficie lunare da lui osservate con nomi di uomini illustri e aveva fatto appello agli astronomi perché accettassero questa nomenclatura; Hevelius, ritenendola offensiva, la sostituì con antichi nomi geografici. Giovanni Battista Riccioli per l'Almagestum novum incaricò il confratello gesuita Francesco Maria Grimaldi (1618-1663) di elaborare una nuova mappa lunare, basandosi sul confronto e sulla correzione di mappe precedenti. Riccioli introdusse una nuova nomenclatura che continuava ad applicare il principio di van Langren, ma la scelta dei nomi era limitata agli astronomi, ai matematici e ai filosofi e l'attribuzione seguiva un criterio sistematico: i nomi erano raggruppati per epoca, nazionalità, orientamento filosofico. Questa nomenclatura fu subito accettata nei paesi cattolici; nell'Europa settentrionale fu usata accanto a quella di Hevelius per centocinquant'anni e poi adottata in maniera esclusiva.
L'aspetto di Saturno, rilevato per la prima volta da Galilei, rappresentò un altro oggetto di studio. Gassendi, Hevelius, Francesco Fontana, Eustachio Divini e altri disegnarono ciò che essi credevano di vedere, senza risolvere l'enigma. Nel 1655 Huygens puntò su Saturno un telescopio con capacità di ingrandimento di 50 volte e presto scoprì il più grande satellite del pianeta, Titano. Nel 1656 era in grado di interpretare le ansae come apparenze prodotte da un anello sul piano equatoriale di Saturno, che scoprì essere parallelo a quello della Terra. Prevedere le apparenze future si ridusse quindi a un problema geometrico, e le previsioni piuttosto accurate di Huygens per gli anni seguenti furono pubblicate nel Systema Saturnium (1659).
Questo libro includeva anche i suoi calcoli sulle dimensioni dei pianeti, ottenuti con l'aiuto di un orologio a pendolo che perfezionò negli anni 1655-1660. Sul piano focale del telescopio collocò un diaframma con un'apertura leggermente più piccola di quella dell'oculare. Il bordo d'entrata del pianeta appariva a quel punto nitidamente delineato; il tempo impiegato per il suo passaggio attraverso l'apertura era accuratamente misurato con l'orologio a pendolo. I risultati ottenuti da Huygens dimostrarono che nessuna 'armonia' di stile kepleriano che considerasse le dimensioni dei pianeti come funzione della distanza solare media era sostenibile: Marte era più piccolo di Venere e Giove più grande di entrambi.
Il virtuoso delle scoperte telescopiche fu Gian Domenico Cassini, professore di astronomia all'Università di Bologna dal 1650 fino al 1669, anno in cui Luigi XIV lo convinse a entrare nell'Académie des Sciences di Parigi, da poco istituita. Negli anni Sessanta del XVII sec., utilizzando i telescopi ideati da Giuseppe Campani, Cassini scoprì l'appiattimento di Giove, la rotazione assiale di Giove e Marte e i principî che governano le eclissi dei satelliti di Giove, riuscendo a calcolarne le latitudini; nel 1668 pubblicò le prime tavole ragionevolmente accurate per la previsione di queste eclissi. Dopo il 1669 proseguì le esplorazioni telescopiche in Francia, scoprendo la 'divisione di Cassini' nel sistema degli anelli di Saturno (1675) e quattro satelliti dello stesso pianeta (1671-1672, 1684).
A partire dal 1671, inoltre, Cassini elaborò, con l'aiuto di due artisti, una serie di disegni della superficie lunare, fino a produrre, nel 1679, una mappa lunare completa, la più esatta tra tutte quelle realizzate nel secolo; nel 1693, come risultato di questi studi, fu in grado di formulare le leggi geometriche che regolano la librazione lunare.
L'Académie des Sciences di Parigi
Il primo istituto per la ricerca scientifica a giovarsi di un finanziamento pubblico fu l'Académie des Sciences di Parigi, fondata nel 1666. L'astronomia era uno dei punti principali del suo programma, per il contributo pratico che essa offriva ai fini della navigazione e della rappresentazione cartografica del regno di Luigi XIV. Tra i primi membri eletti all'Académie vi furono Huygens, il cui orologio d'altura avrebbe fornito ai naviganti, come si sperava, un'accurata misura della longitudine; Adrien Auzout (1622-1691), che aveva perfezionato il micrometro filare e Jean Picard (1620-1682), un astronomo di vasta esperienza. Tutti e tre concordavano nel considerare le tavole di Kepler come le migliori esistenti, ma il loro scopo era di ottenere risultati ancora più precisi attraverso l'ausilio di nuovi strumenti.
Uno dei primi impegni di Picard fu di superare i problemi di collimazione che comportava l'applicazione al mirino dei telescopi di archi graduati, ciascuno dei quali dotato di micrometro; nel 1669 era pronto a iniziare una serie regolare di osservazioni con tali strumenti. Propose inoltre la costruzione di un grande quadrante meridiano, al fine di cronometrare i transiti dei pianeti con un orologio a pendolo per la determinazione delle ascensioni rette e la misurazione delle altezze dei transiti; ma questo strumento non fu completato se non dopo la sua morte.
Già prima di entrare a far parte dell'Académie, Huygens aveva utilizzato l'orologio a pendolo per eliminare un errore di Kepler. Quest'ultimo riteneva che l'equazione annuale dei moti della Luna dipendesse dal fatto che la rotazione della Terra sul suo asse fosse leggermente più veloce in inverno che in estate, e aveva così introdotto un errore nell''equazione del tempo', la relazione per correggere il tempo apparente in tempo medio. L'orologio a pendolo, misurando il tempo medio da mezzogiorno a mezzogiorno per tutto l'anno, dimostrò che l'equazione di tempo di Kepler era errata: l'equazione prekepleriana o tolemaica era quella valida.
Fondamentali per la scienza astronomica furono le correzioni delle osservazioni in relazione a rifrazione e parallasse, due effetti che svanivano allo zenit, ma che in ogni altro luogo erano inestricabilmente confusi; la teoria solare, come già indicato in precedenza, dipendeva dalla precisione di queste correzioni. Cassini aveva effettuato alcune ricerche su questo problema durante la sua permanenza a Bologna, utilizzando un grande gnomone che egli stesso aveva costruito nella basilica di S. Petronio, e una tavola delle rifrazioni, calcolata secondo la legge di Snell. Egli aveva tratto la conclusione che, nel caso in cui la parallasse orizzontale del Sole fosse di 12″ o minore, poteva essere utilizzata durante l'anno un'unica tavola di rifrazioni, oppure, qualora la parallasse orizzontale del Sole fosse pari a 1′ (il valore di Kepler), sarebbe stato necessario usare diverse tavole di rifrazione a seconda delle diverse stagioni dell'anno.
Un altro punto da affrontare era la misurazione della parallasse di Marte al suo avvicinamento massimo alla Terra, nel periodo tra agosto e ottobre 1672: sarebbe allora stato possibile calcolare la parallasse solare a partire dalle distanze relative Terra-Sole e Marte-Sole. Una spedizione alla Caienna, situata a 5° nord dall'equatore, fu programmata per il 1672, per effettuare questa misurazione contemporaneamente ai tropici e a Parigi. Come Cassini previde, la spedizione poteva anche essere utilizzata per raggiungere l'obiettivo che si era posto: fare in modo che i solstizi fossero osservati ai tropici, dove entrambi, quello d'estate e quello d'inverno, avvenivano a elevazioni di 60° o superiori. Le correzioni per la rifrazione e la parallasse avrebbero dovuto essere tali da fornire la stessa obliquità per l'eclittica alla Caienna e a Parigi, e localizzare l'equatore celeste a metà strada fra i due solstizi, precisamente a 90° dal polo. Le osservazioni di Jean Richer (1630-1696) alla Caienna dimostrarono che la prima delle soluzioni alternative di Cassini era corretta: la parallasse solare orizzontale era 12″ o minore, e le rifrazioni non variavano in maniera rilevante dall'inverno all'estate.
L'avvicinamento di Marte nel periodo agosto-ottobre 1672 fu osservato da Richer alla Caienna, da Cassini a Parigi e da Flamsteed a Derby. Dalle osservazioni in Francia, Cassini dedusse una parallasse solare orizzontale di 9,5″; Flamsteed, sulla base delle proprie osservazioni, decise per 10″. Questi valori, come gli stessi Cassini e Flamsteed rilevarono più tardi, erano alquanto incerti; le osservazioni non furono mai pubblicate e la portata dei probabili errori rimase sconosciuta.
Inoltre, Richer aveva portato con sé alla Caienna un orologio a pendolo, regolato a Parigi per effettuare una mezza oscillazione al secondo; una volta giunto a destinazione, scoprì che il pendolo doveva essere accorciato di 1,25 linee (pari a 2,8 mm) per poter continuare a battere i secondi. Huygens e Cassini ritennero che il risultato di Richer fosse errato, ma una spedizione effettuata successivamente ne confermò la validità. L'idea precedentemente proposta da Huygens e Picard, secondo cui la lunghezza del pendolo che misura i secondi doveva essere considerata come campione di misura, si dimostrò così insostenibile.
Le effemeridi di Cassini per i satelliti di Giove furono in breve tempo adottate dall'Académie per determinare le differenze nella longitudine terrestre (a causa delle difficoltà nelle osservazioni, il metodo non era utilizzabile in mare). Picard si recò a Uraniborg nel 1671-1672, per determinare le coordinate dell'osservatorio di Tycho in relazione a quelle di Parigi, in modo tale che fosse possibile fare il confronto con le osservazioni ticoniche. Le osservazioni simultanee di Cassini e Picard delle eclissi dei satelliti di Giove diedero una differenza in longitudine pari a 40′ 26″, superiore ai valori attuali del 4,3%. Gli stessi mezzi furono usati da Richer e Cassini per calcolare la differenza di longitudine tra Parigi e la Caienna.
Picard tornò da Copenaghen portando con sé l'astronomo danese Ole Christensen Rømer, che rimase all'Académie come collaboratore fino al 1681. Avendo riscontrato alcune discrepanze tra le osservazioni delle eclissi dei satelliti di Giove e le previsioni di Cassini, Rømer nel 1675 scoprì che era possibile spiegarle attribuendo alla luce una velocità finita: le eclissi sarebbero avvenute prima di quanto previsto quando la Terra si stava avvicinando a Giove, e più tardi del previsto quando se ne allontanava. Cassini rifiutò questa ipotesi, aggiungendo invece una deviazione annuale al moto di ciascun satellite. In Inghilterra, Flamsteed, Halley e Newton adottarono l'ipotesi di Rømer, che sarebbe stata successivamente confermata dalla scoperta di James Bradley (1693-1762) dell'aberrazione della luce.
Il quadrante murale che Picard aveva desiderato fu finalmente installato nel 1684; per alcuni anni esso fu principalmente utilizzato da Philippe de La Hire (1640-1718), le cui osservazioni furono, in quanto a precisione, all'altezza di quelle della fine del XVIII secolo. Nella realizzazione di tavole per la Luna e i pianeti, La Hire si basò soprattutto sulle osservazioni, collegate da innumerevoli interpolazioni lineari; non accettò l'ellisse e la legge delle aree kepleriane, rifiutando anche la simmetria orbitale intorno alle linee apsidali. Le sue tavole furono ripetutamente pubblicate nel secolo successivo in tedesco e in francese. Tuttavia, la loro base osservativa era alterata dall'aberrazione della luce e dalla nutazione dell'asse terrestre (allora ancora sconosciute), come pure da correzioni errate per la rifrazione.
Cassini diede finalmente una risposta a Mercatore nel 1690, proponendo per le orbite planetarie non una ellisse, in cui la somma delle distanze di un punto dai due fuochi è costante, ma un nuovo genere di curva (più tardi denominata 'cassinoide') in cui era il prodotto di queste distanze a essere costante. Cassini sperava che una curva così definita avrebbe reso la legge delle aree valida per un fuoco e la proprietà dell'equante valida per l'altro.
Le tavole planetarie e lunari di Gian Domenico Cassini furono finalmente pubblicate nel 1740 da suo figlio Jacques, il quale probabilmente apportò alcune revisioni. Le equazioni del centro furono calcolate non a partire dal principio dell'equante, ma da un'approssimazione alla legge delle aree, formulata per la prima volta nel 1632 da Bonaventura Cavalieri, che sosteneva l'immobilità della Terra in conformità ai dettami del Sant'Uffizio. Le tavole planetarie dei Cassini possono essere utilizzate indipendentemente da qualsiasi presa di posizione sull'immobilità o mobilità della Terra. Sembra che nell'Académie di Parigi su questo argomento abbia regnato un prudente silenzio fino agli anni Trenta del XVIII secolo.
I Cassini nella loro teoria lunare mantennero l'ipociclo ticonico per l'evezione, e dovettero quindi introdurre un meccanismo epiciclico ad hoc per far concordare le distanze Terra-Luna con i diametri osservati della Luna, in modo tale da non disturbare l'evezione lunare nella longitudine. La teoria che ne risultò fu probabilmente la più complicata mai formulata sui corpi celesti tra quelle precedenti a Newton.
Flamsteed e Halley
L'inglese John Flamsteed (1646-1719), sofferente sin dalla gioventù di una malattia cronica che gli impedì di seguire un regolare corso di studi, fu autodidatta in astronomia. Verso la fine del 1669 iniziò a trasmettere alla Royal Society le sue previsioni, basate sull'Astronomia Carolina di Streete, di imminenti appulsi della Luna rispetto alle stelle fisse e di altri eventi nella volta celeste. Nel giugno del 1670 Sir Jonas Moore gli donò il micrometro di Richard Towneley. Flamsteed lo incorporò in un telescopio di sette piedi, con cui intraprese una serie di misurazioni di piccole distanze, quali i diametri dei pianeti e dei luminari, le massime digressioni dei satelliti di Giove e ‒ per determinare la parallasse di Marte ‒ le distanze del pianeta dalle stelle più vicine.
Il suo calcolo dei diametri per la Luna dimostrò che la teoria lunare di Horrocks era più precisa di quelle di Boulliau, Wing e Streete. I dati numerici da lui ottenuti, che si adattavano alla teoria di Horrocks, furono allegati all'Opera posthuma (1672) di quest'ultimo, così come la sua dissertazione sull'equazione di tempo, in cui sosteneva ‒ in contrasto con Kepler, Boulliau, Wing e Streete, e come già aveva fatto Huygens in precedenza ‒ che bisognava ritornare all'antica "irregolarità dei giorni solari".
Questi risultati fecero sì che nel 1675 Flamsteed fosse designato astronomo reale con l'incarico di dirigere un nuovo osservatorio a Greenwich, di realizzare un catalogo stellare accurato e di elaborare una teoria lunare, mediante la quale si potesse determinare la longitudine in mare. Nel luglio del 1676 prese il suo posto a Greenwich e a settembre diede inizio a regolari osservazioni con un sestante e due orologi a pendolo.
Fu lo stesso Flamsteed a incoraggiare gli studi astronomici del giovane Edmond Halley, la cui prima impresa astronomica fu una spedizione all'isola di Sant'Elena, negli anni 1676-1678, per realizzare una mappa delle stelle dell'emisfero meridionale. In questa isola il 7 novembre 1677 osservò un transito di Mercurio sul disco solare. James Gregory gli aveva suggerito di utilizzare tale transito per determinare la parallasse del pianeta e da questa dedurre quella solare.
Halley si rese presto conto che le misurazioni della parallasse di Marte si sarebbero dimostrate troppo imprecise per poter fornire un valore attendibile della parallasse solare. La parallasse di Mercurio, di dimensioni piccole quanto quelle solari, era anch'essa scarsamente adatta allo scopo. In un'appendice al suo Catalogus stellarum australium (1678), Halley propose di utilizzare il successivo transito di Venere ‒ che si sarebbe verificato nel 1761 ‒ per risolvere la questione. Egli ritornò sull'argomento nel 1691, nelle "Philosophical Transactions", fornendo gli elementi orbitali, appena aggiornati, per Venere e Mercurio e preannunciando che un altro transito di Venere si sarebbe verificato nel 1769.
Nel frattempo, Flamsteed aveva continuato a osservare diligentemente la posizione di stelle, pianeti e luminari. Nel 1681 pubblicò la Doctrine of the sphere, in cui forniva parametri solari e lunari rivisti. Per il calcolo delle equazioni del centro, fu il primo, dopo Kepler, a utilizzare la legge delle aree; ridusse la massima equazione del centro del Sole dal valore di Horrocks (1°59′) a 1°55′0″ e, dopo il 1689 ‒ quando fu finalmente installato a Greenwich l'arco murale meridiano ‒ controllò nuovamente i suoi dati sul Sole, ottenendo per il valore finale dell'equazione del centro solare 1°56′20″ (in eccesso per 35″ nel 1700), lo stesso valore che sarebbe poi stato utilizzato da Newton.
Fu Halley che nel 1684 incoraggiò Newton a intraprendere il progetto che sarebbe poi diventato i Principia; nel corso della redazione dell'opera, Flamsteed fornì importanti informazioni sulla cometa del 1680-1681, sui satelliti di Giove e sulla distanza di Saturno dal Sole. Già in questi anni Halley stava realizzando, su incarico di Flamsteed, nuove tavole dei pianeti. Dopo aver letto i Principia, Halley iniziò una ricerca sulla storia delle comete e verso la metà degli anni Novanta del Seicento concluse che le comete del 1531, del 1607 e del 1682 erano un'unica cometa (la 'cometa di Halley').
Con l'accumularsi delle sue osservazioni lunari, Flamsteed scoprì che le differenze fra la sua teoria e le osservazioni raggiungevano talvolta i 20′, dieci volte il margine di errore consentito per una teoria che potesse essere usata per determinare la longitudine a meno di 1°. Nell'estate del 1694 chiese aiuto a Newton, il quale, lavorando su una notevole quantità di osservazioni fornite da Flamsteed, dedusse nuovi parametri per la teoria lunare e aggiunse un certo numero di nuovi termini di perturbazione. Il risultato, la Theory of the moon's motion (1702) di Newton, rappresentava ‒ come è stato dimostrato di recente e contrariamente a numerosi giudizi precedenti ‒ un notevole progresso rispetto alle teorie lunari più antiche, malgrado il margine di errore fosse ancora superiore a 2′.
Nel 1689 Flamsteed annunciò di aver scoperto la parallasse annuale nella Stella Polare; in realtà, come il giovane Jacques Cassini presto dimostrò, i moti annuali della Stella Polare, individuati da Flamsteed, erano incompatibili con le caratteristiche richieste per la parallasse.
Nel 1693 Halley scoprì, dallo studio di antiche eclissi, che la Luna era soggetta a un'accelerazione secolare. Sembrerebbe che prima del 1717 egli avesse affermato che Giove fosse soggetto a un'analoga accelerazione secolare e Saturno a una decelerazione. Questi due problemi furono risolti nel 1785 da Pierre-Simon de Laplace (1749-1827), che peraltro nel 1787 sostenne di poter spiegare l'accelerazione secolare della Luna. Tuttavia la sua argomentazione, accettata per settant'anni, sarebbe, in seguito, risultata incompleta.
Bibliografia
Kollerstrom 2000: Kollerstrom, Nicholas, Newton's forgotten lunar theory. His contribution to the quest for longitude, Santa Fe (N.M.), Green Lion, 2000.
Stephenson 1987: Stephenson, Bruce, Kepler's physical astronomy, New York, Springer, 1987.
Taton 1989: Planetary astronomy from the Renaissance to the rise of astrophysics, edited by René Taton and Curtis Wilson, Cambridge-New York, Cambridge University Press, 1989-1995, 2 v.; v. I: Tycho Brahe to Newton, 1989.
Van Helden 1985: Van Helden, Albert, Measuring the universe. Cosmic dimensions from Aristarchus to Halley, Chicago-London, University of Chicago Press, 1985.
Voelkel 2001: Voelkel, James R., The composition of Kepler's Astronomia Nova, Princeton (N.J.), Princeton University Press, 2001.
Wilson 1989: Wilson, Curtis, Astronomy from Kepler to Newton. Historical studies, London, Variorum, 1989.