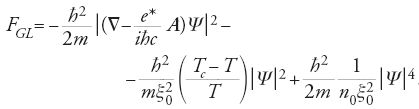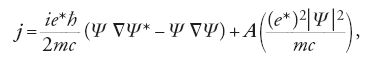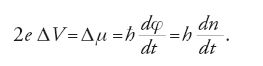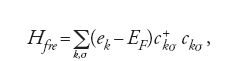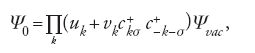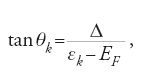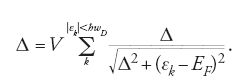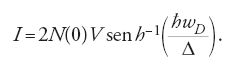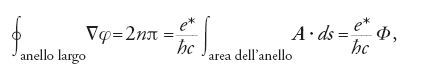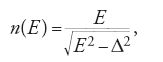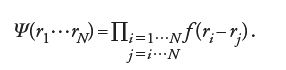La grande scienza. Superconduttività e superfluidità

La grande scienza. Superconduttivita e superfluidita

Superconduttività e superfluidità

La superconduttività è stata scoperta da Heike Kamerlingh Onnes nel 1911, mentre la prima indicazione della superfluidità, vale a dire la cosiddetta transizione di fase lambda, è stata osservata da Wilhelmus Hendrikus Keesom nel 1927. Nello stesso periodo, la teoria quantistica, che peraltro andava conseguendo grandi successi nello spiegare le proprietà della materia a livello atomico, sembrava inadeguata a fornire, sia pure a livello qualitativo, un'interpretazione teorica dei due fenomeni che si presentano nella materia a livello macroscopico.

La comprensione dello stato superconduttore e dello stato superfluido della materia come stati quantistici macroscopicamente coerenti, appartiene interamente alla seconda metà del secolo scorso.

Forse una buona dimostrazione dell'importanza relativa di questa attività è rappresentata dal fatto che nella seconda metà del Novecento siano stati assegnati 16 premi Nobel per lavori correlati a tali fenomeni. Per quanto riguarda la superconduttività vanno ricordati i premi assegnati a John Bardeen, Leon Neil Cooper e John Robert Schrieffer nel 1972, a Ivar Giaever e Brian David Josephson nel 1973, e infine a Georg J. Bednorz e Karl Alexander Muller nel 1987. Nel 1996 furono insigniti del premio D.D. Osheroff, R.C. Richardson e D.M. Lee per le loro ricerche sulla superfluidità dell'He-3, mentre il premio del 1962 a Lev Davidovič Landau e quello a Pëtr Leonidovič Kapitsa del 1978 hanno riguardato lavori sulla superfluidità dell'He-4. Il Nobel conferito ad Aage Niels Bohr e Benjamin Roy Mottelson nel 1975 premiava, almeno in parte, la spiegazione dell'accoppiamento tra nucleoni, simile a quello dei superconduttori, che si verifica nella materia nucleare, mentre quello del 1979 fu assegnato ad Abdus Salam e Steven Weinberg per il loro contributo all'elaborazione della teoria elettrodebole che sfrutta una proprietà del vuoto simile alla superfluidità (si noti inoltre che il premio del 2001 a Eric A. Cornell, Wolfgang Ketterle e Carl Weiman è stato assegnato per lavori sui gas atomici superfluidi).

Ciò che la scienza ereditava nel 1950 dalla metà del secolo precedente era essenzialmente una buona base euristica su questi due fenomeni. Per quanto riguarda la superconduttività, l'esperimento di Walter Meissner (Meissner e Ochsenfeld 1933) fu brillantemente estrapolato da Cornelis J. Gorter e Hendrik Brugt Gerhard Casimir (1934) in modo da fornire una descrizione di tale stato come uno stato d'equilibrio termodinamico di un materiale diamagnetico perfetto, mentre i fratelli London ponevano le basi per lo studio del comportamento dinamico postulando la famosa equazione:

[1] j=4πA/λ²,

fra la densità di supercorrente j e il vettore potenziale A del campo magnetico.

La [1] può essere combinata con le equazioni di Maxwell per evidenziare che λ rappresenta la profondità di penetrazione di un campo magnetico entro un superconduttore. Il valore di questa lunghezza è molto vicino, e ciò può generare qualche confusione, a quello che si potrebbe dedurre se tutti gli elettroni fossero liberi di accelerare in un campo elettrico senza subire alcun urto, vale a dire 1/λ²=ne²/mc² in cui n è il numero di elettroni per unità di volume, e la carica e m la massa dell'elettrone, c la velocità della luce nel vuoto. Questa espressione non contiene né la costante di Planck né alcuna grandezza di scala sufficientemente piccola da poter essere confrontata con la temperatura di transizione, che è molto esigua se paragonata con l'energia di Fermi, E_f, espressa, in termini della temperatura termodinamica, dalla relazione E_f=k_BT_f in cui k_B, è la costante di Boltzmann.

Il livello raggiunto dalle ricerche negli anni Cinquanta è stato ben riassunto in due libri che apparvero attorno al 1950: Superfluids, di Fritz Wolfgang London (1950-1954), che trattava gli aspetti teorici e conteneva molte intuizioni dei futuri sviluppi e Superconductivity, di David Shoenberg (1952), relativo alla parte sperimentale.

Jack Allen e, contemporaneamente, Kapitsa al Mond Laboratory di Cambridge scoprirono che lo stato anomalo dell'He-4 al disotto del punto lambda, 2,18 K, ha quelle strane proprietà per descrivere le quali Kapitsa coniò il termine superfluidità. Egli rientrò a Mosca nel 1938 dove elaborò una serie di esperimenti ingegnosi per dimostrare queste proprietà. Il liquido sembrava essere costituito da due fluidi interpenetranti, di cui uno mostrava un comportamento normale, mentre l'altro era privo di entropia e in grado di fluire senza alcuna dissipazione, concetti, questi, associati con i nomi di London, László Tisza e Landau. Il suggerimento di London del 1936, secondo cui il punto lambda sarebbe una manifestazione della condensazione di Bose-Einstein, concetto questo che era la base delle idee di Tisza e che era assolutamente corretto, fu attaccato da Landau; ciononostante la teoria euristica di Landau del fluido normale, che si rivelò corretta, era completamente coerente con le ipotesi di London. Entrambe le teorie erano modelli 'a due fluidi', che consideravano due fluidi interpenetranti, uno dei quali privo di entropia, mentre l'altro, il fluido normale, composto in gran parte da eccitazioni, che Landau chiamò 'rotoni' e che avevano uno spettro con un minimo in corrispondenza di un certo valore del momento della quantità di moto e con un'energia di circa 8 K superiore al potenziale chimico. Fenomeni spettacolari come il secondo suono, che comportano oscillazioni relative dei due fluidi, oppure il superflusso del film o anche l'effetto fontana, erano tutti spiegati da questa teoria. Si può citare nuovamente il libro di London, il cui primo volume, del 1950, è una meravigliosa sintesi di questo periodo, mentre la storia delle aspre controversie tra questi tre scienziati teorici è riportata nella biografia di Kostas Gavroglu redatta da London (1995).

Alcune osservazioni sulla fisica sperimentale delle basse temperature

Gli anni del secondo dopoguerra videro uno sviluppo considerevole di tutta una serie di ricerche riguardanti la fisica delle basse temperature. Il fatto che questo sviluppo possa essere riassunto attraverso le teorie che produsse non deve oscurare il fatto che "la fisica è una scienza sperimentale", come John Hopfield faceva notare ai suoi colleghi a Princeton. In realtà il rifiorire dopo la guerra della fisica della materia condensata derivava dall'applicazione simultanea di nuove tecniche sperimentali, molte delle quali erano il risultato degli sviluppi ingegneristici dell'industria bellica e di fondi resi disponibili grazie al fatto che la guerra aveva evidenziato il valore militare ed economico della ricerca. Era evidentemente collegato a obiettivi militari il reattore nucleare, grazie al quale fu possibile eseguire misure di diffrazione e di diffusione dei neutroni, che giocarono un importante ruolo negli argomenti qui trattati; ma il reattore nucleare fornì anche isotopi di metalli quali Hg e Pb, che furono cruciali nei primi anni dello studio della superconduttività. Un protagonista importante fu la spettroscopia coerente alle frequenze radio e alle microonde, derivante dallo sviluppo dei radar, e che più tardi giocò un ruolo importante nello sviluppo dei computer elettronici. Forse però lo strumento più importante nella fisica delle basse temperature fu l'apparecchio per la liquefazione dell'elio realizzato da Arthur D. Little, un riadattamento del progetto originale di Kapitsa, che rese disponibili le temperature dell'elio liquido al 'fisico medio' dell'industria e dell'università e che solo la nuova atmosfera favorevole ai finanziamenti rese economicamente possibile. Fino a che punto lo sviluppo di questa macchina sia stato legato al lavoro sulla bomba H e sui missili alimentati a idrogeno liquido non è stato ancora chiarito. Successivamente, queste tecnologie evolsero verso metodi più sofisticati e oggi il laser rende possibile la condensazione di Bose-Einstein di gas atomici, che è una manifestazione completamente nuova di coerenza macroscopica, mentre le sorgenti di luce di sincrotrone sono sensori di cruciale importanza per i moderni superconduttori.

In questa nuova atmosfera la maggior parte degli esperimenti determinanti fu condotta all'interno di laboratori industriali, e più tardi governativi, laddove l'idea stessa di criogenia sarebbe stata precedentemente inconcepibile; così il gap energetico fu dimostrato da M.P. Garfunkel alla Westinghouse, il magnete ad alta intensità di campo fu sviluppato da J.E. Kunzler, l'effetto Josephson fu dimostrato da J.M. Rowell alla Bell e il tunneling superconduttivo fu ottenuto alla General Electrics da Giaever.

Prima della Seconda guerra mondiale la fisica delle basse temperature era dominata da non più di una mezza dozzina di centri accademici e da un piccolissimo nucleo di ricercatori, la maggior parte dei quali avevano avuto contatti con l'Università di Leida. Questi centri erano Oxford, Cambridge, Berkeley e pochi altri; sorprendentemente la Rutgers University era tra questi. Dopo la guerra e nella seconda metà del Novecento questo ramo della fisica si trasformò, uscendo da quella minuscola aristocrazia della fisica fino al punto in cui i congressi, denominati ILT, divennero i congressi internazionali più frequentati dai fisici.

Superconduttività classica

All'inizio degli anni Cinquanta sia la superfluidità sia la superconduttività, che a lungo erano state circondate dal mistero, cominciarono a rivelare i loro segreti. Nel caso della superconduttività, due sviluppi cruciali si realizzarono quasi simultaneamente nel 1950: la scoperta sperimentale dell'effetto isotopico e una descrizione fenomenologica corretta e completa da parte di Vitalij Lazarevič Ginzburg e Landau.

B. Serin e altri ricercatori della Rutgers University osservarono per primi che la variazione della massa isotopica m di Hg influenza la temperatura di transizione della superconduttività, quasi proporzionalmente al fattore m^−1/2 relativo all'energia di punto zero delle vibrazioni del reticolo: ciò rappresenta un suggerimento importante sui possibili meccanismi microscopici. Questo fenomeno, però, fu erroneamente interpretato da Bardeen e, in una teoria essenzialmente equivalente (elaborata prima che venisse reso noto il risultato sperimentale) da Herbert Frohlich. Entrambe le teorie si basavano sulle instabilità della superficie di Fermi dovute a un accoppiamento elettrone-fonone che, come ora sappiamo, provocano onde associate alla variazione di densità di carica, e in realtà competono con la superconduttività, anziché causarla. Già nel 1953, al Congresso di Kyoto, i due scienziati avevano abbandonato tali ipotesi.

La teoria di Ginzburg-Landau era un tentativo, da un lato, di fornire un più robusto significato microscopico all'equazione [1] di London e, dall'altro, di comprendere la natura dei confini normale-superconduttore che appaiono nello 'stato misto' di molti superconduttori quando si trovano in un campo magnetico. Essa impiegava il concetto di Landau di 'parametro d'ordine', che è una variabile locale macroscopica che descrive il grado d'ordine di una fase condensata. La brillante intuizione di Ginzburg e Landau era rappresentata dall'idea che questo parametro d'ordine Ψ per la superconduttività fosse un numero complesso e obbedisse a una equazione d'onda molto simile a quella di Schröndinger, nonostante il fatto che esso fosse una variabile macroscopica. Questa equazione può essere ottenuta minimizzando la seguente espressione dell'energia libera, F_GL:

Eseguendo la derivata di [2] rispetto ad A, possiamo dedurre un'equazione per la corrente:

che concorda con l'equazione [1] di London nel limite macroscopico, in cui i gradienti di Ψ possono essere trascurati se assumiamo che ∣Ψ∣² per T=0 sia la n di London, cioè la densità elettronica totale. Ciò è garantito dalla scelta dei parametri nell'equazione [2], che a loro volta risultano contenere due lunghezze fondamentali, la seconda delle quali è una 'lunghezza di coerenza', ξ, che determina il costo energetico per creare i gradienti del parametro d'ordine. L'aspetto interessante di ξ è che l'energia cinetica che essa rappresenta è un'energia piccola, dell'ordine della temperatura critica T_c, e non dell'energia di Fermi.

Questa teoria euristica e la funzione del nuovo parametro ξ ottennero un crescente sostegno sperimentale negli anni che seguirono, ma la loro piena comprensione fu molto ritardata da problemi di comunicazione, alcuni dei quali favoriti dal clima della guerra fredda, altri probabilmente connessi con l'atteggiamento impositivo di Landau. Poco dopo la formulazione della teoria Ginzburg-Landau, un giovane collaboratore di questi, Aleksej Alekseevič Abrikosov, nel 1957 risolse le equazioni [3] nel caso, allora considerato inusuale, in cui ξ fosse più piccolo della lunghezza λ che compare nella [1]. Questo caso rende negativa l'energia di un'eventuale parete normale-superconduttore, e pertanto, in presenza di un forte campo magnetico, diventa stabile uno stato microscopicamente disomogeneo. Egli risolse le equazioni e dapprima nel caso di un campo relativamente debole, sulle cui linee di forza Ψ=0, ciascuna associata con un flusso magnetico ħc/e* (sebbene, stranamente, questa quantità non venisse dichiarata esplicitamente). Queste linee di forza formano quindi un reticolo regolare. In corrispondenza di campi elevati, lo stato assomiglia a bolle isolate di superconduttore che si sovrappongono, ma nuovamente esiste un 'flusso quantico' per valori nulli del parametro d'ordine Ψ. È molto strano che in nessun punto dell'articolo siano menzionate le idee di Lars Onsager (1949) e London (1950) sulla quantizzazione della vorticità.

Abrikosov chiamò lo stato con un campo magnetico penetrante 'superconduttività di tipo II', e la sua teoria spiegava bene misure precedenti di L.V. Schubnikov sulle leghe metalliche pubblicate nel 1937. Landau, tuttavia, pensò che la teoria fosse troppo azzardata e ritardò la sua pubblicazione fino al 1956, anno in cui lesse il lavoro di Richard Phillips Feynman sui vortici quantizzati in He-4, concludendo che Abrikosov aveva scoperto l'equivalente superconduttivo.

La storia successiva della superconduttività di tipo II procede quasi indipendentemente dalla teoria microscopica. Ai Bell Telephone Laboratories, un gruppo spinto da motivazioni empiriche composto da B.T. Matthias, Kunzler e T.H. Geballe sfidò i pregiudizi dei teorici occidentali dimostrando, nel 1959, che una lega di niobio rimane superconduttiva mentre permette a un campo con un'intensità fino a 8 Tesla di penetrarla. Solo più tardi essi si resero conto che la maggior parte di queste leghe è materiale di tipo II. Il loro lavoro generò il magnete superconduttore che incontrò un enorme successo economico e medico. Poco dopo (1962), Y.B. Kim e altri, che lavoravano a loro volta ai Bell Telephone Laboratories, dimostrarono che la fisica di queste leghe, da cui dipendono i magneti superconduttivi in campi ad alta intensità, è una 'superconduttività dura', che vincola le linee di flusso quantizzato dello stato di Abrikosov mediante imperfezioni del reticolo.

L'equazione cruciale è quella di Gor´kov-Josephson

L'attenzione su questa equazione, in cui n è il numero di vortici all'istante t, fu richiamata da Lev P. Gor´kov per primo, nella sua derivazione della teoria di Ginzburg-Landau, come un'ovvia conseguenza dell'invarianza di gauge. Se Ψ rappresenta un campo di coppie di elettroni, come ora sappiamo, la sua fase φ deve coniugarsi a un numero pari e pertanto deve ruotare a una velocità che è μ/ħ volte il potenziale elettrostatico V. La differenza di potenziale ΔV tra due punti deve essere quindi esattamente uguale, in media, alla velocità alla quale i vortici attraversano la linea di flusso che li congiunge.

Il moto dei vortici è il meccanismo dissipativo fondamentale della superconduttività. Le prime leghe mantenevano notevoli supercorrenti in presenza di campi magnetici solo perché erano relativamente impure. Quando furono provate leghe più pure, fu possibile osservare un 'fluire del flusso' - linee di flusso relativamente mobili una volta che la corrente sia in grado di superare le forze che le vincolano - piuttosto che il 'moto lento del flusso' delle prime osservazioni.

Il funzionamento di un magnete superconduttore viene interrotto dai cosiddetti 'salti di flusso', provocati da diversi modi di rottura del reticolo vincolato dei vortici. Questi vengono minimizzati nei magneti moderni grazie a un'idea di Geballe che consiste nell'incorporare un normale filamento di rame nelle espansioni polari del magnete, consentendo di dissipare l'energia di un salto locale di flusso senza che possa disperdersi verso altri filamenti superconduttivi.

Nello stesso decennio venne portata a termine la teoria microscopica, grazie all'ostinata perseveranza di Bardeen. Assieme a David Pines, egli mostrò nel 1954 che l'interazione elettrone-fonone genera un'interazione attrattiva elettrone-elettrone del secondo ordine; egli si convinse che gli esperimenti con le microonde indicano l'esistenza di un gap energetico nello spettro in corrispondenza della superficie di Fermi. Cooper, un teorico delle particelle, che lavorava sotto la guida di Bardeen con una borsa di post-dottorato, mise in rilievo che una coppia di elettroni al di sopra del mare di Fermi, dotata di un'interazione di questo tipo, si trova in uno stato vincolato se il momento risultante delle loro quantità di moto è nullo; pertanto il semplice mare di Fermi delle particelle libere è instabile rispetto alla formazione di tali coppie vincolate. La sua lettera apparve nel 1956 e, sebbene Bardeen fosse preso da altre occupazioni per aver ricevuto proprio quell'anno il premio Nobel per l'invenzione del transistor, con il suo allievo Schrieffer elaborò una teoria dello stato fondamentale impiegando una statistica appropriata per un sistema di 'coppie di Cooper' con momento della quantità di moto nullo. I tre scienziati pubblicarono tale risultato sotto forma di lettera durante il mese di marzo (Bardeen et al. 1957a) e come articolo completo nel dicembre del 1957 (Bardeen et al. 1957b).

In retrospettiva, il brillante successo di questa teoria consisteva nel fatto di evitare completamente il problema di dover condensare le coppie di elettroni in uno stato superfluido, mentre si focalizzava sulla formazione di coppie dagli stati elettronici liberi, ipotizzando che una volta formate esse fossero automaticamente parte del condensato. Ciò veniva ottenuto imponendo arbitrariamente il 'criterio di Schrieffer', in base al quale le uniche interazioni mantenute sono quelle che legano coppie di elettroni con momento e spin totali esattamente pari a zero; vale a dire

La somma nella [5] si limitava alle energie

relative a un insieme di stati all'interno dell'energia fononica ħw_D della superficie di Fermi. In sostanza si trattava di un modello approssimato dell'effetto fononico.

Successivamente, si dimostrò che quest'ipotesi era assolutamente corretta per i superconduttori metallici convenzionali noti fino ad allora. Ginzburg, per esempio, dimostrò che l'intervallo di temperature per le fluttuazioni termiche del momento della quantità di moto è del tutto trascurabile. A quei tempi questa era solo un'ipotesi, in qualche modo sostenuta dalla teoria di Landau dei 'liquidi di Fermi', che apparve grosso modo in quel periodo, secondo la quale gli stati a bassa energia possono essere descritti esattamente da 'quasi particelle' libere.

Data l'interazione [5], assieme all'hamiltoniana per gli elettroni liberi

si desume che la soluzione di campo medio è sostanzialmente esatta.

Lo stato fondamentale veniva espresso come prodotto di funzioni d'onda

con

[9] u_k=cosθ_k/2, v_k=senθ_k/2

e

dove Δ è un parametro che esprime il gap energetico, determinato a T=0 dalla 'equazione di gap' (assumendo V costante)

L'integrazione di questa equazione dà

Le eccitazioni possono essere derivate in maniera molto semplice. Un modo facile è notare che

[13] α_k=v_kc⁺_kσ+u_kc_-k-σ

annichila Ψ₀, vale a dire α_kΨ₀=0. Allora, α⁺_k=v_kc_kσ+u_kc⁺_-k-σ crea una 'quasi particella' costituita da una miscela coerente di un elettrone e un buco. La sua energia è

La teoria fu rapidamente riformulata in modo più conveniente da Nikolai N. Bogoljubov (Bogoljubov et al. 1959) e da Valatin, che introdusse l'operatore di quasi-particella α_k, e in un'altra forma da Yoichiro Nambu (1960). Ma di fatto, sebbene il formalismo di BCS (Bardeen, Cooper, Schrieffer) fosse un po' involuto, essi portarono a termine tutti i calcoli necessari per il confronto con gli esperimenti.

Fin dall'inizio questa teoria mostrava un accordo eccellente con quasi tutti i dettagli sperimentali ed era quindi una follia mettere in dubbio la sua validità di fondo. I 'fattori di coerenza' inseriti negli elementi della matrice per varie risposte fisiche, come il rilassamento nucleare magnetico, l'attenuazione acustica e successivamente molti altri effetti, entro pochi mesi dalla prima pubblicazione risultarono in ottimo accordo con la realtà sperimentale, così come la predizione della dimensione del gap di energia relativo alla temperatura critica T_c. La teoria conteneva due lunghezze - sebbene Bardeen pare non avesse immediatamente accettato la relazione con la teoria di Ginsburg-Landau - quella di 'coerenza' hv_f/Δ che entra in molte risposte, e una profondità di penetrazione, che entra nell'equazione [1] di London, la quale veniva facilmente derivata dalla stessa teoria.

Come si è detto, in retrospettiva, era irragionevole opporsi a questa teoria; ma questo atteggiamento accomunò molti eminenti scienziati: Eugene Wigner e John Slater, per esempio, non l'accettarono mai, mentre Felix Bloch vi si oppose pubblicamente nel discorso per la presidenza dell'APS (1966); ma l'opposizione più ragionata - che veniva da G. Wentzel, W. Kohn e altri - era incentrata sulla questione dell'invarianza di gauge. Il problema è ovvio: la teoria, così come fu elaborata, fornisce l'equazione di London nella forma [1] che è nongauge-invariante, con la densità di supercorrente proporzionale ad A, il vettore potenziale. Tuttavia solo il rotore di [1] può essere realmente corretto, come proposto originariamente dai fratelli London. Per semplificare i calcoli BCS mantennero solo i termini di interazione con il momento risultante della quantità di moto di una coppia di elettroni nullo (il 'criterio di Schrieffer'), violando così non solo l'invarianza di gauge ma anche quella galileiana. Chiaramente il problema deve essere risolto introducendo le altre interazioni in maniera corretta, ed è ciò che proposi in due articoli del 1958 (i contributi di Bogoljubov e D.V. Shirkov e quello di Nambu erano indipendenti ma apparvero successivamente e non erano del tutto corretti, in particolare perché non mettevano in evidenza l'equivalente superconduttivo del 'fenomeno di Anderson-Higgs'; presi letteralmente, essi predicevano un modo di Goldstone che sembrava un fonone di He-4 e ciò avrebbe avuto conseguenze negative piuttosto rilevanti). Questi sviluppi sembrano un po' fuori tema in una storia della superconduttività, ma vale la pena menzionare che, da questi articoli e dai lavori di Nambu (Nambu e Jona-Lasinio 1961) e di Jeffrey Goldstone (1961), le idee sulle simmetrie infrante e sui 'bosoni di Goldstone' e sul 'fenomeno di Anderson-Higgs' (Anderson 1963; Higgs 1964), entrarono nel mondo della teoria delle particelle elementari, dove giocano un ruolo importante nel modello standard. Il bosone di Higgs è fondamentalmente un condensato superconduttivo del vuoto.

Il ruolo del cambio di simmetria nelle transizioni di fase fu sottolineato per la prima volta nella teoria formulata da Landau negli anni Trenta, ma assunse un'importanza particolare quando la simmetria che cambia è meno ovvia rispetto al semplice caso del ferromagnetismo, come nel fenomeno della coerenza quantica macroscopica dei campi di particelle che si verifica nei superfluidi. La conservazione delle particelle rappresenta e impone una simmetria di gauge della relativa hamiltoniana, che la funzione d'onda [8] viola - localmente, se non globalmente - in ragione del fatto che è una miscela coerente di stati con diversi numeri di coppie. L'aver spiegato e sostenuto tali idee fu il contributo principale di questi articoli e, in parte, della scoperta successiva dell'effetto Josephson.

Questi sforzi divennero sostanzialmente irrilevanti nei confronti della superconduttività - sebbene fossero abbastanza importanti nel contesto generale della teoria quantistica dei campi - quando, l'anno dopo, il collega di Landau, Gor´kov, mostrò che la teoria di Ginzburg-Landau, che era stata esplicitamente scritta in una forma gauge-invariante, poteva essere derivata dalle idee di BCS (Gor´kov 1959). Egli interpretò il parametro d'ordine Ψ di Ginzburg-Landau come l'ampiezza media del campo di coppie di elettroni di BCS, che può variare lentamente da punto a punto. Di conseguenza il parametro di carica e* nella [2] diventa 2e, in accordo con le misure della quantizzazione del campo magnetico in unità di _hc/2e, riportate nel 1961 (Deaver e Fairbank 1961; Doll e Nabauer 1961). Il criterio, affinché il parametro d'ordine abbia un unico valore, stabilisce che la sua fase deve variare in unità di 2π quando passa attorno a un anello superconduttivo o a un vortice di Abrikosov, il che implica una quantizzazione del flusso in questa unità. Poiché la densità di supercorrente j è proporzionale a ∇φ−(e*/ħc) e l'energia a ∣j∣², l'unico modo affinché il limite macroscopico rimanga finito è che questi due termini si cancellino in media. Quindi:

dove Φ è il flusso magnetico attraverso l'anello superconduttivo.

La dimostrazione sperimentale del tunneling quantico attraverso uno strato isolante tra campioni metallici, portata a termine da Giaever nel 1960, contribuì in modo notevole al rapido progresso della nostra comprensione della superconduttività mediante la teoria BCS. Il tunneling tra due metalli normali fornisce una corrente priva di caratteristiche, e quindi una conduttanza di tunneling costante o che varia lentamente, e che sostanzialmente riflette la densità costante degli stati a singolo elettrone in un metallo. Quando un metallo è superconduttore, si apre un gap nella densità degli stati in corrispondenza della sua superficie di Fermi e la conduttanza di tunnel per voltaggi bassi tende a zero. Infatti in prima approssimazione la conduttanza di tunnel di una giunzione tra un metallo normale e uno superconduttore riproduce la predizione della BCS per la densità degli stati

dove il parametro che descrive il gap energetico è Δ e l'energia dell'elettrone è E=eV. Nel caso di una giunzione superconduttiva, la conduttanza è ancor più singolare. Tutti questi effetti potrebbero essere ottenuti in modo pulito col metodo dell''hamiltoniana di tunneling' di M.H. Cohen, L.M. Falicov e J.C. Phillips (1962). Tuttavia, se si esamina la conduttanza in maggior dettaglio si possono notare due caratteristiche aggiuntive. La prima è rappresentata dall'effetto Josephson, predetto nel 1962 quando Josephson era allievo di Pippard a Cambridge (Josephson 1962). Egli dimostrò che per V=0 è possibile che si generi un flusso di una supercorrente di tunneling, l'ampiezza della quale dipende dalla fase relativa ϕ dei due parametri d'ordine, ed è straordinariamente sensibile ai campi elettromagnetici. Ciò fu presto verificato sperimentalmente da Rowell e collaboratori, e più tardi è stato ampiamente sfruttato per la misura di e/ħ tramite l'equazione [4] (utilizzata per la prima volta dal gruppo all'Università della Pennsylvania), nonché in strumentazioni sensibili in forma di SQUID (superconductive quantum interference device), il cui impiego fu dimostrato da Zimmerman e sviluppato da J. Clarke. Il voltaggio standard di Josephson è un elemento chiave del moderno sistema di misura, nel quale unità arbitrarie sono sostituite da unità standard basate su quantità fondamentali tipo e, h, c, m_e, eccetera. Tuttavia l'effetto Josephson ha avuto probabilmente il suo impatto più rilevante come base di una serie di esperimenti di interferenza che non lasciarono più alcun dubbio sul fatto che la superconduttività sia una manifestazione della coerenza quantica macroscopica delle onde di materia, così come la luce laser mostra la coerenza delle onde luminose.

La seconda caratteristica delle osservazioni di tunneling, notata per la prima volta da Giaever ma studiata in dettaglio da Rowell e collaboratori, fu chiamata con il nome poco attraente di 'protuberanze fononiche'. C'è una struttura significativa nella conduttanza del tunnel alle energie dell'ordine delle frequenze di vibrazione tipiche del reticolo. Ciò è degno d'attenzione, perché la teoria presuppone e gli esperimenti confermano che nel normale tunneling metallico sono trascurabili gli effetti causati dai fononi o da qualunque altra interazione. In parallelo con gli sviluppi sperimentali, un progresso notevole si realizzò nel calcolo di soluzioni realistiche (opposte a quelle euristiche, qualitative) dell''equazione di gap' di BCS per le eccitazioni elettroniche, generalizzata per includere interazioni fononiche realistiche e, in particolare, per tener conto del ritardo di eccitazione. Ciò fu realizzato da Schrieffer assieme ad alcuni suoi allievi e da P. Morel e me, utilizzando sofisticati formalismi sviluppati da Nambu e G.M. Eliashberg. Schrieffer e io capimmo che queste soluzioni contengono le 'protuberanze fononiche' che erano state osservate e, ancor più importante, che esse dipendono fortemente dalle frequenze e dalle costanti di accoppiamento dei fononi rilevanti. Prendendo un modello approssimato dello spettro conosciuto dei fononi nel piombo, ottenemmo risultati in totale accordo con le misure di Rowell. W.L. McMillan, ai Bell Telephone Laboratories, sviluppò ulteriormente la ricerca calcolando lo 'spettro' della costante d'accoppiamento a partire dai dati di tunneling e mostrando che dallo stesso può essere dedotta la resistività fononica e la temperatura di transizione, oltre che lo spettro fononico misurato di diversi elementi e leghe superconduttive. Egli seguì questo lavoro con un'analisi meno precisa, ma molto utile, del verificarsi generale della superconduttività, sviluppando una formula per la temperatura critica T_c che funzionava per la maggior parte dei metalli allora noti. Essa era basata sulla teoria fondamentale, ma conteneva parametri semiempirici con intervalli di variabilità molto ristretti.

Un punto importante, a mio parere, fu un'osservazione di Schrieffer riguardo al fatto che un teorema di Migdal può essere applicato alla porzione fononica di queste equazioni, dimostrando che le correzioni, dovute alle interazioni fra più corpi, che si dovrebbero apportare a questi calcoli dovrebbero essere solo di ordine m/M, ovvero del rapporto tra la massa dell'elettrone e quella dello ione.

A quell'epoca la gran parte dell'opposizione residua alla teoria BCS - come quelle di Bloch e di Matthias - era incentrata sull'obiezione che essa rappresentava solo un modello utile, ma non una teoria fondata su principî primi. Il lavoro di McMillan parve la risposta finale a tale affermazione e per questo motivo il 1965 può essere definito- usando un'espressione sportiva americana - il momento in cui 'the fat lady sang', vale a dire il punto in cui il gioco dei superconduttori metallici ordinari giungeva a conclusione.

Nei decenni successivi sono stati scoperti pochissimi superconduttori di origine fononica con valori di T_c abbastanza alti (fino a 40 K), del genere dei recenti MgB₂, e del K₃C₆₀ degli inizi degli anni Novanta. È significativo che i parametri della formula di McMillan abbiano bisogno soltanto di correzioni marginali per poter descrivere queste apparenti anomalie - il fattore cruciale è rappresentato dalle masse relativamente piccole degli elementi B e C, piuttosto che da anomalie derivanti dalle costanti di accoppiamento o da altri artifici. Alcune di esse pongono questioni che continuano ad avvincere i teorici delle interazioni fra molti corpi, non tanto per quanto riguarda il meccanismo della superconduttività (la maggior parte dei supercondutori, per esempio, ha una forte struttura fononica nella sua conduttività di tunneling) ma piuttosto per quanto concerne i fenomeni collaterali. I composti di struttura A15 quali il V₃Si e Nb₃Ge, così come gli intercalati di dicalcogenuri (NbSe₂, ecc.) mostrano un'avvincente competizione tra le onde di densità di carica e le fasi superconduttive.

I 'composti a cluster', come le strutture chevrel (XMo₆S₈, con X=Pb, Ba, Ho, e altri), e gli (alcali)₃(C)₆₀ si dimostrano estremamente insensibili rispetto alla natura e all'ordinamento dei cationi, anche quando questi sono estremamente magnetici: gli elettroni metallici paiono completamente confinati nei cluster. Un altro composto curioso, che vive sul margine dell'instabilità del reticolo è (Ba−K)BiO₃, con una T_c di 30÷40 K.

Un'importante caratteristica dei semplici conduttori BCS è la loro scarsa sensibilità alle impurezze e allo scattering dovuto al disordine (che, come ho dimostrato, è provocato dal fatto che i due elettroni di una coppia sono correlati da una simmetria a inversione temporale, una correlazione che non è influenzata da questo tipo di scattering, ma che dipende in maniera notevole dallo scattering magnetico). È proprio la scarsa sensibilità a quest'ultimo a rappresentare una caratteristica peculiare dei composti a cluster.

La superfluidità nell'elio-4

La storia della superfluidità si è sviluppata in modo molto diverso. Non vi è stata alcuna intuizione folgorante come la teoria BCS, che cambiò completamente la direzione delle ricerche. La ragione consiste forse nel fatto che l'idea della condensazione di Bose-Einstein, che rappresenta la reale natura del fenomeno, apparve troppo presto, come una congettura teorica piuttosto che in risposta a una esigenza sperimentale, rendendo necessario adattare in qualche modo la confusa situazione sperimentale a quest'idea fin troppo semplice.

Due lavori molto importanti per la comprensione della superfluidità apparvero attorno al 1950. Il primo era di Bogoljubov (1947) e trattava il problema in un gas di Bose, piuttosto rarefatto e scarsamente interagente, di particelle neutre a bassa temperatura. Lo scienziato fu in grado di dimostrare, utilizzando metodi correlati con l'approssimazione di fase casuale sviluppata da David Bohm e da Pines nello stesso periodo, che un gas di questo tipo ha eccitazioni di onde di densità quantizzata che corrispondono ai fononi quantici di Landau. La condensazione di Bose fa sì che queste onde siano mescolate con eccitazioni di singole particelle, che consentono un unico modo alle basse energie, con una legge di dispersione lineare (per es., un 'modo di Goldstone'). In questa teoria perturbativa, però, non c'è segno dei rotoni di Landau costituenti il 'fluido normale'.

Il secondo lavoro era un contributo di Oliver Penrose (1951) al quale si unì Onsager in una coppia di articoli scritti da entrambi negli anni successivi (Onsager 1954; Penrose e Onsager 1956). Penrose introdusse il concetto di ODLRO (off-diagonal long-range order) del condensato di Bose-Einstein. Egli mostrò che, mentre la densità della singola particella o la funzione di correlazione fra due particelle di un gas di Bose di questo tipo non ha alcun carattere a raggio lungo, la matrice di densità

[17] ϱ(r,r′)

possiede una struttura inusuale: essa ha un unico grande autovalore, ovvero ha un termine che si può fattorizzare nel prodotto di due funzioni degli argomenti r e r′ aventi un raggio d'azione infinito; tale autovalore costituisce l'autofunzione a energia minima di una singola particella su cui tutte le particelle si sono condensate. Egli propose, inoltre, che questa proprietà potesse sopravvivere all'introduzione di interazioni forti tra le particelle, così come accade nell'elio liquido reale. Con Onsager, Penrose ipotizzò una funzione d'onda effettiva, per un gas con interazioni forti, detta 'funzione di Jastrow', che è semplicemente il prodotto di funzioni delle mutue distanze tra tutte le particelle:

La funzione definita dalla [18] era stata introdotta da Jastrow nel contesto della materia nucleare. Dal momento che gli atomi di elio sono bosoni, tutte le funzioni devono essere positive in corrispondenza dell'energia minima. La classica funzione di distribuzione di un gas interagente ha esattamente la stessa forma [18], con f(r, r′)=exp−(V(r, r′)/kT), cosicché le stime dei vari integrali che coinvolgono questa funzione d'onda possono sfruttare i calcoli preesistenti, per esempio, sui liquidi classici a sfere rigide. In questo modo Onsager e Penrose stimarono quella che oggi è nota come 'la frazione di condensato', vale a dire la grandezza relativa dell'unico autovalore, prossima al 10%, non lontana dalle stime più recenti.

In un certo senso, dunque, già nel 1954 quello dell'elio liquido non costituiva un problema di principio. Tuttavia il modo in cui queste intuizioni potessero condurre alle proprietà reali dell'elio superfluido richiedeva ancora approfondimenti, molti dei quali furono forniti da Feynman nel 1954, e gran parte di quanto rimaneva nella tesi di McMillan del 1965. Questo argomento portò anche a scoperte sperimentali notevoli.

Le prime teorie a due fluidi ipotizzavano che il superfluido fosse irrotazionale:

[19] ∇×v≡0.

Nel 1949 Onsager aveva suggerito che, piuttosto che essere nulla, in un campione toroidale la circuitazione potesse essere quantizzata in unità di h/m e definita come

[20] ∮v ∙ ds.

Ciò fu dimostrato nel 1960 da W.F. Vinen in un notevole esperimento.

Due progressi fondamentali furono opera di Feynman. Il primo (Feynman 1954) consistette nel derivare un metodo di calcolo approssimato dello spettro di eccitazione semplicemente ponendo una delle particelle in uno stato di momento k e stimando l'energia media dello stato risultante mediante operazioni di somma. Ciò può essere facilmente posto in relazione con la funzione di correlazione fra due particelle, misurabile dallo scattering diffuso dei raggi X, la quale ha un picco in corrispondenza del minimo dello spettro rotonico. Inoltre il metodo fornisce un valore dell'energia che è quasi corretto. Le moltissime speculazioni successive sulla natura dell'eccitazione rotonica hanno aggiunto poco a questo semplice metodo di calcolo, che fu migliorato nel 1956 da Feynman e Cohen.

Il secondo progresso (Feynman 1955) derivò dall'approfondire l'osservazione di Onsager del 1949, secondo il quale ci sarebbe stato un risparmio di energia per l'elio presente in un contenitore rotante se si fosse approssimato uno stato di rotazione rigida dividendo la circuitazione necessaria in una serie uniforme di vortici quantizzati, ognuno dei quali contenente il quanto di circuitazione h/m. Nell'He-4, diversamente da quanto accade nei superconduttori, la supercorrente non è autoschermante, non c'è una lunghezza corrispondente alla profondità di penetrazione e pertanto il sistema rompe sempre la circuitazione in vortici minimi se possibile. Ben presto la comunità scientifica cominciò a rendersi conto che la creazione e il moto di linee di vortice potrebbero essere responsabili di effetti dissipativi non lineari e che la capacità di materiali porosi di vincolare le linee di vortice può contribuire alla comprensione di altri effetti dinamici quale l''effetto fontana'. Io stesso mostrai nel 1965 che esiste un'equivalenza formale con il teorema di Josephson per il moto dei vortici. Tuttavia le stesse linee di vortice non sono state osservate direttamente se non negli anni Ottanta, da R. Packard e il suo gruppo.

Ancora sul finire degli anni Cinquanta vennero pubblicati alcuni articoli - di Pines e N.M. Hugenholz, S.T. Beljaev e altri - che formulavano questi diversi concetti nei termini delle teorie di campo di sistemi a molti corpi, che allora riscuotevano molti consensi ma che - diversamente da quanto accadde per la teoria della superconduttività - poco aggiungevano alla comprensione fisica del sistema in modo paragonabile, per esempio, all'uso del teorema di Migdal nella superconduttività. Non c'è modo di evitare il fatto che l'elio liquido sia essenzialmente un sistema fortemente accoppiato e che quindi nessuno sviluppo perturbativo può essere di grande ausilio. Pertanto ogni ulteriore progresso emerse lentamente, attraverso una sperimentazione raffinata e calcoli numerici.

Presumibilmente il calcolo più convincente che confermò la sostanziale correttezza delle idee di Onsager e Feynman fu condotto da McMillan nella sua tesi. McMillan seguì Onsager nell'uso dell'approccio di Jastrow per la funzione d'onda dello stato fondamentale (anticipando il metodo di Laughlin per l'effetto Hall quantico), ma variò la sua funzione f per minimizzare l'energia calcolata, stimando l'energia mediante l'effettiva hamiltoniana. In questo modo egli ottenne una buona approssimazione dell'energia di legame sperimentale, ma migliori erano i valori delle energie relative, così come la sua stima della pressione della transizione di fase liquido-solida e i suoi calcoli dell'intero spettro e della frazione condensata. Se dovessi esprimere nuovamente la mia opinione su quale sia stato il momento terminale del 'gioco', direi che si ebbe nel 1964, anno in cui questa tesi fu completata (McMillan 1965). I suoi risultati furono in qualche modo raffinati da altri, come per esempio L. Velez, ma mai messi seriamente in dubbio.

Uno dei risultati sperimentali degni di nota fu il miglioramento ottenuto da G. Ahlers delle vecchie misure di W.M. Fairbank del calore specifico al punto lambda. Gli esponenti osservati sono in ottimo accordo con ciò che ci si aspetta da un modello xy tridimensionale, confermando ulteriormente la natura del parametro d'ordine.

Un superfluido che è distinto in via di principio da He-4 condensato è il creeping film a due dimensioni, che contiene pochi strati atomici di He-4. Tra le prime osservazioni della superfluidità una delle più sorprendenti è la capacità da parte di un recipiente di He-4 di svuotarsi o riempirsi fluendo sopra i bordi, quando questi vengano mantenuti al di sotto di T_λ. Un'osservazione di Peierls (elevata recentemente al rango di 'teorema di Mermin-Wagner') sottolineava che una simmetria continua in due dimensioni non può avere un ordine a lungo raggio del suo parametro d'ordine, a causa della divergenza delle fluttuazioni termiche a bassa energia. D.J. Thouless e J.M. Kosterlitz nel 1972 osservarono che un sistema a due dimensioni di tipo adeguato - con difetti a forma di vortice - potrebbe avere un ordine topologico a lungo raggio nel senso che la rigidità di fase - che causa il flusso superfluido - può mantenersi finita a meno che alcuni vortici possano venire generati e fluire (Kosterlitz e Thouless 1973). Ciò risulta chiaro se si considera l'onnipresente equazione di Gor´kov-Josephson. In particolare, per il modello xy, il costo energetico di un vortice diverge logaritmicamente al crescere del suo raggio cosicché la rigidità si mantiene finché una densità finita di vortici viene prodotta per via termica. Infatti esiste una temperatura critica in corrispondenza della quale la crescita logaritmica dell'entropia del vortice compensa per eccesso l'energia logaritmica e i vortici proliferano.

Questo aspetto fu verificato per il creeping film sei anni più tardi da D.J. Bishop e J.D. Reppy (1978), con tutti i dettagli quantitativi. Questo fu il primo esempio provato della vecchia idea di una transizione di fase provocata dalla proliferazione cooperativa di difetti.

Con la precisione resa possibile da questi metodi, fu possibile dimostrare che i primi atomi nel film - meno di un monostrato - non condensano ma occupano siti localizzati, ma da quel punto in poi la densità del superfluido cresce linearmente con lo spessore del film.

Esperimenti affascinanti eseguiti da Reppy, Chan e altri utilizzarono il 'giroscopio a superfluido', un recipiente di materiale poroso nel quale il componente superfluido ruota senza decadere.

La superfluidità della materia nucleare

Ben presto emersero varie generalizzazioni della teoria BCS a materiali diversi dai metalli. Una delle prime era contenuta in una lettera del 1959 di Bohr, Mottelson e Pines nella quale si sottolineava che la 'materia nucleare', la sostanza idealizzata della quale i nuclei non sono altro che piccole parti, è un gas di fermioni a interazioni relativamente deboli e che, poiché le forze internucleari sono attrattive alle lunghe distanze, ci si potrebbe attendere che esse formino delle coppie di Cooper, neutroni con neutroni e protoni con protoni. Tale caratteristica, in effetti, era stata osservata da lungo tempo come 'alternanza pari-dispari' delle energie di legame nucleare. Infatti si potrebbe argomentare che Maria Goeppert-Mayer, nel 1949, interpretando questa alternanza come un fenomeno di accoppiamento, abbia per prima introdotto l'idea delle 'coppie di Cooper'. Tali autori dimostrarono che una spiegazione di questo tipo era sensata anche in termini di spettri nucleari rotazionali. Sono stato informato da R. Broglia che la velocità di fissione nucleare è enormemente influenzata dalle grandi fluttuazioni quantiche implicate nella superfluidità.

Questo argomento ha avuto una rinascita nei primi anni Settanta dopo la scoperta di 'anomalie' nella velocità rotazionale delle stelle di neutroni. Questi sono eventi improvvisi di accelerazione che interrompono il sorprendentemente stabile rallentamento della velocità di pulsazione, che è la velocità di rotazione della parte visibile della stella, costituita da protoni e da una crosta protonica. Il modello di stella di neutroni sviluppato da M.A. Ruderman, J.W. Negele e altri ipotizzava un nucleo liquido neutronico superfluido e una 'crosta solida di Wigner' di nuclei ricchi di protoni all'interno di un secondo liquido neutronico superfluido. Pines si rese conto che la maggior parte di questi improvvisi eventi di rallentamento comportano una variazione di energia troppo piccola per essere considerati 'terremoti stellari', in accordo con l'interpretazione originale, cosicché insieme a N. Itoh proposi il modello secondo cui questi fenomeni sono da ritenersi episodi di 'salti di vorticità', equivalenti ai ben noti 'salti di flusso' dei magneti superconduttori.

In questo scenario il nucleo superfluido è visto come rotante con la crosta, poiché in esso i vortici sono liberi. Ma i vortici del superfluido neutronico nella crosta sono vincolati alla crosta stessa, mantenendo costante la velocità di rotazione del fluido mentre la crosta rallenta relativamente a esso. Ciò ingenera una grande forza di Magnus sui centri di vincolo che talvolta provocano un riequilibrio delle velocità di rotazione della crosta e del superfluido. Stime basate su dati sperimentali mostrano che circa l'1% del momento di inerzia è vincolato in questo modo e ciò è in accordo con il modello del pulsar di Ruderman. In una serie di articoli M.A. Alpar, J. Shaham, Pines e altri consolidarono questa ipotesi.

La superfluidità dell'elio-3

Nei tardi anni Cinquanta l'He-3 cominciò a essere disponibile in grandi quantità (a causa del decadimento a He-3 del trizio prodotto per il programma per la bomba H). Si tratta del canonico 'liquido di Fermi' e fu presto confermato che esso obbedisce alla teoria di Landau. Il primo articolo a suggerire che esso manifesta un accoppiamento BCS di un nuovo tipo, costituito da coppie anisotrope con momenti angolari orbitali finiti, fu quello di K.A. Brueckner e altri nel 1960, seguito a breve e per via indipendente da quelli di V.J. Emery e A.M. Sessler; tuttavia le stime grossolane della temperatura critica T_c riportate in questi articoli risultarono essere troppo alte, dal momento che in un decennio la misura della temperatura fu abbassata ai mK da J.C. Wheatley (più tardi uno studio dimostrò che egli aveva di poco attraversato la transizione ma non se ne era accorto). La teoria concernente una fase di questo tipo fu elaborata dapprima da Morel e da me stesso nel 1960 (Anderson e Morel 1961) e più tardi in forma assai più sofisticata da R. Balian e N.R. Werthamer (1963) e da Anthony J. Leggett (1965). Insieme a Morel mostrai correttamente che T_c, che è determinata da una equazione di 'gap lineare', sarebbe la stessa per qualunque fase descritta da un'armonica sferica di momento angolare totale L, dal che deriva S=0 per L pari oppure S=1 per L dispari, essendo S una componente dello spin. I termini di ordine più elevato (in Δ o T_c−T) differenzierebbero però le diverse funzioni sferiche, così che fasi multiple dovrebbero esistere in corrispondenza della medesima T_c.

Il nostro articolo ignorò le componenti M=0, S=1 dello spin e questa omissione fu corretta nel 1963 da Balian e Werthamer i quali derivarono uno stato di tripletto S=1 completamente gapped (S+L=J=0). Ciononostante l'applicazione di questo risultato ai superconduttori elettronici non trovò validità in quelli allora noti a causa della loro sensitività alle impurezze. Nel 1965 Leggett corresse queste prime teorie di campo medio per i fenomeni nel liquido di Fermi, correzioni che sono grandi in He-3.

La ragione per l'enorme rinormalizzazione di T_c consisteva nelle fluttuazioni di spin, come suggerito da Schrieffer e spiegato in modo più convincente da Emery e da A. Layzer e D. Fay. In particolare questi autori identificarono lo stato fondamentale in uno stato di tripletto con ℓ=1, piuttosto che in un'onda d di singoletto come proposto dai primi autori. Nonostante questo impianto teorico, Osheroff, Richardson e Lee (1972), sembrarono sorpresi quando la superfluidità finalmente si manifestò a Cornell nella loro cella a pressione raffreddata con il metodo di Pomeranchuk a 2,8 mK; fu una sorpresa tale che essi attribuirono dapprima il fenomeno alla fase solida (che era necessariamente presente nella loro cella). Dopo un anno o due di esperimenti intensi (forse quello definitivo fu lo studio della magnetizzazione e della risonanza nucleare di He-3) e con il lavoro parallelo di un certo numero di teorici, essi, assieme a Wheatley, ricavarono il complesso diagramma di fase e le caratteristiche fisiche del sistema. Ci sono non meno di tre fasi in competizione, tutte con la medesima T_c, le cui proprietà direzionali sono determinate da forze dipolari ultradeboli, che accoppiano gli orientamenti relativi dei momenti orbitali e di spin, che altrimenti sarebbero liberi, con gli ancora più deboli effetti di asimmetria buco-particella.

L'osservazione di due fasi, una stabile per campi e temperature più alte, suggerì immediatamente l'esistenza di un superfluido anisotropico; e il fatto che una fase (detta fase 'A') avesse una suscettibilità di spin nucleare che non varia quando la temperatura attraversa T_c rese evidente che il tripletto (S=1) previsto da Emery, Layzer e Fay, era corretto. Questa fase mostrava un significativo spostamento di frequenza all'NMR, circostanza che indicava che le funzioni d'onda dello spin e dell'orbita sono anisotropiche e accoppiate attraverso l'interazione dipolare dei due spin. Tale fase, che era stata presa in considerazione da me stesso e da Morel, mancava della componente M=0 dello spin; ma W.F. Brinkman mostrò che, nel dettaglio, i nostri dati non erano del tutto corretti e così la teoria divenne 'ABM'.

La fase 'B', a bassa temperatura e bassa intensità di campo, era quasi del tutto simile a quella studiata da Balian e Werthamer (BW) e le correzioni di Landau alla sua suscettibilità, per esempio, erano state calcolate correttamente da Leggett nel 1965. La dinamica della risonanza nucleare in entrambe le fasi era stata spiegata in maniera brillante mediante le equazioni 'del modello σ non lineare' di Leggett. Infine, un effetto di feedback sulle fluttuazioni di spin delle modifiche a lunghezze d'onda elevate della suscettibilità nel superfluido fornì una spiegazione quantitativa del diagramma di fase, così come mostrato da Brinkman, J.W. Serene e da me stesso.

Questa storia è ben riassunta in due articoli di rassegna: quello di Leggett sulla fenomenologia macroscopica (1975) e quello mio e di Brinkman (Anderson e Brinkman 1975) sulla fisica microscopica. Altri fisici, tra i quali V. Ambegaokar, N.D. Mermin e M.C. Cross, contribuirono con idee importanti.

Da questo lavoro derivarono due sviluppi fondamentali. Il primo fu la teoria topologica dei difetti del parametro d'ordine, che fu proposta in maniera indipendente nel 1975 da G. Toulouse e Maurice Kleman (1976), e Gregori E. Volovik e V.P. Mineev (1976), con alcuni contributi da parte di Pierre-Gilles De Gennes (1973). La complicazione relativa al parametro d'ordine dell'He-3 è tale che divenne fondamentale sviluppare una teoria generale che comprendesse oggetti così diversi quali le linee di vortice, i confini del dominio, i 'porcospini' e simili, che in precedenza erano stati considerati singolarità di sistemi individuali. È interessante notare che, di nuovo, come era avvenuto nel caso delle simmetrie infrante, i teorici delle particelle abbiano sviluppato un interesse per i 'meroni', gli 'istantoni', gli 'skyrmioni' e simili e che per un breve periodo i due campi abbiano comunicato tra loro.

Il secondo sviluppo fu rappresentato dal fatto che Cross (Cross e Anderson 1975) capì e Volovik codificò, nel 1979, il ruolo dei nodi del parametro d'ordine in uno spazio come sorgenti di interconversione tra flusso normale e superfluido; pertanto la definizione di superfluidità diventa considerevolmente più sottile rispetto ai criteri ingenui, come quello della velocità di Landau o le idee del gap energetico di Bardeen. Alla fine appare chiaro che il criterio è semplicemente l'esistenza di un parametro d'ordine complesso, cioè ottenuto da un campo che porta con sé una quantità di energia che si conserva.

Sebbene la fenomenologia mirabile dell'He-3 continui a essere argomento di studio (per es., gli esperimenti con il criostato rotante del gruppo di ricerca finlandese; Mineev et al. 1986), non si sono ottenuti progressi fondamentali dopo i primi, significativi, 3-5 anni; in particolare l'He-3, come l'He-4, costituisce intrinsecamente un caso di accoppiamento molto forte e la definizione delle proprietà fondamentali di un tale sistema di fermioni continua a sfidare le nostre capacità.

Superconduttori esotici: elettroni pesanti e metalli organici

Verso la fine degli anni Settanta l'immagine di una superconduttività mediata da fononi, incorporata nella formula di McMillan, sembrava aver spento la maggior parte delle controversie sulla superconduttività. Tuttavia proprio allora furono individuate due classi di superconduttori che in maniera evidente non rientrano in questa descrizione.

Coloro che studiavano i comportamenti della materia alle basse temperature erano interessati a un'ampia classe di composti metallici noti come 'sistemi a valenza mista', o meglio, 'fluttuante', o, in casi estremi, 'composti a elettroni pesanti'. Il componente rilevante è un elemento con livelli elettronici f tipo Ce o U, circondato da elementi metallici convenzionali quali Al, Cu, Ge. Questi ultimi contribuiscono a un 'mare di Fermi' di elettroni liberi, che alle alte temperature sono diffusi in maniera significativa dagli spin dello strato interno degli elettroni f. Alle temperature più basse - tipicamente per gli elettroni pesanti, dell'ordine di 10÷100 K - gli spin scompaiono gradualmente e gli strati f sembrano 'ibridizzarsi' nella banda degli elettroni liberi, creando bande elettroniche eccessivamente strette con calori specifici, propri degli elettroni liberi, molto grandi. Nei casi superconduttivi, questi corrispondono a masse effettive dell'ordine di 100÷1000 volte la massa dell'elettrone.

Frank Steglich osservò per primo un fenomeno di superconduttività vicino a 1 K nel composto CeCu₂Si₂ (Steglich et al. 1979). È però difficile ottenere dati affidabili per questo composto. Infatti esso rappresenta ancora un enigma, poiché gli stati magnetici appaiono più o meno alla stessa concentrazione della superconduttività. Pertanto, solo quando, pochi anni dopo, vennero scoperti i composti UPt₃ e UBe₁₃ fu possibile accorgersi che tale effetto è abbastanza generale. Attualmente si conoscono una dozzina di materiali di questo tipo. La caratteristica più notevole è rappresentata dalle vistose singolarità del calore specifico in corrispondenza della temperatura critica T_c, che dimostrano come le strette bande f e gli elettroni quasi liberi siano accoppiati e che, in un certo senso, queste T_c siano abbastanza vicine alla scala dell'energia di Fermi: se le energie di Fermi E_F fossero normali le T_c sarebbero ben al di sopra della temperatura ambiente! È sempre più plausibile che la maggior parte di questi materiali abbia accoppiamenti non convenzionali, di tipo 'non-onda-s'. Nell'UPt₃, il materiale studiato in maniera più significativa, ci sono diverse fasi superconduttive che appaiono con le variazioni del campo magnetico e che hanno due temperature di transizione leggermente diverse. Questo è un argomento quasi definito, come per l'He-3. Molti altri casi mostrano un'estrema sensibilità alle impurezze. Alcuni, il CeCd₂Si₂ per esempio, come dimostrato da G.G. Lonzarich, si associano con una funzione d'onda di densità di spin in un modo che suggerisce 'fluttuazioni critiche antiferromagnetiche' in analogia con il caso dell'He-3, ma con una superconduttività apparentemente di singoletto, forse un'onda-d.

A parte quest'unica possibilità, nessuna teoria microscopica è stata proposta in modo plausibile. È chiaro che i fononi non sono coinvolti; in effetti gli 'elettroni' f, che sono sostanzialmente puro spin, sono accoppiati molto debolmente ai fononi, che tendono a provocare una frattura delle coppie nel caso di superconduttori anisotropici. Vale la pena notare il fatto, che non è mai stato spiegato, che la maggior parte dei superconduttori sono materiali a elettroni pesanti, piuttosto che a valenza mista, cioè si può supporre che il modello appropriato sia l'hamiltoniana di un reticolo di Kondo e non quella di un reticolo asimmetrico di Anderson.

Un vecchio (e probabilmente non corretto) suggerimento di Little, secondo cui i composti a catena organica potrebbero supercondurre, stimolò (insieme ad altre motivazioni più valide) una ricerca sui materiali metallo-organici che, dopo alcune deviazioni, diede i suoi frutti con una serie di esemplari scoperti verso il 1985 da D. Jerome e altri. Le T_c variano tra 1 e 13 K. Le loro strutture hanno poco in comune con il concetto di catena polimerica: si tratta in generale di molecole aromatiche planari di dimensioni modeste assemblate in serie lineari lungo una direzione esterna al piano molecolare, intercalate con anioni che impartiscono loro una densità netta di portatori di lacune elettroniche. Alcuni sono all'incirca monodimensionali, altri sono buoni conduttori in un piano e hanno una sola 'direzione dura'. Il diagramma di fase (in funzione di pressione, temperatura e intensità del campo magnetico) di un sale di Bechgaard, che è uno dei materiali metallo-organici più recenti, sembra la più complessa fra tutte le sostanze conosciute. La loro fisica di base come materiali metallici è ancora misteriosa, ed è remota la possibilità di identificare il loro meccanismo di accoppiamento. Almeno uno, detto 'ET' a causa della sua formula complicata, così come suggerito da una invariata suscettibilità di spin, è noto oggi essere un accoppiamento a tripletto ovvero una parità dispari nello spazio e pertanto non mediata da fononi. La rapidità con la quale questa fenomenologia bizzarra è stata scoperta e il basso livello di comprensione teorica, ne impediscono in questa sede un esame approfondito.

Cuprati superconduttivi ad alta T_c

Nonostante gli sviluppi ricordati e il mercato crescente per i magneti superconduttori a intensità di campo elevata, derivante dal loro impiego nelle industrie medica e chimica, la superconduttività a metà degli anni Ottanta veniva considerata come una palude intellettuale, almeno tra le agenzie che gestivano i fondi. Per questo motivo la comunità scientifica accolse con grande entusiasmo la scoperta, da parte di Bednorz e Muller (1986), di quelli che oggi sono noti come i 'superconduttori ad alta T_c', o in modo più appropriato i 'cuprati'. Rispetto agli standard odierni il composto scoperto da questi due scienziati, il (La-Ba)₂CuO₄, non ha una temperatura critica T_c particolarmente alta, al massimo 35 K, ma bisogna ricordare che allora nessun semiconduttore aveva superato i 23,2 K. Inoltre il materiale scoperto ha un gran numero di composti chimici analoghi, che pertanto poterono essere investigati. Era anche plausibile che, in virtù di alcune sue inattese proprietà, esso fosse il capostipite di una nuova classe di materiali e di un nuovo meccanismo. Infatti tale 'irragionevole esuberanza' si rivelò completamente giustificata, poiché in meno di 6 mesi C.W. Chu e i suoi collaboratori (Chu et al. 1987), in competizione con gruppi di ricerca giapponesi (Hikami et al. 1987) e cinesi (Zhao et al. 1987) riuscirono a scoprire con vantaggio di pochi giorni il YBa₂Cu₃O₇, caratterizzato da T_c di oltre 90 K. Sviluppi ulteriori hanno spinto le temperature al di sopra dei 150 K, per le quali è ancora richiesto un raffreddamento con azoto liquido, ma che consentono di operare in maniera più agevole. Diversamente da molti USO (unidentified superconducting objects) che vantano proprietà spettacolari e che vengono proposti di tanto in tanto, i materiali del tipo di Bednorz e Muller sono robusti e riproducibili. Essi non richiedono grandi abilità da parte dei chimici né l'impiego di apparecchiature complesse, anche se sono abbastanza fragili dal punto di vista meccanico. Inoltre questi materiali sembrano essere in grado di tollerare campi magnetici elevati e correnti approssimativamente proporzionali alle loro T_c.

La scienza delle alte T_c ha prodotto un'intera generazione di sofisticati sensori per i materiali e ha portato la metodologia della teoria quantistica a molti corpi a nuovi livelli di sofisticazione, ma non ha trovato una sintesi che fosse considerata soddisfacente dalla comunità scientifica come, per esempio, la BCS. La fisica fondamentale che è alla base del fenomeno fu rapidamente identificata da me e da altri ricercatori, sotto forma del cosiddetto 'isolatore drogato di Mott'. Le entità elettricamente attive sono i piani CuO₂, strutture semplici con ossigeni ligandi compresi tra coppie di ioni Cu²⁺. Questi piani, quando sono stechiometrici, sono antiferromagnetici e isolanti. Quando essi vengono 'drogati', attraverso ioni Cu³⁺ inseriti alterando la stechiometria degli strati inerti che fungono da 'serbatoio', i portatori di carica risultanti diventano superconduttivi, raggiungendo un 'drogaggio ottimale' pari circa al 20%, in corrispondenza del quale la T_c è massima. In precedenza era stato suggerito da diversi gruppi di ricercatori (per es., K. Miyake e collaboratori, J.E. Hirsch e altri) che uno scambio antiferromagnetico tra gli elettroni mobili potesse produrre una superconduttività a 'onda-d' e quando fu stabilito, attraverso diversi metodi sperimentali, che i cuprati sono veramente di tipo onda-d sembrò che la fisica su cui si fonda questa fenomenologia fosse chiara. Tuttavia la strada che partendo da tali nozioni fisiche sarebbe dovuta arrivare a una comprensione quantitativa delle proprietà manifestate dai materiali reali non si è rivelata univoca e sta divenendo sempre più evidente che il nostro modello concettuale della teoria degli elettroni con interazioni forti ha bisogno di un aggiornamento. La caratteristica più notevole dei risultati sperimentali è l'osservazione di uno 'pseudogap' o di un regime di gap di spin per temperature al di sopra della T_c, per i sistemi al di sotto delle condizioni ottimali di doping. Appare un gap nello spettro elettronico attorno all'energia di Fermi, che però non è netto e non mostra fenomeni di coerenza. Ha l'effetto di far scomparire progressivamente la superficie di Fermi, lasciandone un residuo vicino alla direzione a 45° nella zona di Brillouin (questo risultato fu ottenuto utilizzando una fotoemissione a risoluzione d'angolo, usando sorgenti di luce di sincrotrone, metodo che si è sviluppato in maniera eccezionale come risposta alle esigenze della comunità scientifica). Lo pseudogap si estende a temperature sempre più alte mano a mano che si riduce il doping; pertanto il gap stesso è ampio.

G. Baskaran e altri, infatti, suggerirono molto presto che l'accoppiamento avrebbe potuto generare un liquido di coppie di singoletti, o RVB, che perderebbe coerenza di fase a causa della debole rigidità di fase ai bassi doping, e G. Kotliar e altri estesero queste idee alle onde-d. Una parte critica di questa teoria è l'ipotesi di una separazione spin-carica che rende necessaria l'introduzione di variabili di gauge per imporre i vincoli più rilevanti. Tuttavia la forma precisa della teoria di gauge è ancora oggetto di controversia, in quanto M.P.A. Fisher e collaboratori, P.A. Lee e X.G. Wen e altri gruppi sostengono diverse posizioni nella disputa. Sembra plausibile per diverse ragioni sperimentali che la vera risposta potrà emergere dall'unione di idee che si svilupperanno attorno al concetto di RVB, ma non è ancora stato scoperto esattamente il modo di fornire una dimostrazione che possa essere accolta con soddisfazione dall'intera comunità scientifica.

In modo piuttosto singolare, l'aspetto quantitativo - la ragione per cui la T_c è così alta e se il modello di Hubbard sia in grado di prevederlo - non appare troppo controverso. Varie forme di simulazione computazionale sono in grado di trovare una superconduttività di onda-d mediante modelli semplici; perfino stime grossolane ottenute utilizzando l'idea dell'RVB e la prevista rigidità di fase sono numericamente corrette, almeno come ordine di grandezza. Una conseguenza inattesa della superconduttività alle alte T_c è stato un rapido progresso della fisica teorica o, perlomeno, una notevole proliferazione di nuove idee. Entriamo nel XXI sec. senza che l'enigma della superconduttività sia stato completamente risolto.

I gas di Bose-Einstein

Per molti anni alcuni scienziati - per esempio T.J. Greytak (Masuhara et al. 1988) e collaboratori al Massachusetts Institute of Technology (MIT) e J.T.M. Walraven (van Roijen et al. 1988) e collaboratori in Olanda - hanno cercato di accumulare, con densità finite, gas monoatomici quali l'idrogeno atomico polarizzato (che è un bosone), ma sono stati frustrati dagli effetti superficiali, dalle collisioni a tre corpi e da altri percorsi di ricombinazione a idrogeno molecolare, che è molto più stabile. È soltanto con lo sviluppo di sofisticate manipolazioni laser - incluso il raffreddamento a temperature dell'ordine dei nK - di nuvole rarefatte di atomi da parte di S. Chu, W.D. Phillips e altri (Chu 1998) che il fenomeno della condensazione di Bose-Einstein di un gas essenzialmente perfetto, quale fu originariamente definito, poté finalmente essere osservato. I primi esperimenti riusciti risalgono agli ultimi mesi del 1995 e furono eseguiti da Wieman, Cornell e altri (Anderson et al. 1995) al laboratorio del National Institute of Standards and Technology in Colorado, su Na atomico. A questo seguirono gli esperimenti del gruppo di K. Metterle al MIT (Davis et al. 1995) utilizzando dapprima Rb, in seguito, in questo e altri laboratori, estesi a un numero notevole di specie atomiche. La scoperta iniziale si è espansa in modo enorme e tutte le caratteristiche del comportamento quantistico macroscopico sono state dimostrate su questi campioni che possono essere agevolmente manipolati. Si ha l'impressione che molti di questi lavori siano in tale accordo con le previsioni teoriche da avere quasi un carattere da manuale, anche se c'è stato ampio spazio per l'inventiva ingegneristica e per la creatività. Sono state poste alcune questioni fondamentali e a qualcuna è stata data risposta, per esempio Leggett e io stesso abbiamo discusso se due condensati de novo possano avere una fase relativa distinta. Vedo anche la possibilità che vengano condotte misure sperimentali, ancora non disponibili, specialmente sulla gravitazione, poiché per questi atomi liberi neutri il campo gravitazionale assume il ruolo che un campo elettrico ha per i superconduttori.

Notiamo che il settore della 'superconduttività e superfluidità', che corrisponde sostanzialmente alla coerenza quantica dei campi di particelle, è maturato nel corso di cinque decenni ma è ancora gravido di nuove possibilità sperimentali e di profondi quesiti teorici.

Conclusioni

Finora penso di aver enfatizzato gli aspetti teorici a spese dei dati sperimentali. La conseguenza non voluta di ciò è il fatto che i nomi degli scienziati teorici e, cosa per me particolarmente imbarazzante, il mio e quello dei miei collaboratori, appaiono più frequentemente di quelli degli sperimentatori e soprattutto più di quanto sarebbe giusto. Forse posso rimediare parzialmente evidenziando aspetti e risultati sperimentali che mi sembrano di particolare rilevanza se si guarda in retrospettiva il mezzo secolo che è appena trascorso.

Prima di tutto, per quanto riguarda la superconduttività vanno ricordati gli scienziati che hanno scoperto i materiali e successivamente li hanno prodotti in forme utili e scientificamente interessanti quali i monocristalli, i film orientati epitassialmente, le superfici ultrapulite e così via. In quest'ambito il nome che emerge è quello di Matthias, anche se nella sua carriera trentennale mancò l'obiettivo personale principale - riuscendo solo ad aumentare la temperatura massima di transizione superconduttiva di meno di un fattore 2 - vale a dire quello di scoprire materiali superconduttori con temperatura critica prossima alla temperatura ambiente. Ciononostante egli scoprì letteralmente centinaia di nuovi composti superconduttori, stabilì un'euristica affidabile almeno per i superconduttori BCS (Matthias 1955), scoprì il contrasto per questi superconduttori tra dispersione magnetica e non magnetica, assunse un ruolo centrale nelle scoperte che permisero di ottenere i magneti superconduttori per applicazioni pratiche e permise molti altri importanti sviluppi scientifici. Soprattutto formò studenti e ricercatori, stimolando l'entusiasmo che ci consentì di uscire dall''era BCS' dopo il 1980: Arthur Sleight, Zachary Fisk, Chu, Steglich, H.-R. Ott, Brian Maple, Bertram Batlogg e molti altri. Morì improvvisamente nel 1980 prima che fosse chiaro che il mondo è pieno di meravigliosi superconduttori che non sono di tipo BCS, non obbediscono alle regole di questa teoria e corrispondono esattamente a quella speranza che lo aveva motivato negli anni.

Fisk, con il suo amico e collaboratore Ott, eseguendo in molti casi le misure, utilizzò le straordinarie risorse di materiali di Los Alamos per creare dozzine di nuovi materiali, soprattutto i superconduttori a elettroni pesanti tipo UBe₁₃ e UPt₃, che dimostrano che il caso del CeCu₂Si₂ non è un 'mostro della Natura'. Egli riuscì a caratterizzare al meglio il misterioso stato metallico 'a elettroni pesanti'.

La storia del miglioramento graduale della crescita monocristallina per i materiali ad alta T_c è stata importante per l'enorme anisotropia delle proprietà e per le singolari anomalie delle proprietà di trasporto, per gli spettri infrarossi e per lo scattering di neutroni polarizzati. Il primo a ottenere cristalli singoli di YBa₂Cu₃O₇ capaci di garantire proprietà di trasporto accurate fu Z.Z. Wang a Princeton (Hagen et al. 1988; Clayhold et al. 1989), che fornì materiali per il gruppo di N.P. Ong che eseguiva le misurazioni; ci sono stati poi miglioramenti costanti fino alla situazione attuale, nella quale D.A. Bonn e W.A. Hardy producono cristalli sufficientemente privi di difetti a diverse concentrazioni di O cosicché le loro proprietà sembrano completamente di natura intrinseca (Liang et al. 1998). Fondamentali sono stati i cristalli enormi di I. Aksay adatti allo scattering neutronico anelastico, che permise a B. Keimer e altri di misurare in maniera affidabile lo spettro di eccitazione magnetica (Fong et al. 1995).

Il (La-Sr)₂CuO₄ è stata una specialità giapponese; da tempo su questo caso molto particolare è disponibile un lavoro neutronico, grazie ai cristalli prodotti da T. Muratami e più tardi da altri.

Per quanto riguarda il percorso piuttosto tortuoso che ha portato allo sviluppo dei superconduttori organici, esso è stato ben riassunto in un libro del 1992, intitolato Organic Superconductor, scritto da Williams e altri. Un altro risultato notevole che riguarda i materiali è la produzione da parte di C.C. Tsuei di film epitassiali di YBCO, con confini dei granuli in forma di piani costruiti deliberatamente. Questo risultato ha permesso di ottenere una chiara dimostrazione del carattere a onda-d del parametro d'ordine, utilizzando il microscopio a scanning flux per dimostrare che alcuni vortici lungo i confini contengono semiflussi quantici.

Passiamo ad altri risultati sperimentali significativi: ricostruendo la storia dei primi studi sulla superfluidità in HeII, avrei potuto segnalare l'esperimento di E.L. Andronikashvili quale primo test quantitativo del modello a due fluidi (1946). Egli intrappolò il fluido normale in una serie di dischi rotanti che scorrevano in assenza di attrito attraverso il composto superfluido. Il 'giroscopio superfluido di Reppy' è sostanzialmente una variante di questo schema. A parte gli esempi che ho presentato, c'è stata una serie molto significativa di esperimenti che ha permesso di ricostruire la curva di dispersione delle eccitazioni naturali con una accuratezza notevole. Un metodo ingegnoso fu sviluppato da R.C. Dynes e V. Narayanamurti, rendendo possibile misurare la curva di dispersione dei fononi in He utilizzando i fononi di ricombinazione da film superconduttivi con gap energetici noti. Un'altra affascinante serie di esperimenti fu quella di Moses Chan sull'elio in un aerogel, una forma di silice così esile da essere costituita per più del 99% da pori. In questo modo si possono verificare gli effetti di una specie di 'scattering da impurezza' su entrambe le forme isotopiche di elio, nelle quali nulla si dissolverebbe in altro modo.

Nel descrivere il rapido consenso con cui venne accettata la teoria BCS, forse avrei dovuto menzionare l'experimentum crucis di Chuck Hebel e C.P. Slichter mediante il quale essi dimostrarono che, contrariamente a quanto sembrava suggerire l'intuizione, il tempo di rilassamento NMR aumenta appena al di sotto della T_c, confermando sorprendentemente il fattore di coerenza predetto dalla BCS.

Il lavoro di Maeno e altri su un composto scoperto recentemente, analogo al LASCO, il La₂RuO₄, ha stabilito in modo molto esplicito che questo materiale a 'bassa T_c' è un superconduttore a tripletto che, pertanto, presenta un gap di simmetria orbitale dispari (Maeno et al. 2001), sebbene la sua forma effettiva sia ancora oggetto di discussione. Un altro caso che è stato studiato in maniera intensiva, mediante una gran varietà di metodi sperimentali, è l'UPt₃. Colui che ha dato i contributi più importanti è stato il teorico Jim Sauls, il quale ci ha convinti del fatto che si tratta di un altro caso anomalo.

È appropriato concludere questa sezione con una generalizzazione storica. L'osservazione di Thouless, che è stata sviluppata in un modello da parte di Morel e altri e in un 'teorema' da Kohn e Luttinger, sembrava suggerire che l'interazione diretta repulsiva tra elettroni dovesse sempre provocare una superconduttività di tipo non BCS, anche in assenza di 'attrazione' fononica (gli apici sono stati inseriti perché è solo un effetto di ritardo che la fa sembrare un'attrazione). Il fatto che ciò non sia mai stato osservato non sembrava un mistero, poiché i superconduttori di tipo non BCS sono sempre estremamente sensibili allo scattering da parte di tutti i difetti, possibilità che è stata considerata come osservabile solo in condizioni non specificate ma molto particolari.

Quello di cui non ci siamo resi conto è il fatto che il costante progresso nella preparazione dei materiali ci avrebbe prima o poi raggiunti. Per esempio, si sarebbero ottenuti il composto rutenato e probabilmente anche i superconduttori organici come classe di composti che tendono a essere straordinariamente puliti in quanto sintetizzati (effettivamente ci sono anche condizioni speciali, che sembrano essere operative nell'intera classe dei materiali a elettroni pesanti, nel senso che essi, essendo per lo più spin, non vengono facilmente diffusi da potenziali ordinari); e infine, e questo è il vero mistero, i cuprati ad alta T_c, che, come si è dimostrato, sono a onda-d ma sono insensibili allo scattering da parte delle impurezze, fatto questo che mi spinse a intraprendere una caccia disperata per 5 anni.

Ho suggerito, ma non stabilito in forma definitiva, una risposta a questo mistero, che certamente non è stata universalmente accettata. Il punto storicamente rilevante è che è ormai chiaro che la classe dei superconduttori anomali, non-fononi, non è vuota, ma anzi rappresentativa forse quanto i casi convenzionali.

Bibliografia

Abrikosov 1957: Abrikosov, Alekseij Aleksevič, On the magnetic properties of superconductors of the second group, "Zhurnal eksperemental'noj i teoreticheskoj fiziki", 32, 1957, pp. 1442-1452 (trad. ingl.: "Soviet physics JETP", 5/6, 1950, pp. 1174-1182).

Anderson 1995: Anderson, M.H. - Ensher, J.R. - Matthews, M.R. - Wieman, C.E. - Cornell, E.A., Observation of Bose-Einstein condensation in a dilute atomic vapor, "Science", 269, 1995, 5221, pp. 198-201.

Anderson 1958a: Anderson, Philip W., Coherent excited states in the theory of superconductivity: gauge invariance and the Meissner effect, "Physical review", 110/4, 1958, pp. 827-835.

Anderson 1958b: Anderson, Philip W., Random phase approximation in the theory of superconductivity, "Physical review", 112/6, 1958, pp. 1900-1916.

Anderson, Morel 1961: Anderson, Philip W. - Morel, P., Generalized Bardeen-Cooper-Schrieffer states and the proposed low-temperature phase of liquid He³,"Phisical review",123/6, 1961, pp. 1911-1934.

Anderson 1963: Anderson, Philip W., Plasmons, Gauge invariance and Mass, "Physical review", 130/1, 1963, pp. 439-442.

Anderson, Brinkman 1975: Anderson, Philip W. - Brinkman, William F.,Theory of anisotropic superfluidity, in: Proceedings of the 15^th Scottish Universities summer school in Phisics - Nato scientifics Affairs Division, University of St Andrews 1974, edited by Jonathan G.M. Armitage and Ian E. Farquhar, London, Academic Press, 1975.

Andronikashvili 1946: Andronikashvili, E.L., "Journal of physics Moscow", 10, 1946, p. 201.

Balian, Werthamer 1963: Balian, Roger - Werthamer, N.R., Superconductivity with pairs in a relative p-wave, "Physical review", 131/4, 1963, pp. 1553-1564.

Bardeen 1957a: Bardeen, John - Cooper, Leon N. - Schrieffer, John Robert, Microscopic theory of superconductivity, "Physical review", 106/1, 1957, pp. 162-164.

Bardeen 1957b: Bardeen, John - Cooper, Leon N. - Schrieffer, John Robert, Theory of superconductivity, "Phisical review", 108/5, 1957, pp. 1175-1204.

Bednorz, Muller 1986: Bednorz, Johannes Georg - Muller, Karl Alexander, Possible high T_c superconductivity in the Ba-La-Cu-O system, "Zeitschrift für Physik", B64, 1986, pp. 189-193.

Bishop, Reppy 1978: Bishop, David J. - Reppy, John D., Study of the superfluid transition in two-dimensional ⁴He films, "Physical review letters", 40/26, 1978, pp. 1727-1730.

Bloch 1966: Bloch, Felix, Some remarks on the theory of superconductivity, "Physics today", 13 May 1966, pp. 27-29.

Bogoljubov 1947: Bogoljubov, Nikolai N., On the theory of superfluidity, "Journal of physics, Moscow", 11/1, 1947, pp. 23-32.

Bogoljubov 1959: Bogoljubov, Nikolai N. - Tolmachev, Vladimir - Shirkov, Dimitri V., A new method in the theory of superconductivity, New York, Consultants Bureau, 1959.

Chu 1987: Chu, Ching Wu e altri, Superconductivity above 90 K in the square-planar compound system A Ba₂Cu₃ 306+x with A= La, Y, Nd, Sm, Eu, Gd, Ho, Er and Lu, "Physical review letters", 58, 1987, pp. 1891-1894.

Chu 1998: Chu, Steven, The manipulation of neutral particles, "Review of modern physics", 70/3, 1998, pp. 685-706.

Clayhold 1989: Clayhold, J. - Ong, Nai Phuan - Wang, Zuo Zhang - Tarascon, Jean Marie - Barboux, P., Hall effect anomaly in the high T_c copper based perovskites, "Physical review", B39/10, 1989, pp. 7324-7327.

Cohen 1962: Cohen, Michael H. - Falicov, Leo M. - Phillips, James C., Superconducting tunneling, "Physical review letters", 8/8, 1962, pp. 316-318.

Cooper 1956: Cooper, Leon, Bound electron pairs in a degenerate Fermi gas, "Physical review", 104/4, 1956, pp. 1189-1190.

Cross, Anderson 1975: Cross, M.C. - Anderson, P.W., Orbit waves in the ABM phase of superfluid 3He, in: Proceedings of the 14^th International conference on low temperature physics, edited by Matt Krusius and Matt Vuorio, Amsterdam, North-Holland, Oxford-New York, Elsevier, 1975, pt. 1, pp. 29-32.

Davis 1995: Davis, Kendall B. - Mewes, Marc-Oliver - Joffe, Michael A. - Andrews, Michael R. - Ketterle, Wolfgang W., Erratum: evaporative cooling of sodium atoms, "Physical review letters", 75, 1995, p. 2909.

De Gennes 1973: De Gennes, Pierre-Gilles, The order parameter in liquid 3 He, in: Collective properties of physical systems, Proceedings of the 24th Nobel symposium, Lerum, Sweden 1973, edited by Bengt Lundqvist and Stig Lundqvist, Stockholm, Nobel foundation, New York, Academic Press, 1973, pp. 112-115.

Deaver, Fairbank 1961: Deaver, Bascom - Fairbank, William M., Experimental evidence for quantized flux in superconducting Cylinders, "Physical review letters", 7/2, 1961, pp. 43-46.

Doll, Nabauer 1961: Doll, Richard - Nabauer, M., Experimental proof of magnetic flux quantization in a superconducting ring, "Physical review letters", 7/2, 1961, pp. 51-52.

Feynman 1954: Feynman, Richard P., Atomic theory of the two fluid model of liquid helium, "Physical review", 102/2, 1954, pp. 262-277.

Feynman 1955: Feynman, Richard P., Application of quantum mechanics to liquid helium, "Progress in low temperature physics", Amsterdam, North Holland, 1, 1955, pp. 17-53.

Feynman, Cohen 1956: Feynman, Richard P. - Cohen, Michael, Energy spectrum of the excitations in liquid helium, "Phisical review", 102, 1956, pp. 1189-1204.

Fong 1995: Fong, Hung Fai e altri, Phonon and magnetic neutron scattering at 41 meV in Yba₂Cu₃O₇, "Physical review letters", 75/2, 1995, pp. 316-319.

Gavroglu 1995: Gavroglu, Kostas Fritz, London, a scientific biography, Cambridge, Cambridge University Press, 1995.

Ginsburg, Landau 1950: Ginsburg, Vitali L.- Landau, Lev D., On the theory of superconductivity, "Zhurnal eksperemental' noj i teoreticheskoj fiziki", 20, 1950, p. 1064 e segg. (rist. in: Collected papers of L.D. Landau, New York, Gordon and Breach, 1965, pp. 546-568).

Goldstone 1961: Goldstone, Jeffrey, Field theory with "superconductor" solutions, "Nuovo cimento", 19, 1961, pp. 154-164.

Goppert-Mayer 1949: Goppert-Mayer, Maria, On closed shells in nuclei. II, "Physical review", 75/12, 1949, pp. 1969-1970.

Gor´kov 1959: Gor´kov, Lev P., Microscopic derivation of the Ginzburg-London equations in the theory of superconductivity, "Soviet Physics JETP", 36/9, 1959, pp. 1364-1367.

Gorter, Casimir 1934: Gorter, Cornelis J. - Casimir, Hendrick G.B., Zur thermodynamik des supraleitenden Zustandes, "Physicalische Zeitschrift", 35, 1934, pp. 963-969.

Hagen 1988: Hagen, Stephen J. - Jing, T.W. - Wang, Zuo Zhang - Horvath, J. - Ong, Nai Phuan, Out of phase conductivity in single crystal Y Ba₂Cu₃O₇, "Physical review", B37/13, 1988, pp. 7928-7931.

Higgs 1964: Higgs, Peter W., Broken symmetries and the masses of gauge bosons, "Physical review letters", 13/16, 1964, pp. 508-509.

Hikami 1987: Hikami, S. - Hirai, T. - Kagoshima, S., High transition temperature superconductor: Y-Ba-Cu oxide, "Japenese journal of applied physics", 26, 1987, pp. L314-315.

Josephson 1962: Josephson, Brian D., Possible new effects in superconductive tunneling, "Physics letters", 1/7, 1962, pp. 251-253.

Kosterlitz, Thouless 1973: Kosterlitz, J. Michael - Thouless, David J., Ordering metastability and phase transitions in two-dimensional systems, "Journal of physics", C6, 1973, pp. 1181-1203.

Legget 1965: Legget, Anthony J., Theory of a superfluid Fermi liquid I. General formalism and static properties, "Physical review", 140/6A, 1965, pp. 1869-1888.

Legget 1975: Legget, Anthony J., A theoretical descrption of the new phases of liquid ³He, "Review of modern physics", 47/2, 1975, pp. 331-414.

Liang 1998: Liang, Ruixing - Bonn, D.A. - Hardy, W.A., Growth of high quality YBCO single crystals using BaZrO₃ crucibles, "Physica", 304C, 1998, pp. 105-111.

London 1950-54: London, Fritz Wolfgang, Superfluids, New York, Wiley VCH, 1950-1954.

Maeno 2001: Maeno, Yoshiteru - Ong, Nai Phuan - Bhatt, Ravin M., More is different, Princeton, Princeton University Press, 2001, p. 135.

Masuhara 1988: Masuhara, Naoto e altri, Evaporative cooling of spin polarized atomic hydrogen, "Physical review letters", 61, 1988, pp. 935-938.

Matthias 1955: Matthias, Bernd T., Empirical relation between superconductivity and the number of valence electrons per atom, "Physical review", 97/1, 1955, pp. 74-76.

McMillan 1965: McMillan, William L., Ground state of liquid He⁴, "Physical review", 138/2A, 1965, pp. 442-451.

Meissner, Ochsenfeld 1933: Meissner, Walter - Ochsenfeld, Robert, Ein neuer Effekt bei Eintritt der Supraleitfähigkeit, "Naturwissenschaften", 21, 1933, pp. 787-788.

Mineev 1986: Mineev, Vladimir P. - Salomaa, M.M. - Lounasmaa, O.V., Superfluid ³He in rotation, "Nature", 324, 1986, pp. 333-340.

Nambu 1960: Nambu, Yoichiro, Quasi-particles and gauge invariance in the theory of superconductivity, "Physical review", 117/3, 1960, pp. 648-663.

Nambu, Jona-Lasinio1961: Nambu, Yoichiro - Jona-Lasinio, Gianni, Dynamical model of elementary particles based on an analogy with superconductivity. I, "Physical review", 122/1, 1961, pp. 345-358.

Onsager 1949: Onsager, Lars, The two fluid model for Helium II, Commento alla relazione di Cornelis J. Gorter, "Nuovo cimento", 6, 1949, pp. 249-250.

Onsager 1954: Onsager, Lars, Introductory talk, in: Proceedings international conference of theoretical physics, Kyoto-Tokyo, Science council of Japan, 1954, pp. 877-880.

Osheroff 1972: Osheroff, D.D. - Richardson, R.C. - Lee, D.M., Evidence for a new phase of solid He³, "Physical review letters", 28/14, 1972, pp. 885-888.

Penrose 1951: Penrose, Oliver, On the quantum mechanics of helium II, "Philosophycal magazine", 42, 1951, pp. 1373-1377.

Penrose, Onsanger 1956: Penrose, Oliver - Onsager, Lars, Bose-Einstein condensation and liquid helium, "Physical review", 104/3, 1956, pp. 576-584.

Phillips 1998: Phillips, William D., Laser cooling and trapping of neutral atoms, "Review of modern physics", 70/3, 1998, pp. 721-741.

Schoenberg 1952: Schoenberg, David, Superconductivity, Cambridge, Cambridge University Press, 1952.

Steglich 1979: Steglich, Frank e altri, Superconductivity in the presence of strong Pauli paramagnetism: Ce Cu₂ Si₂, "Physical review letters", 43/25, 1979, pp. 1892-1896.

Toulouse, Kleman 1976: Toulouse, Gerard - Kleman, Maurice, Principles of a classification of defects in ordered media, "Journal de physique lettres", 37, 1976, pp. 149-151.

van Roijen 1988: van Roijen, R. - Berkhout, J.J. - Jaakkola, S. - Walraven, J.T.M., Experiments with atomic hydrogen in a magnetic trapping field, "Physical review letters", 61, 1988, pp. 931-934.

Volovik, Mineev 1976: Volovik, Grigori E. - Mineev, Vladimir P., Hydrodynamic of the A-phase of superfluid ³He, "Soviet physics JETP", 44/3, 1976, pp. 591-598.

Volovik 1979: Volovik, Grigori E., Superfluid ³He. Hydrodynamics and nonuniform status, "Soviet Scientific Reviews, Sec. A, Physics reviews", Chur, Harward Academic Publishers, 1979, 1, p. 23.

Wu 1987: Wu, M.K. e altri, Superconductivity at 93 K in a new mixed phase Yb-Ba-Cu-O at ambient pressure, "Physical review letters", 58, 1987, pp. 908-910.

Zhao 1987: Zhao, Zhong-Xian e altri, "Kexue Tongbao", 32, 1987, pp. 661-664.