La grande scienza. Semiconduttori
La grande scienza. Semiconduttori
Semiconduttori
Il modo di comunicare e produrre nella società di oggi è stato a tal punto influenzato dalle tecnologie informatiche da indurre conseguenze confrontabili con quelle prodotte dalla rivoluzione industriale nell'Ottocento e dallo sviluppo delle telecomunicazioni nella prima metà del Novecento.
La rivoluzione informatica si è sviluppata nella seconda metà del Novecento sulla scia del progresso delle conoscenze scientifiche riguardanti il mondo microscopico, il cui fondamento concettuale è la meccanica quantistica. Essa deriva però dall'applicazione di tale disciplina alla comprensione dei processi elettronici in una classe particolare di materiali solidi indicati con il nome generico di semiconduttori.
L'esistenza di materiali di questo tipo, cattivi coibenti (isolanti) e non buoni conduttori, era stata segnalata da Alessandro Volta (1745-1827) nei suoi studi sull'elettricità già alla fine del Settecento. I composti più comuni di questo tipo sono il solfuro d'argento Ag2S, il solfuro di piombo PbS (galena), i solfuri e seleniuri di zinco e cadmio ZnS, CdS, ZnSe e CdSe, e molti altri successivamente scoperti. Tra essi preminente è il silicio, oggi il semiconduttorre tipico, ipotizzato da Antoine-Laurent Lavoisier (1743-1794) alla fine del Settecento come componente della sabbia (silex), e isolato da Joseph-Louis Gay-Lussac (1778-1850) e Jöns Jacob Berzelius (1779-1848) agli inizi dell'Ottocento.
La comprensione teorica dei fenomeni fisici che avvengono nei semiconduttori è iniziata negli anni Trenta ed è stata approfondita per tutto il resto del Novecento, portando a nuovi concetti sui fondamenti della fisica, particolarmente nel campo della teoria dei molti corpi e dell'interazione tra radiazione e materia, e aprendo inoltre nuove possibilità applicative con l'estrema miniaturizzazione dei dispositivi elettronici e optoelettronici. Al momento attuale l'industria dei semiconduttori è di fondamentale importanza nel sistema economico di ogni nazione tecnologicamente avanzata. Essa è caratterizzata da un fatturato annuo globale diretto di oltre mille miliardi di dollari, in costante crescita per il progressivo aumento delle necessità di eseguire calcoli e di accumulare e trasmettere informazioni.
Lo sviluppo della vicenda scientifica e sociale che ha condotto a questi risultati è una storia affascinante e di grande valore educativo, anche per l'interdipendenza strettissima tra fisica e tecnologia da cui è connotata.
Le origini
Nel corso dei suoi studi sul trasferimento di elettricità da un corpo all'altro, Volta fece uso di isolanti non perfetti per scaricare più o meno lentamente un conduttore elettrizzato (si veda, per es., la Memoria letta alla Royal Society di Londra il 14 marzo 1782, e pubblicata sulle "Philosophical Transactions" del 1782). Egli introdusse la locuzione 'deferenti (conduttori) imperfetti' per tali materiali, e più sovente utilizzò il termine 'semicoibenti'. Alcune parole specifiche impiegate nella traduzione francese della stessa memoria sono ancora attuali per indicare la proprietà tipica di tali sostanze: "les corps qui tiennent le juste milieu entre les déférents (conduttori) et les cohibents (isolanti) […], qui sont à la vérité perméables au fluide électrique, mais qui opposent une assez grande résistence à son passage".
Volta aveva avuto alcuni precursori, tra cui Stephen Gray (1666-1736) e Jean-Théophile Desaguliers (1683-1744). Il primo, in uno scritto del 1731 a Cromwell Mortimer, segretario della Royal Society, argomentò sulla capacità del sughero umido, quindi non totalmente isolante, a contatto col vetro elettrizzato di attirare oggetti. Il secondo introdusse il concetto di conduttore elettrico e la dizione relativa (conducteur d'électricité) in una dissertazione premiata dall'Académie Royale des Belles Lettres et Arts a Bordeaux nel 1742.
È tuttavia con la pila di Volta che intensi flussi di elettricità diventano disponibili e consentono, nei primi decenni dell'Ottocento, a Humphry Davy (1778-1829), padre dell'elettrochimica, di condurre esperimenti sulla conducibilità dei metalli più comuni (Cu, Ag, Fe, Pt, ecc.), osservando che in tutti essa diminuisce all'aumentare della temperatura. Michael Faraday (1791-1867), suo allievo, estenderà le misure di conducibilità a materiali non metallici, quali ossidi, carbonati, solfati, e in particolare allo ioduro di mercurio HgI2, per scoprire che l'aumento di temperatura provoca in essi un grande aumento di conducibilità, contrariamente a quanto accade con i metalli. George Busch ha analizzato recentemente (1986) gli esperimenti descritti da Faraday, e più tardi da Johann Wilhelm Hittorf su Ag2S e Cu2S, riscontrandovi la conferma di un andamento esponenzialmente crescente con l'aumento della temperatura, come riportato nella fig. 1.
A questo risultato si attribuì grande importanza per la comprensione del trasporto elettrico, anche se per lungo tempo non fu chiaro quali fossero i portatori di corrente (elettroni o ioni di argento interstiziali in Ag2S). Furono effettuati per molti decenni esperimenti in merito con metodi elettrochimici, che nella maggior parte dei sali ionici avevano consentito di misurare una variazione di peso agli elettrodi corrispondente al numero degli ioni trasportati. Nel caso dei semiconduttori menzionati non si rivelava apprezzabile variazione di peso.
È utile ricordare che la densità di corrente elettrica J è legata al campo elettrico E applicato dalla relazione:
[1] J =ne⟨v⟩=σE,
dove ⟨v⟩ è la velocità media nella direzione del campo elettrico, e la conducibilità σ è proporzionale al numero di portatori per unità di volume n, alla loro carica e alla mobilità μ, velocità di un portatore per unità di campo elettrico, secondo la relazione
[2] σ=neμ .
Per capire i processi da cui hanno origine le proprietà di conduzione elettrica nei corpi solidi era quindi necessario avere la possibilità di misurare con precisione, oltre alla carica elettrica, il numero dei portatori. Questo divenne possibile, nel 1879, con la scoperta di Edwin H. Hall (1855-1938), che la corrente, in presenza di un campo magnetico perpendicolare alla direzione del flusso di cariche, produce un campo elettrico perpendicolare alle due direzioni e proporzionale alla corrente e al campo magnetico, tale da compensare la forza di Lorentz. La costante di proporzionalità, come si può subito vedere, ricordando che la forza di Lorentz vale e⟨v⟩B/c, è 1/nec, da cui è immediato ricavare il segno e la densità n dei portatori.
L'effetto Hall, misurabile contemporaneamente alla corrente elettrica, con un assetto sperimentale del tipo mostrato nella fig. 2, fu ed è tuttora di importanza fondamentale per lo studio dei metalli e dei semiconduttori. Esso consentì di stabilire definitivamente che nei metalli e nei semiconduttori la corrente elettrica è trasportata da elettroni. Carl V.E. Riecke (1845-1915) mostrò infatti nel 1901, all'Istituto di fisica dell'Università di Gottinga, che il peso del materiale trasferito nei semiconduttori, sulla base del numero dei portatori misurato con l'effetto Hall, sarebbe stato enorme se i portatori fossero stati ioni, mentre in realtà era quasi trascurabile, e corrispondeva al valore di e/m trovato da Joseph J. Thomson nel 1898 per l'elettrone libero. La teoria della conducibilità elettrica venne quindi formulata da Riecke e da Paul Drude (1863-1906) con il modello di un gas di elettroni liberi, la cui mobilità diminuisce linearmente con la temperatura. Fu poi perfezionata nel 1913 da Johann Koenigsberger per ossidi e solfuri, postulando che nei semiconduttori la resistività diminuisce esponenzialmente con la temperatura secondo un'energia di attivazione che dipende dalla sostanza, quando ancora l'origine di tale energia di attivazione era oscura.
Un risultato importante e allora del tutto inspiegabile fu evidenziato da Karl Baedeker (1877-1914) nello ioduro di rame (CuI) nel 1909, e successivamente confermato da Orso Mario Corbino (1876-1937) in altre sostanze. Si trattava di anomalie nell'effetto Hall, e in particolare nel segno positivo della costante di Hall, come se i portatori fossero elettroni con carica positiva anziché negativa. Inoltre il loro numero variava grandemente con la concentrazione di iodio, raggiungendo valori molto bassi, incompatibili con la corrente trasportata. Oggi sappiamo che questo è dovuto alla presenza di due tipi di portatori di segno opposto (elettroni e buche con carica positiva), che contribuiscono alla produzione di campi elettrici di Hall di segno opposto.
Il dibattito sulla natura della conducibilità nei semiconduttori, e sull'esistenza stessa di materiali semiconduttori non metallici, continuò a lungo dopo la Prima guerra mondiale senza significativi progressi. Mentre la teoria della conducibilità dovuta ai difetti (posti vacanti) e agli ioni interstiziali nei cristalli ionici faceva grandi progressi, grazie ai contributi di Jakov I. Frenkel, Carl Wagner, Walter Schottky, Walter Jost e Robert W. Pohl, la comprensione del trasporto elettrico nei semiconduttori era carente, ed era oscurata dal fatto che spesso i risultati ottenuti da autori diversi non erano concordi. Tale non riproducibilità fu un ostacolo che condizionò a lungo la fisica dei semiconduttori, anche dopo che i concetti della meccanica quantistica già affermatisi avrebbero potuto fornire le basi per una comprensione almeno qualitativa. L'aspetto dei semiconduttori era spesso simile a quello dei metalli, tanto che ancora nel 1940 si riteneva che il silicio fosse un metallo. In una rassegna del 1930, e ancora nel 1939, Bernhard Gudden asseriva che sostanze pure non possono essere semiconduttori, e che le proprietà di trasporto elettrico di sostanze non metalliche sono riconducibili alle impurezze presenti. In questa affermazione c'è un elemento di verità, ma è soltanto nel fatto che la comprensione delle proprietà elettriche dei composti semiconduttori richiede la disponibilità di sostanze pure possibilmente monocristalline, e un controllo delle diverse impurezze che esse contengono. Solo con la possibilità di fabbricare tali sostanze, dopo la Seconda guerra mondiale, ha inizio l'avvincente capitolo della fisica dei semiconduttori.
Prima di allora però il fisico tedesco Ferdinand Braun (1850-1918), lo scopritore dei raggi catodici, che doveva condividere nel 1909 il premio Nobel con Guglielmo Marconi per i contributi alla trasmissione delle onde elettromagnetiche, aveva scoperto, già nel 1874, all'Università di Lipsia, il potere di raddrizzare la corrente dei cristalli di galena (PbS) e di altri cristalli semiconduttori. In tali cristalli la corrente fluiva quando il campo elettrico era applicato in una direzione e non quando esso era applicato in direzione opposta. Invertendo il campo elettrico spariva la corrente. Tale proprietà darà origine al primo dispositivo a semiconduttore, in quanto verrà utilizzata per rivelare le onde elettromagnetiche.
Rivelatori di onde elettromagnetiche
Negli esperimenti originari di comunicazioni a distanza condotti da Guglielmo Marconi (1874-1937) e da altri, a partire dal 1895 fino agli inizi del secolo, le onde elettromagnetiche che si propagavano nello spazio venivano rivelate dal coherer di Edouard-Eugène Branly (1844-1940), un tubo di ferro vuoto, a contatto con carbone pressato, contenente limatura di ferro, che, quando era orientata dal campo elettrico, migliorava il contatto e aumentava la conducibilità, permettendo quindi la rivelazione del segnale, anche mediante scrittura su carta. Una variante molto utilizzata fu il coherer della Marina italiana, sviluppato alla fine dell'Ottocento da Paolo Castelli e Luigi Solari, nel quale la limatura di ferro per il contatto elettrico era sostituita da gocce di mercurio che si dilatavano a ogni impulso di campo elettrico aumentando la conducibilità al contatto. Questo faceva sì che non fosse necessario ristabilire la situazione precedente dopo ogni impulso, perché la goccia di mercurio ritornava spontaneamente a dimensione e forma normali. Tale apparecchio della Marina italiana fu usato come rivelatore nella prima trasmissione transatlantica di Marconi nel 1901.
All'inizio del Novecento venne però riconosciuta la necessità di raddrizzare la corrente alternata dei campi elettrici irradiati per ottenere una versione elettroacustica dei segnali ottici, per esempio con cuffie acustiche magneticamente attivate, che richiedono una durata dell'impulso di corrente in una direzione compatibile con l'inerzia del sistema meccanico. Venne così utilizzata la proprietà rettificante dei semiconduttori, scoperta da Braun. Il fisico e tecnologo indiano Jagdish C. Bose, dopo molte ricerche nel suo laboratorio di Calcutta, ottenne nel 1901 il brevetto per l'uso della galena (PbS) come raddrizzatore di corrente. Anche se meno sensibili dei coherer, i rivelatori a cristallo divennero presto di uso generale per la ricezione acustica dei segnali.
Dopo la Prima guerra mondiale, per rivelare le onde elettromagnetiche vennero comunemente usate le valvole raddrizzatrici a vuoto (diodi), perché consentivano una migliore riproducibilità dei risultati e fornivano la possibilità di amplificare la corrente con l'inserimento di una griglia interna (triodi). Tuttavia i rivelatori a semiconduttore (particolarmente selenio e ossido di rame, ma anche silicio) non furono mai totalmente abbandonati, per il loro basso costo e per il fatto di non richiedere un circuito ausiliario per il loro funzionamento. Mentre infatti nelle valvole a vuoto occorre riscaldare il filamento per ottenere la corrente di elettroni, nei cristalli semiconduttori la corrente fluisce naturalmente in una direzione e non nella direzione opposta. Comunque, la riproducibilità dei risultati ottenuti con i semiconduttori non era buona, a causa del fatto che essi erano policristallini e contenevano un'elevata densità di impurezze, e in uno stesso cristallo occorreva trovare il punto adatto per il contatto con un filo sottile (a baffo di gatto). Le valvole a vuoto erano invece affidabili e consentivano amplificazioni di corrente.
Sia i buoni cristalli sia le valvole a vuoto avevano una risposta non lineare per campi intensi, proprietà che venne subito utilizzata da Reginald A. Fessenden, a partire dal 1902, per inserire un circuito oscillante ausiliario (eterodino), a causa del quale un segnale di frequenza prefissata, combinandosi con le frequenze principali trasmesse dalle antenne, produceva battimenti di bassa frequenza, e quindi consentiva la recezione di frequenze nel dominio udibile. Questo principio fu poi perfezionato da Edwin H. Armstrong e Shottky nel 1918, utilizzando vari stadi di amplificazione con triodi a vuoto ad alta frequenza e successiva conversione con il circuito eterodino a frequenze udibili. Le trasmissioni radiofoniche furono pertanto possibili.
Nel periodo tra le due guerre l'uso delle valvole a vuoto consentì lo sviluppo delle telecomunicazioni e i grandi progressi dell'elettronica, che poi condussero allo sviluppo dei calcolatori, a partire dagli anni Quaranta. Rimase tuttavia vivo l'interesse riguardo ai rivelatori a semiconduttore, anche se la loro scarsa affidabilità e la limitata comprensione delle loro proprietà contribuirono a dare una pessima fama alla fisica che li studiava, denominata da Wolfgang Pauli negli anni Trenta 'fisica sporca'.
Il silicio e il radar
Alla soglia della Seconda guerra mondiale i magnetron e i klystron di elevate prestazioni consentirono di produrre intensi fasci impulsati di onde ultracorte, le cosiddette microonde di lunghezze d'onda centimetriche. Si presentò pertanto il problema della loro efficiente rivelazione in connessione con lo sviluppo del radar. Toccò a due giovani inglesi, l'ingegner Denis Robinson e il fisico H.W.B. Skinner, in un laboratorio segreto, scoprire nel 1939 il modo di rivelare microonde di dieci centimetri, mediante l'uso di cristalli di silicio e contatti di tungsteno. Essi furono guidati da un libro di H.E. Holmann sulle onde ultracorte, apparso nella letteratura tedesca nel 1936, e realizzarono il primo circuito eterodino che rendeva possibile ridurre la frequenza del segnale di ritorno dell'impulso radar a un valore praticamente utile per successive amplificazioni. L'elemento non lineare nel circuito eterodino era il diodo cristallino rettificante di silicio, con contatto di tungsteno.
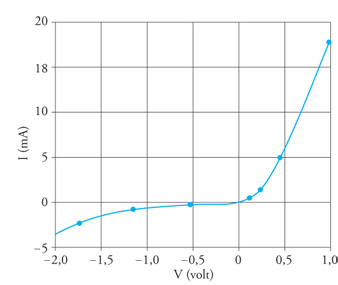
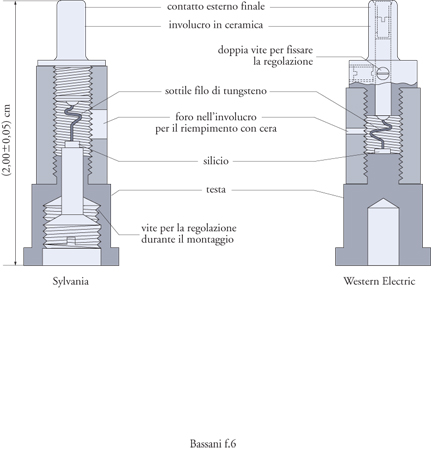
Non era banale scegliere i cristallini di silicio utili tra molti disponibili e già usati dalla fine dell'Ottocento nella siderurgia. Soltanto alcuni di essi rettificavano la corrente, e le ragioni delle proprietà rettificanti del silicio non furono allora comprese, tanto che ancora all'inizio degli anni Quaranta lo si riteneva un metallo. Quando la tecnologia radar venne condivisa dall'Inghilterra con gli Stati Uniti, e affidata al Radiation Laboratory creato presso il Massachussets Institute of Technology (MIT) di Boston nel 1940, e diretto da Lee A. Du Bridge, le ricerche sui semiconduttori vennero potenziate e si ottenne una buona riproducibilità dei risultati. In particolare, silicio relativamente puro e di migliore qualità cristallina venne prodotto dalla società Du Pont, e si scoprì che una concentrazione opportuna di impurezze di boro e alluminio ne migliorava le proprietà rettificanti. Una storica curva corrente-voltaggio di un diodo silicio-tungsteno e tipici rivelatori di onde radar del 1942 sono riportati rispettivamente nelle figg. 3 e 4.
Parallelamente alle ricerche sul silicio si svilupparono alla General Electric, all'University of Pennsylvania e ai Laboratori della Bell Telephon ricerche sul germanio, preferito allora al sili-cio per l'elevata mobilità dei portatori di carica. In questo ambito si misurò il numero e il segno dei portatori con l'effetto Hall e si scoprì l'esistenza di una conducibilità intrinseca (nei cristalli puri) con dipendenza esponenziale dalla temperatura ed energia di attivazione di 0,33 eV, e di una conducibilità estrinseca predominante a più basse temperature, legata al contenuto e alla natura delle impurezze. Tali risultati valevano anche per il silicio, con un valore di circa 0,6 eV per l'energia di attivazione. In tal modo l'interesse tecnologico per i cristalli semiconduttori tornò a essere predominante e si concentrò l'attenzione sui cristalli elementari appartenenti al gruppo IV (C, Si, Ge, Sn), e successivamente sui composti binari dei gruppi III-V e II-VI di simmetria nota e particolarmente semplice (ogni atomo è situato al centro di un tetraedro regolare).
Da questi primi risultati nacque e si sviluppò la fisica dei semiconduttori nell'immediato dopoguerra, principalmente nei gruppi di Frederick Seitz all'University of Pennsylvania, di Karl Lark-Horovitz alla Purdue University, e del gruppo dei Laboratori Bell Telephone, chiaramente interessati all'uso del germanio nelle telecomunicazioni.
Teoria dei processi elettronici
La comprensione teorica dei processi elettronici nei semiconduttori si è sviluppata gradualmente a partire dall'affermarsi della meccanica quantistica negli anni Venti. All'inizio della seconda metà del Novecento i concetti di base erano sostanzialmente acquisiti, anche grazie alla disponibilità di materiali di elevata purezza e in forma di monocristalli, la cui tecnologia di produzione si era grandemente affinata negli anni Quaranta.
Anzitutto il concetto delle bande di energia quali stati disponibili per gli elettroni nei cristalli. Un teorema scoperto da Felix Bloch (1905-1983) nel 1928 stabilisce che le autofunzioni dell'equazione di Schrödinger nei cristalli, dalle quali si ottengono le energie possibili, ammettono come buon numero quantico il vettore k dello spazio reciproco, confinato nella zona di Brillouin del cristallo, nella quale due valori di k differiscono per meno di un vettore del reticolo reciproco (2π/a nella direzione degli assi in un reticolo cubico, dove a è il parametro reticolare). Tali vettori k sono uniformemente distribuiti e in numero uguale al numero di celle del cristallo (la metà del numero di atomi nel silicio e nel germanio, che hanno due atomi per cella elementare, ciascuno al centro di un tetraedro regolare). I valori degli stati di energia disponibili agli elettroni sono quindi distribuiti su bande En(k). Ogni stato k definisce un impulso ħk, dove ħ è la costante di Planck ridotta; esso corrisponde a una lunghezza d'onda di De Broglie degli elettroni λ=2π/k. Tali bande di energia possono essere associate agli stati atomici o agli stati molecolari, ai quali si riducono all'aumentare delle distanze interatomiche. Nel caso di C, Si e Ge, per esempio, tutti elementi del quarto gruppo, si possono associare per gli stati di valenza s1p3 due bande agli stati s (una per ognuno dei due sottoreticoli cubici a facce centrate che formano i tetraedri) e sei bande agli stati p (tre per ogni sottoreticolo). Ogni banda contiene un numero di stati uguali al numero di celle del cristallo (la metà del numero di atomi).
Il secondo concetto fondamentale è il principio di esclusione di Wolfgang Pauli (1900-1958) del 1925, per il quale ogni stato può essere occupato da un solo elettrone (due elettroni se caratterizzati da stati quantici con spin, ossia i momenti angolari intrinseci, opposti). Tale principio fu formulato per spiegare le proprietà chimiche degli atomi, ma fu subito utilizzato per spiegare le proprietà elettroniche dei metalli e degli isolanti. Allo zero assoluto gli elettroni si distribuiscono sugli stati di più bassa energia e all'aumentare della temperatura si distribuiscono sugli stati con la distribuzione statistica di Fermi (1926). I cristalli sono isolanti quando le bande totalmente occupate sono separate dalle bande vuote da un 'gap' Eg (intervallo di energia proibita) abbastanza grande da non consentire in esse presenza di elettroni liberi a ogni temperatura. Nei metalli il livello a energia più alta occupato (livello di Fermi) è interno a una banda, e questo consente agli elettroni di tale energia di trasferirsi sui livelli vicini con un comportamento in tutto simile a quello di elettroni liberi. Negli isolanti il livello di Fermi è all'interno del gap proibito; gli elettroni non possono trasportare corrente perché se uno di essi si sposta da uno stato all'altro, per il principio di esclusione, l'elettrone che prima occupava quello stato farà lo spostamento inverso, dato che tutti gli stati sono occupati nelle bande di energia sottostanti al livello di Fermi. Il campo elettrico non conferisce agli elettroni energia sufficiente a passare da una banda all'altra, e quindi non si ha conducibilità elettrica.
La teoria delle bande è la base per la comprensione di tutte le proprietà dei solidi, ed è merito di Alan H. Wilson averla utilizzata per spiegare anche le proprietà fondamentali dei semiconduttori. Nel 1931, mentre era a Lipsia nel gruppo dove era nata e si sviluppava la meccanica quantistica presso la scuola di Werner Heisenberg, egli pubblicò due classici lavori nei quali le proprietà dei semiconduttori trovavano la loro spiegazione, secondo i concetti sopra indicati. I semiconduttori sono isolanti allo zero assoluto, ma il loro gap Eg è di valore sufficientemente piccolo (minore di circa 2 eV) da consentire che per effetto dell'alta temperatura un numero di elettroni per unità di volume si trovi nella banda normalmente vuota (di conduzione) a energie superiori al livello di Fermi e si comporti come nei metalli, producendo quindi la corrente elettrica in presenza di un campo applicato. Gli elementi del gruppo IV si distinguono in isolanti (C) o semiconduttori (Si, Ge, Sn grigio) soltanto in base al valore del gap Eg. Semiconduttori sono anche i composti III-V e II-VI nella stessa struttura e molti ossidi e sali quando Eg è sufficientemente piccola.
A titolo di esempio riportiamo nella fig. 5 le bande di energia del Si, calcolate con tecniche matematiche opportune sviluppate negli anni Cinquanta da vari autori (C. Herring, F. Hermann, T.O. Woodruff, F. Bassani ecc.), e poi ricalcolate per decenni con tecniche sempre più raffinate. Si può osservare che gli otto elettroni di valenza per cella (quattro per atomo) occupano tutti gli stati di quattro bande fino al massimo γ25′ al punto γ(k=0), e un gap Eg ≈1,2 eV li separa dagli stati vuoti di conduzione. Simili risultati, ma con il minimo della banda di conduzione in posizioni diverse nello spazio k, e diversi valori di Eg, si ottengono per il germanio e per tutti i composti a simmetria zincoblenda (gruppo IV, III-V, II-VI, e alcuni I-VII quali il CuCl).
Un ulteriore fondamentale concetto è quello di 'buca' di elettrone, introdotto da Heisenberg e da R. Peierls per i solidi nel 1931. Uno stato elettronico vuoto in una banda in cui tutti gli stati sono normalmente occupati si comporta come una particella di carica positiva, e come tale è un portatore di corrente. La situazione è analoga a quella delle antiparticelle di Dirac (i positroni), ma in questo caso le 'masse effettive' m* di elettroni e buche sono diverse da quelle di elettroni e positroni liberi, perché sono determinate dalla curvatura delle bande En(k) al minimo o al massimo delle bande di conduzione o di valenza, rispettivamente per gli elettroni o le buche. Il comportamento degli elettroni nel cristallo vicino agli estremi è infatti determinato dalla relazione:
[3] E(k)=E0±[(ħ2k2/2m*)],
con il segno + o − riferito al minimo o al massimo delle rispettive bande, e con valori diversi di m* per elettroni e buche.
L'esistenza di buche ha consentito di spiegare l'effetto Hall anomalo, con costante di segno positivo anziché negativo, descritto precedentemente e rimasto un mistero per decenni. La conducibilità in tal caso è dovuta alle buche di carica positiva e la costante di Hall acquista segno positivo. Se entrambi i tipi di portatori sono presenti prevarrà l'uno o l'altro, e la costante acquisterà un valore che risulta dai contributi di segno opposto dei due tipi di portatori, e dipende dalle rispettive densità e mobilità. Evidentemente nei semiconduttori intrinseci (senza impurezze) il numero di elettroni nella banda di conduzione è uguale al numero delle buche nella banda di valenza. Questo fatto, unitamente all'uso della distribuzione di Fermi per gli elettroni, consente di ottenere per il numero di elettroni di conduzione e di buche per unità di volume l'espressione:
[4] ne=nh=Ce-Eg/2kT,
dove la costante C dipende dalle masse efficaci di elettroni o buche, e debolmente dalla temperatura T. Dalla dipendenza sperimentale della conducibilità intrinseca si può determinare Eg (1,2 eV, per il Si e 0,66 eV per il Ge, a temperatura ambiente).
Si deve a Wilson anche la distinzione tra semiconduttori intrinseci, nei quali la conducibilità è propria del cristallo puro, e semiconduttori estrinseci, nei quali la conducibilità è dominata dalle impurezze. La presenza di impurezze che sostituiscono atomi del reticolo introduce elettroni aggiuntivi se gli elettroni di valenza nell'atomo di impurezza sono in numero maggiore di quelli dell'atomo che sostituiscono, e introduce buche se gli elettroni di valenza sono in numero minore. Così, impurezze del gruppo III (per es., B e Al) in silicio e germanio introducono buche, e impurezze del gruppo V (per es., P e As) introducono elettroni. Tali buche, o elettroni aggiuntivi, sono legati ai loro atomi da un'attrazione di tipo coulombiano, ma la costante dielettrica che scherma l'attrazione è grande (in genere superiore a 10, considerando uguale a 1 quella nel vuoto) e la massa effettiva m* è più piccola di quella dell'elettrone libero, in modo che l'energia di legame è molto piccola (da alcuni meV ad alcune decine di meV). Pertanto gli stati sono parzialmente ionizzati e molti degli elettroni aggiuntivi (o mancanti) sono nelle bande di conduzione (o di valenza) già a temperatura ambiente, e sono portatori di corrente. Mentre ad alte temperature la conducibilità è determinata soltanto dalla struttura delle bande di energia, a temperature relativamente basse e a temperature ambiente il numero e il tipo dei portatori è dominato dal numero e dal tipo delle impurezze. È perciò evidente che il controllo delle impurezze consente di controllare il tipo di conducibilità e il suo valore attraverso il numero di portatori di ogni tipo (elettroni o buche), ricordando che la conducibilità σ è data dall'espressione [2] e sommando il contributo di elettroni e buche. Poiché vale la legge per cui il prodotto nenh rimane costante a ogni temperatura, e segue l'espressione che si ottiene dalla [4], aggiungendo impurezze del gruppo V (donatori) in Si e Ge si eliminano le buche oltre ad aggiungere elettroni, e viceversa per impurezze del gruppo III (accettori). Si possono ottenere così semiconduttori di tipo n (con portatori negativi) e di tipo p (con portatori positivi). Le mobilità μ influiscono molto poco sulla conducibilità rispetto alla densità dei portatori, che è controllata da Eg e dal tipo di impurezze presenti nel cristallo.
Questo semplice schema concettuale si rese disponibile e fu verificato in pochi anni, già nella prima metà del secolo, anche se il suo definitivo trionfo è dovuto alle ricerche del periodo successivo alla Seconda guerra mondiale sui semiconduttori silicio e germanio. Tra i principali artefici delle idee che portarono alla comprensione dei processi elettronici nei semiconduttori, oltre ai già menzionati Bloch, Peierls, Wilson, Seitz, Lark-Horowitz, occorre ricordare H.A. Bethe, J. Bardeen, W.B. Shockley, W. Kohn e C. Kittel. Quest'ultimo sviluppò nel 1952 un metodo che consentì di misurare direttamente le masse efficaci dei semiconduttori, e quindi calcolare le mobilità e verificare la struttura a bande. Tale metodo è la risonanza di ciclotrone, che consiste nell'indurre transizioni con microonde tra livelli quantici discreti prodotti da un campo magnetico B applicato e misurare i picchi d'assorbimento corrispondenti (la frequenza di ciclotrone che separa i livelli nel caso isotropo è ωc = eB/m*c).
La determinazione teorica dell'effettiva struttura a bande di ogni semiconduttore, con la spiegazione del ruolo della simmetria del cristallo e della struttura elettronica degli atomi che lo costituiscono, ha richiesto ulteriori decenni, e per alcuni tipi di semiconduttori è ancora in corso (Bassani e Pastori-Parravicini 1975). A titolo di esempio viene mostrato nelle figg. 6 e 7 lo schema a bande calcolato per il germanio e per l'arseniuro di gallio. È immediato osservare che il massimo degli stati di valenza è sempre a k=0 (punto γ), mentre il minimo degli stati di conduzione è nel punto L(2π/a (1/2,1/2,1/2), stato L-6), nel caso del Ge (Eg=0,66 eV), e nel punto γ (k=0, stato γ6) nel GaAs (Eg=1,41 eV).
La struttura delle bande di energia, i valori delle masse efficaci e le proprietà dielettriche e ottiche sono stati calcolati teoricamente e misurati con esperienze di vario tipo (conducibilità, assorbimento ottico, risonanze di ciclotrone ecc.) nei semiconduttori più comuni già citati, ma anche in ossidi e sali semiconduttori organici. Le ricerche di questo tipo hanno impegnato i fisici dello stato solido durante tutta la seconda metà del XX sec., e per alcuni composti di semiconduttori sono ancora in corso e di grande attualità. Anche nei composti più studiati, continui perfezionamenti teorici sono necessari per tenere conto degli effetti a molti corpi legati alla densità elettronica, W. Kohn - 1972 - e degli effetti dovuti alle interazione tra stati elettronici e stati vibrazionali.
Il transistor
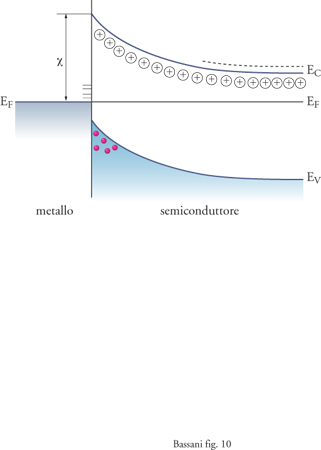
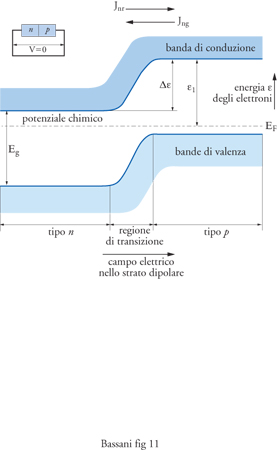
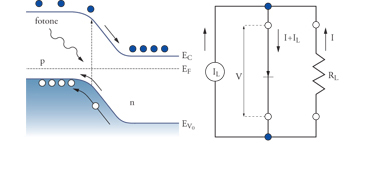
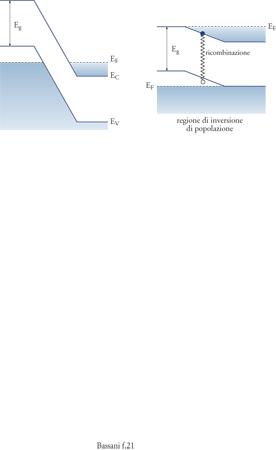
La teoria delle bande ha anzitutto permesso di capire la ragione della rettificazione di corrente nella giunzione metallo-semiconduttore. Essa è riconducibile alla creazione di una barriera di potenziale all'interfaccia, dovuta alla curvatura delle bande di energia verso la superficie, a causa della migrazione di elettroni dal metallo agli stati dei livelli accettori vuoti, o dai livelli donori occupati verso il metallo -W. Schottky, 1939. Tale barriera di potenziale, visualizzata nella fig. 8 per i semiconduttori di tipo n, consente il passaggio attraverso la superficie di separazione (interfaccia) solo agli elettroni che hanno energia superiore a essa, o alle buche di energia inferiore a essa nel caso di semiconduttori di tipo p. Applicando un campo esterno si crea un potenziale all'interfaccia V, che in una direzione abbassa la barriera, e nell'altra la aumenta. Poiché il numero di elettroni di energia superiore a quella della barriera viene variato per effetto statistico nel rapporto e±eV/kT, soltanto nella direzione in cui il potenziale abbassa la barriera, cioè in una direzione del campo elettrico, si ha un grande aumento del numero dei portatori e quindi si ha corrente. Per lo stesso motivo si ottiene rettificazione a una giunzione tra semiconduttori di tipo n e di tipo p; in questo caso la barriera di potenziale è dovuta al fatto che il livello di Fermi (energia di separazione tra stati occupati e stati vuoti) è vicino alla banda di conduzione e alla banda di valenza rispettivamente nei semiconduttori di tipo n e p. Lo schema della giunzione n-p è mostrato nella fig. 9, dove si evidenzia che il potenziale chimico coincide con il livello di Fermi e ha lo stesso valore nei semiconduttori a contatto. In opportuni diodi p-n, con elevati campi elettrici applicati nella direzione che normalmente non porterebbe corrente, Leo Esaki scoprì, nel 1958, che è possibile ottenere correnti per 'effetto tunnel'.
Era naturale aspettarsi che da queste conoscenze scaturisse la possibilità di produrre un dispositivo simile al triodo per amplificazione di corrente o di tensione. Tale dispositivo fu realizzato da Bardeen, W.H. Brattain e Shockley nel 1947 ai Bell Telephone Laboratories di Murray Hill. Il primo esemplare consiste di due giunzioni metallo-semiconduttore e semiconduttore-metallo molto vicine, come indicato nella fig. I.1 (transistor con contatti a punte metalliche). La corrente nel circuito della prima giunzione è amplificata nel circuito principale in conseguenza del fatto che si applica alla base (cristallo) un potenziale diverso rispetto all'emettitore (prima giunzione) e al collettore (seconda giunzione), e che i portatori minoritari sopravvivono e attraversano la base. Furono subito ottenuti guadagni di corrente di ca. 50 e di voltaggio di ca. 100. Il nome transistor fu proposto da J.R. Pierce dei Bell Telephone Laboratories sulla base del fatto che il trasferimento di cariche dall'emettitore al collettore richiede la presenza di un resistore di trasferimento nel circuito.
Un secondo transistor, più semplice e pratico, fu presto inventato da Schockley combinando due giunzioni, per esempio secondo lo schema n-p-n, e utilizzando il fatto che portatori minoritari in una giunzione diventano portatori principali nell'altra. In tale caso la prima giunzione n-p funge da emettitore (iniettore), la seconda p-n da collettore, e il potenziale di base che consente l'amplificazione è sullo strato intermedio p, come mostrato nella fig. I.2. Questa versione del transistor, chiamata bipolare a giunzioni, diede origine ai dispositivi che sostituirono le valvole amplificatrici nei circuiti elettronici e nei calcolatori. Il loro grande vantaggio è dovuto alla grande miniaturizzazione (pochi micron per ogni elemento) e all'eliminazione del filamento caldo, che consente di evitare la presenza di grandi quantità di calore.
Un ulteriore sviluppo fu il transistor a effetto di campo (FET, field effect transistor), inizialmente suggerito e brevettato da Bardeen nel 1950 e poi sviluppato da G.C. Dacey e I.M. Ross nel 1953. In esso si applica un campo elettrico alla base (chiamata anche porta), per attirare o respingere gli elettroni, favorendo o impedendo il trasporto di cariche attraverso la base stessa, e di conseguenza controllando la corrente che fluisce. Una variante estremamente importante del transistor bipolare e del transistor a effetto di campo utilizza l'isolamento prodotto dall'ossido per separare i contatti su una sola superficie e quindi costruire un transistor alla superficie di un monocristallo di silicio o germanio. Lo schema di un tale transistor è mostrato nella fig. I.3.
I vari tipi di transistor, e particolarmente i transistor superficiali, che possono essere costruiti intaccando l'ossido di superficie con un agente chimico in regioni speciali non protette, sulle quali si evapora poi metallo per il contatto elettrico, hanno aperto la strada all'elettronica della seconda metà del secolo XX. È stabilita la possibilità della miniaturizzazione, enormemente accresciuta, al limite della risoluzione con la quale si può segnare, con esposizione alla luce o a un fascio di elettroni, la superficie da scavare nell'ossido (fig. I.4). L'applicazione di un campo elettrico mediante un contatto sulla base del transistor planare (porta) fa sì che gli elettroni si concentrino sulle superfici dell'interfaccia ossido-semiconduttore, e consente di ottenere una dipendenza dell'effetto transistor dal valore del campo applicato (MOSFET, metal oxide semiconductor field effect transistor).
Queste considerazioni e i vantaggi dei transistor planari spiegano il trionfo del silicio come materiale di base. L'ossido di silicio è infatti un ottimo isolante, e non è igroscopico come altri ossidi e l'ossido di germanio. Inoltre, dopo l'ossigeno, è l'elemento più abbondante sulla crosta terrestre.
Un risultato importante di queste ricerche per la fisica fondamentale è la scoperta di un'anomalia dell'effetto Hall quando gli elettroni o le buche sono confinate a un piano per effetto di campo elettrico (MOSFET) o altro. In tal caso la curva del potenziale di Hall indotto in funzione del campo magnetico perpendicolare al piano presenta gradini in corrispondenza a valori che sono sottomultipli interi o frazionari della grandezza universale h/e2 (K. von Klitzing, 1982). Tale effetto Hall quantizzato, oltre a fornire uno standard assoluto di resistenza elettrica, ha rivelato nuovi stati del gas di elettroni o di buche dipendenti dalle correlazioni elettroniche.
Circuiti integrati e microprocessori
Come sviluppo dei transistor planari, nasce nella seconda metà del Novecento l'idea di costruire interi circuiti e calcolatori estremamente compatti, utilizzando soltanto una piccola superficie di silicio monocristallino, opportunamente incisa nel suo ossido protettivo con canali di collegamento tra resistori e transistor in essa inseriti. Già negli anni Quaranta erano diffusi circuiti stampati su una base ceramica, con dimensioni ridotte rispetto ai circuiti abituali, ma la capacità di ottenere interi sistemi circuitali con procedimenti chimici alla superficie di cristalli, eliminando i fili di collegamento, apriva nuove possibilità. Jack Kilby (Texas Instruments) e Robert Noyce (Fairchild Semiconductor) dimostrarono per primi nel 1959 la fattibilità di tale concetto e avviarono i processi di grande integrazione, ottenendo circuiti con resistenze, condensatori e transistori inseriti alla superficie del silicio in quantità sempre crescenti. In particolare, transistor a effetto di campo, con un substrato metallico isolato nella base che può ricevere per effetto tunnel, con un campo applicato tra collettore e base, elettroni che schermano il campo applicato e impediscono il funzionamento del dispositivo, agendo come memorie. Ciò consente di inserire anche le memorie alla superficie del semiconduttore, con enormi capacità di accumulare dati ed eseguire calcoli. Le prime memorie nei chip semiconduttori comparvero all'inizio degli anni Settanta, e prima della fine del decennio avevano raggiunto la capacità di contenere 64 kilobit di informazione binaria.
Negli anni Settanta nasce così, sempre nei laboratori della Texas Instruments, della Fairchild e della nuova Società Intel, il microprocessore. Si tratta di un singolo chip (superficie di silicio, generalmente del diametro di un pollice, ossia di 2,54 cm), che esercita e controlla tutte le funzioni di un calcolatore (con circuiti, resistori, condensatori, transistor, memorie) e per questo è anche chiamato microcontrollore. All'origine di tali ricerche fu Gary Boone, della Texas Instruments, che per primo nel 1972 realizzò un microcontrollore. All'Intel le stesse idee furono implementate da Ted Hoff, che, in collaborazione con Mashatoshi Shima, dell'azienda giapponese di calcolatori Busicom, realizzò un microprocessore basato su quattro chip, e da Federico Faggin, il quale nel 1972 realizzò la logica e il disegno che permisero la creazione del primo microprocessore a singolo chip.
Tali realizzazioni sono state ottenute grazie all'impegno di grandi gruppi industriali, il che ha consentito di apportare ai dispositivi realizzati continui miglioramenti e ne ha favorito la produzione su larga scala. Il rapido progresso tecnologico nel settore ha agevolato la nascita di molte nuove società interamente dedicate alla produzione di dispositivi a semiconduttore; è emblematico il caso della concentrazione di tali società nella cosiddetta Silicon Valley negli Stati Uniti. Tale dinamica fornisce un'esemplificazione significativa dello stretto rapporto tra scienza, tecnologia e industria nella società moderna. Lo sviluppo e l'impiego dei circuiti integrati e dei microprocessori è in continua crescita: l'aumento del numero dei transistor inseribili in un singolo chip segue la cosiddetta legge di Moore, di raddoppio ogni anno, con un aumento esponenziale nel tempo, che ha portato a superare il miliardo di unità nel 2002. Contemporaneamente, a fronte di un aumento esponenziale del costo di un singolo impianto di fabbricazione (nel 2002 è di quasi 2 miliardi di dollari), si è avuta una diminuzione, pure esponenziale nel tempo, del costo di un singolo bit di informazione. Questo processo continua a essere valido e lo sarà per molto tempo, perché il suo limite teorico è ancora lontano, essendo rappresentato dalle dimensioni lineari atomiche (10−8 cm). Attualmente la dimensione lineare minima dei componenti è di 0,2 μm (=2·10−5 cm).
Proprietà ottiche e laser
I semiconduttori si sono rivelati molto importanti anche per le loro proprietà ottiche, che hanno consentito di realizzare microlaser e dispositivi per la fotonica (controllo della luce).
I processi di assorbimento di luce hanno luogo quando un elettrone viene eccitato dalla banda occupata di valenza alla banda vuota di conduzione e i processi di emissione di luce quando un elettrone da quest'ultima si ricombina con una buca nella banda di valenza. Tali processi richiedono anche la conservazione dell'impulso, per cui sono assai probabili soltanto quando le transizioni sono verticali (Δk=0), l'impulso del fotone di luce h/λ essendo trascurabile rispetto a quello degli elettroni ħk.
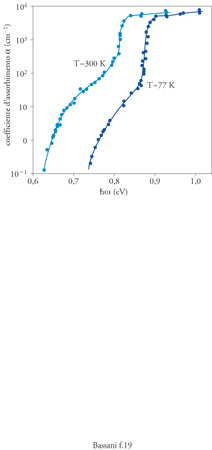
Questo spiega perché silicio e germanio sono molto vantaggiosi per le proprietà di trasporto, in quanto gli elettroni al minimo della banda di conduzione difficilmente si ricombinano con le buche al massimo della banda di valenza con diverso valore di k. Il tempo di vita dei portatori è quindi relativamente grande e consente i fenomeni di trasporto anche quando elettroni e buche sono spazialmente vicini. I processi di assorbimento e di ricombinazione indiretta (con Δk dell'ordine di grandezza di 2π/a) sono tuttavia possibili, anche se meno probabili, con un meccanismo suggerito da Bardeen negli anni Cinquanta, grazie al quale le vibrazioni del cristallo forniscono l'impulso necessario, con l'assorbimento o la creazione di un fonone (quanto di vibrazione), contestuale all'emissione o assorbimento di un fotone. Un'esemplificazione di entrambi i processi è mostrata nella fig. 10 con lo spettro della soglia di assorbimento del Ge. Le strutture dell'assorbimento ottico a frequenze superiori a quella di soglia rivelano uno spettro di eccitazione con dei picchi che sono stati interpretati in tutti i semiconduttori studiati, a partire dal lavoro di F. Bassani, D. Brust e J.C. Phillips sul germanio del 1962. Essi hanno confermato la struttura delle bande di energia anche a energie lontane dal livello di Fermi. Con elevati campi elettrici è stato possibile trasferire elettroni dal minimo della banda di conduzione a minimi secondari a energia superiore rendendo possibili le oscillazioni di corrente osservate da J.B. Gunn nel GaAs nel 1963.
I semiconduttori a gap diretta (tipo GaAs) sono particolarmente efficaci per i processi di interazione radiazione-materia con assorbimento o produzione di luce. In essi, oltre agli stati delle bande di energia, occorre anche tener conto di stati eccitati discreti che si formano entro il gap proibito a causa dell'attrazione coulombiana tra l'elettrone e la buca. Tali stati, evidenziati da Wannier e Mott nei semiconduttori inorganici e da Frenkel e Peierls in quelli organici già nei primi anni Trenta, sono gli 'eccitoni'. Essi possiedono un momento di dipolo elettrico che si combina con il campo elettrico della radiazione per produrre un nuovo tipo di particella, il 'polaritone', introdotta da U. Fano, V.M. Agranovich e J. Hopfield alla fine degli anni Cinquanta e da allora oggetto di intenso studio. I polaritoni nei semiconduttori sono l'analogo dei fotoni nel vuoto, ma presentano una legge di dispersione ω(k) caratteristica di ogni materiale e ben diversa dalla legge lineare che si ottiene lontano dalla risonanza quando l'indice di rifrazione è costante.
Transizioni interbanda ed eccitoni costituiscono gli elementi di base per agire sulla radiazione elettromagnetica producendo vari tipi di dispositivi. Un dispositivo molto usato è basato sull'assorbimento di luce e consente di trasformare direttamente la radiazione elettromagnetica in corrente elettrica (fig. 11). L'assorbimento di luce in vicinanza di una giunzione produce corrente elettrica in quanto disturba l'equilibrio statistico dei portatori, che può essere ristabilito soltanto con passaggio di corrente a circuito chiuso, o con produzione di differenza di potenziale a circuito aperto. Tale effetto fotovoltaico fu rivelato originariamente nel selenio da W.G. Adams e R.E. Day già nel 1877 e fu utilizzato da allora nelle apparecchiature fotografiche per tarare l'intensità luminosa. Nel 1954 furono realizzate da D.M. Chapin, C.S. Fuller e G.L. Pearson le prime celle al silicio per la conversione della radiazione solare in corrente elettrica, con un rendimento del 6%. Da allora il rendimento ha raggiunto in GaAs il 24%. Le celle fotovoltaiche sono oggi il dispositivo più promettente per la produzione di energia elettrica dall'energia della radiazione solare.
Il dispositivo optoelettronico più importante, anche dal punto di vista applicativo, è però il laser a semiconduttori, scoperto negli anni Sessanta. I primi laser funzionanti furono realizzati con giunzioni di GaAs nel 1962 da quattro gruppi diversi, rispettivamente guidati da R.N. Hall e da N. Holonyak ai laboratori della General Electric, da Marshall I. Nathan ai laboratori IBM e da T.M. Quist al Radiation Laboratory del MIT. L'idea essenziale è di produrre inversione di popolazione di elettroni in una giunzione p-n con alta concentrazione di impurezze, per ottenere, quando il campo elettrico agisce favorendo il trasporto di corrente, una sovrapposizione spaziale delle regioni con prevalenza di buche e di elettroni (fig. 12). Al passaggio di corrente, elettroni e buche si ricombinano emettendo fotoni, ma l'inversione di popolazione rimane per la continua iniezione di cariche. Utilizzando specchi, o le stesse superfici del semiconduttore, in modo da formare cavità risonanti, si ottiene emissione coerente stimolata con guadagno considerevole, cioè il laser. La frequenza della luce emessa può essere modificata scegliendo semiconduttori diversi con Eg opportuni, dall'infrarosso di InSb al violetto di nitruri tipo AlN o GaN.
Il vantaggio dei laser a semiconduttore rispetto ai laser atomici è nella loro praticità, per le ridotte dimensioni, nel minimo consumo, e nella semplicità con cui si ottengono la duplicazione e la moltiplicazione di frequenza e altri effetti non lineari, tra i quali la bistabilità ottica.
Le nanostrutture
Negli ultimi due decenni del XX sec. la fisica dei semiconduttori ha ricevuto nuovo impulso dalla possibilità di produrre sostanze artificiali nelle quali alcune parti sono costituite da un tipo di semiconduttore e altre da un semiconduttore diverso. Tali sostanze vengono prodotte con crescita epitassiale da fasci atomici (MBE, molecular beam epitaxy) che incidono sulla superficie di un substrato ad alta temperatura, o con deposizione chimica da vapori opportuni (CVD, chemical vapor deposition). Non sono termodinamicamente stabili in Natura ma, una volta prodotte, hanno tempi di vita praticamente infiniti a temperatura ambiente.
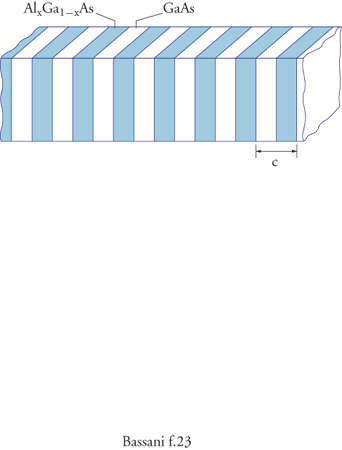
La prima e più semplice di tali strutture è il superreticolo, introdotto da L. Esaki e R. Tsu nel 1970, costituito da sequenze di n piani di un semiconduttore di parametro reticolare a e di m piani di un altro semiconduttore di parametro b, con una periodicità in una direzione na+mb. In questo modo, in tale direzione dello spazio reciproco il parametro reticolare può essere grande a piacere, l'intervallo dei valori di k è molto ridotto e le bande di energia sono strette a piacere (minibande).
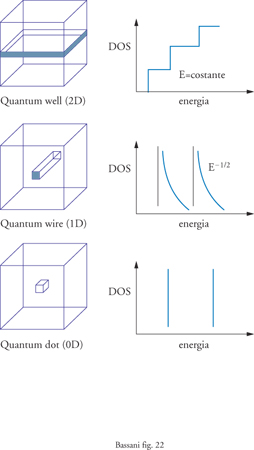
Altre nanostrutture si ottengono confinando alcuni piani di un tipo di semiconduttore con un semiconduttore a gap maggiore. Esse sono chiamate pozzi quantici (QW, quantum well), perché gli elettroni tendono ad andare nel semiconduttore confinato, collocandosi su bande di energia bidimensionali (sottobande), ognuna associata a un livello discreto prodotto dal confinamento per effetto quantistico. È evidente che in tal caso, controllando lo spessore del pozzo, si può controllare la frequenza delle transizioni tra sottobande di elettroni, o tra sottobande di valenza e di conduzione, ottenendo laser di frequenza desiderata, rivelatori nell'infrarosso ecc. La prima osservazione sperimentale delle transizioni ottiche nei pozzi quantici è stata di R. Dingle (1974), e da allora l'ottica con le nanostrutture ha costituito il settore di avanguardia della fisica dei semiconduttori. Un'importante applicazione è il laser a doppia eterostruttura realizzato da Z.I. Alferov (1969).
Se il confinamento da parte del semiconduttore a gap maggiore è in due direzioni si hanno i cosiddetti fili quantici (QWW, quantum well wire) e si ottengono sottobande unidimensionali En(k), come nelle lunghe molecole lineari (tipo il transpoliacetilene). Se il confinamento è in tre direzioni si hanno i punti quantici (QD, quantum dot), a livelli discreti come gli atomi, ma controllabili variando le dimensioni della nanostruttura. Precise osservazioni sperimentali di transizioni ottiche nei QWW e QD nello stesso campione sono state realizzate da G. Abstreiter (1997). Uno schema sintetico delle tre più comuni nanostrutture è riportato nella fig. 13. Il superreticolo può essere visto come una sequenza periodica di pozzi quantici ravvicinati (fig. 14).
Un'ulteriore nanostruttura è la microcavità, che si ottiene quando si costruisce uno strato semiconduttore di larghezza multipla di una mezza lunghezza d'onda della radiazione nel materiale, confinato con pareti totalmente riflettenti, coperte da un film metallico o, meglio ancora, formate da sequenze di strati alternati di due materiali a indice di rifrazione diversi di lunghezza λ/4 (specchi di Bragg), come esemplificato nella fig. 15. In tal caso si ottiene un'elevata concentrazione di luce di lunghezza d'onda scelta, e anche i polaritoni vengono opportunamente modificati (forte accoppiamento). I primi esempi di tali microcavità sono stati ottenuti da C. Weisbuch nel 1992. Accoppiamenti di eccitoni nella cavità (con i suoi modi ottici) producono polaritoni anomali che possono raggiungere densità elevate nel livello più basso. Studi per ottenere la condensazione di Bose-Einstein sono attualmente in corso (Deng et al. 2002).
L'utilizzazione di nanostrutture idonee alla produzione degli effetti ottici più diversi è di attuale interesse. Una possibilità segnalata teoricamente da V.M. Agranovich e G. La Rocca (1994) è quella di formare giunzioni di nanostrutture organiche e inorganiche, ottenendo strutture ibride con risposta non lineare ingigantita, e con trasferimento dell'eccitazione dalla nanostruttura inorganica e conduttrice a quella organica non conduttrice ma molto più luminescente. Si tratta di un nuovo processo di elettroluminescenza.
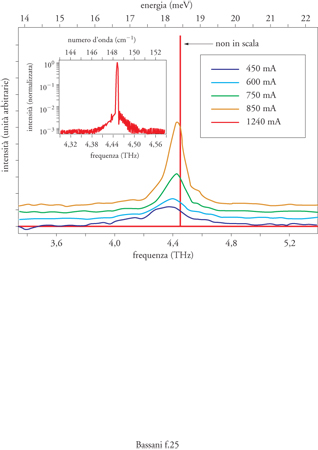
Un'ulteriore recentissima utilizzazione è quella dei laser a cascata, ottenuti da pozzi quantici e superreticoli accostati in elevato numero e spostati in energia con un campo elettrico, in modo che, una volta ottenuta l'inversione di popolazione, l'elettrone che effettua la transizione stimolata si trasferisca al livello eccitato vicino e di nuovo si trovi in inversione di popolazione per una nuova transizione, come l'acqua nei gradini di una cascata. Il processo continua tante volte quanti sono i pozzi e i superreticoli accostati. L'idea dei laser a cascata risale a R. Kazarinov e R. Suris (1971) mentre le prime realizzazioni (1994) sono di F. Capasso dei Bell Telephone Laboratories. Una recentissima applicazione di A. Tredicucci (Scuola Normale Superiore, Pisa, 2002) ha consentito di ottenere, con opportuni superreticoli, laser a cascata di ottima risoluzione spettrale, come mostrato nella fig. 16, nella regione di frequenze dei terahertz (lunghezze d'onda millimetriche e submillimetriche), di estremo interesse per la rivelazione spettroscopica di molecole complesse e per la loro capacità di attraversare la maggior parte delle sostanze.
Conclusioni
I semiconduttori, da Volta ai giorni nostri, hanno impegnato sempre maggiormente i fisici e hanno consentito risultati di grande rilievo in fisica fondamentale e applicata.
Molti premi Nobel sono stati conferiti per i risultati ottenuti nello studio dei semiconduttori: nel 1956 a Shockley, Bardeen e Brattain per il transistor; nel 1973 a Esaki per la scoperta di fenomeni di effetto tunnel nei semiconduttori; nel 1985 a K. Von Klitzing per l'effetto Hall quantizzato; nel 1988 a R.B. Laughlin, H.L. Störmer e D.C. Tsui per la scoperta di fluidi quantistici con eccitazioni a carica frazionaria; nel 1998 a Kohn per la teoria del funzionale densità; nel 2000 a J.S. Kilby per l'invenzione del circuito integrato e a Z.I. Alferov e H. Kroemer per i laser a semiconduttori e l'optoelettronica nelle eterostrutture semiconduttrici.
Nella seconda metà del Novecento, grazie ai semiconduttori, si è sviluppata una tecnologia totalmente nuova, che ha enormemente potenziato il calcolo elettronico e l'accumulazione e la trasmissione dell'informazione. Concetti fondamentali della meccanica quantistica hanno trovato nei semiconduttori la loro naturale verifica e hanno consentito molteplici applicazioni. Nuove possibilità nel campo della fotonica e dell'optoelettronica sono nate con i laser semiconduttori, in particolare utilizzando le eterostrutture.
Si può prevedere che i semiconduttori porteranno importanti risultati anche nei prossimi decenni. Nell'elettronica al silicio si è ancora lontani dal limite teorico, che è quello di poter trasmettere informazioni al livello del singolo elettrone e del singolo atomo. Nella fotonica le nuove nanostrutture promettono molto, sia per quanto riguarda la produzione di luce (laser ed elettroluminescenza), sia per effetti non lineari nelle microcavità e nei sistemi ibridi organico-inorganico. La trasmissione dell'informazione e lo sviluppo del calcolo mediante l'ottica anziché la corrente è un ambizioso obiettivo che potrà essere realizzato soltanto con ulteriori progressi nel campo dei semiconduttori.
Bibliografia
Bassani, Pastori-Parravicini 1975: Bassani, Franco - Pastori-Parravicini, Giuseppe, Electronic states and optical transitions in solids, Oxford, Pergamon, 1975.
Bassani, La Rocca 1996: Bassani, Franco - La Rocca, Giuseppe, Semiconductors, elemental-electronic properties, in Encyclopedia of applied physics, New York, V.C.H., 1996, p. 403.
Bassani 1998: Bassani, Franco, Semiconduttori, proprietà generali, in Enciclopedia del Novecento, Roma, Istituto dell'Enciclopedia Italiana, 1998, Suppl. II, p. 633.
Bassani, Grassano 2000: Bassani, Franco - Grassano, Umberto M., Fisica dello stato solido, Torino, Bollati Boringhieri, 2000.
Bastard 1991: Bastard, Gérald, Quantum mechanics of microstructures and superlattices, Paris, Editions de Physique, 1991.
Busch 1993: Busch, George, Early history of physics and chemistry of semiconductors: from doubts to facts in a hundred years, "Condensed matter news", 2, 1993, pp. 15-27.
Deng 2002: Deng, Hui - Santori, Charles - Bloch, Jacqueline - Yamamoto Yoshihisa, Condensation of semiconductor microcavity exciton polaritons, "Science", 298, 2002, pp. 199-202.
Frova, Perfetti 1997: Frova, Andrea - Perfetti, Paolo, Semiconduttori, proprietà ed applicazioni elettroniche, Roma, Veschi, 1997.
Ivchenko, Pikus 1997: Ivchenko, Eohgenius L. - Pikus, Grigori E., Superlattices and other heterostructures, Berlin-New York, Springer, 1997, 2. ed. (1. ed.: Berlin-London, Springer, 1995).
Seitz, Einspruch 1998: Seitz, Frederick - Einspruch, Norman G., Electronic genie, the tangled history of silicon, Urbana, University of Illinois Press, 1998 (trad. it.: La storia del silicio: elettronica e comunicazione, Torino, Bollati Boringhieri, 1998).
Yu, Cardona 1995: Yu, Peter Y. - Cardona, Manuel, Fundamentals of semiconductor physics, Berlin, Springer, 1995.