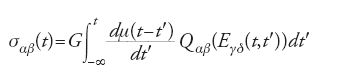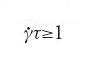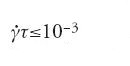La grande scienza. Materia condensata soffice
La grande scienza. Materia condensata soffice
Materia condensata soffice
La fisica della materia condensata soffice si occupa di colloidi, soluzioni polimeriche, emulsioni, schiume, soluzioni tensioattive, polveri e materiali simili. Si tratta di sistemi largamente presenti nella nostra vita quotidiana: ne sono esempi le vernici, l'olio per motori, la maionese, la crema da barba, il talco e così via. In tutti questi casi, la composizione molecolare precisa del sistema ha solo una limitata influenza sul comportamento fisico, che è controllato dalla struttura su scala mesoscopica, cioè su lunghezze che vanno da 1 nm (10−9 m) a 1 μm (10−6 m), facilmente modificabile da agenti esterni quali le sollecitazioni meccaniche. Le peculiari proprietà meccaniche di tali fasi condensate soffici sono ampiamente sfruttate sia dalla Natura sia dall'uomo, tanto direttamente quanto nei processi di trasformazione. Un esempio di queste ultime applicazioni è la modellatura di un oggetto di plastica dura per stampa da una colata: i fusi polimerici rappresentano la materia condensata soffice per eccellenza.
Nella seconda metà del XX sec., e specialmente negli ultimi due decenni, la comprensione della fisica della materia condensata soffice ha compiuto notevoli progressi. Le ragioni determinanti sono molteplici.
In primo luogo, molti elementi propulsori per la ricerca in questo campo sono venuti dall'industria. Infatti, la larga disponibilità di campioni sintetici di materiali polimerici e colloidali ben controllati risale solo agli anni Quaranta e Cinquanta e può essere vista come un sottoprodotto della nascita, all'incirca contemporanea, dell'industria della plastica. In precedenza, gli interessi vertevano su materiali reperibili in Natura, come la gomma naturale, o dotati di scarsa riproducibilità; dagli anni Cinquanta in avanti, invece, è emersa con chiarezza la motivazione industriale per una più profonda comprensione delle proprietà fisiche dei polimeri, stimolata da numerosi fattori trainanti come, dagli anni Sessanta in poi, la produzione di alimenti a livello industriale, che ha richiesto un approccio di gran lunga più scientifico alla comprensione della stabilità meccanica dei materiali soffici. Successivamente, la crescente attenzione per le tematiche dell'ambiente e della salute ha mantenuto alto questo interesse; per esempio, vernici e rivestimenti che tradizionalmente erano composti con solventi organici nocivi, sono ora principalmente a base di acqua; molti cibi, cui di solito erano addizionati conservanti chimici o grassi idrogenati artificialmente, non contengono più tali componenti. In molti di questi casi è la migliore applicazione della fisica, vale a dire il controllo della struttura sotto lavorazioni meccaniche o termiche, che consente un minor ricorso a metodi chimici di stabilizzazione del prodotto.
Al di là di queste motivazioni industriali, lo studio della materia condensata soffice ha fortemente tratto beneficio da sviluppi scientifici più ampi. Molti progressi sono derivati dall'evoluzione dei metodi sperimentali, in particolare dalla diffusione di luce laser, di raggi X e di neutroni, usati per esaminare la struttura statica e dinamica dei materiali. La diffusione della luce laser è risultata particolarmente preziosa, in quanto permette di risolvere scale di lunghezza adatte per sondare la struttura mesoscopica; inoltre, da un punto di vista dinamico, lo studio dei tempi di correlazione dell'intensità della luce diffusa consente di caratterizzare dettagliatamente il moto sulla scala di lunghezza del micron. Dagli anni Ottanta in poi, la potenza di tali metodi è stata ulteriormente accresciuta con lo sviluppo di tecniche che permettono l'interpretazione dei dati della luce laser diffusa da materiali torbidi o persino opachi.
Di importanza comparabile a questi progressi nei metodi sperimentali è stato l'affermarsi delle simulazioni al calcolatore come valido mezzo di indagine. Le prime simulazioni di liquidi a sfere rigide, assimilabili, come diremo, ai colloidi, furono eseguite alla fine degli anni Cinquanta; i lavori importanti sulla statistica dei polimeri iniziarono negli anni Sessanta e quelli sulla dinamica dei polimeri negli anni Settanta e Ottanta; agli anni Ottanta e Novanta risalgono quelli sui fenomeni di autoorganizzazione. Tutti questi campi di ricerca, insieme a molti altri, si sono sviluppati con la crescita della disponibilità di computer sempre più potenti ma, tuttavia, all'inizio del XXI sec. molti argomenti importanti relativi alla materia condensata soffice risultano eccessivamente complessi per poter essere risolti con le sole simulazioni numeriche.
Un'ultima motivazione per gli importanti progressi in questo campo è stato il perfezionamento dei metodi teorici basati sugli sviluppi della meccanica statistica. Alcuni di essi, come le tecniche di scaling e il gruppo di rinormalizzazione, nati negli anni Sessanta per studiare le transizioni di fase, sono generali e di grande portata. Altri, come il modello a tubo per il groviglio polimerico, furono inventati per problemi specifici della materia soffice e non hanno né precedenti né analoghi in altri campi della fisica. Durante la seconda metà del XX sec. grazie a una prudente combinazione di metodologie teoriche specifiche e generali fu possibile interpretare e, talvolta, prevedere quantitativamente, un numero crescente di proprietà fisiche della materia condensata soffice, in termini di pochi concetti unificanti come l'elasticità entropica e il moto browniano. Dai primi studi degli anni Quaranta e Cinquanta alla fine del secolo, i materiali condensati soffici, quali i colloidi e i polimeri, hanno offerto un importante terreno di prova per idee emergenti in meccanica statistica. Questa simbiosi tra gli esperimenti in materia condensata soffice e gli aspetti teorici della meccanica statistica è un tema ricorrente nella presente trattazione.
La fisica della materia condensata
La fisica della materia condensata descrive il comportamento di sistemi contenenti moltissime particelle, a una densità tanto alta che ciascuna interagisce con numerose altre. Esempi tipici sono i solidi cristallini e i liquidi. Poiché ogni atomo o molecola interagisce con numerosi vicini e ognuno di questi con molti altri, e così via, l'intero sistema di particelle è accoppiato. Questa forte correlazione conferisce speciali proprietà collettive al materiale, quali l'elasticità di un cristallo e la viscosità (resistenza allo scivolamento) di un liquido. Non si possono di solito comprendere tali proprietà riferendosi a singole particelle isolate e neppure a piccoli gruppi di particelle: la fisica della materia condensata è, sostanzialmente, un problema a 1023 corpi.
Durante la prima metà del XX sec. furono compiuti enormi progressi nello studio delle fasi condensate, come i solidi cristallini regolari, applicando alle disposizioni periodiche (reticoli) di atomi le leggi, allora da poco scoperte, della meccanica quantistica. Questo lavoro continua ancora oggi, con l'impiego di tecniche sempre più sofisticate. Tuttavia la meccanica quantistica da sola non è sufficiente: per esempio, la comprensione del magnetismo nei solidi ha richiesto non solo la teoria quantistica ma anche l'impiego degli strumenti della fisica statistica. È stato cioè necessario prendere in considerazione le regole che permettono di calcolare la probabilità che un sistema a molti corpi si trovi in un particolare stato fisico microscopico (uno specifico stato quantistico o 'microstato') a una data temperatura. Le proprietà collettive di una fase condensata sono allora espresse come medie su questa distribuzione di probabilità. Da piccoli cambiamenti nei parametri di controllo, come la temperatura, possono talvolta derivare cambiamenti bruschi in queste proprietà; quando tale comportamento diventa sempre più singolare andando verso il limite termodinamico (di grandi dimensioni del sistema), tali fenomeni sono detti 'transizioni di fase'.
Poiché, all'equilibrio termico, un sistema grande visita molti microstati, il suo comportamento dipende sia dal numero di microstati esistenti in un dato intervallo di energia, sia dalle caratteristiche fisiche dei microstati stessi. Per esempio, il fatto che un materiale ferromagnetico (spin su un reticolo) perda completamente la sua magnetizzazione quando riscaldato al di sopra di una temperatura critica (la temperatura di Curie) si può spiegare qualitativamente come segue. A bassa temperatura, il sistema resta negli stati energetici di bassa energia E, stati che sono tutti magnetizzati (gli spin, in media, sono allineati lungo uno stesso asse); ad alta temperatura, il sistema campiona stati che sono collocati in un intervallo di energia più ampio, la maggior parte dei quali sono non magnetizzati (non allineati). La scomparsa della magnetizzazione segnala il prevalere della tendenza a massimizzare l'entropia S (che è, quantitativamente, il logaritmo del numero di microstati che il sistema può campionare) sulla tendenza a minimizzare l'energia. La magnetizzazione va a zero con continuità nel punto di transizione di fase ma la sua forma funzionale cambia, così che, per esempio, la sua derivata rispetto alla temperatura è discontinua.
Questa fondamentale competizione è quantificata nella celebre formula di Hermann von Helmholtz (1821-1894) per l'energia libera:
[1] F=E−TS.
Lo stato di equilibrio termodinamico alla temperatura T in un sistema di composizione fissata (e per un fissato volume V) è quello che minimizza l'energia libera F. Questo rappresenta un enunciato conciso delle leggi della meccanica statistica dell'equilibrio, come concepite da Ludwig Boltzmann (1844-1906) e da Josiah Willard Gibbs (1839-1903). La ricerca negli ultimi anni del XX sec., per esempio nei sistemi magnetici disordinati, ha continuato a occuparsi della competizione tra energia ed entropia, rivelando un 'campo di battaglia' di sorprendente complessità.
Ugualmente vitale è stato il problema relativo alla dinamica: capire come un sistema a molti corpi si avvicina al suo stato di equilibrio e se può restare 'intrappolato' lontano dall'equilibrio; oppure che cosa accade se il sistema viene costantemente 'forzato' da un'immissione di energia dall'esterno.
Materia condensata soffice: una definizione preliminare
Non esiste per la materia condensata soffice una definizione su cui vi sia un accordo generale, ma una possibilità è la seguente: un corpo è costituito di materia condensata soffice se resiste fortemente alla compressione, ma debolmente al taglio. Un esempio è dato da un pezzo di gomma naturale a legami incrociati (lattice): esso può essere facilmente deformato a volume costante ma, forse sorprendentemente, la sua resistenza a cambiamenti di volume, misurata dal modulo di compressibilità, è alta quanto quella di un solido cristallino. È in questo senso che possono essere qualificati come materia condensata soffice i seguenti materiali: gel polimerici (gelatina), emulsioni (maionese), soluzioni detergenti viscoelastiche (shampoo), reticoli cristallini di grassi (margarine), colloidi concentrati (vernici), soluzioni di polimeri (olio per motori multigrade) e cristalli liquidi liotropici (per es., la poltiglia prodotta da una saponetta quando è lasciata in una pozza d'acqua). È meno immediato qualificare come materia soffice la schiuma da barba e la spuma della birra, che sono anch'esse relativamente incompressibili finché non è permessa la fuga del gas intrappolato al loro interno.
Rientrano in questa categoria anche i colloidi densi (come le salse collose che si ottengono mescolando maizena - amido di mais - con acqua). Questi possono sviluppare, sotto forti pressioni, un'alta resistenza alle deformazioni di taglio (un fenomeno chiamato 'ispessimento al taglio', shear thickening), ma sono comunque più facili da deformare trasversalmente piuttosto che da comprimere. Il caso delle polveri secche è leggermente anomalo, in quanto possono assumere vari volumi a seconda di come il campione è stato agitato - questa è la ragione per cui un pacchetto di fiocchi di mais quando arriva nei negozi è meno pieno rispetto al momento in cui viene confezionato - e tendono anche a dilatarsi quando sono sottoposte a taglio ('dilatanza'). Perciò esse non si adattano facilmente alla definizione scelta sopra ma vengono tradizionalmente fatte rientrare nel campo della materia condensata soffice, perché molti aspetti del loro comportamento sono strettamente simili a quelli dei colloidi densi.
Tutti questi materiali differiscono dai liquidi semplici, come l'acqua. Quest'ultima non si comprime facilmente e, si potrebbe dire, oppone poca resistenza alle sollecitazioni di taglio, ma in un modo puramente viscoso: lo sforzo interno è proporzionale alla velocità della deformazione. Questo comportamento è detto 'newtoniano', dal nome di Isaac Newton (1642-1727), che per primo lo descrisse. Al contrario, la maggior parte dei materiali elencati in precedenza si oppone alle sollecitazioni secondo una modalità detta 'viscoelastica': la loro risposta alla deformazione mostra una mescolanza di caratteristiche elastiche e viscose. Per esempio, una soluzione polimerica, cui sia applicata una piccola forza di taglio, dapprima risponde elasticamente, cioè con uno sforzo di taglio proporzionale alla forza applicata per unità di superficie (la pressione di taglio) ma, dopo un tempo limitato (un secondo o due o, in alcuni casi, molto di più), inizia a fluire come un liquido, con una velocità di deformazione (non la deformazione stessa) proporzionale allo sforzo. Ne sono un esempio alcuni giocattoli divertenti quale lo 'stucco sciocco' (silly putty), che rimbalza come una palla di gomma ma che, se lasciato a sé, si estende fino a formare sul piano d'appoggio una frittella sottile. Il primo studioso che considerò tale comportamento teoricamente fu James C. Maxwell (1831-1879), che ne diede una semplice descrizione teorica, oggi conosciuta come 'modello di Maxwell'.
La distinzione che abbiamo fatto è basata sulle scale di tempo: anche l'acqua dapprima risponde elasticamente, ma per un tempo così breve che la maggior parte degli esperimenti non riesce a rilevarlo. I materiali soffici mostrano invece un qualche grado di elasticità su scale temporali facilmente osservabili (dai millisecondi ai giorni). Si noti che molti materiali soffici, tra i quali tutti gli esempi elencati, sono formati principalmente da un fluido semplice, come l'acqua, nel quale sono sospesi oggetti 'mesoscopici', la cui struttura si estende su una scala che varia dal nanometro al micron e la cui dinamica lenta prolunga la risposta elastica. Esempi importanti sono i polimeri (lunghe molecole a catena) o le particelle colloidali (grumi sferici o irregolari di materia dura). In entrambi questi casi, gli oggetti in sospensione hanno caratteristiche permanenti: a meno che non siano applicate loro condizioni estreme, essi rimangono intatti per tutta la vita del materiale. Casi differenti, in cui gli oggetti in sospensione sono transitori, verranno trattati più avanti.
L'equilibrio termico
Uno dei risultati più importanti raggiunti negli ultimi decenni del XX sec. è stata la comprensione, almeno a un livello schematico, della meccanica statistica d'equilibrio dei principali materiali soffici, tra i quali le soluzioni polimeriche e le sospensioni colloidali. In molti casi interessanti la fisica è dominata dal termine entropico dell'equazione [1].
I polimeri
Una catena polimerica lineare è una lunga sequenza non ramificata di unità chimicamente identiche collegate da legami e dotata di una certa flessibilità. Una tale catena può essere esaminata semplicemente, su una scala abbastanza grande, come una linea a zig zag: c'è un numero cospicuo di microstati (corrispondenti a varie sequenze di configurazioni di legami nella catena) con energie simili. Su questa scala i dettagli della chimica locale non sono rilevanti: le proprietà di un polimero possono essere considerate 'universali'. Sotto tali condizioni, è solo la massimizzazione dell'entropia a essere importante nella minimizzazione dell'energia libera; da questo punto di vista ogni catena può essere vista come un 'cammino casuale' (random walk). Questo termine sta a denotare un cammino composto da una sequenza di passi, ognuno dei quali è fatto in una direzione casuale rispetto a quello precedente. In due dimensioni, si può illustrare il cammino casuale come la passeggiata di un ubriaco che si allontana barcollando da un bar, senza sapere dove è stato o dove sta andando. In tre dimensioni, il percorso tracciato da un polimero è simile, con la condizione limitativa importante che le catene non possono intersecarsi l'una con l'altra né autointersecarsi. L'effetto dettagliato di questo vincolo di 'volume escluso' sulla statistica della catena è sottile a intendersi, ma l'effetto complessivo è che la catena si espande riempiendo una regione più grande di spazio.
Si noti che un singolo polimero esplora costantemente il gran numero di microstati a esso accessibili (attraverso il moto browniano); perciò ben poche proprietà significative possono essere definite se non come una media sugli stati visitati. Tutto questo differisce significativamente da ciò che si verifica per gli atomi o le molecole in un materiale duro 'convenzionale', come il ferro, dove le fluttuazioni entropiche possono essere viste come piccoli spostamenti (chiamati 'fononi') da un ben definito stato di base (il reticolo periodico). Per i polimeri, così come accade sempre nella materia condensata soffice, le fluttuazioni costituiscono, invece, la base delle proprietà fisiche. Ciò rende l'uso della meccanica statistica particolarmente stimolante e importante.
Molti progressi nella comprensione della meccanica statistica dei polimeri sono stati compiuti, tra gli altri, da Paul J. Flory, premio Nobel per la chimica nel 1974, Pierre-Gilles de Gennes, premio Nobel per la fisica nel 1991 e Samuel F. Edwards, medaglia Boltzmann 1998. Per esempio, Flory ha ideato una sottile trattazione approssimata del problema del volume escluso, che è stato in seguito tradotto nel formalismo della teoria dei campi da Edwards; de Gennes ha sfruttato questa intuizione per collegare il problema a una transizione di fase magnetica in un certo limite (Flory 1953; de Gennes 1979; Doi e Edwards 1986).
I colloidi
Un altro esempio di fisica dominata da fattori entropici è quella dei colloidi di sfere rigide, vale a dire colloidi in cui le particelle colloidali sono schematizzabili come sfere rigide. Si consideri una sospensione di sfere di raggio dell'ordine del micron, le cui interazioni sono puramente repulsive e attive su distanze molto corte. Ciò equivale a dire che sono vietate le distanze da centro a centro più piccole del diametro di una particella (sfere rigide) ma non si esercita alcuna forza tra le sfere a separazioni più grandi. Ne consegue che tutti i microstati permessi, che sono quelli senza sovrapposizioni tra le sfere, hanno esattamente la stessa energia. Perciò, minimizzare l'energia libera F equivale semplicemente a massimizzare l'eutropia S; anche la temperatura T è irrilevante.
Lo stato di equilibrio dipende dalla concentrazione delle sfere, espressa di solito attraverso la loro 'frazione di volume' φ=4/3π R3N/V, dove N è il numero delle sfere nel volume V e R il loro raggio. Un modo semplice di vedere la massimizzazione dell'entropia consiste nel farla corrispondere allo stato di massimo disordine. Tuttavia questo punto di vista è fuorviante in tale contesto: infatti, per alte concentrazioni, tali che 0,545≤φ≤0,74 (nessuna concentrazione maggiore di 0,74 è possibile per le sfere rigide), si trova che lo stato di entropia più alta è un reticolo regolare, detto 'cristallo colloidale'. Un tale cristallo ha proprietà notevoli: per esempio, i suoi piani reticolari causano la diffusione della luce visibile, analogamente alla diffusione di Bragg dei raggi X comunemente utilizzata per sondare la struttura dei solidi atomici. Questa proprietà conferisce al materiale un aspetto iridescente e variopinto, cui ci si riferisce con il termine 'opalescenza', che deriva dall'analogia con l'aspetto della luce diffusa dagli opali.
La possibilità che le sfere rigide potessero cristallizzare in assenza di interazioni attrattive venne suggerita sul finire degli anni Trenta da John G. Kirkwood; a questo seguì la prima prova sperimentale, la pionieristica simulazione al computer fatta da Berni J. Alder (medaglia Boltzmann 2001) alla fine degli anni Cinquanta. Un argomento strettamente collegato, cioè la presenza di un ordine di orientamento nei fluidi a bacchette dure, fu risolto da Lars Onsager, premio Nobel per la chimica nel 1968.
Per comprendere come la massimizzazione dell'entropia possa portare a una fase ordinata, occorre distinguere due contributi differenti all'entropia. Il primo è l'entropia associata alla densità media di particelle ϱ(r) che dipende dalla posizione r. Questo contributo, Sϱ=−k∫ϱlnϱd3r, è massimo per una densità media uniforme, cioè per ϱ=costante, come quella che si presenta nello stato fluido (k è la costante di Boltzmann). La fase cristallina, nella quale ϱ è fortemente accentuata sui siti reticolari, è nettamente sfavorita in termini di Sϱ. Tuttavia vi è un secondo contributo all'entropia, che è molto più difficile da calcolare: un termine collettivo SC. Questo termine riflette la difficoltà che le particelle hanno nell'evitare localmente i loro vicini. In un fluido denso colloidale, poche sfere possono essere spostate a una distanza significativa senza richiedere che si muovano anche molte sfere vicine. In altri termini, il moto delle sfere nello stato fluido è estremamente correlato; ciò significa che il numero di microstati (o le configurazioni distinte di sfere) realmente disponibili per un dato valore della frazione di volume φ è molto minore di quanto il termine Sϱ potrebbe suggerire. Se, d'altra parte, le sfere occupano un reticolo ordinato (in media), allora ognuna ha una maggiore libertà di effettuare piccoli spostamenti dalla sua posizione nel reticolo, senza interferire con i suoi vicini, rispetto a un fluido della stessa frazione di volume. Qualitativamente, questo si verifica perché l'ordine a lungo raggio di un reticolo cristallino è molto efficace per impacchettare le sfere e quindi rimane più spazio per l'esplorazione locale. Pertanto, SC è molto più grande per il cristallo che per il fluido, se la densità è alta. Il risultato è che quando φ è abbastanza elevata, Sϱ+SC è più grande per il cristallo che per una fase fluida disordinata e, perciò, il cristallo è stabile. Argomenti simili si applicano a casi più complessi, come una sospensione mista di sfere colloidali di diverse dimensioni.
Benché il colloide di sfere rigide sia sospeso in un solvente, al fine di valutare l'energia libera F il solvente può essere quasi ignorato, poiché esso contribuisce all'energia libera per una quantità grande ma pressoché costante. Per sfere rigide ideali a una data frazione di volume, la minimizzazione di F può essere perciò effettuata come se le sfere si trovassero nel vuoto; ciò è stato tacitamente assunto finora. Tali calcoli sono stati effettuati per la prima volta in un contesto diverso, vale a dire per un modello semplice di un fluido atomico - ma sono ben più sensati per i colloidi, perché le particelle colloidali sono più assimilabili a sfere rigide di quanto lo siano gli atomi. Il lavoro sperimentale sulle sospensioni colloidali ha perciò rappresentato (dal 1980 ca.) un terreno di verifica fertile per le teorie classiche dello stato liquido e della cristallizzazione. Mediante esperimenti su opportune miscele, per esempio colloidi più polimeri, si possono manipolare le interazioni colloidali per verificare queste teorie in maggiore dettaglio, per esempio aggiungendo una componente attrattiva alle interazioni tra le particelle colloidali.
Questo approccio, che considera i colloidi come 'modelli di sistemi atomici', è stato esaminato da Peter N. Pusey (1991) e, più recentemente, da Valerie J. Anderson e Henk N.W. Lekkerkerker (2002).
L'elasticità entropica
I materiali citati finora (gel, emulsioni, colloidi, ecc.) sono tutti soffici; tuttavia ci si chiederà che cosa conferisca loro una certa elasticità e perché il modulo di taglio statico (elasticità trasversale) non è nullo, come nei fluidi semplici.
La prima risposta soddisfacente a questa domanda è stata data per il caso degli elastomeri, quali le gomme a legami incrociati e i gel polimerici. Un elastomero è formato da una rete di trefoli polimerici, a ognuno dei quali è associato un cammino casuale, tenuti insieme nei punti di congiunzione. Se il gel è improvvisamente deformato a temperatura costante, i trefoli, che si muovono a caso, devono cambiare la loro forma media: essi si stirano nella direzione di allungamento. L'entropia di un insieme di trefoli deformati è inferiore a quella di un insieme non deformato perché, per definizione, il cammino casuale originario è lo stato più casuale possibile (in questo caso l'argomento semplice, cioè che la casualità massima equivalga all'entropia massima, risulta corretto). Pertanto, l'energia libera di Helmholtz F aumenta in seguito a una deformazione. L'entità dell'aumento è calcolabile con modelli statistici; per una piccola deformazione di taglio, caratterizzata da un piccolo angolo di deformazione γ (misurato in radianti), la variazione di energia libera è ΔF≃kTNγ2, dove k è la costante di Boltzmann e N è il numero di trefoli della rete. Uguagliando questa energia libera immagazzinata a VGγ2/2 si definisce il modulo di elasticità di taglio G; questo è dell'ordine di kTN/V, vale a dire kT volte il numero di 'gradi di libertà elastici' (N) per unità di volume V. I valori di G per un gel polimerico tipico si collocano nell'intervallo (10,104) Pa, a seconda della concentrazione del polimero e della quantità di legami incrociati. Il limite superiore di questo intervallo si trova numerosi ordini di grandezza al di sotto del modulo di taglio di un comune metallo. Al limite inferiore, un valore G≃10 Pa rappresenta un materiale la cui elasticità somiglia a quella di un albume d'uovo a metà cottura.
Queste stime sull'ordine di grandezza del modulo degli elastomeri derivano dal lavoro pionieristico realizzato nel 1953 da Flory e altri. Dagli anni Settanta in poi sono state sviluppate sofisticate teorie quantitative per il comportamento elastico degli elastomeri per tener conto, per esempio, dell'effetto di 'aggrovigliamento'. Quest'ultimo deriva dal fatto che le catene polimeriche non possono intersecarsi; ne risulta un accorciamento effettivo dei trefoli della rete e un aumento del loro numero.
Valori ancora più piccoli (G≤1 Pa) possono presentarsi nel caso di cristalli colloidali. Per questi, si applica una formula simile: G≃kTN/V dove N è il numero delle sfere. Confrontata con un coefficiente così piccolo, anche la forza di gravità, agente su un campione largo alcuni millimetri, è rilevante. Di solito un campione più grande di questo crollerà sotto il proprio peso, formando in una provetta un menisco quasi piatto, in modo tale che a un occhio inesperto può sembrare un fluido (Pusey 1991).
Sia negli elastomeri sia nei cristalli colloidali, il piccolo valore del modulo di taglio G deriva dal piccolo numero di gradi di libertà elastici (catene o sfere) per unità di volume. In un solido convenzionale i gradi di libertà elastici corrispondono ad atomi o a piccole molecole; il numero di questi oggetti per unità di volume è di gran lunga più alto, conferendo a G valori dell'ordine di 108 Pa o maggiori. Si noti che simili argomenti non si applicano al 'modulo di compressibilità' di volume K, il quale controlla la risposta in energia libera, ΔF=1/2 K(ΔV)2, a cambiamenti di volume ΔV in un sistema di composizione fissata. Esso è determinato non dai polimeri o dai colloidi, ma dal liquido circostante, che è acqua o qualche altro materiale molecolare 'normale' (per cui, di solito, K≥108 Pa). D'altra parte, lo sperimentatore può scegliere di studiare, invece di K, il 'modulo di osmosi'
Questo è definito (e misurato) confinando un materiale soffice all'interno di una cella semipermeabile di volume variabile. In questo caso la composizione del sistema non è fissata: il solvente può entrare e uscire, mentre i polimeri o le particelle colloidali sono confinati nella cella. Il contributo del solvente alla compressibilità di volume è perciò eliminato e si trova che
è di nuovo molto piccolo, all'incirca paragonabile a G.
Le miscele
In molti materiali sono contemporaneamente presenti sia polimeri sia colloidi. Essi possono essere accompagnati da goccioline di emulsione o aggregati tensioattivi o da ulteriori tipi di materia in sospensione, praticamente in ogni combinazione possibile. Tali componenti possono interagire in modo fortemente non additivo: vale a dire che un materiale di questo tipo è molto di più della somma delle sue parti.
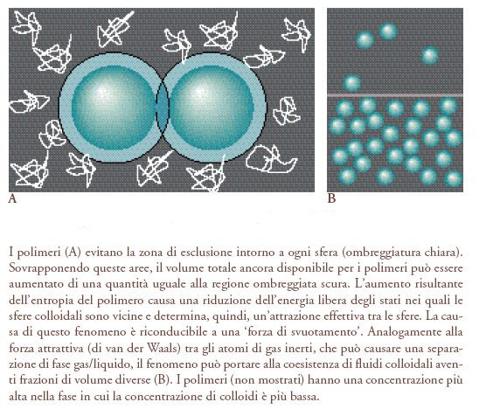
Si supponga che siano miscelate in una soluzione grandi sfere e piccoli polimeri. Le spirali del polimero non possono avvicinarsi troppo alle sfere senza appiattirsi lungo la superficie - una deformazione che farebbe perdere loro entropia. Per evitare ciò, i polimeri tendono a stare fuori da una 'zona di esclusione' intorno a ogni sfera; anche questo fa perdere ai polimeri l'entropia, sebbene non in grande quantità. È possibile però una combinazione ancora più economica: cioè la sovrapposizione delle zone di esclusione di diverse particelle colloidali. Tali sovrapposizioni significano che il 'volume escluso' totale (il volume in cui i polimeri non possono entrare senza deformarsi fortemente) è ridotto, cosicché l'entropia del polimero aumenta (fig. 2). L'argomento mostra che l'energia libera dei polimeri è minimizzata negli stati in cui le grandi sfere sono vicine. Ne consegue che è proprio come se ci fosse una forza attrattiva tra le sfere. Il raggio d'azione di questa 'attrazione entropica' mediata dai polimeri dipende dalla dimensione media della catena, la sua intensità dalla concentrazione del polimero.
La fisica delle particelle colloidali in una tale miscela è strettamente analoga a un sistema di atomi inerti (come l'argon). Questi si respingono fortemente quando le loro nuvole elettroniche si sovrappongono ma, a distanze leggermente più grandi, si attraggono debolmente. Regolando la concentrazione del polimero, si possono progettare sperimentalmente gli analoghi delle diverse fasi di un sistema atomico. Come nel caso della transizione tra fluido colloidale e cristallo colloidale, si trova ora una transizione 'gas-liquido' tra due fluidi colloidali che hanno diverse frazioni di volume φ. Variando con attenzione la dimensione del polimero si può mostrare che, quando le interazioni attrattive sono di portata abbastanza lunga, esiste solo lo stato liquido. Oltre a essere importante per la comprensione dei colloidi, tale lavoro è illuminante per una questione fondamentale di fisica molecolare: l'origine dello stato liquido (Pusey 1991; Anderson e Lekkerkerker 2002).
Forze coulombiane e di dispersione
In molti materiali soffici le interazioni coulombiane, cioè elettrostatiche, sono vitali: i polimeri, i colloidi e i tensioattivi possono contenere gruppi chimici che si ionizzano se messi in acqua. Le forze di Coulomb si pongono, insieme all'entropia, come un fattore determinante delle proprietà fisiche, almeno nei sistemi acquosi e specialmente in quelli biologici. Altrettanto fondamentali sono le forze di dispersione, interazioni attrattive causate dalla correlazione di momenti di dipolo fluttuanti su vari atomi o molecole.
Teorie sulle soluzioni ioniche semplici (come il cloruro di sodio) sono state sviluppate all'inizio del XX sec. e completate più tardi, introducendo le forze di dispersione, nelle teorie sulle interazioni di superficie dovute a Lev D. Landau, premio Nobel per la fisica nel 1962, e altri (Israelachvili 1985). Dalla fine del XX sec. i problemi rilevanti in quest'area hanno principalmente riguardato gli effetti delle forti correlazioni fra le cariche; per esempio, le teorie correnti non possono trattare adeguatamente i sistemi 'macroionici' nei quali una catena polimerica o una particella colloidale portano centinaia di cariche, le cui posizioni sono, perciò, fortemente correlate. In alcuni regimi di forte correlazione di carica, anche la semplice determinazione del segno dell'interazione (attrattiva o repulsiva) rimane ancor oggi problematica.
La dinamica
Anche quando le particelle in sospensione sono permanenti (come nei sistemi colloidali e polimerici) e della stessa taglia, il loro comportamento dinamico può essere piuttosto complicato. In particolare, la risposta del materiale a un flusso dipende da quanto velocemente la sua struttura interna può riorganizzarsi per adattarsi alla forma mutevole del campione.
Il meccanismo di base di questa riorganizzazione è il moto browniano: il lento e tortuoso procedere di un corpuscolo in sospensione causato dalle collisioni casuali e continue con le molecole del fluido circostante. La definizione di moto browniano deriva dal nome del botanico Robert Brown (1773-1858), che per primo osservò il fenomeno su grani di polline sospesi in acqua; il moto browniano fu spiegato nel 1905 da Albert Einstein, premio Nobel per la fisica nel 1921. Tra l'altro, l'effetto fu utilizzato da Jean-Baptiste Perrin per determinare il valore della costante di Boltzmann k, lavoro per il quale egli ricevette il Nobel per la fisica nel 1926.
Il moto browniano nella materia condensata soffice è complicato dal fatto che (a) i corpuscoli in sospensione si scontrano l'uno con l'altro così come con le molecole del solvente; (b) nel caso di oggetti flessibili come i polimeri, le collisioni ne cambiano la forma, oltre che la posizione. Una delle conseguenze è che i polimeri in soluzione, al di sopra di una certa concentrazione, si 'aggrovigliano' irrimediabilmente l'uno con l'altro: il sistema assomiglia a spaghetti scotti (o, volendo dare una immagine più forte, a un barattolo di vermi). Il flusso di un fluido polimerico è dominato dalla lentezza con cui questi grovigli possono essere districati dal moto browniano. Una proposta tecnica ad hoc, per la prima volta presentata da de Gennes, è stata sviluppata da Edwards e Doi in una teoria semplificata ma quantitativa della viscoelasticità dei polimeri, chiamata 'modello a tubo' (Doi e Edwards 1986). Ogni catena polimerica è immaginata come confinata in un tubo formato dal groviglio con le catene vicine; le collisioni la tengono all'interno del tubo, ma il moto browniano le consente ancora di strisciare lentamente lungo l'asse del tubo (Tav. I).
Con il modello a tubo si può spiegare la seguente evidenza sperimentale. Si prenda un materiale soffice polimerico; lo si deformi trasversalmente di un piccolo angolo γ, che sia poi mantenuto costante, e si misuri la tensione di taglio risultante, σ(t), come funzione del tempo t a partire dal momento in cui viene applicata la tensione. Per un solido elastico, come il gel polimerico a legami incrociati sopra considerato, la tensione soddisfa in ogni istante la relazione σ=Gγ. Per un materiale viscoelastico, si trova σ=Gγμ(t) dove μ(t) è una funzione decrescente di t. Per convenzione μ(0)=1 cosicché G rappresenta un coefficiente di elasticità istantaneo e μ(t) il suo decadimento. Il modello a tubo predice, con precisione ragionevole, la forma di μ(t) e la sua dipendenza sia dalla lunghezza media della catena polimerica sia dallo stato di aggrovigliamento. Ancora più significativa è la capacità del modello di predire il comportamento viscoelastico non lineare del sistema quando sia sottoposto a grandi tensioni. Nei polimeri questo comportamento è caratterizzato dall'effetto di 'fluidificazione da taglio' (shear thinning) o pseudo-plasticità se è applicata una grande tensione (deformando il campione tangenzialmente di un angolo γ che supera, diciamo, 0,1 radianti) allora il materiale diventa, temporaneamente, anche più soffice di prima. Più in generale, le predizioni del modello a tubo sono riassunte in una 'equazione costitutiva' (equazione di Doi-Edwards), che collega lo stato di tensione al tempo t (formalmente, il tensore di tensione σαβ(t)) alla storia delle deformazioni precedentemente applicate (formalmente, il tensore di gradiente di velocità ϰαβ(t′⟨t)). L'equazione costitutiva di Doi-Edwards ha avuto grande successo nel predire molti fenomeni fino ad allora inspiegati. Tra questi vi è l'osservazione che se una soluzione polimerica è mescolata con una bacchetta, la sua superficie superiore sale sulla bacchetta. Questo è esattamente il comportamento opposto a quello di un fluido newtoniano nelle stesse condizioni. Una versione semplificata, ma meno precisa, della teoria (chiamata 'approssimazione degli allineamenti indipendenti') è espressa dalla relazione
dove Qαβ è una funzione tensoriale specificata dal tensore cumulativo di deformazione Eγδ(t,t′) tra un tempo precedente t′ e il tempo corrente t, la cui derivata logaritmica è il tensore di velocità di deformazione ϰγδ.
Il modello a tubo e i modelli più raffinati, elaborati successivamente, ma basati direttamente su di esso, sono un valido punto di riferimento su ciò che una buona teoria dinamica sulla materia condensata soffice dovrebbe cercare di ottenere. Il modello offre una comprensione semplificata ma quantitativa della relazione tra le proprietà del materiale e la disposizione molecolare sottostante.
Fino a oggi, però, per nessun altra classe di materiali soffici è stato ottenuto un successo paragonabile. In effetti il modello a tubo è vincente perché sfrutta il fatto che, anche sotto flussi abbastanza forti, le catene polimeriche aggrovigliate rimangono vicine all'equilibrio sulla scala mesoscopica che definisce il tubo. In molti altri materiali soffici, come le emulsioni dense (per es., la maionese), questo non accade: il regime di flusso forte porta a deviazioni marcate dall'equilibrio, persino su scala locale (Larson 1999).
Autoorganizzazione
Passiamo ora a considerare il caso in cui gli oggetti mesoscopici in un fluido sono di carattere non permanente ma transitorio, come può verificarsi durante l'autoorganizzazione (o autoassemblaggio) di piccole molecole in grandi gruppi.
Per esempio, una molecola detergente semplice ha una coda idrocarburica, che respinge l'acqua, cui si sovrappone un gruppo di testa idrofilo. La propensione all'autoorganizzazione e all'assorbimento in superficie di questo tipo di molecola, detta 'anfifilica', affascinò Irving Langmuir, premio Nobel per la chimica nel 1932. Se messe in acqua, tali molecole formano spontaneamente aggregati che minimizzano l'area di contatto tra le code e il liquido circostante. Questi aggregati sono transitori, poiché il moto browniano è sufficiente per romperli; in molti casi essi si creano e si distruggono su una scala di tempo del microsecondo. A seconda delle dimensioni relative di testa e coda, l'impacchettamento ottimale può essere una piccola sfera ('micella'), un lungo cilindro flessibile ('micella gigante') o una lamina piatta ('doppio-strato'). Le micelle giganti sono oggetti simili ai polimeri, ma la loro natura transitoria porta a una dinamica più complessa (Cates e Candau 1990): il processo reversibile di divisione e ricostituzione delle catene modifica il processo di disimpigliamento browniano. In alcuni sistemi, le micelle possono ramificarsi, formando una rete fluida di tubetti cilindrici unidimensionali. Questi e altri stati di organizzazione per aggregati cilindrici sono mostrati nel diagramma di fase schematico della Tav. II.
Il doppio strato esteso si può riconnettere topologicamente a formare una pellicola spugnosa a connessioni multiple, sulla quale le molecole detergenti vivono come se fossero un fluido bidimensionale. Vi è una sorprendente e profonda analogia fra questa pellicola e l'interfaccia fra gli spin 'su' e 'giù' in un solido ferromagnetico. La pellicola a doppio strato divide lo spazio in due domini che sono di volume uguale ad alte concentrazioni di detergente (la 'spugna simmetrica', analoga a un paramagnete) ma di volume diverso a concentrazioni inferiori (la 'spugna asimmetrica', analoga a un ferromagnete). In alcuni sistemi a doppio strato queste due fasi distinte, entrambe fluidi isotropi, sono collegate da una transizione di fase in cui sono state osservate varie anomalie, per esempio nella torbidezza e nella diffusione della luce.
Le stesse strutture locali cilindriche o aggregati laminari possono presentarsi anche in fasi ordinate, come una disposizione regolare di cilindri o una pila regolare di lamine; entrambi sono cristalli liquidi. I cilindri mostrano un ordine periodico (cristallinità) in due direzioni, ma una configurazione simile a un fluido nella terza direzione, cioè lungo l'asse del cilindro. Nel caso del doppio strato, le estese pellicole bidimensionali di fluido assumono un ordinamento a 'mazzo di carte', con un ordine periodico nella terza direzione (quella di accatastamento). Questa cosiddetta fase 'lamellare' è in effetti la struttura della poltiglia di sapone bagnato citata precedentemente; la sua melmosità deriva dalla facilità con cui gli strati possono scivolare l'uno sull'altro (esattamente come in un mazzo di carte).
Nel caso di micelle cilindriche esiste una terza possibilità, chiamata cristallo liquido 'nematico'. In questa fase le micelle puntano tutte più o meno nella stessa direzione, rompendo spontaneamente la simmetria rotazionale di un fluido isotropo, senza però un ordine posizionale a lungo raggio in una qualche direzione.
Tutte queste fasi di cristallo liquido hanno tipi speciali di elasticità che riflettono il loro insolito stato di ordine. Le loro proprietà sono state studiate, tra gli altri, da Landau, de Gennes e Onsager (de Gennes 1972) e, proprio come nei sistemi polimerici e colloidali sopra descritti, l'entropia e le fluttuazioni termiche giocano un ruolo importante. Per esempio, nel cristallo liquido lamellare il moto browniano fa sì che ogni doppio strato oscilli leggermente intorno alla sua posizione media; queste fluttuazioni sono limitate dal fatto che nessuno di essi può attraversare i suoi vicini. Quanto più i doppi strati sono flessibili e vicini, tanto maggiore è il prezzo da pagare in termini di entropia. Così, sebbene una pila di doppi strati molto flessibile si pieghi facilmente, è molto più difficile comprimerla, persino se si consente la fuga del solvente (test di 'compressibilità osmotica'). Questo è, incidentalmente, il motivo per cui le strutture a doppio strato simili a cipolle, mostrate nella fig. 4, assumono forme poliedriche e non sferiche: benché una sfera minimizzi la curvatura, un poliedro, facendo il miglior uso possibile dello spazio, minimizza la compressione.
La compressibilità osmotica e le altre proprietà delle fasi autoorganizzate possono, in molti casi, essere collegate quantitativamente alle costanti elastiche locali degli aggregati che esse contengono. Tali costanti elastiche sono poco numerose e il loro controllo delle proprietà macroscopiche rappresenta un notevole esempio del concetto di universalità citato nell'introduzione. Questa intuizione chiave è stata alla base del lavoro pionieristico di Wolfgang Helfrich, il quale negli anni Settanta per primo ha applicato tali idee alle membrane lipidiche che si incontrano in biofisica; l'approccio è esaminato, insieme a molti degli sviluppi successivi descritti sopra, da Gerhard Gompper e Michael Schick (1994). Fin dai primi anni Novanta, lo studio di sistemi anfifilici autoorganizzati ha sempre più coinvolto applicazioni biofisiche, nelle quali i doppi strati lipidici semplificati sono ampiamente studiati come modelli per le membrane cellulari (Lipowsky e Sackmann 1995).
Aggregati frattali e gel colloidali
Un tipo piuttosto diverso di aggregazione spontanea si verifica nelle sospensioni colloidali, quando siano presenti forze attrattive tra le particelle colloidali (sfere adesive). Queste ultime possono attaccarsi formando strutture tenui filiformi, solitamente di natura frattale. Un esempio di strutture frattali è fornito dai domini ferromagnetici al punto critico: qui le regioni di spin allineati positivamente o negativamente formano strutture autosimili nel senso che, finché non si riescono a distinguere i singoli spin, è impossibile rilevare da un'immagine del campione quale ingrandimento o risoluzione sia stato usato. Osservazioni simili si applicano alle fotografie di aggregati colloidali formati cambiando improvvisamente la temperatura o il pH, in modo che tra le particelle colloidali, precedentemente repulsive l'una rispetto all'altra a causa, per esempio, di una repulsione coulombiana, si presenti una forte attrazione, quale quella prodotta dalle forze di dispersione.
Negli anni Ottanta la percezione che i concetti della geometria frattale possono essere utilizzati per descrivere l'aggregazione colloidale ha prodotto, tra i fisici, un vivo interesse. Ciò è accaduto in seguito al lavoro pionieristico di Thomas A. Witten, il quale ha riconosciuto per primo che nelle strutture frattali di non equilibrio, viste in semplici modelli di aggregazione, si evidenzia un fenomeno critico, analogo a quello trovato nelle transizioni di fase continue. È rilevante che le simulazioni al computer abbiano avuto un ruolo chiave in questo lavoro; il confronto diretto tra i dati sperimentali e quelli simulati è diventato il principale strumento per verificare una teoria in questo campo (Vicsek 1989).
Ogni volta che questi aggregati frattali si uniscono in una trama continua si presenta una rete, chiamata 'gel colloidale'. A seconda della forza delle interazioni, gli aggregati possono rompersi gradualmente e riconnettersi attraverso il moto browniano oppure no; spesso, essi possono essere facilmente rotti applicando una tensione. Il tipo di viscoelasticità che può di conseguenza manifestarsi è diverso da quello descritto in precedenza per i polimeri. In questo caso il materiale rimane un solido elastico quasi a tempo indeterminato (μ(t)=1), finché la tensione applicata σ=Gγ permane sotto una certa soglia. Solo se si supera questa 'tensione di snervamento' il materiale inizia a fluire. Un'ulteriore complicazione consiste nel fatto che la tensione di snervamento può lentamente evolvere nel tempo per un processo detto di 'invecchiamento'.
La formazione, il flusso e il comportamento di invecchiamento dei gel colloidali rimangono relativamente poco compresi, in parte perché, diversamente da quanto assunto nei semplici modelli di aggregazione, affinché il gel sia in grado di fluire i legami non possono formarsi in un modo del tutto irreversibile (Haw e Poon 1997).
Transizioni di fase indotte dal flusso
Sia gli aggregati anfifilici sia quelli colloidali possono mostrare un accoppiamento forte tra il loro stato di organizzazione e lo stato di flusso nel materiale. Ciò può avere conseguenze spettacolari. In alcuni casi è possibile convertire un fluido isotropo, contenente un doppio strato anfifilico a forma di spugna, in un cristallo liquido lamellare, semplicemente scuotendo leggermente il campione in una provetta. Allo stesso modo, molti cristalli colloidali possono essere convertiti rapidamente in uno stato fluido, applicando una leggera deformazione di taglio. Entrambi i fenomeni sono esempi di 'transizioni di fase indotte dal flusso'.
Nei casi più semplici la forza di taglio produce una trasformazione che si potrebbe realizzare anche cambiando una variabile termodinamica, come la temperatura o la pressione. In entrambi gli esempi precedenti lo stesso effetto potrebbe essere ottenuto modificando leggermente la concentrazione, piuttosto che applicando la deformazione di taglio. Molte transizioni indotte dal flusso sono ora ben comprese in questi termini.
In una seconda classe di sistemi (tra i quali le micelle giganti) è richiesta dall'equazione costitutiva una transizione repentina da uno stato di flusso a un altro, in funzione della velocità di flusso. Questa intrinseca instabilità del flusso può essere accompagnata da un cambiamento dello stato termodinamico o meno, per esempio in un cristallo liquido esagonale o nematico.
In una terza classe di sistemi l'applicazione di un flusso produce uno stato di organizzazione che è completamente nuovo. Un esempio spettacolare si verifica quando un cristallo liquido lamellare è sottoposto a una deformazione di taglio stabile e prolungata (fig. 4). Piuttosto che rimanere ordinati secondo una pila regolare, gli strati si riorganizzano lentamente in gusci chiusi di topologia sferica (ma forma poliedrica), uno annidato nell'altro, formando un insieme di 'cipolle'. Ogni cipolla di solito è larga alcuni micron e contiene centinaia di strati. Questa trasformazione è reversibile: riducendo la velocità di taglio, si ritorna alla struttura precedente. Tuttavia, se la forza di taglio improvvisamente cessa, cosicché non c'è più un'immissione stabile di energia dall'esterno, le cipolle non riescono a ritornare rapidamente alla loro struttura precedente; in alcuni casi, esse sono stabili per mesi. Questo fenomeno suggerisce un'interessante tecnologia per incapsulare piccole molecole, come i prodotti farmaceutici, consistente nell'aggiungerle alla miscela prima che le cipolle si siano formate.
Un altro esempio di transizione di fase indotta dal flusso si verifica in soluzioni di micelle giganti, per concentrazioni al di sotto della soglia di aggrovigliamento. Una tale soluzione è a stento viscoelastica, però, quando viene deformata lentamente e per un tempo lungo, si trasforma in un nuovo stato gelatinoso. Teoricamente ci si aspetterebbe che le sollecitazioni trasversali abbiano un effetto forte in un sistema come questo, ma solo quando la velocità di taglio
,
dove τ è il tempo di rilassamento più lungo osservabile nel sistema in quiete (qui, τ è il tempo di rilassamento rotazionale per le micelle, dell'ordine dei micro o dei millisecondi). Invece in questo caso la velocità di taglio minima richiesta è piccolissima:
la comprensione di tale fenomeno sembra ancora molto lontana.
I primi studi sperimentali sistematici sulle transizioni di fase indotte dal flusso in materiali autoorganizzati sono stati condotti negli anni Ottanta (Rehage e Hoffmann 1991); la transizione a cipolla è stata invece scoperta più tardi (Diat et al. 1992). Malgrado il notevole sforzo teorico, i progressi nella comprensione di queste transizioni sono stati relativamente modesti, salvo pochi casi limite, alcuni dei quali esaminati da Ronald G. Larson (1999).
Stati bloccati e mezzi granulari
Sotto certe condizioni, una sospensione colloidale di sfere rigide può subire una transizione di fase indotta dal flusso, da una fase libera di fluire a uno stato 'bloccato' (jamming). Per illustrare questo fenomeno si pensi agli ingorghi stradali: su un'autostrada molto trafficata c'è una velocità media al di sopra della quale il traffico non può scorrere liberamente; anche se tutti i conducenti volessero andare più rapidamente non potrebbero, perché il flusso è instabile e le piccole fluttuazioni conducono a intasamenti spontanei.
Un esperimento classico secondo queste linee può essere eseguito in cucina: si metta un cucchiaio di maizena (amido di mais) in una tazza e si aggiunga acqua goccia a goccia, fino a quando tutto il materiale non si è sensibilmente inumidito; si mescoli ora con un cucchiaio. Se la composizione è proprio quella giusta, e finché il cucchiaio viene spostato lentamente, la sospensione fluisce quasi senza resistenza; viceversa, se il mescolamento è rapido, non si può ottenere lo stesso risultato: il tutto si muove come un unico pezzo solido. Alcuni lavori alla fine degli anni Novanta hanno iniziato a far luce su tali processi, ma la fisica di questi fenomeni rimane tutt'altro che chiara.
La natura di tale transizione nei colloidi suggerisce anche un collegamento con un'altra classe di materiali che facilmente si bloccano: i mezzi granulari, tra i quali figurano le polveri secche, come la sabbia. C'è uno spettro continuo che va dalle polveri asciutte allo stato colloidale, passando per le malte e le paste. Attraverso questo spettro, durante gli anni Novanta, hanno cominciato a emergere alcuni aspetti comuni, come una caratterizzazione della geometria locale basata su 'catene di forza', costituite da intense interazioni locali. Tuttavia, non si può dire che esista una struttura teorica veramente unificata.
Dinamica bloccata
Molti materiali soffici, come le gocce fluide deformate in un'emulsione densa o le cipolle della fig. 4, restano intrappolati in uno stato 'bloccato', lontano dal vero equilibrio ma tanto vicino a un minimo metastabile di energia libera da permettere una trattazione termodinamica locale o su brevi intervalli temporali. Su scale di tempo più lunghe, tali materiali possono mostrare processi di rilassamento assai lenti; in molti casi, per quanto a lungo si possa osservare il sistema, le sue proprietà continueranno a evolvere.
Dagli anni Settanta in poi un comportamento fortemente analogo a questo è stato osservato in altri settori della fisica della materia condensata, in particolare in magneti disordinati chiamati 'vetri di spin'. Tale campo di ricerca è stato a sua volta parzialmente ispirato da precedenti studi sperimentali sui 'vetri strutturali'; questi ultimi si presentano sovraraffreddando fluidi molecolari, come il glicerolo, in un regime vetroso. Negli anni Ottanta si è mostrato che le sospensioni colloidali dense sono esse stesse vetri strutturali, nel senso che le particelle rimangono intrappolate vicino a posizioni fisse che non formano un reticolo ordinato (Pusey 1991). Negli anni Novanta è stato proposto che il paradigma del vetro possa spiegare uno spettro più ampio di dinamiche bloccate nella materia condensata soffice, come per le emulsioni dense o per le fasi cristalline liquide a trama (per es., le cipolle), nelle quali si può prevedere un'evoluzione lenta del sistema attraverso una sequenza di stati metastabili, vicini all'equilibrio. È stato anche ipotizzato che la transizione di jamming possa essere collegata a un passaggio dalla fase fluida a quella vetrosa, in seguito all'applicazione di una tensione. Queste e altre idee sono state esaminate in un recente compendio (Cates e Evans 2000).
Cinetica delle transizioni di fase
Una forma di metastabilità più semplice di quella trovata nei vetri si presenta, per esempio, in un vapore sovraraffreddato. In questo caso il sistema si attarda in uno dei pochi minimi di energia libera, corrispondenti alle varie fasi termodinamiche, anche se il passaggio a un altro stato potrebbe far diminuire la sua energia libera F. La transizione può alla fine manifestarsi per mezzo della nucleazione di una piccola goccia della fase preferita. Un meccanismo diverso si presenta quando, a causa di un cambiamento improvviso dei parametri - come una variazione della temperatura o un 'congelamento' (quenching) - un sistema, che era originariamente in un minimo di energia libera, improvvisamente si trova in un massimo o nelle sue vicinanze e inizia a evolvere di conseguenza. Questo caso si verifica, per esempio, quando una miscela stabile di due fluidi è raffreddata e inizia a smescolarsi in un processo detto di 'decomposizione spinodale' (Bray 1994).
La cinetica di smescolamento di liquidi e solidi semplici è un argomento importante della fisica della materia condensata. Nel caso delle leghe metalliche c'è una conoscenza empirica ragionevole di come il processo di formazione del materiale influisca sulla microstruttura risultante. Malgrado ampie ricerche, una comprensione simile dei canali di sviluppo di un processo nella materia condensata soffice non è stata ancora raggiunta, anche se progressi notevoli sono stati compiuti alla fine degli anni Novanta, almeno per una classe importante di sistemi (miscele colloidi-polimeri). Questo argomento è esaminato da Anderson e Lekkerkerker (2002). Un colloide o una pasta (sia essa vernice, shampoo o salsa di pomodoro) può essere inutilizzabile se si separa prematuramente in un blocco solido e in uno strato di solvente sovrapposto. Il verificarsi o meno di ciò dipende dalla microstruttura del materiale che, a sua volta, è determinata dalla storia della sua formazione.
Ugualmente interessante, ma meno studiato in altri campi della fisica degli stati condensati, è il processo inverso. Come si mescolano fasi inizialmente separate se si cambiano le condizioni termodinamiche ad hoc? Un comportamento peculiare è quello di un cristallo liquido a doppio strato che, mentre si dissolve in un eccesso di acqua, può mostrare diversi tipi di instabilità. Tra queste vi è l'instabilità 'mielinica', così chiamata dalle strutture osservate, a forma di dita, che somigliano strettamente alle guaine mieliniche che rivestono le cellule nervose nel corpo umano. Tale instabilità non è stata ancora sistematicamente studiata o spiegata, malgrado sia nota fin dalla metà del XIX sec. negli studi di Rudolf Virchow, ma si può realisticamente sperare in progressi più rapidi nell'attuale secolo.
Conclusioni e prospettive
La fisica della materia condensata soffice entra poco nei curricula universitari e rimane di interesse minoritario (sebbene crescente) tra i fisici che si occupano di materia condensata. Tra questi ultimi essa ha la reputazione, immeritata, di argomento 'confuso', intendendo forse che molti materiali soffici devono essere studiati chimicamente e fisicamente prima di arrivare a una comprensione completa dei fenomeni. Non c'è dubbio che sia così, ma in quasi tutti i sistemi ricorrono problematiche fisiche quali le fluttuazioni termiche di grande entità, i moti browniani vincolati e l'elasticità entropica. Ciò significa che la comprensione si fonda su un'unica struttura concettuale, all'interno della quale si possono poi differenziare le varie caratteristiche chimiche. Benché scienziati dei materiali, chimici e ingegneri chimici abbiano giocato un ruolo importante, sono stati i fisici, durante la seconda metà del XX sec., ad aver riconosciuto le universalità fondamentali e ad aver costruito la struttura dei collegamenti tra gli esperimenti e la meccanica statistica.
Gli anni Ottanta e Novanta hanno visto un dialogo crescente tra i fisici della materia soffice e i biologi (Lipowsky e Sackmann 1995). Tuttavia è inevitabile che fisica della materia soffice e biologia differiscano tra loro. I fisici sono abituati a considerare le caratteristiche generali di un problema e, quindi, ad applicare le acquisizioni ottenute ad altre situazioni simili nel complesso, ma diverse nel dettaglio. D'altro canto, le strutture biologiche sono state selezionate dall'evoluzione in modo che l'eccezione fisica risulti spesso la norma biologica. In tali circostanze, gli strumenti concettuali esistenti devono essere modificati e ne devono essere inventati di nuovi; questa prospettiva di ricerca si proietta lontano nel XXI secolo.
La fisica della materia condensata soffice è stata (e continua a essere) una disciplina di grande problematicità, proponendo sfide tanto agli sperimentali, quanto ai teorici, quanto a coloro che si occupano di simulazioni numeriche. Si tratta di un campo molto interessante soprattutto perché si occupa delle proprietà di materiali che si incontrano ogni giorno: materiali che mangiamo, che frizioniamo sulla nostra pelle, con cui decoriamo le nostre case e, in parte, di cui siamo fatti. Mi auguro di aver trasmesso attraverso questa rassegna, la curiosità intellettuale e scientifica che l'argomento ha destato. Non v'è dubbio che una comprensione più profonda e il controllo di queste proprietà possano recare benefici significativi.
Lo studio della materia condensata soffice riguarda materiali familiari e la familiarità, si dice, genera disprezzo. Forse questa è la ragione per cui, almeno durante gli anni Ottanta e Novanta, la stampa non scientifica sembrava spesso più interessata a produrre titoli divertenti ma imprecisi ("scienziati matti spendono i soldi del governo agitando barattoli di salsa di pomodoro") che a fornire ai lettori una qualche idea di cosa comportasse la ricerca. Si è anche rilevato più volte, durante quel periodo, un atteggiamento dispregiativo tra colleghi di aree più tradizionali. Al contrario, parte del pubblico ha mostrato piacere nel sapere che neanche gli scienziati professionisti hanno ancora capito perché la salsa di pomodoro qualche volta non voglia uscire fuori dalla bottiglia e pochi di loro dubitano che risolvere questo piccolo problema, a fianco di mille più grandi, potrebbe rendere la loro vita nel XXI sec. un po' più facile.
Bibliografia
Anderson, Lekkerkerker 2002: Anderson, Valerie J. - Lekkerkerker, Henk N.W., Insights into phase transition kinetics from colloid science, "Nature", 416, 2002, pp. 811-815.
Bray 1994: Bray, Alan J., Theory of phase ordering kinetics, "Advances in physics", 43, 1994, pp. 357-459.
Cates, Candau 1990: Cates, Michael E. - Candau, Sauveur J., Statics and dynamics of wormlike surfactant micelles, "Journal of physics condensed matter", 2, 1990, pp. 6869-6892.
Cates, Evans 2000: Cates, Michael E. - Evans, Martin R., Soft and fragile matter: nonequilibrium dynamics, metastability and flow, Briston, IOP Publishing, 2000.
Diat 1992: Diat, Olivier - Roux, Didier - Nallet, Frederic, Effect of shear on a lyotropic lamellar phase, "Journal de physique", 3, 1992, pp. 1427-1452.
Doi, Edwards 1986: Doi, Masao - Edwards, Samuel F., The theory of polymer dynamics, Oxford, Clarendon Press, 1986.
Flory 1953: Flory, Paul J., Principles of polymer chemistry, Ithaca-New York, Cornell University Press, 1953.
de Gennes 1972: Gennes, Pierre-Gilles de, The physics of liquid crystals, Oxford, Clarendon Press, 1972.
de Gennes 1979: Gennes, Pierre-Gilles de, Scaling concepts in polymer physics, Ithaca-New York, Cornell University Press, 1979.
Gompper, Schick 1994: Gompper, Gerhard - Schick, Michael, Self-assembling amphiphilic systems, London-New York, Academic Press, 1994.
Haw, Poon 1997: Haw, Mark D. - Poon, Wilson C.K., Mesoscopic structure formation in colloidal aggregation and gelation, "Advances in colloid and interface science", 73, 1997, pp. 71-126.
Israelachvili 1985: Israelachvili, Jacob, Intermolecular and surface forces, London-New York, Academic Press, 1985.
Larson 1999: Larson, Ronald G., The structure and rheology of complex fluids, Oxford, Oxford University Press, 1999.
Lekkerkerker 2000: Lekkerkerker, Henk N.W., Phase separation and aggregation in colloidal suspension, in: Soft and fragile matter, nonequilibrium dynamics, metastability and flow, edited by Michael E. Cates and Martin R. Evans, Briston, IOP Publishing, 2000.
Lipowsky, Sackmann 1995: Lipowsky, Reinhard - Sackmann, Erich, Structure and dynamics of membranes: from cells to vesicles, Amsterdam-Oxford, Elsevier, 1995.
Pusey 1991: Pusey, Peter N., Colloidal suspensions, in: Liquids, freezing and glass transition, 51st Session: Papers, edited by Jean-Pierre Hansen, Denis Levesque and Jean Zinn-Justin, Amsterdam-New York, Elsevier, 1991, pp. 767-942.
Rehage, Hoffmann 1991: Rehage, Heinz - Hoffmann, Heinz, Viscoelastic surfactant solutions - Model systems for rheological research, "Molecular physics", 74, 1991, pp. 933-973.
Vicsek 1989: Vicsek, Tamás, Fractal growth phenomena, Singapore, World Scientific Publishing, 1989.