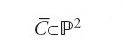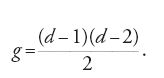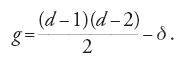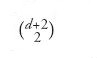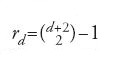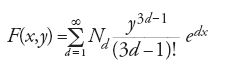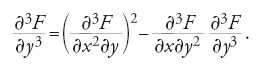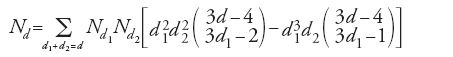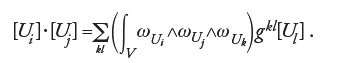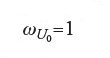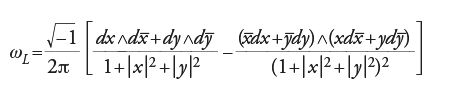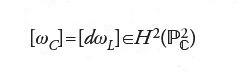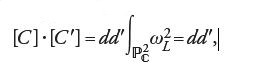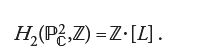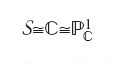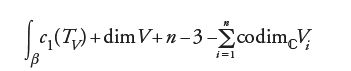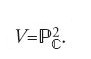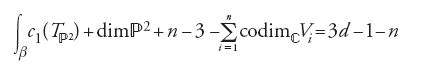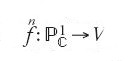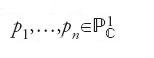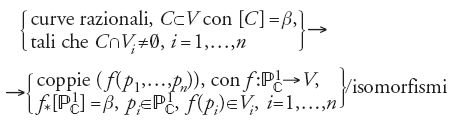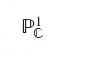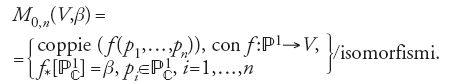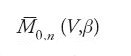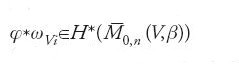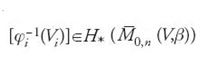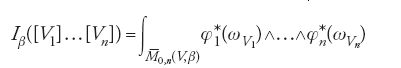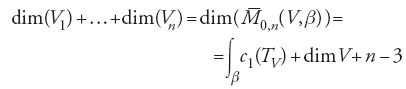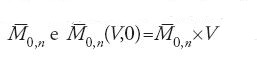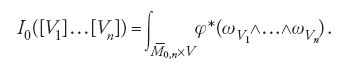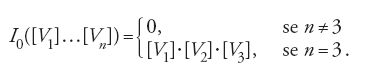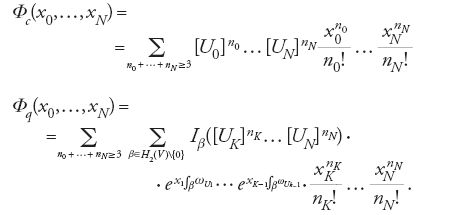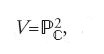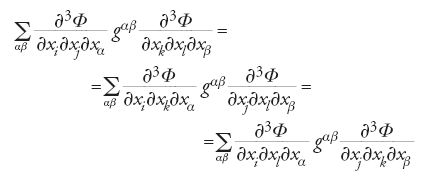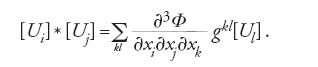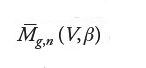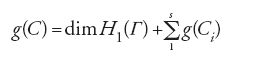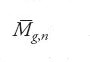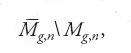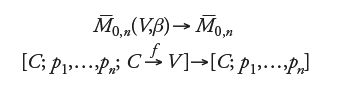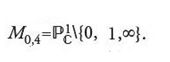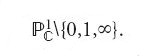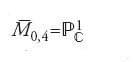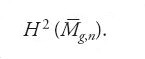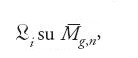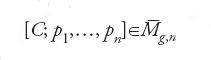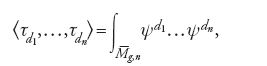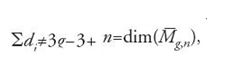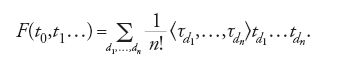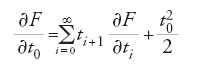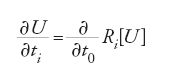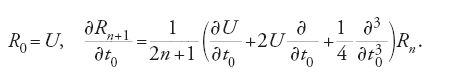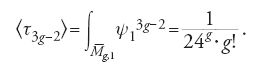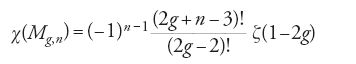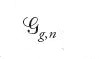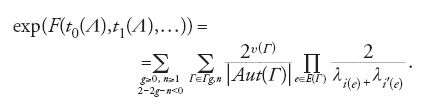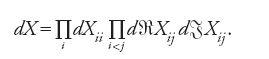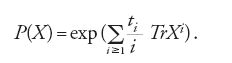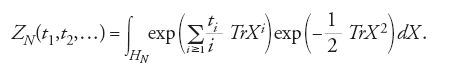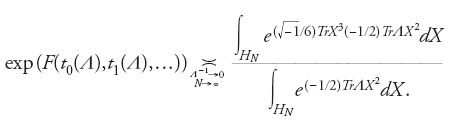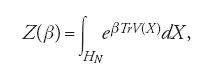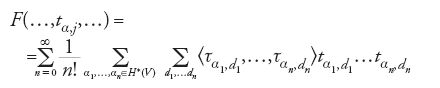La grande scienza. Geometria numerativa e invarianti di Gromov-Witten

La grande scienza. Geometria numerativa e invarianti di Gromov-Witten

Geometria numerativa e invarianti di Gromov-Witten

Nel trattato Le coniche, Apollonio di Perge (262-180 a.C. circa) affronta i primi problemi di geometria numerativa. Una delle 387 proposizioni del trattato stabilisce che per 5 punti generici del piano passa una e una sola conica. Un'altra asserisce che vi sono al più 8 circonferenze tangenti a tre circonferenze assegnate. Il trattato di Apollonio era ancora in auge all'epoca di Johannes Kepler (1571-1630) e di Isaac Newton (1642-1727) che lo lessero e ne fecero uso. Fu solo nel 1820 che Michel Chasles (1793-1880) stabilì che vi sono esattamente 3264 coniche tangenti a 5 coniche date e in posizione generica. Circa venti anni dopo, Hermann Schubert (1848-1911) trovò che vi sono 666841088 quadriche dello spazio proiettivo tridimensionale tangenti a nove quadriche in posizione generica.

Gli esempi appena citati riguardano la teoria delle curve algebriche e, più in generale, la teoria delle varietà algebriche, la quale prese corpo con il consolidarsi di alcuni fondamentali punti di vista. Il primo, dovuto a René Descartes (1596-1650), consiste nel tradurre le nozioni geometriche in nozioni algebriche. Dunque, per esempio, una curva algebrica piana C non è altro che l'insieme degli zeri di un polinomio P(x,y) di due variabili reali x e y:

[1] C={(x,y)∈ℝ²:P(x,y)=0}.

Si dice che C ha grado d, se d è il grado del polinomio P(x,y). Una retta è l'insieme degli zeri di una equazione lineare (curva di grado 1)

[2] ax+by+c=0.

Una conica è l'insieme degli zeri di una equazione quadratica (curva di grado 2)

[3] ax²+by²+cxy+dx+ey+f=0.

Il secondo punto di vista è quello proiettivo, introdotto da Albrecht Dürer negli Elementorum geometricorum libri (1500) e da Leon Battista Alberti nel De pictura (1435). Esso è essenziale per dare consistenza alla teoria dell'intersezione, poiché nell'intersecare due curve algebriche è possibile che alcune intersezioni 'vadano all'infinito' come avviene nel caso di due rette parallele del piano cartesiano. Un altro modo in cui, eventualmente, si possono perdere alcune intersezioni è quello di limitarsi alle soluzioni reali. I numeri complessi, che compaiono in algebra con le opere di Gerolamo Cardano (1545) e Raffaele Bombelli (1572), fecero irruzione in geometria per opera di Caspar Wessel (1764). È l'ambito della geometria proiettiva complessa quello in cui si pongono nel modo più naturale le questioni di teoria dell'intersezione. Un tipico teorema nella teoria dell'intersezione è il teorema di Bézout: due curve algebriche complesse e proiettive di gradi n e m si intersecano in nm punti, contati con opportune molteplicità (potendo esservi tangenze di vari ordini), oppure hanno una componente in comune (come accade, per es., a due coniche, entrambe spezzate in coppie di rette e aventi una di queste rette in comune). Il teorema può generalizzarsi in dimensione superiore: siano date r ipersuperfici algebriche V₁,…,V_r nello spazio proiettivo r-dimensionale ℙ^r. Sia n_i il grado di V_i (e cioè il grado del polinomio omogeneo in r+1 variabili di cui V_i è luogo di zeri); allora V₁ ∩…∩V_r consta di n₁n₂…n_r punti, contati con opportune molteplicità, oppure è un insieme infinito. In un certo senso, una qualsiasi questione di geometria numerativa che cerchi la risposta a una domanda come: "quante sono le figure di un certo tipo che soddisfano determinate condizioni" si riduce a un problema di teoria dell'intersezione. Per esempio, poiché le coniche del piano dipendono da 5 parametri omogenei e il passaggio di una conica per un punto si traduce in una condizione lineare, il fatto che per 5 punti generici del piano passa una sola conica si traduce nel fatto che 5 piani generici di ℙ⁵ si intersecano in un punto.

È difficile formarsi un'idea intuitiva di una curva complessa immersa nel piano proiettivo. Se si pensa al caso reale, tutto è più semplice perché si sa disegnare il grafico di un'equazione algebrica. Nel disegnare il grafico della stessa equazione nel piano complesso bidimensionale, si deve visualizzare una superficie bidimensionale reale in uno spazio quadridimensionale reale. Siano z=x+iy e w=u+iv variabili complesse. Sia P(z,w) un polinomio, che si può scrivere nella forma P(z,w)=F(x,y,u,v)+iG(x,y,u,v), separandone la parte reale e la parte immaginaria. Allora, la curva piana complessa

[4] C={(z,w)∈ℂ²:P(z,w)=0}

deve essere riguardata come il luogo

[5] C={(x,y,u v)∈ℝ⁴:F(x,y,u,v)=G(x,y,u,v)=0}

e dunque come l'intersezione di due ipersuperfici nello spazio quadridimensionale reale. Fu Bernhard Riemann, nella sua tesi del 1846, a capire come si debba pensare una curva algebrica piana. Un tale oggetto è costituito da due dati: il primo è quello che si usa ormai chiamare una superficie di Riemann. Con ciò si intende una superficie S compatta orientabile bidimensionale dotata di una struttura complessa e cioè di un insieme di funzioni ℳ(S), dette funzioni meromorfe. Questo insieme di funzioni deve soddisfare un certo numero di proprietà che permettono di svolgere, sulla superficie S, una teoria delle funzioni olomorfe e meromorfe completamente analoga a quella classica. Il secondo dato è costituito da due funzioni meromorfe z e w di ℳ(S). Questi dati definiscono un'applicazione

[6] f:S{poli di z e w}→C⊂ℂ²

la cui immagine è C. Se invece di partire da C⊂ℂ², si fosse partiti dalla sua chiusura proiettiva

allora si sarebbe ottenuta una estensione

Dunque, Riemann 'toglie' la curva dal piano, ne costruisce un'immagine astratta S che poi immerge, mediante f, nel piano.

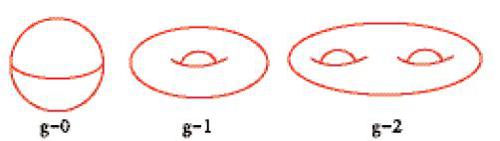
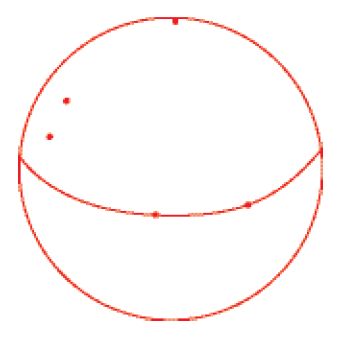
Una superficie di Riemann compatta S appare come una ciambella con g buchi e il numero g si chiama 'genere' di S. Cosicché, una superficie di genere zero è una sfera, una superficie di genere 1 è un toro e cosí via (fig. 1).

Il genere della superficie di Riemann S associata a una curva algebrica piana C si calcola facilmente. Supponiamo che C sia di grado d e che

incontri la retta all'infinito in d punti distinti. Se la curva piana C è non singolare (e cioè se in nessun punto di C si annullano simultaneamente le due derivate parziali del polinomio P) allora il genere di S è dato dalla formula

Nel caso in cui C è singolare la formula è più complicata. Il calcolo è più semplice se ci si limita al caso in cui le singolarità di C siano 'nodi'. Un nodo è un punto p=(a,b)∈C in cui lo sviluppo in serie di Taylor del polinomio P che definisce C è della forma

[9] P(z,w)=α(z−a)²+β(z−a)(w−b)+γ(w−b)²+…

e in cui il discriminante β²−4αγ è non nullo. Dal punto di vista reale, un nodo appare come nella fig. 2.

Ebbene, il genere della superficie di Riemann associata a una curva algebrica piana di grado d avente come singolarità δ nodi è dato da

Dal punto di vista complesso, una superficie di Riemannn S di genere 1 che nell'immergersi nel piano produce una curva con un nodo può raffigurarsi come nella fig. 3.

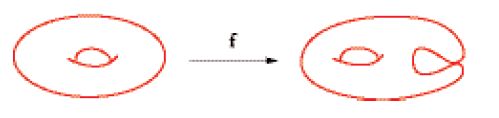
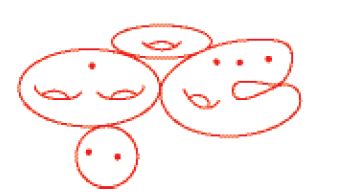
Le curve algebriche piane che hanno superficie di Riemann di genere zero si dicono razionali. La terminologia deriva dal fatto che il campo delle funzioni meromorfe di una superficie di Riemann di genere zero è il campo delle funzioni razionali in una variabile. Dalla formula del genere segue che, tra le curve piane, vi sono curve razionali: le rette, le coniche, le cubiche con un nodo, le quartiche con tre nodi e in generale le curve di grado d con (d−1)(d−2)/2 nodi. Le curve razionali possono essere considerate una generalizzazione delle rette, nel senso che, come le rette, sono immagini di applicazioni della sfera di Riemann (superficie di genere 0) nel piano proiettivo (fig. 4).

Si descriverà ora un problema di geometria numerativa, riguardante le curve piane razionali, risolto da Maxim Kontsevich nel 1992. Si considerino le curve algebriche piane di un dato grado d. Un polinomio in due variabili di grado d dipende da

parametri complessi. Dunque, posto

le curve algebriche piane di grado d possono pensarsi come i punti di uno spazio proiettivo complesso

Richiedere che una curva abbia un nodo si traduce in una condizione algebrica. Geometricamente, le curve con un nodo descrivono una ipersuperficie algebrica in questo spazio proiettivo. Similmente, le curve di grado d con δ nodi descrivono una sottovarietà algebrica di codimensione δ in

Si considerino le curve di grado d e di genere 0 e ci si limiti al caso delle curve nodate. Dalla formula del genere segue che queste curve hanno δ=(d−1)(d−2)/2 nodi e dunque descrivono, in

,

una sottovarietà V di dimensione 3d−1=r_d−(d−1)(d−2)/2. Si fissino ora 3d−1 punti nel piano. Poiché il passaggio per un punto equivale a una condizione lineare sui coefficienti del polinomio che definisce una curva piana, le curve piane, nodate, di grado d e genere 0 che passano per 3d−1 punti assegnati corrispondono ai punti di intersezione della varietà (3d−1)-dimensionale V con 3d−1 iperpiani in

Questo insieme è, in generale, finito e la sua cardinalità si denota con N_d. Esaminando i primi casi si ottiene:

N₁=1: vi è una sola retta per 2 punti del piano (Euclide).

N₂=1: vi è una sola conica per 5 punti del piano (Apollonio).

N₃=12: vi sono 12 cubiche nodate per 8 punti del piano (Chasles).

Si può calcolare direttamente, con i metodi classici, anche N₄=620, ma i calcoli diventano virtualmente impossibili nei casi successivi. I metodi di geometria numerativa sviluppati da Hieronymus Zeuthen, ma soprattutto da Hermann Cäsar Hannibal Schubert, seguendo le idee originali di Chasles e Jean-Philippe-Ernest Fauque de Jonquières, trovano, in problemi del tipo appena descritto, limiti che non sembrano superabili.

Intorno al 1990, nell'ambito della teoria conforme dei campi e della teoria delle stringhe, si è scoperto che le funzioni di partizione di numerosi modelli matematici di teoria dei campi possono essere espresse in serie asintotiche i cui coefficienti hanno significato geometrico. Questi invarianti geometrici, così organizzati, si riescono a calcolare, per ricorrenza, non appena si trovino equazioni differenziali soddisfatte dalla funzione di partizione. Si ritorni all'esempio appena trattato. Si consideri la serie

dove N_d è il numero delle curve piane, nodate, di grado d e genere 0 che passano per 3d−1 punti assegnati. Il fatto notevole, dimostrato da Kontsevich, è che la serie F soddisfa l'equazione differenziale di WDVV (Witten, Dijkgraaf, Verlinde, Verlinde)

Usando questa equazione si ottiene la relazione

con d_1, d₂>0 e d>1.

Tramite questa relazione, i numeri N_d si calcolano, ricorsivamente, a partire da N₁=1 e si ottiene: N₂=1, N₃=12, N₄=620, N₅=87304, N₆=26312976, N₇=14616808192, N₈=13525751027392,…

Per comprendere il significato della serie F definita dalla [11] e dell'equazione [12] da essa soddisfatta, bisogna dare un'interpretazione matematica più profonda dei numeri N_d. In effetti, i numeri N_d sono un caso molto particolare degli invarianti di Gromov-Witten. Prima di introdurre questi invarianti è opportuno richiamare alcuni elementi della classica teoria dell'intersezione.

Si consideri una varietà analitica complessa e compatta V come l'ambiente in cui si svolge la geometria che vogliamo studiare. Nelle considerazioni precedenti questa varietà era il piano proiettivo complesso

Si ricordi che una varietà analitica complessa di dimensione s è uno spazio topologico di Hausdorff che può essere ricoperto da carte locali, ognuna delle quali è copia omeomorfa di un polidisco in ℂ^s, in modo tale che il passaggio da un carta a un'altra possa essere espresso da applicazioni analitiche. Una superficie di Riemann è una varietà analitica complessa di dimensione 1. Il piano proiettivo

è una varietà analitica complessa di dimensione 2.

Una struttura algebrica che cattura molte informazioni sulla teoria dell'intersezione, e dunque sulla geometria numerativa della varietà V, è 'l'anello di coomologia di V', che si denota usualmente con il simbolo H*(V). Gli elementi di H*(V) sono classi di equivalenza di forme differenziali 'chiuse' modulo forme differenziali 'esatte' su V. Se x₁, x₂,…,x_2s sono le coordinate reali di una carta locale di V, una forma differenziale ω di grado k su V si scrive in questa carta nella forma ω=∑_If_Idx_I, dove I=(i₁,…,i_k) è un multiindice, dx_I=dx_i1 ∧…∧dx_ik e le f_I sono funzioni C^∞ a valori complessi. L'operatore di differenziazione d è definito localmente da dω=∑_I df_I ∧dx_I, dove df=∑(∂f/∂x_i)dx_i. Una forma differenziale ω si definisce 'chiusa' se dω=0 e 'esatta' se ω=dφ. Si denota con H^k(V)⊂H*(V) il sottogruppo delle classi di equivalenza delle forme differenziali chiuse di grado k. Si ha una decomposizione:

[14] H*(V)=⊕_kH^k(V).

La struttura moltiplicativa dell'anello di coomologia di V è data dal prodotto esterno di forme e con questa moltiplicazione H*(V) diventa un anello graduato: dati [ω]∈H^k(V) e [φ]∈H^h(V), si ha

[15] [ω][φ]=_def[ω∧φ]∈H^h+k(V).

La struttura moltiplicativa dell'anello di coomologia riflette la teoria dell'intersezione su V in virtù del teorema di dualità di Poincaré. Si ricordi innanzi tutto che, date una sottovarietà W di V di dimensione k e una k-forma differenziale ω, la teoria dell'integrazione su V permette di definire l'integrale ∫_Wω. Inoltre, il teorema di Stokes afferma che, se W è una sottovarietà chiusa e se ω è chiusa, questo integrale non dipende dalla classe di coomologia di ω. Una delle conseguenze più importanti del teorema di dualità di Poincaré è la seguente. Sia W⊂V una sottovarietà chiusa di dimensione k e sia d la dimensione complessa di V. Allora esiste una classe di coomologia, rappresentata da una d−k forma differenziale chiusa ω_W, che prende il nome di 'classe duale di Poincaré di W', che ha la seguente proprietà: per ogni forma chiusa φ su V, di grado k si ha:

[16]  ∫_Wφ=∫_Vω_W⋀φ.

Lo spazio dei funzionali (complessi) su H^k(V) prende il nome di k-esimo spazio di omologia di V e si denota con il simbolo H_k(V). Si assumerà, come ipotesi semplificativa, che H_k(V) abbia una base costituita da funzionali della forma: φ→∫_Wφ, dove W è una sottovarietà k-dimensionale chiusa di V. Un tale funzionale prende il nome di 'classe di omologia' di W e si denota col simbolo [W]. Per dare sostegno intuitivo all'idea di classe di omologia, si può ricordare che due sottovarietà chiuse W e W′ che costituiscano il bordo di una varietà k+1-dimensionale rappresentano la stessa classe di omologia. La dualità di Poincaré è dunque un isomorfismo lineare tra H_k(V) e H^2d−k(V) che associa alla classe di omologia [W] la classe di coomologia [ω_W]. Volendo studiare la teoria dell'intersezione delle sottovarietà analitiche complesse, e dunque di dimensione reale pari, si può concentrare l'attenzione sul sottoanello

[17] H^2*(V)⊂H*(V)

costituito dalle classi di coomologia di grado pari. È questo un anello commutativo con unità 1∈H⁰(V). Per comprendere come la struttura moltiplicativa di H^2*(V) si trasferisca, tramite l'isomorfismo di Poincaré, in una struttura moltiplicativa su H_2*(V) si fissi una base [U₀],…,[U_N] di H_2*(V), si ponga

e si denoti con (g^ij) la matrice inversa della matrice (g_ij). Si verifica allora che la moltiplicazione in H_2*(V), indotta per dualità di Poincaré da quella in H^2*(V), è data da

L'elemento neutro di questa moltiplicazione è dato dalla 'classe fondamentale' [V] e, d'ora in poi, si assumerà che [U₀]=[V] o, equivalentemente, che

Un'importante osservazione è la seguente: se U e W sono sottovarietà analitiche complesse chiuse di V con dimensioni complementari e se U e W si intersecano trasversalmente in ∣U∩W∣ punti, allora:

[20]  ∣U⋂W∣=∫_Vω_U⋀ω_W.

Ciò giustifica la seguente definizione di numero di intersezioni. Siano date le sottovarietà analitiche complesse V₁,…,V_k di V, rispettivamente, di dimensioni (complesse) d₁,…,d_k. Si assuma d₁+…+d_k=dim(V); allora il numero di intersezione [V₁]…[V_k] è il prodotto

[21]  [V₁]…[V_k] = ∫_Vω_V1⋀…⋀ωV_k .

Per esempio, ritornando al caso in cui la varietà ambiente V è il piano proiettivo complesso ℙ² con coordinate proiettive X, Y, Z, si consideri come sottovarietà la retta L di equazione Z = 0. Si verifica che la classe duale di Poincaré di L è rappresentata dalla 2-forma

dove x=X/Z e y=Y/Z. Si verifica inoltre che, data una curva algebrica piana proiettiva C di grado d, allora

In particolare, se C′ è un'altra curva piana e se d′ è il suo grado, si ha

in accordo con il teorema di Bezout. Dietro questo calcolo vi è il fatto che il secondo gruppo di omologia di

è generato da [L]:

La conoscenza dei numeri di intersezione [21] è equivalente a quella della struttura moltiplicativa dell'anello di coomologia della varietà ambiente V e questa, a sua volta e sotto opportune ipotesi, determina il tipo di omotopia razionale della varietà stessa. Dunque i numeri di intersezione permettono, entro certi limiti, di ricostruire la varietà stessa. Il punto di vista degli invarianti di Gromov-Witten è diverso. Invece di cercare numeri di intersezione vengono ricercati numeri, apparentemente più riposti, che rispondano a problemi di geometria numerativa del tipo illustrato precedentemente e che esprimano il numero di curve razionali, contenute nella varietà ambiente V, soddisfacenti a certe condizioni algebriche.

Invarianti di Gromov-Witten

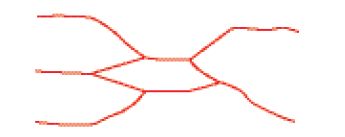
Il punto di vista degli invarianti di Gromov-Witten trae origine dalla geometria simplettica e dalla teoria delle stringhe. Il modello descritto dalla teoria delle stringhe ha per oggetto fondamentale un laccio o stringa, che per il momento si può immaginare chiuso, e i cui possibili modi di vibrazione sono rappresentazioni delle particelle elementari associate alle forze fondamentali esistenti in Natura (forze della meccanica quantistica, forze elettromagnetiche, forze di gravità). Così come la traiettoria descritta da un certo numero di particelle puntiformi è una curva unidimensionale, che si biforca e si ricongiunge a seconda di processi di creazione e annichilazione (fig. 5), la traiettoria descritta da un certo numero di stringhe chiuse può essere immaginata come una superficie bidimensionale (fig. 6).

Dal punto di vista geometrico la varietà ambiente in cui vive la stringa è una varietà V proiettiva, compatta e non singolare. Nella teoria delle stringhe la cancellazione di anomalie detta condizioni piuttosto restrittive su V, per esempio quella di essere una varietà di Calabi-Yau. Dal punto di vista matematico questa restrizione non è necessaria.

Il primo caso che è naturale studiare è quello delle curve razionali contenute in V. Si considerano quindi applicazioni analitiche f:S→V, dove

è una copia della sfera di Riemann (superficie di Riemann di genere 0) o, equivalentemente, della retta proiettiva complessa. L'immagine C=f (S) è una curva razionale contenuta in V. Nel caso delle curve piane, si concentrava l'attenzione su curve razionali di un determinato grado. Ricordando la [24], il grado di una curva piana non è altro che la classe di omologia intera della curva stessa. Dunque, nel caso generale di una varietà ambiente V qualsiasi, si fissa una classe β∈H₂(V, ℤ) e si concentra l'attenzione sulle curve razionali C⊂V tali che [C]=β. Nel caso delle curve piane, fissati n punti generici in

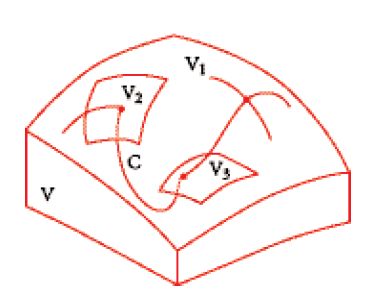
si consideravano le curve piane, razionali, nodate, di grado d, passanti per questi punti. È noto inoltre che, se n=3d−1, vi è solo un numero finito di curve piane, razionali, nodate, di grado d che passano per questi punti o, equivalentemente, che la famiglia di curve piane, razionali, nodate, di grado d, dipende da 3d−1 parametri complessi. Nel caso generale si fissano n sottovarietà analitiche V₁,…,V_n di V e si cercano le curve razionali C in V tali che [C]=β e che abbiano intersezione non vuota con V₁,…,V_n (fig. 7).

Un calcolo, che comporta conoscenze di geometria algebrica e in particolare di teoria delle deformazioni, porta alla conclusione che la famiglia delle curve razionali in V con [C]=β e che hanno intersezione non vuota con V₁,…,V_n, dipende da

parametri. È opportuno soffermarsi su questa formula.

Anzitutto è utile ricordare il concetto di 'prima classe di Chern di un fibrato vettoriale olomorfo'. Un fibrato vettoriale olomorfo F, di rango r su una varietà analitica V, consta di una famiglia F={F_p}_p∈V di spazi vettoriali complessi di dimensione r, uno per ogni punto p∈V, che variano olomorficamente al variare del punto p in V. Una sezione C^∞ di un fibrato consta di una famiglia di vettori v={v_p∈F_p}_p∈V, che variano in modo C^∞ al variare di p in V. Un fibrato della forma V×ℂ^r si dice banale. Naturalmente, un fibrato banale possiede r sezioni linearmente indipendenti. Per avere una prima misura di quanto un fibrato si discosti dall'essere banale, si prendano r sezioni generiche s¹,…,s^r e si consideri il luogo D_r dei punti p in V in cui s¹_p,…,s^r_p non sono linearmente indipendenti. Non è difficile vedere che questo luogo, se non è vuoto (ciò che accade per un fibrato banale), consta di una sottovarietà D_r di codimensione reale 2 in V. Il duale di Poincaré della sottovarietà D_r è una classe di coomologia in H²(V) che si denota con il simbolo c₁ (F) e prende il nome di prima classe di Chern del fibrato F.

Caso notevole di fibrato vettoriale olomorfo è quello del fibrato tangente olomorfo T_V. Se z₁,…,z_s sono coordinate locali olomorfe intorno a un punto p di V, allora lo spazio T_V,p, tangente olomorfo a V in p, ha come base le derivazioni

e al variare di p descrive il fibrato T_V.

Si ritorni alla formula [25]. Alla luce delle considerazioni appena fatte, si osservi cosa essa dice nel caso in cui

Anzitutto, una basilare formula della geometria algebrica, che prende il nome di 'formula di aggiunzione', afferma che c₁(T_ℙ2)= =3[ω_L], dove ω_L è definita dalla [22]. Nel caso in cui si vogliano contare curve piane di grado d, la classe β non è altro che d[L]. Poiché la dualità di Poincaré dice che ∫_L ω_L=1, il contributo del primo addendo in [25] è uguale a 3d. D'altro canto, nel caso delle curve piane le sottovarietà V₁,…,V_n sono punti e dunque hanno codimensione 2. Ne segue, come si era già constatato, che per n punti generici del piano passano

curve piane, razionali, di grado d.

Ritornando al caso generale, si può dare la seguente definizione provvisoria degli invarianti di Gromov-Witten. Si supponga che l'insieme delle curve razionali C⊂V, con [C]=β e C∩V_i≠/0, sia finito; si definisce l'invariante di Gromov-Witten I_β([V₁]…[V_n]) ponendo:

[28] I_β([V₁]…[V_n])=#{curve razionali C⊂V con: [C]=β e C∩V_i≠/0, i=1,…,n}.

Per dare una definizione rigorosa degli invarianti di Gromov-Witten è opportuno esprimere la definizione provvisoria [28] in termini di teoria dell'intersezione, in analogia con i numeri di intersezione definiti dalla formula [21]. Si consideri una curva razionale C⊂V, con [C]=β, e si supponga x₁∈C∩V₁,…,x_n∈C∩V_n. La curva C è l'immagine di una applicazione analitica

Siano

tali che f(p_i)=x_i, per i=1,…,n. Si ha una biezione di insiemi

dove un isomorfismo tra (f(p₁,…,p_n)) e (f(p′₁,…,p′_n)) è una applicazione bianalitica φ di

in sé stesso tale che f=f′o φ e tale che φ(p_i)=p′_i, per i=1,…,n. Dunque, secondo la definizione provvisoria, l'invariante di Gromov-Witten I_β ([V₁]…[V_n]) non è che la cardinalità degli insiemi sopra descritti, ove essi siano finiti. Si dimentichino, per il momento, le sottovarietà V₁,…,V_n, e si consideri solamente l'insieme

Risulta che:

a) M_0,n (V,β) ha una struttura di varietà analitica (eventualmente singolare, ma con singolarità non severe).

b) La dimensione di M_0,n(V,β) è uguale a ∫_βc₁(T_V)+dim V+n−3.

c) M_0,n (V,β) ammette una compattificazione

per la quale vale la dualità di Poincaré e sulla quale, dunque, è possibile sviluppare una teoria dell'intersezione.

L'esempio più semplice di uno spazio del tipo di M_0,n (V,β) è quello in cui la varietà V si riduce a un punto {p}, il che implica β=0. Dal punto di vista della teoria delle stringhe, il caso considerato è quello della gravità pura. In esso lo spazio M_0,n ({p},0), che si denota semplicemente con il simbolo M_0,n, è lo spazio che parametrizza le n-ple di punti distinti in ℙ¹ a meno di proiettività. Poiché, tramite una proiettività, si possono sempre fissare tre punti in

la dimensione di M_0,n è uguale a n−3, il che è in accordo con la formula enunciata nel punto (b). Lo spazio M_0,n è il più semplice esempio di spazio dei moduli di curve n-puntate. Esso corrisponde al caso di genere 0 e sarà oggetto di esame nel prossimo paragrafo, insieme con il caso più generale dello spazio dei moduli M_g,n delle curve n-puntate di genere g.

Dato un punto [f(p₁,…,p_n)]∈M_0,n (V,β), si pone

Ciò definisce applicazioni analitiche

[32]  φ_i:M_0,n(V,β)→V, i=1,…,n

che si possono estendere alla compattificazione

Dalla [29] segue che, secondo la definizione provvisoria,

[33] I_β([V₁]…[V_n])=∣φ₁^-1(V₁)⋂…⋂φ^-1n(V_n)∣.

D'altro canto, se la classe di coomologia ω_Vi ∈H*(V) è la duale di Poincaré di [V_i]∈H*(V), la classe di coomologia

è la duale di Poincaré di

e dunque è del tutto naturale definire gli invarianti di Gromov-Witten tramite la formula integrale

non appena φ*₁ (ω_V1)⋀…⋀φ*_n(ω_V1) sia una forma di grado massimo e cioè quando

(Si pone invece, convenzionalmente, I_β ([V₁],…,[V_n])=0 quando non vale questa uguaglianza). In effetti, in virtù delle [20], [21] e [33], la definizione [34] coincide con quella provvisoria [28] nel caso in cui φ^-1₁(V₁),…,φ^-1_n(V_n) si incontrino trasversalmente in un numero finito di punti.

Con l'introduzione degli invarianti di Gromov-Witten la teoria dell'intersezione si trasferisce dalla varietà ambiente V allo spazio dei moduli

o meglio all'insieme di tutti gli spazi dei moduli

al variare di n e di β. È effettivamente la considerazione simultanea di tutti questi spazi di moduli che consente di definire le funzioni generatrici dei numeri di intersezione del tipo di quelle descritte nel precedente paragrafo relativamente al caso delle curve piane.

È importante osservare che gli invarianti di Gromov-Witten generalizzano i numeri di intersezione [21]. In effetti, si consideri la classe β=0. Gli elementi di M_0,n (V,0) sono classi [f(p₁,…,p_n)], dove f è una applicazione costante. Dare una tale f è come dare un punto in V. Dunque se M_0,n denota la varietà delle n-ple di punti distinti in

si ha una identificazione M_0,n (V,0)=M_0,n×V. Le applicazioni di valutazione φ_i coincidono tutte con la proiezione φ:M_0,n×V→V.

Inoltre la varietà M_0,n ha, come si vedrà, una naturale compattificazione

In conclusione

Questo integrale può essere diverso da 0 solo se il grado della forma ω_V1⋀…⋀ωV_n coincide con la dimensione di

Ma se ciò accade, la dimensione di

deve essere uguale a zero. In questo caso

è un punto e

In definitiva:

Così come i numeri di intersezione determinano la struttura moltiplicativa di H_2*(V), gli invarianti di Gromov-Witten determinano una 'deformazione' della struttura moltiplicativa di H_2*(V).

Come si è già accennato, gli invarianti di Gromov-Witten appaiono quali coefficienti di una serie formale che soddisfa l'equazione WDVV [12] e, a partire da questa è possibile, in casi notevoli, calcolare i coefficienti della serie stessa. D'ora in poi si supporrà che tutti i gruppi di omologia di grado pari siano generati da classi di omologia di sottovarietà analitiche della varietà ambiente V. Ritornando alle notazioni della sezione precedente, sia [U₀]=[V],…,[U_N] una base per H_2*(V). Si definisce il potenziale di Gromov-Witten Φ ponendo

Si può separare in questa espressione una parte classica e una parte 'quantistica'. Sia [U₁],…,[U_K-1] una base di H₂(V). Allora Φ=Φ_c+Φ_q, dove

Nel caso in cui

si ha

dove L è una retta, e [U₂]=[p], dove p è un punto. Se si pone x₀=1, x₁=x e x₂=y allora, in virtù della [24], il potenziale Φ_q coincide con la serie F definita in [11].

Come si è già affermato, ciò che, in molti casi, rende calcolabili gli invarianti di Gromov-Witten è il fatto che il potenziale Φ soddisfa l'equazione WDVV [12]. È questo un sistema di equazioni differenziali che può scriversi nel modo seguente

per ogni scelta di i, j, k, l. Nel caso in cui

restringendo l'attenzione alla parte quantistica del potenziale di Gromov-Witten, questo sistema di equazioni si riduce all'equazione [12] o, equivalentemente, alla relazione ricorsiva [13].

Si definisce un 'prodotto quantico' ponendo

Questo prodotto introduce una struttura di algebra commutativa e unitaria nel modulo H_2*(V) ⊕ ℚ [x₀, x₁,…,x_N]. Il fatto molto notevole è che le equazioni WDVV [40] equivalgono all'asserzione che questa algebra è associativa. Per questo le equazioni WDVV prendono anche il nome di equazioni dell'associatività. Porre, nel prodotto definito dalla [41], tutte le variabili x_i uguali a zero è come sostituire il potenziale Φ con la parte classica Φ_c. Nel fare ciò si riottiene l'usuale struttura moltiplicativa in H_2*(V). È in questo senso che gli invarianti di Gromov-Witten determinano una deformazione della struttura moltiplicativa di H_2*(V).

Gli invarianti di Gromov-Witten, così come definiti dalla [34], coinvolgono lo studio delle curve razionali (cioè di genere 0) all'interno di una varietà ambiente. È del tutto naturale estendere questo studio alle curve di genere qualsiasi. Allo spazio M_0,n (V,β) deve essere sostituito lo spazio M_g,n (V,β) i cui elementi sono classi di isomorfismo [C, f, p₁,…,p_n], dove C è una curva di genere g, i p_i sono punti distinti di C e f è un morfismo da C a V tale che f [C]=β. In questo quadro, gli invarianti di Gromov-Witten sono definiti esattamente come in [34], dove però il dominio di integrazione deve ora essere una opportuna compattificazione di M_g,n (V,β). La definizione generale di invarianti di Gromov-Witten richiede dunque una buona teoria dell'intersezione per la compattificazione

dello spazio M_g,n (V,β). Ora, mentre le varietà M_0,n (V,β) e le loro compattificazioni sono irriducibili e con singolarità molto semplici, le varietà M_g,n (V,β) sono estremamente singolari e presentano molte componenti di varie dimensioni. Per definire gli invarianti di Gromov-Witten nel caso di genere g>0 è necessario poter disporre di una teoria dell'intersezione sulle varietà dei moduli M_g,n (V,β) e sulle loro compattificazioni. Tramite la teoria degli 'stack algebrici' è in effetti possibile definire su queste varietà una teoria dell'intersezione. Le notevoli difficoltà tecniche per giungere a questa definizione sono state superate nel 1997 da Kai Behrend e Barbara Fantechi.

Un caso già molto interessante e comunque di grande rilevanza geometrica è quello in cui la varietà V si riduce a un punto. In questo caso il dato del morfismo f:C→V è pleonastico, nel senso che la classe β non può che coincidere con la classe nulla e lo spazio M_g,n ({p}, 0) si denota semplicemente con M_g,n e prende il nome di 'spazio dei moduli delle curve n-puntate di genere g'. I punti di questo spazio sono le classi di isomorfismo di superfici n-puntate (C; p₁,…,p_n) dove C è una superficie di Riemann di genere g e i p_i sono punti distinti di C. Si ricordi che due superfici n-puntate (C; p₁,…,p_n) e (C′; p₁′,…,p_n′) sono isomorfe se vi è un isomorfismo φ:C→C′ tale che φ(p_i)=p_i′, per i=1,…,n. All'inizio dell'ultimo decennio del XX sec. e principalmente per opera di Witten e Kontsevich, la teoria dell'intersezione e la geometria numerativa degli spazi dei moduli di curve algebriche (gli spazi M_g,n) hanno ricevuto un impulso notevole e hanno portato alla sorprendente scoperta che i numeri di intersezione di questi spazi possono essere calcolati tramite l'equazione di Korteweg- de Vries. A questa scoperta è dedicato il paragrafo sucessivo, nel quale si descrivono alcuni degli elementi che consentono di trattare gli invarianti di Gromov-Witten più generali e cioè la geometria degli spazi dei moduli M_g,n(V,β).

La geometria numerativa dello spazio dei moduli delle curve algebriche

Il termine curva designerà una curva completa non singolare definita su ℂ o, ciò che è lo stesso, una superficie di Riemann compatta. Si considerano, d'ora in poi, curve n-puntate (C; p₁,…,p_n) di genere g, tali che 2−2g−n⟨0. Questa condizione numerica assicura che vi è solo un numero finito di automorfismi di C che fissano i punti p_i. L'insieme M_g,n delle classi di isomorfismo delle curve n-puntate di genere g prende il nome di 'spazio dei moduli delle curve n-puntate di genere g'. Riemann osservò che questo insieme possiede una naturale struttura di varietà analitica di dimensione complessa uguale a 3g−3+n. Per capire perché una curva n-puntata di genere g dipende da 3g−3+n parametri è utile considerare separatamente i casi g=0, g=1 e g>1.

L'unica superficie di Riemann di genere 0, a meno di isomorfismi, è la sfera di Riemann o, equivalentemente, la retta proiettiva complessa ℙ¹. Gli automorfismi di ℙ¹ sono le proiettività e vi è esattamente una proiettività che fissa tre punti di ℙ¹. Ne segue che lo spazio dei moduli delle curve n-puntate di genere g=0 coincide con lo spazio delle (n−3)-ple di punti distinti in

e dunque ha dimensione uguale a n−3 (fig. 8).

Una curva di genere 1 è isomorfa al gruppo quoziente di ℂ modulo un suo reticolo massimale Λ, ed è quindi un toro complesso. Si può sempre pensare che il reticolo Λ sia generato da due vettori 1 e τ, dove Im(τ)>0. Si indica con X_τ il toro complesso ℂ/Λ. Una curva 1-puntata di genere 1 è isomorfa a una coppia del tipo (X_τ,0) e si verifica che (X_τ,0) e (X_τ′, 0) sono isomorfe se e solo se

dove a,b,c,d sono interi e ad−bc=±1. Ne segue che le curve 1-puntate di genere 1 dipendono da un parametro complesso e che quindi le curve n-puntate di genere 1 dipendono da n parametri complessi (fig. 9).

Per comprendere il caso di genere g>1 è necessario capire, almeno intuitivamente, perché una superficie di Riemann di genere g dipenda da 3g−3 parametri complessi o, se si vuole, da 6g−6 parametri reali. Sia dunque S una superficie di Riemann di genere g. Si decomponga S in 2g−2 'pantaloni' come nella fig. 10. Si consideri su S una metrica riemanniana compatibile con la struttura complessa di S (cioè una metrica nella quale la rotazione di 90° di un vettore tangente complesso coincida con la moltiplicazione per i). La decomposizione in pantaloni fornisce le 3g−3 lunghezze dei bordi dei pantaloni e i 3g−3 angoli che determinano il modo in cui questi bordi devono attaccarsi tra loro. Poiché un pantalone in cui siano fissate le lunghezze dei bordi è analiticamente rigido, questi 6g−6 numeri sono i moduli (reali) di S.

I punti dello spazio dei moduli M_g,n rappresentano classi di isomorfismo di curve non-singolari n-puntate e di genere g. Per compattificare lo spazio M_g,n è necessario aggiungere punti che corrispondano a curve singolari. Queste curve sono ottenute facendo tendere a zero la lunghezza di uno o più cicli su una curva non-singolare. Ciò che è in un certo senso sorprendente, è che si può sempre supporre che al bordo dello spazio dei moduli vi siano punti che corrispondono a curve con singolarità molto semplici e cioè con singolarità nodali. Per una curva algebrica, un nodo è una singolarità che, dal punto di vista analitico locale, è isomorfa alla singolarità del tipo xy=0. Una curva nodata n-puntata è una coppia (C; p₁,…,p_n), dove C è una curva dotata al più di singolarità nodali mentre p₁,…,p_n è una n-pla di punti distinti e non-singolari di C. Una curva nodata n-puntata può essere quella nella fig. 11.

Una curva nodata n-puntata si dice 'stabile' se è connessa e possiede solo un numero finito di automorfismi. Quest'ultima condizione si traduce nel richiedere che ogni componente di genere zero contenga almeno tre punti che siano marcati o singolari. Ebbene, un risultato fondamentale (detto 'lemma di riduzione stabile') afferma che si può compattificare M_g,n aggiungendo al bordo solamente classi di isomorfismo di curve stabili n-puntate.

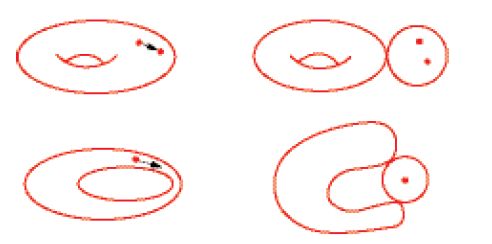
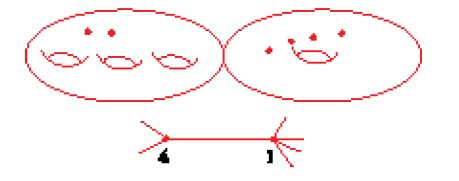
Non solo è sorprendente che la compattificazione di M_g,n possa essere definita esclusivamente in termini di curve nodali senza dover ricorrere a singolarità più complicate, ma è anche sorprendente che ci si possa limitare al caso in cui gli n punti marcati si possono supporre distinti e non-singolari. La fig. 12 mostra cosa accade al limite, quando si considera una famiglia di curve in cui due punti marcati si avvicinano tra loro o quando un punto marcato si avvicina a un nodo: in ambedue i casi la curva stabile limite presenta una 'bolla' (superficie di Riemann di genere 0) che ospita il limite dei punti marcati.

È utile considerare il grafo duale di una curva stabile puntata (C; p₁,…,p_n). Un tale grafo Γ ha tanti vertici quante sono le componenti irriducibili di C, mentre i suoi lati si dividono in due classi. Anzitutto, per ogni nodo di C vi è un lato che congiunge i vertici corrispondenti alle componenti di C contenenti quel nodo. Vi sono poi lati con un vertice solo. Essi corrispondono ai punti marcati di C. Se il lato corrisponde a un vertice p_i il suo vertice corrisponde alla componente di C e lo si decora con l'indice i. Nella fig. 13 si illustra il grafo duale della curva disegnata nella fig. 11.

Il genere di una curva stabile C è definito dalla formula

dove C₁,…,C_s, sono le componenti irriducibili di C. La curva della fig. 11 ha genere 6. Lo spazio dei moduli delle curve stabili n-puntate di genere g, compattificazione dello spazio M_g,n, si denota con il simbolo

e ha la struttura di varietà algebrica compatta di dimensione 3g−3+n. Il bordo ∂M_g,n di M_g,n in

cioè il luogo

è l'unione di un certo numero di sottovarietà di codimensione 1 che si possono descrivere nel modo seguente. Vi è anzitutto il luogo Δ_irr, il cui punto generico corrisponde a una curva stabile irriducibile con un solo nodo. Nella fig. 14 si mostra una tale curva e il suo grafo duale.

Inoltre, per ogni decomposizione P=A∪B dell'insieme delle marcature P={p₁,…,p_n} e per ogni i∈{1,…,n} vi è il luogo Δ_i,A il cui punto generico corrisponde a una curva stabile costituita da una curva di genere i, marcata dai punti p_s con s∈A, e da una curva di genere g−i marcata dai punti p_s con s∈B, che si incontrano in un punto, come mostrato nella fig. 15.

Si ha

È istruttivo considerare il caso di genere 0. In esso le componenti del bordo sono del tipo Δ_0,A. Ciò che rende il caso di genere 0 particolarmente interessante è il fatto che l'anello di coomologia di

è un anello di polinomi nelle classi δ_A, duali di Poincaré di Δ_0,A, modulo un ideale R di relazioni molto semplici:

Le relazioni sono le seguenti

per ogni scelta di indici i,j,k,l. Queste relazioni sono l'essenza geometrica delle equazioni WDVV soddisfatte dal potenziale di Gromov-Witten. In effetti, si può dimostrare che le equazioni [13] si riducono alle equazioni [46] per mezzo della applicazione naturale

che 'dimentica' la mappa f.

Si può anche dimostrare che le relazioni [46] si riducono al caso più semplice in cui n=4. Si osservi che

In effetti, poiché a meno di isomorfismi della retta proiettiva, si può trasformare una terna di punti nella terna {0,1,∞}, dare una curva 4-puntata di genere 0, a meno di isomorfismi, è come dare un punto di

Ne segue che

e che ∂M_0,4={0,1,∞}. I tre punti del bordo di M_0,4 corrispondono alle tre curve stabili, 4-puntate e razionali, i cui diagrammi duali sono raffigurati nella fig. 16.

Le relazioni [46] in questo caso si leggono nel modo seguente: δ₁₂=δ₁₃=δ₂₃ e ci dicono semplicemente che due punti in ℙ¹_ℂ sono omologicamente equivalenti. In un certo senso questa è l'essenza geometrica delle equazioni WDVV.

Nel momento in cui scriviamo, né l'anello di coomologia di M_g,n né quello di

sono pienamente conosciuti. Per quello che riguarda la conoscenza dell'anello di coomologia pari

un sostanziale progresso si è avuto con la dimostrazione, dovuta a Kontsevich, di una importante congettura di Witten. Per illustrare questo risultato conviene anzitutto descrivere alcune classi notevoli in

Si denota con il simbolo ψ_i la classe di Chern del fibrato lineare

la cui fibra sul punto

è lo spazio cotangente T*Pi(C) in p_i a C:

Una prima osservazione, dovuta a Witten, è che, mediante operazioni di tipo algebro-geometrico effettuate a partire da polinomi nelle classi ψ₁,…,ψ_n e applicazioni di inclusione degli strati del bordo ∂M_g,n in

o di proiezione da

a

si può costruire un sottoanello di

contenente i più notevoli cicli algebrici di

come, per esempio, le classi di Mumford-Morita-Miller o le classi di bordo. Le classi appartenenti a questo sottoanello prendono il nome di 'classi tautologiche'. La seconda osservazione è che la struttura di questo anello è completamente determinata dai numeri di intersezione delle sole classi ψ₁,…,ψ_n, considerate però per ogni valore di g e di n. In altri termini, il punto di vista di Witten è il seguente: invece di concentrare l'attenzione sulla teoria dell'intersezione di tutte le classi tautologiche in un singolo spazio di moduli

è più conveniente determinare la teoria dell'intersezione su tutti gli spazi di moduli

delle sole classi ψ₁,…,ψ_n.

Seguendo un formalismo suggerito dalla teoria topologica dei campi, Witten pone

dove si intende che

è uguale a zero se

e definisce la funzione generatrice dei numeri di intersezione ponendo

Witten mostra che F soddisfa l''equazione della stringa':

e congettura che la funzione U=∂²F/∂t²₀ soddisfi la gerarchia di equazioni di Korteweg-de Vries scritta nella forma di Gel'fand-Dikii

dove i polinomi differenziali R_i[U] sono definiti da

Questa congettura di Witten è stata dimostrata da Kontsevich nel 1992. Ponendo x=t₀ e t=t₁, la prima equazione di questa gerarchia è, a meno di una normalizzazione, la classica equazione di Korteweg-de Vries che governa il moto delle onde solitoniche

[54]  U_t=-6UU_x-U_xxx.

È importante notare che l'equazione della stringa e la gerarchia KdV permettono il calcolo esplicito dei numeri

Per esempio

Il fatto che un numero razionale, e non un intero, appaia come numero di intersezione dipende dal fatto che gli spazi

presentano singolarità che sono localmente isomorfe al quoziente di un polidisco per un gruppo finito.

Allo stesso ordine di idee appartiene il calcolo della caratteristica di Euler-Poincaré di M_g,n, effettuato da Harer e Zagier circa dieci anni prima della formulazione della congettura di Witten. Il calcolo porge un risultato notevole:

dove ζ(s)=∑_n>01/n^s è la funzione zeta di Riemann.

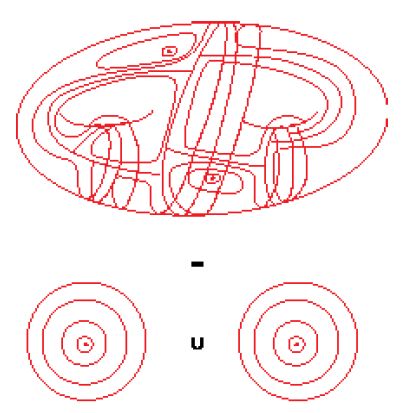
Come si è detto, una delle idee fondamentali della coomologia quantistica è che gli spazi dei moduli M_g,n (V, β), e dunque in particolare gli spazi M_g,n, vanno considerati simultaneamente per tutti i valori di g e n. La dimostrazione della congettura di Witten, dovuta a Kontsevich, mette bene in evidenza questo aspetto. Il primo passo della dimostrazione consiste nel dare una decomposizione cellulare dello spazio dei moduli M_g,n. Per un teorema dovuto a K. Strebel, data una superficie di Riemann n-puntata (C; p₁,…,p_n) e una n-pla di numeri reali positivi (r₁,…,r_n), è unicamente determinato un grafo Γ⊂C avente le seguenti proprietà. Anzitutto CΓ è unione di n dischi Δ₁,…,Δ_n di centri p₁,…,p_n. Inoltre è possibile introdurre in C una metrica che è piatta in C{p₁,…,p_n} e che ha singolarità in p₁,…,p_n. Ciò può essere visto come un modo di discretizzare il dato di una metrica riemanniana su C (e dunque di una struttura complessa) concentrandone la curvatura nei vertici del grafo Γ (fig. 17).

La metrica introdotta induce una metrica sul grafo Γ. Se L(Γ) è l'insieme dei lati di Γ, si consideri la cella

Il gruppo (finito) Aut(Γ) degli automorfismi di Γ agisce su c_Γ e si ottiene una decomposizione

dove

è l'insieme dei grafi connessi che si possono immergere in una superficie di Riemann di genere g e tali che CΓ è unione di n dischi. Grafi di questo tipo si chiamano 'grafi a nastro connessi di genere g, con n componenti di bordo'. In questo modo lo spazio M_g,n è decomposto in celle. All'interno di una cella indicizzata da Γ ci si muove variando le lunghezze dei lati di Γ.

Questa decomposizione cellulare di M_g,n permette di ridurre l'integrazione che interviene nella definizione [49] a una somma di integrazioni lungo le celle di dimensione massima (che corrispondono a grafi con vertici trivalenti). Per effettuare questa integrazione Kontsevich trova una espressione combinatoria per le classi ψ_i e mediante il cambiamento di variabili

ottiene la seguente espressione combinatoria per l'esponenziale della funzione di partizione [50]:

In questa formula Λ è la matrice diagonale: diag(λ₁,…,λ_N). Con il simbolo Γ_g,n si denota l'insieme dei grafi a nastro trivalenti (non necessariamente connessi) di genere g, con n componenti di bordo colorate con i colori λ₁,…,λ_N. Infine si denotano con i(e) e i′(e) i colori delle componenti di bordo di cui e è lato.

A questo punto interviene un'idea originariamente dovuta a 't Hooft.

Nello studiare reazioni nucleari che comportano un numero elevato di livelli di energia, si suole prendere come hamiltoniana una matrice hermitiana N×N, con N molto grande, i cui elementi siano variabili aleatorie. La misura di probabilità sullo spazio H_N delle matrici hermitiane N×N deve soddisfare due proprietà: l'indipendenza statistica e l'invarianza unitaria. Queste proprietà costringono la misura a essere (a meno di normalizzazione) del tipo

dove c e λ sono reali positivi e

I livelli di energia sono gli autovalori λ₁,…,λ_N di una matrice hermitiana aleatoria. Le quantità fisiche che si vogliono calcolare, come per esempio le funzioni di partizione, si ottengono per integrazione di opportune funzioni di λ₁,…,λ_N o, equivalentemente, di funzioni P(X) che siano invarianti per l'azione del gruppo unitario U(N). Tipicamente si considerano funzioni P delle tracce di X. Per esempio, si può considerare la funzione

Se come distribuzione di probabilità si considera la misura

la corrispondente funzione di partizione è, in questo caso, espressa come segue:

L'osservazione di 't Hooft, in seguito sviluppata da Brézin-Itzykson-Parisi-Zuber è la seguente. Così come nella teoria di Feynman è possibile calcolare lo sviluppo asintotico di integrali del tipo

(dove A è una matrice simmetrica definita positiva) in termini di diagrammi di Feynman, quando allo spazio ℝⁿ si sostituisce lo spazio delle matrici hermitiane H_N si ottengono sviluppi asintotici espressi in termini di grafi a nastro.

Usando questa idea e lo sviluppo [60], Kontsevich riesce a esprimere l'esponenziale della funzione generatrice [50] dei numeri di intersezione di M_g,n in forma di integrale matriciale, ottenendo la seguente notevole uguaglianza asintotica

L'ultimo passo nella dimostrazione di Kontsevich consiste nel far vedere che il logaritmo dell'integrale matriciale che appare alla destra della [66] soddisfa l'equazione KdV. Un legame tra integrali matriciali ed equazione KdV era già stato stabilito intorno agli anni 1989-1990 nei lavori di Kazakov, Brézin-Kazakov, Gross-Migdal, Douglas e Douglas-Shenker, nei quali si è scoperto che il modello matriciale può essere usato per una descrizione non perturbativa della 2D-gravità. La funzione di partizione di questo modello risulta del tipo

dove V(X)=∑g_iXⁱ è il potenziale. Per calcolare questo integrale si può usare il metodo dei polinomi ortogonali. Nel fare ciò l'equazione di Toda fa la sua comparsa. Passando da parametri discreti a parametri continui si ottiene l'equazione KdV. Ispirandosi a questo ordine di idee Kontsevich conclude la sua dimostrazione.

Ritornando alla coomologia quantistica di una varietà proiettiva V e ispirandosi al caso appena illustrato della gravità pura, in cui V si riduce a un punto, si è condotti a considerare invarianti di Gromov-Witten che includano come casi particolari sia i numeri definiti nella [34] sia i numeri definiti nella [49]. Si pone allora

dove le classi ψ_i sono definite su

nello stesso modo in cui lo erano su

Anche in questo caso si può formare una serie generatrice

e ci si può porre il problema di determinare le equazioni che essa soddisfa. Alexander B. Givental (2001) dimostra che questa serie generatrice soddisfa equazioni di tipo KdV almeno nel caso in cui V appartenga a una certa classe di varietà proiettive che, in ogni caso, include gli spazi proiettivi

e le grassmanniane. Queste equazioni, scritte per la prima volta da Eguchi, Hori e Xiong, da una parte contengono le equazioni WDVV e dall'altra la gerarchia KdV. Nel momento in cui scriviamo non è ancora stato risolto il caso di una varietà proiettiva liscia qualsiasi.

Bibliografia

Arbarello 2002: Arbarello, Enrico, Sketches of KdV, in: Symposium in honor of C.H. Clemens, Salt Lake City (UT), 2000 (Contemporary mathematics, 312), Providence (RI), American Mathematical Society, 2002, pp. 9-69.

Fulton, Pandharipande 1997: Fulton, William - Pandharipande, Rahul, Notes on stable maps and quantum cohomology, in: Algebraic geometry, Symposium, Santa Cruz 1995, "Proceedings symposia in pure mathematics", 62, 1997, pp. 45-96.

Givental 2001: Givental, Alexander B., Semisimple Frobenius structures at higher genus, "International mathematics research notices", 23, 2001, pp. 1265-1286.

Kontsevich 1992: Kontsevich, Maxim, Intersection theory on moduli spaces and matrix Airy function, "Communications in mathematical physics", 147, 1992, pp. 1-23.

Kontsevich 1995: Kontsevich, Maxim, Enumeration of rational curves via torus action, in: The moduli space of curves, edited by Robbert Dijkgraaf, Carol Faber, Gerard van der Geer (Progress in mathematics, 129), Boston-Basel-Berlin, Birkhäuser, 1995, pp. 335-368.

Manin 1999: Manin, Jurij I., Frobenius manifolds, quantum cohomology and moduli spaces (American Mathematical Society. Colloquium Publications, 47), Providence (RI), American Mathematical Society, 1999.

Witten 1991: Witten, Edward, Two-dimensional gravity and intersection theory on moduli space, in: Survey in differential geometry, proceedings of the Conference on geometry and topology, Harvard University 1990, edited by Chuan-Chih Hsiung, Stephen Yau, Bethlehem (PA), Lehigh University, 1991, pp. 243-310.