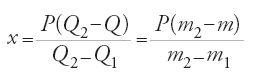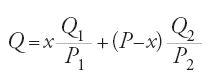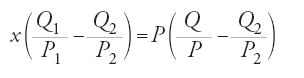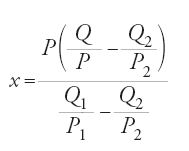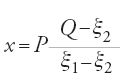La civiltà islamica: teoria fisica, metodo sperimentale e conoscenza approssimata. Statica

La civilta islamica: teoria fisica, metodo sperimentale e conoscenza approssimata. Statica

Statica

La statica è quella parte della meccanica che si occupa dell'equilibrio dei corpi. Al pari di tutta la meccanica, essa ha origine nell'Antichità, anche se la parola 'meccanica' possiede oggi un senso diverso da quello che aveva per gli Antichi e per gli autori arabi. La parola greca méchanḗ indicava originariamente una macchina, vale a dire un insieme di dispositivi atti a eseguire un determinato lavoro. Per gli studiosi dell'Antichità, la 'meccanica' era l'arte di costruire congegni, relativamente primitivi, a partire da cinque 'macchine semplici' (argano, leva, carrucola, cuneo e vite) che permettevano di spostare carichi pesanti con poco sforzo. La locuzione araba ῾ilm al-ḥiyal, ovvero la scienza dei procedimenti ingegnosi, traduce il greco méchanḗ. Il termine 'meccanica' ha continuato a designare la scienza delle macchine fino al Medioevo, quando si cominciò a studiare il moto dei corpi, per divenire poi, con Newton, la scienza del moto. Tuttavia è soltanto tra il XIX e il XX sec. che questo termine designerà la scienza di ogni tipo di movimento: la statica e la teoria delle macchine ne costituiscono solamente casi particolari.

Nell'Antichità, la statica era la scienza 'del peso'; come l'aritmetica, la scienza del calcolo, era suddivisa in due parti, una teorica e una pratica, corrispondenti a due diverse impostazioni: una si basava su leggi geometriche mentre l'altra su leggi dinamiche, le leggi del moto. La prima corrente risale ai Mechanica dello Pseudo-Aristotele, che è probabilmente la più antica opera di meccanica in nostro possesso. Nonostante non siano note traduzioni arabe o latine, l'opera ha avuto un ruolo molto importante nell'evoluzione delle idee in campo meccanico. Il suo contenuto è stato trasmesso attraverso altri lavori come i Mechanica di Erone d'Alessandria (attivo nel 62 a.C. ca.) e si caratterizza per un approccio dinamico ai problemi della statica e per l'assenza di rigore nelle dimostrazioni. L'autore, per esempio, non si preoccupa di dare una dimostrazione rigorosa della forma matematica della legge del moto di una leva, ma vuole piuttosto spiegare il fenomeno fisico e giustificare la teoria con le leggi della Natura utilizzando concetti dinamici a partire dalla legge di Aristotele, secondo la quale la velocità del moto è proporzionale alla forza motrice. I principî dell'equilibrio sono studiati su una leva a partire dalla rottura del suo equilibrio.

La seconda corrente, detta euclideo-archimedea, si fa risalire agli scritti sulla bilancia e sulla leva attribuiti a Euclide (III sec. a.C. ca.). Non è impossibile infatti che il Libro della bilancia romana, che studiosi arabi attribuiscono a Euclide, sia stato il primo trattato a presentare un approccio puramente statico alla teoria della leva. Tale trattato ci è pervenuto soltanto in lingua araba, in una versione dovuta verosimilmente a Ṯābit ibn Qurra. La sua impostazione esclusivamente di natura statica deriva dal fatto che le leggi dell'equilibrio sono studiate su una leva in equilibrio stabile, non mediante le nozioni di forza e di velocità ma soltanto in termini di distanze e pesi. Tale corrente si caratterizza anche per il ricorso alla teoria del baricentro, che la qualifica come strettamente archimedea, e per il rigore delle dimostrazioni geometriche.

L'eredità greca: le tradizioni aristotelica e archimedea

Da quando è stata proposta l'esistenza di due tradizioni o correnti nella meccanica antica, una aristotelica e l'altra archimedea, si è spesso cercato di classificare le opere arabe di statica secondo l'una o l'altra tradizione. Non sembra che i matematici arabi abbiano avuto direttamente accesso ai Mechanica dello Pseudo-Aristotele, cui non si fa mai allusione, e del quale non si conoscono versioni in lingua araba. Non sembra nemmeno che i matematici arabi siano venuti a conoscenza dei trattati di Archimede più avanzati in materia, né di quelli in cui il principio della leva è stabilito o utilizzato in dimostrazioni geometriche riguardanti la teoria del baricentro, come l'Equilibrio dei piani, il Metodo, la Quadratura della parabola o altre opere sul baricentro dei solidi andate perdute. È possibile, tuttavia, che essi le abbiano conosciute sotto forma di frammenti anonimi, di parafrasi o attraverso altri trattati, come i già citati Mechanica di Erone, il Kitāb fī 'l-qarasṭūn (Libro della bilancia romana) di Ṯābit ibn Qurra (IX sec.) o, ancora, il Libro VIII della Collezione matematica di Pappo di Alessandria (IV sec.), tutte opere di impronta fortemente aristotelica. In effetti, i matematici arabi conoscevano sicuramente i Mechanica di Erone, di cui ci è pervenuta soltanto una versione araba del IX sec., dovuta a Qusṭā ibn Lūqā. È un trattato estremamente ricco che fornisce numerose informazioni sulla meccanica greca, con vari riferimenti alla statica di Aristotele e di Archimede. Gli Arabi conoscevano anche un trattato di meccanica che il biografo e bibliografo Ibn al-Nadīm attribuisce a Pappo e che si intitola Madḫal ilā ῾ilm al-ḥiyal yuḏkaru fī-hi ῾ilm marākiz al-ṯiqal wa-kayfa yurfa῾u al-ṯiql al-῾aẓīm bi-'l-miqdār al-yasīr min al-quwwa (Introduzione alla scienza della 'meccanica' nella quale si parla della teoria del baricentro e di come sollevare un grande peso con una piccola forza). Quest'opera ‒ che tratta di problemi meccanici e in particolare del baricentro e della leva ‒ corrisponde probabilmente al Libro VIII della Collezione matematica di Pappo.

Per di più, siamo oggi in possesso di vari testi arabi e latini di origine greca che trattano della leva e della bilan-cia. Essi coincidono in certi punti, divergono in altri, si ricongiungono per il senso o per il testo e potrebbero risalire ‒ non è ancora ben chiaro ‒ a un'opera di Euclide o di Archimede. In ogni caso, che si tratti di Euclide, di uno dei suoi discepoli o del primo Archimede, queste opere rappresentano una tappa necessaria e importante nell'evoluzione della teoria della leva e della meccanica compresa tra i Mechanica dello Pseudo-Aristotele e l'Equilibrio dei piani o il Metodo di Archimede.

Se non ci si vuole limitare ad affermare l'esistenza di due correnti profondamente diverse, i vari modi d'impostare il problema dell'equilibrio vanno visti nel quadro di un processo evolutivo complessivo. In questo modo si spiega perché, malgrado le apparenti differenze, gli studiosi alessandrini e arabi sembrano non preoccuparsi di tale dicotomia, né esprimono alcuna riserva in proposito. Per fare un esempio, Erone include nella propria opera sia elementi dinamici, tratti dai Mechanica, sia principî puramente archimedei (riguardanti il baricentro), senza manifestare alcun disagio o riserva e senza avere l'impressione di trasgredire qualche legge particolare. Allo stesso modo, Ibn Qurra, nel Kitāb fī 'l-qarasṭūn, unisce lo studio della leva all'analisi dinamica dell'equilibrio. Il principio della leva è qui, in effetti, dimostrato in due modi diversi. Il primo si avvale di un'impostazione dinamica basata sulla legge del movimento di Aristotele e consiste nel confrontare due settori circolari descritti dal moto di una leva in rottura di equilibrio; il secondo affronta invece il problema in modo statico-geometrico, facendo appello al teorema di sostituzione o di ridistribuzione dei pesi.

Considerazioni di carattere dinamico e statico si trovano anche nel Kitāb MĪzān al-ḥikma (Libro della bilancia della saggezza), opera enciclopedica di ῾Abd al-Raḥmān al-Ḫāzinī (XII sec.), che raccoglie vari scritti di autori greci e arabi.

Ricordiamo in particolare il testo che al-Ḫāzinī attribuisce ad Abū Sahl al-Qūhī (X sec.) e ad al-Ḥasan ibn al-Hayṯam (X-XI sec.) e che si apre con la definizione aristotelica del centro del mondo e del movimento naturale dei gravi verso questo centro, per concludersi con l'espressione geometrica della legge della leva e con la definizione di baricentro. Le due impostazioni compaiono dunque in entrambe le tradizioni, quella greca e quella araba, senza che ciò significhi necessariamente l'appartenenza a una delle due.

Si può dunque dire che, se gli studiosi dell'Occidente tardo medievale si sono occupati di meccanica seguendo due tradizioni ‒ quella aristotelica, detta 'dinamica' (quando si trattava di studiare e spiegare in ambito fisico il concetto di forza), e quella archimedea, detta 'statica' (nel caso di problemi di equilibrio) ‒, è spesso impossibile, se non addirittura fuori luogo, voler ascrivere i lavori degli autori dell'Antichità e del primo Medioevo all'una o all'altra di queste tradizioni. Opere come i Mechanica di Erone, il Kitāb fī 'l-qarasṭūn di Ibn Qurra o il Kitāb MĪzān al-ḥikma di al-Ḫāzinī rifiutano questo tipo di classificazione.

La statica araba e il suo posto tra le scienze

Le condizioni storiche hanno particolarmente favorito lo sviluppo della statica araba nel Medioevo. Il miglioramento economico e, in particolare, l'aumento degli scambi commerciali richiedevano bilance e metodi di pesata sempre più perfezionati e ciò poteva realizzarsi soltanto attraverso la ricerca e l'approfondimento della teoria dell'equilibrio. Lo sviluppo della scienza dei procedimenti ingegnosi (῾ilm al-ḥiyal) è stato invece causato dalla necessità di migliorare le tecniche di spostamento e di sollevamento di grossi carichi (per scopi sia bellici sia civili) e quelle di sollevamento dell'acqua per l'irrigazione.

La statica araba del Medioevo si divide in tre indirizzi. Il primo è quello riguardante la statica teorica, che nasce dalla necessità di sviluppare la teoria dell'equilibrio sulla base dell'impostazione assiomatica e sui metodi infinitesimali della geometria greca. I due principali temi di ricerca, strettamente legati tra loro, sono la teoria della leva e la teoria del baricentro. La tradizione archimedea si associa qui a quella della fisica aristotelica: nelle opere arabe, la tradizione cinematica e quella statica coesistono e sono tra loro complementari. Il secondo indirizzo è relativo all'idrostatica, che consiste nello sviluppo della teoria di Archimede dei corpi galleggianti e degli studi di Aristotele sul movimento dei corpi in un fluido; l'applicazione pratica dell'idrostatica di Archimede porta alla nozione di peso specifico e ai metodi per determinarlo. Il terzo indirizzo, infine, riguarda la scienza delle macchine semplici e delle loro diverse combinazioni e comprende anche la scienza del sollevamento dell'acqua. Nella maggior parte delle enciclopedie arabe medievali la meccanica aveva essenzialmente questo significato.

La sintesi delle tradizioni archimedea e aristotelica è la caratteristica più significativa della statica araba. Il brillante studioso di meccanica al-Ḫāzinī è testimone di questa sintesi: "Quest'arte [la statica] include l'arte della geometria e l'arte della fisica, perché comprende lo studio delle cose quantitative e qualitative" (Kitāb MĪzān al-ḥikma, p. 7).

Dopo averne definito l'oggetto, esaminiamo quale posto occupava la statica tra le altre scienze secondo gli studiosi arabi del Medioevo. Secondo al-Fārābī la statica, che fa parte della matematica, come la geometria, l'aritmetica, l'astronomia e la musica, si divide in due branche: scienza dei gravi e ῾ilm al-ḥiyal; il significato di ῾ilm al-ḥiyal era però ampio e comprendeva anche i metodi aritmetici e geometrici dell'ingegneria e i metodi di costruzione delle bilance. Avicenna considera ῾ilm al-ḥiyal una branca della matematica, dove per branca di una scienza egli intende l'insieme dei metodi pratici relativi alle sue applicazioni. In questo senso, egli considera la scienza dei pesi e delle bilance, la scienza dello spostamento dei pesi mediante piccole forze e quella del sollevamento dell'acqua come facenti parte di una stessa branca della geometria, la meccanica. La statica teorica è, di fatto, considerata da tutti gli studiosi una branca della matematica.

A proposito del problema del baricentro, una delle due parti principali della statica teorica, al-Ḫāzinī dichiara che "la nozione di baricentro è la più grande e la più nobile delle nozioni delle scienze matematiche" (ibidem, p. 6). Questa collocazione della statica si ritrova in numerose enciclopedie arabe medievali. Secondo una delle più antiche, Mafātīḥ al-῾ulūm (Le chiavi delle scienze) di Muḥammad ibn Aḥmad al-Ḫwārizmī (X sec.), ῾ilm al-ḥiyal fa parte delle otto discipline scientifiche fondamentali (come la filosofia, la logica, l'astronomia, ecc.) e si divide in due branche: la prima studia le macchine semplici e i congegni che permettono di spostare pesi mediante piccole forze, mentre la seconda si occupa dei meccanismi per il sollevamento dell'acqua e dei meccanismi pneumatici. Quindi si può affermare che comprende due campi di ricerca strettamente legati tra loro, la teoria del baricentro e quella della leva.

È importante sottolineare che nel Medioevo, in Oriente come in Occidente, la statica non era separata dalle altre scienze. Gli studiosi di meccanica non erano esperti soltanto di questa disciplina ma anche di matematica, di astronomia, di filosofia, di medicina, ecc.; spesso, in una stessa opera, molte di queste scienze sono presenti insieme.

Siamo oggi in possesso di oltre sessanta opere di statica dell'Oriente medievale, alcune di paternità certa, altre anonime. Alcuni lavori e piccoli trattati, traduzioni di trattati antichi andati perduti, frammenti spesso quasi completi di predecessori arabi sono inclusi in opere di altri autori e sono giunti a noi soltanto in questa forma.

La statica teorica

La teoria della gravità e del baricentro

La nozione di baricentro compare per la prima volta in modo esplicito nelle opere di Archimede. Egli definisce il baricentro di un corpo come quel punto in cui, se vi è sospeso, il corpo resta in equilibrio, qualunque sia la sua posizione. Erone e Pappo attribuiscono ad Archimede, rispettivamente nella prop. 24 dei Mechanica e nel Libro VIII della Collezione matematica, la seguente definizione geometrica del baricentro di un corpo: esso è il punto di intersezione di tutti i piani di equilibrio del corpo, cioè il punto attorno al quale le parti del corpo si equilibrano reciprocamente. A partire da questa definizione, Archimede giunge alla geometrizzazione di tutta la statica teorica, rappresentando i pesi per mezzo di forze a essi proporzionali e sostituendo la leva con un segmento e i gravi con determinate figure geometriche.

In altre opere è data una diversa definizione del baricentro, di carattere fisico e legata ai principî aristotelici di moto e luogo naturale. Si deve ricordare al riguardo che i matematici greci dividevano i moti meccanici in due categorie: i moti naturali e quelli forzati. I moti forzati sono provocati da un intervento esterno mentre quelli naturali, che come la caduta dei gravi hanno luogo senza interventi esterni, dipendono da una certa inclinazione o tendenza insita nel corpo. Un grave, nel suo moto naturale, ha un'inclinazione verso il suo luogo naturale, che secondo Aristotele è il centro del mondo (corrispondente con il centro della Terra). Secondo questa definizione, il baricentro di un corpo pesante è il punto del corpo che coincide con il centro dell'Universo quando il corpo è in stato di quiete, al termine del suo moto naturale. Si tratta di una definizione che è data in modo esplicito soltanto nel Kitāb MĪzān al-ḥikma, anche se alcuni riferimenti a essa si trovano nei Mechanica di Erone e nel Libro VIII della Collezione matematica di Pappo. Per definire il baricentro, i due autori greci si richiamano infatti sia all'inclinazione dei corpi verso il centro del mondo sia all'intersezione di un corpo con piani passanti per il centro del mondo.

Secondo al-Ḫāzinī e i suoi predecessori, al-Qūhī e Ibn al-Hayṯam, la pesantezza, o la gravità (al-ṯiqal), è una categoria variabile che dipende dalla distanza tra il corpo e il centro del mondo; la distanza è definita come il segmento di retta che collega il baricentro del corpo al centro del mondo. Tali autori non forniscono la forma concreta di questa relazione, ma suppongono che la gravità sia nulla al centro del mondo e che cresca allontanandosi da esso. "Ogni corpo il cui peso è noto per una data distanza rispetto al centro del mondo vede variare il proprio peso in funzione di questa distanza. Più è lontano, più è pesante. Se si avvicina, diventa più leggero. Così il rapporto tra i pesi è come il rapporto tra le distanze" (Kitāb MĪzān al-ḥikma, p. 20). Al-Ḫāzinī spiega che la variazione della gravità in funzione della distanza dal centro del mondo dipende dalle variazioni di densità del mezzo che circonda la Terra, cioè dell'aria. "I gravi sono ostacolati dall'aria e nell'aria sono più leggeri del loro peso reale. Se si spostano verso un'aria più rarefatta sono più pesanti e viceversa se si spostano verso un'aria più densa sono più leggeri" (ibidem). Questa densità è massima sulla superficie della Terra ed è nulla alla periferia del Cosmo. Il peso di un corpo è allora massimo alla periferia del Cosmo ed è nullo al centro dell'Universo. In un dato punto del Cosmo si ha P=a+br, dove r è la distanza del punto dal centro del mondo e b è una costante. Nel caso ideale, in cui a=0, si ha ΔP=bΔr e P₁/P₂=r₁/r₂.

Il primo trattato conosciuto nel quale si trovano considerazioni di questo genere è il Kitāb MĪzān al-ḥikma; il concetto di gravità qui presente è simile al moderno concetto di energia potenziale. Si tratta però di una teoria che non ha avuto sviluppi nella meccanica medievale, né in Oriente né in Occidente. Il fenomeno della variazione della gravità dei corpi in funzione della distanza dal centro della Terra fu scoperto soltanto nel XVIII sec., grazie ai progressi compiuti nella teoria della gravitazione.

Nelle opere di Archimede a noi note non vi è alcuna definizione di baricentro. Egli si limita a determinare le caratteristiche geometriche di questo punto o a utilizzarlo come uno strumento in alcune dimostrazioni geometriche, senza definirlo esplicitamente. Archimede non sembra riferirsi a esso come a un principio nuovo, ma piuttosto come a una nozione già acquisita. Non sappiamo se la definizione di baricentro si trovi in un'opera andata perduta ‒ come sembrano sostenere alcuni commentatori quali Pappo, Erone ed Eutocio (quest'ultimo nel commento al Libro I dell'Equilibrio dei piani) ‒ o se essa sia stata data per scontata senza mai essere definita esplicitamente.

Il baricentro è una delle principali questioni trattate dalla statica araba. I matematici arabi hanno ereditato pochissimi lavori greci sul baricentro; oltre ai Mechanica di Erone, al Libro VIII della Collezione matematica di Pappo e verosimilmente a un testo di Archimede, non vi è traccia di alcun'altra opera chiaramente attestata sul soggetto. In questo modo, pochi matematici arabi hanno affrontato tale difficile problema il quale, non avendo alcuna fonte di partenza, richiedeva una grande competenza e una notevole abilità tecnica, in particolare nella determinazione del baricentro delle figure geometriche di rotazione, che comporta l'uso dei metodi della geometria infinitesimale. È quanto attesta Abū Isḥāq al-Ṣābi᾽ nella sua corrispondenza con al-Qūhī: "perché su questa scienza, quella del baricentro, non ci sono pervenute opere complete (kitāb kāmil) né lavori soddisfacenti (῾amal šāfī) di autori antichi o moderni" (Berggren 1983, p. 120). Se ne ha conferma da al-Qūhī che, nell'introduzione alla Risāla fī istiḫrāǧ misāḥat al-muǧassam al-mukāfi᾽ (Sulla determinazione del volume del paraboloide), parla dei "baricentri di numerosi corpi pesanti, che non sono stati determinati prima di noi da nessuno degli Antichi che si sono distinti in geometria, né a maggior ragione da nessuno dei moderni che sono loro inferiori; e che sappiamo non essere stati determinati da nessuno fino a oggi" (Rashed 1996, I, p. 850).

La corrispondenza di al-Qūhī e l'introduzione al suo trattato sul volume del paraboloide presentano, a questo riguardo, un duplice interesse storico; esse infatti non soltanto attestano l'esistenza di un trattato di al-Qūhī sul baricentro, fornendo informazioni sul contenuto e sul contesto nel quale fu scritto, ma danno anche ragguagli sulle conoscenze e sulle attività scientifiche dell'epoca. D'altra parte, l'enciclopedista al-Anṣārī menziona questo trattato assieme a uno di Ibn al-Hayṯam sullo stesso argomento, nella nota che egli dedica alla scienza del baricentro. Sembra dunque che questi due testi fossero le sole opere arabe complete e soddisfacenti sul baricentro e che fossero molto apprezzate. È probabilmente per tale ragione che al-Ḫāzinī cita soltanto queste opere, parlandone nello stesso capitolo del suo trattato. Non ci resta purtroppo alcuna traccia del trattato di Ibn al-Hayṯam, oltre al testo cui fa riferimento al-Ḫāzinī.

Complessivamente, sono tre le fonti arabe che ci permettono di studiare il problema del baricentro: il Kitāb fī 'l-qarasṭūn di Ṯābit ibn Qurra, il Kitāb MĪzān al-ḥikma di al-Ḫāzinī e la corrispondenza scientifica di Abū Sahl al-Qūhī. L'argomento principale del trattato di Ibn Qurra è il qarasṭūn, che noi chiamiamo comunemente bilancia romana. Si tratta essenzialmente di determinare il peso da applicare a una estremità di una sbarra omogenea sospesa in un punto perché resti in equilibrio. La risoluzione di questo problema richiede che ne sia risolto un altro: la dimostrazione della legge generale della leva nel caso di un giogo reale. Si attribuiscono opere con lo stesso titolo anche ai fratelli Banū Mūsā (IX sec.), a Qusṭā ibn Lūqā e Ibn al-Hayṯam, delle quali però non resta traccia.

Nel Kitāb fī 'l-qarasṭūn, Ibn Qurra non affronta esplicitamente il problema del baricentro ma ci si avvicina molto quando dimostra la legge dell'equilibrio per una leva reale. Egli considera il peso di una parte del giogo come un carico distribuito uniformemente per tutta la sua lunghezza, sostituendolo con un peso uguale sospeso al centro di questa parte. A tale scopo, suddivide la sbarra in parti uguali contraendo il peso di ciascuna parte nel centro della stessa e utilizzando il metodo relativo ai pesi sospesi dello Pseudo-Euclide.

Il metodo, che consiste nel suddividere una sbarra in parti uguali mediante sezioni parallele, era stato utilizzato da Archimede nella prop. 9 dell'Equilibrio dei piani, per determinare il baricentro di un parallelogramma. Anche l'idea di sostituire un insieme di pesi uguali disposti alle medesime distanze con pesi disposti al centro degli intervalli di suddivisione è presente in Archimede, nelle propp. 4, 5 e 6 dello stesso trattato, dove egli considera i pesi come puntiformi e applicati ai baricentri; si tratta dello stesso principio usato dal matematico greco nella dimostrazione geometrica della legge della leva. Senza conoscere il trattato di Archimede, Ibn Qurra era dunque andato molto vicino al concetto di baricentro, aprendo la via ad alcuni autori arabi successivi che riuscirono a determinare geometricamente il baricentro di varie figure, come il segmento di un paraboloide di rotazione. I suoi successori arabi ebbero, in effetti, accesso al suo Kitāb fī 'l-qarasṭūn, pervenutoci in numerosi manoscritti e citato anche da al-Qūhī nella sua corrispondenza con Abū Isḥāq al-Ṣābi᾽.

Il Kitāb MĪzān al-ḥikma di al-Ḫāzinī è un'opera di carattere enciclopedico, fondamentale nella storia della statica, in cui l'autore riporta i lavori di molti dei suoi predecessori arabi e greci, lasciandoci traccia di numerose opere di statica andate perdute e fornendo preziose informazioni sulle conoscenze degli Arabi nel campo della statica, dell'idrostatica, della scienza dei metalli e delle costruzioni meccaniche. Nel primo capitolo al-Ḫāzinī presenta, in nove sezioni, una lista di proposizioni, senza dimostrazione, che egli attribuisce ad Abū Sahl al-Qūhī e a Ibn al-Hayṯam, non precisandone i rispettivi contributi. Il testo definisce la gravità come una forza intrinseca a un corpo solido che lo attira verso il centro del mondo e studia il legame tra la densità e la forza di un corpo e tra il peso e il movimento dei solidi nei liquidi. Alla fine della quarta sezione è data la seguente definizione di baricentro: "un corpo che si trovi al centro del mondo lo ha nel proprio centro. L'inclinazione delle parti di questo corpo in tutte le direzioni e verso il centro del mondo è sempre la stessa. Ogni piano passante per il centro del mondo divide questo corpo in due parti i cui pesi sono in equilibrio rispetto al piano. In ogni corpo pesante, il punto che coincide con il centro del mondo quando il corpo vi si trova in quiete è il baricentro" (Kitāb MĪzān al-ḥikma, p. 17). Si tratta di una definizione che prende le mosse da considerazioni di tipo aristotelico, come l'inclinazione dei corpi verso il centro del mondo, per arrivare al concetto strettamente archimedeo di baricentro. A partire da essa, l'autore deduce alcune proposizioni di carattere puramente statico. È, ancora una volta, la dimostrazione che gli studiosi arabi passavano senza problemi da un'impostazione all'altra, considerandole piuttosto come approcci complementari. In effetti, non si può definire il baricentro di un solido senza ricorrere alla nozione di equilibrio, la quale a sua volta rinvia a nozioni dinamiche come quelle di movimento e di inclinazione naturale verso il centro del mondo.

Abbiamo visto come Erone e Pappo attribuiscano ad Archimede considerazioni molto simili sulla definizione di baricentro: l'equilibrio di un corpo rispetto a un piano o attorno a una retta passante per il suo baricentro e per il centro del mondo.

I lavori di Abū Sahl al-Qūhī sul baricentro

Come si è visto, nel Kitāb MĪzān al-ḥikma, al-Qūhī aveva studiato il problema dell'equilibrio e definito il baricentro in termini sia fisici sia geometrici. Numerose testimonianze dello stesso al-Qūhī relative ad altri suoi lavori in campo matematico forniscono ulteriori ragguagli sulle sue ricerche di statica e ci informano del fatto che egli si occupò del baricentro redigendo un trattato in più volumi sull'argomento. Nelle sue lettere ad Abū Isḥāq al-Ṣābi᾽, per esempio, al-Qūhī non dà la dimostrazione dei risultati riportati, rinviando ad alcuni libri sul baricentro da lui scritti, e fa riferimento a un trattato in sei libri ai quali alcuni altri avrebbero dovuto aggiungersi, in particolare un Libro VII, che doveva essere superiore agli altri per volume e contenuto.

Nell'introduzione al suo trattato sul volume del paraboloide, al-Qūhī annuncia che interromperà le ricerche sul baricentro, dopo aver determinato quello di numerose figure geometriche come il settore sferico e l'ellissoide, per lavorare al calcolo del volume del paraboloide; risultato che gli sarebbe poi servito per la determinazione del baricentro di questa stessa figura. Da questa testimonianza si può cogliere il livello tecnico e scientifico raggiunto da al-Qūhī nel momento in cui si occupa del baricentro: livello che non potrà essere inferiore a quello del trattato sul volume del paraboloide. È naturale che prima di determinare il baricentro di figure solide egli abbia dovuto studiare questa nozione e tutto ciò che essa implica, come la nozione di equilibrio e la teoria della leva. Ciò è confermato dal testo del Kitāb MĪzān al-ḥikma a lui attribuito, nel quale non è presente il calcolo dei baricentri di figure geometriche ma in cui si trovano le definizioni fisiche e geometriche di baricentro e numerose proposizioni riguardanti il fenomeno dell'equilibrio. È da notare che al-Ḫāzinī ebbe certamente accesso a una parte di questi scritti, se non a tutti.

È possibile chiedersi ora quale sia stato il contributo di al-Qūhī a questi importanti risultati. Nell'introduzione al trattato Fī ῾amal al-musabba῾ al-mutasāwī al-aḍlā῾ (La costruzione dell'ettagono regolare) vi è un passo che dimostra il grande interesse dei matematici dell'epoca per l'opera di Archimede; in particolare sono citati alcuni trattati allora disponibili, come La sfera e il cilindro, e un libro sul baricentro. Sappiamo, d'altra parte, dall'introduzione alla Risāla fī istiḫrāǧ misāḥat al-muǧassam al-mukāfi᾽, che l'individuazione da parte di al-Qūhī del baricentro del paraboloide ‒ e probabilmente anche di quello della semisfera, dell'ellissoide e di altre "cose" non precisate ‒ era del tutto indipendente dai risultati di Archimede, di cui al-Qūhī non era a conoscenza. Sempre in questa introduzione egli dichiara di non occuparsi di problemi già risolti dai suoi predecessori, poiché il suo scopo era quello di risolverne di nuovi. Così, lavorando da solo, al-Qūhī riscopre alcuni importanti risultati di Archimede, ai quali ne aggiunge due interamente nuovi sul baricentro di un arco di cerchio e di un settore circolare.

La teoria della leva

Nell'Antichità come presso gli Arabi, la statica si basava sul principio della leva, che si riduceva a sua volta al problema dell'equilibrio di un sistema di due corpi. Nelle opere a noi pervenute, Archimede si era occupato soltanto della leva ideale in equilibrio, rappresentandola mediante un segmento di retta fissato a uno dei suoi punti e all'estremità del quale pendono alcuni pesi. Il principio di Archimede è dunque direttamente legato al concetto di baricentro. Un'altra impostazione della teoria della leva risale alla tradizione dei Mechanica dello Pseudo-Aristotele e consiste nello studio di una leva in rottura di equilibrio. In questo caso, la dimostrazione del principio della leva si basa sul fatto che, se l'equilibrio della leva si rompe, in virtù della legge del moto di Aristotele, l'estremità descrive un arco di cerchio la cui lunghezza è inversamente proporzionale al peso sospeso.

Gli autori arabi seguono entrambe le tradizioni. Le due versioni del principio della leva si possono trovare in uno stesso trattato, come nel caso del Kitāb fī 'l-qarasṭūn e del Kitāb MĪzān al-ḥikma, le due principali opere arabe di statica. A partire dal XII sec., il Kitāb fī 'l-qarasṭūn esercitò una grande influenza sugli studiosi medievali di lingua latina grazie alla traduzione a opera di Gherardo da Cremona, dal titolo Liber Karastonis. L'origine di questo testo è controversa. In effetti, nell'epilogo della versione tradotta da Gherardo da Cremona, Ṯābit ibn Qurra ci informa che il suo libro è soltanto una revisione e uno sviluppo di un trattato di origine greca, ritrovato in pessimo stato, intitolato Causae Karastonis. Secondo il parere di alcuni storici, non c'è ragione di pensare che Ibn Qurra si sia servito dei Mechanica dello Pseudo-Aristotele: il Kitāb fī 'l-qarasṭūn potrebbe avere avuto origine dai frammenti sulla bilancia attribuiti a Euclide. Altri storici pensano invece a un trattato di Archimede sulle bilance andato perduto, del quale il Causae Karastonis costituirebbe una parte.

In ogni caso, gli studiosi arabi trovarono nel Kitāb fī 'l-qarasṭūn numerose tracce dell'opera di Aristotele sulla statica, e in particolare l'uso della legge del moto per stabilire il principio della leva. Il testo è anche contraddistinto da un notevole rigore matematico, contenendo dimostrazioni di carattere puramente statico analoghe a quelle che dà Archimede nell'Equilibrio dei piani. Sono fornite in effetti due diverse dimostrazioni del principio della leva, una di carattere dinamico e una di carattere statico. La prima affronta il problema dal punto di vista della dinamica, essendo basata sulla legge del moto di Aristotele e consistendo nel confronto di due settori circolari descritti dal moto di una leva in rottura di equilibrio. Si parte dal fatto che una retta AB, animata da un moto attorno a un punto O, descrive due settori circolari simili di raggi OA e OB. Se la sbarra è in rottura di equilibrio, sia A nella posizione superiore e B in quella inferiore. Per riportare la sbarra alla posizione iniziale occorrono pesi inversamente proporzionali agli archi AA e BB che essi percorrono in tempi uguali. È qui che interviene la legge del moto di Aristotele, in quanto ciascuno dei pesi viene spostato dalla forza esercitata dall'altro. Poiché essi percorrono distanze diverse in tempi uguali, queste forze devono essere proporzionali al percorso che esse determinano. Per alcuni storici, questa dimostrazione costituisce una tappa importante nella direzione di quello che più tardi sarà chiamato il 'principio dei lavori virtuali'; essa, d'altra parte, è molto simile a quella che dà lo Pseudo-Aristotele nei Mechanica, anche se sembra che Ibn Qurra non conoscesse quest'opera.

La seconda dimostrazione è di natura geometrica e ricorda il metodo usato nel Libro della bilancia romana attribuito a Euclide e che si basa sul teorema di sostituzione, o ridistribuzione, dei pesi che, come abbiamo osservato sopra, si avvicina molto al concetto di baricentro. Esistono però importanti differenze tra il metodo di Ibn Qurra e quello dello Pseudo-Euclide. Quest'ultimo dimostra il principio della leva per pesi commensurabili e soltanto per un giogo ideale. La sbarra viene divisa in un numero qualunque di parti uguali, si considerano poi pesi uguali appesi ai punti di divisione, e si dimostra geometricamente che i pesi così distribuiti equivalgono a un peso uguale alla loro somma posto al centro di tutti i punti di divisione. Attraverso una successione di spostamenti dei pesi, si giunge al principio di proporzionalità tra i pesi e le distanze. Ibn Qurra prende probabilmente le mosse da una fonte vicina al trattato dello Pseudo-Euclide, alla quale apporta però aggiunte importanti. Egli determina dapprima la risultante di due forze uguali; quindi generalizza il risultato a un numero finito qualunque di forze uguali, e poi a un numero infinito (lā nihāya) di tali forze. Studia poi il caso di un giogo reale, considerandone il peso come un carico distribuito uniformemente per tutta la sua lunghezza: la sbarra viene divisa in parti uguali e il peso concentrato nei punti di mezzo delle singole parti. Questo metodo, come abbiamo visto, era stato utilizzato da Archimede sia per determinare il baricentro di alcune figure piane sia per dimostrare la legge della leva.

Nel Kitāb MĪzān al-ḥikma al-Ḫāzinī riporta alcuni testi sulla teoria dell'equilibrio che egli attribuisce ad Abū Sahl al-Qūhī, ad Ibn al-Hayṯam, a Euclide, a Ibn Qurra e ad al-Muẓaffar al-Isfizārī. Questi scritti contengono numerose proposizioni prive di dimostrazioni, che ci permettono comunque di conoscere la portata del contributo arabo alla teoria dell'equilibrio e di ottenere alcune interessanti informazioni su varie opere andate perdute.

Vediamo più da vicino alcuni passi del Kitāb MĪzān al-ḥikma e cerchiamo di stabilire da quali opere traggano origine alcune delle proposizioni in esso contenute e quale sia stato il contributo originale degli studiosi arabi.

Al-Muẓaffar al-Isfizārī (XI-XII sec.) scrisse un trattato, andato perduto ma in parte riportato da al-Ḫāzinī, sulla costruzione e l'utilizzazione della bilancia idrostatica. Lo studio di questo testo rivela come l'autore abbia elaborato un'introduzione alla teoria del qarasṭūn, spiegando e semplificando alcuni passi del Kitāb fī 'l-qarasṭūn e vari frammenti dello Pseudo-Euclide. Vi si incontrano anche teoremi non riportati né nel libro di Ibn Qurra né in quello dello Pseudo-Euclide. È possibile che questi teoremi siano ispirati ai lavori di alcuni predecessori arabi come al-Qūhī e Ibn al-Hayṯam. Si tratta anzi di un'eventualità molto probabile: al-Ḫāzinī riproduce infatti nel Kitāb MĪzān al-ḥikma alcuni testi che attribuisce a questi due studiosi. Riprendendo i lavori di al-Isfizārī sulle bilance e lavorando nello stesso luogo (alla corte di Marw, capitale del Khurasan), al-Ḫāzinī doveva avere sotto mano gli stessi documenti sui quali aveva lavorato il suo predecessore; è dunque ragionevole pensare che anche al-Isfizārī conoscesse questi testi.

Dopo la definizione in termini fisici del baricentro, al-Ḫāzinī studia l'interazione di due corpi al centro del mondo e ne deduce le loro posizioni rispetto a questo centro, quando essi sono in quiete. Studia quindi il baricentro di un sistema di due corpi tridimensionali non rigidamente collegati esaminando il loro comportamento durante il moto verso il centro del mondo. Per giustificare le proprie conclusioni, l'autore non fornisce dimostrazioni facendo soltanto uso di esempi. Per comprendere l'interazione di due corpi in quiete al centro del mondo, egli suggerisce di considerare i due esempi che seguono. Il primo consiste nel far rotolare in un recipiente semisferico due corpi di forma sferica, contemporaneamente o uno dopo l'altro, e nell'immaginare una linea retta che congiunga il centro del recipiente al centro C del mondo.

Nel caso di un solo corpo, il suo baricentro si trova sulla retta verticale. Nel caso di due corpi uguali, i loro baricentri si trovano a uguale distanza, da una parte e dall'altra della verticale. Se i due corpi sono diversi, il baricentro del sistema formato dai due corpi sta sulla verticale e si applica la legge dei rapporti inversi tra pesi e distanze: OI/Io=p/P. Si tratta della legge della leva applicata ai corpi solidi e dipendente dalle distanze dei loro baricentri; legge che risulta una generalizzazione sia di quella dello Pseudo-Euclide (che non fa intervenire il concetto di baricentro) sia di quella di Archimede (che riguarda solo figure piane).

Per quanto riguarda il secondo esempio, bisogna immaginare due corpi di forma sferica sospesi a uno stesso punto e una retta che congiunge questo punto con il centro dell'Universo. Nel caso di un solo corpo sospeso, il baricentro di questo sta sulla verticale, come Archimede (prop. 6 del trattato La quadratura della parabola) afferma di aver dimostrato in un'opera precedente, che non ci è pervenuta. Nel caso di due corpi, il baricentro del sistema è posto sulla verticale, e si può applicare la legge dei rapporti inversi. Si ottiene così un altro risultato che Archimede afferma di aver dimostrato, secondo cui il baricentro di un sistema di due corpi si trova sulla retta che congiunge i loro centri.

Nel testo in questione vi è soltanto la definizione fisica aristotelica di baricentro, mentre non appare alcun riferimento alla definizione geometrica che abbiamo visto in al-Qūhī e in Ibn al-Hayṯam (equilibrio attorno a un piano, intersezione delle rette di equilibrio), e ciò lascia supporre che l'autore fosse interessato soltanto al fenomeno dell'equilibrio e non al calcolo del baricentro delle figure geometriche. Si nota in ogni caso una notevole padronanza del concetto di baricentro e di come esso interviene nel fenomeno dell'equilibrio.

Il testo del Kitāb MĪzān al-ḥikma attribuito ad al-Qūhī e a Ibn al-Hayṯam contiene, come abbiamo detto, un insieme di proposizioni senza dimostrazione ‒ riguardanti i gravi e facenti riferimento alla nozione di baricentro ‒ che non sono dissimili, anche se più generali, da quelle dell'Equilibrio dei piani di Archimede.

Nelle proposizioni seguenti al-Ḫāzinī si occupa delle nozioni di equilibrio e di baricentro di un sistema di solidi nello spazio: "Se si aggiungono a pesi in equilibrio rispetto a un dato centro pesi in equilibrio rispetto allo stesso centro senza modificare il baricentro del sistema, allora il sistema resta in equilibrio rispetto a questo centro […]. Se si sottraggono pesi in equilibrio a pesi in equilibrio senza modificare il baricentro, i pesi che restano sono in equilibrio" (Kitāb MĪzān al-ḥikma, p. 18). Si tratta di proposizioni analoghe alla prop. 5 dell'Equilibrio dei piani (e ai suoi corollari), nella quale però si considera soltanto l'equilibrio di coppie di pesi uguali ed equidistanti da uno stesso punto e tali che i baricentri siano tutti allineati. È perciò l'estensione di questa proposizione al caso di coppie di pesi qualunque in equilibrio, e allo spazio.

La proposizione seguente, di carattere puramente statico, è dedotta dalla definizione di baricentro attribuita ad al-Qūhī e a Ibn al-Hayṯam nello stesso testo e ricorda una proposizione analoga di al-Isfizārī, salvo il fatto che egli considera i corpi al termine del loro movimento naturale, cioè al centro del mondo: "Dati due gravi collegati tra loro, il rapporto tra il peso dell'uno e il peso dell'altro è uguale al rapporto inverso dei due segmenti della retta sulla quale giacciono i tre baricentri, quelli di ciascuno dei due gravi e quello del sistema che essi formano" (ibidem, p. 19).

Nella sezione 9 troviamo la seguente proposizione: "Se due corpi qualunque sono in equilibrio rispetto a un dato punto, il rapporto fra il peso dell'uno e il peso dell'altro è uguale al rapporto inverso dei due segmenti della retta che passa per questo punto e per i due baricentri" (ibidem, p. 20). Essa corrisponde alla prop. 6 dell'Equilibrio dei piani, relativamente però a corpi solidi, e alla prop. 4 dello Pseudo-Euclide, ma con maggiore precisione e facendo intervenire la nozione di baricentro. Richiamandosi al concetto di baricentro, l'autore elimina la concezione fisica della bilancia e la legge della leva diventa astratta e puramente geometrica.

Questi esempi dimostrano che vi è un'importante differenza tra il Libro della bilancia romana (attribuito a Euclide) e l'Equilibrio dei piani (che Erone e Pappo attribuiscono ad Archimede) e le proposizioni che al-Ḫāzinī fa risalire ad al-Qūhī e a Ibn al-Hayṯam. Queste ultime estendono ai corpi solidi in equilibrio nello spazio molte delle proposizioni contenute nell'Equilibrio dei piani, precisano la legge dell'equilibrio dello Pseudo-Euclide ricorrendo al concetto di baricentro e rendono astratta e puramente geometrica la legge dell'equilibrio, eliminando la concezione fisica della bilancia. Questi fondamentali sviluppi della teoria della leva e del baricentro contenuti nel Kitāb MĪzān al-ḥikma e nell'opera di al-Qūhī si possono considerare la logica prosecuzione dei frammenti sulla leva attribuiti ad Archimede e a Euclide. Molte testimonianze suggeriscono, d'altra parte, che al-Qūhī lavorava sul baricentro senza avere alcuna conoscenza dei risultati ottenuti da Archimede. È chiaro altresì, sulla base della sua corrispondenza, che egli non conosceva né la dimostrazione della legge della leva data da Archimede né quella dello Pseudo-Euclide. I matematici arabi non conoscevano quindi alcuna opera greca che trattasse i problemi dell'equilibrio in relazione al concetto di baricentro o della determinazione del baricentro di una figura solida. Gli sviluppi che essi determinarono in questo campo furono interamente frutto dei loro sforzi.

La nozione di momento nella statica araba

Gli assiomi di Archimede e il principio della leva non soltanto sono alla base della teoria generale dell'equilibrio, ma rappresentano anche il primo passo verso l'elaborazione della nozione di momento di una forza (rispetto a un punto). Questa nozione è utilizzata implicitamente da Archimede; la si ritrova in particolare nell'Equilibrio dei piani, dove compare per la prima volta il prodotto di una forza (il peso) per la distanza tra il punto di applicazione di questa e il punto di sospensione del giogo; quantità che più tardi sarà chiamata appunto il 'momento' della forza rispetto al punto di sospensione. Anche l'autore del Kitāb fī 'l-qarasṭūn fa implicitamente uso di questa nozione. Egli introduce quella che chiama 'forza del peso' (quwwat al-ṯiql), associandola a ciascun elemento di lunghezza della leva e notando che essa varia proporzionalmente alla distanza di questi elementi dal punto di sospensione del giogo. Altri autori arabi hanno utilizzato implicitamente la nozione di 'momento', applicandola non solo a un segmento puramente geometrico, come aveva fatto Archimede, ma anche a una leva pesante. Ṯābit ibn Qurra ha sviluppato più di ogni altro questa teoria nel suo Kitāb fī 'l-qarasṭūn. Mentre Archimede e i tardi autori greci ne avevano fatto uso soltanto nel caso di un giogo orizzontale, dove il braccio è semplicemente il segmento di retta che congiunge l'asse al punto di applicazione del peso, Ṯābit ibn Qurra generalizzò la nozione di 'braccio' considerando anche una leva a gomito, nella quale la parte che sorregge il peso forma un angolo qualunque con la parte principale del giogo. Il braccio è allora definito come la più breve distanza tra l'asse di rotazione della leva e la direzione di azione della forza: si tratta della prima definizione precisa del 'braccio di una forza'.

Applicazioni pratiche della teoria della leva

Al-Ḫāzinī formula il principio della leva riportando le dimostrazioni di Ṯābit ibn Qurra e di al-Isfizārī in modo così completo da poter passare direttamente alle applicazioni pratiche. Presenta la bilancia come un sistema di gravi: il giogo, i piatti, il cui numero può arrivare fino a cinque, e l'ago. Si tratta della 'bilancia della saggezza', cioè di una bilancia a bracci uguali munita di cinque piatti e di un peso equilibrante posto sopra il giogo graduato. Al-Ḫāzinī ne esamina le condizioni di equilibrio e di stabilità basandosi sulla teoria del baricentro, da lui esposta in precedenza.

Il suo studio si divide in tre parti. Egli considera dapprima un giogo cilindrico pesante, sospeso a un asse parallelo all'asse orizzontale e in equilibrio, e tre possibili posizioni del giogo alla 'rottura' dell'equilibrio, a seconda che l'asse di rotazione passi sotto sopra, o per il baricentro del giogo. Le tre posizioni sono dette rispettivamente asse di rotazione (miḥwar al-inqilāb), asse di vincolo (miḥwar al-iltizām) e asse di equilibrio (miḥwar al-i῾tidāl) e, in linguaggio moderno, corrispondono alle posizioni di equilibrio instabile, stabile e indifferente. Esse vengono descritte da al-Ḫāzinī nel modo seguente.

a) Asse di equilibrio. Se l'asse passa per il baricentro del giogo, cioè nel suo punto di mezzo, ed è perpendicolare al giogo, quest'ultimo ruoterà liberamente. La posizione di quiete è quella nella quale si trova alla fine di una rotazione e appare evidente che questa posizione è quella orizzontale, in quanto la freccia che passa per il centro dell'Universo e per il baricentro del giogo divide quest'ultimo in due parti uguali.

b) Asse di rotazione. L'asse è situato tra il centro dell'Universo e il baricentro del giogo. Se il giogo viene mosso si rovescerà perché la freccia che passa per il centro dell'Universo divide il giogo in due parti disuguali. La parte inclinata verso il basso sarà la più pesante ed è per questa ragione che il giogo si ribalta.

c) Asse di vincolo. L'asse si trova al di sopra del baricentro del giogo. Se il giogo si muove, la freccia che passa per il centro dell'Universo lo divide in due parti disuguali. La parte inclinata verso l'alto sarà la più pesante e tornerà verso il basso per fermarsi parallelamente all'orizzonte, in quanto la freccia dividerà in quel momento il giogo in due parti uguali. Questo sarà allora vincolato a restare parallelo all'orizzonte.

Nella seconda parte della sua analisi, al-Ḫāzinī studia un sistema composto da un giogo di bilancia e da un ago, trascurando dapprima l'effetto dei piatti e dei pesi. Le condizioni di equilibrio di un tale sistema sono ridotte a quelle di una leva di bilancia libera ma con un altro baricentro. Si tratta di una riduzione legittima soltanto se il sistema è simmetrico rispetto all'asse di sospensione, cioè quando l'ago è di forma romboidale ed è fissato al baricentro del giogo. In caso contrario, i baricentri del giogo e dell'ago non coincidono, le condizioni diventano più complesse e lo saranno in misura ancora maggiore in presenza dei piatti. Al-Ḫāzinī non lo dimostra, motivando che sarebbe troppo lungo farlo. Il metodo usato ci permette tuttavia di supporre che la dimostrazione si basava su certi postulati dei Corpi galleggianti di Archimede e più precisamente sulle leggi dell'equilibrio dei corpi di varie forme immersi in un liquido. Al-Ḫāzinī conosceva sicuramente la versione araba di quest'opera, che era stata riportata per intero nel Kitāb MĪzān al-ḥikma. Questo punto ci conduce a un altro problema fondamentale della statica araba, l'equilibrio di un corpo in un liquido, ovvero l'idrostatica.

L'idrostatica e il calcolo del peso specifico

I matematici arabi si sono interessati alla bilancia non soltanto per la sua utilizzazione negli scambi commerciali ma anche per il suo impiego come strumento di misura delle densità specifiche dei metalli e delle pietre preziose.

L'idrostatica fu fondata da Archimede, che fu il primo a proporre una teoria dell'equilibrio dei corpi immersi nei liquidi e a studiarne la stabilità. Tra i suoi predecessori non vi sono tracce di leggi o di tentativi di formalizzare questo fenomeno fisico. Vitruvio riferisce nel De architectura che la vicenda storica della corona del re Erone di Siracusa sarebbe all'origine della teoria idrostatica di Archimede. Il re gli avrebbe chiesto di verificare se una certa corona era di oro puro e Archimede, avendo capito mentre faceva il bagno il principio della spinta che subisce un corpo immerso in un liquido, ne avrebbe dedotto la soluzione del problema della corona. La storia della corona è riportata da Ǧābir ibn Ḥayyān (VIII-IX sec.) nel trattato di alchimia Kitāb al-Baḫt (Libro della fortuna), nel quale viene attestata l'esistenza di una versione araba del trattato che Archimede avrebbe scritto su richiesta del re per esporre il suo metodo intitolata Kitāb Wazn al-tāǧ (Libro del peso della corona). Ǧābir ibn Ḥayyān dichiara di aver redatto un commento a questo libro, che egli definisce difficile.

I soli lavori di idrostatica di Archimede a noi pervenuti sono i due libri dei Corpi galleggianti, nei quali sono studiate le leggi della statica dei fluidi e le condizioni di equilibrio di un solido immerso in un liquido. Gli studiosi arabi ne possedevano un frammento che conteneva la definizione di peso specifico, che è assente nel testo greco, e una versione del postulato di base della pressione idrostatica migliore di quella che si trova nel testo originale. Questo frammento contiene anche gli enunciati di sette delle nove proposizioni del Libro I e della prop. 1 del Libro II. Oltre a questo, gli Arabi conoscevano anche alcuni scritti di Menelao e di Pappo sulla densità specifica. Secondo al-Ḫāzinī, Menelao descrive la bilancia di Archimede e anche il suo metodo per distinguere le due componenti di una lega. L'autore del Kitāb MĪzān al-ḥikma attribuisce inoltre a Pappo uno strumento di misura dei pesi specifici, che egli descrive e di cui spiega il funzionamento.

Quanto agli studi degli scienziati arabi, disponiamo, per darne un giudizio, di due fonti principali: il trattato di al-Bīrūnī sul peso specifico e il già citato Kitāb MĪzān al-ḥikma di al-Ḫāzinī. Grazie a tali opere abbiamo testimonianze di numerosi studi di scienziati arabi, come Sanad ibn ῾Alī (IX sec.), Yūḥannā ibn Yūsuf (X sec.) della Scuola di Baghdad, Abū al-Faḍl al-Buḫārī (X sec.) ‒ del quale al-Bīrūnī si considerava successore diretto ‒, al-Nayrīzī (X sec.) ‒ del quale ci è pervenuta un'opera ‒, al-Rāzī (IX-X sec.), Avicenna (X-XI sec.) e al-Ḫayyām (XI-XII sec.).

L'idrostatica

È chiaro quale sia il principio che ha ispirato al-Ḫāzinī nella scelta delle fonti per il capitolo sull'idrostatica del Kitāb MĪzān al-ḥikma. Egli espone le proprie versioni dei lavori di Archimede e Menelao per enunciare i principî fondamentali dell'idrostatica. Includendo nel suo trattato il Libro di Archimede sul pesante e il leggero, egli rende familiare al lettore il movimento dei corpi in un mezzo diverso dall'aria: "Se un corpo pesante si sposta in un liquido, il suo peso decresce di una quantità che dipende dal volume, per cui nel liquido diventa più leggero di una quantità pari al peso del volume del liquido spostato" (Kitāb MĪzān al-ḥikma, p. 24). Più grande è il volume del corpo in moto, maggiore è l'ostacolo al movimento. D'altra parte, la differenza di velocità in un liquido di due corpi di pari densità e volume è determinata dalla differenza di forme che implica una differenza di forze motrici: "Se le forme sono diverse le forze che muovono i corpi sono diverse" (ibidem). In questo modo, al-Ḫāzinī distingue due forze agenti sui corpi in moto in un mezzo diverso dall'aria. Una è determinata dal peso e dalla forma del corpo e, secondo l'insegnamento di Aristotele, offre una resistenza al moto. L'altra è la spinta verso l'alto definita da Archimede, che dipende dal volume del corpo e da quello del liquido spostato (che è, a sua volta, determinato dalla differenza tra la densità del corpo e quella del mezzo). A parità di volume, una maggiore densità implica una maggiore gravità in un dato mezzo. Corpi che hanno lo stesso peso in un mezzo possono averne diversi in un altro. Si tratta di affermazioni senza dubbio fondate sulla teoria di Archimede: al-Ḫāzinī applica infatti la prop. 7 del Libro I dei Corpi galleggianti al caso di corpi immersi in mezzi di diversa densità. In questo modo, combinando l'idrostatica di Archimede con la teoria aristotelica del moto dei corpi, al-Ḫāzinī sviluppa una teoria del moto dei corpi solidi nei liquidi che tiene conto sia della resistenza del mezzo al moto dei corpi sia della spinta di Archimede. Particolarmente interessanti sono le sue osservazioni sulle variazioni di peso che subisce un corpo passando da un mezzo all'altro. Esse gli servono da giustificazione teorica al metodo di determinazione del peso specifico, che consiste nel pesare un corpo prima nell'aria e successivamente nell'acqua.

Al-Ḫāzinī estende poi l'idrostatica archimedea al caso di corpi galleggianti che presentano una cavità vuota o con un carico; in altre parole, egli sviluppa la teoria della barca. Il suo ragionamento si svolge in tre tappe, considerando dapprima il caso di un corpo solido pieno, poi quello di un corpo solido con una cavità e infine il caso di un corpo solido con una cavità contenente un carico. Dopo aver preso un volume d'acqua uguale al volume del corpo pieno, denominato 'acqua campione', egli considera tre casi: nel primo, il peso del corpo con una cavità è pari a quello dell'acqua campione e il corpo, in questo caso, galleggia; nel secondo, il peso del corpo con una cavità è superiore a quello dell'acqua campione, il corpo viene detto allora 'corpo immerso' e il suo peso nell'acqua, quello che eccede il peso della parte immersa, è dato dalla differenza tra il peso del corpo nell'aria e il peso di un uguale volume d'acqua; nel terzo, infine, il peso del corpo con una cavità è inferiore a quello dell'acqua campione, è il caso del corpo emergente, il cui peso nell'acqua è uguale al peso del volume d'acqua spostato dalla parte immersa del corpo.

In questo modo al-Ḫāzinī perviene alla nozione di forza di spinta, che egli definisce come la differenza tra il peso dell'acqua campione e il peso del volume d'acqua spostato dalla parte immersa del corpo. Si può determinare questa forza poggiando sul corpo emergente un carico, in modo tale che la superficie superiore del corpo coincida con la superficie dell'acqua. Il peso del carico misura allora la forza di spinta. Al-Ḫāzinī studia poi l'influenza della dimensione della cavità, definendo 'acqua della cavità' il suo contenuto d'acqua; se il peso è pari al peso del corpo, la cavità è detta 'equivalente' (al corpo). Egli considera tre casi: nel primo, la cavità è equivalente e il corpo galleggia; nel secondo, la cavità è maggiore della cavità equivalente e il corpo perciò va a fondo; nel terzo, la cavità è minore e il corpo allora risale alla superficie. Al-Ḫāzinī considera infine un corpo con una cavità aperta contenente un carico, riducendone il modello a quello di un corpo con una cavità senza carico e questo a sua volta a quello di un corpo pieno: la 'teoria della barca carica' si riallaccia così alla teoria di Archimede dei corpi galleggianti.

Il peso specifico

Un certo numero di trattati è dedicato al problema della determinazione del peso specifico dei metalli e dei minerali e ne contiene soluzioni sia teoriche sia pratiche. Si tratta di questioni centrali nel Kitāb MĪzān al-ḥikma di al-Ḫāzinī alle quali al-Bīrūnī dedica alcuni lavori (Maqāla fī 'l-nisab allatī bayna al-filizzāt wa-'l-ǧawāhir fī 'l-ḥaǧm, Trattato sui rapporti tra i metalli e le pietre in volume). Il peso specifico di un corpo non è mai stato esplicitamente definito come il rapporto tra il peso e il volume, né nell'Antichità né dai predecessori arabi di al-Ḫāzinī. Tutti coloro che quest'ultimo menziona e che sono citati nell'introduzione del trattato di al-Bīrūnī hanno fatto un uso implicito di questa nozione. Si deve ad al-Ḫāzinī la prima definizione precisa: "Il peso di un corpo relativamente piccolo, di qualunque sostanza esso sia, ha con il volume del corpo lo stesso rapporto di un corpo più grande (della stessa sostanza) con il proprio volume" (Kitāb MĪzān al-ḥikma, p. 86).

Per determinare il peso specifico di un campione occorreva conoscere e confrontare i suoi pesi nell'aria e nell'acqua e dunque misurare il peso dell'acqua spostata. Per farlo si può procedere in due modi, entrambi equivalenti a un'applicazione del principio di Archimede, secondo il quale il peso di un corpo immerso in un liquido diminuisce di una quantità pari al peso del liquido spostato. Il primo modo consiste nel pesare il campione nell'aria e poi nell'acqua: lo strumento privilegiato per queste misure è la bilancia idrostatica. Il secondo consiste nel recuperare il volume del liquido spostato e pesarlo. A questo scopo al-Bīrūnī prevede un vaso conico (al-āla al-maḫrūṭa): si riempie il vaso d'acqua fino a che questa non scorre da un condotto laterale, si immerge poi il campione nell'acqua, si raccoglie l'acqua spostata in un recipiente posto sotto il condotto e la si pesa. Il peso specifico è calcolato confrontando il peso del corpo nell'acqua ‒ la differenza tra il peso del corpo nell'aria e il peso dell'acqua spostata ‒ con quello del corpo misurato nell'aria.

Al-Bīrūnī descrive gli esperimenti compiuti e le misurazioni, come pure gli strumenti di misura e il modo di utilizzarli, e presenta i risultati ottenuti in alcune tabelle. Studia dapprima i metalli, poi le pietre preziose e infine altre sostanze come il sale, la cera e l'avorio. Per calcolare il peso specifico, egli prende campioni di metallo e di minerali di peso pari a 100 miṯqāl (1 miṯqāl=4,424 g) o di volume uguale a quello occupato da 100 miṯqāl d'oro. In una tabella riporta il peso dell'acqua spostata da campioni di metalli e di minerali aventi lo stesso peso nell'aria; in un'altra i volumi di campioni aventi lo stesso peso nell'acqua, ecc. A partire da queste tabelle si poteva determinare il peso specifico di una sostanza tramite operazioni aritmetiche.

Come sostanza di riferimento al-Bīrūnī non prendeva l'acqua ma il metallo più pesante (l'oro) per i metalli e il minerale più duro (lo zaffiro) per i minerali. I suoi risultati sono piuttosto vicini a quelli attuali. Alcune deviazioni da questi ultimi si possono spiegare con la presenza di impurità nei campioni e con differenze di temperatura nel corso degli esperimenti, nei quali veniva trascurata la temperatura dell'acqua. Al-Bīrūnī determinò anche il peso specifico di alcuni liquidi, stabilendo la differenza tra i pesi specifici dell'acqua a seconda che sia fredda, calda, salata o dolce e mettendo poi in evidenza una certa relazione esistente tra la densità dell'acqua e il suo peso specifico. Di fatto, egli fu il primo nella storia della scienza a introdurre procedimenti di verifica nella pratica sperimentale.

Un altro autore che si occupò del problema della determinazione del peso specifico fu ῾Umar al-Ḫayyām, in un'opera dal titolo Mīzān al-ḥikam (Bilancia delle saggezze), interamente inclusa nel trattato di al-Ḫāzinī. In quest'opera sono proposti due metodi di calcolo: la teoria dei rapporti e il metodo algebrico (al-ǧabr wa-'l-muqābala) per restaurazione e opposizione, quest'ultimo analogo ai moderni metodi di risoluzione delle equazioni lineari. Il peso specifico è determinato a partire dal rapporto tra il peso di una sostanza nell'aria e nell'acqua. Se P, P₁, P₂ e Q, Q₁, Q₂ sono i pesi di una lega e quelli delle sue componenti rispettivamente nell'aria e nell'acqua e d, d₁, d₂ i corrispondenti pesi specifici, i rapporti P/Q, P₁/Q₁ e P₂/Q₂ sono uguali ai rapporti dei pesi specifici d/(d−d_a), d₁/(d₁−d_a), d₂/(d₂−d_a), dove d_a è il peso specifico dell'acqua. Le proporzioni che si ottengono sono illustrate in una figura nella quale i valori numerici sono rappresentati da segmenti di varia lunghezza.

Anche al-Ḫāzinī apportò un contributo essenziale alla teoria e alla pratica della determinazione del peso specifico, dedicando a questo problema una parte importante del suo trattato. Dopo aver descritto in dettaglio i metodi dei suoi predecessori (al-Bīrūnī e al-Ḫayyām), al-Ḫāzinī espone il proprio, fondato sull'uso della 'bilancia della saggezza' e sulle tavole di al-Bīrūnī. Al-Ḫāzinī pesava i campioni (d'oro, d'argento o di loro leghe) nell'aria e nell'acqua con la bilancia della saggezza e ne determinava poi il peso specifico mediante i tre metodi seguenti.

Nel primo metodo, di natura aritmetica, al-Ḫāzinī utilizzava la teoria euclidea dei rapporti, tramite la quale otteneva il peso x di un componente della lega nella forma

e le relazioni

[2] F=P−Q=cm, F₁=P₁−Q₁=cm₁ e F₂=P₂−Q₂=cm₂ ,

dove P, P₁, P₂ e Q, Q₁, Q₂ sono i pesi della lega e dei suoi due componenti, rispettivamente nell'aria e nell'acqua; F, F₁, F₂ sono le spinte archimedee della lega e dei suoi componenti; c è il valore di una divisione della graduazione; m, m₁, m₂ sono i numeri di divisioni per la lega e per i due componenti.

Il secondo metodo consisteva nell'utilizzare la seguente costruzione geometrica. Si tracciano due rette parallele EG e HF e si prendono su di esse, secondo una data scala, i segmenti: EG=P, pari al peso della lega nell'aria; LF=Q, parial peso della lega nell'acqua; HF=ξ₁=P Q₁/P₁, pari al peso nell'acqua delprimo componente della lega; KF=ξ₂=P Q₂/P₂, pari al peso nell'acqua del secondo componente della lega.

Si tracciano poi le rette EH e GK e si prolungano fino a che non si incontrano (si può facilmente dimostrare che non sono parallele). Sia X il punto d'incontro e sia KM la parallela a HE. La figura MEHK che si ottiene è un parallelogramma nel quale la somma degli angoli GEH ed EMK è uguale a due angoli retti e l'angolo EXK è acuto. Essendo l'angolo EMK esterno al triangolo MGK, anche l'angolo EGX è acuto. Si traccia poi una retta XL, dove L è tale che LF=Q, e che taglia il segmento EG in un certo punto O. Il segmento EG viene diviso da O in due parti di lunghezza in generale diversa. Allora, se XO passa al di sopra della retta XHE, il campione controllato è di oro puro; se passa al disotto della retta XKG, il campione è di argento puro, e se interseca la retta EMG, il campione è una lega di questi due metalli. I segmenti EO e OG sono proporzionali alle percentuali di ciascun metallo nella lega. Al-Ḫāzinī fu il secondo studioso, per quanto ne sappiamo, a utilizzare il metodo geometrico; il primo, come già si è detto, fu al-Ḫayyām. Il metodo di quest'ultimo si può però considerare una pura illustrazione geometrica di una tecnica aritmetica, mentre al-Ḫāzinī offre un metodo geometrico dettagliato e una dimostrazione rigorosa per risolvere i problemi dei composti. La figura che egli propone si può considerare un prototipo di nomogramma.

Nel terzo metodo egli utilizzava al-ǧabr e al-muqābala, cioè risolveva equazioni algebriche del primo ordine. L'equazione che al-Ḫāzinī aveva formulato a parole si può esprimere come segue:

dove Q₁/P₁ e Q₂/P₂ sono le frazioni che rappresentano i pesi dei componenti della lega e x è il peso cercato di uno dei due. Seguendo il procedimento di 'restaurazione e opposizione' si può trasformare questa equazione come segue:

da cui:

ovvero

La soluzione algebrica fornisce un risultato uguale a quelli ottenuti in modo aritmetico e geometrico.

Il Libro IV del Kitāb MĪzān al-ḥikma è interamente dedicato alle varie bilance idrostatiche realizzate dai predecessori di al-Ḫāzinī. Vi si trova la descrizione della bilancia di Archimede, così come viene riportata da Menelao, che permetteva di misurare direttamente le proporzioni d'oro e di argento in una lega di questi due metalli. L'autore descrive anche la bilancia fisica (al-mīzān al-ṭabī῾ī) di Abū Bakr Muḥammad ibn Zakariyyā al-Rāzī, come la bilancia idrostatica assoluta (al-mīzān al-ǧāmi῾) di ῾Umar al-Ḫayyām.

La statica applicata

La statica pratica riguarda un insieme di problemi concernenti l'utilizzo di strumenti e mezzi meccanici, di cui uno dei più rilevanti è l'uso delle bilance. Una porzione importante della statica teorica, la cui parte pratica riguarda la determinazione dei pesi specifici, è già stata descritta nella trattazione dei pesi specifici. In questo paragrafo ci occuperemo di strumenti e macchine e, in particolare, dei problemi della bilancia e della pesata.

Le macchine semplici e la meccanica

Una delle fonti arabe più antiche che trattano delle macchine semplici è l'enciclopedia Mafātīḥ al-῾ulūm di Muḥammad ibn Aḥmad al-Ḫwārizmī, pervenutaci anche in traduzione latina con il titolo Le chiavi delle scienze. Essa contiene descrizioni di congegni meccanici che permettono di spostare carichi pesanti con piccole forze; macchine che, rientrando nella categoria di quelle che permettevano di sollevare oggetti, suscitavano all'epoca un notevole interesse.

Altri studiosi si sono interessati alla statica applicata. Oltre all'enciclopedia di al-Ḫwārizmī, le opere più note sono il Kitāb al-Ḥiyal (Libro della scienza meccanica) dei fratelli Banū Mūsā (IX sec.), Mi῾yār al-῾aql (La misura dell'intelletto) di Avicenna (XI sec.), il Kitāb fī ma῾rifat al-ḥiyal al-handasiyya (Il libro della conoscenza dei procedimenti ingegnosi) di al-Ǧazarī (XII sec.), come pure il Kitāb Mīzān al-ḥikma.

I lavori di Avicenna sono molto interessanti, in particolare i capitoli dedicati alla meccanica nella sua opera enciclopedica e il trattato Mi῾yār al-῾aql, che si basano sui Problemi di meccanica dello Pseudo-Aristotele e sui Mechanica di Erone. Mi῾yār al-῾aql si compone di due sezioni, nelle quali sono descritte cinque macchine semplici. La prima sezione deve al trattato di Erone i nomi e le definizioni delle macchine semplici, i materiali necessari per costruirle, le condizioni che ne assicurano la stabilità e la sicurezza nel funzionamento. La seconda sezione contiene descrizioni di combinazioni di macchine semplici. Come Erone, Avicenna classifica queste combinazioni secondo la compatibilità dei gruppi di macchine semplici che ne fanno parte. Tuttavia, contrariamente a Erone, che aveva considerato soltanto alcune di queste combinazioni, Avicenna analizza tutte quelle possibili. Anche se puramente pratico, il suo trattato è di grande importanza nella storia della meccanica. Fu infatti il primo tentativo riuscito di classificazione delle macchine semplici e delle loro combinazioni; classificazione il cui interesse non era casuale, né per Avicenna né più in generale per la sua epoca.

Una nuovo modo di affrontare lo studio delle macchine tende ad affermarsi tra l'XI e il XII secolo. Gli autori di questo periodo considerano una particolare macchina semplice, elaborano in rapporto a essa una teoria rigorosa, per poi descrivere e classificare i diversi apparecchi ottenuti modificando il tipo di macchina prescelto. Altri autori considerano una suddivisione particolare di una branca della scienza e descrivono diverse macchine, meccanismi e strumenti relativi a questa branca o associati a essa. Il Kitāb MĪzān al-ḥikma di al-Ḫāzinī è un esempio tipico di questo genere di trattati di meccanica. Esso espone in modo esaustivo i principali problemi teorici e di applicazione pratica della macchina semplice più comune, la leva, e della sua modificazione più diffusa, la bilancia.

Riassumendo, l'evoluzione della scienza delle macchine semplici nell'Antichità e nell'Oriente medievale ha conosciuto varie tappe. A partire dalle descrizioni del principio di funzionamento delle macchine semplici e delle loro combinazioni, si è cercato di classificarle per arrivare a descrizioni che ne permettessero la teorizzazione e consentissero la costruzione di modelli e di tutte le loro modificazioni. È a partire da questi aspetti che si costituirà più tardi la meccanica industriale.

Le bilance e la pesata

Nel trattato Kitāb MĪzān al-ḥikma, al-Ḫāzinī menziona Ṯābit ibn Qurra ma il testo citato è diverso da quello del Kitāb fī 'l-qarasṭūn e proviene verosimilmente da un'opera di divulgazione che espone in generale le condizioni necessarie per la costruzione di una bilancia a bracci, dapprima uguali e poi diversi. Vi si spiega come utilizzare una bilancia in modo conveniente, cioè come evitare gli errori che ne possano falsare la pesata, quali la non omogeneità del mezzo o il fatto che il giogo non sia orizzontale. Si tratta senza dubbio di un testo di Ibn Qurra che si rivolgeva agli artigiani e ad altri utilizzatori di bilance privi di conoscenze matematiche. L'esistenza di un trattato di questo tipo dimostra come gli scienziati arabi, anche i più eminenti, si interessassero non solo agli aspetti teorici della statica ma anche a quelli pratici, per rispondere alle esigenze di un'economia fiorente.

Il Kitāb MĪzān al-ḥikma è il testo che contiene le informazioni più complete sulla bilancia e sulla tecnica della pesata. L'autore definisce il trattato nei termini seguenti: "abbiamo dunque voluto raccogliere su quest'arte [le bilance e i metodi di pesata] ciò che è stato fatto dagli Antichi e da coloro che sono venuti dopo e vi abbiamo aggiunto il risultato della nostra riflessione, con l'aiuto di Dio" (p. 6). Al-Ḫāzinī divide le bilance in due gruppi, quelle a bracci uguali e quelle a bracci diversi. Il modello più semplice di bilancia a bracci uguali è costituito da un giogo e due piatti. Il peso è posto su uno dei piatti ed è misurato mediante contrappesi posti sull'altro piatto o su entrambi. Egli propone, per questo tipo di bilancia, una serie di contrappesi che permettono di misurare il massimo peso con il minimo numero di pesi. L'aspetto importante è che, quando si utilizza un solo piatto, i pesi sono scelti tra le potenze di 2 (le unità di peso sono 1, 2, 2², 2³, ...) o tra le potenze di 3 (1, 3, 3², 3³, ...). Si tratta di casi particolari del problema della rappresentazione di un numero intero per mezzo della somma algebrica di differenti potenze di un altro numero intero. Al-Ḫāzinī dà in questo modo la soluzione del problema della pesata, riscoperta soltanto molto più tardi in Occidente.

La bilancia a bracci uguali pone un altro problema: come si può rappresentare matematicamente l'operazione della pesata? Poiché tale operazione consiste nel posare su un piatto un carico di cui non si conosce il peso e sull'altro piatto i contrappesi in modo che il giogo sia in equilibrio, essa può essere considerata come una forma iniziale del metodo al-ǧabr wa-'l-muqābala, che è all'origine dell'algebra moderna e che prevede, in un'equazione, la trasposizione dei termini negativi e la riduzione dei suoi termini simili. Nel caso presente, l'equazione da risolvere è un'equazione algebrica di primo grado. Il caso più semplice è quello in cui l'incognita (il carico da pesare) è posta su uno dei piatti sospeso a una estremità della bilancia e il contrappeso è nel piatto sospeso all'altra estremità. È il caso dell'opposizione. Se la somma dei contrappesi è uguale al peso del carico, la bilancia è in equilibrio, cioè i due membri dell'equazione sono uguali e la quantità incognita è determinata. A volte occorre mettere alcuni contrappesi sul piatto dove si trova il carico da pesare. È il caso, più complesso, del complemento. È possibile che il metodo al-ǧabr wa-'l-muqābala sia connesso con la pratica della pesata e con l'uso di bilance semplici a bracci uguali.

Le bilance a bracci diversi sono suddivise da al-Ḫāzinī in due tipi: qarasṭūn, bilancia munita di due piatti o di una cremagliera per appendere i pesi e qabbān, bilancia munita di un piatto e di un contrappeso che si può spostare lungo il braccio opposto al piatto. La teoria di questo tipo di bilance è esposta nei commenti ai lavori di Ṯābit ibn Qurra e di al-Isfizārī inclusi nel Kitāb MĪzān al-ḥikma. I due tipi di bilance, qarasṭūn e qabbān, ammettevano a loro volta alcune varianti, a seconda delle applicazioni cui erano destinate. Il tipo qabbān, per esempio, possiede due varianti: la bilancia giusta (al-qusṭās al-mustaqīm) per pesate molto precise e la bilancia-orologio astronomico.

Bilancia-orologio con serbatoio ad acqua

La bilancia-orologio consta di un giogo formato da due scale solidali (una graduata per le ore e l'altra per i minuti), di due pesi diversi che si spostano lungo le scale e di un vaso sospeso all'estremità del giogo, contenente acqua o sabbia. La bilancia è appesa al soffitto in un luogo chiuso e permette la misura del tempo sia di giorno sia di notte. Dopo aver equilibrato la bilancia spostando i due pesi lungo le scale, si apre l'orifizio del vaso; l'acqua o la sabbia fuoriescono e la bilancia è di nuovo squilibrata. Per riequilibrarla si spostano un'altra volta i pesi lungo le scale e la differenza delle posizioni dei pesi dà il tempo astronomico trascorso.

Al-Ḫāzinī non è l'inventore di questo strumento. Descrizioni di orologi dello stesso tipo, di cui uno è attribuito ad Archimede, si trovano, infatti, nelle opere di al-Sā῾ātī e di al-Ǧazarī. Tuttavia, nessuno di questi è graduato per dare il tempo astronomico, come avviene, invece, per la bilancia-orologio di al-Ḫāzinī, che è uno dei primi strumenti scientifici che permettono di effettuare tale calcolo.

Al-Ḫāzinī descrive poi le varie versioni del tipo qarasṭūn: la bilancia di conversione, in cui il giogo è diviso in due parti nel rapporto di 10 a 7, che è il rapporto del dīnār al dirham, permette di convertire le due monete; la bilancia geodetica, i cui bracci sono uguali e che consente di dare a certe superfici una posizione perfettamente orizzontale, essenziale in particolare per la taratura degli strumenti astronomici; la bilancia idrostatica, che serve a pesare campioni di metallo e di minerali nell'aria e nell'acqua, per determinarne il peso specifico e stabilire la composizione delle leghe.

Particolare attenzione è dedicata alla bilancia idrostatica. Una parte essenziale del trattato di al-Ḫāzinī è dedicata alla sua utilizzazione e alla questione della determinazione dei pesi specifici. Ne vengono considerati tre tipi: il primo è una bilancia comune, a bracci uguali e a due piatti; il secondo è a tre piatti, di cui due sono uno sopra l'altro per pesate nell'acqua; il terzo ha cinque piatti, tre fissati alle estremità del giogo come nel caso precedente e due che si possono spostare lungo il giogo per equilibrarlo.

Al-Ḫāzinī fornisce un rendiconto dettagliato della storia dell'evoluzione della bilancia idrostatica e dei metodi di pesata in un arco di circa quindici secoli, a partire dalla bilancia di Archimede, utilizzabile solamente per due metalli ( per es., oro e argento) e in un'acqua di densità data. La descrizione di questa bilancia si ha soltanto nel Kitāb MĪzān al-ḥikma, come nel caso della bilancia di al-Rāzī, conosciuta soltanto grazie ad al-Ḫāzinī.Quest'ultima è una bilancia a due piatti, uno fisso e l'altro mobile. Contrariamente a quella di Archimede, nella quale uno dei due piatti è immerso nell'acqua, nella bilancia di al-Rāzī nessun piatto è immerso: essi sono invece pieni d'acqua. Una tale bilancia poteva essere utilizzata per due metalli qualsiasi e con un'acqua qualunque, ma non era molto precisa; era difficile, infatti, fabbricare due piatti dello stesso volume e dello stesso peso. La bilancia idrostatica migliorò con l'aggiunta di un terzo piatto, riservato particolarmente alla pesata di campioni di metallo nell'acqua. Al-Ḫāzinī afferma che alcune bilance idrostatiche a tre piatti erano già state utilizzate nel passato nei paesi islamici.

Al-Isfizārī aumentò a cinque il numero dei piatti e costruì una bilancia universale che chiamò mīzān al-ḥikma (bilancia della saggezza). Si tratta di una bilancia a bracci uguali, graduata secondo due scale, con cinque piatti semisferici, un peso mobile e un ago fissato al centro del giogo. L'ago è collegato a un supporto, non mediante un asse ma secondo un ingegnoso sistema di sospensione libera, costituito da una sbarra trasversale unita a un pezzo a forma di braccio a squadra. Questo sistema di sospensione permetteva di diminuire l'effetto dell'attrito sulla precisione della misurazione. L'alta precisione era assicurata anche da una conveniente scelta delle dimensioni degli elementi costitutivi dell'apparecchio. Al-Ḫāzinī dedica un intero capitolo alla descrizione della bilancia della saggezza ‒ degli elementi che la costituiscono e dei metodi di assemblaggio di questi ‒ e ai problemi di equilibratura e di precisione. Due dei piatti fissi erano riservati alle pesate nell'aria, il terzo alle pesate nell'acqua. I due piatti mobili fungevano da cavalierini per portare la bilancia nella posizione di equilibrio, prima della taratura e della pesata.

La bilancia della saggezza fu migliorata da al-Ḫāzinī, che ne sviluppò anche le basi teoriche e i metodi sperimentali. Nella sua opera è descritta in modo dettagliato la tecnica per determinare il peso specifico di un campione; tecnica che si riduce essenzialmente al calcolo della spinta, che dipende dal peso misurato nell'aria e nell'acqua. Egli procede come segue. Prima della pesata, la bilancia viene messa in equilibrio, avendo cura di immergere il terzo piatto fisso nell'acqua. Si pone poi il campione da pesare su un piatto fisso, diciamo a sinistra di chi guarda, bilanciandolo con alcuni pesi sul piatto fisso di destra. Il campione viene poi spostato nel piatto immerso nell'acqua e, poiché il suo peso nell'acqua è inferiore a quello nell'aria, a causa della spinta dell'acqua l'equilibrio si rompe. Al-Ḫāzinī propone due metodi per riequilibrare la bilancia e determinare la spinta. Il primo consiste nell'aggiungere pesi noti, per esempio dei dirham, al piatto fisso di destra: la somma di tutti questi pesi è pari alla spinta. Il secondo metodo consiste nel trasferire i pesi dal piatto fisso di destra al piatto mobile di destra e nel riportare la bilancia in equilibrio spostando il piatto mobile lungo il giogo della bilancia. Il punto sul quale si trova il piatto mobile, in condizioni di equilibrio, corrisponde al peso specifico della sostanza pesata. Al-Ḫāzinī insiste sulla qualità dei campioni e sulle proprietà fisico-chimiche dell'acqua, precisando che le misure di una data serie devono essere fatte sempre con la stessa acqua, proveniente cioè dalla stessa fonte, e alla stessa temperatura, se si vuole che abbia senso confrontare i risultati.

L'importanza storica della bilancia della saggezza è dovuta, oltre alla sua grande precisione, ai molteplici usi ai quali si prestava. Essa era utilizzata non soltanto per il calcolo del peso specifico e per la determinazione della composizione di una lega, ma anche per provare l'autenticità e la purezza dei metalli e delle pietre preziose. Con due soli piatti e il peso mobile sulla parte sinistra del giogo, essa poteva essere utilizzata come un comune qarasṭūn o qabbān, come una bilancia per convertire dirham in dīnār o come una bilancia di precisione (qusṭās mustaqīm). Si trattava di uno strumento molto sensibile, con un campo di applicazione estremamente ampio, considerato il più perfetto tra quelli conosciuti nel XII e XIII secolo.

Abbiamo esaminato in questo capitolo la formazione dei fondamenti teorici e dei metodi pratici della statica araba. È un processo che non si riduce alla semplice traduzione e trasmissione delle opere dell'Antichità. I metodi di Archimede e quelli dei Problemi di meccanica sono in effetti approfonditi e migliorati e, tra il IX e il XV sec., viene sviluppato il contenuto dinamico dell'insegnamento di Aristotele. Sfruttando vari strumenti matematici ‒ come la teoria delle proporzioni, le tecniche di carattere infinitesimale ereditate dai Greci e i metodi algebrici e le tecniche di calcolo da loro stessi perfezionati ‒ gli scienziati arabi hanno portato la statica a un alto livello di sviluppo. La teoria del baricentro è stata generalizzata ai corpi solidi e ai sistemi di corpi nello spazio e la teoria della leva ideale è stata estesa in modo da tenere conto del peso della leva. La scienza del peso viene così fondata prima di svilupparsi nell'Occidente medievale. Nasce un filone scientifico che unisce l'impostazione dinamica con l'idrostatica archimedea e che si potrebbe definire idrodinamica medievale. La statica archimedea costituisce una base sulla quale si fonda la scienza dei pesi specifici, grazie allo sviluppo di numerosi metodi di calcolo. Le opere di al-Bīrūnī e di al-Ḫāzinī possono essere considerate l'inizio dell'applicazione dei metodi sperimentali nella scienza del Medioevo. La statica araba ha avuto un ruolo importante nella storia della meccanica classica dell'Occidente medievale; essa è stata un anello essenziale nella catena dell'evoluzione della scienza, senza il quale la meccanica classica non avrebbe probabilmente potuto svilupparsi.

Bibliografia

Bancel 2001: Bancel, Faïza, Les centres de gravité d'Abū Sahl al-Qūhī, "Arabic sciences and philosophy", 11, 2001, pp. 45-78.

Berggren 1983: Berggren, John L., The correspondence of Abū Sahl al-Kūhī and Abū Isḥāq al-Ṣābi᾽. A translation with commentaries, "Journal for the history of Arabic science", 7, 1983, pp. 39-123.

Carra de Vaux 1893: Carra de Vaux, Bernard, Les mécaniques de Héron, "Journal asiatique", s. IX, 1893.

Clagett 1959: Clagett, Marshall, The science of mechanics in the Middle Ages, Madison (Wis.), University of Wisconsin Press; London, Oxford University Press, 1959.

Drachmann 1963: Drachmann, Aage G., Fragments from Archimedes in Heron's Mechanics, "Centaurus", 8, 1963, pp. 91-146.

Duhem 1905-06: Duhem, Pierre M.M., Les origines de la statique, Paris, Hermann, 1905-1906, 2 v.

Hall 1973: Hall, Robert E., Al-Khāzinī, in: Dictionary of scientific biography, edited by Charles C. Gillispie and Frederich L. Holmes, New York, Scribner, 1970-1990, 18 v.; v. VII, 1973, pp. 335-351.

Al-Hassan 1979: al-Jazarī, A compendium on the theory and practice of the mechanical arts, edited by Ahmad Y. al-Hassan, Aleppo, University of Aleppo Press, 1979.

Heath 1921: Heath, Thomas L., A history of Greek mathematics, Oxford, Clarendon, 1921, 2 v. (rist.: New York, Dover, 1981, 2 v.).

Jaouiche 1976: Jaouiche, Khalil, Le livre du Qarasṭūn de Thābit ibn Qurra. Étude sur la notion de travail et du calcul du moment statique d'une barre homogène, Leiden, E.J. Brill, 1976.

Knorr 1978: Knorr, Wilbur R., Archimedes and the Elements. Proposal for a revised chronological ordering of the Archimedean Corpus, "Archive for the history of exact sciences", 19, 1978, pp. 211-290.

‒ 1982: Knorr, Wilbur R., Ancient sources of the medieval tradition of mechanics. Greek, Arabic and Latin studies of the balance, Firenze, Istituto e Museo di Storia della Scienza, 1982.

Moody 1952: Moody, Ernest A. - Clagett, Marshall, The medieval science of weights (Scientia de ponderibus). Treatises ascribed to Euclid, Archimedes, Thabit ibn Qurra, Jordanus de Nemore and Blasius of Parma, edited and translated by Ernest A. Moody and Marshall Clagett, Madison (Wis.), University of Wisconsin Press, 1952.

Rashed 1996: Rashed, Roshdi, Math. inf. I.

‒ 1997: Rashed, Roshdi, Déterminations infinitésimales, quadrature des lunules et problèmes isopérimétriques, in: Histoire des sciences arabes, sous la direction de Roshdi Rashed avec la collaboration de Régis Morelon, Paris, Seuil, 1997, 3 v.; v. II: Mathématiques et physique, pp. 93-120 (ed. orig.: Encyclopedia of the history of Arabic science, London-New York, Routledge, 1996, 3 v.).

Rozhanskaya 1976: Rožanskaja, Mariam M., Mechanika na srednevekovom Vostoke, Moskvà, 1976.

‒ 1983a: Rožanskaja, Mariam M. - Levinova, I.S., Al-Chazini i ego Kniga vesov mudrosti, "Naučnoe nasledstvo", 6, 1983, pp. 229-275.

‒ 1983b: Rožanskaja, Mariam M. - Levinova, I.S., U istokov mechaniki mašin, in: Issledovanija po istorii mechaniki, Moskvà, 1983, pp. 28-43.

‒ 1987a: Rozhanskaya, Mariam M. - Rozenfeld, B.A., On al-Bīrūnī's densymetry, in: From deferent to equant: a volume of studies in the history of science in the ancient and medieval Near East in honor of E.S. Kennedy, edited by David A. King and George Saliba, New York, New York Academy of Sciences, 1987, pp. 403-417.

‒ 1987b: Rozhanskaya, Mariam M., On a mathematical problem in al-Khāzinī's Book of the Balance of Wisdom, in: From deferent to equant: a volume of studies in the history of science in the ancient and medieval Near East in honor of E.S. Kennedy, edited by David A. King and George Saliba, New York, New York Academy of Sciences 1987, pp. 427-435.

‒ 1992: Rozhanskaya, Mariam M., Abū-l-Fatḥ ῾Abd al-Raḥmān al-Khāzinī, Moskvà, 1992.

‒ 1997: Rozhanskaya, Mariam M., La statique, in: Histoire des sciences arabes, sous la direction de Roshdi Rashed avec la collaboration de Régis Morelon, Paris, Seuil, 1997, 3 v.; v. II: Mathématiques et physique, pp. 263-292.

Sezgin 1974: Sezgin, Fuat, Geschichte des arabischen Schrifttums, Leiden, E.J. Brill, 1967-; v. V: Mathematik (bis 430 H.), 1974.

Wiedemann 1912: Wiedemann, Eilhard, Die Schrift über den Qarastun, "Bibliotheca mathematica", s. III, 12, 1912, pp. 11-29.

‒ 1918: Wiedemann, Eilhard - Hauser, Fritz, Uhr des Archimedes und zwei andere Vorrichtungen, "Nova acta leopoldina. Abhandlungen der kaiserlich leopoldinisch-carolinisch deutschen Akademie der Naturforscher", 103, 1918, 5, pp. 163-203.

‒ 1970: Wiedemann, Eilhard, Aufsätze zur arabischen Wissenschaftsgeschichte, Hildesheim-New York, Olms, 1970, 2 v.; v. I.

Woepcke 1851: Woepcke, Franz, Notice sur des traductions arabes de deux ouvrages perdus d'Euclide, "Journal asiatique", s. V, 4, 1851, 18, pp. 217-247.

Würschmidt 1925: Würschmidt, Joseph, Die Schrift des Menelaos über die Bestimmung der Zusammensetzung von Legierungen, "Philologus", 80, 1925.

Youschkewitch 1964a: Youschkewitch, Adolf P., Note sur les déterminations infinitésimales chez Thabit ibn Qurra, "Archives internationales d'histoire des sciences", 17, 1964, 66, pp. 37-45.

‒ 1964b: Youschkewitch, Adolf P., Geschichte der Mathematik im Mittelalter, Leipzig, Teubner, 1964 (ed. orig.: Istorija matematiki v srednie veka, Moskvà, 1961).

Zotenberg 1879: Zotenberg, Hermann, Traduction arabe du 'Traité des corps flottants' d'Archimède, "Journal asiatique", 7, 1879, 13, pp. 509-515 (trad. ingl. in: The medieval science of weights (Scientia de ponderibus). Treatises ascribed to Euclid, Archimedes, Thabit ibn Qurra, Jordanus de Nemore, and Blasius of Parma, edited and translated by Ernest A. Moody and Marshall Clagett, Madison (Wis.), University of Wisconsin Press, 1952, pp. 52-55).