La civiltà islamica: teoria fisica, metodo sperimentale e conoscenza approssimata. Ibn al-Hayṯam e la nuova fisica
La civilta islamica: teoria fisica, metodo sperimentale e conoscenza approssimata. Ibn al-Haytam e la nuova fisica
Ibn al-Hayṯam e la nuova fisica
Apartire dalla fine del XIX sec., il lavoro di ricerca sull'opera ottica di Abū ῾Alī al-Ḥasan ibn al-Hayṯam (m. dopo il 1040) non ha cessato di registrare nuovi sviluppi. Fino a questo periodo, nonostante le traduzioni in latino e in italiano del magnum opus di questo autore, il Kitāb al-Manāẓir (Libro dell'ottica, tradotto in latino con il titolo di De aspectibus, da ora in poi solo Ottica), che esercitarono una profonda influenza sullo sviluppo del pensiero scientifico e filosofico nel corso del Medioevo e fino alla nascita della scienza moderna, e quella della Maqāla fī 'l-marāyā al-muḥriqa bi- 'l-quṭū῾ (Trattato sugli specchi ustori parabolici), realizzata da Gherardo da Cremona (1114 ca.-1187), le altre sezioni dell'Ottica erano rimaste sconosciute agli studiosi europei. Nel mondo musulmano, l'opera ottica di Ibn al-Hayṯam era stata meno ignorata di quanto si sia stati inclini a pensare. La sua conoscenza, tuttavia, si era diffusa soprattutto attraverso il commento critico dell'Ottica redatto da Kamāl al-Dīn al-Fārisī (m. 718/1319), il Tanqīḥ al-manāẓir (La revisione dell'Ottica), che, oltre a includere gran parte del testo commentato, contiene le 'recensioni' di altri trattati di Ibn al-Hayṯam da cui si può ricavare un'immagine rappresentativa della sua opera in questo campo. È a partire dal testo di Kamāl al-Dīn e da alcuni trattati di Ibn al-Hayṯam che, verso la fine del XIX sec., gli studiosi europei sarebbero tornati ad affrontare lo studio dei lavori di quest'ultimo autore. Tuttavia, il principale evento registrato dalla ricerca moderna su Ibn al-Hayṯam è la pubblicazione nel 1942-1943 del libro di Mustafa Nazif che contiene un'analisi approfondita quasi dell'intera opera ottica di Ibn al-Hayṯam, basata sul testo stesso dell'Ottica da lui riscoperto così come su altri trattati. Tutta la ricerca su Ibn al-Hayṯam condotta nella seconda metà del XX sec. si pone nel solco di questa indagine magistrale.
Le indagini condotte nel corso degli ultimi tre decenni consentono di valutare tutta l'opera di Ibn al-Hayṯam e, in particolare, quella dedicata all'ottica, a partire da basi più solide. Da questi studi emerge l'immagine di un matematico di eccezionale levatura, i cui lavori coronano, tra l'altro, la tradizione archimedea, e di un astronomo, le cui riflessioni sui rapporti che legavano l'astronomia alla fisica segnano l'inizio di una ricerca che, quasi tre secoli più tardi, condurrà all'invenzione dei modelli non tolemaici. In questa sede ci occuperemo della sua opera ottica e soprattutto della riforma da lui apportata a questa disciplina. È grazie a essa e al progetto di cui essa faceva parte che si verifica un cambiamento di status: con le indagini di Ibn al-Hayṯam, l'ottica, da sempre considerata una scienza geometrica, si trasforma in una scienza fisica. In questo capitolo prenderemo in esame l'origine, il significato e l'importanza di tale cambiamento.
Si può tentare di riassumere il programma della riforma di Ibn al-Hayṯam con la seguente formula: sostituire la teoria geometrica della visione con la teoria geometrica dei fenomeni luminosi. Questa formula presenta il grande vantaggio di porre il concetto di luce al centro di tutto il progetto di Ibn al-Hayṯam; essa, infatti, esclude l'idea secondo cui la riforma di Ibn al-Hayṯam sarebbe stata imperniata soltanto sul fenomeno della visione e avrebbe avuto lo scopo di sostituire la teoria 'emissionista' dei matematici (secondo cui la visione si verificava attraverso i raggi visivi emanati dagli occhi) con quella 'immissionista' mutuata dai filosofi, secondo la quale la visione si produceva grazie all'impressione negli occhi delle forme, dei colori e delle luci degli oggetti visibili.
Tuttavia, tale formula tiene conto solamente di alcuni aspetti della riforma di Ibn al-Hayṯam senza precisarne, come ha osservato Roshdi Rashed (1993a), "le condizioni di possibilità", né le modalità di attuazione. Dal momento che lo stesso Ibn al-Hayṯam si riferisce, in almeno tre occasioni, alla necessità di operare una 'composizione' delle scienze fisiche e di quelle matematiche per descrivere i fenomeni legati alla luce e alla visione, alcuni storici hanno pensato di aver trovato in queste affermazioni la soluzione, o alcuni elementi della soluzione, della questione relativa alla natura della sua riforma dell'ottica. Ora, bisogna sottolineare che la riforma di Ibn al-Hayṯam non può essere compresa senza cogliere il preciso significato di queste osservazioni e soprattutto quello attribuito dall'autore al termine 'composizione'.
In effetti, alcuni storici hanno pensato di poter presentare il progetto di Ibn al-Hayṯam come un compromesso volto alla risoluzione dell'"enigma della posizione della matematica all'interno dello schema aristotelico delle scienze" (Pinès 1974, p. 80). Altri invece ritengono che esso rappresenti "una sintesi delle due dottrine che si contendevano il dominio del campo dell'ottica prima di Ibn al-Hayṯam, quella dei geometri Euclide e Tolomeo e quella dei filosofi peripatetici" in cui "l'approccio dei matematici dominava la forma dell'indagine, mentre le loro dottrine dovevano essere alterate, se non capovolte, alla luce di quelle dei fisici" (Sabra 1972, p. 191). Tuttavia, la questione della composizione della matematica e delle scienze fisiche non può essere risolta a priori; bisogna innanzi tutto tentare di comprendere nel modo più preciso possibile la riforma realizzata da Ibn al-Hayṯam.
Fino a non molto tempo fa, una tale indagine si sarebbe scontrata con due ostacoli, uno di carattere storiografico e uno di natura concettuale, del resto legati tra loro. A causa di un'inadeguata conoscenza della storia dell'ottica tra il II e il X sec., infatti, si riteneva che Ibn al-Hayṯam fosse il diretto erede di Tolomeo. Ora, dal momento che quest'ultimo aveva dedicato una sua importante opera allo studio della visione e l'opera fondamentale di Ibn al-Hayṯam trattava soprattutto di questo fenomeno, si tendeva a spiegare la 'rivoluzione copernicana' compiuta da Ibn al-Hayṯam attraverso una serie di influenze esterne e, in particolare, quella della filosofia peripatetica. A ciò si aggiungeva un errore commesso da alcuni bio-bibliografi antichi che aveva portato fuori strada la maggior parte degli storici moderni. Ci riferiamo alla confusione tra il matematico al-Ḥasan ibn al-Hayṯam e il filosofo chiamato Muḥammad ibn al-Hayṯam. Poiché quest'ultimo aveva affermato di essere un fedele discepolo di Tolomeo, di Galeno e di Aristotele e nel testo dell'Ottica erano chiaramente riproposte le tesi e i metodi dei primi due autori, spesso ci si accontentava di assumere le influenze di Aristotele o della filosofia peripatetica come le prove tendenti a dimostrare che il tentativo di Ibn al-Hayṯam era fondato su una combinazione di concetti e di metodi matematici e filosofici. È in questo contesto che la questione della 'composizione' è stata alterata e affrontata in modo tutt'altro che soddisfacente.
Queste imprecisioni storiografiche sono state accompagnate da una scorretta impostazione concettuale. Non ci si è limitati, infatti, a presentare la storia dell'ottica da Tolomeo a Ibn al-Hayṯam come un periodo vuoto, privo di ogni interesse o di qualsiasi elemento in grado di gettare nuova luce sull'opera di Ibn al-Hayṯam, ma anche a considerare la storia dell'ottica dell'Antichità, nelle rare analisi in cui era presa in considerazione da questa prospettiva, soltanto dal punto di vista della teoria della visione. In questo modo sono state trascurate altre aree di ricerca strutturalmente legate a questa teoria.
Tale lacuna è stata in larga misura colmata dagli studi pubblicati in questi ultimi anni, che hanno chiarito non solo gran parte della storia della teoria della visione da Tolomeo a Ibn al-Hayṯam, ma anche la storia dello studio geometrico della luce e quella degli strumenti ustori, aree di ricerca i cui molteplici e conflittuali rapporti con la tradizione euclidea e quella tolemaica sono essenziali per comprendere più a fondo la storia dell'ottica.
Luce e visione prima di Ibn al-Hayṯam
Il paesaggio mutevole dell'Antichità
Per quanto riguarda il suo oggetto e i mezzi proposti per il suo studio, l'ottica geometrica antica, i cui migliori esempi sono rappresentati dai trattati di Euclide e Tolomeo, può essere presentata come un tentativo di 'geometrizzazione dello sguardo'. Questa geometrizzazione è operata con l'aiuto di raggi visivi discreti o di un cono visivo solido, entrambi costruiti a partire dal centro dell'occhio. Benché accanto a questa disciplina esistesse una fisiologia dell'occhio, usata in campo medico, che a volte tentava di spiegare il ruolo svolto da quest'ultimo nell'atto della visione, l'ottica geometrica dell'Antichità riduceva quasi sempre l'occhio a un punto geometrico; nella maggior parte dei casi, infatti, si riteneva che la sensazione visiva si producesse in ultima analisi al di fuori di questo organo e che fossero le estremità sensibili dei raggi visivi a 'vedere' l'oggetto, esplorandolo.
Sebbene i filosofi peripatetici avessero severamente criticato questa teoria e, in particolare, il concetto di raggio visivo (o flusso visivo), essa era riconducibile a una concezione essenzialmente aristotelica della fisica, concentrandosi in modo particolare sul senso della vista. Come tutti gli altri sensi, quest'ultimo aveva un suo oggetto sensibile, il colore. Questa disciplina, tuttavia, non poteva ignorare del tutto la luce, se non altro perché nell'oscurità non si può vedere nulla; essa, però, era considerata soltanto una delle condizioni della visione. Benché la visione non potesse fare a meno della presenza della luce, quest'ultima non aveva alcun ruolo nel suo funzionamento e quindi non era oggetto di geometrizzazione.
Il contributo dell'ottica geometrica fu immenso. Nell'Ottica, il primo documento di questa tradizione giunto fino a noi, Euclide, per rendere conto di certi fenomeni legati alla prospettiva, si basa su alcuni principî fondamentali come, per esempio, l'aspetto apparente delle cose, le loro figure e le loro relazioni spaziali nella visione diretta. Con l'Ottica di Tolomeo il campo d'indagine di questa disciplina registra un notevole ampliamento, giungendo a comprendere non soltanto lo studio della visione diretta, ma anche quello della visione indiretta, di cui sono presi in esame due casi. Il primo è quello della visione per raggi riflessi che si verifica quando i raggi visivi emessi dall'occhio cadono su mezzi levigati, come, per esempio, gli specchi. Nel corso di questa analisi, Tolomeo formula le leggi della formazione delle immagini negli specchi e inizia una ricerca sperimentale destinata a localizzare l'immagine in tutti i tipi di specchi: piani, concavi e convessi (ma sempre sferici). Segue quindi l'analisi della visione per raggi rifratti che si verifica quando i raggi visivi emessi dall'occhio attraversano una superficie trasparente. In questa occasione, Tolomeo studia mediante un dispositivo sperimentale il luogo apparente dell'oggetto e compila la prima tavola numerica dei cambiamenti dell'angolo di rifrazione in funzione dell'angolo di incidenza.
A questo punto, attribuendo un peso eccessivo al ruolo svolto dalla visione nell'ottica antica si rischierebbe di tralasciare due importanti questioni. Ci riferiamo, in primo luogo, alla relativa autonomia della struttura geometrica concepita per spiegare la visione, sia nelle differenti teorie emissioniste, sia nello stesso dibattito tra i sostenitori delle teorie emissioniste e quelli delle teorie immissioniste sulla natura della visione. Questa autonomia è evidente soprattutto nel trattato ottico di Euclide, secondo cui il ruolo dei raggi visivi, così come quello dei raggi del Sole ai quali l'autore fa riferimento una sola volta, si riduce a garantire l'esistenza del segmento di retta che unisce "un punto-origine (l'occhio o il Sole) a un punto-oggetto". Questa circostanza è confermata dalla seconda questione, la cui importanza potrebbe essere occultata da uno studio esclusivamente incentrato sulla visione. Ci riferiamo all'esistenza nell'Antichità della scienza degli specchi ustori, una disciplina che ha come oggetto non i raggi visivi ma quelli luminosi emanati dagli oggetti brillanti e soprattutto dal Sole che, cadendo su superfici dotate di una certa forma (paraboloidica, sferica o costituita da un insieme di superfici piane), provocano la combustione in un determinato punto o in un insieme di punti.
Nello studio degli specchi ustori si constata un capovolgimento dell'ordine di priorità: l'occhio, che nello studio della visione svolgeva un ruolo di primo piano, qui serve soltanto a prendere atto del processo di combustione, mentre la luce è elevata dal rango di semplice condizione a quello di oggetto primario di studio. Ciò avviene attraverso l'istituzione di un'omologia tra la propagazione dei raggi luminosi e quella dei raggi visivi, ritenute soggette alle stesse leggi della propagazione rettilinea e della riflessione. Questa omologia era giustificata nel Libro I, andato perduto, dell'Ottica di Tolomeo, a partire da una serie di osservazioni filosofiche sulla comune natura della luce e del flusso visivo, entrambe considerate specie appartenenti allo stesso genere.
Coloro che si occupavano dello studio degli specchi ustori non si interessavano a tale genere di considerazioni. Nei testi più antichi di questa tradizione oggi a nostra disposizione, il Sole è già assimilato a un punto geometrico e di conseguenza tutti i raggi solari che cadono sugli specchi sono considerati paralleli. Grazie a questa semplificazione, gli autori dei testi dedicati agli specchi ustori potevano limitarsi a considerare un insieme di raggi, tutti paralleli all'asse dello specchio, avvalendosi della geometria del cerchio e di quella della parabola. In tal modo, al contrario dello studio dell'immagine negli specchi sferici, questa disciplina si fondava su una delle branche più avanzate della matematica (la teoria delle sezioni coniche) contribuendo, al tempo stesso, al suo arricchimento.
Impiegando un linguaggio moderno, potremmo dire che il suo obiettivo era quello di studiare l'immagine di un oggetto situato all'infinito, nella fattispecie il Sole, in uno specchio paraboloidico o sferico. Benché anacronistica, questa formulazione presenta un duplice vantaggio. Da un lato, essa mette in luce una delle potenzialità di questa disciplina e, dall'altro indica la strada che sarà necessario percorrere per giungere a realizzarla. In effetti, il punto di combustione di uno specchio paraboloidico si avvicina, più di qualsiasi altra immagine studiata da Tolomeo nel suo esame della riflessione dei raggi visivi negli specchi, all'odierna concezione dell'immagine reale di un oggetto in uno specchio concavo. Tuttavia, nulla ci autorizza a pensare che gli autori antichi lo studiassero in tale prospettiva.
È per questo che, malgrado i loro impliciti legami ontologici e l'omologia delle loro strutture geometriche, gli studi geometrici della visione e della luce rimasero, nel corso dell'Antichità, due discipline ben distinte tra loro. È in un'altra epoca, sotto un altro cielo e su un altro piano che queste due discipline inizieranno ad avvicinarsi.
Dagli specchi ustori agli strumenti ustori
Gli antecedenti dell'ottica geometrica araba vanno ricercati esclusivamente nell'ottica geometrica ellenistica. Il numero delle opere greche tradotte in arabo e riguardanti tutti i campi dell'ottica, cioè la teoria della visione, l'ottica atmosferica e gli specchi ustori, alcune delle quali attualmente sono disponibili solamente in versione araba, rappresenta la prova del grande interesse mostrato nel corso di questa epoca per tutte le questioni legate alla luce e alla visione. A partire da questi testi, gli studiosi del IX e del X sec. hanno aperto nuove strade di ricerca delle quali soltanto oggi iniziamo a valutare l'importanza.
In un trattato recentemente scoperto e pubblicato (Rashed 1993a), il matematico del X sec. Ibn Sahl amplia il campo dello studio della combustione includendovi non soltanto il caso della combustione provocata dalla riflessione dei raggi solari in uno specchio ellissoidale, ma anche quello in cui la combustione è prodotta dalla rifrazione di raggi luminosi. Quest'ultimo studio conduce l'autore a formulare per la prima volta la legge della rifrazione della luce, generalmente conosciuta con il nome di 'legge di Snell'. Questa estensione produce un duplice effetto. Da un lato, essa stabilisce un legame fra lo studio geometrico della rifrazione, da sempre legato alla visione, e quello riguardante la propagazione della luce; a questo punto la rifrazione dei raggi luminosi non è più considerata una proprietà deducibile esclusivamente a partire dalla rifrazione dei raggi visivi, sulla base della comune natura della luce e della visione, ma un fenomeno autonomo che, come la riflessione, può essere sottoposto a un trattamento geometrico. Dall'altro lato, questa estensione del campo di applicazione della geometria allo studio della luce è accompagnato dalla moltiplicazione delle fonti luminose. Invece di occuparsi soltanto del gruppo dei raggi paralleli provenienti da una sorgente situata all'infinito, Ibn Sahl si interessa, nello studio degli specchi ustori ellissoidali, all'effetto di combustione provocato in un determinato punto dai raggi provenienti da una sorgente situata non all'infinito, ma in un altro punto determinato. Ora, sebbene sia implicita in quest'analisi, l'idea della propagazione rettilinea della luce in tutte le direzioni non è mai enunciata da Ibn Sahl. Inoltre, essendo un matematico, l'autore seguita a considerare la sorgente luminosa come puntiforme, assimilandola in effetti ai raggi da essa emessi. Tuttavia, la legge della riflessione della luce, che postula l'uguaglianza dell'angolo d'incidenza e dell'angolo di riflessione rispetto alla normale, e la legge secondo cui il raggio incidente, il raggio riflesso e la retta normale alla superficie riflettente giacciono sullo stesso piano, anche se non sono formalmente enunciate in questo studio esclusivamente geometrico, sono all'origine dell'interesse mostrato da Ibn Sahl per l'ottica geometrica.
Del resto, Ibn Sahl non soltanto seguita a considerare le sorgenti come puntiformi, ma si limita a esaminare alcuni gruppi privilegiati di raggi per giungere alla scoperta della legge di rifrazione nelle lenti: i raggi "paralleli all'asse nel caso della lente piana-convessa, e quelli provenienti dal fuoco di una delle facce iperboliche nel caso della lente biconvessa" (Rashed 1993a, p. XLII). Un passo decisivo verso una concezione più generale e più fisica della propagazione della luce era stato già compiuto da al-Kindī nell'ambito dell'analisi della visione.
Al-Kindī e il primato operativo della luce
La profonda influenza esercitata da al-Kindī, grande filosofo ed erudito del IX sec., sullo sviluppo dell'ottica nel corso del Medioevo è legata al De aspectibus, traduzione latina di una sua opera andata perduta. Tuttavia, soltanto di recente, attraverso lo studio delle altre sezioni dell'opera, si è potuta evidenziare l'ampiezza del suo contributo a questa disciplina così come i suoi legami con i successivi sviluppi. Questa situazione ha registrato un decisivo cambiamento in seguito alla pubblicazione del primo volume delle opere filosofiche e scientifiche di al-Kindī curata da Roshdi Rashed nel 1997, che contiene non soltanto una nuova edizione del De aspectibus, ma anche un altro importante testo, finora sconosciuto, intitolato Kitāb fī taqwīm al-ḫaṭā᾽ wa-'l-muškilāt allatī li-Uqlīdis fī 'l-Manāẓir (Sulla rettifica degli errori e delle difficoltà riscontrabili nell'Ottica di Euclide) e il Kitāb fī 'l-šu῾ā῾āt [al-šamsiyya] (Libro sui raggi [solari]). Grazie ad alcuni frammenti di al-Kindī e ad altri testi risalenti alla stessa epoca, questo volume mette in luce sia l'estensione della sua opera ottica sia l'interesse allora suscitato da questa scienza.
L'opera di al-Kindī è conosciuta sia nei suoi aspetti di difesa della teoria emissionista, sia in quelli relativi alla teoria della visione. In questa sede riprenderemo lo studio di alcuni degli argomenti impiegati da al-Kindī, esaminandoli, però, in una prospettiva completamente diversa, per evidenziare gli aspetti legati alle questioni che ci interessano, ossia il rapporto tra la luce e la visione, la natura delle 'esperienze' dell'autore, le differenze riscontrabili tra queste ultime e quelle di Ibn al-Hayṯam e soprattutto la natura dei rapporti che legavano l'ottica geometrica alla fisica.
La caratteristica distintiva dell'ottica di al-Kindī è rappresentata dall'"interpretazione in senso fisico dell'ottica euclidea" (Rashed 1997, p. 75). Il filosofo, infatti, grazie soprattutto alla sua insistenza sull'accordo esistente tra l'ottica geometrica e la fisica, interpretò il testo di Euclide, e in particolare i brani relativi alla natura dei raggi visivi, in modo da metterne in luce i presupposti fisici. Questa esigenza, tuttavia, invece di indurlo a limitare le sue indagini al concetto di cono visivo, lo portò a stabilire un nuovo rapporto tra la luce e la visione, grazie al quale "lo studio della propagazione rettilinea della luce giunge ormai a occupare una posizione paritaria all'interno di quest'area di indagine" (ibidem, p. 80). L'assunzione di questa posizione era a sua volta determinata da ciò che abbiamo definito il primato operativo della luce nello studio della visione. Ma in che cosa consiste questo primato?
In al-Kindī, l'interpretazione in termini fisici dell'ottica euclidea è ispirata dall'esigenza di accordare tra loro l'ottica e la filosofia. L'autore elogia Teone di Alessandria e Tolomeo che, pur essendo "pervenuto alla perfezione nel campo della matematica […] utilizza nelle sue condizioni e nelle sue dimostrazioni matematiche le condizioni e le dimostrazioni filosofiche" (Kitāb fī taqwīm al-ḫaṭā᾽, p. 172). Al-Kindī fa questa osservazione quando confuta la dottrina euclidea secondo cui i raggi visivi erano discontinui; ciò equivaleva ad affermare che tra due raggi vicini esisteva uno spazio e che i punti situati in questo spazio non erano visibili. Per confutare questa dottrina, al-Kindī utilizza l'analisi puntuale della visione: l'origine dei raggi visivi non va ricercata soltanto nel centro dell'occhio, ma in tutta la superficie della pupilla. Da ogni punto della pupilla, che presenta la forma di una calotta sferica, emana un numero infinito di raggi (al-Kindī non parla esplicitamente della propagazione sferica, ma tutta la sua esposizione sembra suggerire questa idea). Ogni punto della superficie della pupilla, quindi, corrisponde al vertice di un cono la cui base si trova sulla superficie dell'oggetto visibile. Così, ogni punto della superficie dell'oggetto si trova, a sua volta, all'intersezione di un numero infinito di basi di cono; tuttavia, ciò non significa che tutti i punti di questa superficie siano ugualmente visibili. Dal momento che la pupilla è convessa, infatti, i soli raggi che possono raggiungere un dato punto della superficie dell'oggetto saranno quelli non ostacolati dalla convessità della pupilla. In tal modo, nella misura in cui ci si allontana, sulla superficie dell'oggetto, dall'asse della visione (cioè dalla retta tracciata perpendicolarmente dal centro dell'occhio alla superficie dell'oggetto), il numero dei 'raggi' (termine con cui al-Kindī spesso indica i diversi coni visivi) che la raggiungono diminuisce e, di conseguenza, anche la visibilità si riduce.
Ora, la ragione che induce al-Kindī a rifiutare il concetto euclideo di raggio e a elaborare la sua analisi puntuale è di carattere filosofico, indicata in un argomento proposto nel Kitāb fī taqwīm e illustrato in dettaglio nel De aspectibus. I raggi erano gli 'organi' attraverso cui l'occhio percepiva gli oggetti. Secondo 'tutti i matematici e tutti i filosofi', però, la linea geometrica era un ente esteso nel senso della sola lunghezza, privo di larghezza e di spessore; essa quindi non poteva percepire nulla. Allo stesso modo, il punto a cui perveniva una linea geometrica, essendo privo di lunghezza, di larghezza e di spessore non poteva in alcun modo essere percepito.
Tale critica del concetto di raggio visivo sollevava un problema. Dal momento che quest'ultimo era l'unico elemento che rendeva possibile la geometrizzazione della visione, bisognava trovare il modo di giustificarne in ogni caso l'impiego. La soluzione di al-Kindī è indicata all'inizio del De aspectibus. Essa è costituita da una serie di argomenti volti a dimostrare la propagazione rettilinea della visione che, tuttavia, si basa su esempi relativi alla luce; è analizzando i raggi luminosi che al-Kindī giunge a definire i raggi visivi.
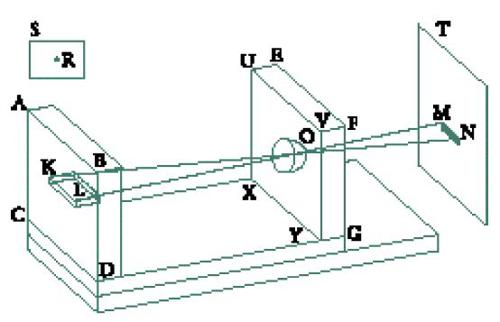
Questi argomenti, in qualsiasi modo li si voglia chiamare, si fondano, con una sola eccezione, sulla formazione delle ombre dei corpi estesi. Al-Kindī, infatti, riteneva che la tesi secondo la quale "il tragitto percorso dai raggi provenienti dai corpi luminosi è rettilineo" era confermata da due fenomeni, quello in base al quale "i limiti in estensione delle ombre dei corpi sono rettilinei" e quello delle "luci [che] passano attraverso le aperture" (De aspectibus, in: Rashed 1997, pp. 440-444). L'autore a questo punto menziona alcune esperienze molto semplici, senza dubbio ispirate al concetto di cono d'ombra impiegato dagli astronomi per spiegare le eclissi. Al-Kindī, tuttavia, compie le sue esperienze su oggetti terrestri. Dopo aver descritto una sorgente luminosa, costituita da una candela perfettamente sferica (condizione difficilmente rispettabile) di diametro D, e un oggetto anch'esso perfettamente sferico, di diametro d, l'autore indica tre casi: (1) D>d, l'ombra assume la forma di un cono il cui vertice si trova dal lato dell'oggetto; (2) D=d, l'ombra assume la forma di un cilindro; (3) D⟨d, l'ombra assume la forma di un cono il cui vertice si trova dal lato della sorgente luminosa.
Dietro queste esperienze si intravede chiaramente l'idea della propagazione sferica della luce. Dal momento che la luce si propaga a partire dalla sorgente luminosa in tutte le direzioni, il ruolo dell'oggetto è quello di ritagliare in questa sfera omogenea uno spazio, che presenta la forma di un cono o di un cilindro. A questo punto, l'interesse di al-Kindī non è rivolto all'interno della zona d'ombra così prodotta, ma alla superficie definita da questa zona. Trovandosi nell'interfaccia che divide la parte luminosa dalla parte oscura, questa superficie, infatti, indica il limite di ciascuna di esse e, di conseguenza, corrisponde alla definizione geometrica di superficie data da Euclide nel Libro I degli Elementi. L'intersezione di questa superficie conica o cilindrica con il piano che passa per l'asse comune della sorgente luminosa e dell'oggetto è una linea retta che rappresenta un raggio nel senso euclideo del termine.
L'obiettivo di queste 'esperienze' non è il tentativo di isolare un raggio luminoso, ma quello di giustificare l'impiego delle linee rette nello studio della luce. I raggi così ottenuti sono unicamente oggetti geometrici, mentre il principale oggetto 'fisico' rimane per al-Kindī la sfera creata dalla propagazione della luce o, nel caso dell'illuminazione di un oggetto ben definito, il cono prodotto dall'intersezione di questa sfera con la superficie esteriore dell'oggetto.
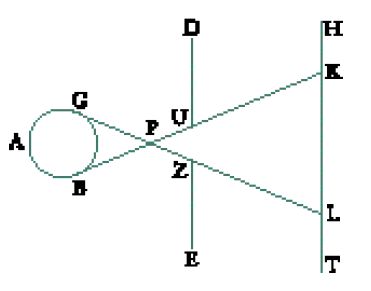
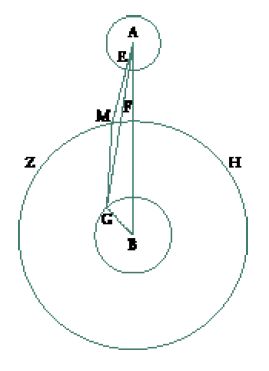
Come abbiamo già osservato, al-Kindī indica come prova della propagazione rettilinea anche le "luci [che] penetrano nelle aperture". Egli illustra questa proprietà attraverso la seguente esperienza (fig. 2).
La luce emanata da una candela rappresentata dal cerchio GB passa attraverso l'apertura UZ praticata nella tavola DE, fino a cadere sulla superficie HT. Al-Kindī scrive: "Se, partendo dal bordo della luce, che cade attraverso l'apertura della tavola parallela alla luce, si traccia la linea retta che unisce uno dei due lati della luce in larghezza [punto L o K] al bordo della candela, dal lato opposto in larghezza [punto G o B], questa linea toccherà il bordo dell'apertura praticata nella tavola. Ciò certamente non accadrebbe se i limiti dei raggi non procedessero lungo linee rette" (ibidem, p. 450).
Questa esperienza merita di essere sottoposta a un esame dettagliato. In effetti, al contrario di quelle che la precedono, essa non è fondata sul contrasto tra la luce e l'ombra, ma tra la luce e l'oscurità. È evidente, infatti, che il suo successo è legato alla possibilità di 'vedere' le tracce delle linee GL e BK. Ora ciò è possibile soltanto nel caso in cui la tavola HT si trovi immersa nell'oscurità, una condizione che sembra anticipare l'idea della camera oscura. Al-Kindī tuttavia non valuta tutte le conseguenze della sua ipotesi; in primo luogo, perché né la sorgente luminosa né l'apertura sono puntiformi. Dal momento che l'apertura ha una certa larghezza, il punto P, in cui si incontrano le linee GL e BK si trova davanti all'apertura stessa. Secondariamente, come nelle esperienze precedenti, al-Kindī non si interessa alla luce che proviene da ogni punto della sorgente, benché disponga già dell'analisi puntuale della luce. Così, egli non parla dei raggi provenienti dai punti che si trovano tra G e B e che si incrociano nell'area vicina al punto P.
In ogni caso, questa e altre esperienze non devono indurre a pensare che l'autore non fosse riuscito a conseguire gli scopi che si prefiggeva. La sua ricerca è ovviamente condizionata dall'intento originario, quello di dimostrare che "gli estremi dei raggi seguono linee rette". Per quanto essenziale alla fondazione dell'ottica geometrica, questo proposito nasceva soltanto dall'esigenza di giustificare l'impiego delle linee rette come raffigurazioni degli 'estremi dei raggi'.
Il De aspectibus è indubbiamente un trattato dedicato alla visione e non alla luce. Queste 'esperienze' quindi dovevano servire solamente a confermare attraverso "prove sensibili" la tesi secondo cui tutti i raggi seguono linee rette. Tuttavia, la scelta di fare ricorso all'analisi della luce indica un nuovo approccio, le cui conseguenze possono essere rilevate in tutta l'opera di al-Kindī che ha imposto a questo trattato una struttura diversa da quella delle opere in precedenza dedicate all'ottica. Constatiamo, in primo luogo, che al-Kindī inverte l'ordine stabilito con ogni probabilità da Tolomeo nel Libro I dell'Ottica. Invece di assumere come dato fondamentale la visione rettilinea per poi giungere a dedurne la propagazione rettilinea della luce, al-Kindī opta per un'indagine fondata sulle modalità di propagazione della luce per giungere alla conclusione che anche i raggi visivi seguono linee rette. Si può persino dire che è proprio la scelta di questo procedimento 'sperimentale' a imporre l'inversione dell'ordine di priorità. Come abbiamo già osservato, infatti, la confutazione della teoria dei raggi visivi discreti imponeva la giustificazione dell'impiego delle linee rette in campo ottico attraverso lo studio dei ritagli effettuati in un mezzo omogeneo, nella fattispecie nell'aria, ritagli che dividevano l'aria in due parti, una oscura e una luminosa. Ora, questo fenomeno non si produceva nella visione. L'atto della visione, infatti, non dava luogo nel mezzo trasparente a nessun effetto visibile utilizzabile come base di questa giustificazione. Dal momento che aveva optato per una dimostrazione di carattere sperimentale, al-Kindī non poteva che ricorrere all'analisi della luce.
Non bisogna stupirsi, dunque, nel constatare che il grande passo in avanti compiuto da al-Kindī nello studio della visione, vale a dire l'introduzione dell'analisi puntuale, sia giustificato a partire dall'esame della propagazione della luce. Come già notato, l'analisi puntuale era, infatti, strettamente legata alla confutazione della teoria euclidea della visione basata sull'esistenza di raggi visivi discreti. Tuttavia, è attraverso l'esame della propagazione della luce che al-Kindī giunge prima all'enunciazione del concetto della propagazione puntuale e sferica, la quale si produce a partire da ogni punto della superficie del corpo luminoso in tutte le direzioni, e poi, attraverso l'implicito riconoscimento della comune natura della luce e della visione, all'estensione di questo concetto alla visione. A questo scopo al-Kindī impiega un metodo indiretto: dopo aver descritto tre diversi casi possibili, egli li rifiuta uno alla volta con l'aiuto di una dimostrazione per assurdo.
a) Primo caso: la luce emana soltanto dal centro della sorgente luminosa. Se ciò fosse possibile, il vertice del cono d'ombra si troverebbe sempre nel lato dell'oggetto illuminato e mai in quello della sorgente luminosa, una circostanza smentita dall'esperienza.
b) Secondo caso: la luce emana dalla superficie della sorgente luminosa secondo rette parallele. Se ciò fosse possibile, la luce illuminerebbe esclusivamente gli oggetti che si trovano da uno dei lati della sorgente, una circostanza anche questa volta smentita dall'esperienza (al-Kindī prende in esame solamente il caso in cui la sorgente è più grande dell'oggetto).
c) Terzo caso: la luce non si diffonde a partire dal centro del corpo luminoso ma segue direzioni privilegiate, nel senso che alcune luci che provengono da certe parti del corpo luminoso sono parallele, mentre altre non lo sono. Ciò significa che un solo e unico corpo dovrebbe produrre, muovendosi nello spazio, coni d'ombra di forma sia conica sia cilindrica. Questa circostanza, però, è smentita dall'esperienza.
Dopo aver rifiutato le sopra menzionate ipotesi, al-Kindī presenta la sua tesi relativa alla propagazione della luce: "rimane quindi una sola [possibilità]: la luce si diffonde dal corpo luminoso a tutta l'aria che lo circonda e ogni luogo da cui è possibile tracciare una linea retta che giunge a toccare un punto del corpo luminoso è illuminato dalla luce del corpo luminoso" (De aspectibus, in: Rashed 1997, p. 480).
Il modo in cui al-Kindī nega queste differenti possibilità è molto più sistematico di quanto si possa pensare. Con il primo caso, egli dimostra che il corpo luminoso non può ridursi a una sorgente puntiforme; con il secondo caso rifiuta l'assimilazione di tutte le sorgenti luminose a punti situati all'infinito (il postulato fondamentale della teoria degli specchi ustori) e con il terzo sottolinea la differenza esistente tra l'emanazione della luce da una sorgente luminosa e la riflessione di questa in un corpo levigato (in cui sono riscontrabili direzioni privilegiate).
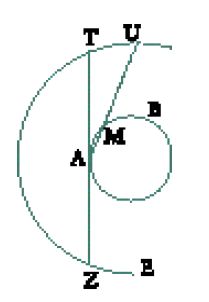
La sola limitazione cui è soggetta l'emanazione omogenea è che il raggio possa pervenire a un punto, vale a dire che il suo tragitto non attraversi il corpo luminoso. Nella fig. 3, per esempio, i punti Z e T indicano i limiti della parte della sfera EU che può essere illuminata dalla luce proveniente dal punto A della sorgente sferica B; le rette che si trovano al di là di questi limiti attraversano la sorgente e quindi non possono raggiungere nessun punto dell'oggetto, come, per esempio, la retta AU, un raggio luminoso che rappresenta il limite del cono luminoso: dal momento che attraversa la sorgente nel punto M, questa retta non può raggiungere il punto U.
È vero che, essendo completamente simmetrica, una sorgente sferica e omogenea non può che produrre un'illuminazione omogenea. Il 'numero' dei raggi che pervengono a ogni punto dello spazio, infatti, è uguale a quello dei raggi la cui propagazione è impedita dalla convessità della sfera. In compenso, questa analisi porta a concludere che lo spazio soggetto all'illuminazione di una sorgente luminosa non sferica, o di una sorgente parzialmente sferica, non è illuminato in modo uniforme e che i punti più illuminati sono quelli più vicini all'asse della sorgente. Così, sebbene al-Kindī non dedichi una specifica analisi al tema della distribuzione non omogenea della luce di una sorgente non sferica, l'argomento presentato nel De aspectibus e riproposto, come abbiamo già accennato, nel Kitāb fī taqwīm (probabilmente redatto in una data posteriore), per rendere conto dell'intensità della visione in prossimità dell'asse visivo e della sua attenuazione alle estremità del campo visivo, potrebbe essere impiegato anche per spiegare l'intensità dell'illuminazione in prossimità dell'asse del campo luminoso. Questa proprietà, considerata da Tolomeo una delle differenze specifiche che distinguevano la luce dal flusso visivo, avrebbe così potuto trovare una spiegazione nella struttura geometrica dell'occhio. Tanto più che al-Kindī illustra la sua dimostrazione in un linguaggio in cui la luce e la visione sono confuse tra loro: egli parla della "luce intensa, che cade nel centro del cerchio che contiene la base dell'aria che subisce l'azione della vista", determinata dall'"illuminazione" del "luogo chiamato centro della visione" grazie a "un maggior numero di parti della vista". Il risultato della dimostrazione è quindi presentato in un linguaggio ambivalente.
Ci sembra di poter dire che il primato della luce nello studio della visione di al-Kindī non è un primato ontologico. Per al-Kindī lo studio della visione non si riduce a quello della luce, né si può subordinare il secondo al primo. Inoltre, il suo scopo non è "negare l'esistenza dei raggi visivi o conferire ai raggi luminosi un ruolo prioritario nel processo della visione" (Lindberg 1976, p. 20). Questo studio è ancora basato sulla tradizione euclidea, secondo cui "propagazione della luce e visione non si escludono reciprocamente, ma rispondono alle stesse condizioni di possibilità" (Rashed 1997, p. 72), e forse è proprio in questa circostanza che va ricercato il suo significato storico.
La dottrina della luce di Avicenna
All'inizio della Maqāla fī 'l-ḍaw᾽ (Trattato sulla luce), Ibn al-Hayṯam, parlando della 'composizione' delle scienze fisiche e matematiche, asserisce che, se lo studio dell'aspetto cosiddetto 'geometrico' della luce spetta alle scienze matematiche, l'indagine sull'essenza della luce, dei raggi e della trasparenza rientra nel campo delle scienze fisiche, lasciando intendere che senza il contributo di queste ultime lo studio della luce sarebbe rimasto incompleto. Per avere un'idea più precisa di quale contributo le dottrine dei filosofi potevano dare alla nuova scienza della luce, sarà opportuno analizzare in modo dettagliato la dottrina della luce di Avicenna (980-1037). Quest'analisi ci consentirà non solo di mettere in evidenza ciò che Ibn al-Hayṯam doveva ai filosofi, ma anche e soprattutto il modo in cui egli utilizzò le loro analisi, nella cornice del suo progetto, e le questioni in cui, spesso senza riconoscerlo esplicitamente, l'elaborazione del suo sistema gli impose di prendere le distanze dalle loro posizioni.
La dottrina della luce di Avicenna è importante in questa indagine per tre ragioni principali. In primo luogo, pur rimanendo nel solco di Aristotele, la sua teoria della visione si discosta dalla dottrina aristotelica per l'approfondimento di alcune idee dello Stagirita che sono arricchite dalle riflessioni dell'autore o da quelle ereditate dalla tradizione peripatetica. In secondo luogo, grazie alla sua indifferenza nei riguardi dei problemi tecnici dell'ottica geometrica, il discorso di Avicenna si colloca a un livello unicamente filosofico o, per usare il linguaggio dell'epoca, esclusivamente fisico. L'autore affronta il dibattito con i seguaci di questa o quella teoria della visione o della luce soltanto quando sono in discussione i fondamenti dell'ottica. In terzo luogo, la sua dottrina documenta lo stato del discorso filosofico sulla visione e sulla luce nel periodo in cui Ibn al-Hayṯam intraprendeva la sua riforma. L'esame della teoria di Avicenna dal punto di vista della luce ci può consentire infine di mettere in evidenza una serie di aspetti che potrebbe sfuggire a un'indagine incentrata esclusivamente sulla visione.
Al contrario di al-Kindī, Avicenna non ha redatto alcun testo specificatamente dedicato all'ottica geometrica. In effetti, il suo interesse per l'ottica non è altrettanto vivo quanto quello che egli mostra per altre discipline matematiche; è senza dubbio per questo che l'ottica riveste un'importanza secondaria nella sua sintesi filosofica. A eccezione di un certo numero di osservazioni personali, e di interessanti commenti su alcuni fenomeni legati alla visione e, in particolare, sull'arcobaleno, tema riguardo al quale l'autore riconosce di essere in disaccordo con i suoi 'amici peripatetici', le analisi di Avicenna sulla visione e sulla luce sono esposte nella Fisica di al-Šifā᾽ (La guarigione), la sua grande enciclopedia filosofica, e, in particolare, nel Libro III del De anima, la sezione dedicata alla teoria della percezione, dove la visione (al-ibṣār) è presa in esame in quanto facoltà dell'anima. Egli, dunque, si occupa della luce solamente perché questo tema poteva contribuire a chiarire quello della visione: come Aristotele, infatti, Avicenna riteneva che "per prendere in esame la visione" fosse necessario "parlare della luminosità (al-ḍaw᾽), della trasparenza (al-mušiff) e del colore (al-lawn)" (al-Šifā᾽, ed. Anawati, VI, p. 79). È a causa di questo rapporto di dipendenza che la dottrina avicenniana della luce non è esposta in modo sistematico; i suoi elementi, infatti, emergono via via che l'autore procede nella discussione del tema della visione.
Il termine al-ḍaw᾽, che Ibn al-Hayṯam impiega sempre per designare la luce, è quindi uno dei concetti che, secondo Avicenna, è necessario spiegare prima di affrontare la questione filosofica della visione. I due autori impiegano questo termine in due diverse accezioni. Nell'opera di Ibn al-Hayṯam, al-ḍaw᾽ è un termine generico che indica diversi generi di luce, mentre in quella di Avicenna esso è impiegato soltanto per designare la luce che risiede nei corpi visibili in sé (è per questo che qui abbiamo deciso di tradurlo con 'luminosità'): "La luminosità (al-ḍaw᾽) […] è una qualità che l'occhio percepisce nel Sole e nel fuoco, senza che si possa dire che essa sia nerezza, bianchezza, rossezza o un altro colore; la luce (al-nūr) […] è qualcosa che emana da un tale corpo e che si immagina cada sui corpi, presentandosi allora come bianchezza, nerezza o come verde" (ibidem).
Nella misura in cui indicano la luce che risiede in un corpo, certamente luminoso in sé, e la luce che da esso emana, i vocaboli qui tradotti con 'luminosità' e 'luce' corrispondono rispettivamente ai termini lux e lumen che si ritroveranno più tardi nelle opere degli studiosi del Medioevo latino. In Avicenna, tuttavia, questa distinzione non presuppone un preciso ordine ontologico: egli, infatti, non afferma che i due concetti rientrano nello stesso genere, né che uno è subordinato all'altro. In effetti, è attraverso altri due concetti, il corpo e la visione, che questi termini, così come altri vocaboli relativi al lessico dell'ottica ‒ 'trasparenza', 'raggio', 'splendore' ‒ entrano in relazione tra loro. Tutti questi termini fanno la loro comparsa nel momento in cui Avicenna divide il corpo, che costituisce un concetto fondamentale, in base ai rapporti che lo legano a un altro concetto importante, quello della visione.
Innanzi tutto i corpi si dividono in tre gruppi principali: quelli che sono assolutamente non visibili, anche quando sono illuminati ‒ cioè i corpi trasparenti ‒, quelli visibili in sé ‒ ossia i corpi luminosi ‒ e quelli che per poter essere visti devono essere illuminati ‒ appartenenti cioè alla categoria dei corpi colorati.
Avicenna indica la proprietà essenziale dei corpi trasparenti nella non visibilità, mentre definisce in modo più esplicito le altre due categorie: "il corpo è visibile in sé quando è dotato di luminosità, altrimenti esso è visibile soltanto quando è investito dalla luce: in questo caso, esso si chiamerà colorato (mulawwan)" (ibidem, p. 81).
In queste formule troviamo la definizione di due concetti. L'impiego dei due termini ‒ luminosità e luce ‒ corrisponde a una distinzione tra due entità che si presenta sotto la forma dell'asimmetria delle loro azioni: ciò che nei corpi luminosi si presenta come luminosità, investendo i corpi opachi risveglia un'altra proprietà, il colore. Quest'ultimo diviene così la proprietà dominante e mette in ombra la luce che l'ha attualizzato, come testimonia il seguente brano di al-Šifā᾽: "Noi diciamo: la luminosità è una parte (ǧuz᾽) di quel visibile che chiamiamo colore, [vale a dire] essa è qualcosa che, quando si mescola al colore in potenza (iḏā ḫālaṭa 'l-lawn bi-'l-quwwa), il prodotto, la loro fusione (imtizāǧ), dà origine alla cosa che è la luce in atto. Ora, se questa disposizione non esiste, si producono solo l'illuminazione e il bagliore. La luminosità è dunque in qualche modo una parte di quella cosa che è il colore, una parte che si combina con esso, nello stesso modo in cui la bianchezza e la nerezza si combinano in un certo modo producendo colori intermedi" (ibidem, p. 91).
Di conseguenza, è in rapporto ai corpi luminosi e colorati che Avicenna definisce luminosità e colore: la luminosità è la proprietà distintiva della prima categoria di corpi (quella dei corpi luminosi) e il colore è la proprietà distintiva della seconda categoria (quella dei corpi colorati).
Tuttavia, la luminosità svolge anche un altro ruolo nella dottrina di Avicenna:
La luminosità è una qualità, ed essa è in sé stessa una perfezione per il trasparente in quanto trasparente. Essa è anche una qualità di ciò che è visibile in sé e non per una causa esterna. Ed è certo che ciò che è visibile in sé impedisce al tempo stesso alle cose che si trovano dietro di esso di essere viste. Quanto alla luce, essa è una qualità che il corpo trasparente riceve dal corpo luminoso, ed è grazie a essa che il trasparente [in potenza] si perfeziona e diviene trasparente in atto. Quanto al colore, esso è una qualità che si perfeziona con l'aiuto della luce, ed esso è tale che il corpo [a cui esso appartiene] può impedire l'azione del [corpo] luminoso su altri corpi, se si interpone tra essi e il [corpo] luminoso. Dunque i corpi si dividono in luminosi, colorati e trasparenti. (ibidem, p. 92)
Esaminando più da vicino questo passaggio, si osserva che il termine 'luminosità' indica la luce nella sua appartenenza a un corpo, mentre il termine 'luce' designa la luce nel suo processo di propagazione. Tuttavia, non è da questo punto di vista che Avicenna affronta il problema. Egli, infatti, definisce l'azione del mezzo trasparente in modo da porre in questione ogni idea di propagazione della luce. Nello stesso modo in cui il concetto di luce, che non ha un equivalente in Avicenna, si divide immediatamente in due concetti ‒ la luminosità e la luce ‒, quest'ultima si caratterizza in due modi ben distinti tra loro, a seconda che si trovi in un mezzo trasparente o che cada su un corpo non luminoso. In entrambi i casi, la sua azione è definita dalla perfezione che essa conferisce al mezzo trasparente e al corpo colorato. Per quanto riguarda quest'ultimo, tale azione è facilmente comprensibile, poiché è a opera della luce che i colori, prima di allora invisibili, si rivelano all'occhio o, come dice Avicenna, "si attualizzano". Così, il corpo colorato acquisisce, attraverso la presenza della luce, una qualità, quella della visibilità, di cui era privo prima di essere illuminato. Che cosa intende Avicenna con l'espressione "perfezione del mezzo trasparente"?
È evidente che questo perfezionamento non si può identificare con la visibilità, perché, come già detto, i corpi trasparenti sono assolutamente invisibili. Quest'azione è definita da alcuni autori come una trasformazione qualitativa del mezzo trasparente, un'espressione che potrebbe suggerire l'idea di un movimento, nel senso aristotelico del termine, che si produrrebbe nel mezzo trasparente illuminato dalla sorgente luminosa. Tuttavia, il testo di Avicenna non può essere interpretato in questo senso. Al contrario, l'autore tenta di scartare, attraverso un'analogia, ogni idea di trasformazione causata dall'azione della luce nel mezzo trasparente:
Quanto alla trasparenza, essa può essere in potenza o in atto. Tuttavia, per essere in atto, il trasparente non ha bisogno di una trasformazione interna, ma piuttosto di una trasformazione [che si produce] in qualcos'altro o di un movimento di qualcos'altro. Esso è, sotto questo aspetto, simile a un orifizio (al-manfaḏ) o a una strada (al-maslak) che non hanno bisogno, per esistere in atto, di una nozione in sé stessi, ma dell'esistenza in atto di qualcosa che penetri nell'orifizio o di qualcuno che percorra la strada. (ibidem, pp. 81-82)
Questo passaggio dimostra che il perfezionamento del mezzo trasparente attraverso la luce non è un movimento naturale, nel senso di un cambiamento il cui principio si trova all'interno del mezzo trasparente stesso. Esso non è neppure un cambiamento che interviene nel mezzo trasparente sotto l'azione di un agente esterno. La presenza della luce non solo non rende visibile il mezzo trasparente, ma non lo trasforma in alcun modo. L'analogia della strada serve a illustrare questo rapporto, o piuttosto questa assenza di rapporto dal punto di vista causale tra la luce e il mezzo in cui essa si propaga.
Il mezzo trasparente non agisce sulla luce né risente del suo passaggio; il suo unico ruolo è dunque quello di non 'impedire' e di facilitare l'azione del corpo luminoso sul corpo che subisce questa azione. È quindi lecito dire, come potrebbero suggerire le analogie dell'orifizio e della strada, che il mezzo trasparente veicola la luce, consentendole di propagarsi, di trasmettersi da un corpo all'altro?
La risposta di Avicenna a questo interrogativo emerge dal suo dibattito con i sostenitori della tesi secondo cui la luce è costituita dai corpuscoli emanati dagli oggetti luminosi. La sua analisi critica, quindi, è rivolta in un primo momento alla teoria atomistica della luce e, in effetti, in alcuni argomenti si fa riferimento in maniera esplicita a essa. Avicenna, tuttavia, presenta anche altri argomenti non esclusivamente incentrati sulla critica della teoria atomistica. Al contrario, l'assenza di ogni riferimento a questa o quella teoria conferisce a tali argomenti un valore generale, grazie al quale essi, superando i limiti di questa particolare analisi, si trasformano in tesi volte alla confutazione non soltanto dell'esistenza del flusso dei corpuscoli, ma anche e soprattutto di ogni idea relativa all'emanazione di qualsiasi tipo di raggi sia dai corpi sia dagli occhi.
In breve, la risposta data attraverso questi argomenti all'interrogativo summenzionato può essere considerata affermativa soltanto se con l'espressione 'propagazione della luce' ci si limita a suggerire che quest'ultima possa, grazie al mezzo trasparente, manifestarsi sul corpo che si trova di fronte alla sorgente luminosa. In caso contrario, è evidente che ogni idea di propagazione come spostamento di qualcosa e persino come effetto rimane del tutto estranea alla dottrina della luce di Avicenna.
Disponiamo già di alcuni elementi che anticipano questa risposta. Abbiamo visto, per esempio, che definendo la trasparenza nei termini della 'perfezione' del mezzo trasparente, Avicenna esclude ogni legame tra la propagazione della luce e il movimento. Altri elementi emergono nel corso della sua confutazione del concetto di raggio. All'inizio della sua analisi dedicata alla visione, Avicenna scrive: "il raggio (al-šu῾ā῾) è qualcosa che si immagina nei corpi come di scintillante (yataraqraqu) che fa da schermo (yasturu) al colore dei corpi e che da loro emana (yufīḍu)" (al-Šifā᾽, ed. Anawati, VI, p. 79). Il modo in cui egli descrive questo concetto, così come la successiva distinzione tra due tipi di raggi ‒ il raggio in senso proprio (al-šu῾ā῾), che proviene dai corpi luminosi, e il bagliore (al-barīq), che ha origine dai corpi illuminati, come per esempio gli specchi ‒, dimostra che la sua critica non è diretta esclusivamente contro il raggio in senso tecnico, vale a dire né contro quello di tipo euclideo né contro il raggio così come è concepito da al-Kindī. Ciò che Avicenna scrive a questo proposito riguarda non solo le opinioni di coloro che credevano nella corporeità dei raggi, ma anche ogni idea di propagazione, indipendentemente dal suo significato fisico e dalla sua rappresentazione geometrica:
Il raggio non è né un corpo né una forza che si trasmette dal Sole alla Terra spostandosi nel mezzo; al contrario, esso è qualcosa che si produce simultaneamente (daf῾atan) in ciò che si trova di fronte [al Sole o a un corpo luminoso], a condizione che quest'ultimo ammetta la luce e che tra i due intervenga un corpo che non impedisca l'azione dell'uno sull'altro, vale a dire un corpo trasparente. […]
Dicendo che il raggio emana, che esce o entra, ricorriamo a metafore (alfāẓ maǧāzī). […] In effetti, il raggio si produce istantaneamente in ciò che si trova di fronte. Ora, poiché si produce a partire da qualcosa che si trova in alto, si è immaginato che esso discenda da questo, benché, con ogni evidenza, [sia più corretto dire che esso] non discende ma si produce, perché non è visibile lungo il suo tragitto né ha bisogno di impiegare un tempo percettibile [per compiere questo percorso]. (ibidem, p. 84)
Come vedremo, Avicenna tenta sempre di esimersi dall'analizzare il mezzo intermedio e di passare direttamente dal corpo che emette la luce a quello che la riceve. La sua preferenza per il verbo 'prodursi', che a suo parere dovrebbe essere usato in sostituzione di 'discendere', non è quindi una semplice questione terminologica. L'uso del primo infatti gli consente di associare la luce ai corpi, dissociandola dal mezzo intermedio. L'iniziale definizione della luce nei termini della perfezione del trasparente non svolgerà in seguito un ruolo di primo piano nella sua analisi. La luce, infatti, è visibile solamente al suo punto di partenza e d'arrivo, mentre "non è visibile lungo il suo tragitto". Ancora una volta, emerge il ruolo decisivo svolto da quella che, in un altro linguaggio, potrebbe essere chiamata propagazione istantanea della luce, che in questo brano e nei successivi passaggi dell'argomentazione di Avicenna è alla base del suo rifiuto di ogni teoria dell'emanazione: "ora, [quelli che credono che i raggi emanano dai corpi] forse dispongono di una prova in grado di dimostrare la loro emanazione; se è così, dove si trova questa prova? Forse ciò è dimostrato dalle sensazioni ed essi si basano sui sensi; in questo caso come potrebbero i sensi percepire il movimento di un mobile, il cui tempo di movimento sfugge ai sensi e che non è percepibile lungo il suo tragitto?" (ibidem, pp. 84-85).
Così, allo spostamento dei raggi (sempre confuso con lo spostamento della luce) è attribuito un significato molto particolare, che li riduce all'ombra di sé stessi:
quanto allo spostamento del raggio, esso è dello stesso genere dello spostamento dell'ombra, [cioè se il raggio fosse qualcosa che si può spostare] allora anche l'ombra sarebbe necessariamente un corpo in grado di spostarsi. Ma né l'uno né l'altra si producono per spostamento bensì per annichilazione (buṭlān) e rinnovamento (taǧaddud), producendosi di nuovo entrambi ogni volta che si crea una situazione di frontalità. […] L'ombra non annichila la luce ed entrambe non sono corpi. E se si spostano è per rinnovamento e non perché si tratti di cose che si spostano. (ibidem, p. 85)
Come si può constatare, in questo passaggio la descrizione della propagazione della luce in termini di attualizzazione del mezzo trasparente è messa in ombra dall'importanza attribuita alla creazione di una situazione di frontalità tra la sorgente luminosa e l'oggetto illuminato. I termini 'annichilazione' e 'rinnovamento' impiegati in questo nuovo contesto allontanano ancora di più la propagazione della luce dal movimento, inteso come cambiamento che si produce gradualmente. La propagazione della luce è, quindi, un fenomeno che si produce istantaneamente.
Tuttavia, in Avicenna la svalutazione del ruolo del mezzo trasparente riguarda soprattutto la dottrina della luce. Nella sua teoria della visione, infatti, l'attualizzazione del mezzo trasparente riacquista una grande importanza come unica garanzia della veridicità della visione. Per quanto riguarda tale questione, egli si schiera dalla parte dei 'sostenitori dell'impressione' (aṣḥāb al-inṭibā῾) e si contrappone ai 'sostenitori del raggio' (aṣḥāb al-šu῾ā῾), spiegando la visione attraverso la tesi secondo cui l'occhio è colpito dall'immagine (al-šabāḥ) dell'oggetto. Così, l'idea della trasmissione di 'qualcosa' attraverso l'attualizzazione del mezzo s'impone nel momento in cui egli si trova a descrivere la visione. In ogni caso, anche per quanto riguarda quest'ultima, si preoccupa di distinguere l'attualizzazione dal cambiamento qualitativo del mezzo trasparente stesso, come dimostra il seguente passaggio di al-Šifā᾽:
La trasformazione di cui ha bisogno il trasparente in potenza per divenire trasparente in atto è costituita dal fatto che il corpo colorato sia illuminato e che il suo colore si manifesti in atto. Quanto al movimento [di cui ha bisogno il trasparente in potenza per divenire trasparente in atto], esso consiste nello spostamento del corpo luminoso [verso il trasparente] senza che questo si trasformi in sé. E quando una di queste cose si realizza, la visione si produce e [il trasparente] diviene trasparente in atto grazie all'esistenza di qualcos'altro. (ibidem, pp. 81-82)
Inoltre, alcuni passaggi di al-Šifā᾽ dimostrano che lo scarto esistente tra la teoria della visione e la dottrina della luce è meno rilevante di quanto possa sembrare. In effetti, Avicenna interpreta l'idea dell'impressione delle immagini in modo da attribuire un'importanza molto ridotta al ruolo svolto dal mezzo trasparente e da assegnare una posizione predominante al corpo luminoso e alla creazione di una situazione di frontalità. Egli pensa in tal modo di riuscire a giustificare la visione rettilinea. Quest'idea è chiaramente enunciata nel brano in cui Avicenna risponde alla seguente obiezione: come conciliare la dottrina della trasmissione delle immagini con la circostanza per cui esse pervengono a certi occhi e non ad altri? Egli risponde così a questo interrogativo:
In effetti, noi non diciamo che l'aria trasmette nel senso che essa riceve certe figure (rusūm) e immagini (ašbāḥ) di un oggetto per condurle verso un altro oggetto. Noi diciamo che il luminoso (al-nayyir) è tale che esso è in grado di trasmettere la sua immagine a ciò che si trova di fronte a lui, a condizione che tra essi esista non un ostacolo (῾ā᾽iq), vale a dire un corpo colorato (mulawwan), ma un corpo trasparente. Poiché se il corpo che si interpone (al-wāsiṭa) fosse prima ricettore e poi trasmettitore, esso trasmetterebbe [le immagini] a tutti gli occhi, come avviene nel caso del calore che si trasmette a tutti coloro che toccano, qualunque sia la loro posizione. (ibidem, p. 119)
Aggiungeremo per inciso che, quasi due secoli più tardi, Šihāb al-Dīn al-Suhrawardī (549-587/1155-1191) spiegherà la visione in un modo sotto molti aspetti analogo alla dottrina avicenniana della propagazione della luce. Secondo questo autore, la creazione di una situazione di 'frontalità' tra l'occhio e ciò che è visibile assicura in sé all'anima la possibilità di procurarsi l'immagine dell'oggetto, senza che altri elementi, come per esempio l'attualizzazione del mezzo, svolgano alcun ruolo in questo processo.
La spiegazione di Avicenna della riflessione dei raggi si concilia perfettamente con lo spirito che anima la sua dottrina della luce: "anche la riflessione del raggio ha un senso metaforico. Ogni corpo, se è illuminato e se è levigato, ammette che ogni altro corpo che si trova di fronte a lui si illumini a sua volta, senza che vi sia uno spostamento" (ibidem, p. 85). La sua dottrina della luce non è esattamente identica a quella elaborata da Aristotele, anche se è allo scopo di attribuire un maggior peso ad alcuni elementi della teoria aristotelica della visione che Avicenna si sente obbligato ad affrontare, ai margini dell'esposizione di questa teoria, il dibattito relativo alla natura della luce.
Tra queste discordanze la più rilevante è quella relativa alla descrizione del mezzo trasparente, che nella visione ha un ruolo diverso da quello svolto nella 'propagazione' della luce. Nel primo caso il mezzo trasparente assicura sempre la trasmissione dell'immagine dell'oggetto all'occhio, mentre nel secondo esso non trasmette nulla. L'assenza di simmetria tra il ruolo svolto dal mezzo nella dottrina della visione e in quella della luce ha senza dubbio la sua origine nel rifiuto di ogni teoria volta ad attribuire alla propagazione della luce un significato materiale. Portando alle loro logiche conseguenze alcune idee aristoteliche, Avicenna perviene a conclusioni che oggi sarebbero considerate assurde, in cui la propagazione della luce si trova degradata al rango di epifenomeno. La ragione di ciò va ricercata nel fatto che egli è interessato non tanto alla propagazione della luce quanto piuttosto alle condizioni della visibilità degli oggetti, tra le quali naturalmente figura l'illuminazione da parte di una sorgente luminosa. Quest'ultima, a sua volta, si realizza attraverso la creazione di una situazione di frontalità; il resto sfugge ai sensi così come a ogni ragionamento teorico.
Avicenna non tenta quindi di definire i fondamenti 'fisici' sui quali basare l'elaborazione dell'ottica geometrica; al contrario, la sua analisi rende impossibile un tale tentativo. Non è soltanto l'ottica fondata sulla dottrina dell'immissione che gli sembra contraria ai principî fisici; in effetti, il suo atteggiamento, nei confronti del tipo di ottica in corso di elaborazione nell'opera di Ibn al-Haytam, non sarebbe stato diverso da quello adottato in ogni periodo storico dai filosofi peripatetici nei confronti dell'ottica di Euclide e di Tolomeo: egli avrebbe ritenuto di trovarsi in presenza di uno strumento che poteva efficacemente 'salvare i fenomeni' ma si sarebbe rifiutato, al tempo stesso, di attribuire una realtà fisica alle sue costruzioni teoriche. Ciò che dice David C. Lindberg (1976) a proposito dell'atteggiamento adottato da Avicenna nei confronti della teoria euclidea dei raggi visivi può essere applicato anche a quello che il filosofo avrebbe tenuto nei confronti dell'ottica di Ibn al-Hayṯam: evitando di mettere in dubbio la sua utilità matematica, egli avrebbe sostenuto che essa non rappresenta la natura fisica della luce.
Le idee fondazionali della scienza della luce
Salvare i fenomeni o fondare una scienza dimostrativa?
Quanto è stato detto finora consente di spiegare l'esistenza all'epoca di Ibn al-Hayṯam di due movimenti paralleli ma orientati in direzioni opposte. Nel campo dell'ottica matematica si registra un forte aumento del numero dei fenomeni da studiare attraverso metodi geometrici. L'opera di Ibn Sahl ‒ vale a dire sia il trattato sugli strumenti ustori sia lo studio della trasparenza del corpo celeste ‒ è soltanto un esempio, fortunatamente giunto fino a noi, di questa tendenza. Le indagini di questo studioso si distinguono non soltanto per il trattamento matematico in forme inedite della luce, inclusa quella rifratta, ma anche per il riconoscimento della necessità di giungere a un'esplicita formulazione delle leggi di propagazione della luce.
Ritroviamo tale formulazione nell'opera di al-Kindī, il quale tentò di dotare di una solida base la legge della propagazione rettilinea della visione. Ispirata a un analogo esame della luce, l'analisi puntuale della visione di al-Kindī è accompagnata da una concezione fisica della sorgente luminosa. La moltiplicazione delle fonti, che in Ibn Sahl dipende dalla geometria delle situazioni prese in considerazione, rinvia in al-Kindī all'intento di rafforzare la legge della propagazione rettilinea della luce attraverso 'prove sensibili'. Dal momento che è più facilmente utilizzabile in questo genere di 'protoesperimenti', la luce finisce per acquisire un primato operativo sulla visione.
Così, le due principali branche dell'ottica geometrica iniziano ad avvicinarsi l'una all'altra, anche se in modo non sistematico e seguendo strade diverse. Le questioni fondamentali, infatti, rimangono ancora irrisolte: ci riferiamo alla precisa natura del rapporto esistente tra la visione e la luce, così come tra l'oggetto fisico e l'oggetto matematico, e soprattutto alla natura dell'ottica come scienza fisica basata sull'utilizzazione di strumenti matematici. Si delinea così "una situazione conflittuale che esploderà soltanto centocinquant'anni più tardi" (Rashed 1997, p. 76).
Questa esplosione si riflette nell'opera ottica di Ibn al-Hayṯam, la quale non può essere ridotta a nessuno dei suoi elementi costitutivi. In tal caso ci troviamo in presenza di un vero e proprio progetto, la cui estensione non si limita a ciò che Ibn al-Hayṯam afferma, a questo proposito, né nella Maqāla fī 'l-ḍaw᾽ né nella sua opera principale, l'Ottica, un testo dedicato alla visione in cui tuttavia l'autore tenta costantemente di dimostrare, al di là di ogni ambiguità, che la formulazione della teoria della visione può essere intrapresa soltanto all'interno della scienza della luce. Il progetto di Ibn al-Hayṯam, però, non è riducibile a questo preciso disegno; la sua realizzazione impone non soltanto il riesame di alcune questioni già considerate all'interno di diverse branche dell'ottica, ma anche l'analisi di problemi fino allora irrisolti o rimasti inaccessibili per qualsiasi tipo di indagine scientifica.
È nella cornice della costituzione di questa scienza che Ibn al-Hayṯam solleva la questione della composizione delle scienze matematiche e fisiche. Ora, ci auguriamo di aver dimostrato, attraverso l'analisi della dottrina della luce di Avicenna, che la filosofia peripatetica di quel periodo non poteva riconoscere questa scienza, se non nel caso in cui essa non avesse preteso di conferire uno status ontologico ai suoi concetti.
Tuttavia, non è su una tale concezione che Ibn al-Hayṯam costruisce la sua teoria ottica, e ciò per due principali ragioni. In primo luogo, per quanto riguarda la luce e la sua propagazione la sua opera è contrassegnata da un rigoroso realismo. Non soltanto la luce, come proprietà dei corpi in cui risiede, è assolutamente reale, ma anche il fenomeno a cui lo studioso è più interessato, quello della propagazione della luce, non ha nulla di immaginario. Ciò vale anche per il colore, qualità ben distinta dalla luce, dalla quale, tuttavia è sempre veicolato. Su tali questioni Ibn al-Hayṯam è estremamente chiaro. Se a volte parla delle 'linee immaginarie' lungo le quali la luce si propaga è solamente, come vedremo più avanti, per operare una distinzione tra l'oggetto fisico, il fascio di luce e l'oggetto matematico a cui è associato. Affermando che queste linee sono immaginarie egli intende dire che esse partecipano dello stesso genere di realtà fisica di ogni altro oggetto geometrico. In secondo luogo, la sua concezione della 'scienza', così come è esposta nella Maqāla fī 'l-ma῾lūmāt (Trattato sui noti), non è conciliabile con questo approccio definito 'positivistico'. Da tale concezione, così come essa è presentata in questo trattato, discendono tre elementi: (a) la scienza è una credenza (i῾tiqād) o un'opinione (ẓann) che si fonda su un oggetto ("una nozione": ma῾nā); (b) Ibn al-Hayṯam aderisce a una sorta di teoria della corrispondenza: a suo parere, un'opinione falsa, che non corrisponde cioè a "una nozione, così come è", non può essere considerata una scienza; (c) un'opinione che cambia con il tempo, a causa del cambiamento del suo oggetto, non è una scienza, se non nel caso in cui la si "limiti nel tempo".
Sono queste le condizioni necessarie e sufficienti a cui un'opinione deve rispondere per poter essere considerata scienza. Ora, bisogna distinguere tra la scienza, vale a dire tra un'opinione vera e non soggetta al cambiamento, e la strada da percorrere per giungere alla sua definizione. A questo punto Ibn al-Hayṯam introduce il criterio in base al quale distinguere le scienze che sappiamo essere immutabili da quelle che, pur essendo altrettanto vere, sono per così dire prive di questo 'secondo grado' di consapevolezza.
Benché la corrispondenza tra l'opinione che si ha di una "nozione" e "la nozione così com'è" sia in sé sufficiente ad assicurarne la verità, non si può 'riconoscere' la verità di una proposizione se quest'ultima non è accompagnata da una dimostrazione. In questo caso, essa dovrà essere considerata un'opinione, almeno fino a quando non si giunga alla definizione della questione attraverso la dimostrazione. Quest'ultima quindi non è la causa della verità dei nostri enunciati, ma è il solo strumento attraverso cui tale verità può essere riconosciuta e imposta all'attenzione degli altri.
Ibn al-Hayṯam ripropone questa idea anche in altri contesti. Nella sezione iniziale della Maqāla fī ḍaw᾽ al-qamar (Trattato sulla luce della Luna), dopo aver asserito che tutti i grandi sapienti, sia nel campo della matematica sia in quello della fisica, credevano che la Luna mutuasse la sua luce dal Sole, egli aggiunge che questa tesi, benché evidente (ẓāhir) necessita di una dimostrazione. A suo parere, infatti, "finché non si sarà dimostrata la sua necessità, è ammessa una sola conclusione: siamo in presenza di una cosa non necessaria (wāǧib ḍarūrī) ma contingente (imkānī), non certa (mutayaqqan) ma congetturale (maẓnūn)".
Una scienza dimostrata si distingue non solo da ciò che conosciamo "senza dimostrazione né necessità, ma per sentito dire e per imitazione, sulla fiducia, o per intuizione" (Maqāla fī 'l-ma῾lūmāt, p. 95), ma anche da ciò che ci sembra evidente (ẓāhir). Per quanto riguarda questo punto, le osservazioni summenzionate della Maqāla fī ḍaw᾽ al-qamar riprendono, completandola, la teoria di cui erano stati annunciati gli elementi fondamentali nella Maqāla fī 'l-ma῾lūmāt.
Così, il passaggio dall'opinione alla scienza, che segna la transizione dal dubbio alla certezza, è assicurato dalla dimostrazione e unicamente da essa. Al contrario della certezza intuitiva, che dipende dall'evidenza immediata, la certezza che emerge dalla dimostrazione si fonda non su una soddisfazione di carattere psicologico, ma sulla corrispondenza esistente tra le nostre 'opinioni' e le "quiddità delle cose che esistono", le "nozioni così come sono".
La concezione qui esposta a grandi linee può essere considerata una teoria sia della conoscenza sia della scienza. Questi discorsi, infatti, valgono sia per la scienza nel senso attribuito a tale termine nella Maqāla fī 'l-ma῾lūmāt, ossia quello di una conoscenza vera che può essere basata su qualsiasi oggetto, sia per la scienza intesa come indagine sistematica che ha come oggetto una classe ben definita di fenomeni, nella fattispecie quelli legati alla visione o alla luce.
Questa teoria si avvicina, almeno per la sua insistenza sulla dimostrazione, al concetto aristotelico di scienza come conoscenza dimostrativa. Tuttavia, in Ibn al-Hayṯam l'idea di scienza dimostrativa non si identifica necessariamente con il sistema deduttivo descritto da Aristotele negli Analitici secondi, vale a dire con una concatenazione di ragionamenti in cui ogni passaggio dipende dal precedente e tutta l'argomentazione è riconducibile a un ristretto numero di principî. Infatti, se il ragionamento geometrico svolge un ruolo di primo piano nell'ottica di Ibn al-Hayṯam, tuttavia, prima di imboccare la strada della geometrizzazione, è necessario assicurarsi che i principî scelti siano realmente degni di questo nome, che siano cioè 'dimostrati'.
Su questo punto Ibn al-Hayṯam prende le distanze da Aristotele, secondo il quale la nozione di dimostrabilità dei principî condurrebbe a conclusioni assurde, implicando sia un regresso all'infinito sia un circolo vizioso. Questo status dei principî, questa assoluta anteriorità, presuppone che l'individuazione dei principî sia operata con strumenti diversi dalla dimostrazione. Basandosi su ciò che dice Aristotele alla fine degli Analitici secondi, bisogna quindi riconoscere l'esistenza di un''intuizione razionale' in grado di cogliere i principî, oppure optare per la tesi secondo cui questi sono colti, in ultima analisi, dalle sensazioni, ammettendo così che esse non possono ingannare.
Ora, nell'opera ottica di Ibn al-Hayṯam è riscontrabile lo sforzo sistematico di dimostrare la proprietà fondamentale della luce, ossia la sua propagazione rettilinea, così come le proprietà generali della luce e della visione. La dimostrazione di questi principî si basa su due strumenti: l'induzione e la sperimentazione. Non è attraverso la tesi dell'infallibilità delle sensazioni che Ibn al-Hayṯam giunge all'elaborazione di tali strumenti; al contrario, il ricorso a questi ultimi è dettato dal riconoscimento della fallibilità delle sensazioni. Ciò conferisce una certa problematicità a tutto il modo di procedere di Ibn al-Hayṯam. Prima di affrontare questo problema, però, è necessario analizzare il modo in cui egli definisce i concetti fondamentali della scienza della luce, vale a dire le nozioni di luce, di trasparenza e di raggio.
La definizione dei concetti
Nell'Ottica (I, 3, 20), troviamo una sola asserzione sulla natura della luce, secondo cui, da un lato, quest'ultima è una forma, dall'altro lato essa esiste indipendentemente dalla visione e la sua esistenza si presenta in diverse forme, tra cui si distinguono la forma sostanziale e quella accidentale. Per il resto, la luce è studiata attraverso la sua proprietà essenziale, costituita dalla propagazione da tutti i punti dell'oggetto luminoso in ogni direzione. All'inizio della Maqāla fī 'l-ḍaw᾽, Ibn al-Hayṯam presenta due definizioni della luce, quella adottata dai filosofi e quella a cui ricorrevano i matematici. Riportiamo di seguito la definizione della luce secondo i filosofi:
noi possiamo enunciare in relazione a queste nozioni una proposizione universale, cioè che ogni nozione che si trova in un corpo, tra le nozioni che ne costituiscono l'essenza, è chiamata forma sostanziale ‒ poiché la sostanza di ogni corpo è costituita dall'insieme di tutte le nozioni che in esso si trovano e che non sono separabili fintantoché la sua sostanza non cambia. È così che la luce di ogni corpo luminoso in sé è una delle nozioni che costituiscono la sua essenza: la luce di ogni corpo luminoso in sé è dunque una sua forma sostanziale e la luce accidentale che appare sui corpi opachi illuminati da altri è una loro forma accidentale: è questa l'opinione dei filosofi. (Maqāla fī 'l-ḍaw᾽, p. 207)
Benché appaia naturale, la distinzione 'sostanziale-accidentale' può essere concepita soltanto nella cornice di una teoria che ha come punto di partenza il concetto di luce. Nelle analisi incentrate sulla visione, per esempio, quella di Avicenna, il concetto unitario di luce, suscettibile in seguito di dividersi in sostanziale e accidentale, non è un dato di base. Come abbiamo visto, nell'analisi di Avicenna l'interesse per la visione e per i corpi come supporto di ogni qualità, ostacola l'identificazione della luce e della luminosità, così come una netta distinzione tra luce e colore. Ciò porta Avicenna a dividere i corpi in luminosi, trasparenti e colorati, benché egli riconosca l'esistenza dei colori in certi oggetti luminosi terrestri, come il fuoco, o in alcuni astri, come Marte e Giove. Anche se in alcuni casi Avicenna parla del 'bagliore' (al-barīq) che emana dai corpi colorati, l'esistenza di quest'ultimo è spesso oscurata dalla dicotomia 'luminoso-colorato', al punto che si potrebbe pensare a due proprietà reciprocamente esclusive: per ciò che concerne la visione, i corpi luminosi sono presentati come se fossero incolori e quelli colorati come se fossero privi di luce.
Nonostante la divisione della luce in sostanziale e accidentale ‒ una divisione nuova almeno per quanto riguarda le sue conseguenze ‒ ciò che interessa Ibn al-Hayṯam non è la luce nella sua appartenenza a un certo corpo. La luce sostanziale e quella accidentale lo interessano solamente in quanto fonti di altri due tipi di luce, ossia quella emessa da un corpo luminoso in sé, detta "la luce prima", e quella emessa da un corpo illuminato da una luce prima, chiamata "la luce seconda" (egli indica anche la luce terza, quarta, ecc.). Scompaiono così tutti quei termini ‒ luminosità, luce, raggio, bagliore ‒ che indicavano l'assenza di un concetto unificatore in Avicenna: egli preferisce rimanere al livello dei fenomeni, per cedere il passo al solo concetto di luce, mentre le suddivisioni intervengono soltanto in un secondo momento.
Come nasce il concetto di luce? Esso si impone, come dimostra sia il testo dell'Ottica sia quello della Maqāla fī 'l-ḍaw᾽, attraverso il riconoscimento dell'esistenza di fenomeni che non hanno omologhi né nella teoria emissionista né in quella immissionista della visione. In effetti, l'induzione dimostra che esiste una vasta categoria di fenomeni in cui l'illuminazione si produce anche quando l'oggetto e la sorgente luminosa non si trovano l'uno di fronte all'altra. Inoltre, questi fenomeni sono tali che non possono essere spiegati né con la riflessione né con la rifrazione dei raggi luminosi. Tra questi fenomeni figura l'aurora, nel corso della quale una parte della superficie della Terra è illuminata prima che il Sole sorga, così come l'apparizione di una debole luce negli ambienti che si trovano di fronte a un muro illuminato. Dal momento che in questi casi l'illuminazione non si produce secondo direzioni privilegiate, Ibn al-Hayṯam giunge alla conclusione che le parti illuminate dell'aria e del muro agiscono come gli oggetti luminosi in sé, ossia che la luce si propaga da ogni punto della loro superficie in tutte le direzioni. D'altronde, l'autore si servirà di questa descrizione per spiegare la propagazione dei colori, considerati indipendenti dalla luce.
L'origine sperimentale del concetto di 'luce seconda' che nell'Ottica e nella Maqāla fī 'l-ḍaw᾽ è in parte occultata dalla struttura sintetica dell'esposizione, si rivela nella Maqāla fī ḍaw᾽ al-qamar grazie al modo in cui Ibn al-Hayṯam affronta questo tema. L'impossibilità di classificare la luce della Luna nelle categorie della 'luce riflessa' e della 'luce rifratta' ‒ le sole ammesse dall'analogia tra luce e flusso visivo e studiate dall'ottica geometrica ‒ richiede la creazione di una nuova categoria di luce. Ibn al-Hayṯam solleva questo problema nella cornice della dicotomia 'luce riflessa-luce rifratta', giungendo alla conclusione che soltanto trascendendo questa cornice si può risolvere in modo soddisfacente la questione. Egli s'interroga sul modo in cui la luce della Luna si diffonde verso la Terra: "per riflessione, come accade nei corpi levigati, e come crediamo ritengano i matematici? Per penetrazione, come accade nei corpi trasparenti?". Ora, benché questi due modi di diffusione della luce siano "proprietà di tutti i corpi in grado di trasmettere la luce, che non sono certamente luminosi in sé", egli si chiede se non ne esista un terzo "ben distinto dagli altri". Dopo aver eseguito un esame sperimentale e matematico di cui parleremo più avanti, Ibn al-Hayṯam finisce per rispondere in senso affermativo a questo interrogativo, dimostrando che la luce della Luna è una luce seconda, nel senso che essa emana da ogni punto della superficie di un corpo non luminoso in tutte le direzioni.
La distinzione tra luce prima e seconda non sarà mantenuta a lungo. A eccezione di alcune differenze derivanti dalle loro proprietà osservabili (quali per esempio la debolezza della luce seconda rispetto alla prima), queste due specie di luce sono soggette alle stesse leggi di propagazione, di riflessione e di rifrazione. Così, l'indipendenza della luce dalla sua sorgente è assicurata, ma su un piano più generale.
La luce seconda quindi è quella che emana da ogni punto della superficie di un corpo illuminato seguendo linee rette e in tutte le direzioni. È in questi termini che Ibn al-Hayṯam spesso definisce la luce seconda. A volte, tuttavia, egli ne parla impiegando un linguaggio un po' ostico ma più preciso, affermando che la luce seconda è quella che emana dalla 'luce accidentale', o che emana da ogni punto della luce che si insedia in un corpo dopo che quest'ultimo è stato illuminato dai raggi provenienti da una sorgente luminosa. Ponendo l'accento sulla luce ricevuta dal corpo illuminato e non sul corpo stesso, egli stabilisce un legame tra la luce e le proprietà del corpo su cui essa cade.
A prescindere dai corpi luminosi in sé, vale a dire il Sole, il fuoco (cioè ogni sorgente terrestre di luce) e le stelle, gli altri corpi si dividono in trasparenti e opachi, una divisione basata sul modo in cui essi agiscono in relazione alla luce. Tuttavia, questi due tipi di corpi partecipano della stessa proprietà, la facoltà o capacità di recepire la luce. Essi si differenziano per il modo in cui ciascuno trasmette la luce recepita: "i corpi trasparenti possono in effetti essere attraversati dalla luce interamente o parzialmente" (Maqāla fī 'l-ḍaw᾽, p. 210), mentre "l'assenza di questa capacità [...] distingue i corpi opachi dai corpi trasparenti" (ibidem). L'esistenza di una capacità ricettiva della luce sia nei corpi trasparenti sia in quelli opachi è dimostrata dal fatto che la luce 'si fissa' o 'permane' tanto negli uni quanto negli altri, in funzione dell'opacità che esiste in loro. Nel caso dei corpi opachi, questa proprietà si manifesta attraverso la luce che si vede sulle loro superfici, mentre nei corpi trasparenti, essa si manifesta quando un "corpo opaco ne attraversa uno trasparente, ovunque si trovi il loro punto di intersezione". In seguito a questo attraversamento "la luce apparirà sul corpo opaco. Questa proprietà si rivela nel caso in cui il corpo trasparente è l'aria o l'acqua" (ibidem).
È grazie al permanere della luce in un corpo opaco che questo giunge a essere dotato di 'luce accidentale', diviene cioè sorgente di luce seconda (come vedremo più avanti, questa idea influenzerà le esperienze condotte da Ibn al-Hayṯam sulla luce). L'impiego dell'espressione 'capacità ricettiva' ‒ del resto attestata nella letteratura filosofica dell'epoca ‒ non deve indurre a trascurare la singolarità di questa idea. Da un lato, infatti, il concetto di attualizzazione del mezzo trasparente, che occupa una posizione centrale nell'analisi filosofica della luce, è completamente assente, dall'altro lato il ruolo svolto da questo mezzo non può essere ridotto a quello di una semplice 'strada' che permette il transito della luce, o, per essere più precisi, che consente alla luce di manifestarsi sul corpo che ha di fronte. In effetti, con queste distinzioni Ibn al-Hayṯam si propone di trattare la luce come un oggetto reale, come qualcosa che si muove, che si insedia nei corpi, che è presente ovunque lungo il suo percorso e la cui presenza può essere dimostrata per mezzo dell'esperienza. Non è attraverso l'approfondimento del problema dell'essenza della luce che Ibn al-Hayṯam giunge a certificare la realtà fisica dell'oggetto della sua ricerca; al contrario, è evitando questo genere di discussioni che egli riesce a conseguire un tale obiettivo.
Inoltre, nella sua analisi la trasparenza stessa registra un cambiamento di status: essa non è più un concetto puramente teorico, ma una proprietà che risiede in alcuni corpi e che è sempre mescolata all'opacità. Non esistono quindi corpi assolutamente trasparenti, ma più o meno trasparenti. Come ogni proprietà fisica, la trasparenza ha un certo limite che coincide con quello del corpo del cielo. Così, Ibn al-Hayṯam giunge a stabilire un compromesso tra la tesi aristotelica secondo cui il corpo del cielo è l'oggetto più trasparente che possa esistere e la tesi sostenuta da Ibn Sahl, il quale, attraverso un argomento puramente matematico, dimostra che è possibile immaginare una trasparenza superiore a quella del cielo.
La ricerca di Ibn al-Hayṯam sui raggi è ispirata dalla stessa preoccupazione che lo aveva condotto a formulare la tesi sulla trasparenza del cielo, vale a dire dal riconoscimento della necessità di distinguere l'oggetto matematico dall'oggetto fisico. Ibn al-Hayṯam applica questa idea, già presente nella confutazione del concetto di raggio euclideo di al-Kindī (v. sopra), alla propagazione della luce.
Sebbene egli parli della propagazione della luce a partire da ogni punto degli oggetti luminosi o illuminati, ciò che emette la luce non è un punto nel senso geometrico del termine. Nell'Ottica, dopo aver dimostrato che la luce emana da ogni parte, per quanto piccola, del corpo luminoso, egli afferma che ciò che è vero per le parti sensibili di un corpo lo è anche per le sue parti invisibili. La luce, quindi, è emessa da ogni parte, per quanto piccola, dell'oggetto luminoso. Un tale corpo, infatti, "non è un insieme di parti", ma un corpo "unico e continuo". Inoltre, poiché il corpo luminoso ha una sola natura, le sue parti partecipano della stessa natura del suo insieme. Ora, nonostante la sua confutazione della concezione atomistica dei corpi e la sua insistenza sulla infinita divisibilità delle grandezze, Ibn al-Hayṯam ritiene che i corpi naturali dotati di certe proprietà non possano essere divisi oltre un determinato limite. Le parti di un corpo, infatti, conservano le loro proprietà soltanto se non sono troppo piccole. Egli quindi conclude che esiste una "parte più piccola del corpo" in grado di emettere la luce, la quale, tuttavia, è completamente differente dalla luce più debole che si possa vedere. Quest'ultima, infatti, dipende da molti fattori e, in particolare, dall'acutezza della visione, dall'intensità della luce ambientale e così via.
L'idea dell'esistenza dei minima naturalia, ovvero delle più piccole parti di un corpo che potrebbero presentare una certa 'forma', risale ad Aristotele. Nelle opere di quest'ultimo troviamo tuttavia due tesi differenti: in alcuni casi, egli lascia intendere che i corpi fisici siano divisibili all'infinito, come i corpi in quanto grandezze, mentre in altri opera una distinzione tra le grandezze, che sono divisibili all'infinito, e i corpi fisici, che possono essere divisi solamente fino a un certo limite, oltre il quale il corpo perderebbe le sue forme. La prima tesi si iscrive nel progetto "di presentare la scienza naturale come una disciplina scientifica fondata sulla solida base della scienza della geometria" (Glasner 2001, p. 12), mentre la tesi dell'esistenza dei minima naturalia rientra in un periodo più tardo dello sviluppo della sua concezione della fisica.
In Ibn al-Hayṯam, invece, è l'idea dell'esistenza di un elemento minimo dei corpi in grado di emettere la luce che assicura un solido supporto all'ottica geometrica. A questa idea, infatti, corrisponde quella della 'più piccola luce' e quest'ultima si risolve nella definizione del raggio in senso fisico. Nel Libro IV dell'Ottica tale idea trova espressione in un argomento: dopo aver constatato che la luce si propaga soltanto in un corpo e che ogni corpo, anche se molto sottile, presenta sempre una certa larghezza, il ragionamento di Ibn al-Hayṯam sposta l'accento sulla luce stessa, concludendo che anche 'la più piccola luce' presenta una certa larghezza. Questa 'più piccola luce' è tale che "non può esistere luce più sottile della sua considerata isolatamente (iḏā kāna munfaridan)" ed "essa si propaga (yamtaddu) secondo la linea che si può immaginare (yutawahhamu) al suo centro nel senso della lunghezza" (al-Fārisī, Tanqīḥ al-manāẓir, I, 2, 5). La 'più piccola luce' s'identifica dunque con il raggio nel senso fisico del termine ‒ se la si dividesse in due nel senso della lunghezza, infatti, essa perderebbe la sua qualità di luce ‒ mentre il raggio in senso geometrico è la linea retta che le è associata, cioè la retta che divide in due questa luce. Ciò non equivale a dire che tale linea è la sola che si possa immaginare in questa parte minima della luce; al contrario, si possono immaginare altre rette parallele a essa o che la intersecano. Fin quando si ha a che fare con un solo elemento minimo della luce, queste altre rette non indicano le direzioni della propagazione della luce. Ciò non deve indurre a pensare che a ogni luce minima di un corpo corrisponda un solo raggio geometrico, una conclusione che avrebbe avuto conseguenze gravissime per l'ottica geometrica (un numero finito di raggi corrisponderebbe, infatti, a un numero finito di punti del corpo). Ibn al-Hayṯam evita di cadere nella trappola del finitismo impiegando un argomento geniale.
In termini formali, questo argomento (presentato una sola volta in modo piuttosto sommario nella cornice della riflessione sulla luce) può essere formulato nel seguente modo: benché a ogni parte minima della luce si possa associare una sola retta, dal momento che il corpo non è l'insieme di queste parti minime (vale a dire non è composto da atomi) ma un tutto continuo, una parte due volte più larga di quella minima è dotata ugualmente della forma della luce, cosicché la sua luce segue non solo le due linee che dividono in due ciascuna delle sue parti, ma anche la linea che divide in due il loro insieme. Dunque, si avranno almeno tre direzioni della propagazione della luce a partire da una parte due volte più larga della parte minima. Inoltre, se si immaginasse una quarta retta, non parallela alle prime tre, ma che attraversa la parte due volte più larga della parte minima, in modo da essere "circondata da ogni lato da una luce non più sottile della luce più sottile" (ibidem, p. 373), allora anche questa retta indicherebbe una direzione della propagazione della luce, poiché la parte nella quale essa si trova sarebbe a sua volta dotata della forma della luce. Ora, il numero di tali rette è infinito ed esse si propagano in direzioni non tutte parallele tra loro. Estendendo questo argomento a tutto il corpo, si giunge con grande naturalezza al concetto di propagazione della luce a partire da ogni punto di un corpo in tutte le direzioni e secondo linee rette. Nella fig. 5 questo argomento è illustrato in modo generico: a indica la larghezza della parte più piccola della luce, le linee più marcate mostrano alcune delle direzioni che la luce può seguire nella sua propagazione a partire da un corpo tre volte più largo del corpo elementare, mentre le linee tratteggiate indicano alcune delle direzioni che la luce non può seguire, perché non sono "circondate da tutti i lati da una luce non più sottile della luce più sottile".
La 'più piccola luce' è un'entità teorica; di essa sappiamo soltanto che è estremamente piccola e quindi invisibile. Tuttavia, a questa entità teorica corrispondono alcune entità osservabili come, per esempio, i raggi che passano attraverso gli orifizi, la cui larghezza diminuisce in misura direttamente proporzionale alla strettezza degli orifizi. Ciò significa che il raggio ha un limite oltre il quale non può passare attraverso un orifizio. Dunque Ibn al-Hayṯam non prende in considerazione la diffrazione della luce. I raggi abbastanza grandi per poter passare attraverso un orifizio corrispondono in effetti a molti punti del corpo e, di conseguenza, non sono tutti paralleli tra loro. È per questo che, dopo aver attraversato un orifizio, per quanto stretto esso possa essere, i raggi divergono sempre tra loro, disponendosi in forma di due facce di una superficie conica, il cui vertice si trova in corrispondenza dell'orifizio; in caso contrario il raggio non può passare attraverso l'orifizio. Così, la divergenza della luce, uno dei fenomeni che dimostravano la sua propagazione rettilinea, creava una serie di difficoltà sul piano sperimentale: come ottenere un fascio di luce corrispondente al raggio nel senso geometrico del termine?
La formulazione dell'argomento di Ibn al-Hayṯam sottolinea la distanza che lo divideva dalla concezione atomista della luce e della sua propagazione. È grazie a questo argomento, infatti, che egli giunge a mantenere la continuità della luce, giustificando, al tempo stesso, la sua propagazione rettilinea. In seguito, Ibn al-Hayṯam non presenterà più la luce come una forma ma si limiterà a parlare semplicemente di luce. Come abbiamo visto, Ibn al-Hayṯam passa direttamente dall'esistenza della parte minima del corpo a quella della parte minima della luce. D'ora in poi parlerà solamente in termini di quest'ultima, della sua propagazione e delle sue proprietà cinematiche e dinamiche, senza approfondire i problemi che l'attribuzione di queste proprietà a una forma potrebbe sollevare.
In tal modo, evitando di affrontare una discussione filosofica sullo status ontologico della luce, Ibn al-Hayṯam giunge ad assicurare una certa realtà, per non dire una sorta di esistenza materiale, alla propagazione. Non è un caso, infatti, che nel Libro IV dell'Ottica questa giustificazione della luce preceda la spiegazione della riflessione di questa attraverso un'analogia meccanica. Basandosi sulle esperienze compiute con una palla che, lasciata cadere su una superficie, balza in direzione contraria, Ibn al-Hayṯam divide il 'movimento' della luce in due componenti, una verticale e una orizzontale, ottenendo l'uguaglianza degli angoli di incidenza e di riflessione.
La materialità della luce, nel senso della sua esistenza in ogni mezzo, così come la sua azione e il suo movimento si prestavano, del resto, alla sperimentazione; la sua dimostrazione sarà uno degli obiettivi delle esperienze di Ibn al-Hayṯam.
L'elaborazione del metodo
Il Libro I dell'Ottica, nel quale sono prese in esame le proprietà più generali della luce e della visione, è organizzato in base a un piano sistematico. L'autore fa precedere l'esame di ciascun problema ‒ visione rettilinea, propagazione rettilinea della luce, differenti tipi di luce, condizioni generali della propagazione della luce e della visione ‒ dalla presentazione di una serie di osservazioni. Queste ultime dimostrano la generalità del fenomeno in questione soltanto quando sono ripetute in diverse condizioni. È solamente al termine di questo procedimento induttivo, condotto su 'tutto ciò che è visibile e in tutti i momenti', che si raggiunge la certezza di essere in presenza di una regolarità "universale (muṭṭarida) che non cambia (lā taḫtalifu) e non varia (wa-lā tataġayyaru)" (Kitāb al-Manāẓir, I, 2, 5). Nell'accento posto sull'invarianza delle regolarità si può individuare un legame con la teoria della scienza esposta nella Maqāla fī 'l-ma῾lūmāt: è attraverso l'induzione che l'oggetto della nostra conoscenza si eleva al rango di 'oggetto conosciuto' e che l'opinione che noi abbiamo di esso diviene 'scienza'. L'induzione (al-istiqrā᾽) è quindi un mezzo di dimostrazione. Inoltre, nel caso in cui l'oggetto dell'indagine non sia suscettibile di rappresentazione geometrica, l'induzione è il solo mezzo di dimostrazione come, per esempio, nel caso delle condizioni generali della visione. Grazie alla dimostrazione induttiva, queste condizioni, che trovano espressione in un linguaggio non matematico, si rivelano non meno invariabili delle leggi geometriche della propagazione della luce, benché per ottenere queste ultime sia necessario ricorrere a un altro mezzo di dimostrazione, ossia la sperimentazione.
L'induzione, infatti, in alcune occasioni non raggiunge il suo obiettivo se non è accompagnata da un'altra operazione che Ibn al-Haytam chiama al-i῾tibār, la sperimentazione. Quest'ultima è un'osservazione, costantemente ripetuta su diversi oggetti e in differenti condizioni, che spesso si basa sull'uso di uno strumento. La sperimentazione serve a isolare un fenomeno che, in condizioni normali, non può essere colto dalla vista o a studiarne le proprietà che abitualmente sfuggono ai sensi. Essa dunque interviene nei casi in cui ci si trova a dover esaminare le proprietà geometriche della luce. Il campo d'applicazione della sperimentazione è molto diversificato e include sia l'esame del tracciato rettilineo dei raggi visivi attraverso il regolo, sia analisi molto più ricercate condotte con dispositivi sperimentali progettati e fabbricati.
In tal modo, l'induzione è sempre un elemento indispensabile della sperimentazione, nel senso che non bisogna mai basarsi su una sola esperienza o su esperienze condotte solamente in date condizioni. L'induzione, dunque, si distingue dalla semplice osservazione per il fatto di dover essere ripetuta anche in condizioni diverse e la sperimentazione si distingue a sua volta dall'induzione per l'intervento di uno strumento.
In ogni caso, Ibn al-Hayṯam non ritiene che la sperimentazione presupponga necessariamente l'uso di uno strumento: in alcune occasioni, infatti, egli impiega il termine i῾tibār in riferimento a un fenomeno naturale verificatosi senza l'intervento di un dispositivo sperimentale. Per esempio, per dimostrare che la luce del Sole proviene da tutta la sua superficie e non solo dal suo centro egli evoca, tra gli altri, il fenomeno in base al quale il Sole illumina la Terra anche prima di sorgere, quando il suo centro è ancora al di sotto dell'orizzonte. Ibn al-Hayṯam non esita a impiegare il termine i῾tibār in riferimento a questo fenomeno che potrebbe essere considerato un semplice fatto osservabile. Benché egli a volte impieghi l'infinito i῾tibār e i suoi derivati nelle loro accezioni comuni, sembra che nei casi analoghi a quello precedentemente menzionato questo termine mantenga sempre il suo senso tecnico. La sperimentazione, infatti, si distingue dall'osservazione per il fatto di offrire la possibilità di isolare un fenomeno, di vederlo sotto aspetti diversi o sotto un aspetto inconsueto. Ciò accade quando il cambiamento delle condizioni, che introduce un elemento di controllo e che spesso è ottenuto con l'aiuto di un dispositivo sperimentale, si produce nella Natura stessa. Menzioneremo un altro esempio: l'azione dell'eclisse solare è quella di occultare una parte del Sole. Questo fenomeno, quindi, produce esattamente lo stesso effetto che si può ottenere impiegando uno schermo in grado di occultare una parte del Sole; anche l'eclisse, dunque, serve a dimostrare che la luce del Sole proviene da tutta la sua superficie. È per questo che Ibn al-Hayṯam definisce 'esperienza' l'osservazione di questo aspetto dell'eclisse solare.
L'induzione e la sperimentazione possono essere impiegate indipendentemente da altri procedimenti come veri e propri mezzi di dimostrazione. In altri termini, la loro funzione non si riduce né a una semplice verifica di ciò che è già conosciuto, o persino dimostrato, attraverso altri procedimenti, né, come nel caso delle osservazioni astronomiche, alla produzione di risultati numerici.
Tuttavia, i ragionamenti sperimentali di Ibn al-Hayṯam non si sviluppano in un vuoto fisico. Egli non si interessa all'induzione dei fenomeni in quanto tali e impiega questo procedimento solamente in vista di problemi ben definiti. Inoltre, Ibn al-Hayṯam spesso giunge a delimitare il campo delle osservazioni possibili (v. oltre) ricorrendo a una serie di principî di ordine fisico (nel significato allora attribuito a questo termine). Il mondo sensibile e, di conseguenza, le esperienze a cui esso può essere sottoposto, sono già ordinati da tali principî. Questi ultimi, però, non sono mai dello stesso ordine delle regolarità di cui si occupano le indagini di Ibn al-Hayṯam. In altri termini, l'autore non adotta mai un principio dell'ottica senza averlo prima sottoposto a una dimostrazione induttiva o sperimentale. Al contrario, egli accoglie senza alcuna dimostrazione i principî che riguardano le proprietà più generali dei corpi, ossia la continuità, l'omogeneità dei corpi considerati semplici e la loro sfericità.
Le dimostrazioni sperimentali sono effettivamente tali anche perché nel corso del loro svolgimento Ibn al-Hayṯam non ricorre mai ad argomenti di carattere matematico. Sotto questo aspetto le sue dimostrazioni si distinguono nettamente da quelle di al-Kindī, in cui l'esperienza non è che un punto di partenza e l'argomentazione raggiunge il suo obiettivo soltanto attraverso una dimostrazione di carattere matematico. Per Ibn al-Hayṯam, i campi d'applicazione di questi due tipi di dimostrazione sono ben distinti: la dimostrazione sperimentale serve a stabilire le proprietà generali della propagazione della luce, mentre il ruolo della dimostrazione matematica si riduce a quello di giustificare la confutazione di tesi già avanzate, la cui falsità può essere messa in luce solamente da questo genere di dimostrazione.
Ciononostante, il modo in cui Ibn al-Hayṯam sviluppa le sue dimostrazioni matematiche per confutare le tesi che erano in competizione con le sue, necessita a volte di costruzioni geometriche e della messa in scena di situazioni immaginarie, grazie alle quali esse si avvicinano, discostandosi al tempo stesso dalla sperimentazione nel senso ordinario del termine, a un altro genere di esperienza: l'esperimento concettuale. Ma questo è un punto sul quale torneremo in seguito.
Tuttavia, la netta distinzione tra la dimostrazione matematica e quella sperimentale non impedisce a Ibn al-Hayṯam di ricorrere alla matematica nell'ideazione dei suoi dispositivi sperimentali. Al contrario, è proprio per questo che i suoi dispositivi si distinguono dai semplici strumenti d'osservazione.
La dimostrazione sperimentale dei principî dell'ottica
La novità del modo di procedere di Ibn al-Hayṯam non riguarda soltanto l'ampio ricorso alla sperimentazione, ma anche e soprattutto il contesto in cui quest'ultima fa la sua comparsa. Nel Libro I dell'Ottica è riservato un ampio spazio alla dimostrazione sperimentale della proprietà fondamentale della luce, vale a dire alla sua propagazione rettilinea. Attraverso una serie di esperienze, egli dimostra che la visione si produce lungo linee rette e che la luce, in tutte le sue manifestazioni, si propaga secondo linee rette. Il modo di procedere di Ibn al-Hayṯam rivela tutta la sua importanza solamente se raffrontato a quello dei suoi predecessori.
L'Ottica di Euclide si apre con una serie di enunciati che sono effettivamente ipotesi o postulati. Il primo riguarda il principio della visione rettilinea: i raggi provenienti dall'occhio si propagano in linea retta. Mentre nel terzo e nel quarto si legge che ciò che si vede è ciò su cui cadono i raggi visivi, e ciò che non si vede è ciò su cui i raggi visivi non cadono.
A prescindere dal loro status, tali enunciati compaiono all'inizio del trattato perché non rientrano nel genere di problemi preso in esame nel testo. Ciò non è sorprendente: nell'Ottica euclidea, infatti, sono usati soltanto procedimenti geometrici e questi enunciati non rientrano nel campo della geometria. Questo produce un duplice effetto. Da un lato, nonostante la menzione delle 'linee rette generate dall'occhio' che implica un'indubbia inclinazione per la teoria emissionistica della visione, l'autore garantisce la neutralità dei risultati ottenuti nel testo nei confronti di questa o di quella teoria della visione. Dall'altro, questa scelta metodologica implica (o forse presuppone) una sorta di divisione del lavoro: l'ottica, nel senso euclideo del termine, rimane una scienza geometrica, mentre tutti gli altri aspetti della visione sono rinviati ad altre scienze. È per questo che nell'Ottica di Euclide è escluso il ricorso a qualsiasi tipo di esame sperimentale.
Con l'Ottica di Tolomeo la situazione si complica. Dal momento che il Libro I di questo trattato era già andato perduto quando l'opera era stata tradotta in arabo, gli storici hanno tentato di ricostruire il suo contenuto a partire da alcune antiche testimonianze giunte fino a noi. Sappiamo, dallo stesso Tolomeo, che questo libro aveva come oggetto "tutto ciò che permette di legare tra loro le proprietà della vista e della luce, i motivi per cui esse rispondono le une alle altre, le loro mutue similitudini, ciò che appartiene a ciascuna come differenza specifica e i loro accidenti" (Optica, p. 11). Tale libro si sarebbe quindi aperto con l'esame della comune natura della luce e della vista per poi proseguire con l'analisi delle loro proprietà comuni. Queste ultime naturalmente includevano la propagazione in linea retta. Tutto ciò che sappiamo a questo riguardo è che l'autore "sembra essersi sforzato di dimostrarla in modo sperimentale" (Simon 1988, p. 85). Non siamo in grado di stabilire se si trattasse di un esame sperimentale della propagazione rettilinea della luce, in seguito generalizzato fino a comprendere la visione, analogo a quello condotto più tardi da al-Kindī, o di un esame della visione da cui dedurre la propagazione rettilinea della luce o, ancora, di due serie indipendenti di esperienze che avrebbero consentito a Tolomeo di giungere alla dimostrazione della propagazione rettilinea sia della luce sia della visione.
In assenza di altre informazioni, possiamo tentare di chiarire la questione soltanto confrontando i casi in cui i due autori, Tolomeo e Ibn al-Hayṯam, ricorrono, ognuno all'interno del proprio quadro concettuale, all'esperienza. Ciò accade soprattutto nelle loro rispettive analisi della riflessione e della rifrazione. In questi casi gli esami sperimentali di Ibn al-Hayṯam svolgono un duplice ruolo: quello di dimostrare le leggi che governano la riflessione e la rifrazione della luce che cade su una superficie levigata o che passa da un mezzo trasparente a un altro e, in secondo luogo, quello di dimostrare la sua propagazione rettilinea dopo essere stata soggetta alla riflessione o alla rifrazione. In queste esperienze quindi, indipendentemente dagli scopi che con esse intendeva conseguire, Ibn al-Hayṯam non dimentica mai di verificare la propagazione rettilinea della luce; nelle sue esperienze, invece, Tolomeo si propone solamente di verificare i principî della formazione dell'immagine negli specchi e della posizione dell'oggetto visto attraverso un mezzo trasparente. Ibn al-Hayṯam approfitta di tutte le occasioni per dimostrare la propagazione rettilinea della luce, mentre Tolomeo la considera un dato acquisito.
Le esperienze di tipo tolemaico, condotte sulla visione, però, si distinguono da quelle di Ibn al-Hayṯam, che hanno come oggetto la luce, per una caratteristica molto più significativa. Nelle esperienze di Tolomeo, l'occhio si trova sin dall'inizio in una posizione privilegiata, ossia a una delle estremità del percorso del raggio visivo, per ottenere il quale è quindi sufficiente dirigere lo sguardo, molto probabilmente attraverso una diottra (uno strumento per la determinazione della visuale), verso un punto dell'oggetto. Nelle esperienze di Ibn al-Hayṯam, che studia il percorso ottico ‒ ovvero il tragitto della luce che passa da un punto dell'oggetto a un punto dello spazio e che può, lungo il suo percorso, essere soggetta alla riflessione o alla rifrazione ‒, l'occhio può trovarsi in qualsiasi punto idoneo dello spazio. Il problema fondamentale, dunque, è quello di 'isolare' un fascio di luce: un obiettivo che pone seri problemi, sia sul piano tecnico sia su quello teorico. Inoltre, le esperienze di Tolomeo hanno come oggetto soltanto i raggi visivi generati dall'occhio, mentre quelle di Ibn al-Hayṯam riguardano un'ampia gamma di sorgenti luminose: il Sole, la Luna, alcuni astri, il fuoco e soprattutto le sorgenti di 'luce seconda'. Quest'ultima categoria include praticamente tutti gli oggetti terrestri e, come vedremo più tardi, anche alcuni celesti.
Per avere un'idea di tutte queste differenze si può comparare l'unica esperienza presentata nel Libro I dell'Ottica di Ibn al-Hayṯam, che è dedicato alla visione, a quelle descritte negli altri libri. In questo caso il dispositivo sperimentale è costituito da un regolo sul quale è tracciata una linea retta e da un tubo di piccolo diametro (non più grande dell'orbita dell'occhio) che è incollato al regolo lungo il tracciato della linea. Avvicinando l'occhio a una delle estremità della linea, si vede, lungo la prosecuzione della linea, la parte dell'oggetto che corrisponde al diametro del tubo. Coprendo una parte della base del tubo, la parte visibile dell'oggetto si rimpicciolisce. Si può del resto verificare con un regolo il tracciato rettilineo della linea che unisce ogni punto dell'oggetto all'occhio (ma Ibn al-Hayṯam non precisa le modalità di questa operazione. Ora, nel caso in cui il termine 'linea' designasse il confine tra la parte scura e la parte più chiara all'interno del tubo, l'autore avrebbe implicitamente fatto ricorso alla luce!). Inoltre, coprendo tutta la base del tubo, la parte visibile dell'oggetto scompare completamente. Dal momento che in tale caso ogni altra linea che unisce l'occhio a questa parte dell'oggetto non è retta, si può concludere che la visione non si produce se non in linea retta.
Qualunque sia la sua origine, questo dispositivo non serve né a verificare la propagazione rettilinea della visione né, a maggior ragione, quella della luce. Il suo solo scopo è quello di stabilire un legame unico, in forma di una linea retta, tra ogni punto dell'oggetto e l'occhio. Questa sola esperienza potrebbe costituire la base dell'ottica, se quest'ultima fosse riducibile alla geometrizzazione della visione. Così, analizzando questa esperienza di Ibn al-Hayṯam, è possibile avere un'idea dell'esperienza tolemaica sulla propagazione rettilinea della luce.
La semplicità di questa esperienza e la complessità di quelle da cui è seguita dimostrano che la scelta della luce come oggetto di ricerca trasforma il concetto stesso di esperienza. Abbiamo già indicato, a proposito delle 'protoesperienze' di al-Kindī, la causa fondamentale di questa complessità: la propagazione della luce effettua un ritaglio nello spazio, che non ha equivalenti nella teoria dei raggi visivi. Altri elementi dipendono dal concetto stesso di propagazione della luce così come è definito da Ibn al-Hayṯam: la molteplicità dei tipi di luce, la molteplicità delle sorgenti e la divergenza della luce che proviene da un corpo esteso. Vi sono, però, anche alcuni elementi di carattere epistemologico: non bisogna limitarsi a dimostrare la tesi presentata, ma occorre anche invalidare le tesi contrarie. Allo stesso modo, la teoria della percezione sviluppata nel Libro III dell'Ottica presuppone una certa diffidenza nei confronti della semplice osservazione così come nei riguardi della generalizzazione di un risultato ottenuto in una situazione specifica. È per questo che nella successiva sezione analizzeremo queste teorie e soprattutto i loro rapporti con l'induzione e la sperimentazione.
Tuttavia, prima di affrontare tali questioni, bisogna sottolineare il fatto che le esperienze di Ibn al-Hayṯam non servono soltanto a dimostrare le proprietà della luce; esse svolgono anche un'altra funzione, quella di dimostrare l'esistenza stessa della luce nel mezzo in cui si propaga.
Le esperienze minuziosamente descritte nell'Ottica (I, 3, 3) servono al conseguimento di diversi scopi. Compiute sulle luci che fuoriescono da piccoli orifizi, esse dimostrano la propagazione rettilinea della luce, cioè l'esistenza di una corrispondenza unica tra ogni punto della sorgente luminosa e ogni punto dell'oggetto illuminato. Esse, però, hanno un obiettivo ancora più importante. Quando la luce, dopo essere fuoriuscita da un piccolo orifizio, attraversa una camera oscura o un'aria polverosa, il tracciato visibile è la luce stessa e non il colore dell'aria ambientale. Anche nel caso in cui la camera non sia immersa nell'oscurità oppure in cui non ci sia polvere nell'aria, si può sempre rendere manifesta la luce interponendo uno schermo tra la sorgente e l'oggetto visibile in molti punti del suo tragitto. Questo 'ritaglio' trasversale dimostra che in ogni punto del suo tragitto la luce non è meno reale che nei punti di partenza e di arrivo. Ciò che si vede sullo schermo è la luce stessa e non il colore dello schermo attualizzato dalla luce che su esso cade. Inoltre, spostando lo schermo all'interno dello spazio della camera, si può constatare che la luce esiste soltanto nei punti che si trovano lungo la linea retta che unisce l'orifizio a un punto dello schermo. Un'altra esperienza, condotta con l'aiuto di un regolo, dimostra che l'insieme dei punti così individuati costituisce simultaneamente una linea retta.
Non si può non rilevare il legame tra il procedimento sperimentale con cui Ibn al-Hayṯam dimostra l'esistenza della luce e i concetti teorici di cui abbiamo già parlato: la più piccola luce, la capacità ricettiva del mezzo intermedio e la fissazione della luce nel mezzo.
Le origini del procedimento sperimentale di Ibn al-Hayṯam
La dimostrazione s'impone quando manca l'evidenza. Anche le leggi generali dell'ottica non sono 'certe' in virtù della loro evidenza, ma perché, come afferma Ibn al-Hayṯam nella Maqāla fī ḍaw᾽ al-qamar sono "derivate (mustaḫraǧa) per dimostrazione e verificate (muṣaḥḥaḥa) per induzione" (Londra, BL, India office 734, f. 35r-v). Questa diffidenza nei confronti dell'evidenza e questa inclinazione per la ricerca delle prove possono essere attribuite a molte cause. In primo luogo, alla novità dell'oggetto della ricerca, da cui discendono due conseguenze: grazie al suo abbandono della nozione di raggio visivo, Ibn al-Hayṯam si trova ad affrontare un oggetto molto più complesso, privandosi al tempo stesso di tutte le prove ‒ sperimentali, filosofiche e storiche ‒ su cui si basava la teoria dei raggi visivi. Le leggi dell'ottica perdono la loro evidenza e sarà quindi necessario riformularle. È per questo che, nonostante il debito di Ibn al-Hayṯam nei confronti di Tolomeo, le esperienze di quest'ultimo servono al primo soltanto come punti di partenza. Inoltre, benché la tesi già avanzata sull'origine astronomica del concetto di esperienza in Ibn al-Hayṯam spieghi alcuni dei suoi aspetti storici, non si può ridurre il modo di procedere dell'autore alle pratiche degli astronomi. Essi, infatti, non sottoponevano mai alla prova dell'esperienza i fondamenti della loro scienza (il movimento sferico degli orbi), ma si limitavano a effettuare osservazioni destinate a indicare il valore numerico di un parametro.
In questa sezione tenteremo non tanto di effettuare un'indagine storica sull'origine del procedimento sperimentale di Ibn al-Hayṯam, quanto di studiare la sua teoria della percezione, che può gettare una nuova luce sulla sua concezione dell'induzione. Inoltre questa teoria, così come quella dell'errore da cui è accompagnata, conduce l'autore a elaborare una concezione della fallibilità della conoscenza. È nostra intenzione dimostrare che il raffronto tra questa concezione di Ibn al-Hayṯam e la sua teoria della scienza mette chiaramente in luce la necessità di individuare nuovi mezzi di dimostrazione, più efficaci della semplice osservazione.
Il Libro II dell'Ottica è dedicato alla teoria della percezione visiva. Benché quest'ultima sia enunciata nel linguaggio aristotelico e alcuni suoi elementi siano già presenti nell'opera di Tolomeo, le divergenze fra i tre autori sono così grandi da invalidare qualsiasi tentativo di presentare la teoria di Ibn al-Hayṯam come uno sviluppo della teoria di Aristotele o un rimaneggiamento, per quanto profondo, di quella del matematico alessandrino.
Tali divergenze sono riscontrabili sin dall'inizio dell'esposizione. Secondo Tolomeo sono visibili il corpo (o piuttosto, il volume), la grandezza, il colore, la figura, la posizione, il cambiamento e la quiete. A eccezione del colore, sensibile proprio della vista, questi visibili sono definiti da Aristotele 'sensibili comuni' perché non sono propri di alcun senso ma comuni a tutti (Aristotele, De anima, II, 6, 418a 18-20). Ibn al-Hayṯam porta il numero dei visibili a ventidue, fino a comprendere la luce, il colore, la distanza, la posizione, il volume, la forma, la figura, la grandezza, la separazione, la continuità, il numero, il movimento, la quiete, la rossezza, la levigatezza, la trasparenza, l'opacità, l'ombra, l'oscurità, la bellezza, la bruttezza e "la similarità e la differenza in ciascuna delle nozioni particolari considerate separatamente e in tutte le forme composte da nozioni particolari" (Kitāb al-Manāẓir, I, 3, 44). Inoltre, alcune categorie includono molte altre qualità che dipendono da esse.
Esaminiamo più attentamente questo elenco. Esso comprende non solo le qualità considerate visibili da Tolomeo, ma anche altre che Aristotele (De anima, II, 422b 25-30) e i suoi discepoli riconducono al tatto. In questa categoria troviamo non soltanto la rossezza e la levigatezza, che figurano tra le più importanti categorie di Ibn al-Hayṯam, ma anche l'aridità e l'umidità, che rientrano nelle categorie del movimento e della quiete perché sono percepite grazie a questi ultimi e che a tale titolo sono annoverate tra i 'visibili'. Altre, come per esempio la bellezza e la bruttezza, non figurano negli elenchi dei sensibili compilati nel periodo precedente a quello in cui visse Ibn al-Hayṯam. Inoltre, alla fine dell'elenco, troviamo la similarità e la differenza, che appaiono soltanto comparando tra loro almeno due qualità e che tuttavia non sono meno 'visibili' delle altre.
Così, trasferendo certe qualità connesse ad altri sensi e soprattutto a quello del tatto nel campo della visione, Ibn al-Hayṯam non solo sottolinea l'importanza della visione in ogni tipo di percezione, ma soprattutto mostra di voler sostituire la teoria della percezione modellata sul senso del tatto con una teoria che ha come punto di partenza la vista.
L'ampliamento del campo del visibile è accompagnato dalla svalutazione del ruolo che è svolto dalla sensazione nell'atto della visione e, più in generale, nella percezione. Naturalmente, la visione ha inizio con la ricezione delle 'forme' del colore e della luce del visibile, veicolate dai raggi provenienti dalla superficie esteriore del corpo che colpiscono il cristallino. Dal momento che ogni raggio proviene da un punto di questa superficie, è possibile stabilire una corrispondenza, punto per punto, tra le forme così recepite e i diversi punti del corpo visibile. Inoltre, l'ordine in base al quale tali forme si collocano sul cristallino corrisponde esattamente all'ordine in cui sono disposte sulla superficie del corpo visibile. Questo è quanto richiede la geometria della visione.
In seguito, le forme si trasmettono, conservando il loro ordine, all'interno dell'occhio, fino alla cavità del nervo comune, dove ha luogo la percezione immediata. A questo punto, è importante precisare che tali 'forme' sono soltanto quelle del 'colore' e della 'luce' del corpo visibile. Tra le ventidue qualità già menzionate, solamente queste ultime, infatti, sono percepite dalla "sensazione pura" (bi-muǧarrad al-ḥiss), mentre le altre sono colte o dall'"inferenza e dal discernimento" (bi-'l-qiyās wa-'l-tamyīz) o dal "riconoscimento" (bi- 'l-ma῾rifa) (Kitāb al-Manāẓir, II, 3, 40). Questa tripartizione non deve essere confusa con quella operata da Tolomeo, secondo cui vi sono cose viste effettivamente, cose viste 'immediatamente' e cose viste 'mediatamente'. Ora, anche alle espressioni 'forma del colore' e 'forma della luce' è attribuito un significato molto particolare: ciò che è percepito dalla sensazione pura non è questo o quel colore o questa o quella luce. L'oggetto della sensazione pura quindi non è che "il colore in quanto colore" e la "luce in quanto luce". Di conseguenza, "la quiddità del colore, così come il suo grado di intensità o di tenuità, sono percepiti solo dal discernimento, dall'inferenza e dal riconoscimento" (ibidem).
Così nella misura in cui è in questione ogni punto del visibile, il contenuto della percezione sensibile in senso proprio è estremamente limitato, perché le forme dei colori e delle luci così percepite sono prive di ogni determinazione. Ibn al-Hayṯam si discosta pertanto da Avicenna, secondo cui la semplice sensazione è in grado di percepire non solo i colori in tutta la loro ricchezza (e quindi non si limita alla percezione della 'forma del colore in quanto colore'), ma anche tutti i sensibili comuni, la cui percezione dipende da quella del colore (la grandezza, la figura, il numero e la posizione). Soltanto per quanto concerne il movimento e la quiete, l'atto della percezione non può compiersi al livello della sensazione pura, ma sembra richiedere l'intervento di una facoltà diversa dai sensi (quwwa ġayr al-ḥiss).
Secondo Ibn al-Hayṯam il lavoro di queste altre facoltà inizia molto presto, anche se esse, in realtà, più che 'facoltà' sono operazioni e funzioni mentali difficilmente identificabili con facoltà già riconosciute. Tali operazioni servono a completare il lavoro della sensazione pura. I termini impiegati da Ibn al-Hayṯam per designare queste operazioni complementari sono relativamente stabili, ma il loro significato tende a variare. Egli utilizza sempre i termini tamyīz, qiyās e ma῾rifa, il primo dei quali, tuttavia, è impiegato per designare sia la facoltà del discernimento (al-quwwa al-mumayyiza) sia un'operazione, come il secondo, qiyās; in alcuni casi indica invece il risultato del qiyās e in altri è sinonimo di induzione (istiqrā᾽), nel significato attribuito da Ibn al-Hayṯam a questa parola, quello di "percezione di tutte le nozioni contenute nella forma [dei colori e delle luci già percepite dalla sensazione pura]" (ibidem, 26). Il termine qiyās è impiegato da Ibn al-Hayṯam per indicare la comparazione, il ragionamento e, in particolare, il ragionamento sillogistico. Esso è sempre accompagnato da tamyīz, di cui spesso costituisce una fase, benché a volte il primo termine sia utilizzato come sinonimo del secondo. L'impiego del termine ma῾rifa è più univoco: esso designa l'atto di identificazione di un oggetto, sia come tale sia come membro di una classe di oggetti.
Se questa apparente ambiguità esiste, essa è determinata dall'impiego delle parole appena definite nel quadro di una teoria inedita della percezione, in cui si confondono i confini che in precedenza separavano i campi d'applicazione dei diversi concetti. Se il termine qiyās è inserito nel vocabolario della percezione per indicare sia la 'comparazione' sia il 'ragionamento' e, in particolare, il 'ragionamento sillogistico', è perché l'autore riteneva che ogni comparazione fosse accompagnata da un ragionamento, per quanto implicito, e che ogni ragionamento assumesse la forma di un sillogismo, anche quando una delle premesse non era esplicita.
Tenteremo di descrivere a grandi linee questa teoria. Quando un oggetto si presenta all'occhio, esso ne riceve le forme delle luci e dei colori che sono trasmesse alla cavità del nervo comune, dove la 'sensazione pura' le percepisce. Quindi interviene il discernimento, che deve desumere da queste forme tutte le informazioni che riguardano le altre venti qualità che potrebbero essere presenti nell'oggetto. I visibili, infatti, possono essere percepiti soltanto nei corpi e un corpo non reca mai una sola qualità visibile, ma una moltitudine di qualità visibili. Ciò che nel corpo si presenta alla vista non è quindi una sola qualità, ma piuttosto un insieme di qualità differenti e di diversi gradi della stessa qualità. Inoltre, queste 'nozioni', così come si presentano nel corpo, non sono separate. Di conseguenza, "ciascuna forma dei visibili è un insieme di molte nozioni particolari" (ibidem, 4, 1). Il ruolo del discernimento è quello di districare questo insieme, affinché "ogni nozione particolare" appaia separatamente dalle altre.
A tal fine la facoltà del discernimento esegue simultaneamente due operazioni. In primo luogo, essa opera un'induzione (istiqrā᾽) di ciò che è dato nell'atto della visione. In questo caso, Ibn al-Hayṯam impiega il termine istiqrā᾽ in un'accezione molto vicina al suo significato etimologico. Esso, infatti, indica non tanto una sorta di ragionamento quanto un'operazione preliminare a quest'ultimo, nel corso della quale l'occhio esamina esaustivamente l'oggetto dato, in modo da non lasciarsi sfuggire nulla. Ciò avviene sia al livello della sensazione pura sia a quello del discernimento.
In secondo luogo, effettua una serie di operazioni, riunite sotto il nome di qiyās, che consistono nel comparare le 'nozioni' che si trovano nel visibile e distinguerle; a tal fine, il discernimento ricorre sempre a una serie di sillogismi. Fino a che si è al livello del discernimento puro, tutte le operazioni sono eseguite a partire dai dati ricevuti da un solo e unico corpo: il discernimento puro, infatti, non ha termini di riferimento diversi dal corpo che l'occhio ha percepito. Tutti questi giudizi quindi sono sincronici e riguardano lo stesso oggetto. Il discernimento puro non può né identificare l'oggetto né classificarlo. La comparazione dunque è condotta soltanto tra le diverse forme fornite dallo stesso oggetto. Dal momento che non può identificare l'oggetto, il discernimento si limita a 'elencare' le relazioni esistenti tra tali forme. Molto probabilmente è questa la ragione per cui la differenza e la similitudine sono inserite tra le ventidue categorie dei visibili. Tuttavia, benché esaustive, queste 'liste di relazioni' sono molto confuse.
Quello che l'autore definisce 'discernimento puro' non può sussistere da solo. In effetti, esso è sempre aiutato nel suo lavoro da un'altra operazione, un tipo di qiyās che, in virtù del ruolo fondamentale svolto nella percezione, merita il nome di 'riconoscimento'. Tenteremo, a questo punto, di descriverne il funzionamento. Le relazioni individuate dal discernimento puro non cadono nell'oblio, ma sono memorizzate. Tutte le volte che l'occhio percepisce una forma, il discernimento stabilisce alcune relazioni di similitudine e di differenza non soltanto tra i diversi elementi da cui questa forma è costituita, ma anche tra essi e gli elementi costitutivi delle forme già percepite, che sono registrati nella memoria. L'intelletto riesce così a identificare un colore, una luce, una posizione e soprattutto un corpo a partire da una comparazione con le informazioni fornite da forme già percepite. Questa identificazione è operata sia a livello individuale sia a livello della specie: talvolta la visione identifica la forma in questione con qualcosa che ha già percepito, talvolta essa precisa la specie a cui appartiene.
Ora, al contrario del discernimento che percepisce i visibili in seguito a un esame esaustivo di ciò che si presenta alla vista, per identificare una forma il riconoscimento ha bisogno soltanto di alcuni indici (amārāt). Con questo termine Ibn al-Hayṯam intende designare le caratteristiche distintive del visibile, individuate in seguito alla ripetizione della stessa percezione o di percezioni simili. Questi indici non sono stabiliti una volta per tutte; al contrario, essi si formano nel corso del tempo, attraverso un processo di apprendimento durante il quale l'individuo fa sempre più affidamento sulla riserva di indici costituita e registrata nel corso della sua esperienza vissuta.
Le nostre percezioni si compiono quindi in larga misura attraverso il riconoscimento per mezzo di indici e sono, nella maggior parte dei casi, indirette. In effetti, ciò che è recepito al momento della sensazione, cioè prima dell'intervento del qiyās e del riconoscimento, si riduce agli aspetti inediti del visibile, vale a dire a ciò che in esso è singolare e per cui si distingue da visibili simili. Vi è dunque un doppio movimento: da un lato, il discernimento, preceduto dall'induzione, coglie l'oggetto nella sua singolarità; dall'altro, attraverso il qiyās e il riconoscimento, lo identifica con questo o quell'oggetto o lo sussume in un genere universale.
Tutto ciò va inteso in senso 'genetico': a eccezione di una piccolissima parte offerta immediatamente, al momento stesso cioè della visione, tutto il resto rimane da apprendere. Questo apprendimento ha luogo attraverso un processo graduale, a ogni fase del quale interviene una comparazione, un'inferenza o un ragionamento. Dal momento che tutte queste operazioni sono soggette a errore, la percezione è estremamente fallibile.
Lo sviluppo della teoria della percezione è accompagnato in Ibn al-Hayṯam da quello della teoria dell'errore. L'importanza di quest'ultima, che è esposta nel Libro III dell'Ottica, non va ricercata tanto nei dettagli relativi ai differenti tipi di errore che intervengono nella percezione di ognuna delle ventidue nozioni, quanto nella dottrina della fallibilità della percezione di cui costituisce la premessa.
Anche la 'sensazione pura', nonostante il suo limitato campo d'azione, non sfugge all'errore. Ciò che Ibn al-Hayṯam scrive a questo proposito è molto importante perché chiarisce tutta la sua teoria della percezione, soprattutto in relazione alla dottrina aristotelica dell'errore. Secondo Aristotele "i sensi non ingannano, almeno su quanto è loro proprio" (De sensu, 4, 442b 8; Metaphysica, IV, 1010b 2-3): la sensazione non è soggetta a errore perché i sensi non giudicano. Vi è quindi una netta divisione tra le facoltà principali dell'anima: poiché le sensazioni non ingannano, gli errori vanno sempre ascritti all'intelletto. Quest'ultimo interviene o nel corso dell'attribuzione, vale a dire a livello della formazione di un giudizio, o a livello del ragionamento sillogistico. Essendo un tutto semplice e indivisibile, la sensazione pura non è né un giudizio né un ragionamento: essa è dunque infallibile.
Ora, è proprio lo status privilegiato della sensazione pura, la partizione della percezione della cosa sentita in sensazione e interpretazione attraverso l'intelletto, che è messo in dubbio nella teoria della percezione di Ibn al-Hayṯam. Questa messa in discussione della sensazione pura può apparire sorprendente soprattutto perché, secondo l'autore, il discernimento delle nozioni contenute nel visibile ha inizio soltanto quando la sensazione pura ha terminato il suo lavoro e l'identificazione avviene solamente con il riconoscimento. Si delinea così una situazione paradossale, soprattutto perché gli errori della sensazione pura occupano uno spazio tutt'altro che trascurabile nella teoria della percezione di Ibn al-Hayṯam. Tenteremo di chiarire questa situazione.
Nell'Ottica (III, 5, 1-3) Ibn al-Hayṯam rivolge la sua attenzione al modo in cui l'errore può intervenire nella sensazione pura. Esporremo a grandi linee il suo argomento, evitando di entrare nei dettagli. La luce in quanto luce e il colore in quanto colore naturalmente non si identificano con questa o quella luce o con questo o quel colore. Ciò non significa, tuttavia, che questi ultimi non possano variare: essi, infatti, sono dotati almeno di una proprietà, quella di essere più o meno intensi. Quest'analisi non si arresta al livello dei puri concetti. Sia la luce sia il colore, infatti, presentano un certo contenuto sensoriale: la luce come tale corrisponde alla luminosità che accompagna ogni luce, mentre il colore come tale corrisponde a "una certa colorazione (talawwun) simile all'oscurità o all'ombra" (ibidem, II, 3, 54). La luce in quanto luce varia per intensità e il colore in quanto colore varia, da un lato, per intensità, a seconda della luce che l'accompagna e, dall'altro lato, in quanto qualità sensibile, tra due poli opposti.
Nonostante queste precisazioni, la sensazione pura non sarebbe mai accompagnata da un giudizio se ogni volta che si dirigesse lo sguardo verso un visibile si vedesse una sola luce oppure un solo colore. Sembra che Aristotele, così come i filosofi attivi nei periodi successivi, abbia preso in esame soltanto questo caso; a suo parere, l'oggetto della sensazione è un tutto indivisibile. È per questo che il Filosofo preferisce ignorare l'errore minimo in cui può incorrere un senso rivolgendosi ai suoi oggetti propri, assicurando così l'esistenza della sola base su cui elaborare la scienza senza cadere in una serie di trappole di cui era perfettamente cosciente: il ricorso alla conoscenza innata che non può essere appresa attraverso alcun processo logico, il regresso all'infinito, il circolo vizioso e l'assunzione di ipotesi non verificate come principî.
Nell'opera di Ibn al-Hayṯam questo errore minimo si amplifica. Come l'autore afferma in diverse occasioni, i visibili possono essere visti soltanto nei corpi e ogni corpo contiene non solo una moltitudine di visibili, ma anche molteplici gradi dello stesso visibile. Di conseguenza, ciò che si dà nella sensazione pura sono "le forme dei colori in quanto colori" e non "la forma del colore" del visibile nella sua totalità. Ogni raggio, infatti, si limita a trasportare la forma di un punto del corpo (o, più precisamente, della più piccola parte del corpo che può possedere una forma). Sostituendo l'idea aristotelica di un'immagine globale, equivalente al visibile nella sua totalità, con un'immagine puntuale in cui ogni punto corrisponde a un punto dell'oggetto, il colore del corpo visibile finisce per essere sostituito dai colori delle sue parti minime. Così, ciò che è percepito nella sensazione pura non è una superficie monocroma, ma piuttosto una copia in bianco e nero di una tela dipinta secondo la tecnica del puntinismo. Citiamo di seguito ciò che scrive a questo proposito Ibn al-Hayṯam: "Ora ciò che la vista percepisce del colore all'inizio del suo verificarsi nell'occhio è la colorazione. Ma la colorazione è una sorta di oscurità o, se il colore è tenue, è analoga all'ombra. Se l'oggetto ha differenti colori, allora la prima cosa che la vista percepirà della sua forma è un'oscurità le cui parti variano a seconda della intensità e della tenuità, come ombre che variano a seconda dell'intensità e della tenuità" (ibidem, II, 3, 54).
In tal modo, ciò che l'occhio percepisce nella sensazione pura si distingue per l'intensità e la tenuità delle sue parti, senza, tuttavia, identificarsi con questo o quel colore (o con questa o quella luce). Vi è dunque un elemento in cui il giudizio dipende dalla sensazione pura. Ogni giudizio è sempre accompagnato dalla possibilità di incorrere in un errore; anche la sensazione pura quindi può sbagliarsi.
Il trasferimento di una parte della facoltà di giudizio alla sensazione implica la critica della divisione tradizionale delle facoltà dell'anima in sensazioni, che non possono incorrere in errore, poiché la loro funzione si limita alla semplice ricezione di dati che non sono in alcun modo interpretati, e intelletto, che inizia il suo lavoro di interpretazione e giudizio soltanto quando la percezione si è conclusa. In Ibn al-Hayṯam l'interpretazione interviene molto presto nella percezione, tanto che questa divisione perde la sua ragione di essere. Al posto della bipartizione 'percezione-intelletto' troviamo, dunque, una divisione più complessa. Ciò che separa, all'interno di quest'ultima, la sensazione pura dall'inferenza, dal discernimento e dal riconoscimento, non è più la presenza o l'assenza del giudizio, ma il loro oggetto: la sensazione pura ha come oggetto il colore e la luce, mentre la percezione degli altri visibili avviene attraverso l'inferenza, il discernimento e il riconoscimento.
Come abbiamo visto Ibn al-Hayṯam scompone i concetti unitari di 'colore' e 'luce' di un corpo, per sostituirli con le luci e i colori delle sue parti, riuscendo così a identificare una delle principali fonti d'errore della percezione. A questo punto, dedicheremo la nostra attenzione alle altre fonti d'errore che dipendono dalle condizioni della visione. Perché essa abbia luogo, è necessario che "tra l'occhio e l'oggetto esista una certa distanza, […] che l'oggetto si trovi di fronte all'occhio; che l'oggetto sia luminoso, […] che l'oggetto sia dotato di una certa grandezza, […] che tra l'occhio e l'oggetto esista un mezzo trasparente e che il visibile sia dotato di una certa opacità" (ibidem, I, 8, 1).
Tutte queste condizioni sono stabilite attraverso l'osservazione e la sperimentazione. Per quanto riguarda la seconda condizione, Ibn al-Hayṯam dimostra attraverso una serie di argomenti sperimentali e dimostrativi che la visione assiale è più intensa di quella laterale e che la visione diviene sempre meno netta via via che ci si allontana dall'asse del cono dei raggi. Affinché l'occhio possa vedere nettamente un punto, è necessario che esso lo veda attraverso un raggio assiale. Poiché in ogni momento il raggio assiale proviene da un solo punto, per avere una visione netta dell'oggetto o, come direbbe Ibn al-Hayṯam, per 'indurre' queste proprietà, bisogna prendere visione di tutti i suoi punti attraverso l'asse del cono dei raggi. Dal momento che questo spostamento dell'asse sulla superficie esterna del corpo visibile esige un certo tempo, qualsiasi tipo di visione si svolge in un dato periodo di tempo.
A eccezione di quella relativa alla frontalità, che limita la visione netta a una sola direzione, queste condizioni implicano un intervallo. Tutte le qualità che intervengono in queste condizioni presentano infatti una certa 'latitudine' (῾arḍ). Invece di interessarsi ai due estremi di questa latitudine, Ibn al-Hayṯam dedica la sua attenzione alla parte centrale, cioè alle latitudini moderate (῾arḍ al-i ῾tidāl), perché a queste latitudini la visione è più veridica.
Ibn al-Hayṯam non definisce queste 'latitudini moderate' per la semplice, e importante, ragione che esse non sono prestabilite; inoltre, tali latitudini non sono indipendenti tra loro. In ogni condizione, la latitudine moderata è funzione del visibile e dunque dipende dalle altre condizioni. Esse in realtà si apprendono nel corso della vita, sin dalle prime esperienze dell'infanzia. La visione svolge un duplice ruolo in questo apprendimento: essa aiuta gli individui a costruirsi un mondo percettibile che, a sua volta, condiziona tutte le loro percezioni. Le condizioni della visione non sono tali nel senso trascendentale del termine: il loro ruolo non si riduce a quello di predisporre la scena in cui può avere luogo la visione. Non bisogna sorprendersi quindi nel constatare che tali condizioni non sono incluse nella geometria della visione: la loro natura, infatti, sfugge alla geometrizzazione. Esse, tuttavia, intervengono nell'atto della visione per definirne il grado di veridicità e (benché solo qualitativamente) il campo di validità, e soprattutto per precisarne le eventuali fonti di errore. Così, più ci si allontana da questi gradi moderati più si corre il rischio di cadere in errore (come nel caso in cui guardando da lontano una superficie curva la si percepisce come una superficie piatta).
Nell'opera di Ibn al-Hayṯam la teoria dell'errore è sviluppata sotto due aspetti: secondo i tipi di visione (attraverso la sensazione pura, attraverso il riconoscimento, ecc.) e secondo le condizioni in grado di introdurvi un errore. Abbiamo già parlato del tipo di errore che può intervenire nella sensazione pura. Gli errori che interessano le altre fasi della percezione visiva non possono che ampliare le due brecce aperte dalla teoria della visione, esposta da Ibn al-Hayṯam all'interno della teoria tradizionale della conoscenza. Ci limiteremo all'analisi degli errori della percezione per inferenza (qiyās) perché il modo in cui Ibn al-Hayṯam li descrive getta una nuova luce sul suo metodo sperimentale e soprattutto sulla posizione che in esso occupano l'induzione e la sperimentazione.
Il paragrafo 7 del Libro III dell'Ottica, in cui sono presi in esame gli errori che possono intervenire nell'inferenza, si apre con un discorso sulle origini di questo genere di errore. Con il termine 'inferenza', l'autore intende designare, come, del resto, in altre sezioni dell'Ottica, l'inferenza sillogistica. Queste origini sono riconducibili a due tipi: quelle che riguardano l'aspetto materiale del sillogismo e quelle che concernono il suo aspetto formale. Ibn al-Hayṯam afferma di non voler considerare il secondo tipo. La sua indagine quindi è incentrata sull'aspetto materiale del sillogismo, vale a dire sugli errori inerenti alle premesse di un sillogismo. Questi ultimi si dividono in tre tipi; i primi due ‒ assumere come vera una premessa falsa e considerare universale una premessa particolare ‒ dipendono dalla facoltà di giudizio, mentre il terzo dipende dal modo in cui si individuano le premesse (iktisāb al-muqaddamāt). Gli errori che interessano l'individuazione delle premesse attraverso la visione sono, a loro volta, riconducibili a due tipi: o la visione assume come vera una premessa falsa o assume come universale una premessa particolare.
Secondo Ibn al-Hayṯam questi due tipi di errore derivano da un'induzione incompleta. In ogni visibile, infatti, esistono due generi di nozioni (ma῾ānī): quelle manifeste e quelle non manifeste. Queste ultime, secondo l'autore, non sono le proprietà in via di principio invisibili, ma le particolarità dell'oggetto che si impongono all'attenzione soltanto in seguito a un accurato esame. Questo accurato esame, che ha come oggetto tutto il visibile e tutte le sue proprietà visibili, si chiama induzione.
Così, l'induzione fa la sua comparsa almeno in tre diverse occasioni e sotto tre differenti forme. Al livello della visione, essa consiste nel dirigere l'asse della visione verso 'ogni parte' del visibile, in modo da non lasciarsi sfuggire nulla. Al livello del discernimento, essa indica l'azione attraverso cui il discernimento distingue le informazioni trasmesse dalle forme dei colori e delle luci del visibile, discernendo tutte le nozioni in esso contenute, in modo da stabilire tutte le similitudini e le differenze esistenti tra queste nozioni. E infine, come vedremo più avanti, al livello della dimostrazione delle ipotesi, l'induzione indica l'esame di tutti i casi possibili che potrebbero presentarsi. Vi è quindi una corrispondenza tra il concetto di induzione come strumento destinato a ottenere una visione veridica e il concetto di induzione come mezzo di definizione delle ipotesi, corrispondenza tanto più precisa in quanto le ipotesi di cui si occupa Ibn al-Hayṯam riguardano le proprietà visibili degli oggetti.
Ibn al-Hayṯam crede nella possibilità dell'induzione esaustiva che, tuttavia, è limitata da alcune condizioni: "la vista non asserirà la definizione delle proprietà manifeste se è incapace di contemplare l'oggetto interamente, ed è cosciente di questa incapacità; tale definizione le apparirà dubbia e incerta" (ibidem, III, 7, 1). È per questo che nell'analisi degli errori, quelli causati dal fatto che le proprietà dell'oggetto visibile superano le latitudini moderate occupano una posizione di primo piano. Tuttavia, ciò non significa che questi fenomeni rimangano in ogni caso inaccessibili alla ricerca.
Nella sezione successiva vedremo come, combinando l'induzione nella sua terza accezione, la sperimentazione e la matematica, Ibn al-Hayṯam riesca a risolvere il problema della luce della Luna. Vedremo inoltre come questo successo sia determinato dalla sua riforma, grazie a cui la luce della Luna diviene non solo un oggetto autonomo di ricerca, ma anche uno strumento di ampliamento del campo della ricerca scientifica, che inizierà a includere argomenti che fino ad allora non erano mai stati sottoposti a indagini di carattere scientifico.
Esempio di una ricerca fisica
La luce della Luna: nascita di un problema
Il progetto di Ibn al-Hayṯam include non solo l'analisi di quasi tutti i problemi fino ad allora trattati all'interno delle differenti branche dell'ottica ‒ teoria della visione, teoria della combustione e rifrazione atmosferica ‒ che, tuttavia, sono studiati come manifestazioni della propagazione della luce, ma si estende anche ad altri problemi, trovando applicazione a fenomeni diversi e aprendo nuovi campi di ricerca. Si costituisce così un'area di indagine che si propone lo scopo di riesaminare i problemi che, a causa della mancanza di concetti appropriati o di mezzi idonei, non erano stati trattati in modo soddisfacente o a cui non era stata data una soluzione convincente. Tutti questi problemi riguardano i corpi celesti. Tra le opere di Ibn al-Hayṯam, infatti, figura un gruppo di trattati che potremmo definire di carattere ottico-cosmologico: Maqāla fī ḍaw᾽ al-qamar (Trattato sulla luce della Luna), Maqāla fī 'l-atar allaḏī fī waǧh al-qamar (Trattato sulla macchia che appare sulla Luna), Maqāla fī aḍwā᾽ al-kawākib (Trattato sulla luce delle stelle) e Fī 'l-maǧarra (Sulla via Lattea).
In questo insieme, il trattato intitolato Maqāla fī ḍaw᾽ al-qamar occupa una posizione privilegiata per più di una ragione. In primo luogo, il problema della luce della Luna, che era rimasto sempre ai margini della ricerca scientifica, è presentato per la prima volta come degno di uno studio autonomo. In secondo luogo, il metodo impiegato nella prima parte del trattato e il risultato ottenuto nella seconda sono decisamente inediti. In terzo luogo, in questo trattato troviamo la prima applicazione dell'ottica a un problema prima di allora considerato estraneo al campo d'indagine di questa scienza. A tal fine Ibn al-Hayṯam riunisce molti elementi dell'astronomia e della fisica della sua epoca, così come dell'ottica. Il modo in cui egli dimostra le tesi avanzate nelle due parti in cui è divisa l'opera, infine, offre alcuni chiari esempi dell'applicazione della sua concezione della dimostrazione a una delle scienze fisiche.
In questo trattato Ibn al-Hayṯam risponde ai seguenti interrogativi: da dove proviene la luce della Luna? (problema della ricezione); dopo essere stata recepita, in che modo essa emana verso altri corpi e soprattutto verso la Terra? (problema dell'emissione). Le risposte formulate dall'autore si riducono a due tesi dimostrate una dopo l'altra: la Luna riceve la sua luce dal Sole; la Luna, come ogni corpo luminoso in sé, diffonde la luce a partire da ogni punto della sua superficie, in tutte le direzioni e secondo linee rette. La questione fondamentale è che la prima di queste tesi era ampiamente accettata, mentre la seconda contraddiceva un'altra idea molto diffusa. Tutti i grandi sapienti, infatti, avevano sostenuto che la Luna riceveva la sua luce dal Sole, mentre sembra che prima di Ibn al-Hayṯam nessuno avesse messo in dubbio la tesi secondo cui la Luna riverberava la luce del Sole allo stesso modo di uno specchio. Come riuscì Ibn al-Hayṯam a mostrare la natura problematica della prima tesi e a imporre la necessità della sua dimostrazione? Come riuscì a ottenere un risultato che nessuno dei suoi predecessori aveva anticipato?
Il problema della ricezione
Inizieremo la nostra analisi con l'esame della prima tesi. Nella parte iniziale del suo trattato Ibn al-Hayṯam scrive che questa tesi era condivisa da tutti i sapienti nel campo della matematica e della fisica. Tra le ragioni che avrebbero indotto gli studiosi a proporla, egli indica quelle relative a tre gruppi di fenomeni: il fatto che la faccia luminosa della Luna si trovi sempre di fronte al Sole, le fasi della Luna e, infine, le eclissi lunari. Tuttavia, come abbiamo già osservato, egli precisa che questa tesi doveva essere dimostrata. In assenza di una dimostrazione, infatti, non si poteva che ritenere di trovarsi in presenza "di una contingenza e non di una necessità", di un'opinione "congetturale e non di una certezza".
Ciò che scrive Ibn al-Hayṯam trova una conferma nelle testimonianze storiche. Al contrario della questione dell'origine della luce delle stelle, su cui vi erano opinioni discordanti, quella relativa all'origine della luce della Luna registrava da sempre un consenso unanime: tutti ritenevano che essa fosse presa a prestito dal Sole. Questa tesi risaliva ai 'fisiologi' presocratici che, nel corso delle loro ricerche sulla natura delle cose, avevano preso in esame anche questo fenomeno. Secondo uno scritto apocrifo attribuito a Plutarco, il De placitis philosophorum (II, 24), il primo a sostenere che "la Luna deriva la sua luce dal Sole" fu Talete di Mileto, il più antico filosofo ionico. Tuttavia, nonostante questa e altre indicazioni come, per esempio, quella secondo cui Talete si sarebbe riferito alla 'natura terrestre' della Luna, così come un'oscura locuzione di Parmenide sulla "luce presa a prestito" della Luna, è stato accertato che il primo filosofo a esprimersi su questo tema fu Anassagora, al quale, secondo Platone, va attribuita la "recente tesi [secondo cui] la Luna riceve la sua luce dal Sole" (Cratylus, 408a 4-5).
In ogni caso, questa scoperta sarà in seguito giustificata dal punto di vista epistemologico da Aristotele. Negli Analitici secondi, parlando della particolare abilità posseduta dall'anima nel discernere in modo immediato il termine medio di una dimostrazione, e quindi la vera causa di un fenomeno da spiegare, il Filosofo menziona l'esempio della luce della Luna: basandosi sul fatto che la faccia luminosa di quest'ultima si trova sempre di fronte al Sole, un individuo dotato di "prontezza deduttiva" giunge facilmente alla conclusione che la Luna riceve la sua luce dal Sole" (I, 34, 89b 10-15).
Così, il primo fenomeno evocato da Ibn al-Hayṯam, quello relativo alle posizioni reciproche del Sole e della Luna, potrebbe, secondo Aristotele, essere all'origine della scoperta della provenienza della luce della Luna. Tuttavia, le testimonianze di alcuni autori più tardi inducono a pensare che questa scoperta fosse in origine legata all'osservazione degli altri due gruppi di fenomeni evocati da Ibn al-Hayṯam.
Ippolito da Ostia, un teologo cristiano del III sec., per esempio, collega questa scoperta alla spiegazione del modo in cui si verificavano le eclissi lunari. Egli sostiene che, secondo Anassagora, le eclissi lunari sono causate dalla Terra quando fa da schermo alla Luna, mentre quelle solari sono determinate dalla funzione di schermo svolta dalla Luna quando è nuova. Analogamente, secondo Aezio, sin dall'epoca di Anassagora si era iniziato a stabilire un legame tra l'ipotesi secondo cui la Luna riceveva la sua luce dal Sole e le fasi che essa attraversava nel corso di ogni mese lunare. Inoltre, l'autore del De placitis philosophorum (II, 29) scrive che "Platone, Aristotele, gli stoici e i matematici" avevano espresso pareri concordi sulle modalità della produzione delle fasi lunari.
Quanto ai matematici, sembra che essi abbiano ben presto adottato questa tesi per impiegarla nel calcolo delle eclissi, le cui osservazioni si andavano sempre più precisando e che sarebbero a loro volta servite da base a una serie di calcoli astronomici. Così, Aristarco di Samo inserisce all'inizio del suo trattato sulle dimensioni e le distanze del Sole e della Luna un enunciato relativo a questa tesi presentato come un postulato. D'ora in poi questa tesi sarà alla base di tutte le teorie delle eclissi formulate nel corso dell'Antichità e del Medioevo.
Quanto alla dimostrazione richiesta da Ibn al-Hayṯam, sembra che il suo solo esempio sia quello offerto nella Maqāla fī ḍaw᾽ al-qamar. Nel XVII sec. Descartes scriveva ancora che questa tesi era accettata da tutti per la semplice ragione che essa rendeva conto delle fasi della Luna. Ibn al-Hayṯam critica i suoi predecessori che avevano assunto come prove fenomeni che si limitavano a indicare una causa. Con ciò egli non intende dire che questa prova non è valida perché non è conforme alla concezione aristotelica della dimostrazione. Secondo questa concezione, infatti, dimostrare, a partire dalle fasi della Luna, che la sua luce è presa in prestito dal Sole, non era un procedimento accettabile in fisica, perché equivaleva a scoprire la causa a partire dall'effetto, mentre una vera dimostrazione fisica doveva dedurre l'effetto dalla causa. Ibn al-Hayṯam avanza una critica diversa. Secondo l'autore i suoi predecessori non hanno studiato in modo esauriente il campo dei fenomeni che potrebbero essere alla base della produzione delle fasi della Luna o delle eclissi lunari: essi si sono quindi basati su un'induzione 'non esaustiva' dei fenomeni. È possibile, infatti, che altre configurazioni, che potrebbero legittimamente esistere nel cielo, siano alla base della produzione di tali fenomeni, senza dover presumere che la Luna non sia in sé luminosa. La prima questione che l'autore solleva è quindi la seguente: il fenomeno delle fasi lunari è sufficiente a dimostrare che la Luna non è in sé luminosa?
Ibn al-Hayṯam risponde negativamente a questo interrogativo, ipotizzando l'esistenza di due configurazioni alternative: una Luna per metà luminosa che gira intorno a sé stessa (l'autore precisa i dettagli di questo movimento) e un'altra totalmente luminosa, priva di rotazione ma circondata da un corpo emisferico che gira intorno a sé stesso, e dimostrando che ognuna di queste configurazioni potrebbe essere all'origine della produzione delle fasi della Luna, senza dar luogo a nessuna conseguenza in grado di smentire l'esperienza.
Di seguito, Ibn al-Hayṯam si domanda se il fenomeno delle eclissi lunari possa in sé dimostrare che la luce della Luna è presa in prestito dal Sole. Egli risponde in senso affermativo, giungendo, tuttavia, ancora una volta a questa conclusione attraverso l'esame delle eventuali configurazioni che potrebbero dar luogo alle eclissi lunari.
L'autore fa precedere la sua esposizione sulle configurazioni dall'enumerazione dei principî fisici che ogni corpo celeste deve rispettare. Per evitare di seguire la sua esposizione parola per parola, raggrupperemo tali principî in tre classi. (1) Principio di permanenza: i corpi celesti non sono suscettibili di generazione né di corruzione. Da ciò consegue che i corpi celesti non possono dividersi né ammettere alcun tipo di deformazione. (2) Principio del plenum: nel mondo celeste non vi è alcuno spazio vuoto. (3) Principio di circolarità: il solo moto ammesso nel mondo celeste è quello circolare e uniforme (o una combinazione dei moti di questo tipo).
Secondo Ibn al-Hayṯam tali principî sono alla base delle leggi che governano la fisica celeste. Abbiamo già accennato al fatto che queste leggi sono molto importanti per l'autore. In effetti, le critiche che egli rivolge in altri contesti all'astronomia di Tolomeo si fondano in parte sulla presenza, nei modelli geometrici di quest'ultimo, di alcuni moti non uniformi. Del resto, anche gli astronomi della Scuola di Marāġa criticheranno alcuni modelli tolemaici richiamandosi a tali leggi. Si rileva, tuttavia, un grande assente tra i principî elencati: il 'principio di sfericità', secondo cui ogni corpo celeste nel suo insieme, così come ciascuno dei suoi elementi costitutivi, non può che essere sferico. Come abbiamo già osservato, Ibn al-Hayṯam non considerava assurda l'ipotesi dell'esistenza di un corpo emisferico che orbitava intorno alla Luna (in grado di produrre attraverso il suo movimento le fasi di quest'ultima). Al contrario, è proprio la liceità di una tale ipotesi che lo induce a rifiutare la tesi secondo cui il fenomeno delle fasi lunari dimostrerebbe in sé che essa riceve la sua luce dal Sole. Nei successivi brani della sua esposizione, Ibn al-Hayṯam non parla della forma dei corpi che potrebbero fare da schermo alla Luna.
È lecito operare una distinzione nella fisica celeste di Ibn al-Hayṯam tra elementi 'necessari', rappresentati dalle leggi summenzionate, ed elementi 'contingenti' di cui farebbero parte la figura, così come il numero e le posizioni dei corpi celesti? Non vi è nulla nel testo di Ibn al-Hayṯam che induca a pensare il contrario. Tuttavia, 'i corpi che muovono i corpi celesti', ovvero gli orbi celesti, devono essere sferici, poiché essi trascinano con il loro movimento circolare i corpi celesti propriamente detti (le stelle, i pianeti e ogni altro corpo privo di moto proprio).
Al contrario degli elementi necessari che non si lasciano contraddire dall'esperienza, quelli contingenti, e soprattutto il numero e le posizioni dei corpi celesti, possono cambiare in base alle esigenze dell'esperienza e quest'ultima può essere reale oppure immaginaria. Ormai la conformità alle leggi non rappresenta il solo criterio che decide della sorte dei corpi celesti. In altri termini, ciò che accade nei cieli non è indifferente a quanto si osserva sulla Terra: per ogni corpo celeste esistono alcuni fenomeni osservabili prodotti dalla sua esistenza, la cui assenza può essere assunta come prova della sua inesistenza.
Ibn al-Hayṯam ipotizza a questo punto l'esistenza di due configurazioni a cui, a suo parere, si riduce il campo delle configurazioni possibili. Alla prima attribuiremo il nome di "Antisole" e alla seconda quello di "compagno della Luna". L'Antisole è un corpo privo di luce che si troverebbe tra la Luna e la Terra occupando una posizione opposta a quella del Sole (in rapporto, naturalmente, al centro del mondo che si confonde con quello della Terra) e che seguirebbe il suo moto, in modo che nel momento in cui il Sole si trova a est, l'Antisole dovrebbe trovarsi a ovest e viceversa. Trovandosi davanti alla Luna al momento dell'opposizione, questo corpo potrebbe svolgere la stessa funzione dell'ombra della Terra e quindi produrre l'eclissi lunare. Ora, essendo privo di luce, tale corpo dovrebbe essere invisibile. Tuttavia, Ibn al-Hayṯam dimostra che anche un corpo celeste invisibile può produrre conseguenze visibili. Dal momento che l'Antisole può coprire il corpo della Luna, la sua grandezza angolare deve essere almeno uguale a quella della Luna. Un corpo il cui diametro apparente corrisponde a mezzo grado e che si sposta, seguendo il moto del Sole, sullo sfondo delle stelle fisse, dovrebbe però nascondere in alcuni momenti le stelle che si trovano lungo il suo tragitto. Ora, dal momento che questa occultazione non è mai stata osservata, si può concludere che l'Antisole non esiste.
Al contrario dell'Antisole, il compagno della Luna è un corpo in grado di girare intorno a essa; in altri termini, esso sarebbe un satellite della Luna, e insieme formerebbero un piccolo sistema planetario. Non è a causa di questo aspetto inedito che Ibn al-Hayṯam finisce per rifiutare l'ipotesi dell'esistenza del compagno della Luna, ma perché, in caso contrario, esso produrrebbe effetti visibili che in realtà non si verificano. Attraverso un esame minuzioso delle differenti posizioni che questo corpo potrebbe occupare in relazione alla Luna, Ibn al-Hayṯam dimostra che esse determinerebbero tutte situazioni assurde: l'uguaglianza della durata delle eclissi e dell'intervallo tra due eclissi consecutive, ma soprattutto l'esistenza di una parallasse dell'eclissi lunare. Ciò significa che, grazie alla presenza del compagno della Luna e indipendentemente dalla posizione che esso occupa, le eclissi lunari si produrrebbero in momenti diversi per gli osservatori che si trovano in differenti regioni della Terra. Ora, poiché le eclissi lunari non presentano mai una parallasse, la tesi dell'esistenza del compagno della Luna deve essere rifiutata. Così, le eclissi lunari possono essere spiegate in un solo modo: la Luna riceve la sua luce dal Sole e, quando la Terra si interpone tra il suo corpo e il Sole, essa si eclissa.
Il problema dell'emissione
Ibn al-Hayṯam procede quindi alla dimostrazione della tesi secondo cui la luce della Luna emana come luce seconda, ossia si diffonde da ogni punto e in tutte le direzioni. La sua dimostrazione è articolata in due fasi. In un primo momento egli dimostra, attraverso un esame sperimentale, che la luce della Luna emana a partire da ogni punto di quest'ultima; quindi dimostra con un argomento matematico che il modo in cui la luce emana dalla Luna contraddice la tesi ai suoi tempi largamente diffusa secondo cui tale luce si identificherebbe con quella del Sole che giunge fino a noi per riflessione.
Il dispositivo sperimentale impiegato da Ibn al-Hayṯam è costituito da un regolo dotato di due mire (fig. 8). Nella prima (ABCD) pratica la fessura KL e nella seconda un emisfero, il cui centro si trova sulla superficie interna della mira (UVXY) e la cui sommità, l'orifizio O, è situata sulla faccia esterna di essa (EFG). Le dimensioni della fessura e del regolo sono scelte in modo che l'angolo KOL sia almeno uguale alla grandezza apparente della Luna, vale a dire
Osservando la Luna con questo strumento e guardando dal punto O, se ne vedrà l'intero diametro. Sullo schermo T, posto a una distanza adeguata, apparirà allora la macchia luminosa MN. Nell'Ottica (I, 3, 13-15) tale divergenza (inḫirāṭ) della luce figura tra le prove sperimentali, le quali dimostrano che la luce proviene da tutti i punti di un corpo. Tuttavia, nella Maqāla fī ḍaw᾽ al-qamar, la ricerca sperimentale di Ibn al-Hayṯam va al di là di questa dimostrazione: coprendo progressivamente la fessura con un corpo opaco, si osserva che la macchia MN diviene sempre più piccola, fino a che la luce che fuoriesce dalla parte scoperta della fessura non è più visibile. Quindi, se con l'aiuto dello schermo S, sul quale è stato praticato il piccolo foro R, si copre la fessura, in modo che la luce che emana dalla Luna penetri nella fessura soltanto attraverso il foro R, si potrà constatare, osservando tutte le parti della Luna con questo strumento, che la sua luce passa attraverso il foro R e l'orifizio O, raggiungendo lo schermo T. Ibn al-Hayṯam dimostra in questo modo che la Luna emana luce da tutte le sue parti, non dimentica inoltre di precisare che questa esperienza deve essere ripetuta nel corso di molte notti e in differenti regioni della Terra.
Dopo aver stabilito che la luce della Luna emana da ogni punto della sua superficie, Ibn al-Hayṯam si propone di dimostrare che tale emanazione non è il risultato della riflessione dei raggi solari sulla superficie della Luna. Egli ricorre in questo caso a una reductio ad absurdum. Dopo aver ipotizzato che la luce del Sole si riflette sulla superficie della Luna, dimostra che in questo caso la parte visibile della Luna sarebbe molto più piccola di quanto effettivamente non sia. Quindi rifiuta la tesi della riflessione asserendo che essa contraddice l'osservazione. Questa dimostrazione è basata non soltanto sulle leggi dell'ottica, ma anche su alcuni dati astronomici, concernenti le dimensioni relative della Luna, della Terra e del Sole, così come le distanze relative tra la Luna, la Terra e il Sole. Ibn al-Hayṯam prende in considerazione due casi: quello dell'emissione diretta della luce della Luna verso la Terra e quello secondo cui la luce della Luna raggiunge la Terra dopo aver subito una o più rifrazioni (la dimostrazione del caso dei raggi diretti è descritta nella Tav. Ia e Ib).
In base a questa dimostrazione, la parte della Luna la cui luce potrebbe riflettersi verso la Terra sarebbe racchiusa in un quadrilatero sferico le cui dimensioni misurerebbero (1/4)″ e (1/8)″, vale a dire poco più grande di un punto. In questa dimostrazione Ibn al-Hayṯam si basa sulle distanze e sulle grandezze dei corpi luminosi calcolate per la prima volta da Ipparco. Come sappiamo, questi valori sono troppo piccoli; di conseguenza, le dimensioni ottenute per il 'luogo di riflessione' sono molto esagerate: per ottenerne le dimensioni reali, bisogna moltiplicare la distanza tra il Sole e la Terra per il fattore 20; ciò porta a rimpicciolire le dimensioni di questo luogo di un fattore pari a 20.
Confutazione della tesi della riflessione dei raggi solari sulla Luna; il problema della rifrazione atmosferica
Malgrado la sua eleganza, questa dimostrazione è soggetta a due condizioni: essa è valida soltanto in prossimità della quadratura e non tiene conto della rifrazione atmosferica. Nel corso di una parte tutt'altro che irrilevante del resto del trattato, Ibn al-Hayṯam tenta di superare tali limiti e di dimostrare, da un lato, che il risultato ottenuto è valido per tutte le situazioni relative del Sole, della Luna e della Terra e, dall'altro lato, che la rifrazione atmosferica non incide in misura rilevante su questo risultato.
La rifrazione atmosferica interviene quando la luce, emanando dal Sole verso la Luna o dalla Luna verso la Terra, passa da un mezzo all'altro: questi mezzi sono la sfera dell'aria e la sfera celeste (Tav. II).
Dal momento che la sfera celeste è più trasparente dell'aria, sul suo lato convesso si produrrà almeno una rifrazione. Nel caso della tripla rifrazione (rappresentata, nella figura della tavola II, dalla linea GMNPQR), poiché non dispone di misurazioni esatte relative al diametro della sfera dell'aria e a quello della sfera celeste, Ibn al-Hayṯam si limita a mostrare che i raggi che emanano dal Sole verso la Luna non attraversano nella maggior parte dei casi il confine tra il mondo celeste e quello sublunare e che ciò avviene solamente dopo le quadrature. Tuttavia, l'autore tenta di dimostrare che in questo caso, indipendentemente dal numero delle rifrazioni, la parte visibile della Luna sarebbe sempre molto più piccola di quella che si può effettivamente osservare.
Il procedimento si basa ancora una volta sulla delimitazione del 'luogo di riflessione', benché in questo caso Ibn al-Hayṯam impieghi argomenti più indiretti, in cui fa appello non solo alle leggi dell'ottica, ma anche ai fenomeni che dovrebbero verificarsi se il luogo di riflessione presentasse una grandezza non irrilevante. Descriveremo soltanto uno di questi esempi. Per dimostrare che i raggi che raggiungono la Terra rifrangendosi sul corpo celeste non si discostano molto dai raggi diretti, Ibn al-Hayṯam presenta un argomento fondato sull'esistenza della parallasse della Luna. Sappiamo che la posizione della Luna, calcolata in rapporto al centro della Terra, non coincide sempre con quella individuata osservando la Luna a partire da un punto della Terra. Questo scarto è definito dall'angolo di parallasse, vale a dire dall'angolo compreso tra la retta che unisce il centro della Terra a quello della Luna e la retta che congiunge un punto della Terra al centro della Luna (l'angolo GAB nella fig. 9). Considerando la distanza tra la Luna e la Terra e il diametro della Terra, si può dire che la misura di quest'angolo è di circa mezzo grado.
Ora, supponiamo che, invece di seguire la retta AG, la luce che emana dal centro della Luna si spezzi nel punto M del corpo celeste e che, di conseguenza, segua la linea spezzata AMG. Ibn al-Hayṯam dimostra che lo scarto tra le rette MG e AG non può essere più grande dell'angolo di parallasse. Se A∧GM>G∧AB, infatti, la retta GM (che rappresenta la direzione in cui si vede un punto della Luna) e la retta AB non si incontrerebbero e, di conseguenza, la parallasse non potrebbe prodursi. Questa eventualità è smentita dall'osservazione. Il raggio rifratto sarà quindi sempre molto vicino al raggio diretto, e la dimostrazione già presentata per le dimensioni del 'luogo di riflessione' sarà approssimativamente valida anche per i raggi rifratti.
Il caso della tripla rifrazione è molto più complicato. Tuttavia, Ibn al-Hayṯam riesce a dimostrare che in tutti gli esempi illustrati nella figura, se la luce del Sole si riflettesse sulla superficie della Luna, la parte visibile della Luna non sarebbe più grande di un sedicesimo della superficie lunare realmente visibile, un'ipotesi che contrasta con i dati dell'osservazione. Si può quindi concludere che la luce del Sole non si riflette sulla superficie della Luna.
In tutte queste dimostrazioni l'occhio non svolge alcun ruolo: si tratta sempre, come abbiamo visto, della luce che, emanando dalla Luna, raggiunge un punto della Terra. Tali dimostrazioni, tuttavia, sono tutte fondate sul presupposto della sfericità della Luna. Per rispondere alle obiezioni che avrebbero potuto essere sollevate su quest'ultimo punto, Ibn al-Hayṯam decide di presentare una confutazione, diretta e indipendente dalla figura geometrica della Luna, della tesi della riflessione. Questo argomento è essenzialmente ispirato alla tesi sviluppata dall'autore in un'altra sezione del trattato, quella secondo cui le linee seguite dalla luce nella sua propagazione sono le stesse seguite dalla visione dell'oggetto da cui la luce emana.
Per dimostrare che la luce del Sole non giunge fino a noi dopo essersi riflessa sulla superficie della Luna, Ibn al-Hayṯam costruisce due coni tra loro simmetrici. Il primo, che chiameremo cono incidente, C, è il cono solido formato da tutti i raggi che emanando dal Sole raggiungono il punto M della superficie della Luna. Il secondo, il cono riflesso Cr, comprende tutti i raggi che si riflettono in questo punto della Luna. Si tratta in effetti di 'coni luminosi' concepiti sul modello di quelli visivi dei matematici. La costruzione di questi coni e l'argomento da cui è seguita si basano sui seguenti principî: (a) l'unicità della retta normale (il fatto cioè che la normale si trovi allo stesso tempo su tutti i piani normali); (b) la simmetria tra il cono incidente e il cono riflesso. Questa simmetria si definisce in rapporto alla retta normale al piano tangente alla superficie della Luna. Si tratta di una simmetria spaziale, ma che si definisce in rapporto a una retta, cioè alla retta normale alla superficie della Luna.
Basandosi sulla corrispondenza già stabilita fra i tragitti dei raggi luminosi e le rette secondo cui si produce la visione, Ibn al-Hayṯam giunge alla conclusione che ogni punto da cui un osservatore potrebbe vedere il punto M si dovrebbe trovare all'interno di Cr. Questa costruzione gli consente così di calcolare, a partire dai dati astronomici già utilizzati, la grandezza dell'intersezione di Cr con la superficie della Terra. Ora, dato che tale intersezione definisce la parte della superficie della Terra da cui un osservatore terrestre potrebbe vedere il punto M, è evidente che, nel caso in cui la luce del Sole giungesse fino a noi dopo essersi riflessa nel punto M, questo punto sarebbe visibile soltanto per coloro che si trovano lungo l'arco AB. Ora, questo arco non può misurare più di un sesto della circonferenza della Terra. Tale ipotesi, pertanto, è smentita dall'esperienza quotidiana, dato che in ogni momento un certo punto della Luna è visibile da una parte della superficie della Terra molto più grande dell'arco AB.
In seguito, Ibn al-Hayṯam riprende l'argomento così sviluppato applicandolo in questo caso a tutta la superficie visibile della Luna. Dal momento che tale superficie è costituita da tutti i punti omologhi al punto M, è possibile definire per ogni punto un cono incidente e uno riflesso. Così, tutti i punti della circonferenza della Terra da cui si potrebbe vedere il punto M′ si troverebbero lungo l'arco A′B′ e tutti i punti da cui si potrebbe vedere l'arco MM′ si troverebbero lungo l'arco AB′. Ciò vale per ogni altro punto della parte visibile della Luna. Ora, AB′⟨AB: quindi, poiché l'intersezione di tutti gli archi omologhi ad AB è più piccola di AB, allora la parte della superficie della Terra da cui risulterebbe visibile tutta la superficie della Luna sarebbe più piccola di un sesto della sua parte visibile. Tuttavia ciò è smentito dall'osservazione. Ibn al-Hayṯam dimostra infine che anche se la luce della Luna giungesse fino a noi per rifrazione questo risultato rimarrebbe valido, tanto più che il cono rifratto sarebbe più 'stretto' del cono diretto e, di conseguenza, la sua intersezione con la superficie della Terra sarebbe più piccola di quella del cono diretto.
Nascita di una fisica celeste
Gli argomenti impiegati da Ibn al-Hayṯam nella Maqāla fī ḍaw᾽ al-qamar colpiscono soprattutto per la loro semplicità matematica. Il calcolo del luogo di riflessione, il principale saggio di abilità del trattato, non richiede che la conoscenza delle proprietà del cerchio, delle leggi di riflessione della luce, delle dimensioni e delle distanze del Sole e della Luna in rapporto a quelle della Terra, nozioni note già molto prima del periodo in cui visse Ibn al-Hayṯam. Perché tale questione è stata risolta solamente nell'XI secolo? Perché tutte le soluzioni presentate prima che Ibn al-Hayṯam decidesse di riproporla come un vero e proprio problema scientifico si sono rivelate arbitrarie?
Innanzi tutto bisogna dire che questo ritardo non è stato causato dall'influenza della tesi molto diffusa secondo cui esisteva una differenza fondamentale tra i corpi celesti e quelli del mondo terrestre. Infatti tutti sapevano che, come precisa Ibn al-Hayṯam all'inizio del suo trattato, il corpo della Luna si distingueva da ogni altro corpo celeste. La Luna si differenziava dalle altre stelle perché riceveva la luce dal Sole e l'idea ampiamente riconosciuta secondo cui la luce del Sole si rifletteva sulla sua superficie l'allontanava ancora di più dagli altri corpi celesti. Per poter dar luogo alla riflessione della luce, infatti, la Luna doveva essere composta da una materia compatta e non si conosceva l'esistenza di nessun altro specchio nel cielo. Il risultato ottenuto da Ibn al-Hayṯam, quindi, non sovvertiva di per sé la fisica celeste del suo tempo. Esso aprì una breccia in questa disciplina per altre ragioni di cui parleremo più avanti.
In compenso, si può dire che la questione delle modalità di emanazione della luce dalla Luna non avrebbe potuto essere sollevata prima di Ibn al-Hayṯam. La situazione dell'ottica, divisa tra la teoria della visione, da un lato, e la teoria della combustione, dall'altro, non consentiva la formulazione di tale questione. La teoria della visione era ordinata in base alla bipartizione diretta-indiretta e, a sua volta, la visione indiretta era divisa in 'visione per raggi riflessi' e 'visione per raggi rifratti' e la teoria della combustione, pur avvalendosi naturalmente delle leggi generali della riflessione, le impiegava solamente in relazione a situazioni molto specifiche. Questo problema poteva essere sollevato unicamente nel quadro di una teoria basata su un concetto unitario di luce e su una formulazione generale delle leggi della sua propagazione, che fosse in grado inoltre di assimilare la geometria della visione a quella della propagazione della luce. Questa teoria fu enunciata per la prima volta da Ibn al-Hayṯam.
La Maqāla fī ḍaw᾽ al-qamar si distingue per un aspetto inedito: l'elaborazione di un metodo destinato allo studio scientifico del mondo celeste. Con questo trattato la geometria viene a trovarsi per la prima volta nella posizione di potersi pronunciare non solo sui movimenti che si producono nel cielo, ma anche sulla costituzione materiale di questo mondo, anche se gradualmente e in riferimento a una sua sola parte.
Il progetto delineato nella Maqāla fī ḍaw᾽ al-qamar è ripreso nella Maqāla fī 'l-aṯar allaḏī fī waǧh al-qamar. In questo trattato Ibn al-Hayṯam dimostra che la macchia (di cui si fa cenno nel titolo) non fa parte del mondo sublunare e che è causata dalla differenza esistente tra la capacità ricettiva della parte della Luna in cui essa appare e il resto del suo corpo. Per dimostrare questa tesi Ibn al-Hayṯam fa appello a tutte le ipotesi avanzate in relazione all'argomento, rifiutandole una dopo l'altra. Ogni ipotesi è rifiutata in base a una ragione di carattere sperimentale: alcune presuppongono l'esistenza di una parallasse, vale a dire che la macchia appaia in differenti punti della Luna in funzione del luogo da cui la si osserva; altre implicano il cambiamento della forma della macchia e altre ancora che la macchia lasci apparire in trasparenza una parte del cielo. Dal momento che tutte queste conseguenze sono smentite dall'esperienza, Ibn al-Hayṯam giunge alla conclusione che la macchia è causata essenzialmente dalla differenza esistente tra la costituzione materiale delle diverse parti della Luna e tenta di spiegarla attraverso il concetto della capacità ricettiva e della sua irregolare distribuzione sulla superficie della Luna.
Se i due primi trattati indicano la vastità del progetto dell'autore, il terzo (redatto prima della Maqāla fī 'l-aṯar allaḏī fī waǧh al-qamar) ne rivela i limiti. In questo trattato, intitolato Maqāla fī aḍwā᾽ al-kawākib (Trattato sulla luce delle stelle), Ibn al-Hayṯam tenta di dimostrare, sempre a partire da fenomeni visibili, che tutte le stelle sono luminose in sé, a eccezione della Luna. Tra i fenomeni che l'autore menziona come prove di questa tesi, figura il fatto che nessuna stella presenta una serie di fasi. Secondo Ibn al-Hayṯam, infatti, tutte le stelle ci appaiono sempre in forma di cerchi. Se fossero illuminate dalla luce del Sole o da quella di un'altra stella, esse dovrebbero presentare una serie di fasi, allo stesso modo della Luna. Benché nel trattato sia presentata come un dato dell'osservazione, la sfericità delle stelle, da cui derivava il loro aspetto circolare, non era affatto tale: sappiamo, infatti, che la distanza esistente tra le stelle e la Terra è così grande che la loro forma non può essere individuata a occhio nudo. In ogni caso, l'argomento di Ibn al-Hayṯam definisce almeno una delle condizioni necessarie della non luminosità in sé delle stelle: in questo caso esse dovrebbero presentare una serie di fasi (in effetti, soltanto con le indagini di Galilei si è giunti alla conoscenza delle fasi dei pianeti). Anche questo trattato quindi si iscrive nello stesso progetto dei primi due.
In un quarto trattato dedicato allo studio della Via Lattea, Ibn al-Hayṯam si schiera dalla parte di coloro che, al contrario di Aristotele, ritengono che la Via Lattea non sia un fenomeno meteorologico, ma un oggetto che si trova nel mondo celeste. Anche in questo caso il suo argomento è basato sull'osservazione: se facesse parte del mondo sublunare, la Via Lattea dovrebbe subire una parallasse, cioè, osservata da punti diversi della Terra, dovrebbe cambiare posizione in rapporto alle stelle fisse. Come testimonia Tolomeo nell'Almagesto, la Via Lattea, invece, occupa sempre la stessa posizione in rapporto alle stelle fisse.
Il legame esistente tra questa tesi e alcuni autori, come, per esempio, Olimpiodoro, che avevano enunciato idee analoghe, non è molto chiaro. Allo stesso modo, la questione dell'influenza che questo trattato avrebbe potuto esercitare su altri studiosi ‒ come, per esempio, Avempace (m. 1139), Averroè (m. 1198), Abū 'l-Barakāt al-Baġdādī (m. 1164), Faḫr al-Dīn al-Rāzī (m. 1209) ‒ che hanno ripreso questa tesi sotto diverse forme, non è ancora approdata a risultati definitivi. Tuttavia, si può dire che in Ibn al-Hayṯam questa tesi si iscrive in una ricerca sulla natura dei corpi celesti, mentre gli altri autori la prendono in considerazione nel quadro tradizionale della meteorologia. Inoltre, Ibn al-Hayṯam non esita a collocare al di là di ogni ambiguità la Via Lattea tra i corpi celesti, mentre Avempace cerca ancora un compromesso tra questa tesi e quella aristotelica e Averroè ritiene che essa sia una delle tante spiegazioni possibili di questo fenomeno.
I risultati ottenuti nel gruppo dei trattati da noi definiti ottico-cosmologici potrebbero apparire modesti, una circostanza che del resto sottolinea le grandi difficoltà da superare per qualsiasi studio sul cielo che avesse aspirato a essere considerato scientifico. Operando tra un'astronomia che si occupava soltanto del calcolo dei movimenti e delle posizioni degli astri e una cosmologia per così dire negativa, che si accontentava di definire le proprietà delle cose celesti in opposizione agli oggetti terrestri, Ibn al-Hayṯam tenta di aprire una terza strada, lungo la quale sollevare nuove questioni relative al cielo o dare risposte più esatte agli interrogativi ancora irrisolti. Tuttavia, questi risultati apparentemente modesti sono ottenuti solamente al termine di una ricerca che fa ricorso a dati diversi, desunti da differenti campi d'indagine, che riunisce molti principî, leggi e metodi, fino ad allora impiegati in aree ben distinte tra loro, e che utilizza molti tipi diversi di ragionamento.
A questo punto, prima di passare all'esame di questo aspetto sintetico del metodo di Ibn al-Hayṯam, sarà il caso di soffermarsi sulla ricapitolazione che l'autore presenta alla fine del primo trattato.
Dunque la luce che emana dalla Luna verso la Terra è una luce che emana dal suo corpo, quando essa è illuminata dal Sole, nello stesso modo in cui la luce emana dai corpi luminosi in sé. Così, il colore luminoso che le è proprio non appare per riflessione e la riflessione non vi ha nulla a che fare. Esso non è neppure il colore di un corpo che si interpone tra l'occhio e la Luna. Esso è dunque il colore che è proprio alla sua sostanza quando essa è illuminata dal Sole. Come se il Sole, illuminandola, le conferisse una forma, grazie a cui la sua sostanza diviene luminosa in sé e grazie a cui il suo colore diviene a sua volta luminoso. Questa forma vi permane fino a quando il Sole la illuminerà. E come se il Sole, conferendole questa forma, la perfezionasse. (Maqāla fī ḍaw᾽ al-qamar, f. 47r)
In questo, così come in molti altri trattati, l'autore, la cui ricerca aveva come punto di partenza la distinzione tra corpi luminosi in sé e non luminosi in sé, finisce per assimilare il secondo gruppo al primo. Inoltre, il modo in cui Ibn al-Hayṯam impiega i termini 'forma' e 'perfezione' dimostra che la sua ricerca è in grado di fare a meno di questi concetti. Essi servono soltanto a tradurre il risultato ottenuto attraverso una ricerca sperimentale nel linguaggio della filosofia del suo tempo. Dal momento che i ragionamenti attraverso cui tale risultato è ottenuto garantiscono di per sé la sua validità, questo linguaggio ha un valore esclusivamente metaforico: non è che un modo di esprimere concetti spiegabili con altri mezzi e in modo più soddisfacente.
È indubbiamente l'assimilazione dei corpi non luminosi in sé ai corpi luminosi in sé che permette a Ibn al-Hayṯam (Kitāb al-Manāẓir, I, 3, 16) di considerare la Luna come un corpo luminoso in sé, allo stesso titolo del Sole e del fuoco.
Tipologie di dimostrazione nella Maqāla fī ḍaw᾽ al-qamar
Nella Maqāla fī ḍaw᾽ al-qamar si possono individuare almeno quattro tipi di argomentazioni volte a verificare le tesi dell'autore o a confutare idee contrarie. Esse non sono del tutto indipendenti tra loro, ma distinguendole potremo capire più a fondo come certi procedimenti argomentativi cambino significato a seconda delle nuove situazioni in cui Ibn al-Hayṯam li impiega e come si aprano nuove vie di argomentazione che raggrupperemo in quattro categorie: sperimentale, induttiva, per modellizzazione e attraverso l'esperienza concettuale.
Inizieremo a prendere in esame il tipo di argomentazione più caratteristico dell'opera di Ibn al-Hayṯam: quello sperimentale. Come abbiamo visto, è attraverso un dispositivo sperimentale che egli giunge a dimostrare come la luce della Luna provenga da ogni parte del suo corpo. A questo proposito, si rileva una differenza significativa nel modo in cui la luce della Luna è considerata nell'Ottica e nella Maqāla fī ḍaw᾽ al-qamar. Nell'Ottica (I, 3, 15) l'autore inserisce la Luna tra i corpi luminosi in sé, come il Sole e il fuoco. Per dimostrare che la luce della Luna emana da tutte le parti del suo corpo e non solo dal suo centro o da una sola parte, egli evoca la luce emessa dalla falce di Luna, quella emessa durante le eclissi lunari e quella emessa dalla Luna quando una parte del suo corpo si trova ancora al di sotto della linea dell'orizzonte, così come un'altra prova, a cui è attribuito il nome di esperienza (al-i ῾tibār): la divergenza della luce della Luna che passa attraverso i piccoli orifizi. Quest'ultima dimostra non solo che la luce emana da ogni parte della Luna, ma anche che si diffonde secondo linee rette.
Astraendo dai problemi posti dalla diversa presentazione della natura della luce della Luna nelle due opere, di cui abbiamo già parlato, l'esperienza descritta nella Maqāla fī ḍaw᾽ al-qamar è molto più sofisticata. Si tratta, in effetti, di dimostrare che da ogni parte visibile della Luna, per quanto piccola, emana una luce. È per questo che l'esperienza in questione non si limita all'esame della luce che fuoriesce dalla fessura. Coprendo la fessura con il piccolo schermo S, su cui è stato praticato l'orifizio R, Ibn al-Hayṯam dimostra che la luce della Luna proviene da ogni parte del suo corpo. È isolando la luce che proviene da ogni parte della Luna che Ibn al-Hayṯam dimostra che la sua luce non proviene soltanto dal suo centro o da un altro punto privilegiato. Così, l'analisi puntuale, impiegata sul piano teorico, è associata, sul piano sperimentale, all'analisi della superficie della Luna nelle sue parti costitutive. Ibn al-Hayṯam lascia intendere che la luce che passa per l'orifizio R non subirà alcuna divergenza e che raggiungerà ogni volta un solo punto dello schermo. Essa quindi corrisponderà alla più piccola luce così come è definita nel Libro IV dell'Ottica.
Come abbiamo già osservato, la tesi della ricezione è dimostrata attraverso un procedimento logico che possiamo definire induttivo, nella misura in cui è fondato sull'esame esaustivo delle diverse configurazioni che potrebbero essere presentate come la causa delle eclissi lunari. Ora, nonostante ciò che l'uso del termine 'induzione' può suggerire, non si tratta di una ricerca guidata da una teoria che limita il campo delle configurazioni possibili attraverso principî relativi alla costituzione del cielo e dei movimenti in esso ammissibili.
In questa dimostrazione, l'induzione svolge due funzioni complementari: essa è impiegata come mezzo di dimostrazione e, al tempo stesso, come mezzo di confutazione. Questo secondo aspetto, che rimane in qualche modo in secondo piano nelle esperienze dell'Ottica, è chiaramente posto in risalto nella Maqāla fī ḍaw᾽ al-qamar. In effetti, anche nell'Ottica la funzione della sperimentazione non si riduce mai alla verifica di una tesi, ma si estende al rifiuto delle tesi alternative. La dimostrazione sperimentale della propagazione rettilinea della luce, per esempio, è accompagnata dalla confutazione delle tesi che avrebbero potuto essere avanzate per sostenere che la luce segue un percorso non rettilineo.
Attraverso questo secondo aspetto, il genere di ragionamento induttivo utilizzato dall'autore si avvicina alla dialettica nel significato aristotelico del termine, una delle cui funzioni era quella di eliminare, "tra i principî provvisoriamente ammessi", quelli che non è opportuno adattare (Granger 1976, p. 72). Ora, indipendentemente dai legami esistenti tra questa idea aristotelica e la pratica di Ibn al-Hayṯam, il modo in cui quest'ultimo la impiega dimostra che siamo in presenza di un nuovo metodo e non di una nuova applicazione di un metodo già noto da molti secoli. In Ibn al-Hayṯam, infatti, l'esame delle tesi in competizione tra loro non si svolge soltanto sul piano della scelta dei principî e non è condotto attraverso un'analisi del loro contenuto in vista della scoperta di una contraddizione interna. Il criterio della verità è rappresentato dall'esperienza. Tale questione ci porta all'esame del terzo tipo di argomentazione individuabile nella Maqāla fī ḍaw᾽ al-qamar.
Le configurazioni presentate come spiegazioni alternative dell'origine delle eclissi lunari hanno in comune una caratteristica: l'invisibilità. Di conseguenza, né la tesi dell'esistenza dell'Antisole né quella del compagno della Luna sono confutabili attraverso l'osservazione diretta. Come abbiamo già osservato, in questo caso Ibn al-Hayṯam tenta di dimostrare che anche queste configurazioni non osservabili possono produrre effetti osservabili. L'esistenza di ciascuna di esse può quindi essere negata a partire da osservazioni terrestri. La struttura di questo tipo di argomentazione può essere rappresentata dal seguente
In questo schema, cui si fa ricorso in quasi tutte le opere dedicate alla filosofia della scienza, p rappresenta la teoria e q il fenomeno osservabile. Questo modo di presentare il rapporto esistente tra la teoria e l'esperienza, benché sia vero a grandi linee, rischia, tuttavia, di occultarne l'estrema complessità. Esso potrebbe, infatti, lasciar pensare che i risultati osservabili siano desumibili in modo naturale, e attraverso un'argomentazione esclusivamente logica, dalle teorie. Così, ogni persona dotata della capacità di ragionare sarebbe in grado di confutare una teoria.
Questa idea, però, non trova alcun riscontro nella pratica scientifica. Quest'ultima consiste in larga misura nella ricerca dei mezzi attraverso cui si può giungere a dedurre conseguenze osservabili da una teoria, spesso enunciata in un linguaggio matematico e in termini di entità teoriche. Un altro punto, non meno importante, è quello del modo in cui si può verificare, attraverso la sperimentazione, la conseguenza così ottenuta. Vi è dunque un movimento orientato in due direzioni. Per trarre conseguenze in linea di principio osservabili bisogna perfezionare lo studio della teoria: è necessario eseguire calcoli, elaborare modelli e così via. Per verificare le conseguenze, bisogna perfezionare lo studio della realtà: è necessario riprodurre il fenomeno in condizioni sperimentali e isolarlo, occorre ideare e fabbricare dispositivi sperimentali di diversi gradi di complessità e disporre dei mezzi tecnici necessari.
Queste osservazioni preliminari ci consentono di dire che Ibn al-Hayṯam è uno dei primi ricercatori, se non il primo, ad aver riflettuto su questa duplice difficoltà.
Abbiamo già parlato più volte dell'aspetto sperimentale. In effetti, nelle esperienze di Ibn al-Hayṯam e soprattutto in quelle che hanno come oggetto la propagazione della luce seconda, la riflessione e la rifrazione della luce, si rivela una grande abilità artigianale come, del resto, nello strumento impiegato nella Maqāla fī ḍaw᾽ al-qamar. Benché sia ideato, come riconosce lo stesso autore, sul modello del regolo parallattico degli astronomi, quest'ultimo registra tra le mani di Ibn al-Hayṯam un cambiamento di status: da strumento di osservazione si trasforma in dispositivo sperimentale.
In ogni modo, in tutti questi casi, il rapporto esistente tra il fenomeno osservabile e la teoria è relativamente semplice. Il tema di queste sperimentazioni, infatti, è il principio della propagazione rettilinea della luce e l'esistenza di una corrispondenza diretta tra l'oggetto teorico (le rette che rappresentano la direzione della propagazione della luce) e l'oggetto osservabile (il fascio di luce) è già assicurata dal concetto della 'più piccola luce'.
Tuttavia, in Ibn al-Hayṯam, il rapporto tra la teoria e il fenomeno osservabile non è sempre così diretto. Al contrario, il fenomeno osservabile a volte è desunto dalla teoria soltanto dopo che quest'ultima è stata elaborata. Tale elaborazione è operata soprattutto in due modi, di cui troviamo alcuni esempi estremamente chiari nella Maqāla fī ḍaw᾽ al-qamar.
Il primo consiste nel rappresentare la teoria sotto forma di un modello. Così, per confutare la tesi dell'esistenza del compagno della Luna, Ibn al-Hayṯam immagina che l'Universo sia costituito da un insieme di sfere, ciascuna delle quali ruota intorno al suo centro con un moto circolare e uniforme, e gira, in ultima analisi, intorno al centro della Terra. Egli costruisce così una sorta di macchina celeste soggetta ad alcuni principî imposti dalla fisica, destinata soprattutto ad assoggettare il mondo celeste a una sorta di controllo sperimentale. Dal momento che questa macchina serve fondamentalmente a esaminare un'ipotesi (e soprattutto a rifiutarla), il suo grado di complessità dipende dalla natura di quest'ultima e, dal momento che non rappresenta l'Universo in tutta la sua ricchezza, non è una riproduzione del mondo celeste ma un modello di quest'ultimo: si tratta di una rappresentazione semplificata che tiene conto solamente degli elementi pertinenti. È grazie alla sua semplicità che questo modello può essere impiegato in una sorta di esame sperimentale. Affinché un corpo possa essere ammesso in questa macchina, occorre non soltanto che la sua esistenza sia conforme a una serie di principî ma anche che essa non produca nessuna conseguenza tale da poter essere smentita dall'osservazione.
Questa semplificazione è ancora più evidente nel modello presentato da Ibn al-Hayṯam nel corso dell'esame dei raggi rifratti. Questo modello riproduce una parte dell'Universo nella forma di un sistema di due sfere concentriche ‒ il limite tra la sfera terrestre e il cielo (cerchio I nella figura della Tav. II) e l'orbe della Luna (cerchio II) ‒ in quanto la rifrazione si produce soltanto quando la luce passa da una sfera all'altra. In questo caso, il fenomeno osservabile che consente a Ibn al-Hayṯam di delimitare con l'aiuto di questo modello le dimensioni del luogo di riflessione è l'assenza della parallasse della Luna nel caso in cui i raggi rifratti siano molto diversi dai raggi diretti.
Nella misura in cui i modelli precedentemente indicati sono costruiti a partire da oggetti reali ma inaccessibili, questo modo di elaborare la teoria per trarne conseguenze osservabili può essere considerato una forma di sperimentazione. Tuttavia, per distinguerlo dalle sperimentazioni dirette, suggeriamo di designarlo col nome di 'esperienza concettuale'. È vero che questa espressione è quasi sempre impiegata in riferimento a situazioni in cui si tenta di chiarire un concetto attraverso un'esperienza immaginaria, da cui abitualmente non discende nessun effetto osservabile. Tuttavia, se ci prendiamo la libertà di ampliare in una certa misura il campo di applicazione di questo concetto è solamente per facilitare la comprensione di alcune delle argomentazioni di Ibn al-Hayṯam. Almeno per la loro funzione negativa, per il fatto cioè di essere impiegate soprattutto nella confutazione di una serie di tesi, e per il ruolo svolto dall'immaginazione scientifica nella loro ideazione, queste argomentazioni sono molto vicine alla nozione di 'esperienza concettuale', nell'accezione oggi comune dell'espressione. Si tratta, infatti, non della rappresentazione di una configurazione reale (come nel caso della modellizzazione) ma di configurazioni immaginarie che, pur non traducendosi mai in realtà, presuppongono già l'impiego di alcuni dati astronomici (le distanze tra la Luna e la Terra e tra il Sole e la Terra), così come quello delle leggi della propagazione della luce.
Nella categoria delle esperienze concettuali rientrano anche alcune delle argomentazioni già classificate come argomentazioni induttive o per modellizzazione. Tuttavia, il migliore esempio di questo genere di esperienza è contenuto nella Maqāla fī ḍaw᾽ al-qamar: ci riferiamo al modo in cui Ibn al-Hayṯam presenta la sua confutazione generale della tesi della riflessione della luce del Sole sulla superficie della Luna.
Questo genere di argomentazione si distingue dalla semplice modellizzazione anche per l'uso della matematica, evidente soprattutto nel calcolo delle dimensioni del luogo di riflessione (Tav. Ia e Ib). Questo calcolo in effetti è assimilabile al calcolo delle dimensioni dell'immagine di un oggetto (il Sole) in uno specchio sferico convesso (la Luna), che si trova a una data distanza dall'oggetto, così come è osservata da un punto (la Terra), le cui distanze dall'oggetto e dallo specchio siano note.
L'individuazione del punto di riflessione in uno specchio sferico convesso era uno dei quesiti posti nel famoso 'problema di Alhazen', risolto nel Libro V dell'Ottica attraverso l'intersezione di un cerchio e di un'iperbole. Ci si aspetterebbe che, passando da un punto-oggetto a un oggetto dotato di grandezza, il problema diventi matematicamente più complicato. Ma in effetti avviene il contrario. Questa semplicità è determinata dall'obiettivo che Ibn al-Hayṯam si propone: egli, infatti, calcola la grandezza del luogo di riflessione al solo scopo di confutare la tesi della riflessione.
Dal punto di vista formale, l'argomento di Ibn al-Hayṯam potrebbe essere considerato una dimostrazione per assurdo. Tuttavia, come abbiamo già osservato, in questa dimostrazione intervengono molti elementi: le dimensioni e le distanze del Sole e della Luna, così come le leggi della riflessione della luce. È il modo in cui l'autore riunisce elementi diversi, se non disparati, per ottenere un risultato osservabile da una teoria che inizialmente non ne presentava nessuno, che chiamiamo 'perfezionamento dello studio della teoria'. Presentando questo ragionamento come una semplice argomentazione per assurdo si finisce per non cogliere una caratteristica fondamentale del modo di procedere di Ibn al-Hayṯam. È vero che la dimostrazione in questione rivela un perfetto dominio dei metodi del ragionamento matematico, ma bisogna riconoscere che l'argomentazione per conseguire il suo obiettivo deve allontanarsi dal campo della geometria. Al contrario, senza la duplice applicazione dell'ottica all'astronomia e della geometria a entrambe le discipline, senza la possibilità di confrontare tra loro i dati delle diverse scienze dell'epoca, un tale risultato sarebbe inconcepibile.
Nel calcolo del luogo di riflessione, Ibn al-Hayṯam opera come un fisico e non come un matematico. Questa differenza è già stata messa in luce da Roshdi Rashed (1993a) nel contesto delle esperienze, in questo caso reali, dell'autore sulla rifrazione della luce.
Bibliografia
Biard 1997: Descartes et le Moyen Âge, édité par Joël Biard et Roshdi Rashed, Paris, Vrin, 1997.
Bodéüs 1993: Aristoteles, De l'âme, édité par Richard Bodéüs, Paris, Flammarion, 1993.
Bolton 1996: Bolton, Robert, Scepticisme et véracité de la perception dans le 'De anima' et la 'Métaphysique' d'Aristote, in: Corps et âme. Sur le De anima d'Aristote, sous la direction de Gilbert Romeyer Dherbey, études réunies par Cristina Viano, Paris, Vrin, 1996, pp. 295-329.
Dumont 1988: Les présocratiques, édité par Jean-Paul Dumont, avec la collaboration de Daniel Delattre et Jean-Louis Poirier, Paris, Gallimard, 1988.
Federici Vescovini 1965a: Federici Vescovini, Graziella, Studi sulla prospettiva medievale, Torino, Giappichelli, 1965 (rist.: 1987).
‒ 1965b: Federici Vescovini, Graziella, Contributo per la storia della fortuna di Alhazen in Italia. Il volgarizzamento del MS. Vat. 4595 e il 'Commentario terzo' del Ghiberti, "Rinascimento", 5, 1965, pp. 17-46.
‒ 1997: Federici Vescovini, Graziella, Descartes et les sciences curieuses. Le raisonnement ex suppositione et le Moyen Âge, in: Descartes et le Moyen Âge, édité par Joël Biard et Roshdi Rashed, Paris, Vrin, 1997, pp. 119-138.
Glasner 2001: Glasner, Ruth, Ibn Rushd's theory of 'Minima naturalia', "Arabic sciences and philosophy", 11, 2001, pp. 9-26.
Granger 1976: Granger, Gilles-Gaston, La théorie aristotélicienne de la science, Paris, Aubier Montaigne, 1976 (2. ed.: 2000).
Heath 1913: Heath, Thomas L., Aristarchus of Samos. The ancient Copernicus, Oxford, Clarendon, 1913 (rist.: New York, Dover, 1981).
Jolivet 1984: Études sur Avicenne, dirigées par Jean Jolivet et Roshdi Rashed, Paris, Les Belles Lettres, 1984.
Kohl 1924-25: Kohl, Karl, Über das Licht des Mondes. Eine Untersuchung von Ibn al-Haytham, "Sitzungsberichte der Physikalisch-medizinischen Sozietät in Erlangen", 56-57, 1924-1925, pp. 305-398.
Lejeune 1948: Lejeune, Albert, Euclide et Ptolémée, deux stades de l'optique géométrique grecque, Louvain, Bibliothèque de l'Université, Bureau du 'Recueil', 1948.
Lindberg 1976: Lindberg, David C., Theories of vision from Al-Kindi to Kepler, Chicago, University of Chicago Press, 1976.
Lloyd 1996: Lloyd, Geoffrey E.R., Aristotelian explorations, Cambridge-New York, Cambridge University Press, 1996.
Masoumi Hamedani 1999: Masoumi Hamedani, Hossein, Faḫr-e Rāzī wa Ibn Hayṯam, in: Ḫerad-e Jāvdān: Ǧashn-nāmeh ye Ostād Seyyed Jalāl al-Dīn Āštiyānī, édité par A.A. Mohammad-Khani et H. Seyyed Arab, Teheran, 1999, pp. 641-660.
‒ 2002: Masoumi Hamedani, Hossein, Ibn al-Hayṯam et la naissance d'une physique céleste, (Thèse de doctorat, Paris VII, 2002).
Morelon 1999: Morelon, Régis, Astronomie 'physique' et astronomie 'mathématique' dans l'astronomie précopernicienne, in: Les doctrines de la science de l'antiquité à l'âge classique, édité par Roshdi Rashed et Joël Biard, Leuven, Peeters, 1999, pp. 105-129.
Nazif 1942-43: Naẓīf, Muṣṭafā, Al-Ḥasan ibn al-Hayṯam, buhūṯu-hu wa-kušūfu-hu al-baṣariyya, Il Cairo, Ǧāmi῾at Fu᾽ād al-Awwal, 1942-1943, 2 v.
Omar 1977: Omar, Saleh Beshara, Ibn al-Haytham's optics. A study of the origins of experimental science, Minneapolis, Bibliotheca Islamica, 1977.
‒ 1981: Omar, Saleh Beshara, Al-Istiqrā᾽ ῾inda Ibn al-Hayṯam, "Journal for the history of Arabic science", 5, 1981, 1-2, pp. 175-190.
Pinès 1974: Pinès, Shlomo, Philosophy, mathematics and the concepts of space in the Middle Ages, in: The interaction between science and philosophy, edited by Yehuda Elkana, Atlantic Highlands (N.J.), Humanities, 1974, pp. 75-90.
Ragep 1993: Naṣīr al-Dīn al-Ṭūsī's Memoir on astronomy (Al-Taḏkira fī ῾ilm al-hay᾽a), edited and translated by F. Jamil Ragep, New York, Springer, 1993, 2 v.
Rashed 1968: Rashed, Roshdi, Le Discours de la lumière d'Ibn al-Haytham: traduction française critique, "Revue d'histoire des sciences", 21, 1968, pp. 197-224.
‒ 1970a: Rashed, Roshdi, Optique géométrique et doctrine optique chez Ibn al-Haytham, "Archive for history of exact sciences", 6, 1970, pp. 271-298.
‒ 1970b: Rashed, Roshdi, Le modèle de la sphère transparente et l'explication de l'arc-en-ciel: Ibn al-Haytham, al-Fārisī, "Revue d'histoire des sciences", 23, 1970, pp. 109-140.
‒ 1978: Rashed, Roshdi, Lumière et vision chez Ibn al-Haytham, in: Roemer et la vitesse de la lumière, avant-propos de René Taton, Paris, Vrin, 1978, pp. 19-44 (rist. in: Rashed, Roshdi, Optique et mathématiques. Recherches sur l'histoire de la pensée scientifique en arabe, Aldershot, Variorum, 1992, v. IV).
‒ 1984: Rashed, Roshdi, Mathématiques et philosophie chez Avicenne, in: Études sur Avicenne, dirigées par Jean Jolivet et Roshdi Rashed, Paris, Les Belles Lettres, 1984, pp. 29-39.
‒ 1990: Rashed, Roshdi, A pioneer in anaclastics. Ibn Sahl on burning mirrors and lenses, "Isis", 81, 1990, pp. 464-491.
‒ 1992: Rashed, Roshdi, Optique et mathématiques. Recherches sur l'histoire de la pensée scientifique en arabe, Aldershot, Variorum, 1992. 1993a: Rashed, Roshdi, Géométrie et dioptrique au Xe siècle: Ibn Sahl, al-Qūhī et Ibn al-Haytham, Paris, Les Belles Lettres, 1993.
‒ 1993b: Rashed, Roshdi, La philosophie des mathématiques d'Ibn al-Haytham, II: Les connus, "Mélanges de l'Institut dominicain d'études orientales du Caire", 21, 1993, pp. 87-275.
‒ 1993c: Rashed, Roshdi, Math. inf. II.
‒ 1996a: Encyclopedia of the history of Arabic science, edited by Roshdi Rashed, London-New York, Routledge, 1996, 3 v. (trad. franc.: Histoire des sciences arabes, sous la direction de Roshdi Rashed avec la collaboration de Régis Morelon, Paris, Seuil, 1997, 3 v.)
‒ 1996b: Rashed, Roshdi, Geometrical optics, in: Encyclopedia of the history of the Arabic science, edited by Roshdi Rashed, London-New York, Routledge, 1996, 3 v.; v. II: Mathematics and the physical sciences, pp. 643-671.
‒ 1997: Œuvres philosophiques et scientifiques d'al-Kindī, Leiden-New York, E.J. Brill, 1997-1998, 4 v.; v. I: L'optique et la catoptrique, par Roshdi Rashed, 1997.
‒ 1999: Les doctrines de la science de l'antiquité à l'âge classique, édité par Roshdi Rashed et Joël Biard, Louvain, Peeters, 1999.
‒ 2000a: Les catoptriciens grecs, textes établis, trad. et commentés par Roshdi Rashed, Paris, Les Belles Lettres, 2000-; v. I: Les miroirs ardents, 2000.
‒ 2000b: Rashed, Roshdi, Math. inf. III.
Russell 1996: Russell, Gül A., The emergence of physiological optics, in: Encyclopedia of the history of Arabic science, edited by Roshdi Rashed, London-New York, Routledge, 1996, 3 v.; v. II: Mathematics and the physical sciences, pp. 672-715.
Sabra 1966: Sabra, Abdelhamid I., Ibn al-Haytham's criticism of Ptolemy's Optics, "Journal of the history of philosophy", 4, 1966, pp. 145-149.
‒ 1971: Sabra, Abdelhamid I., The astronomical origins of Ibn al-Haytham's concept of experience, in: Actes du XIIe Congrès International d'Histoire des Sciences, Paris 1968, t. IIIA, Paris, Blanchard, 1971, pp. 133-136.
‒ 1972: Sabra, Abdelhamid I., Ibn al-Haytham, Abū ῾Alī al-Ḥasan ibn al-Ḥasan, in: Dictionary of scientific biography, edited by Charles C. Gillispie and Frederich L. Holmes, New York, Scribner, 1970-1990, 18 v.; v. VI, 1972, pp. 189-210.
‒ 1976: Sabra, Abdelhamid I., The physical and the mathematical in Ibn al-Haytham's theory of light and vision, Commemoration volume of Bīrūnī international congress in Tehran, Teheran, 1976, pp. 1-20.
‒ 1978: Sabra, Abdelhamid I., Sensation and inference in Alhazen's theory of visual perception, in: Studies in perception: interrelations in the history of philosophy of science, edited by Peter K. Machamer and Robert G. Turnbull, Columbus, Ohio State University Press, 1978, pp. 217-248.
‒ 1982: Sabra, Abdelhamid I., Ibn al-Haytham's lemmas for solving 'Alhazen's problem', "Archive for history of exact sciences", 26, 1982, pp. 299-324.
‒ 1989a: The Optics of Ibn al-Haytham, Books I-III: On direct vision, edited by Abdelhamid I. Sabra, London, The Warburg Institute, University of London, 1989, 2 v.
‒ 1989b: Sabra, Abdelhamid I., 'Form' in Ibn al-Haytham's theory of vision, "Zeitschrift für Geschichte der arabisch-islamischen Wissenschaften", 5, 1989, pp. 115-140.
‒ 1994: Sabra, Abdelhamid I., Optics, astronomy and logic: studies in Arabic science and philosophy, Aldershot, Variorum, 1994.
Saliba 1996: Saliba, George, Arabic planetary theories after the eleventh century A.D., in: Encyclopedia of the history of Arabic science, edited by Roshdi Rashed, London-New York, Routledge, 1996, 3 v.; v. I: Astronomy-theoretical an applied, pp. 58-127.
Schoy 1925: Schoy, Carl, Über die Natur der Spuren (Flecken) die man auf der Oberfläche des Mondes sieht: Abhandlungen des Schaichs Abu ῾Ali al-Hasan ibn al-Haitham, Hannover, Lafaire, 1925.
Schramm 1962: Schramm, Mathias, Ibn al-Haythams Weg zur Physik, Wiesbaden, Steiner, 1962.
Simon 1988: Simon, Gérard, Le regard, l'être et l'apparence dans l'optique de l'Antiquité, Paris, Seuil, 1988.
‒ 1992: Simon, Gérard, L'Optique d'Ibn al-Haytham et la tradition ptoléméenne, "Arabic sciences and philosophy", 2, 1992, pp. 203-236.
‒ 1997: Simon, Gérard, La psychologie de la vision chez Ptolémée et Ibn al-Haytham, in: Perspectives arabes et médiévales sur la tradition scientifique et philosophique grecque. Actes du colloque de la SIHSPAI, Paris 1993, édités par Ahmed Hasnawi, Abdelali Elamrani-Jamal et Maroun Aouad, Leuven, Peeters; Paris, Institut du monde arabe,1997, pp. 189-207.
Smith 1996: Smith, Mark A., Ptolemy's theory of visual perception. An English translation of the Optics with introduction and commentary, Philadelphia, The American philosophical society, 1996.
‒ 1998: Smith, Mark A., Ptolemy, Alhazen, and Kepler and the problem of optical images, "Arabic sciences and philosophy", 8, 1998, pp. 9-43.
‒ 2001: Smith, Mark A., The Latin source of the fourteenth-century Italian translation of Alhacen's 'De aspectibus' (Vat. Lat. 4595), "Arabic sciences and philosophy", 11, 2001, pp. 27-43.
Viano 1996: Corps et âme. Sur le De Anima d'Aristote, sous la direction de Gilbert Romeyer Dherbey, études réunies par Cristina Viano, Paris, Vrin, 1996.
Wiedemann 1906: Wiedemann, Eilhard, Über die Lage der Milchstrasse nach Ibn al-Haiṯam, "Sirius", 39, 1906, pp. 113-115.
‒ 1907: Wiedemann, Eilhard, Über eine Schrift von Ibn al-Haiṯam. Über die Beschaffenheit der Schatten, "Sitzungsberichte der Physikalisch-medizinischen Sozietät in Erlangen", 39, 1907, pp. 226-248.
‒ 1914: Wiedemann, Eilhard, Über die Camera obscura bei Ibn al-Haiṯam, "Sitzungsberichte der Physikalisch-medizinischen Sozietät in Erlangen", 46, 1914, pp. 155-169.