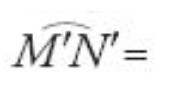La civiltà islamica: teoria fisica, metodo sperimentale e conoscenza approssimata. Cinematica
La civilta islamica: teoria fisica, metodo sperimentale e conoscenza approssimata. Cinematica
Cinematica
Sebbene la cinematica si configuri come scienza solamente molto più tardi, alcuni studiosi di geometria tra i secc. IX e XIII hanno dato importanti contributi a questo capitolo della meccanica. Se il caso di Ibn al-Hayṯam è uno dei più noti, nondimeno ancheṮābit ibn Qurra, al-Qūhī, al-Bīrūnī e Naṣīr al-Dīn al-ṭūsī si sono applicati a problemi di cinematica, sia celeste sia terrestre. Questi ultimi (la vicenda di Ibn al-Hayṯam è differente) hanno affrontato i problemi di meccanica da un punto di vista matematico, analizzando un movimento astratto in tutte le condizioni materiali, un movimento per così dire 'disincarnato'. Non rientrano nel loro approccio premesse fisiche, presupposti ontologici, ricerche sulla causa del movimento, o riflessioni sul motore: il loro studio è puramente cinematico. Il corpo di cui si esamina il movimento è assimilato a un punto, non interessano né ciò di cui è fatto né la sua forma, e il luogo in cui si muove è lo spazio omogeneo della geometria euclidea; di conseguenza le contrapposizioni della fisica aristotelica tra movimento naturale e movimento violento, da un lato, e tra mondo sublunare e mondo celeste, dall'altro, non sono prese in considerazione. Questi studi, che vertono su alcuni aspetti definiti della cinematica, finiscono per mettere in discussione in modo radicale certi punti ‒ tutt'altro che irrilevanti ‒ della Fisica aristotelica.
Ṯābit ibn Qurra, al-Bīrūnī e il concetto di velocità istantanea
Sebbene i trattati pervenutici non contengano alcuna definizione della velocità, inclusa quella media, la maggior parte degli autori, in particolare gli astronomi, fa frequentemente uso della velocità media; si parla di uguaglianza di velocità (quando i corpi in moto percorrono distanze uguali in tempi uguali), di movimento più veloce (quando un punto mobile percorre la stessa distanza di un altro in un tempo più breve o percorre una distanza maggiore nello stesso tempo) o più lento, di movimento uniforme (quando distanze uguali sono percorse in tempi uguali). Inoltre, secondo Aristotele e la tradizione peripatetica, ogni movimento ha luogo in un tempo e non in un istante ‒ in ogni momento l'oggetto in moto occupa soltanto potenzialmente una posizione determinata ‒, la nozione di velocità istantanea o di moto istantaneo è priva di qualsiasi significato.
Tuttavia, nel quadro generale dell'analisi matematica di un movimento accelerato o di un movimento ritardato, il matematico e astronomo Ṯābit ibn Qurra, nel IX sec., seguito poi da al-Bīrūnī nell'XI sec., arriva a definire la nozione di velocità in un punto o, secondo la sua terminologia, quella di movimento in un punto.
Ṯābit ibn Qurra (210-288/826-901), al quale si devono numerosi e pregevoli lavori di matematica infinitesimale, aritmetica e astronomia, è autore di un trattato intitolato Kitāb fī ibṭā᾽ al-ḥaraka fī falak al-burūǧ wa-sur῾ati-hā bi-ḥasab al-mawāḍi῾allatī takūn fī-hā min al-falak al-ḫāriǧ al-markaz (Rallentamento e accelerazione del moto [apparente di un mobile] sull'eclittica a seconda del luogo in cui si produce il moto sull'eccentrico). In questo trattato egli analizza il movimento apparente sull'eclittica di un astro (o di qualsiasi altro oggetto mobile, materiale e non) animato da un movimento circolare uniforme su un eccentrico, determinando il punto in cui il movimento apparente è più lento, quello in cui è più veloce e quello in cui è uguale al movimento medio.
In primo luogo dimostra un teorema enunciato in questi termini: "Quando il movimento di un astro o [del centro] di un'orbita qualunque è uniforme su un eccentrico, il suo movimento apparente più lento sull'eclittica si verifica quando [il mobile] è all'apogeo del suo eccentrico, e il suo movimento apparente più veloce quando è al suo perigeo. Per il resto, il movimento apparente, quando si produce in prossimità dell'apogeo, è più lento rispetto a quando si trova lontano da esso" (Œuvres d'astronomie, p. 73).
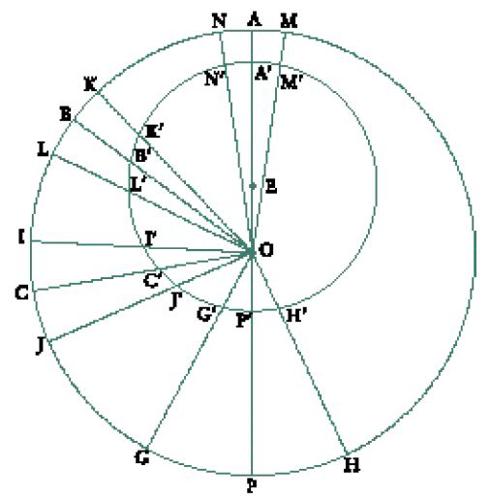
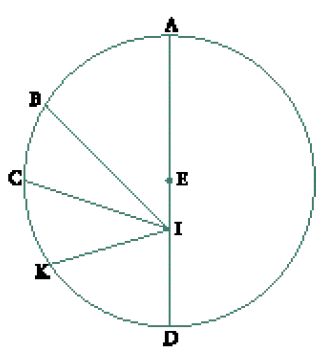
Siano A′, B′, C′, P′ punti sul perimetro di un cerchio di centro E (eccentrico), e A, B, C, P quelli sul cerchio dell'eclittica di centro O, A′ l'apogeo e P′ il perigeo dell'eccentrico (fig. 1). Un qualunque punto mobile descrive l'eccentrico con un movimento circolare uniforme; quando questo mobile è in A′ (rispettivamente B′, C′, P′) è visto in A (rispettivamente B, C, P) sul cerchio dell'eclittica da un osservatore situato in O; supponiamo che il punto B sia più vicino al punto A del punto C. Poiché il punto mobile è animato da un movimento circolare uniforme sull'eccentrico, gli archi uguali M′N′, K′L′, I′J′ e G′H′, centrati rispettivamente in A′, B′, C′ e P′, qualunque essi siano (e quindi per quanto piccoli siano), sono percorsi in tempi uguali. Ṯābit dimostra, con l'ausilio di due lemmi geometrici preliminarmente stabiliti, che se
,
allora
Questi archi dell'eclittica sono percorsi in tempi uguali ‒ quelli durante i quali il punto mobile percorre con moto circolare uniforme sul cerchio dell'eccentrico gli archi uguali M′N′, K′L′, I′J′, G′H′‒; questo risultato è vero qualunque siano gli archi uguali M′N′, K′L′, I′J′ e G′H′, e dunque qualunque sia l'intervallo di tempo considerato (per quanto piccolo sia). Ṯābit ibn Qurra conclude quindi, mediante un implicito passaggio al limite, che "l'avanzamento apparente sull'eclittica è più lento quando [il mobile] si trova nel punto A′, è più rapido quando si trova nel punto P′. In un luogo vicino ad A′ l'avanzamento è più lento che in un luogo lontano da esso" (ibidem).
Il movimento apparente nel punto P è quindi più veloce che nel punto C, a sua volta più veloce che nel punto B, a sua volta più veloce che nel punto A.
La considerazione di un movimento intermedio, vale a dire quello del punto mobile sul cerchio eccentrico, permette a Ṯābit ibn Qurra di far corrispondere ad archi sull'eclittica archi sull'eccentrico e di ricondurre questo problema di cinematica a un problema puramente geometrico. Aver stabilito una disuguaglianza sugli archi (dell'eclittica), valida qualunque siano gli archi corrispondenti dell'eccentrico, e dunque qualunque sia l'intervallo di tempo considerato, gli permette in seguito, con un passaggio implicito al limite e conservando la relazione di ordine, di poter dedurre una disuguaglianza per le velocità istantanee.
Ṯābit ibn Qurra enuncia poi un secondo teorema: "Quanto al movimento medio uniforme sull'eclittica, non si produce realmente in alcun luogo di essa; ma vi sono due punti dell'eccentrico tali per cui quando il movimento medio si produce fra uno di essi e l'apogeo, è sempre superiore al movimento apparente, e quando il movimento medio si produce fra uno di essi e il perigeo, è sempre inferiore al movimento apparente. Questi due punti sono quelli la cui distanza dall'apogeo, in movimento apparente sull'eclittica, è pari a un quarto di cerchio. Più il movimento [apparente] si avvicina a uno di questi due punti, più esso tende a essere uguale al movimento medio; e ogni volta che, da una parte e dall'altra di uno di questi due punti, si prendono 'due archi' di movimento apparente sull'eclittica, in modo tale che siano uguali, la loro somma è uguale, realmente, al movimento medio. Sono questi due punti che assomigliano a due punti del movimento medio" (ibidem, pp. 78-79).
Le velocità che intervengono in questo secondo teorema sono velocità angolari. Il punto mobile, essendo animato da un movimento circolare uniforme sull'eccentrico, percorre archi uguali in tempi uguali; poiché un giro completo del suo movimento apparente sull'eclittica si compie nello stesso tempo di un giro completo sull'eccentrico, la sua velocità angolare media sull'eclittica è uguale alla sua velocità sull'eccentrico. Come nel teorema precedente, il ricorso a un movimento uniforme, quello del punto mobile sull'eccentrico, permette a Ṯābit di dimostrare questo teorema in senso geometrico.
Facendo uso delle notazioni precedenti, sia OB un raggio perpendicolare ad AP che interseca l'eccentrico in B′, H e I due punti dell'eclittica simmetrici rispetto a B, ai quali corrispondono i punti H′ e I′ dell'eccentrico (fig. 2): si ha dunque
Ibn Qurra dimostra quindi che
Di conseguenza, quando il punto mobile si sposta da H′ a B′ sull'eccentrico, è visto da O spostarsi, nello stesso tempo, da H a B sull'eclittica; la sua velocità angolare apparente tra H e B è quindi inferiore alla sua velocità angolare sull'eccentrico, ossia alla sua velocità angolare media sull'eclittica.
Allo stesso modo, poiché
,
la velocità angolare apparente fra B e I è superiore alla velocità angolare media. Ṯābit ibn Qurra afferma quindi quanto segue: "Poiché è così, e poiché abbiamo dimostrato che più il movimento si avvicina al punto A più è lento sull'eclittica, e che più si avvicina al punto P più è veloce, risulta chiaro che in tutto questo vi è un avvicinamento all'uguaglianza con il movimento medio quando vi è avvicinamento al punto B" (ibidem, p. 81).
Poiché la velocità apparente cresce fra A e P, è inferiore alla velocità media prima del punto B e superiore a essa dopo, Ṯābit afferma che la velocità apparente tende verso la velocità media nel punto B, supponendo implicitamente che questa velocità cambi in modo continuo fra A e P. Egli dimostra inoltre che HOI = I'EH';
essendo gli archi HI e H′I′ percorsi nello stesso tempo, la velocità angolare apparente del mobile fra H e I è uguale alla velocità angolare fra H′ e I′, ossia alla velocità media, e questo qualunque sia l'arco HI attorno al punto B (per quanto piccolo sia). Tramite un implicito passaggio al limite, la velocità angolare apparente nel punto B è dunque uguale alla velocità media; Ṯābit può quindi concludere che "il movimento apparente è uguale in questo caso al movimento medio" (ibidem, p. 82).
Da quest'esempio si vede come, senza aver bisogno di definire la velocità ‒ né la velocità istantanea né quella media ‒, ma semplicemente usando le regole abituali di confronto fra le velocità medie (dei movimenti) menzionate all'inizio di questo paragrafo, insieme ad alcuni impliciti passaggi al limite, Ṯābit è in grado non di definire, ma di confrontare le velocità istantanee in diversi punti: gli unici postulati impliciti qui sono che le velocità variano in modo continuo e che i passaggi al limite conservano le relazioni d'ordine. Non è senz'altro un caso che questa dimostrazione sia opera di un matematico che ha dato un contributo notevole alla matematica infinitesimale, e che quindi aveva familiarità con il metodo di esaustione e i passaggi al limite che esso sottende: il punto di una retta o di un arco è il limite di un segmento o di un arco, come l'istante è il limite di una durata, il che riafferma l'equivalenza tra la struttura del tempo e quella della linea.
Sempre su questa equivalenza si fonda la sua dimostrazione del postulato delle parallele in cui una retta è generata dal movimento uniforme di un punto. La nozione di infinito in atto è contenuta in nuce in queste dimostrazioni. Il teorema è ripreso nell'XI sec. da al-Bīrūnī nel suo studio sullo spostamento dell'apogeo solare, contenuto nel cap. VIII del Libro VI della sua enciclopedia astronomica al-Qānūn al-mas῾ūdī (Canone [astronomico] dedicato ad al-Mas῾ūd), un'opera composta a Ghazna fra il 421/1030 e il 427/1036 e dedicata al sultano al-Mas῾ūd. Al-Bīrūnī, che abitualmente cita tutte le fonti cui attinge, non menziona Ṯābit ibn Qurra, una circostanza che sembra attestare come egli non conoscesse il testo di quest'ultimo.
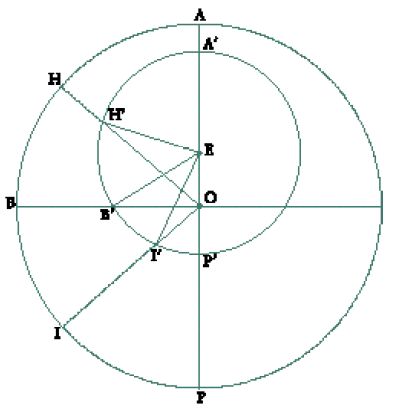
Al-Bīrūnī, avvalendosi di un metodo diverso da quello di Ṯābit, dimostra (fig. 3) che se
,
allora
,
e ne deduce quindi, come Ṯābit, ma senza entrare nei dettagli della dimostrazione, che la velocità minima (o, con le sue parole, la lentezza estrema del movimento) è all'apogeo e che l'estremo della velocità è al perigeo, poiché il rallentamento o l'accelerazione del movimento si producono secondo l'aumento o la diminuzione dell'angolo al vertice I che intercetta un arco di grandezza fissata.
Al-Qūhī, critico di Aristotele
Si devono ad al-Qūhī, insigne studioso di geometria attivo nella seconda metà del X sec., alcuni lavori innovativi riguardanti la matematica infinitesimale e le proiezioni, che egli contribuì a rendere un capitolo autonomo nell'ambito della matematica. Al-Qūhī si interessò inoltre dell'applicazione della matematica all'astronomia e alla statica (studi sul centro di gravità, sulla geometria delle coniche e studio degli strumenti matematici, come l'astrolabio e il compasso perfetto).
Al-Qūhī, presentato dai suoi contemporanei come un eminente studioso che non si occupava né di teologia né di metafisica, faceva parte dell'entourage dell'emiro buwayhide ῾Aḍud al-Dawla a Baghdad. In questo ambiente, che riuniva filosofi e sapienti ‒ fra cui Abū 'l-Faraǧ ibn al-ṭayyib, al quale si deve uno dei commentari alla Fisica di Aristotele ‒ si discuteva di matematica, di astronomia e di filosofia; del resto, al-Qūhī critica proprio due delle proposizioni aristoteliche presentate nella parte del commentario di Abū 'l-Faraǧ pervenutaci: si tratta dell'asserzione secondo cui è impossibile che in un tempo finito abbia luogo un movimento infinito e quella per cui tra due movimenti contrari vi è necessariamente un tempo di quiete (Rashed 1999).
Aristotele, nel Libro VI della Fisica (VI 7, 238a 20-37), dimostra l'impossibilità di percorrere una distanza finita in un tempo infinito e, viceversa, l'impossibilità di percorrere una distanza infinita in un tempo finito. Questa tesi, che nessuno si era azzardato a contestare prima di al-Qūhī, è una vera e propria opinione comune che egli contraddice, affermando in tal modo l'esistenza dell'infinito in atto; è possibile che al-Qūhī, di cui sono note le riserve a proposito della metafisica, così facendo abbia voluto dimostrare la debolezza dei fondamenti della fisica dei filosofi. Per stabilire la possibilità di un movimento infinito in un tempo finito, al-Qūhī concepisce l'esperienza teorica che segue.
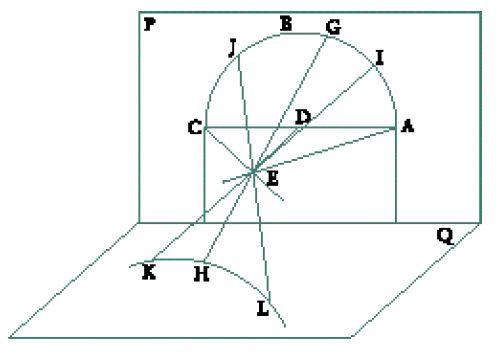
Siano due piani P e Q perpendicolari, si consideri nel piano P un semicerchio ABC, di diametro AC parallelo alla retta d'intersezione dei due piani, e sia D il punto di mezzo di AC (fig. 4). Uno gnomone DE di lunghezza l è perpendicolare al piano P. Quando una sorgente luminosa descrive l'arco ABC (movimento che ha luogo in un tempo finito, poiché l'arco è di lunghezza finita) l'estremità dell'ombra dello gnomone descrive nel piano Q un ramo d'iperbole LHK (proiezione conica studiata da al-Qūhī). Il movimento dell'estremità dell'ombra dello gnomone non ha né inizio né fine (dunque è infinito). In effetti, se H è un punto qualunque del ramo d'iperbole, esso non può essere né "l'inizio" del movimento né la sua "fine" poiché la retta HE interseca il piano P in G, che è distinto da A e C, punti che non danno ombra. Esiste quindi un punto I dell'arco AG, distinto da A e da G, e un punto J dell'arco GC, distinto da G e da C. La sorgente luminosa passa quindi prima in I (proiettando un'ombra in K) poi in G (proiettando un'ombra in H) poi in J (proiettando un'ombra in L) e H non è né l'inizio né la fine del movimento. A ogni punto del semicerchio la proiezione conica fa corrispondere un punto del ramo d'iperbole, e viceversa. Questa proiezione trasforma un insieme limitato ma non chiuso ‒ l'arco aperto AC del cerchio ‒ in un insieme non limitato ‒ il ramo d'iperbole.
Purtroppo il ragionamento di al-Qūhī, per essere corretto, presuppone la propagazione istantanea della luce; poiché la lunghezza IK (rispettivamente JL) tende all'infinito quando il punto I (rispettivamente J) si avvicina al punto A (rispettivamente C), il tempo impiegato dalla luce per percorrere questa distanza tende ugualmente all'infinito. Consideriamo, a giustificazione delle argomentazioni di al-Qūhī, che la propagazione istantanea, sia del raggio luminoso sia del raggio visivo, sembra essere stata generalmente ammessa: si deve attendere Ibn al-Hayṯam, per il quale il movimento nel tempo della luce è una delle premesse necessarie per fondare la sua analogia fra la riflessione di un raggio luminoso e i fenomeni d'urto, perché questa opinione comune sia posta in discussione.
L'oggetto della seconda esperienza consiste nel provare l'esistenza di due movimenti contrari non separati da un tempo di quiete. L'importanza strategica dell'esistenza di un momento di arresto tra due movimenti rettilinei opposti (quies media) è stata già sottolineata. Il problema della quies media, prima di al-Qūhī, aveva interessato anche alcuni matematici: Ibn Karnīb, secondo il biografo e bibliografo al-Nadīm, avrebbe scritto un testo per confutare l'affermazione di Ṯābit ibn Qurra secondo cui tra due movimenti contrari non vi sarebbe quies media; tuttavia questi testi non sono giunti fino a noi.
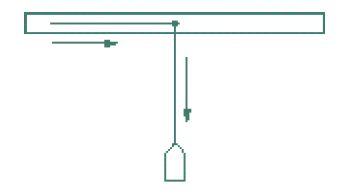
Della seconda esperienza di al-Qūhī purtroppo ci è pervenuta unicamente ‒ e per di più in modo indiretto ‒ la descrizione del processo sperimentale utilizzato, senza riferimento ad alcuna dimostrazione.
Un regolo orizzontale di lunghezza 2a ha al suo centro un foro. Attraverso questo foro passa un filo di lunghezza 2a alla cui estremità è agganciato un peso; quando una navetta sposta con un movimento uniforme l'estremità del filo sul regolo orizzontale, il peso si muove di un moto verticale uniforme, di velocità numericamente uguale a quella della navetta, discendente durante la prima metà del movimento; poi, senza interruzione poiché il movimento della navetta non si interrompe quando essa passa al livello del foro, ascendente durante la seconda metà: "la salita del peso e la sua discesa sono due movimenti contrari, sebbene siano entrambi effetto del medesimo oggetto in movimento che non cessa di muoversi; se dunque sono gli effetti di un oggetto in movimento che non cessa di muoversi, ne consegue necessariamente che esistono due movimenti contrari senza quiete fra di essi" (Rashed 1999, p. 22).
Quest'esperienza mette in luce, in modo assai più agevole da osservare rispetto ai fenomeni d'urto, l'esistenza di due movimenti contrari non separati da un tempo di arresto e dunque di una discontinuità nella velocità.
C'è da osservare che il matematico, contrariamente ai filosofi, non cerca in questi testi di correggere la dottrina fisica con un'argomentazione dialettica, ma fabbrica more geometrico due controesempi che provano la falsità delle tesi proposte. Il valore dimostrativo di queste due esperienze non dipende dal fatto che siano o meno realizzate; lo studioso immagina ‒ senza che vi sia neppure bisogno di realizzarli realmente ‒ due dispositivi materiali che mostrano, l'uno, l'esistenza di un movimento infinito che si compie in un tempo finito, l'altro l'esistenza di due movimenti contrari non separati da un tempo di quiete. L'esperienza, pur essendo di natura speculativa, "consente in questo caso di verificare l'ipotesi fisica e di progredire grazie alla geometria con un duplice controllo, linguistico e sperimentale: l'incontro fra la matematica e la filosofia crea un luogo nuovo in cui le idee meccaniche sono pensate e verificate diversamente" (ibidem, p. 19).
Naṣīr al-Dīn al-ṭūsī e la coppia di al-ṭūsī
Naṣīr al-Dīn al-ṭūsī (1201-1274), matematico e astronomo, all'inizio del cap. 11 della Taḏkira fī ῾ilm al-hay᾽a (Memorandum di astronomia), dimostra un lemma che ha dato origine a una vasta letteratura (Ragep 1993). In questo lemma tecnico egli mostra che, componendo due movimenti circolari uniformi, si può ottenere un movimento rettilineo che è noto con il nome di 'coppia di al-ṭūsī'. Grazie a questo lemma, egli è in grado di eliminare le difficoltà del modello lunare di Tolomeo, in particolare "l'incapacità di questo modello di permettere al centro dell'eclittica di avvicinarsi al centro dell'Universo e di allontanarsene senza aver bisogno di introdurre il meccanismo del girabacchino di Tolomeo" (Saliba 1997, p. 107); questo modello può essere applicato anche ai pianeti superiori.
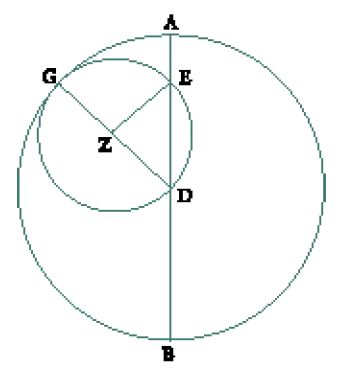
Siano quindi dati due cerchi, il primo (C) di centro D e di raggio DG, l'altro (C′) di centro Z e di raggio ZD=1/2 DG (fig. 6); il cerchio C è animato da un movimento di rotazione verso sinistra e il cerchio C′ è animato da un movimento di rotazione verso destra, due volte più veloce, restando comunque tangente internamente al primo in un punto G assegnato di C; sia AB una retta fissa passante per D e il punto E dato di C′. Si vuole studiare il movimento del punto E.
Per al-ṭūsī, come per gli astronomi venuti prima e dopo di lui, essendo i movimenti studiati per definizione circolari uniformi, confrontare tali movimenti consiste nel confrontare i periodi di rivoluzione: il cerchio C′ effettua due giri (rispettivamente 1/2 giro) quando il cerchio C effettua un giro (rispettivamente 1/4 di giro).
Sarebbe equivalente, in senso geometrico se non fisico, descrivere questo movimento lasciando fisso il cerchio C e immaginando che il cerchio C′ ruoti senza scivolare all'interno del cerchio C, ossia che il centro Z del cerchio C′ ruoti intorno al punto D con un movimento circolare uniforme mentre il cerchio C′ è animato da un movimento di rotazione intorno a Z in senso inverso e due volte più veloce.
Al-ṭūsī dimostra quindi che il punto E descrive il segmento AB: all'inizio del movimento i punti G ed E coincidono con il punto A; a un istante qualunque il punto G ha descritto l'arco AG mentre il punto E ha descritto l'arco GE. Al-ṭūsī afferma dunque che l'arco GE è simile (šabīh) ‒ e non uguale, come appare invece nella traduzione di Ragep ‒ a due volte l'arco GA, precisando poi cosa intende per archi simili: archi di cerchio simili (su cerchi differenti) sono archi intercettati da angoli al centro uguali. Si ha quindi
questa uguaglianza traduce geometricamente la relazione cinematica tra i periodi di rivoluzione o, in altre parole, le velocità angolari. A partire da qui la dimostrazione è puramente geometrica: riferendosi al triangolo isoscele DZE, si ha che
dunque
e i punti D, A, E sono allineati.
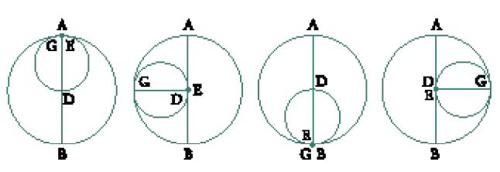
La proposizione reciproca, che non è menzionata da al-ṭūsī, risulta immediata e stabilisce che ogni punto del segmento AB corrisponde a una posizione relativa dei due cerchi a un istante dato. Il punto E descrive dunque il segmento AB oscillando fra A e B (fig. 7).
F. Jamil Ragep (1993, II, p. 432) segnala che il lemma di al-ṭūsī è ripreso da Quṭb al-Dīn al-Šīrāzī nell'opera Tuḥfa al-šāhiyya (Dono regale) per dimostrare l'impossibilità della quies media fra un movimento ascendente e discendente lungo un diametro terrestre.
L'importanza di questo lemma, indipendentemente dal suo scopo immediato ‒ proporre un modello lunare diverso da quello di Tolomeo ‒, è messa in risalto più volte: dato che un movimento rettilineo può essere ottenuto mediante la composizione di due movimenti circolari uniformi, ciò fa apparire un movimento rettilineo nel mondo sovralunare, soggetto in linea di principio ai soli movimenti circolari uniformi eterni.
Conclusioni
Questi esempi di studi sulla cinematica prodotti da geometri ‒ esempi che non sono senz'altro gli unici, dal momento che la conoscenza di questo settore è ben lungi dall'essere completa ‒ sono la dimostrazione dell'interesse che alcuni di loro avevano rivolto a questo tipo di ricerche, assai prima che la disciplina si costituisse in quanto tale: infatti, bisogna attendere Galilei per poter assistere agli esordi della cinematica come disciplina autonoma. I lavori cinematici di questi studiosi di geometria, come si è visto, finiscono per rimettere in discussione certe tesi ‒ non di scarso rilievo ‒ della fisica aristotelica sul movimento. In primo luogo, per gli studiosi di geometria, lo spazio in cui ha luogo il movimento rappresenta lo spazio omogeneo della geometria euclidea e non lo spazio geocentrato della filosofia naturale; pertanto, ai loro occhi, la nozione di 'luogo naturale' perde la sua pertinenza. A quest'epoca, del resto, risale il primo tentativo di geometrizzazione del luogo da parte di Ibn al-Hayṯam (Rashed 2002), con la conseguenza di eludere l'opposizione tra movimento naturale e movimento forzato, o l'opposizione fra mondo sovralunare e mondo sublunare, in quanto quest'ultima era stata ugualmente messa in discussione dall'esistenza della 'coppia di al-ṭūsī'. D'altra parte, la negazione della necessità della quies media ‒ di cui sono state accennate già in precedenza le ricadute ‒ avvalora certe posizioni dei mutaziliti sul movimento e contribuisce a minare, dall'esterno, la fisica aristotelica.
Bibliografia
Hartner 1963: Hartner Willy - Schramm, Matthias, Al-Bīrūnī and the theory of the solar apogee. An example of originality in Arabic science, in: Scientific change. Historical studies in the intellectual, social and technical conditions for scientific discovery and technical invention, from antiquity to the present, edited by Alistair C. Crombie, London, Heinemann, 1963, pp. 206-218.
Morelon 1987: Morelon, Régis, Thābit ibn Qurra, Œuvres d'astronomie, Paris, Les Belles Lettres, 1987.
Ragep 1993: Naṣīr al-Dīn al-Ṭūsī's. Memoir on astronomy (Al-Taḏkira fī ῾ilm al-hay᾽a), edited and translated by F. Jamil Ragep, New York, Springer, 1993, 2 v.
Rashed 1993: Rashed, Roshdi, Géométrie et dioptrique: Ibn Sahl, al-Qūhī et Ibn al-Haytham, Paris, Les Belles Lettres, 1993.
‒ 1996: Rashed, Roshdi, Math. inf. I.
‒ 1999: Rashed, Roshdi, Al-Qūhī vs. Aristotle: on motion, "Arabic sciences and philosophy", 9, 1999, pp. 7-24.
‒ 2002: Rashed, Roshdi, Math. inf. IV.
Saliba 1997: Saliba, Georges, Les théories planétaires en astronomie arabe après le Xe siècle, in: Histoire des sciences arabes, sous la direction de Roshdi Rashed avec la collaboration de Régis Morelon, Paris, Seuil, 1997, 3 v.; v. I: Astronomie, théorique et appliquée, pp. 71-138.