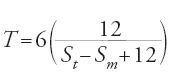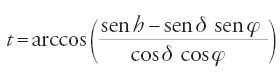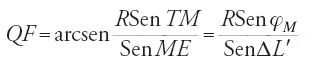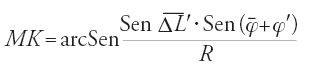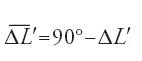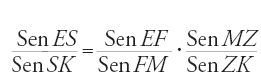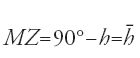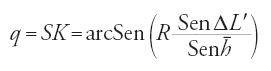La civiltà islamica: osservazioni, calcolo e modelli in astronomia. Mīqāt, qibla, gnomonica

La civilta islamica: osservazioni, calcolo e modelli in astronomia. Miqat, qibla, gnomonica

Mīqāt, qibla, gnomonica

Si può affermare che il contributo più originale dell'astronomia araba si ebbe sul piano teorico. Molti degli studiosi cui si devono progressi significativi si occuparono però anche di problemi di astronomia pratica, alcuni dei quali toccavano aspetti della religione islamica, mentre altri si riferivano a necessità pratiche di interesse generale. Un esempio di queste ultime è la determinazione della posizione di una località rispetto a un'altra, che presupponeva la conoscenza della latitudine e della longitudine delle due località e altre nozioni di geografia matematica. I problemi religiosi erano invece legati al culto e comprendevano la determinazione delle ore delle preghiere (mīqāt), del momento del levar del Sole e del tramonto nei periodi di digiuno, della direzione della Mecca (qibla) e della visibilità della falce di Luna per stabilire l'inizio del mese, nonché i calcoli per il calendario e per la corrispondenza tra l'anno astronomico e il suo valore arrotondato. Le tecniche usate andavano da semplici approssimazioni a metodi matematici complessi; questi ultimi avrebbero anche dato luogo ad analisi teoriche di portata molto più vasta rispetto ai problemi presi in esame.

I primi musulmani non disponevano di metodi matematici avanzati e per risolvere i problemi più comuni posti dalla religione ricorrevano all'astronomia popolare. La tradizione non scientifica forniva regole pratiche per il calendario lunare, per i momenti riservati alle preghiere e per la qibla, che continuarono a essere applicate e anzi raccomandate dai 'giuristi' islamici anche dopo l'introduzione e la diffusione di metodi scientifici più avanzati. Per regolare il calendario lunare bastava l'osservazione della falce di Luna; le ore della preghiera si determinavano con semplici calcoli sulle ombre; e per la qibla bastavano la direzione del vento e alcuni fenomeni osservabili all'orizzonte.

La presenza della tradizione popolare accanto a quella scientifica degli astronomi non diede luogo a conflitti. Con rare eccezioni, giuristi e astronomi si richiamavano alle due tradizioni senza che gli uni cercassero mai di mettere in discussione l'autorità degli altri. Se i giuristi non si attenevano agli standard matematici rigorosi degli astronomi, non per questo cercavano di svalutarli o rigettarli; analogamente, se agli astronomi capitava di rimarcare le inesattezze della tradizione popolare ‒ cosa che accadeva raramente ‒, tali osservazioni erano molto discrete e non miravano a mettere in discussione la validità dell'approccio dei giuristi. Vari fattori possono aver contribuito a questa tranquilla coesistenza; vi ritorneremo più avanti. Diciamo però subito che il motivo più probabile è che ciascuno dei due gruppi era conscio della validità dei metodi usati dall'altro e dei limiti dei propri. I dottori dell'Islam sapevano che i metodi degli astronomi erano più accurati, ma ritenevano giustamente che, spesso, per rispondere alle necessità della religione i loro fossero sufficientemente precisi. Gli astronomi dovevano, d'altra parte, riconoscere che i metodi popolari davano approssimazioni spesso accettabili, mentre i loro erano troppo complicati per godere di un'ampia diffusione. In altri termini, i diversi metodi avevano importanza in ambiti differenti.

Tuttavia, con l'istituzione della figura del muwaqqit (addetto al computo del tempo della moschea) nel XIII sec., il divario cominciò a diminuire. Le conoscenze tecniche divennero più accessibili grazie alla compilazione di tavole dettagliate, che rendevano rapidamente utilizzabili i risultati ottenuti con metodi matematici. La costruzione di speciali strumenti, che permettevano di risolvere comodamente vari problemi di natura religiosa, si può considerare anch'essa un tentativo di estendere a un pubblico più vasto l'utilizzazione delle conoscenze e delle pratiche matematiche degli specialisti. L'uso largamente diffuso di tavole per il computo del tempo, testimoniato dai numerosi esemplari che ci sono pervenuti, dimostra che il tentativo ebbe un certo successo. Le tavole, con centinaia di migliaia di voci, erano opera di muwaqqit alle dipendenze delle maggiori moschee della Siria e dell'Egitto. Prodotte all'interno della massima istituzione religiosa islamica, la moschea, non erano messe in discussione ma, al contrario, utilizzate dai giuristi islamici e da altri funzionari religiosi.

Il corpus delle tavole astronomiche è notevole. Esse si trovano infatti sia nelle compilazioni astronomiche dette zīǧ, sia in raccolte da consultare per problemi specifici, e coprono una grande varietà di argomenti avvalendosi di metodi di calcolo di varia complessità. Tra le più semplici vi sono le tavole di moltiplicazione per il sistema sessagesimale. La maggior parte delle tavole contenute negli zīǧ tratta problemi di astronomia sferica: equazioni dei pianeti, latitudini, parallasse, visibilità della Luna e dei pianeti, calcolo di eclissi. Vi sono anche esempi di tavole di astronomia sferica non incluse in zīǧ, come quelle di Ibn Yūnus (m. 1009), che riguardano l'ascensione obliqua calcolata per ciascun grado di latitudine terrestre e di longitudine dell'eclittica. Altre tavole presentano funzioni ausiliarie per calcoli di astronomia sferica: vi era tabulata una serie di funzioni matematiche che permetteva, con rimandi da una tavola all'altra e mediante semplici operazioni aritmetiche (addizioni e sottrazioni), di risolvere i problemi più comuni. Il primo astronomo a compilarle fu Ḥabaš al-Ḥāsib, nel IX sec.; altre, molto più complicate (contenenti circa 13.000 valori), sono opera di Šams al-Dīn al-Ḫalīlī, uno studioso attivo nel XIV sec. a Damasco. Vi sono anche tavole per astrolabi e quadranti solari, per la qibla e per le ore delle preghiere.

Il corpus più numeroso fra i diversi tipi di tavole riguarda la determinazione delle ore della preghiera per mezzo dell'osservazione del Sole e delle stelle. In genere queste tavole erano indipendenti dagli zīǧ e sono rilevanti per l'alta precisione e la sofisticata abilità matematica (si fa uso di schemi di interpolazione) che esse presuppongono. Ugualmente importante era il loro ruolo sul piano sociale; infatti sulla base delle numerose tavole e copie che ci sono pervenute, si può concludere che la determinazione delle ore della preghiera ebbe il beneplacito delle autorità religiose e che impegnò per lungo tempo numerosi astronomi. Inoltre, a partire dal XIII sec., tale attività si svolse all'interno delle istituzioni religiose.

La scienza del computo del tempo

La scienza del computo astronomico del tempo (῾ilm al-mīqāt) si occupava principalmente di misurare il tempo in base all'osservazione del Sole e delle stelle e di stabilire le ore della preghiera quotidiana, due compiti strettamente collegati. Si trattava quindi di un campo di ricerca nel quale si incontravano religione e scienza. Nei primi tempi dell'Islam era il muezzin a stabilire le ore della preghiera, aiutandosi con semplici tavole delle ombre e con tecniche di astronomia popolare; un'impostazione più scientifica si affermò invece quando gli Arabi ebbero acquisito una maggiore esperienza nell'astronomia matematica. I calcoli degli astronomi, apprezzati all'inizio soltanto da un ristretto gruppo di scienziati, finirono per imporsi e prendere il posto di quelli dei muezzin. La creazione della carica di muwaqqit dimostra chiaramente che l'istituzione religiosa riconosceva ufficialmente l'autorità dei metodi scientifici degli astronomi. Le prime testimonianze di questa carica risalgono al XIII sec., sotto il regno dei Mamelucchi: a partire da questo periodo furono compilate molte tavole e ideati numerosi strumenti, per risolvere problemi sia locali, riferiti a particolari latitudini, sia generali, per latitudini qualsiasi.

Nel XIII e nel XIV sec. il computo del tempo si diffuse come attività ufficialmente riconosciuta in tutta la Siria e l'Egitto dei Mamelucchi, e questa pratica continuò nel periodo ottomano fino al XIX secolo. Essa però è precedente all'istituzione della figura del muwaqqit. Già nel X sec., al Cairo, Ibn Yūnus, autore del celebre manuale di astronomia al-Zīǧ al-ḥākimī al-kabīr (Grandi tavole astronomiche dedicate ad al-Ḥākim), aveva lavorato intensamente in questo campo. A lui si deve la compilazione di tavole dettagliate e un'attività del tutto analoga a quella dei muwaqqit. Il suo lavoro ebbe anche un'influenza diretta sui muwaqqit del periodo successivo; diffusione minore ebbero le tavole compilate a Baghdad nel IX e nel X secolo. In seguito, comunque, non tutti gli astronomi più famosi che si occuparono del computo del tempo assunsero la carica di muwaqqit, benché molti di loro fossero religiosi e alcuni, in particolare, studiosi delle raccolte di tradizioni (ḥadīṯ, attribuite a Muḥammad) e di diritto islamico. Il culmine dell'attività di computo del tempo coincide quindi con una sempre maggiore integrazione dell'astronomia nella società e questa integrazione dimostra, a sua volta, che la validità dei metodi scientifici e la loro superiorità sulle tecniche dell'astronomia popolare erano ormai largamente riconosciute.

Le prescrizioni del Corano riguardo alle preghiere quotidiane non ne specificano il numero e non stabiliscono entro quale intervallo di tempo le singole preghiere devono essere recitate. Maggiori particolari si trovano nei ḥadīṯ. Secondo questi ultimi, in due giorni consecutivi Muḥammad ebbe dall'angelo Gabriele istruzioni diverse su come pregare: durante la sua vita il Profeta doveva quindi aver modificato sia l'orario sia la durata delle preghiere. Fonti diverse concordano sul fatto che egli proibì la preghiera a mezzogiorno, all'alba e al tramonto, ma riguardo all'intervallo di tempo entro il quale doveva avvenire la recitazione le tradizioni superstiti non permettono di trarre conclusioni definitive. Le raccolte di tradizioni attribuite al secondo califfo, ῾Umar (m. 644), e all'imām alide Ǧa῾far al-Ṣādiq (m. 765) riportano altri particolari. Tuttavia, per un accordo generale sui principî in base ai quali determinare le ore della preghiera occorre attendere l'VIII sec., quando questi principî, dopo lunghe discussioni tra le varie scuole di diritto islamico, furono definitivamente stabiliti. La differenza principale fra le tradizioni più antiche e le formulazioni successive delle scuole di diritto sta nel fatto che, mentre le prime facevano riferimento alla lunghezza delle ombre, le seconde, per definire gli intervalli di tempo entro i quali recitare le preghiere diurne, ricorrevano all'incremento di lunghezza delle ombre.

Prima di procedere oltre nella discussione sul problema delle ore delle preghiere, presentiamo le linee generali delle equazioni fondamentali del computo del tempo. Si consideri la sfera celeste con il centro O coincidente con il centro della Terra (fig. 3). Il piano passante per il centro della sfera interseca la superficie secondo un cerchio massimo (per es., i meridiani, l'equatore, l'eclittica e l'orizzonte). Se il piano non passa per il centro, il cerchio è più piccolo (è il caso dell'orbita apparente percorsa in un giorno dal Sole). Per due punti sulla superficie della sfera passa un solo cerchio massimo e la minima distanza tra i due punti è l'arco più corto tra i due staccati su questo cerchio. Un triangolo sferico è un triangolo i cui lati sono archi di cerchio massimo. Indichiamo con M la posizione del Sole in un dato giorno e in un dato istante; il cerchio BMA indica l'orbita apparente percorsa quel giorno dal Sole. Il Sole sorge in A, culmina al meridiano in B e tramonta in C. Inoltre, il tempo trascorso dal momento in cui il Sole sorge a quando si trova in M è proporzionale alla lunghezza dell'arco AM. Sulla superficie della sfera celeste sono definiti diversi archi: MT=δ=declinazione del Sole; EM=λ=longitudine del Sole; QF=ε=obliquità dell'eclittica; NP=QZ=φ=latitudine terrestre locale. E inoltre: MK=h=altezza del Sole in M; MB=t=angolo orario (t dipende da h, δ e φ); AM=d=arco di rivoluzione; AB=D=metà dell'arco diurno (AB=AM+MB, o D=d+t); EK=a=arco azimutale (a dipende da h, δ e φ); EA=amplitudine ortiva.

Si definisce 'ora ineguale' (detta anche 'ora stagionale' oppure 'ora temporaria') un dodicesimo della durata della luce diurna in un dato giorno; essa varia quindi al variare della latitudine del luogo e della declinazione solare. Queste ore sono dette 'ineguali' perché la durata effettiva di dodici ore diurne non è pari a quella di dodici ore notturne. Quando la declinazione è nulla (vale a dire, agli equinozi), le ore sono tutte uguali. La formula generale per determinare l'ora del giorno dal sorgere del Sole (in ore temporarie) è T=6d/D.

Gli archi sulla superficie della sfera celeste sono tra loro dipendenti e i calcoli per il computo del tempo si basano su equazioni che permettono di determinare gli archi incogniti, a partire dalle misure di altri archi che si ottengono facilmente mediante osservazione. In particolare, per una data latitudine e un dato momento dell'anno, si poteva determinare l'ora del giorno osservando la lunghezza dell'ombra di uno gnomone; il valore T è infatti una funzione della lunghezza dell'ombra, che si può calcolare con metodi di vario tipo, sia esatti sia approssimati. Per esempio, ponendo in un punto O uno gnomone OG lungo 12 unità, e denotando con S_m la lunghezza dell'ombra a mezzogiorno (ossia quando il Sole passa al meridiano) e con S_t la lunghezza dell'ombra a un certo istante t, si ha S_t=12cotanh, dove h è l'altezza del Sole in quell'istante. Allora T si può determinare a partire da S_t e da S_m; una formula approssimata è

Se l'ombra è misurata prima di mezzogiorno, il valore di T si riferisce a un'ora del giorno determinata dopo il sorgere del Sole, mentre se la misurazione avviene dopo mezzogiorno, esso corrisponde a un'ora del giorno prima del tramonto. La prima formula esatta per il calcolo di T fu data dal già citato Ḥabaš al-Ḥāsib nel IX sec., ma la dimostrazione si ebbe nel X sec. a opera di Abū 'l-Wafā᾽. In notazione moderna, la formula esatta per il calcolo dell'angolo orario t è

Per h=0 si ha t=D, ossia l'angolo orario è la metà dell'arco diurno, AB; quindi il valore della lunghezza della metà dell'arco diurno è D=arccos(−tgδ tgφ).

La determinazione delle ore della preghiera

Le cinque preghiere prescritte dal Corano devono essere recitate entro limiti di tempo prestabiliti, diversi a seconda dei periodi dell'anno e della località, che sono definiti in base alla posizione apparente del Sole rispetto all'orizzonte del luogo. Questi limiti variano quindi in funzione dell'altezza e della longitudine del Sole e della latitudine della località. Vi erano molti tipi di approccio al problema della determinazione delle ore in cui i fedeli dovevano recitare le preghiere. Oltre ai metodi di computo del tempo basati sulle case lunari, vi erano alcuni semplici schemi che fornivano la lunghezza delle ombre nelle varie località, a ogni ora stagionale o a mezzogiorno. La lunghezza dell'ombra era determinata sia mediante l'osservazione sia con calcoli approssimati. È stata individuata una ventina di trattati che contemplano semplici schemi di questo tipo, ma solo sette di questi sono stati studiati. Alcuni si basano su metodi di origine greca, ma la maggior parte fa uso di una formula indiana che collega ore temporarie e allungamento dell'ombra rispetto alla lunghezza minima che essa ha a mezzogiorno. La formula, approssimata, è T=6n/(Δs+n), dove n è la lunghezza dello gnomone, T l'ora (in ore temporarie) e Δs l'incremento di lunghezza dell'ombra.

Nel calendario lunare islamico, il giorno inizia al tramonto. Gli intervalli di tempo entro i quali devono essere recitate le cinque preghiere sono definiti come segue: per la prima, detta maġrib (tramonto), si va dal tramonto al crepuscolo; per la seconda, detta ῾išā᾽ (crepuscolo), dal crepuscolo all'alba; per la terza, faǧr (alba), dall'aurora al sorgere del Sole; per la quarta, ẓuhr (mezzogiorno), dal momento in cui il Sole passa al meridiano fino all'inizio della preghiera successiva; e infine per la quinta, ῾aṣr (pomeriggio), l'intervallo comincia quando la lunghezza dell'ombra di un oggetto è pari alla sua ombra a mezzogiorno aumentata della lunghezza dell'oggetto stesso e termina o al tramonto, secondo alcune scuole coraniche, oppure, secondo altre, quando l'ombra a mezzogiorno è aumentata di due volte la lunghezza dell'oggetto. In alcune delle prime comunità islamiche era prevista un'altra preghiera, la ḍuḥā, da recitarsi tra l'alba e mezzogiorno. David King ha mostrato come le tre preghiere ḍuḥā, ẓuhr e ῾aṣr corrispondano grosso modo alla fine della terza, sesta e nona ora stagionale diurna, corrispondenza che si può verificare mediante la formula indiana vista sopra. King ha anche osservato che il sistema di regolare le ore della preghiera mediante le ore stagionali era usato anche da alcune comunità cristiane orientali. Delle sette ore canoniche dei cristiani siriaci, la preghiera dell'alba fu espressamente proibita dall'Islam come retaggio di pratiche pagane, mentre la ḍuḥā, che alcuni musulmani ancora recitavano, finì con l'essere soppressa; le cinque preghiere rimanenti corrispondono alle cinque preghiere islamiche.

Le definizioni tradizionali delle ore delle preghiere diurne sono in un certo senso modi pratici di regolare le ore della preghiera in termini di ore stagionali. Una volta definiti gli orari in termini di lunghezza delle ombre, fu possibile affrontare il problema nel quadro dell'astronomia sferica, senza tenere conto delle ragioni che avevano motivato quelle definizioni. E ciò perché la lunghezza dell'ombra di un oggetto è funzione dell'orbita apparente del Sole e varia quindi, durante l'anno, in funzione della longitudine del Sole e della latitudine terrestre. Se si fa uso dell'astronomia sferica, il calcolo dell'ora delle preghiere diurne richiede l'applicazione di complicate formule trigonometriche e metodi altrettanto complessi erano usati per stabilire, in termini della durata del crepuscolo, gli orari delle preghiere notturne. Il passaggio dai metodi basati sulla lunghezza dell'ombra a quelli basati sull'incremento di questa lunghezza è esso stesso un segno della precisione crescente con cui era affrontato il problema.

Le prime tradizioni definivano l'inizio delle preghiere di mezzogiorno e del pomeriggio in termini della lunghezza delle ombre, in modo tale che, per la preghiera di mezzogiorno, la lunghezza s dell'ombra fosse uguale alla lunghezza n dello gnomone (s=n); secondo questo schema di calcolo, il periodo riservato alla preghiera pomeridiana cominciava quando s=2n. Poiché, per un dato giorno, la lunghezza più corta dell'ombra si ha a mezzogiorno, se si definisce l'inizio della preghiera di mezzogiorno in termini di lunghezza dell'ombra e non di incremento di questa lunghezza, l'altezza del Sole a metà giornata dovrebbe essere h_m=45°. Tale condizione non può essere sempre soddisfatta. In alcune località il Sole non raggiunge mai l'altezza di 45°; in molte altre la raggiunge solo in alcuni periodi dell'anno. In altre parole, in molte località, almeno per una parte dell'anno, la lunghezza dell'ombra non diviene mai tanto piccola quanto quella dello gnomone. Solo ai tropici, com'è il caso della Mecca, la condizione s=n è soddisfatta tutti i giorni dell'anno.

Questo problema è illustrato nella fig. 5. La massima lunghezza dell'ombra a mezzogiorno nella località alla quale corrisponde la figura si ha il primo giorno d'inverno, in corrispondenza del punto di minima altezza a mezzogiorno, occupato dal Sole quando la sua orbita apparente coincide con il Tropico del Capricorno. Nella figura,

e

Sia S_m l'ombraa mezzogiorno. Nel primo giorno d'inverno, per una località situata a una latitudine φ, l'altezza del Sole a mezzogiorno è h_m=90°−φ−ε e perciò, per tutte le località per le quali φ>21,5°, avremo h_m⟨45°. Ciò vuol dire che, per tutte le località la cui latitudine è maggiore di 21,5°, la condizione h_m=45° non può essere soddisfatta tutto l'anno. Nuovi principî erano perciò necessari per definire le ore delle preghiere diurne.

Al posto della lunghezza dell'ombra, le scuole islamiche presero a considerare l'aumento della lunghezza rispetto al valore di mezzogiorno. La preghiera di mezzogiorno doveva quindi cominciare quando la lunghezza dell'ombra era pari a quella che si ha a mezzogiorno, più 1/12, 1/5 o 1/4 della lunghezza n dello gnomone. Più importante è la definizione dell'incremento pomeridiano. Tutte le scuole di diritto islamico, a eccezione della Scuola ḥanafita, sostengono che il periodo della preghiera del pomeriggio comincia quando l'incremento rispetto al valore di mezzogiorno, cioè rispetto al valore minimo, è pari a n (2n per la Scuola ḥanafita). Ne segue che, per una località nella quale l'altezza del Sole a mezzogiorno è h_m, e per uno gnomone di lunghezza n, la preghiera del pomeriggio comincia quando l'altezza del Sole raggiunge un valore h tale che cotanh=cotanh_m+n, ovvero h=arccotan(cotanh_m+n). Una volta determinato il valore di h, l'ora corrispondente si può determinare risolvendo rispetto all'angolo orario t le equazioni standard per il calcolo del tempo, di cui si è detto in precedenza. La preghiera della sera termina, a seconda delle scuole, o al tramonto oppure quando la lunghezza dell'ombra aumenta di 2n.

Il periodo della preghiera maġrib, dal tramonto alla completa oscurità, è funzione della durata del crepuscolo. Analogamente, per la preghiera faǧr si va dall'aurora al levar del Sole. L'aurora comincia e la maġrib finisce quando la depressione del Sole sotto l'orizzonte è di un certo numero di gradi. Per questa depressione si assumono diversi valori; il più usato è 18°. La durata dell'alba è quindi data dal tempo che il Sole impiega a salire all'orizzonte orientale da una depressione di 18°. Analogamente la maġrib si recita nell'intervallo di tempo che il Sole impiega dopo il tramonto a raggiungere i 18° sotto l'orizzonte occidentale; qui finisce il crepuscolo e comincia la preghiera ῾išā᾽. La durata delle preghiere dell'alba e del tramonto è quindi funzione della longitudine λ del Sole, della latitudine φ del luogo e dell'inclinazione dell'eclittica. Il primo autore che tenne conto anche dell'effetto della rifrazione all'orizzonte fu Ibn Yūnus, nel X secolo.

La generale necessità di determinare le ore della preghiera favorì lo sviluppo di metodi che permettevano di risolvere facilmente il problema. Gli astrolabi, che si possono considerare gli elaboratori analogici dell'epoca, riportavano spesso curve destinate allo scopo: sono conservate numerose centinaia di astrolabi provenienti da paesi musulmani e molti di essi contengono curve relative alle ore della preghiera. Speciali quadranti, alcune dozzine dei quali sono in nostro possesso, furono progettati con le stesse finalità. E anche in molte delle meridiane giunte fino a noi si trovano segni per le preghiere di mezzogiorno e del pomeriggio. Il metodo più comodo e rapido era però quello delle tavole. Queste davano in genere la durata del periodo destinato a ciascuna preghiera, espressa in gradi equatoriali (360° corrispondono a 24 ore, ovvero 1° equivale a 4 minuti di tempo). Per ogni grado di longitudine solare (corrispondente grosso modo a un giorno) e per una data altezza del Sole (misurata direttamente mediante osservazione), in una tavola di orari della preghiera si trovano in genere: il tempo trascorso dal levare del Sole (angolo orario), la durata di metà del giorno e della notte, l'angolo orario all'inizio della preghiera pomeridiana, la durata dei crepuscoli mattutino e serale e quella dell'oscurità totale. Occorre tuttavia osservare che, sebbene la particolare importanza che assunse il computo del tempo fosse dovuta principalmente al fatto che esso serviva a determinare l'ora delle preghiere, le tavole destinate in particolare a questo scopo costituiscono solo una parte del corpus di tavole per il computo del tempo.

Le tavole per il computo del tempo

Vari tipi di tavole riguardano il computo del tempo e altre funzioni astronomiche. La vasta letteratura sull'argomento affronta anche gli aspetti teorici di tali questioni. L'opera più antica conosciuta sul computo del tempo è quella di al-Ḫwārizmī, risalente ai primi anni del IX sec., mentre si deve a Ṯābit ibn Qurra (m. 901) un testo completo sulla teoria della meridiana. Le opere classiche sulla scienza del computo del tempo, come il celebre Kitāb Ǧāmi῾ al-mabādi᾽ wa-'l-ġāyāt fī ῾ilm al-mīqāt (Libro completo dei principî e degli obiettivi della scienza del computo del tempo) di Abū ῾Alī al-Marrākušī (m. 1280 ca.), comprendono in genere una trattazione teorica di astronomia sferica e delle meridiane, una discussione sulla costruzione e sull'uso di vari strumenti e un ampio insieme di tavole, alcune delle quali universali e valide per tutte le latitudini terrestri. Inoltre, esse spesso includono anche tavole ausiliarie per facilitare la soluzione di problemi di trigonometria sferica. Le tavole del muwaqqit damasceno al-Ḫalīlī rappresentano uno dei migliori risultati di questa tradizione, in quanto forniscono soluzioni numeriche complete ed estremamente accurate per tutti i problemi relativi al calcolo del tempo e alla determinazione della qibla.

Per una data latitudine e per ciascun grado di longitudine solare, nelle tavole si trovano l'equazione per la durata della metà del giorno e funzioni come la declinazione solare, l'ascensione retta, l'altezza meridiana del Sole, la metà dell'arco di visibilità (niṣf qaws al-nahār), il numero delle ore equinoziali, la lunghezza dell'ombra a mezzogiorno, l'altezza del Sole all'inizio della preghiera pomeridiana, la durata dei crepuscoli mattutino e serale e l'angolo orario nel momento in cui il Sole si trova all'azimut della qibla. Per quanto riguarda la latitudine di Baghdad, al-Ḫwārizmī calcolò la lunghezza delle ombre corrispondenti alle ore delle preghiere diurne, per intervalli di 6° di longitudine solare (cioè per intervalli di circa 6 giorni). Le più antiche tavole ancora esistenti per determinare il tempo trascorso dal sorgere del Sole in funzione dell'altezza di questo e dell'altezza meridiana furono compilate nel X sec. da ῾Alī ibn Āmāǧūr; una di queste fa uso di una formula approssimata e fornisce l'ora per ogni latitudine terrestre, mentre un'altra riguarda la latitudine di Baghdad e si basa su una formula esatta. A partire dal IX sec. molti zīǧ riportano descrizioni di metodi accurati per riuscire a determinare l'ora del giorno in funzione delle altezze solari, istantanea e meridiana.

Le prime tavole complete per determinare le ore della preghiera di cui siamo in possesso sono quelle di Ibn Yūnus. La sua opera più importante sul computo del tempo su basi astronomiche ha per titolo Kitāb ġĀyat al-intifā῾ fī ma῾rifat al-dā᾽ir wa-faḍli-hi wa-'l-samt min qibal al-irtifā῾ (Tavole utilissime per stabilire il tempo trascorso dal sorgere del Sole, l'angolo orario e l'azimut del Sole conoscendo la sua altezza). Ibn Yūnus scrisse anche altri due manuali a questo collegati, che sono il Kitāb al-Samt (Libro delle tavole azimutali) e il Kitāb Faḍl al-dā᾽ir (Libro delle tavole per gli angoli orari) e che includono tavole per il computo del tempo per mezzo del Sole e per la determinazione delle ore della preghiera alla latitudine del Cairo. Queste opere sono la base del corpus posteriore di tavole, di cui si servirono a partire dal XIII sec. gli astronomi del Cairo, e da esse traggono ispirazione le tavole compilate in Siria nel XIV sec. e ancora in uso nel XIX secolo. Ibn Yūnus fu anche il primo astronomo che tabulò la durata dei crepuscoli mattutino e serale, la durata dell'oscurità e gli effetti della rifrazione atmosferica sulla durata del crepuscolo.

Il modello di Ibn Yūnus fu sviluppato ulteriormente nell'Egitto e nella Siria del XIII e del XIV sec.: furono compilate numerose tavole che calcolavano l'ora in funzione dell'altezza e della longitudine del Sole, notevoli sia per le dimensioni (contenevano in genere migliaia di voci) sia per la precisione. Naǧm al-Dīn al-Miṣrī (m. 1280 ca.) compilò tavole per tutte le latitudini terrestri con oltre 250.000 voci; esse fornivano il tempo trascorso dal sorgere del Sole in funzione dell'altezza meridiana (ġāyat al-irtifā῾), di metà dell'arco di visibilità (niṣf qaws al-nahār) e dell'altezza istantanea del Sole, per il giorno, e delle stelle, per la notte. Nel suo Kitāb Ǧāmi῾ al-mabādi᾽ wa-'l-ġāyāt fī ῾ilm al-mīqāt, Abū ῾Alī al-Marrākušī, contemporaneo di al-Miṣrī, forniva una trattazione completa degli aspetti pratici del computo del tempo corredata di molte tavole. Le tavole per città come Baghdad, Marāġa e Shiraz, nonostante siano precedenti, non hanno la portata e il significato di quelle per il Cairo del XIII e del XIV secolo. Tra queste ultime si trovano quelle di Šihāb al-Dīn al-Maqsī, costituite da oltre 10.000 voci, che danno l'ora del giorno in funzione dell'altezza e della longitudine solare, e di al-Baḫāniqī, che constano di 30.000 voci e misurano il tempo trascorso dal sorgere del Sole, l'angolo orario, l'azimut e le ore della preghiera.

La produzione delle tavole continuò al Cairo nel XIV sec., ma il centro dell'attività si era ormai spostato in Siria. Come molti dei loro omologhi egiziani, numerosi astronomi siriaci del XIV sec., anche se non tutti, erano addetti al computo del tempo. Alcuni di loro, come Ibn al-Šāṭir, eccellevano in astronomia teorica e pratica; altri lavoravano esclusivamente a problemi di astronomia sferica e di computo del tempo. La crescita della ricerca nel campo dell'astronomia sferica nella Siria del XIV sec. fu stimolata dalla tradizione egiziana. La maggior parte degli astronomi più noti di questo periodo aveva infatti studiato al Cairo: è il caso di Šams al-Dīn Muḥammad al-Mizzī (m. 1350 ca.) e di Ibn al-Šāṭir, entrambi di Damasco; di Zayn al-Dīn al-Karakī, di Gerusalemme, che aveva studiato con al-Mizzī; e di Ibn al-Sarrāǧ, di Aleppo, che soggiornò in Egitto all'inizio della carriera. Fatto salvo questo debito, i successi degli astronomi siriaci furono però superiori a quelli degli egiziani e rappresentano il punto più alto del contributo dell'Islam al computo del tempo su basi astronomiche.

Dopo essere tornato a Damasco dal Cairo, al-Mizzī compilò un serie di tavole per la preghiera e per il computo del tempo per la latitudine di Damasco, sulla falsariga del corpus del Cairo. Anche Ibn al-Šāṭir compilò tavole per il computo del tempo ma, a parte l'opera monumentale di astronomia teorica, il suo principale contributo all'astronomia sferica pratica riguarda la costruzione della magnifica meridiana della moschea omayyade di Damasco e del ṣandūq al-yawāqīt, uno speciale strumento per il computo del tempo (v. oltre). Sulla base di nuove osservazioni, egli ricalcolò altresì alcuni dei parametri di cui si erano serviti gli astronomi precedenti e i nuovi parametri furono poi utilizzati da al-Ḫalīlī per ricalcolare le tavole per la Siria. L'opera di al-Ḫalīlī, ancora utilizzata nel XIX sec., è uno degli esempi più ineccepibili dei risultati ottenuti dalla scienza islamica nel campo del computo del tempo su basi astronomiche. Egli compilò tavole per risolvere problemi di vario tipo, sia per Damasco sia nel caso generale applicabile a tutte le località. Le sue tavole di funzioni matematiche ausiliarie per il computo del tempo mediante il Sole a qualunque latitudine permettono di calcolare facilmente l'angolo orario (che è funzione dell'altezza e della longitudine del Sole e della latitudine terrestre), in quanto le operazioni necessarie sono soltanto addizioni e sottrazioni. Un altro gruppo di tavole di funzioni matematiche ausiliarie riguarda problemi di astronomia sferica per ogni latitudine. Ad al-Ḫalīlī si devono anche tavole per determinare, alla latitudine di Damasco, l'ora del giorno e le ore della preghiera. Altre tavole forniscono l'azimut della qibla in funzione della latitudine e della longitudine terrestri (v. oltre).

Dopo il XIV sec. altri astronomi seguirono l'esempio delle tradizioni egiziana e siriaca e compilarono tavole per altre località, tra cui Gerusalemme, la Mecca, Tripoli e Tunisi, nonché un corpus relativamente numeroso di tavole per Istanbul e alcune città ottomane. Tuttavia, malgrado questa continua produzione, il livello dell'attività del XIV sec. non fu più raggiunto dagli astronomi che seguirono.

Gli astronomi egiziani, e ancor più i siriaci, furono importanti anche per i risultati ottenuti nella costruzione degli strumenti. Dall'inizio del XIV alla fine del XV sec. numerosi astronomi costruirono strumenti innovativi per il computo del tempo; tra questi vanno annoverati griglie trigonometriche, quadranti, meridiane e astrolabi. La figura più importante è quella di Ibn al-Sarrāǧ, che progettò vari quadranti e astrolabi universali per il computo del tempo di giorno e di notte. Anche Ibn al-Šāṭir ideò una meridiana universale e uno strumento per determinare l'ora, il ṣandūq al-yawāqīt li-῾ilm al-mawāqīt (lo scrigno di rubini per il computo del tempo). Si tratta di uno strumento portatile, dotato di una bussola per orientarlo secondo il meridiano e che consta di due meridiane universali, una polare e una equatoriale. Ibn al-Šāṭir scrisse anche un trattato sull'uso di questo strumento.

Un altro problema affrontato in diversi trattati astronomici è quello della visibilità della falce di Luna. Il calendario islamico è lunare; l'anno 1 corrisponde al nostro anno 622. Il mese lunare inizia subito dopo il tramonto con l'avvistamento della falce. Ma la visibilità della falce è a sua volta funzione di diverse variabili, non tutte ugualmente rilevanti, come le coordinate celesti del Sole e della Luna, la latitudine del luogo dove avviene l'avvistamento e la luminosità del cielo. Furono ideati vari metodi per determinare sotto quali condizioni la falce di Luna sarebbe stata visibile. Alcuni di essi prendevano in considerazione solo un numero ristretto di variabili, nel caso particolare della Luna, mentre altri prendevano in esame tutti i possibili fattori che, in generale, influiscono sulla visibilità di un qualunque corpo celeste all'orizzonte immediatamente dopo il tramonto del Sole, trattando come caso particolare il problema della visibilità della falce di Luna.

La determinazione della 'qibla'

La qibla è la direzione verso la quale si rivolgono i musulmani durante la preghiera e nello svolgimento di altri atti rituali. Il monumento più sacro dell'Islam è la Ka῾ba, detta anche 'casa di Dio', una struttura a forma di cubo che si trova alla Mecca, la cui costruzione è attribuita al profeta Abramo e al figlio Ismaele. Durante le cinque preghiere quotidiane i fedeli si debbono rivolgere alla Ka῾ba, ed è per questo che tutte le moschee sono orientate, almeno in teoria, verso di essa. Determinare la qibla era quindi un problema che gli astronomi dovevano affrontare spesso e metodi matematici, che andavano dai più semplici ai più raffinati, furono ideati per risolverlo. La maggior parte dei manuali di astronomia conteneva capitoli dedicati a questo problema, che suggerivano tecniche sia approssimate sia esatte. L'argomento era trattato negli zīǧ, ma furono compilate anche opere dedicate esclusivamente a esso.

Prima di poter disporre, verso la fine dell'VIII sec., di metodi matematici, i musulmani determinavano la qibla basandosi sulle pratiche dei primi compagni del Profeta, sulle tradizioni tramandate dall'astronomia popolare e sul fatto che anche per la Ka῾ba si ha un allineamento astronomico, fondato sulle direzioni cardinali e sul sorgere e tramontare del Sole e delle stelle. Per distanze non troppo grandi dalla Mecca questi metodi fornivano approssimazioni accettabili, ma per località lontane, nell'Africa del Nord e in Iran, l'errore era piuttosto rilevante. L'orientamento di numerose moschee del primo periodo non era quello giusto e, se molte furono lasciate così com'erano, altre furono ricostruite e orientate nella direzione corretta. Metodi semplici, non matematici, furono usati nel primo periodo e continuarono a esserlo anche dopo la comparsa delle scienze matematiche. Queste ultime tuttavia permisero lo sviluppo di metodi di calcolo della qibla per qualunque località, in base alle sue coordinate geografiche e a quelle della Mecca.

Alcuni dei primi metodi per determinare la qibla erano basati semplicemente sull'imitazione del comportamento di Muḥammad. Nel periodo che il Profeta trascorse alla Mecca non vi erano problemi per orientarsi verso la Ka῾ba. A Medina però, quando pregava, egli si rivolgeva verso sud, e per questo motivo molte moschee del primo periodo, a Medina come altrove, furono costruite rivolte a sud, direzione che fu anche la qibla dei primi seguaci del Profeta. Per gli insediamenti del Nord del Higiaz e del basso Eufrate, il sud rappresentava un'approssimazione ragionevole. Inoltre, nei primi tempi per la qibla si prendevano anche direzioni che avevano un significato simbolico: ci si rivolgeva per esempio verso la strada che imboccavano i pellegrini nel lasciare il proprio paese per recarsi alla Mecca. Queste prime generazioni di musulmani erano anche consapevoli delle tradizioni preislamiche riguardo all'orientamento dei muri della Ka῾ba: sapevano cioè che questi muri erano orientati verso il punto in cui sorge la stella Canopo e verso il solstizio d'estate. Una diffusa e radicata tradizione popolare associava poi ciascun muro della Ka῾ba a uno dei principali venti della regione; per questi motivi, la qibla era a volte determinata a partire dalla direzione dei venti e, nella costruzione delle prime moschee, si teneva conto di allineamenti astronomici.

Un'altra tradizione popolare, ancora più diffusa, era basata su schemi geografici secondo i quali la Mecca è posta al centro del mondo, il mondo è suddiviso in zone attorno alla Ka῾ba, e a ciascuna di queste zone è assegnata una direzione definita su basi astronomiche. David King (1996) parla di questa tradizione come della 'geografia sacra' dell'Islam. Oltre alla motivazione religiosa che porta a considerare la Mecca il centro dell'Universo, questi schemi trovano giustificazione nella norma largamente condivisa secondo la quale durante la preghiera il fedele deve sì rivolgersi alla Mecca, ma genericamente, non necessariamente nella direzione esatta. King ha trovato una settantina di questi schemi, che coprono un lungo periodo di tempo. Il più antico è quello elaborato da Ibn Ḫurradāḏbih nella Baghdad del IX sec., che propone una divisione in quattro settori. Nel X sec. il geografo al-Muqaddasī di Gerusalemme ideò uno schema a otto settori e Ibn Surāqa, uno studioso yemenita che si era formato in Iraq, propose schemi con otto, undici e dodici settori. Per ogni regione Ibn Surāqa definisce con precisione la posizione da tenere rispetto al sorgere e al tramontare di determinate stelle e rispetto ad alcuni venti. Gli schemi di questo genere sono numerosissimi ma, a parte l'esame d'insieme svolto da King, il contenuto della maggior parte di essi deve ancora essere studiato.

Tav. I

Tav. II

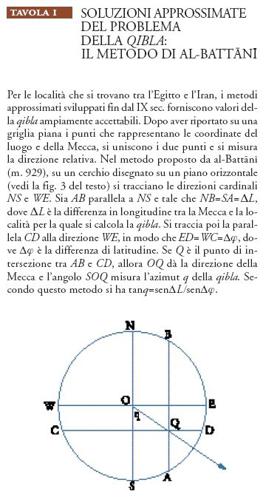
Vari metodi matematici di diverso grado di complessità accompagnarono la tradizione popolare nella determinazione della qibla. Dal punto di vista della geografia matematica, il problema della qibla consiste nel trovare la direzione della Mecca lungo il più breve tra i due archi di cerchio massimo che la uniscono alla località nella quale si effettua la misura. Occorre allora conoscere le coordinate geografiche delle due località e con questi dati a disposizione possono essere utilizzati vari metodi. I primi e più semplici erano approssimati (Tav. I) e si servivano di carte per rappresentare su una griglia piana ortogonale di latitudini e longitudini la posizione della Mecca rispetto a un dato luogo. Si fece poi uso di analemmi (Tav. II), cioè di metodi di proiezione per rappresentare il piano meridiano, il piano dell'equatore celeste e il piano dell'orizzonte su un unico piano: il problema della qibla si risolve in questo caso mediante una serie di rotazioni di questi tre piani. Con una proiezione ortogonale, si proietta la figura spaziale su un piano e, facendo ruotare i piani obliqui fino a sovrapporsi a questo, si ottengono le dimensioni reali delle figure in essi contenute.

Infine, con metodi di trigonometria sferica (il teorema di Menelao o il più semplice teorema dei seni), la qibla si poteva determinare a partire da punti presi sulla sfera e sui cerchi. In quest'ultima soluzione, che ha un alto grado di precisione, il problema viene trasferito sulla sfera celeste, sulla quale si determina la posizione assunta dallo zenit della Mecca rispetto allo zenit del luogo. La direzione della qibla è individuata sull'orizzonte locale come azimut dello zenit della Mecca. Come per molti altri problemi di astronomia, si cercarono anche qui soluzioni universali per tutti i casi possibili, servendosi di procedimenti matematici di notevole complessità. Con questi metodi furono compilate numerose tavole che forniscono la qibla per diverse località, in funzione della latitudine e della longitudine terrestri. La più antica soluzione esatta del problema della qibla in nostro possesso è quella dovuta ad al-Nayrīzī, attivo alla fine del IX sec. a Baghdad, che si ottiene mediante quattro applicazioni del teorema di Menelao; i calcoli, che con questo teorema risultano piuttosto complicati, furono più tardi notevolmente semplificati dall'applicazione della regola dei seni e della tangente. Un altro metodo di uso comune è quello degli zīǧ, che compare in diverse opere dal IX al XV sec. e richiede la definizione e il calcolo di varie funzioni ausiliarie, tra le quali la differenza di latitudine modificata e la longitudine modificata, per arrivare a determinare l'altezza e l'azimut della qibla. Il famoso astronomo al-Bīrūnī (XI sec.) delineò varie soluzioni sulla base di analemmi e di metodi di astronomia sferica. Ibn al-Hayṯam, contemporaneo di al-Bīrūnī, scrisse due trattati sul problema della qibla; in uno di questi si trova la più semplice soluzione geometrica che si conosca, mentre l'altro dà una soluzione universale mediante l'astronomia sferica.

La soluzione esatta del problema della 'qibla' mediante la trigonometria sferica

Il problema della determinazione della qibla a partire dalle coordinate terrestri di una data località e di quelle della Mecca è un problema di geografia sferica che però fu trattato dagli astronomi musulmani come un problema di astronomia. Il problema astronomico equivalente consiste nel considerare lo zenit del luogo e quello della Mecca, per poi determinare l'azimut della Mecca lungo il cerchio dell'orizzonte. L'azimut della qibla è dato quindi dall'intersezione tra l'orizzonte locale e il cerchio massimo passante per lo zenit della Mecca e quello del luogo. Se il punto M della fig. 3 rappresenta lo zenit della Mecca, il problema consiste nel determinare l'azimut della Mecca sul cerchio dell'orizzonte, cioè la misura q dell'arco SK. L'arco SB dà l'altezza della meridiana, l'arco MK l'altezza h dello zenit della Mecca, l'arco MT la latitudine φΜ della Mecca e l'arco QT la differenza di longitudine ΔL tra la Mecca e il luogo in questione.

I metodi esatti, anche se diversi uno dall'altro, fanno quasi sempre intervenire le misure di una serie di archi ausiliari. Uno di questi metodi richiede di determinare due archi, detti 'primo arco' e 'secondo arco' ovvero 'differenza di longitudine modificata' e 'latitudine modificata'. Essi si possono vedere nella fig. 3: tracciando la perpendicolare EMF al meridiano che passa per lo zenit della Mecca, l'arco MF dà la differenza di longitudine modificata ΔL′ e l'arco QF la latitudine modificata φ′. Questi archi si calcolano di solito applicando il teorema di Menelao a quattro insiemi di triangoli sferici e relative trasversali. Riportiamo una tipica applicazione del metodo in notazione moderna.

1) Applicando il teorema di Menelao al triangolo sferico MET e alla trasversale QFP si ha:

Ma EF=EQ=PT=90°, FM=ΔL′ (differenza di longitudine modificata o primo arco), QT=ΔL e MP=90°−φΜ;

dunque

ovvero

,

dove R è il raggio del cerchio di base (e, per definizione, Sen90°=R),

2) Applicando il teorema di Menelao al triangolo sferico PFM e alla trasversale QTE abbiamo

Tuttavia QP=PT=EF=90°, ME=90°−ΔL′ e QF=φ′ (latitudine modificata o secondo arco), per cui

Si consideri poi l'arco ausiliario

3) Applicando ancora il teorema di Menelao, questa volta al triangolo sferico ZFM e alla trasversale EKS, otteniamo:

Ma SZ=ZK=EF=90° e quindi per l'altezza h=MK dello zenit M della Mecca abbiamo

,

dove

4) Applicando infine il teorema di Menelao al triangolo sferico EKM e alla trasversale ZFS otteniamo:

Però ES=EF=ZK=90° e

e perciò

Tavole e strumenti per la determinazione della 'qibla'

A partire dal IX sec. furono compilate tavole che davano la qibla in funzione della longitudine e della latitudine terrestri, alcune basate su metodi approssimati, altre su calcoli esatti che facevano uso di analemmi o di metodi di trigonometria sferica. Le tavole seguono passo passo i calcoli richiesti da ciascuno dei metodi e sono accompagnate da tavole ausiliarie che permettono, date la longitudine e la latitudine di una località, di determinare la qibla semplicemente aggiungendo o sottraendo i valori delle funzioni ausiliarie in esse riportati. Molti zīǧ contenevano tavole per la qibla delle città più importanti. Nel XIV sec. al-Ḫalīlī compilò una tavola universale per la qibla che permetteva di determinare l'azimut della Mecca per ogni grado di latitudine e longitudine terrestri. I calcoli delle oltre tremila voci sono basati su una formula esatta e forniscono una soluzione universale del problema.

La questione della determinazione della direzione della Mecca e degli orari nei quali recitare le varie preghiere dette anche un notevole impulso alla scienza e all'arte della co struzione degli strumenti. Astrolabi, quadranti, bussole e griglie cartografiche di varia precisione furono ideati e utilizzati sia per queste finalità sia per altre osservazioni e calcoli astronomici. Il più importante di tutti è l'astrolabio, strumento molto versatile. Molti astrolabi riportavano sul retro curve per determinare la qibla e in alcuni manuali dedicati a questo strumento vi sono capitoli che spiegano come usarlo a questo scopo. Per risolvere problemi di trigonometria e per lo svolgimento dei calcoli relativi alla qibla erano utilizzati anche quadranti di seni. Un quadrante che permetteva di trovare la qibla per qualunque località fu ideato nel XIV sec. dall'astronomo di Damasco al-Mizzī, prima citato, mentre a Sibṭ al-Mārdīnī si deve un manuale sull'uso del quadrante solare per determinare la qibla; il testo, composto nel 1450 ca., ebbe molto successo e fu oggetto di numerosi commenti. Lo sviluppo di strumenti universali per determinare la qibla continuò oltre il XV secolo. Il più perfezionato fu progettato a Isfahan alla fine del XVII sec. e consiste in una mappa del mondo, incisa su una lastra e centrata sulla Mecca, che riporta circa 150 località, dall'Andalus alla Cina. Puntando un'alidada verso una determinata località si possono leggere direttamente sulla circonferenza della lastra la direzione della Mecca e la sua distanza dalla località presa in considerazione.

Le meridiane

La teoria e la pratica delle meridiane costituiscono un aspetto importante dell'attività di computo del tempo. Per determinare l'ora, erano usate meridiane sia orizzontali (in arabo ruḫāma, marmo) sia verticali (in arabo munḥarifa, inclinata) e nella maggior parte di quelle che ci sono pervenute sono segnate le ore della preghiera di mezzogiorno e del pomeriggio. Informazioni al riguardo si possono ottenere sia direttamente, esaminando le meridiane medievali che ci sono pervenute (ne abbiamo però solamente alcune), sia da opere teoriche, da tavole per la loro costruzione e da strumenti particolari per la determinazione dell'ora.

La maggior parte delle meridiane a nostra disposizione risale al XIII e al XIV sec., periodo in cui, come abbiamo visto, l'attività nel campo della misurazione del tempo fu piuttosto intensa. Esempi notevoli sono la meridiana di Ibn Ṭūlūn della moschea del Cairo, che riporta le ore stagionali e l'ora della preghiera pomeridiana, e la meridiana verticale della Madrasa Qā᾽itbāy di Gerusalemme. La più impor tante tra quelle giunte fino a noi è la stupenda meridiana della moschea omayyade di Damasco, costruita nel 1371-1372 da Ibn al-Šāṭir, nella quale sono segnate sia le ore stagionali sia quelle equinoziali, l'ora del levare del Sole, del mezzogiorno e del tramonto e le ore delle preghiere del pomeriggio, del crepuscolo e dell'alba. Ibn al-Šāṭir ideò e costruì anche un particolare strumento per determinare l'ora, il ṣandūq al-yawāqīt, che consta di due meridiane universali portatili, una polare e una equatoriale, varie tavole e una bussola magnetica. Un manuale che spiega l'uso di questo strumento fu composto al Cairo dall'astronomo del XV sec. al-Wafā᾽ī. Possediamo sia lo strumento di Ibn al-Šāṭir sia il manuale di al-Wafā᾽ī.

Sono molti i manuali che contengono discussioni sulle meridiane e la maggior parte di essi tratta gli aspetti pratici della costruzione di questi strumenti. Per quanto riguarda la teoria, l'opera classica è il trattato di Ṯābit ibn Qurra intitolato Kitāb al-Ruḫāmāt (Libro dei quadranti solari). A differenza di altri, questo non contiene tavole, ma fornisce le formule per il calcolo delle coordinate per i piani orizzontale e verticale della meridiana; a esse aggiunge le formule per le trasformazioni di coordinate per qualsiasi altro piano della meridiana. In particolare, Ṯābit ibn Qurra prospetta soluzioni per i casi in cui il piano della meridiana sia parallelo all'orizzonte, al meridiano, al primo verticale, oppure per piani sghembi rispetto a questi primi tre. A giudicare dagli altri manoscritti finora identificati e studiati, quest'opera offre la trattazione più avanzata sulle meridiane di tutto l'Islam medievale.

Se le opere teoriche rimaste sono relativamente poche, i manuali che forniscono tavole e istruzioni pratiche per la costruzione di meridiane sono invece numerosi. Tali tavole specificano quali coordinate segnare su meridiane disposte in piani diversi tra loro. Le meridiane indicano le ore stagionali, i gradi equatoriali, o una loro combinazione, e in genere riportano l'ora delle preghiere di mezzogiorno e del pomeriggio. Il trattato più antico è quello di al-Ḫwārizmī (primi del IX sec.); esso contiene un gruppo di tavole per disegnare curve su meridiane orizzontali, per dodici diverse latitudini. In ogni tavola sono considerati l'altezza del Sole, la lunghezza dell'ombra e l'azimut del Sole. Per uno gnomone di data lunghezza, al-Ḫwārizmī calcola le coordinate polari, considerando come angolo l'azimut e come raggio la lunghezza dell'ombra, da segnare sul piano orizzontale della meridiana. La lunghezza dell'ombra è ovviamente in funzione dell'altezza del Sole, cioè dell'ora. Dati quindi l'altezza del Sole e l'azimut, le tavole permettono di segnare l'intersezione delle linee orarie con le linee d'ombra per vari intervalli di tempo.

Risalgono al IX sec. altri due manuali sulle meridiane, il primo riguardante la costruzione di una meridiana conica portatile e l'altro, opera di Ibn al-Ādamī, costituito da un insieme di tavole per tracciare curve su meridiane verticali a qualunque latitudine. Un trattato del X sec. contiene tavole per la costruzione di meridiane con uno gnomone orizzontale, relative alla latitudine di Baghdad, le quali riportano i dati per ogni mezz'ora stagionale e ogni 30° di longitudine solare. Come per altri campi dell'attività di computo del tempo, tra il XIII e il XV sec. si assiste alla produzione di numerose opere sulle meridiane. Un classico testo del XIII sec., il Ǧāmi῾ al-mabādi᾽ wa-'l-ġāyāt fī ῾ilm al-mīqāt, di Abū ῾Alī al-Marrākušī, comprende lunghi capitoli sugli aspetti pratici della costruzione di meridiane orizzontali, verticali, cilindriche e coniche; ci sono giunte anche tavole del XIII sec. per meridiane verticali alla latitudine del Cairo, dovute ad al-Maqsī. Per ogni grado di inclinazione al meridiano locale, egli tabulò le coordinate dei punti d'intersezione tra le curve delle ore stagionali e le linee d'ombra agli equinozi e ai solstizi. Nell'Aleppo del XIV sec. Ibn al-Sarrāǧ compilò tavole per molti tipi di meridiane, per tutte le latitudini. Altre furono compilate da Sibṭ al-Mārdīnī (XV sec.) e da al-Tīzīnī (XV sec.). Questa attività continuò nel periodo ottomano, durante il quale si assistette a un aumento del numero di tavole per Istanbul e altre città islamiche.

Poiché fino al XII sec. l'attività scientifica nel mondo musulmano dipendeva essenzialmente dal sostegno pubblico, molti degli scienziati che ricevevano finanziamenti da governanti e dignitari pubblici dovevano piegarsi in qualche misura ai loro umori e desiderata. A partire dal XII sec. la situazione cambiò. I medici e gli astronomi più insigni della Siria e del Cairo erano impiegati soprattutto come giureconsulti e insegnanti in istituzioni mediche simili alle madāris, oppure si occupavano del computo del tempo nelle principali moschee della regione. Entro il quadro istituzionale delle moschee, in particolare, il computo del tempo implicava una vasta attività di carattere aritmetico, computazionale ed empirico, che si estendeva dalla costruzione di strumenti alla compilazione di tavole con centinaia di migliaia di dati e allo sviluppo di complicati schemi d'interpolazione per calcolare quei dati. Si trattò di un impegno di largo respiro all'interno dell'istituzione religiosa e in totale accordo con questa. L'integrazione nell'istituzione non portò però a un'analoga integrazione epistemologica delle conoscenze scientifiche e di quelle religiose nel computo del tempo. Gli astronomi delle moschee dell'Egitto e della Siria continuarono ad applicare standard scientifici rigorosi; invece di scendere a compromessi sui loro metodi scientifici, adottando le semplici tecniche dell'astronomia popolare, cercarono di rendere accessibili ai non specialisti le loro conoscenze matematiche. Così facendo, dettero vita a un corpus di scritti matematici che furono, in modo quasi esclusivo, i testi di riferimento per la soluzione dei problemi di computo del tempo nel mondo islamico. In altri termini, gli astronomi delle moschee furono capaci di delimitare, all'interno della sfera religiosa, un'area dove erano loro, e non gli studiosi religiosi tradizionali, ad avere l'ultima parola.

Bibliografia

Davidian 1983: Davidian, Marie-Louise, Al-Bīrūnī on the time of day from Shadow Lengths, in: Kennedy, Edward S. [et. al.], Studies in the islamic exact sciences, Beirut, American University of Beirut, 1983, pp. 274-279.

Id 1974: Id, Yusuf - Kennedy, Edward S., A letter of al-Bīrūnī: Ḥabash al-Ḥāsib's Analemma for the Qibla, "Historia mathematica", 1, 1974, pp. 3-11.

Ilyas 1984: Ilyas, Muhammad, A modern guide to astronomical calculations of islamic calendar, times and qibla, Kuala Lumpur, Berita, 1984.

Kennedy 1983a: Kennedy, Edward S. [et al.], Studies in the islamic exact sciences, Beirut, American University of Beirut, 1983.

‒ 1983b: Kennedy, Edward S., Al-Bīrūnī on the Muslim times of prayer, in: Kennedy, Edward S. [et al.], Studies in the islamic exact sciences, Beirut, American University of Beirut, 1983, pp. 299-310.

King 1986: King, David A., Islamic mathematical astronomy, London, Variorum, 1986.

‒ 1987: King, David A., Islamic mathematical instruments, London, Variorum, 1987.

‒ 1990: King, David A., A survey of medieval shadow schemes for simple time-reckoning, "Oriens", 32, 1990, pp. 191-249.

‒ 1993: King, David A., Astronomy in the service of Islam, Aldershot-Brookfield (Vt.), Variorum, 1993.

‒ 1996: King, David A., Astronomy and islamic society: Qibla, gnomonics and timekeeping, in: Encyclopedia of the history of Arabic science, edited by Roshdi Rashed, New York-London, Routledge, 1996, 3 v.; v. I: Astronomy-theoretical and applied, pp. 128-184.

Nader 1983: Nader, Nadi, Abū 'l-Wafā᾽ on the solar altitude, in: Kennedy, Edward S. [et al.], Studies in the islamic exact sciences, Beirut, American University of Beirut, 1983, pp. 280-283.

Schoy 1922: Schoy, Carl, Abhandlung über die Ziehung der Mittagslinie, dem Buch über das Analemma entnommen, samt dem Beweis dazu von Abū Sa῾īd aḍ-Ḍarīr, "Annalen der Hydrographie und maritimen Meteorologie", 50, 1922, pp. 265-271.

‒ 1923: Schoy, Carl, Die Gnomonik der Araber, Berlin-Leipzig, de Gruyter, 1923.

‒ 1924: Schoy, Carl, Sonnenuhren der spätarabischen Astronomie, "Isis", 6, 1924, pp. 332-360.

Sédillot 1844: Sédillot, Louis-Amélie, Mémoire sur les instruments astronomiques des Arabes, "Mémoires de l'Académie Royale des Inscriptions et Belles-Lettres de l'Institut de France", 1, 1844, pp. 1-29.