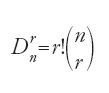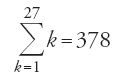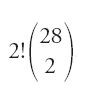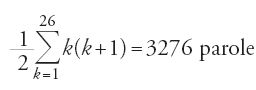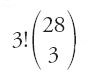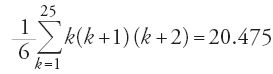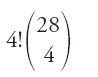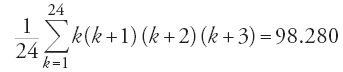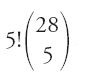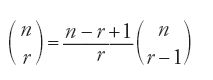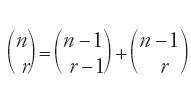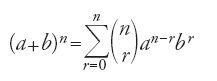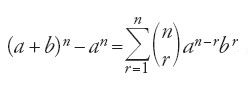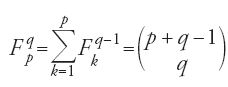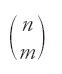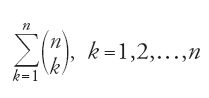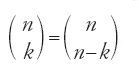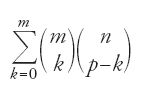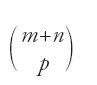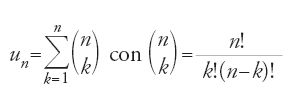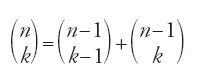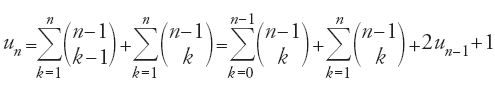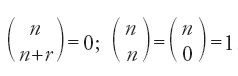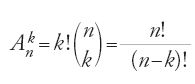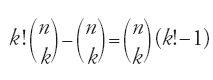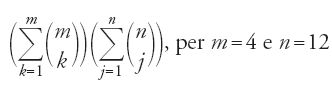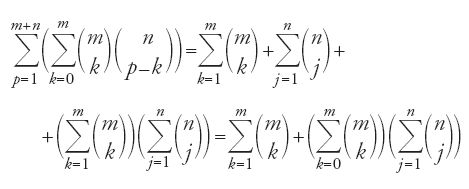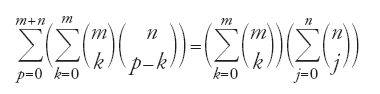La civiltà islamica: condizioni materiali e intellettuali. Algebra e linguistica. Gli inizi dell'analisi combinatoria

La civilta islamica: condizioni materiali e intellettuali. Algebra e linguistica. Gli inizi dell'analisi combinatoria

Algebra e linguistica. Gli inizi dell'analisi combinatoria

Intorno alla metà del XVII sec. lo studio delle combinazioni si afferma come un campo di ricerca a sé stante, al quale sono destinati lavori specifici. Basti citare, tra molte altre opere, l'Abrégé des combinaisons di Bernard Frénicle de Bessy (1605 ca.-1675), redatta in quel periodo ma pubblicata più tardi (Parigi 1693); gli scritti di calcolo delle probabilità e in particolare quelli dovuti a Blaise Pascal (1623-1662) quali l'opuscolo sulle Combinationes (Parigi 1903) e, più tardi, la seconda parte dell'Ars conjectandi di Jacques Bernouilli (1654-1705), pubblicato postumo, a Basilea, nel 1713; e infine la Dissertatio de arte combinatoria di Gottfried Wilhelm Leibniz (1646-1716). La ricerca sulle combinazioni trae origine dal neonato calcolo delle probabilità (che si presenta dapprima come dottrina del caso e in seguito come un vero e proprio calcolo del probabile), dalle ricerche di aritmetica e dagli studi di filosofia teoretica sulla lingua universale e sulla caratteristica universale. Ma se è vero che più di ogni altra disciplina sono state le esigenze del calcolo delle probabilità a dare un nuovo impulso alla ricerca sulle combinazioni, è anche vero che ci troviamo davanti a una effettiva presa di coscienza che fa sì che l'oggetto 'combinazione' sia studiato in sé, indipendentemente dal contesto in cui si trova. È in questa presa di coscienza che risiede, per così dire, l'autonomia dell'analisi combinatoria.

Si pone allora la domanda se sia legittimo fissare l'inizio di questi studi alla metà del XVII secolo. Certo, se ci si limita a tentare di raccogliere qua e là qualche combinazione operata da logici, linguisti o alchimisti si va fuori strada; occorre invece cercare situazioni dove il calcolo delle probabilità è assente, dove cioè questa materia, fondamentale per lo sviluppo dell'analisi combinatoria, ancora non compare. Una di queste situazioni è data dalla matematica araba, nella quale l'assenza del calcolo delle probabilità è evidente. Infatti, per quanto oggi ne sappiamo, i matematici arabi non hanno sviluppato studi di calcolo delle probabilità e sono stati gli studi di linguistica, le ricerche di algebra e poi di aritmetica, e gli scritti di filosofia teorica che hanno portato i matematici a considerare le combinazioni e, come sembra accertato, a dedicare a esse alcuni trattati monografici. Ne conosciamo almeno un esempio, l'opera di Ibrāhīm al-Ḥalabī (XVI sec.) Fī istiḫrāǧ ῾iddat al-iḥtimālāt al-tarkībiyya min ayy ῾adad kāna (Sulla determinazione delle eventualità combinabili a partire da un numero qualunque [di oggetti]), che la buona sorte ci ha permesso di reperire.

Tuttavia, di queste ricerche, che esordiscono a partire dai primi dell'VIII sec., non viene fatto mai cenno da chi si occupa di classificazione delle scienze; non ne parlano gli antichi biobibliografi e neppure i moderni, da al-Fārābī a Ibn al-Akfānī. Esse non sono state considerate nemmeno dalla moderna storiografia della matematica e della scienza, e solo recentemente ‒ tre decenni fa - ci siamo permessi di cominciare a parlare di analisi combinatoria nella matematica araba, senza tuttavia sollevare la questione della legittimità di questa scelta terminologica; essa non è stata affrontata, d'altra parte, neppure da coloro che sono venuti dopo di noi e finora non ci si è chiesti come mai questa grande assente non avesse mai cessato di fatto di essere presente. La risposta a questa domanda ci permetterà probabilmente di capire meglio le condizioni della nascita della disciplina, in assenza del nome di battesimo.

Linguistica e combinatoria

Un nome domina molti capitoli della linguistica araba a partire dall'VIII sec., ed è quello di Ḫalīl ibn Aḥmad. Matematico, è autore di un libro di aritmetica; musicologo, è il fondatore della fonologia dell'arabo, della prosodia e della lessicografia, per non parlare dei contributi dati alla grammatica e ad altre discipline linguistiche. Il caso è eccezionale e meriterebbe un grosso volume; noi considereremo qui soltanto la lessicografia. Ḫalīl concepì per primo, per quanto ne sappiamo, il progetto di comporre un dizionario della lingua, e non solo un lessico. A questo progetto rispondeva il suo Kitāb al-῾Ayn (Libro della lettera ῾ayn ), il primo dizionario conosciuto. Forse egli ne redasse solo una parte, il resto potrebbe allora essere opera del suo allievo al-Layṯ ibn al-Muẓaffar; vi furono probabilmente interventi anche di altri. Gli studiosi che discutono di queste attribuzioni sono d'accordo tuttavia nell'ammettere che il progetto è di Ḫalīl, che a lui si deve l'elaborazione dei mezzi per realizzarlo e che una parte del libro è di sua mano.

Il progetto di Ḫalīl è chiaro e preciso: razionalizzare la pratica empirica dei lessicografi ed estenderla per far sì che in un solo libro sia contenuto l'intero vocabolario della lingua. Occorre dunque trovare il modo di enumerare in modo esaustivo le parole della lingua, e far sì che vi sia una corrispondenza biunivoca tra l'insieme delle parole e le voci del dizionario. Ḫalīl elabora allora la teoria che possiamo così delineare: la lingua è una parte foneticamente realizzata della lingua possibile. Le parole di quest'ultima si ottengono per combinazione e permutazione delle lettere; le parole della prima sono quelle della lingua possibile che soddisfano le regole di compatibilità fonetica e sono effettivamente utilizzate. Il lessicografo si trova dunque davanti a un duplice compito: uno espressamente e unicamente combinatorio, l'altro fonologico. Ḫalīl ne aggiunge in seguito altri, di carattere etnolinguistico, storico, e così via.

L'autore comincia con il ricordare che le radici delle parole arabe constano di un numero di lettere variabile da due a cinque. Se la disposizione delle 28 lettere dell'alfabeto nella radice r, dove r varia da 2 a 5, ci dà l'insieme delle radici e dunque delle parole della lingua possibile, solo una parte del risultato, quella limitata dalle regole della fonologia, cioè dalla compatibilità dei fonemi delle radici, formerà la lingua. Compilare un dizionario significa quindi in primo luogo costruire la lingua possibile per estrarne poi, secondo tali regole, tutte le parole della lingua reale. Egli comincia dunque con il calcolo del numero delle combinazioni senza ripetizione di n lettere dell'alfabeto in gruppi di r, dove r varia da 2 a 5, per poi passare a quello del numero delle permutazioni di ogni gruppo di r lettere. In termini moderni egli calcola quattro valori D_n², ..., D_n⁵ (ossia le disposizioni senza ripetizione di 28 elementi presi a 2 a 2, a 3 a 3, a 4 a 4 e a 5 a 5) dati dalla

con n=28 e 1≤r≤5.

Ciò che interessa sapere è se per ottenere questi risultati Ḫalīl abbia proceduto per semplice enumerazione diretta, cioè empiricamente, o se prima abbia elaborato regole per il calcolo delle combinazioni e delle permutazioni. Soltanto in questo modo potremo giudicare se egli ha effettivamente contribuito all'analisi combinatoria. La questione è delicata perché alcuni suoi scritti sono andati perduti ma, per fortuna, ci resta una citazione di un linguista posteriore, Ḥamza al-Iṣfahānī, che ci è stata trasmessa dal celebre linguista al-Suyūṭī nel suo al-Muẓhir fī ῾ulūm al-luġa wa-anwā῾i-hā (Il chiarificatore delle scienze della lingua e dei loro tipi): "Al-Iṣfahānī scrive: Ḫalīl dice nel Kitāb al-῾Ayn che il numero di queste forme [radici] della lingua degli Arabi, quelle utilizzate e quelle non considerate, siano esse di due, tre, quattro e cinque lettere, senza ripetizione, è di dodicimila migliaia, trecentomila, cinquemila, quattrocentododici" (al-Muẓhir, I, pp. 74-75). E ci viene riferito anche che al-Iṣfahānī continua precisando che quelle bilittere sono 756, quelle trilittere 19.656, quelle quadrilittere 491.400, quelle di cinque lettere 11.793.600: la somma è dunque 12.305.412. Tale citazione non si trova nel Kitāb al-῾Ayn così come ci è pervenuto. Essa forse figurava in un'altra versione o in un altro libro di Ḫalīl andati perduti. Comunque sia, è stata ripresa da successori, come al-Suyūṭī, e corrisponde effettivamente al lavoro contenuto nel Kitāb al-῾Ayn.

I numeri riportati sono giusti e non possono essere ottenuti per enumerazione diretta. Senza dubbio Ḫalīl procedeva mediante un vero e proprio calcolo. Ma quale? Per rispondere a questa domanda facciamo appello a un autore più tardo, che sembra però perpetuare una vecchia tradizione. Si tratta di Ibn Ḫaldūn (1332-1406) e della sua Muqaddima (Introduzione alla sua opera storico-sociologica, il Kitāb al-'῾Ibar, Libro dei moniti esemplari). Secondo Ibn Ḫaldūn, per ottenere le radici a due lettere Ḫalīl combina una prima lettera con tutte le seguenti, lo stesso fa con una seconda lettera, e così via, sommando quindi il tutto "secondo il procedimento noto agli studiosi di aritmetica" (al-Muqaddima, p. 548). Egli considera cioè le combinazioni formate da una lettera e dalle 27 che seguono, da una seconda e dalle 26 seguenti e così di seguito. Si ottiene in tal modo la somma

"che va raddoppiata in ragione dell'inversione delle radici di due lettere", da cui il numero 756. In altri termini, in realtà egli calcola

Per ottenere le radici di tre lettere si procede allo stesso modo. A una data coppia di lettere (a,b) si combinano tutte le lettere seguenti, e così per tutte le coppie. Il totale sarà:

Tuttavia poiché per ogni lessema di tre lettere si ottengono, permutando le lettere, sei lessemi, abbiamo in tutto 6×3276=19.656. Anche qui si calcola

Analogamente, per quattro lettere, si ha:

da cui 24×20.475=491.400, il totale ottenuto da Ḫalīl, cioè

Con cinque lettere, infine, si ha:

,

da cui 120×98.280=11.793.600, ovvero

Resta la difficoltà di sapere come abbia effettivamente operato Ḫalīl, se per combinazioni e permutazioni o calcolando somme di interi. In quest'ultimo caso, la domanda che si pone riguarda le relazioni tra le combinazioni e le somme. Se egli conosceva tali relazioni, bisogna supporre che sapesse costruire i numeri figurati e conoscesse la relazione tra questi numeri e la formula delle combinazioni, oppure che sapesse calcolare la somma delle potenze degli interi naturali per la quarta e la quinta potenza. Un calcolo di questo tipo si incontra però solamente in Ibn al-Hayṯam (m. dopo il 1040), ai primi dell'XI sec., e in un contesto matematico molto diverso.

Quanto riferito da Ibn Ḫaldūn sembra non lasciare dubbi su questo punto: egli vuole suggerire che Ḫalīl, malgrado la confusione e gli errori, procedeva per combinazioni e permutazioni. Tale indicazione gli viene direttamente dalle fonti alle quali si ispira. Sembra infatti che egli abbia preso l'informazione da Ibn al-Bannā᾽ al-Marrākušī (m. 1321), in particolare dal libro di aritmetica di quest'ultimo Raf῾al-ḥiǧāb (Il sollevamento del velo), nel quale Ibn al-Bannā᾽ mette esplicitamente in rapporto le combinazioni utilizzate in lessicografia, nella tradizione di Ḫalīl, e i numeri figurati. Egli stabilisce così, per n=28 lettere dell'alfabeto e r da 2 a 5, la formula

dove F^r_k è il k-esimo numero figurato di ordine r. Nel corso della dimostrazione, ottenuta mediante un'induzione di tipo arcaico presente negli studi arabi di aritmetica, egli utilizza l'uguaglianza:

e conosce le regole che possiamo esprimere, nelle nostre notazioni, nel modo seguente: (n)_r=n(n−1)...(n−r+1) e (n)_n=n! (Rashed 1984). Certo, Ibn al-Bannā᾽ non studia i numeri figurati nella loro generalità, come fa invece il suo contemporaneo al-Fārisī, tuttavia, sebbene la trattazione riguardi r compreso tra 2 e 5, il principio vi è presente. Ciò che importa rilevare qui è l'articolazione delle formule combinatorie fondate sulla conoscenza del triangolo aritmetico (detto 'triangolo di Pascal'), la sua legge di formazione e la lessicografia di Ḫalīl. Non vi è dunque dubbio sull'interpretazione combinatoria delle formule, né sul modo di ottenere la somma degli interi naturali presente nell'opera di Ibn al-Bannā᾽, che è adoperato probabilmente da Ibn Ḫaldūn, anche se in modo un po' maldestro.

Lo stesso Ibn al-Bannā᾽ sembra appartenere a una tradizione che collega la combinatoria del lessicografo e la conoscenza del triangolo aritmetico. Anche Ibn al-Mun῾im (m. 1228) cercava tutte le parole della lingua, non soltanto le radici. Dopo aver richiamato il progetto di Ḫalīl, egli dichiara di volerlo estendere a tutte le parole arabe, la cui lunghezza massima non superi le 10 lettere su un alfabeto di 28. Concepisce un modello originale: "Si dispone di sete di 10 colori. Si vuole comporre dei ciuffi [šarārīb], dei quali alcuni sono costituiti da un solo colore, altri da due, altri ancora da tre, e così via finché l'ultimo gruppo consta di 10 colori, e si vuole conoscere il numero dei ciuffi di ciascun tipo" (Lamrabet 1994, p. 215). Ibn al-Mun῾im fornisce di seguito il triangolo aritmetico. Per quanto riguarda invece Ḫalīl, è verosimile che egli abbia ottenuto formule combinatorie, sebbene soltanto per induzione: era un matematico e un linguista geniale, e quelle formule non sembrano essere fuori della sua portata.

In quanto lessicografo, Ḫalīl considera l'alfabeto di 28 lettere. Lascia da parte molti fonemi, così, il fonema hamza non è considerato una lettera che entra in combinazione con altre. Questo fonema non aveva una forma fissa: si scrive con la lettera alif come nella parola bada᾽ (incominciò), si scrive con la wāw come in yū᾽min (crede), con la yā᾽ come in yastanbi᾽ūna-ka (ti chiedono informazioni) e talvolta, infine, è presente senza lettera 'di sostegno' come nella parola binā᾽ (costruzione). È questo il motivo per il quale alcuni linguisti come al-Mubarrad non lo considerano una lettera ed è forse anche il motivo che spinse Ḫalīl a scartarlo nella composizione del dizionario. Tuttavia, in quanto fonologo, Ḫalīl reintegra hamza come fonema e il numero dei fonemi sale in questo modo a 29.

Oltre al calcolo di combinazioni, si è visto che egli procede anche per permutazioni. Nel Kitāb al-῾Ayn, Ḫalīl, citato dal suo allievo al-Layṯ, scrive:

Sappi che una parola di due lettere prende due forme come qd, dq; šd, dš, mentre le parole di tre lettere prendono sei forme e si chiamano quindi masdūsa, 'in forma di sei', come ḏrb, ḏbr, brḏ, bḏr, rḏb, rbḏ. La parola di quattro lettere ha ventiquattro forme perché le sue lettere, che sono quattro, sono moltiplicate per il numero delle forme di quelle di tre lettere, che sono sei: si hanno ventiquattro forme […]. La parola di cinque lettere prende centoventi forme perché le sue lettere che sono cinque sono moltiplicate per le forme di quelle a quattro lettere che sono ventiquattro; ne risultano centoventi forme delle quali un piccolo numero viene utilizzato, mentre il più grande scartato. (p. 66)

Questa citazione, che ci svela ancora una volta come ragiona Ḫalīl (in accordo con l'interpretazione che è stata suesposta), mostra anche che egli conosceva le due espressioni per le permutazioni P_n=1.2.3…n e P_n=nP_n-1. Il fatto che n assuma solamente i valori 2, 3, 4 e 5 non incide sulla generalità dell'espressione; ciò d'altra parte accade anche negli studi di combinatoria del XVII secolo.

tab. 1

Dopo aver ottenuto, tramite queste combinazioni e permutazioni, la lingua possibile, Ḫalīl applica le proprie conoscenze fonologiche ed etnolinguistiche per isolare da questa la lingua reale. Una volta individuati due livelli di analisi, ossia segni e significati, e una volta ricostituita la lingua possibile a partire dal solo livello dei segni, egli procede a un'ulteriore distinzione tra i suoni: suono periodico, musicale, e suono irregolare, aperiodico; vale a dire la distinzione tra vocali e consonanti. Le consonanti sono poi ordinate in classi secondo il punto di articolazione. Egli elenca le varie classi, partendo dalle laringali per terminare con le labiali (tab. 1), e per alcune classi distingue tra sorde e sonore. Così, nella prima classe la consonante ῾ayn (῾) è sonora, mentre ḥā᾽ (ḥ) è sorda; e nella quinta classe dāl (d) è sonora e tā᾽ (t) sorda. Un esame della sua classificazione e delle spiegazioni date nel Kitāb al-῾Ayn alla luce della fonetica moderna mostra chiaramente che la suddivisione dei suoni in classi secondo il punto di articolazione e l'opposizione sorde/sonore è, nel complesso, affrontata correttamente. L'ordine delle consonanti all'interno di ciascuna classe resta tuttavia piuttosto approssimativo; gli allievi di Ḫalīl, come Sībawayh, riprenderanno quest'analisi per perfezionarla.

Ḫalīl troverà in quest'analisi fonologica le condizioni necessarie per riconoscere, tra le parole della lingua possibile, quelle che possono essere reali. Ma tra le parole che soddisfano queste condizioni non tutte sono necessariamente utilizzate, ed è qui che interviene l'etnolinguistica, la conoscenza della letteratura preislamica, quella del primo secolo dell'Islam, del Corano e di tutti i tesori linguistici che permettono di distinguere tra parole utilizzate e parole trascurate (muhmal). Non va poi dimenticato che questo studio fonologico gli ha permesso di scoprire una proprietà dell'arabo e, più in generale, delle lingue semitiche, essenziale per il suo progetto lessicografico. Egli scoprì infatti una caratteristica morfologica dell'arabo, e cioè l'importanza delle radici nella derivazione del vocabolario e il loro numero relativamente ridotto. La radice, come raggruppamento di consonanti e solo di consonanti, nucleo semantico al quale è spesso associato un significante generico, non poteva apparire come un'unità teorica di analisi prima delle distinzioni tra senso e significato e tra vocali e consonanti. Le radici sono inoltre di forma limitata, ossia si presentano nelle quattro forme richiamate prima: contengono al più cinque lettere e la maggior parte ne contiene tre.

A partire da quest'analisi, Ḫalīl concepirà il progetto del dizionario e i mezzi per realizzarlo come, per esempio, la possibilità di tralasciare le semivocali, che avrebbero reso la combinatoria molto più complicata. L'analisi gli fornisce anche le regole di incompatibilità tra fonemi all'interno di una radice. Non possiamo qui descrivere nei particolari queste regole di incompatibilità ma le riassumiamo per grandi linee. Le prime due consonanti di una radice non possono appartenere alla stessa classe, né in generale a classi contigue; le ultime due sono soggette alla stessa regola ma possono essere simili. La derivazione delle parole a partire dalle radici si ottiene per schemi finiti, anch'essi oggetti di combinatoria. Tali schemi e combinazioni saranno identificati con lo sviluppo della ricerca, cioè quando la fonologia e la morfologia dell'arabo saranno considerate in sé e non solo come ausiliarie della lessicografia. Questa sarà l'opera degli allievi e dei successori di Ḫalīl.

Il Kitāb al-῾Ayn non solo sopravviverà a Ḫalīl ma diventerà un modello per una lunghissima tradizione. Si può dire che tutti i lessicografi dell'arabo sono in un modo o nell'altro allievi di Ḫalīl. Certo, sono stati corretti gli errori commessi nel raccogliere le parole della lingua reale, vi sono state variazioni nella forma del dizionario ed è stata perfezionata la composizione: ma il metodo resta essenzialmente lo stesso. Per fare un solo nome tra i successori di Ḫalīl citiamo Ibn Durayd (m. 321 h.). Nato meno di mezzo secolo dopo Ḫalīl, membro come lui della Scuola di Bassora, scrive al-Ǧamhara (La raccolta), nella quale calcola n^r per n=28 lettere e r variabile da 1 a 5. Egli ripartisce le classi di forme ottenute a seconda che contengano o meno una o più lettere cosiddette 'deboli' quali wāw, yā᾽, hamza, e sistema quindi le varie classi secondo un principio morfologico. Consideriamo il calcolo di Ibn Durayd per r=2: ottiene 28²=784 forme; ne toglie 28, cioè le forme ottenute per ripetizione di una stessa lettera, e ne restano

756=28x27=D²₂₈

(si veda la formula [1] per D_n^r); sottolinea che le 28 forme sono invarianti per permutazione (qalb). Egli esamina quindi la morfologia di tutte le forme e ne trova

600=24x25=D²₂₅

senza lettere deboli; 150 forme ciascuna delle quali contenente una lettera debole; poi 6 forme ciascuna contenente due lettere deboli; e infine 3 forme composte di una lettera debole ripetuta due volte; prosegue quindi il calcolo per le forme di tre, quattro e cinque lettere. Come Ḫalīl, e in modo esplicito, egli definisce questo studio combinatorio 'una sorta di calcolo' (bi-ḍarbin min al-ḥisāb) e scrive: "Ti spiego ciò che ottieni dalle forme a due, tre, quattro e cinque lettere, se Dio l'Altissimo lo vuole, con una sorta di calcolo [ḥisāb] chiaro" (al-Suyūṭī, al-Muẓhir, p. 72).

È possibile seguire questa tradizione lessicografica ancora per un millennio attraverso un buon numero di dizionari come quelli di Aḥmad ibn Fārīs (Mu῾ǧam maqāyīs al-luġa, Dizionario dei paradigmi della lingua), Ibn Manẓūr (Lisān al-῾Arab, La lingua degli Arabi) e al-Zabīdī (Tāǧ al-῾arūs, La corona della sposa). I lessicografi arabi, che avevano cominciato a occuparsi di combinatoria a partire dall'VIII sec., possedevano quindi già i primi elementi di questa nuova materia, corrispondenti, nella notazione moderna, a

Fin da Ḫalīl si aveva la consapevolezza che questi procedimenti ed espressioni rientravano in 'una sorta di calcolo': si tratta di un calcolo di combinazioni. Un calcolo che si impose naturalmente quando si cercò di risolvere da un punto di vista teorico il problema pratico della composizione di un dizionario. Il linguaggio si rivela essere un terreno privilegiato sia per l'elaborazione sia per la pratica di questo nuovo calcolo. Tale circostanza appare legata alla storia dell'analisi combinatoria elementare. La lingua è infatti uno dei campi immediatamente disponibili nel quale si trovano il discreto e il finito: le lettere sono oggetti discreti e sono in numero finito. Più tardi, gli algebristi e gli studiosi di teoria dei numeri cercheranno di ritornare proprio alla lingua per trovare esempi, notazioni e metodi allo scopo di illustrare la combinatoria, che essi elaborano, a quanto sembra, indipendentemente dai linguisti.

La lessicografia non è però la sola disciplina ad avere avuto bisogno di una combinatoria per costituirsi. Un procedimento analogo è seguito dallo stesso Ḫalīl per quanto riguarda la prosodia ed è sempre a lui che viene attribuito uno dei primi trattati di criptografia e di criptoanalisi, discipline i cui inizi datano da quel periodo e che, pur non rientrando nel campo delle ricerche linguistiche, sono strettamente legate a esse. Sono numerosi i linguisti che si occuparono di criptografia e di criptoanalisi. In queste discipline, come nella lessicografia e nella prosodia, si cerca di risolvere in modo teorico un problema pratico: si tratta in questo caso di creare algoritmi efficienti per nascondere il contenuto di un testo o di un messaggio. Di qui il nome di al-ta῾miya dato alla disciplina, dal verbo ῾amiya che significa 'perdere completamente la visione di qualcosa'.

A partire al più tardi dal IX sec. con al-Kindī, questa disciplina non soltanto fu designata con un nome specifico ma ebbe anche un proprio vocabolario tecnico. Da quel momento, e fino alla metà del XVIII sec., vedrà la luce un'immensa letteratura specialistica, com'è attestato dagli scritti di al-Zabīdī, autore del famoso dizionario di arabo e di un trattato sui fondamenti della criptografia. Tra i nomi più famosi troviamo ῾Alī ibn ῾Adlān (583-661/1187-1263), Isḥāq ibn Ibrāhīm ibn Wahb, Ibn Ṭabāṭabā (m. 322/934), ῾Alī ibn Muḥammad ibn al-Durayhim (712-762/1312-1361), autori che per i loro algoritmi fanno uso, come si può intuire, di trasposizioni, sostituzioni e permutazioni. Anche se non arricchiscono di nuove regole la combinatoria, essi da un lato dimostrano che questa è uno strumento utilizzabile anche in campi che non siano la lessicografia o la prosodia, dunque non è legata a un campo in particolare e, dall'altro, contribuiscono alla sua diffusione presso un pubblico che non è solo quello dei linguisti. Inoltre, essi mettono in luce il significato propriamente combinatorio delle permutazioni, delle trasposizioni e delle sostituzioni.

Si potrebbero fare numerosi altri esempi, tratti o meno dai campi di ricerca menzionati, al fine di testimoniare la diffusione della conoscenza e della pratica della combinatoria tra gli studiosi e i filosofi. Così, il letterato Abū 'l-Ḥayyān al-Tawḥīdī, nelle sue Muqābasāt, ricorda l'esempio del filosofo Yaḥyā ibn ῾Adī, suo contemporaneo, il quale cercava i numeri della 'divisione logica' secondo cui si organizzano gli elementi della frase inna al-qā᾽ym ġayr al-qā῾id (chi sta in piedi non sta seduto), vale a dire il numero delle configurazioni ottenute a partire da una frase di quattordici lettere (dove hamza non è una lettera; in questa frase vanno infatti contate solamente le lettere che hanno valore consonantico; soltanto queste e non le vocali sono, per la lingua araba, lettere in senso proprio). Questo problema corrisponde a quello della distribuzione di 14 palline in 2 urne; Yaḥyā ibn ῾Adī trova che esse sono

Al-Bīrūnī, nell'opera Kitāb Taḥdīd nihāyāt al-amākin li-taṣḥīḥ masāfāt al-masākin (Libro sulla determinazione delle coordinate delle località per rettificare il valore delle distanze fra loro), conferma questa testimonianza e procede egli stesso a un semplice calcolo di combinazioni per trattare l'eclissi di Luna.

Calcolo algebrico e combinatorio

Dal canto loro, gli algebristi, impegnati nel movimento di 'aritmetizzazione dell'algebra', come pure nello sviluppo del calcolo algebrico astratto, concepiscono nuove tecniche, tra le quali lo sviluppo delle potenze del binomio di grado qualunque. Proprio l'elaborazione di queste tecniche portò gli algebristi alla tavola dei coefficienti binomiali, alla regola di formazione di questa e alla formula binomiale per potenze intere. Sappiamo infatti da al-Samaw᾽al che, alla fine del X sec., al-Karaǧī conosceva le formule

,

per n intero e che aveva anche dimostrato il teorema del binomio per induzione finita completa. Dalla fine del X sec., le espressioni come la [15] vengono continuamente incluse, con qualche leggera variante, nei libri di algebra e di ḥisāb (calcolo). Siamo quasi sicuri che ῾Umar al-ḫayyām (1042-1131) conosceva queste espressioni. Egli scrive infatti:

Gli indiani conoscono metodi per determinare i lati dei quadrati e dei cubi che basano su un'induzione [che poggia] su pochi numeri, cioè la conoscenza dei quadrati di nove cifre, vale a dire il quadrato di uno, di due, di tre […], come pure i prodotti di uno per l'altro, cioè il prodotto di due per tre, e analogamente per casi simili. Abbiamo scritto un libro per dimostrare che questi metodi sono esatti e conducono all'oggetto cercato. Ne abbiamo inoltre moltiplicato le forme, voglio dire per determinare i lati del quadrato-quadrato, del quadrato-cubo, del cubo-cubo, e ciò fin dove si vuole, cosa nella quale nessuno ci aveva preceduto. Si tratta di dimostrazioni numeriche, fondate sui libri aritmetici degli Elementi. (Risāla fī 'l-ǧabr wa-'l-muqābala, pp. 129-200)

Nel XIII sec., queste stesse formule, a meno di qualche piccola differenza, saranno riscoperte. Così, Naṣīr al-Dīn al-ṭūsī (1201-1274), nei Ǧawāmi῾ al-ḥisāb bi-'l-taḫt wa-'l-turāb (Compendio del calcolo con la tavoletta e la polvere), dà la formula:

La medesima espressione si ritroverà nel XV sec. nel Miftāḥ al-ḥisāb (La chiave del calcolo) di Ǧamšīd al-Kāšī. Si tratta però di formule ben note ad al-Zanǧānī, al-Fārisī (m. 1319), Ibn al-Mālik al-Dimašqī, al-Yazdī e Taqī al-Dīn ibn Ma῾rūf tra molti altri. Quindi, sin dalla fine del X sec. il triangolo aritmetico o di Pascal, come pure il teorema del binomio facevano parte delle conoscenze dei matematici arabi. Non è poi raro trovare regole riguardanti le permutazioni nei libri di ḥisāb, dopo l'esposizione delle regole elementari dell'aritmetica e della somma di una progressione aritmetica, e prima dello studio dell'estrazione di radice (quadrata, cubica o di potenza superiore). Certo, una cosa è conoscere questo triangolo, la sua regola di formazione e il teorema del binomio e vederli come strumenti matematici necessari per l'algebra dei polinomi, per l'estrazione della radice n-esima di un intero, ecc. e altra cosa è considerarli come elementi di una nuova disciplina che si occupa delle partizioni di un insieme finito. Soltanto quando questi strumenti sono interpretati da un punto di vista combinatorio si può parlare di una nuova branca degli studi matematici. Tale passaggio fondamentale segna proprio l'atto di nascita della nuova disciplina.

Tuttavia, sarebbe errato pensare che gli algebristi non avessero colto relativamente presto quest'interpretazione, anche se solo implicitamente. Un buon esempio è fornito da uno studio di al-Samaw᾽al sul seguente problema. Date dieci incognite x₁, ..., x₁₀, si cerca un sistema di equazioni lineari a sei incognite; egli ottiene

equazioni a sei incognite; poi, esaminando il problema della loro compatibilità e applicando delle combinazioni, trova 5040; eliminando le ripetizioni, queste condizioni si riducono a 504. In questo studio al-Samaw᾽al rappresenta le incognite x_i mediante la cifra i, cioè mediante gli 'indici', come diremmo oggi. La tesi secondo la quale questi algebristi ignoravano tutto dell'interpretazione combinatoria delle regole da loro espresse viene dunque smentita da questa applicazione del calcolo combinatorio data da al-Samaw᾽al. Siamo convinti che l'interpretazione combinatoria non fosse loro sfuggita; nulla però li obbligava a formularla esplicitamente. Questa formulazione non tarderà a emergere quando gli algebristi procederanno a nuove ricerche di aritmetica o si occuperanno di filosofia. L'analisi combinatoria si presenta inizialmente proprio in questa diversità dei campi di applicazione ‒ algebra, ricerche aritmetiche, filosofia, linguistica, criptografia ‒, prima che emerga la coscienza della sua unità; e non malgrado la diversità delle applicazioni, ma proprio grazie a essa. Soltanto allora si pubblicheranno i primi scritti interamente dedicati all'analisi combinatoria come quello di al-Ḥalabī.

Ricerche di aritmetica e di combinatoria

A cominciare da Naṣīr al-Dīn al-ṭūsī, e molto probabilmente prima di lui, viene ripetutamente riscoperta l'interpretazione combinatoria del triangolo aritmetico e della sua legge di formazione; e si ritrovano anche le regole elementari dell'analisi combinatoria. Durante tutto il XIII sec., infatti, e in particolare negli ultimi anni, quell'interpretazione è presente nelle ricerche di aritmetica. Alla fine del secolo Kamāl al-Dīn al-Fārisī, in una memoria di teoria dei numeri, ritorna su quest'interpretazione e stabilisce l'uso del triangolo aritmetico per gli ordini numerici, cioè il risultato che si attribuisce generalmente a Pascal. Per i numeri figurati egli stabilisce una relazione equivalente alla:

,

dove F^q_p è il p-esimo numero figurato di ordine q, F^q_{p = 1} per ogni q, presentando quindi in questo modo un legame tra i numeri figurati di ordine qualunque e le combinazioni. Per conoscere il numero dei divisori propri di un intero è quindi possibile rifarsi alla tavola dei numeri figurati. Questa è la spiegazione di al-Fārisī:

Il metodo per conoscere le parti aliquote binarie (combinazioni di due termini) o ternarie, o di altre a un numero qualunque di lati, a condizione che siano primi e tutti distinti, consiste nel cercare nella successione delle somme omonime del numero di volte [῾adad al-ta᾽līf] meno uno per il quale si combina, il numero il cui rango ‒ cioè i primi numeri [nelle successioni] delle somme (indici delle colonne) ‒ è omonimo del numero di lati meno il numero di volte per le quali si combina. È il numero delle combinazioni. (Rashed 1983, par. 17)

Per cogliere il senso di questo passo supponiamo che il dato intero si decomponga in n fattori primi distinti e si cerchi il numero di parti aliquote prodotto di m interi, con 0⟨m⟨n. Si cerca allora nella tavola l'elemento che si trova all'incrocio tra la (m−1)-esima riga e la (n−m)-esima colonna. Si ottiene allora F^m_n-m+1 che, per la formula precedente, è uguale a

Per dimostrare questa proposizione al-Fārisī opera in modo interamente combinatorio, per applicazioni successive del triangolo aritmetico, le cui 'celle' sono interpretate esplicitamente come combinazioni di p oggetti in gruppi di k. Lo stile combinatorio di al-Fārisī sembra essere un tratto comune dell'epoca, ed è precisamente di questo stile che egli aveva bisogno per stabilire il teorema sulle funzioni aritmetiche elementari, il numero dei divisori propri di un numero. Nel calcolo delle combinazioni per determinare il numero delle parti aliquote di un intero al-Fārisī riprende i coefficienti binomiali, e ne dà un'interpretazione decisamente combinatoria. Un atto che è tra quelli fondanti dell'analisi combinatoria e che permetterà di considerare i numeri figurati in modo incomparabilmente più generale di quello dei predecessori e dei contemporanei di al-Fārisī che conosciamo.

Filosofia e combinatoria

Linguistica, criptografia e ricerche di aritmetica non sono i soli campi nei quali compaiono i procedimenti combinatori in un'interpretazione espressamente combinatoria. Anche la filosofia teorica ha infatti avuto un ruolo particolarmente importante nella formazione dell'analisi combinatoria. Molto prima di Leibniz, e in modo incomparabilmente più efficace di Raimondo Lullo (1234 ca.-1315), il matematico del XIII sec. Naṣīr al-Dīn al-ṭūsī, per far parlare l'ontologia di Avicenna in una lingua precisa, applica le regole e le formule delle quali aveva fatto uso nei Ǧawāmi῾ al-ḥisāb bi-'l-taḫt wa-'l-turāb. Come abbiamo già ricordato, in questo libro egli riproponeva il triangolo aritmetico e il teorema del binomio. In un trattato di metafisica dal titolo Fī bayān kayfiyyat ṣudūr al-ašyā᾽ al-ġayr al-mutanāhiya῾an al-mabda᾽ al-awwal al-wāḥid (Sulla dimostrazione del modo di emanazione delle cose [in numero infinito] a partire dal principio primo unico) al-Ṭūsī si propone di risolvere il problema dell'emanazione di una molteplicità da un principio primo; si tratta quindi dell'emanazione degli 'intelletti'. Al-Ṭūsī rappresenta questi intelletti con lettere dell'alfabeto, quindi applica le regole delle combinazioni. Egli comincia con l'introdurre il lemma che afferma che il numero totale delle combinazioni di n elementi a k a k è pari a

e per calcolare questo numero usa l'uguaglianza

Procede quindi al calcolo degli esseri derivati, rango per rango, utilizzando l'espressione

per 1≤p≤16, m=4, n=12, il cui valore è il coefficiente binomiale

questo calcolo si esegue con la [34].

Il contributo di al-Ṭūsī sarà riportato nel primo trattato conosciuto di analisi combinatoria, di cui ci occuperemo.

Un trattato di analisi combinatoria

L'interpretazione espressamente combinatoria del triangolo aritmetico e del teorema del binomio è presente in al-Ṭūsī come qualcosa di ovvio. Egli si esprime in una terminologia tecnica che si ritroverà nei suoi successori, come al-Fārisī e Ibn al-Bannā᾽. Tutto lascia pensare che all'epoca di al-Ṭūsī, e forse anche prima, gli algebristi avessero adottato quest'interpretazione nelle applicazioni di questo tipo di formule alle diverse discipline, algebra compresa. Tali formule, e in particolare il triangolo e il teorema, si ritrovano spesso riprodotte nei libri di ḥisāb e di algebra. Si trovano fra gli altri nel Miftāḥ al-ḥisāb di al-Kāšī; nel libro di Ibn al-Mālik al-Dimašqī, al-Is῾āf al-atamm (L'assistenza perfetta); in quello di Taqī al-Dīn ibn Ma῾rūf, Buġyat al-ṭullāb (Il desiderio degli studiosi), che prende esempi dalla linguistica per illustrare certe regole; e nell'opera di al-Yazdī, ῾Uyūn al-ḥisāb (Le fonti del calcolo).

Presenza massiccia e applicazioni frequenti: tutto indica che era giunto il momento perché l'analisi combinatoria raggiungesse una propria indipendenza e si presentasse con una certa autonomia. Essa era ormai maturata al punto di diventare argomento di una dissertazione. Quando successe tutto ciò precisamente? Non lo sappiamo. È noto però che un matematico e filosofo, Ibrāhīm al-Ḥalabī, redasse il già citato Fī istiḫrāǧ ῾iddat al-iḥtimālāt al-tarkībiyya min ayy ῾adad kāna, che è in ogni caso il primo trattato a tutt'oggi conosciuto interamente dedicato alla combinatoria. Le regole di questa disciplina non vi compaiono più semplicemente come regole di calcolo algebrico e non si fa più appello a esse solo per applicarle all'algebra, alla linguistica o alla filosofia. Esse sono considerate in sé, in un libro con un titolo che rinvia alle permutazioni, alle disposizioni, alle combinazioni, e così via, cioè a tutti gli argomenti di combinatoria allora studiati. In questo trattato il testo di al-ṭūsī, ripreso e amplificato, occupa un posto di riguardo: funge da metodo per determinare e stabilire le combinazioni.

Al-Ḥalabī incomincia con l'interrogarsi sui vari metodi per studiare le 'eventualità combinabili' (al-iḥtimālāt al-tarkībiyya). Il suo obiettivo è chiaro: "determinare quante sono le eventualità combinabili per un numero qualunque di oggetti" (Risāla fī istiḫrāǧ ῾iddat al-iḥtimālāt al-tarkībiyya, f. 69v). Egli scarta il metodo empirico che consiste nell'enumerare, per esempio, per un insieme di tre elementi a,b e c, le sette eventualità combinabili a,b,c,ab,ac,bc,abc; le difficoltà sono chiare quando l'insieme ha n elementi (f. 70r). Il secondo metodo (ff. 70r-71v) fornisce invece una regola generale, della quale egli va fiero. Si tratta di un'espressione equivalente a u_n=2u_n−1+1, dove u_n è l'insieme di tutte le eventualità combinabili di n elementi; in linguaggio moderno,

per 1≤k≤n.

Il metodo è verosimilmente stabilito a partire dalla regola seguente, nota dalla fine del X sec.:

Sommando si ottiene:

Al-Ḥalabī però si discosta anche da questo metodo che richiede un calcolo complicato, quello di tutti gli u_i per 1≤i ≤n−1. Per ottenere un metodo migliore egli prende come punto di partenza l'espressione [21], sapendo che

Al-Ḥalabī definisce quindi diverse eventualità combinabili e le corrispondenti regole di calcolo: (a) la 'materia' (al-mādda) (f. 71v) delle eventualità di ordine k, cioè le combinazioni degli elementi senza ripetizione in gruppi di k, il cui numero è

(b) la 'materia e la forma' (maǧmū῾ al-mādda wa-'l-ṣūra) (f. 72r) delle eventualità di classe k, cioè le disposizioni senza ripetizione:

(c) la 'forma' (al-ṣūra) (ff. 72v-73r) delle eventualità di classe k: si sottrae la materia (a) da 'la materia e la forma' (b):

(d) la forma delle eventualità indipendentemente dalla classe, cioè le permutazioni di n oggetti:

[31] n!=n (n−1)....2∙1,

e infine (e) la materia, la forma e la ripetizione di ordine k, cioè le disposizioni con ripetizione di n oggetti presi in gruppi di k, che sono in numero di n^k.

Il lessico tecnico della lingua dell'analisi combinatoria che usa al-Ḥalabī in questo trattato si compone di termini già utilizzati da al-ṭūsī (per es., tarkīb, composizione); di termini a lui propri come iḥtimālāt (eventualità) o tikrār (ripetizione); e anche di prestiti dal linguaggio aristotelico, come mādda e ṣūra. Gli ultimi due termini gli impongono però di introdurre problemi estranei all'argomento in questione, e anche superflui in tale contesto, temi che recano pregiudizio alla chiarezza dell'esposizione, come quando al-Ḥalabī si chiede se materia e forma si possano separare.

Una volta poste queste regole al-Ḥalabī scrive: "Per determinare le eventualità 'materiali' [al-iḥtimālāt al-māddiyya] (ossia le combinazioni senza ripetizione) esiste un altro metodo, al quale si è fatto appello per determinare gli 'intelletti accidentali' [al-῾uqūl al-῾araḍiyya]". È allora che egli incorpora il testo di al-ṭūsī sia in verbis sia nello sviluppo del calcolo. Egli traccia il triangolo aritmetico fino a 12 e fa la somma degli elementi della diagonale che chiama 'combinazioni semplici' (al-iḥtimālāt al-basīṭa) ottenendo il numero 4095 menzionato da al-ṭūsī e chiama 'combinazioni composte' (al-iḥtimālāt al-murakkaba) l'espressione

,

e mostra che alla formula [22] corrisponde la somma delle combinazioni semplici e composte. In altre parole, si ha:

quando si sottrae 1 da tutte e due le parti si ottiene:

da cui, tenendo conto dell'equivalenza con la sommatoria da p=0 a p=m+n come la [22], ottiene l'uguaglianza 2^m+n=2^m2ⁿ.

Al-Ḥalabī procede poi ad altri calcoli sui dati forniti da al-ṭūsī, e si abbandona a riflessioni sul testo del suo predecessore, tutte riguardo a proprietà combinatorie. Siamo molto lontani dal problema dell'emanazione della molteplicità a partire dall'Uno, del quale non resta che un pallido ricordo. Già attenuato in al-ṭūsī, il contenuto ontologico scompare completamente da questo trattato di analisi combinatoria: restano soltanto i metodi e i risultati necessari o anche solo utili al trattato. Se dunque l'aspetto 'assiomatico' della dottrina di Avicenna, e una propensione per l'ontologia formale, permettono ad al-ṭūsī di sperare in una soluzione matematica di questo problema metafisico, tale soluzione si è venuta a trovare poi inserita in lavori di matematica, indipendentemente dal problema metafisico da cui essa scaturiva. Ciò è stato possibile in quanto gli oggetti della combinatoria possono essere Intelletti o oggetti qualunque: la sola condizione è che siano distinti e in numero grande a piacere ma finito.

Sulla storia dell'analisi combinatoria

La storia del costituirsi dell'analisi combinatoria come disciplina autonoma tra Ḫalīl nell'VIII sec. e al-Ḥalabī nel XVI si presenta come la storia di oggetti appartenenti a campi differenti che si spogliano di ogni dimensione ontologica per conservare soltanto componenti formali: si riducono a un insieme di oggetti qualunque, in numero finito e discreti. Come abbiamo visto, è proprio grazie alla varietà e alla diversità di questi campi di interesse che tali elementi formali sono potuti emergere e hanno potuto acquisire la loro indipendenza. È facile capire come, per via di questa varietà, la storia dell'analisi combinatoria degli inizi non si configuri affatto come un cammino in linea retta che porta alla scoperta delle proprietà essenziali di un oggetto particolare dato in anticipo. Per la loro neutralità ontologica e il loro aspetto, le lettere dell'alfabeto si prestavano direttamente a uno studio di carattere combinatorio. Ma questo studio, per quanto se ne possa dire, non è stato fatto subito, come in seguito a una presa di possesso eidetica, bensì soltanto quando Ḫalīl si propose di risolvere teoricamente il problema pratico della composizione di un dizionario della lingua. È probabile che i procedimenti da lui ideati e le formule da lui stabilite verosimilmente riguardassero soltanto la formazione delle parole e non avessero il carattere di generalità necessario alla costruzione di una disciplina autonoma riguardante le combinazioni. Resta però il fatto che Ḫalīl e i suoi successori, come Ibn Durayd, sensibili al carattere formale di questi procedimenti e di queste formule, vi riconoscevano 'una specie di calcolo' (ḍarbun min al-ḥisāb). Come disciplina autonoma, l'analisi combinatoria non è ancora nata mentre in quanto calcolo è in avanzato stato di gestazione. Tra i criptografi la combinatoria si trova nella stessa situazione.

Alla fine del X sec. gli algebristi (al-Karaǧī e i suoi successori) avevano dal canto loro stabilito il triangolo aritmetico, la regola di formazione e il teorema del binomio. Anche se i matematici sapevano di manipolare procedimenti combinatori, li utilizzavano, come afferma al-Samaw᾽al, soltanto come mezzi ausiliari per il calcolo algebrico astratto che stavano allora sviluppando. Tuttavia dopo la fine del X sec. e prima del XIII si compie un atto essenziale per la storia dell'analisi combinatoria: il riconoscimento esplicito, e non solo implicito, che le regole applicate dai linguisti, dai criptografi e da altri ancora sono le stesse stabilite dagli algebristi e, inoltre, che si possono applicare a varie situazioni: ricerche di aritmetica, filosofia, ecc. Sarebbe azzardato al momento cercare di stabilire chi ha fatto il gran passo; sappiamo però che già Naṣīr al-Dīn al-Ṭūsī si muoveva a suo agio in questo nuovo universo di pensiero. A questo stesso universo appartengono i lavori dei suoi successori quali al-Fārisī e Ibn al-Bannā᾽.

L'ultimo passo da compiere, che però non presenterà difficoltà particolari, è quello di parlare delle regole e delle formule in un linguaggio combinatorio, senza riferimento a questo o a quel campo di applicazione. È tale passo che identifica una disciplina e ne fonda l'autonomia. Si tratta di un passo più epistemico che tecnico, compiuto da al-Ḥalabī nel suo libro, la cui importanza risiede appunto in questo gesto epistemico. Ideando un linguaggio tecnico, certo ancora pesante, che sarà riscoperto più tardi da Leibniz nell'Orizzonte della natura umana (1693), al-Ḥalabī dimostra una volta di più la volontà di riconoscere nell'analisi combinatoria una branca indipendente del sapere. È stato il primo? In ogni caso per noi, limitatamente alle nostre conoscenze, lo è stato. La storia dell'analisi combinatoria araba si ferma qui. Questa disciplina rinascerà quando verrà applicata al nuovo e vastissimo campo della probabilità; ma per questo bisognerà attendere Fermat, Pascal, Jacques Bernouilli e tutti gli altri.

Bibliografia

Kennedy 1973: Kennedy, Edward S., A commentary upon Bīrūnī's Kitāb Taḥdīd al-amākin, an 11th century treatise on mathematical geography, Beirut, American University of Beirut, 1973 (ed. ar.: Kitāb Taḥdīd nihāyāt al-amākin, [a cura di] P. Bulgakov, "Maǧalla al-maḫṭūṭāt al-῾arabiyya / Revue de l'Institut des manuscrits arabes", 6, 1962; trad. ingl.: The determination of the coordinates of positions for the correction of distances between cities: al-Bīrūnī᾽s Taḥdīd al-amākin, Beirut, American University of Beirut, 1967; rist. in: "Islamic Geography", 26, 1992).

Lamrabet 1994: Lamrabet, Driss, Introduction à l'histoire des mathématiques maghrébines, Rabat, Driss Lamrabet, 1994.

Mrayati 1987: Mrayātī, Muḥammad Yaḥyā Mīr ῾Alam, Ḥassān al-Ṭayyān, Origins of Arab cryptography and cryptanalysis, v. I: Analysis and editing of three Arabic manuscripts: Al-Kindī, Ibn ῾Adlān, Ibn al-Durayhim, Damasco, The Arab Academy, 1987.

Rashed 1972: Rashed, Roshdi, L'induction mathématique. Al-Karaǧī, As-Samaw᾽al, "Archive for history of exact sciences", 9, 1972, pp. 1-21.

‒ 1973: Rashed, Roshdi, Algèbre et linguistique. L'analyse combinatoire dans la science arabe, in: Logical and epistemological studies in contemporary physics, edited by Robert Cohen, Boston, Reidel, 1973, pp. 383-399 (rist. in: Rashed, Roshdi, Entre arithmétique et algèbre. Recherches sur l'histoire des mathématiques arabes, Paris, Les Belles Lettres, 1984, pp. 245-257).

‒ 1982: Rashed, Roshdi, Matériaux pour l'histoire des nombres amiables et de l'analyse combinatoire, "Journal for the history of Arabic science", 6, 1982, pp. 209-278.

‒ 1983: Rashed, Roshdi, Nombres amiables, parties aliquotes et nombres figurés aux XIII^e-XIV^e siècles, "Archive for history of exact sciences", 28, 1983, pp. 107-147 (rist. in: Rashed, Roshdi, Entre mathématique et algèbre. Recherches sur l'histoire des mathématiques arabes, Paris, Les Belles Lettres, 1984, pp. 259-299).

‒ 1984: Rashed, Roshdi, Entre arithmétique et algèbre. Recherches sur l'histoire des mathématiques arabes, Paris, Les Belles Lettres, 1984 (trad. ingl.: The development of Arabic mathematics. Between arithmetic and algebra, Dordrecht-Boston, Kluwer, 1994).

‒ 1999a: Rashed, Roshdi - Vahabzadeh, Bijan, Al-Khayyām mathématicien, Paris, Blanchard, 1999 (trad. ingl.: Omar Khayyam. The mathematician, New York, Bibliotheca Persica, 2000).

‒ 1999b: Rashed, Roshdi, Combinatoire et métaphysique: Ibn Sīnā, al-Ṭūsī et al-Ḥalabī, in: Les doctrines de la science de l'antiquité à l'âge classique, édité par Roshdi Rashed et Joël Biard, Leuven, Peeters, 1999, pp. 61-86 (trad. ted.: Kombinatorik und Metaphysik: Ibn Sīnā, aṭ-Ṭūsī und al-Ḥalabī, in: Mathesis, Festschrift zum siebzigsten Geburtstag von Matthias Schramm, hrsg. von Thiele Rüdiger, Berlin-Diepholz, GNT, 2000, pp. 37-54; trad. ingl.: Metaphysics and mathematics in classical Islamic culture: Avicenna and his successors, in: God, life and the cosmos: christian and islamic perspectives, edited by Ted Peters, Muzaffar Iqbal and Sayed Nomanul Haq, Aldershot-Burlington, Ashgate, 2002, pp. 151-171).