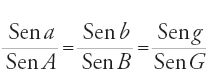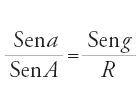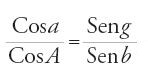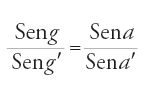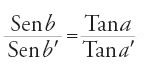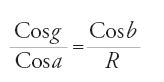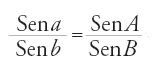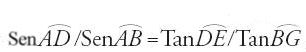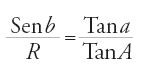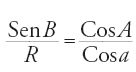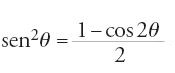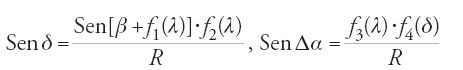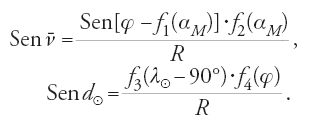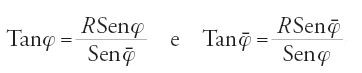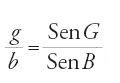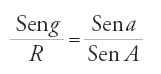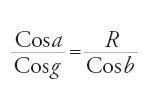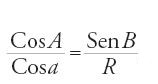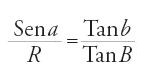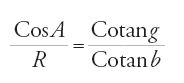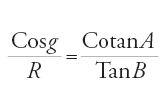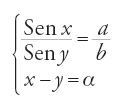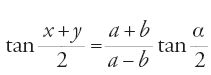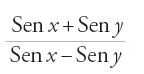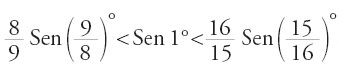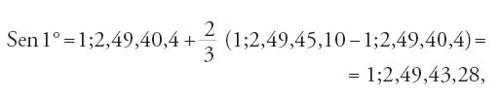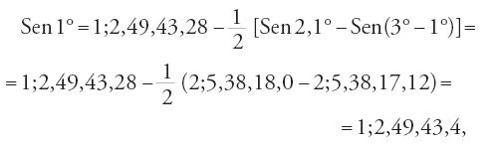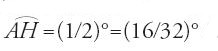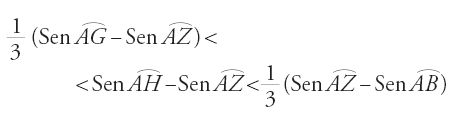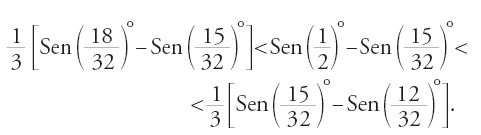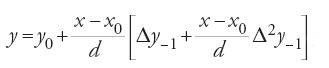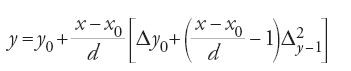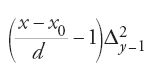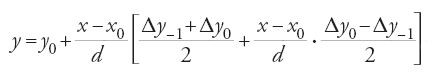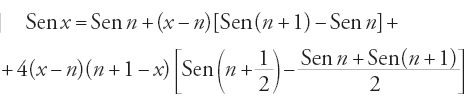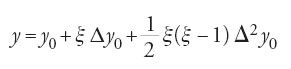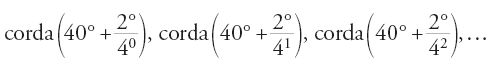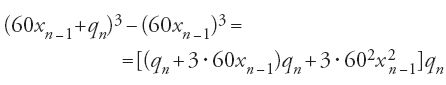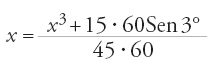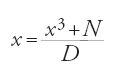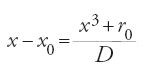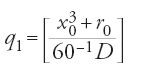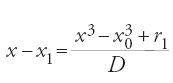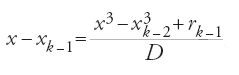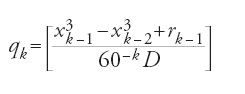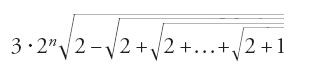La civiltà islamica: antiche e nuove tradizioni in matematica. Trigonometria

La civilta islamica: antiche e nuove tradizioni in matematica. Trigonometria

Trigonometria

Dalla geometria alla trigonometria

La trigonometria, scienza ausiliaria dello studio del moto degli astri, ha origini che risalgono almeno a Ipparco, al quale è attribuita la prima tavola delle corde. Già verso il VI sec. gli studiosi indiani sostituiscono la vecchia corda dell'arco doppio con la metà, cioè con R volte il nostro seno (scriveremo Sen per Rsen), dando al raggio R del cerchio della sfera diversi valori (60, 150, 3438, 120, ecc.). Nonostante il contributo della scienza indiana in questo campo non si limiti alla sola introduzione del seno, ciò non toglie che per gli astronomi arabi del IX sec. l'Almagesto non tarderà a soppiantare i Siddhanta indiani. Il trattato greco seduce per il rigore dell'esposizione, le dimostrazioni e i programmi di osservazione che suggerisce. Per quanto paradossale possa sembrare, l'enorme edificio costruito da Tolomeo nell'Almagesto, la celebre Syntaxis mathematica, si basa essenzialmente su alcune proposizioni geometriche molto elementari. I calcoli piuttosto complessi riguardanti i modelli planetari si riducono sempre al teorema di Pitagora e alla corda che rappresenta questo o quel cateto di un triangolo rettangolo la cui ipotenusa è uguale al diametro del cerchio di riferimento (con raggio R pari a 60, comodo nella numerazione sessagesimale). Lati e angoli di triangoli piani sono ottenuti in questo modo. Lo stesso linguaggio geometrico si ritrova, applicato alla costruzione della tavola delle corde, nel capitolo 10 del Libro I, dove esprime implicitamente le formule di addizione degli archi. Quanto all'astronomia sferica, essa sembra ridursi a una dozzina di applicazioni del teorema di Menelao.

Questo è, per sommi capi, e senza menzionare per ora alcuni artifici più sottili, l'apparato trigonometrico dell'Almagesto. Preparati sui testi greci e indiani, i primi astronomi arabi si doteranno in qualche decennio di un'astronomia sferica che, se può disorientare per la terminologia e i temi affrontati, si rivela comunque in grado di risolvere qualunque problema. Soltanto un secolo e mezzo dopo, verso l'anno 1000, la riforma intrapresa troverà una formulazione matematica con la comparsa delle prime relazioni tra gli elementi del triangolo sferico. Saranno allora precisate le nozioni, in particolare quella di funzione tangente introdotta a partire dal IX secolo. Contemporaneamente si prenderà coscienza dell'importanza di poter disporre di un metodo e di un linguaggio specifici. In questo periodo di regno dei Buwayhidi, durante il quale i centri di ricerca scientifica sono numerosi e molto attivi, si può effettivamente parlare di un'affermazione della trigonometria. Da allora la nuova scienza sarà oggetto di opere dedicate esclusivamente a essa; si assiste anche alla ricerca di una maggiore precisione nella lettura e nella costruzione della tavola dei seni, che darà origine ad altri lavori.

Nel presente capitolo seguiremo il percorso che ha portato alla nascita di questa tecnica particolare che è la trigonometria. Faremo riferimento ai testi riportando qualche formula; lo stato attuale delle nostre conoscenze, infatti, non ci permette di fare un inventario completo. Eviteremo di andare sistematicamente alla ricerca dei precursori di Regiomontano (1436-1476), François Viète (1540-1603), Retico (1514-1576) e altri fondatori della trigonometria in Europa. I confronti sono rischiosi, in quanto in Occidente la trigonometria si è formata a partire da un sapere già costituito, al di fuori del contesto astronomico nel quale era sorta cinque secoli prima in terra abbaside. Secondo l'uso che se ne fa, una stessa formula può in effetti avere significati diversi ed essere più o meno interessante. È un punto sul quale torneremo a proposito delle formule del triangolo sferico e della nozione di triangolo polare. Sarebbe inoltre un abuso confondere, per esempio, le semplificazioni occasionali di Ibn Yūnus (m. 1009) o ǧamšīd Ġiyāṯ al-Dīn al-Kāšī (m. 1429), quando in alcune regole di astronomia sostituiscono prodotti di seni e coseni con somme, con la 'prostaferesi' (un metodo che consiste nel sostituire la moltiplicazione con l'addizione mediante formule del tipo cosa cosb=1/2 [cos(a+b)+cos(a−b)]), conosciuta in Europa nel XVI sec. e che si rivelò utile prima dell'introduzione dei logaritmi.

Succede spesso in matematica che nozioni utili in un certo periodo cadano poi in disuso. Nell'epoca della quale ci occupiamo abbiamo l'esempio del senoverso Versθ=R(1-cosθ), che gli autori arabi prendono dalla scienza indiana e che nei loro trattati ha un po' il ruolo del nostro coseno. In mancanza di una qualunque nozione di orientamento e di segno, il senoverso ha il vantaggio di assumere valori distinti per angoli acuti od ottusi. Analogamente, ancora recentemente si mettevano in forma logaritmica formule di trigonometria sferica; tale forma non si applica più e la risoluzione dei triangoli ha anch'essa perduto il posto che aveva nei manuali di astronomia. Come altre discipline, la trigonometria ha subito l'evoluzione unificatrice della matematica. È opportuno, quindi, considerare singolarmente le fasi del suo sviluppo. Per noi il periodo arabo rappresenta il periodo delle prime formule del triangolo, delle prime definizioni e dell'introduzione della funzione tangente. Dimenticheremo il contenuto che assumeranno in seguito in analisi le funzioni circolari, per tornare invece all'epoca nella quale la trigonometria prende forma distinguendosi dalla geometria.

Il calcolo sferico degli 'zīǧ'

La doppia eredità, indiana e greca, dell'astronomia sferica araba, i problemi dei quali progressivamente si arricchisce e le strade scelte nel IX sec. per risolverli, saranno determinanti nella formazione dello strumento matematico destinato a facilitarne la risoluzione. È quindi importante conoscerne le componenti, anche se dovremo allontanarci leggermente dal quadro del nostro studio.

Un primo elemento costitutivo del calcolo sferico, come appare abbondantemente sviluppato negli zīǧ (le tavole astronomiche), proviene dall'eredità greca. Riguarda il ruolo fondamentale dell'eclittica, il cerchio di riferimento dei movimenti planetari. Si avvia in questo modo una tecnica di decomposizione dei problemi che riduce in anticipo il numero delle formule utili. Come nell'Almagesto, tutto viene, per così dire, riferito all'eclittica: gli angoli con le verticali (per la parallasse) e con l'orizzonte (visibilità); i punti o 'gradi' dell'eclittica associati a ogni astro ('grado', 'grado di passaggio' al meridiano, 'gradi di levata e di tramonto'); i punti situati in un dato istante al meridiano o all'orizzonte (da cui l'ascendente degli astrologi) che fissano la posizione della sfera nel suo moto diurno. Una nozione importante è quella di ascensione obliqua, la cui tavola è richiesta nell'Almagesto per ottenere la longitudine dell'ascendente (che deve essere tabulata per ciascuna latitudine). Non resta allora che applicare il teorema di Menelao a problemi semplici, il più delle volte a partire da un quadrilatero formato da quarti di cerchi massimi.

La prop. 1 del Libro III degli Sphaerica di Menelao di Alessandria (I sec. d.C.) stabilisce una relazione tra sei archi di tre cerchi massimi sostegno dei lati di un quadrilatero completo; quando i lati formano i quadranti la relazione equivale a una formula del triangolo rettangolo sferico. Chiunque conoscesse l'astronomia degli zīǧ sapeva, per esempio, che il seno della declinazione del Sole ‒ o di un 'grado'‒ si ottiene dividendo per il raggio della sfera il prodotto del seno della longitudine del Sole per il seno della sua declinazione massima (l'obliquità dell'eclittica). Questa regola per la declinazione del Sole, che lega l'ipotenusa, un cateto e l'angolo opposto di un triangolo rettangolo sferico, risulta dall'applicazione del teorema di Menelao al quadrilatero che si configura non appena il problema viene posto (fig. 2a, quadrilatero ZBAD e secante AGD o triangolo rettangolo ABG). Sono calcoli dello stesso tipo di quelli dell'Almagesto, con la differenza che nell'opera di Tolomeo, a partire dalle lettere di una figura, si indica come calcolare la corda del doppio di un dato arco sapendo che un certo rapporto di corde è composto da altri due rapporti. Pur non disponendo di un simbolismo come quello creato successivamente, la formulazione delle regole rappresentò un passo importante per cogliere analogie e per l'idea di enunciati matematici generali che aiuta a formare.

Regole come questa per la declinazione del Sole si trovano nei testi provenienti dall'India, come il Khaṇḍakhādyaka di Brahmagupta (598-dopo il 665), che era noto prima dell'Almagesto e delle Tavole manuali di Tolomeo. Il contesto è però molto diverso. Nelle opere indiane non si ha nessuna dimostrazione, nessuna figura, nessuna rappresentazione sulla superficie della sfera, bensì enunciati in versi che esprimono la similitudine di triangoli rettangoli piani i cui cateti sono seni, seniversi, ombre dello gnomone, raggio della sfera o somme di queste quantità. Nel caso della declinazione del Sole (fig. 2b), i due triangoli simili, che vanno pensati appartenenti a due piani paralleli all'interno della sfera, hanno per ipotenusa rispettivamente il seno della longitudine del Sole e il raggio della sfera, e per cateti omologhi il seno della declinazione del Sole e quello della declinazione massima. Senza altri mezzi a disposizione, l'astronomia sferica dei Siddhanta è più rudimentale di quella dell'Almagesto, ma fornisce nondimeno altre regole, come quella per l'ascensione retta, che nel simbolismo moderno si può scrivere senα_⊙=senλ_⊙∙cosε/cosδ_⊙ (v. fig. 2b), la quale, collegando archi di quattro cerchi, non può risultare da una sola applicazione del teorema di Menelao. Essa contiene soprattutto la nozione di azimut e l'idea importante di collegare per mezzo di una formula la misura del tempo e l'altezza di un astro di declinazione data. Il metodo indiano dei triangoli piani ha in effetti successo là dove noi faremmo appello alla formula dei coseni: calcolo dell'angolo orario in funzione dell'altezza, relazione tra azimut e altezza.

Forti dei due insegnamenti ricevuti, i pionieri dell'astronomia che si crea nel IX sec. non si limitano a produrre una sintesi che dia agli enunciati la forma di istruzioni chiare, espresse per mezzo del seno e del senoverso indiani con R=60, il valore dell'Almagesto: la lettura approfondita del libro di Tolomeo porta ad affinarne le tecniche. Ciò è vero per il calcolo sferico, dove vengono soppresse alcune approssimazioni ottenute mediante triangoli piani (parallasse, visibilità, eclissi). Ci si libera del vincolo rappresentato dalla tavola delle ascensioni oblique: negli zīǧ il problema dell''ascendente senza tavole'non ha necessariamente una connotazione astrologica. Grazie all'azimut, misurato sul 'cerchio indiano', che con la qibla diventa una nozione comune, si collega la posizione degli astri alla misura delle loro coordinate locali: il calcolo classico delle 'ascensioni dell'azimut' altro non è che la determinazione dell'angolo orario, noto l'azimut. Le coordinate sull'eclittica sono calcolate a partire dalla declinazione e dal 'grado di passaggio'; nell'Almagesto erano calcolate in modo approssimato per mezzo della posizione di astri vicini.

Un argomento che dà luogo a un'abbondante letteratura, la qibla, si aggiunge alle questioni puramente astronomiche. Si tratta di un calcolo simile a un cambiamento di coordinate (azimut, conoscendo le coordinate orarie) e che è visto come tale quando usa la determinazione dell'altezza dello zenit della Mecca nel luogo considerato. Sebbene gli zīǧ affrontino molti altri argomenti, concludiamo qui quest'incursione nel campo piuttosto tecnico dell'astronomia sferica. Notiamo tuttavia che, quando si considera lo sviluppo di questa scienza nell'epoca araba, gli storici della scienza citano di solito la qibla, e in questo modo non ci si rende conto della complessità del calcolo sferico degli zīǧ, dovuta alla sua formazione composita e allo sviluppo prodigioso dell'astronomia nel IX secolo. Quanto all'astrologia, essa non acquisirà le tecniche sferiche se non dopo la semplificazione apportata dalle formule del triangolo.

Alcuni dei nuovi problemi dipendono dalla risoluzione di triangoli qualunque; come sono risolti? Vi sono tentativi infruttuosi, che conosciamo attraverso le critiche che suscitano: gli autori di tavole si faranno concorrenza nel fornire varie soluzioni. L'idea più importante è senza dubbio l'impiego di funzioni ausiliarie; vi ritorneremo a proposito della tangente. Ai diversi metodi geometrici si aggiunge il procedimento grafico noto come 'analemma', che si collega alle procedure della moderna geometria descrittiva.Tutto ciò porta a regole per calcolare archi incogniti di cui vogliamo ricordare soltanto quelle che seguono da ragionamenti 'sulla superficie della sfera', come nell'Almagesto. La procedura per superare le difficoltà è piuttosto naturale: passa di cerchio in cerchio fino a ottenere l'arco cercato, ed è una tecnica la cui particolarità sfugge ai commentatori arabi medievali, tanto è loro familiare. Tutta una terminologia applicata agli archi ausiliari entra nella pratica corrente, tracciando per così dire la strada ai metodi più usuali. Fino alla fine del X sec. si accumuleranno negli zīǧ regole di tutti i tipi; i vari passi che queste prevedono sono suscettibili nella maggior parte dei casi di una dimostrazione mediante il teorema di Menelao, e corrispondono quasi sempre alle medesime formule del triangolo sferico rettangolo.

Verso le formule del triangolo

Se l'introduzione della funzione tangente nel IX sec. passerà quasi inosservata, la scoperta di teoremi con i quali sostituire il quadrilatero è invece un avvenimento che segnerà quel periodo, e che sarà accompagnato da dispute di priorità. Per i testimoni di questo rinnovamento delle tecniche dell'astronomia, il teorema di Menelao è incontestabilmente la sola formula sferica applicata dai predecessori. Nel corso dei primi due secoli la ricerca matematica sembra infatti cristallizzarsi intorno a questo teorema, anche se forse alcune regole degli zīǧ furono già ottenute altrimenti, 'lette' in qualche modo sulla superficie della sfera. Nello stesso tempo gli astronomi cominciano a liberarsi del teorema di Menelao stabilendo direttamente le formule usuali.

Occorre ricordare che un buon numero di testi di astronomia dei secc. IX e X è privo di dimostrazioni. Alcuni saranno oggetto di studi ulteriori. Sappiamo, per esempio, che Abū 'l-Rayḥān al-Bīrūnī (973-dopo il 1050) compose due voluminosi commenti ‒ entrambi andati perduti ‒ delle tavole di due autori del IX sec., al-Ḫwārizmī e Ḥabaš al-Ḥāsib. È chiaro, e l'abbiamo visto a proposito della declinazione del Sole, che uno stesso risultato si può ottenere in molti modi, ed è il contesto che suggerisce all'autore in quale modo dimostrarlo. Così, Ibn Yūnus, che basa le sue ricerche su quanto precedentemente formulato da al-Battānī e da Ḥabaš, nei suoi Zīǧ al-ḥākimī al-kabīr (Grandi tavole astronomiche dedicate ad al-Ḥākim), fa uso di metodi 'all'interno della sfera'(ossia di formule ottenibili mediante una figura nello spazio o un analemma), poiché le numerose varianti proposte per la soluzione dei singoli problemi si leggono su un medesimo analemma. Quando una formula è applicata più volte a una stessa configurazione sferica semplice, ci si può domandare se l'autore ritorni ogni volta a una dimostrazione diretta o a un teorema così disagevole da applicare come quello di Menelao, o se più semplicemente non operi una trasposizione della regola ottenuta una prima volta. Paul Luckey (1941) ha posto questa domanda a proposito degli enunciati di ṯĀbit ibn Qurra sul quadrante solare. La questione si pone ancora più nettamente riguardo a tutto il calcolo sferico degli zīǧ di Ḥabaš. I vari passi del ragionamento 'sulla superficie della sfera', che passa per il calcolo di archi ausiliari, corrispondono in effetti a quattro regole elementari, enunciate all'inizio, e delle quali una, e cioè la regola indiana sull'ascensione retta del Sole, non segue immediatamente dal teorema di Menelao. Se questo è effettivamente il procedimento seguito dall'autore, si spiega la facilità con la quale vengono risolte in questo trattato le difficoltà del passaggio da coordinate locali a coordinate equatoriali o eclittiche.

Comunque, Ḥabaš non enuncia formule applicabili a un triangolo; parleremo in seguito dell'importante contributo dato da questo astronomo. Il grande ṯĀbit ibn Qurra (826-901), la cui attività si estendeva a tutti i campi della matematica e dell'astronomia, fu uno dei numerosi autori a interessarsi al teorema di Menelao, conosciuto da allora nel testo degli Sphaerica e la cui dimostrazione occupa il capitolo 13 del Libro I dell'Almagesto. A tal proposito, al-Bīrūnī dichiara:

Nuovi sviluppi riguardo a questa figura e ai diversi casi da considerare si devono ad Abū 'l-῾Abbās al-Faḍl ibn Ḥātim al-Nayrīzī e Abū ǧa῾far Muḥammad ibn al-Ḥusayn al-Ḫāzin nei rispettivi commenti all'Almagesto […]. Abū 'l-Ḥasan ṯĀbit ibn Qurra dedicò un libro al rapporto composto, ai suoi diversi tipi e applicazioni, e un altro alla figura di intersezione o 'quadrilatero completo' [al-šakl al-qaṭṭā῾], rendendo più agevole l'uso di questo teorema. Sono numerosi gli autori moderni che hanno approfondito tale questione: Ibn al-Baġdādī, Sulaymān ibn ῾Iṣma, Abū Sa῾īd Aḥmad ibn Muḥammad ibn ῾Abd al-ǧalīl al-Siǧzī e molti altri. Rivolgevano a essa un interesse particolare perché si trattava in un certo senso della pietra angolare dell'astronomia. Senza di essa nessuno dei calcoli menzionati in precedenza [i calcoli degli zīǧ] sarebbe stato possibile (Kitāb Maqālīd ῾ilm al-hay᾽a, pp. 92-94).

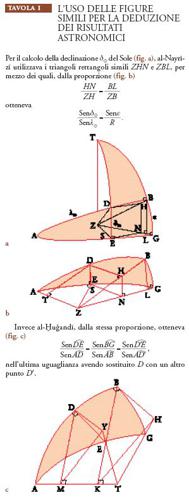
Unica formula sferica del prestigioso Almagesto, la prop. 1 del Libro II degli Sphaerica di Menelao, si presta agli studi matematici per via dei casi ai quali dà luogo l'uso di un rapporto composto, in assenza di simbolismo. Infatti, l'uguaglianza a/b=c/d∙e/f si enuncia nel seguente modo: il rapporto di a a b è composto dal rapporto di c a d e dal rapporto di e a f; è dunque necessario disporre di regole per il calcolo di uno qualunque dei sei numeri, noti gli altri cinque. Come negli Sphaerica e nell'Almagesto (ma senza le corde), il teorema è enunciato e dimostrato in due forme, ognuna delle quali esprime che un rapporto di seni è composto di altri due rapporti (v. fig. 1): nella forma detta tafṣīl (dieresi), si tratta di

o di

nell'altro caso, tarkīb (sintesi), si tratta invece di

o di

Nel primo caso si ha

e nel secondo si ha

Gli autori arabi fanno altre distinzioni, in particolare in funzione dell'arco cercato. ṯĀbit ibn Qurra considera diciotto casi, dopo una dimostrazione peraltro molto elegante che, invece di fare appello al teorema piano, riduce il teorema sferico all'identità a/b=a/c∙c/b che lo traduce per proiezione su una retta. Studi di questo genere, come si vede, se da un lato rivelano l'aspetto disagevole del teorema, dall'altro valorizzano in astronomia il ragionamento 'sulla superficie della sfera' e sono un primo passo verso l'elaborazione di una tecnica matematica specifica.

Abū 'l-῾Abbās al-Nayrīzī (m. 922 ca.), uno degli autori citati da al-Bīrūnī, ha, per la qibla, un metodo che fa uso del teorema di Menelao. Possediamo pochi testi come questo, con calcoli originali svolti esplicitamente mediante il quadrilatero; ne abbiamo però di Abū Naṣr ibn ῾Irāq e di Abū 'l-Wafā᾽ al-Būzǧānī, i due principali artefici, assieme ad Abū Maḥmūd al-Ḫuǧandī, del rinnovamento che ha luogo alla fine del X secolo. In altre parole, non vi sono stati enunciati matematici intermedi che precedano quella che è detta, più o meno giustamente, la scoperta del teorema generale dei seni. Per spiegare la coincidenza dei contributi dei tre astronomi del Khwarizm, di Baghdad e di Rayy, è stata presa in considerazione anche la possibilità di una fonte comune. L'ipotesi contrasta con la testimonianza di al-Bīrūnī nella sua opera Kitāb Maqālīd ῾ilm al-hay᾽a (Libro delle chiavi dell'astronomia), dedicata all'introduzione dei nuovi teoremi. In realtà, la somiglianza degli enunciati è dovuta soltanto al contenuto dei testi astronomici, e forse non è un caso che i tre sistemi di formule che dovranno sostituire il teorema di Menelao siano proposti nel quadro di importanti studi astronomici.

Tav. I

Il nome di Abū Maḥmūd al-Ḫuǧandī (m. 1000 ca.) resta legato al famoso sestante faḫrī, alto più di venti cubiti, graduato in minuti d'arco e costruito a Rayy (vicino all'odierna Teheran) sotto il patronato del buwayhide Faḫr al-Dawla. Questo strumento è stato descritto da al-Bīrūnī, che ebbe occasione di esaminarlo assieme allo stesso al-Ḫuǧandī. Nel Kitāb Maqālīd ῾ilm al-hay᾽a egli riporta le discussioni che agitavano allora la piccola comunità scientifica di Rayy, a proposito di un teorema del quale al-Ḫuǧandī contende la priorità ad Abū 'l-Wafā᾽ al-Būzǧānī e che chiama 'il canone dell'astronomia'; si tratta della formula che conosciamo come 'regola delle quattro quantità' (v. oltre). Al-Ḫuǧandī presenta ad al-Bīrūnī un trattato sull'osservazione degli astri, all'inizio del quale viene enunciato questo teorema che viene poi applicato in tutto il libro. A Rayy si trova anche un altro astronomo, Kūšyār ibn Labbān (970 ca.-1030 ca.), che riprende in una delle sue opere l'esposizione di Abū Maḥmūd al-Ḫuǧandī, rimaneggiandola e definendola al-šakl al-muġnī (lett., la figura che dispensa ossia dispensa dal teorema di Menelao), un appellativo che rimarrà (si noti che il termine al-šakl significa sia figura sia teorema). Come osserva al-Bīrūnī, la lunga dimostrazione di al-Ḫuǧandī è molto diversa da quelle di Abū 'l-Wafā᾽ al-Būzǧānī; essa evoca invece le figure simili, caratteristiche per la presenza del rettangolo, tramite le quali 'in modo molto più semplice', già Abū 'l-῾Abbās al Nayrīzī e Abū ǧa῾far al-Ḫāzin (m. 961/971 ca.) ritrovavano le regole dell'Almagesto (Tav. I). Per vie diverse, l'astronomia degli zīǧ conduce alle medesime formule del triangolo. Abū Maḥmūd al-Ḫuǧandī non è però un matematico di primo piano. La necessaria riforma sarà opera congiunta di Abū Naṣr ibn ῾Irāq e di Abū 'l-Wafā᾽ al-Būzǧānī.

I teoremi di Abū Naṣr ibn ῾Irāq e di Abū 'l-Wafā᾽ al-Būzǧānī

Le semplificazioni apportate all'epoca alle tecniche astronomiche si riducono per al-Bīrūnī e i suoi contemporanei a una 'figura', che, come si può dimostrare, è sufficiente a sostituire il quadrilatero. L'espressione significativa al-šakl al-muġnī che le viene attribuita sta a indicare sia l'aspetto indispensabile del teorema ‒ regola delle quattro quantità e relazione dei seni nel triangolo rettangolo ‒ sia la sua estensione, giudicata notevole ma di minore interesse, e cioè il teorema generale dei seni. Un'altra formula accolta, la regola delle tangenti di Abū 'l-Wafā᾽, prenderà il nome di al-šakl al-ẓillī (al-ẓillī, l'ombra, designa la tangente, v. oltre). All'inizio l'impostazione di Abū Naṣr è piuttosto diversa da quella di Abū 'l-Wafā᾽.

L'emiro Abū Naṣr ibn ῾Irāq (m. 1036 ca.) non ha lasciato, come l'illustre allievo al-Bīrūnī, un'opera che abbracci tutti i campi del sapere del suo tempo. I suoi scritti riguardano l'astronomia, soprattutto l'astronomia matematica, e alcuni punti particolari di geometria. A lui si deve la prima versione completa degli Sphaerica di Menelao, abbandonata dai predecessori per alcune difficoltà incontrate nel Libro III; la sua traduzione è considerata la più vicina al testo greco, oggi perduto. Quest'uomo, di elevata condizione sociale, seppe capire le qualità eccezionali del giovane al-Bīrūnī, che formò negli studi di matematica. La loro collaborazione si sviluppò nel Khwarizm, prima che i due autori condividessero, con altri studiosi di Kath, l'esilio di Ghazna, alla corte di Maḥmūd, il potente capo del nuovo impero ghaznavide. La storia del Kitāb Maqālīd ῾ilm al-hay᾽a risale a quel periodo.

Abū 'l-Wafā᾽ al-Būzǧānī (940-997 o 998) era all'epoca molto famoso. Stabilitosi in gioventù a Baghdad, dove gli zii erano astronomi, aveva dedicato tutta la vita all'astronomia e alla matematica. Al-Bīrūnī riporta le osservazioni che fece, tra cui quella di un'eclissi di Luna effettuata congiuntamente a Baghdad e a Kath per dedurne la differenza di longitudine tra le due città. Abū 'l-Wafā᾽ è anche autore di opere di matematica, teoriche e pratiche. Il calcolo trigonometrico occupa un posto importante nell'opera che egli compose alla fine della sua vita, intitolata Kitāb al-Maǧisṭī (Libro dell'Almagesto) e che forse rimase incompiuta, poiché il solo manoscritto in nostro possesso contiene i sette trattati dei quali parla al-Bīrūnī e nient'altro.

Al-Bīrūnī riporta le circostanze dell'introduzione dei nuovi teoremi. Due di essi, relativi al triangolo rettangolo, furono dapprima stabiliti da Abū Naṣr nel Kitāb al-Samt (Libro degli azimut); tuttavia, poiché il suo proposito era quello di ritrovare le dimostrazioni di varie regole raccolte da Abū Sa῾īd al-Siǧzī, Abū Naṣr applica soprattutto il teorema di Menelao, e le due formule non sono nemmeno enunciate. Questo impiego del quadrilatero e del rapporto composto è criticato da Abū 'l-Wafā᾽, che si era fatto mandare il libro a Baghdad; egli sostiene che i metodi del suo al-Maǧisṭī sono più concisi e migliori. In risposta, Abū Naṣr dedica ad al-Bīrūnī la Risāla fī 'l-qusīyy al-falakiyya, nota come Epistola sugli archi sferici, nella quale espone le idee che non ha potuto sviluppare nel Kitāb al-Samt; tuttavia, il titolo datole da Abū Naṣr, Sui triangoli sferici, corrisponde meglio al contenuto. Un anno più tardi, al-Bīrūnī riceverà i primi sette trattati del Kitāb al-Maǧisṭī di Abū 'l-Wafā᾽. Composto poco dopo (tra il 994 e il 1004), il Kitāb Maqālīd ῾ilm al-hay᾽a riporta la polemica sollevata da questi vari scritti, la quale testimonia sia l'importanza data all'evento sia la vivacità di tutti i centri scientifici sparsi da un capo all'altro del califfato abbaside. Ma torniamo agli enunciati della Risāla e a quelli del Kitāb al-Maǧisṭī di Abū 'l-Wafā᾽, nel primo capitolo del Libro II.

L'esposizione della Risāla parte dal teorema generale dei seni, il quale afferma che in ogni triangolo sferico formato da archi di cerchi massimi, i seni dei lati sono proporzionali ai seni degli archi che misurano gli angoli loro opposti. Abū Naṣr dimostra quattro formule distinte, che applica ai problemi dell'Almagesto. La prima esprime il teorema generale dei seni, ossia, dato un triangolo ABG formato dagli archi a, b, g,

la seconda è la relazione corrispondente per il triangolo rettangolo (in G), ossia

,

dimostrata in precedenza nel Kitāb al-Samt.

Le ultime due, sempre per un triangolo rettangolo in G, sono due relazioni vicine alla moderna formula cosA=cosa∙senB:

,

che è la seconda relazione già presente nel Kitāb al-Samt e

[6] 90° - A = δ_B (90° - a),

dove Cos indica il seno dell'angolo complementare e δ_B(x) l'inclinazione dell'arco x per un'inclinazione massima uguale a B. Nella Risāla, soltanto il teorema dei seni è dimostrato direttamente, con una dimostrazione non priva di eleganza e che comprende come caso particolare la relazione [4] già dimostrata per il triangolo rettangolo. Le relazioni [5] e [6] sono dedotte immediatamente dalla [4] per mezzo di triangoli sferici associati.

Mentre tutte le formule di Abū Naṣr sono relazioni del triangolo, Abū 'l-Wafā᾽ introduce un doppio teorema fondamentale che collega invece gli archi formati da una coppia di triangoli rettangoli associati: se due archi di cerchi massimi si tagliano sulla superficie di una sfera e se si prendono su uno di questi dei punti qualunque, i rapporti dei seni degli archi compresi tra questi punti e il punto d'intersezione sono uguali ai rapporti rispettivi dei seni delle loro inclinazioni prime e delle ombre (v. oltre) delle loro inclinazioni seconde. Si riconoscono in questo enunciato la regola delle quattro quantità

e la regola delle tangenti

Dalla regola delle quattro quantità si ricavano i risultati seguenti: una relazione del triangolo rettangolo (in G), ossia

e il teorema generale dei seni

Il teorema dei seni è introdotto, quindi, senza passare per l'enunciato intermedio della relazione [4] per il caso del triangolo rettangolo. Le due parti del teorema principale sono dimostrate direttamente, la prima in due modi diversi, uno dei quali si ispira alla dimostrazione dell'Almagesto per il teorema di Menelao (la fig. c della Tav. I, relativa alla regola delle tangenti, corrisponde all'altro metodo, del tipo di quelli che vengono usati nel Kitāb al-Samt:

,

da MD/KB=DY/BH).

I modelli elaborati da Abū Naṣr e Abū 'l-Wafā᾽ sono di ispirazione diversa. Tuttavia, dal punto di vista delle applicazioni si riducono a quattro teoremi: al-šakl al-muġnī, che corrisponde alle formule [3], [4] e [7]; al-šakl al-ẓillī, che corrisponde alla formula [8], la quale prenderà anche la forma

e infine due teoremi di minore interesse, la relazione [9] e le varianti [5] e [6] della relazione SenB/R=CosA/Cosa. Queste formule, che provengono dalle regole degli zīǧ, rispondono ampiamente alle necessità del calcolo astronomico. Al-Bīrūnī lo dimostra nel Kitāb Maqālīd ῾ilm al-hay᾽a risolvendo tutti i problemi classici per mezzo della sola 'figura che dispensa [dal quadrilatero]'. Nel Kitāb al-Maǧisṭī di Abū 'l-Wafā᾽ il calcolo sferico trattato con una profusione di metodi nei Libri dal II al V rivela l'efficacia e la duttilità delle formule del capitolo 1 del Libro II. Più tardi gli autori arabi enunceranno le sei relazioni del triangolo rettangolo, ma i loro testi astronomici continueranno a riportare soltanto lo strumento elaborato da Abū 'l-Wafā᾽ e Abū Naṣr. Così, in un'opera del XV sec., gli Zīǧ-i Ḫāqānī (Le tavole astronomiche per Ḫāqān) di al-Kašī, uno degli ultimi grandi matematici e astronomi dell'Islam, si trovano applicati solo i primi tre teoremi, e soprattutto la regola delle quattro quantità. Uno dei più famosi trattati di astronomia dell'Occidente arabo, Iṣlāḥ al-Maǧisṭī (La rettifica all'Almagesto) di ǧĀbir ibn Aflaḥ al Išbīlī (noto in latino come Geber, XII sec.), non fa nemmeno uso della tangente. Tradotto in latino, questo testo è stato una delle fonti del De triangulis di Regiomontano. La relazione

del trattato di ǧĀbir fu nota in Occidente con il nome di 'teorema di Geber'.

La funzione tangente

La nozione di triangolo sottende tutta la trigonometria di Abū Naṣr, e l'adozione del triangolo come configurazione di base si ritroverà nei trattati dedicati specificamente a tale disciplina matematica. Con la 'figura dell'ombra' di Abū 'l-Wafā᾽, la tangente entra definitivamente nel calcolo astronomico. Ci fu bisogno di molto tempo perché potesse emergere l'idea apparentemente semplice di utilizzare il rapporto tra il seno di un angolo e il seno dell'angolo complementare liberandosi dalla nozione di ombra dello gnomone. Malgrado il termine 'ombra' con cui è chiamata, non sembra che questa idea ne provenga direttamente. Per uno di quegli strani fenomeni dei quali esistono altri esempi nella storia della matematica, la tangente compare sulla scia di funzioni ausiliarie più sofisticate, nate dall'analisi di calcoli sferici dipendenti, come la tangente, da due parametri.

Rileggendo i testi che precedono l'introduzione della tangente si resta sorpresi dalla quantità di occasioni che si erano presentate per definire e tabulare questa funzione. Intanto, il teorema di Menelao la richiede in alcune applicazioni. In mancanza di una tavola che desse la tangente di un angolo α in funzione di α, o la sua equivalente corda2α/corda(180°−2α), nell'Almagesto il calcolo della latitudine del luogo, φ, in funzione della durata maxd_⊙ del giorno più lungo dell'anno, non si può fare utilizzando la formula tanφ=sen(maxd_⊙)cotε, mentre più volte viene applicata la formula, con le corde, equivalente alla formula più generale send=tanφtanδ, per determinare l'equazione del giorno solare d.

Un altro calcolo, facilitato dalla tavola delle tangenti, è quello di un angolo di un triangolo rettangolo piano di cui sono dati i cateti. Il problema si pone a proposito dei modelli planetari, in particolare per la costruzione di tavole di equazioni. Inoltre, il calcolo dell'altezza del Sole a partire dall'ombra dello gnomone obbliga a ricorrere continuamente al teorema di Pitagora e a estrarre una radice quadrata, e abbiamo visto in precedenza il ruolo crescente che hanno le coordinate locali nell'astronomia indiana e araba.

Nei primi testi arabi il calcolo dell'altezza del Sole passa ancora per l'ipotenusa del triangolo determinato dallo gnomone e dalla sua ombra, il 'diametro dell'ombra'. Per uno gnomone verticale g che getta un'ombra o su un piano orizzontale, l'altezza h del Sole si calcola con la formula Senh_⊙=Rg/d, dove

Si arriva rapidamente a tabulare l'ombra in funzione dell'altezza. Il più delle volte lo gnomone è suddiviso in 12 dita, secondo una tradizione indiana, ma esistono altre suddivisioni (per es., in 6 e mezzo o 7 piedi, o in 60 parti). Negli zīǧ di al-Ḫwārizmī (compilati a Baghdad ai primi del IX sec.) e di al-Battānī (Raqqa, fine del IX sec.) s'incontra una tavola dell'ombra in funzione dell'altezza, a due posizioni, in gradi, per uno gnomone di 12 dita, che corrisponde dunque alla funzione θ→12cotθ; in entrambi i trattati viene applicata soltanto ai calcoli reciproci dell'altezza e dell'ombra. Lo gnomone, grandezza arbitraria come lo è il raggio della sfera, con unità di misura proprie, è apparentemente di ostacolo a qualunque idea di generalizzazione e all'introduzione dell'utile funzione tan o Rtan. Nello stesso periodo, Ḥabaš al-Ḥāsib non ha tavole per l'ombra del Sole nei suoi zīǧ, e calcola l'altezza mediante il tradizionale 'diametro dell'ombra' per uno gnomone di 12 dita. Tuttavia è proprio in questo trattato, senza dubbio uno dei più importanti a noi pervenuto dell'astronomia del IX sec., che compare la nozione generale di tangente di un arco, con una sua definizione, una tavola e applicazioni varie. Il modo in cui Ḥabaš la introduce fa pensare che non la debba a un predecessore. Infatti, a prescindere dalla difficile questione dello status da attribuire alle tavole dell'ombra del Sole rispetto all'introduzione effettiva della tangente, nel lavoro di Ḥabaš il contesto serve a spiegare l'introduzione della nuova funzione e, paradossalmente, lo scarso interesse che essa suscita prima di andare a occupare negli zīǧ un posto paragonabile a quello della funzione seno.

Aḥmad ibn ῾Abd Allāh Ḥabaš al-Ḥāsib al-Marwazī appartiene a quella generazione di astronomi che scoprono l'Almagesto dopo essersi formati con metodi indiani. Contemporaneo sia di al-Ḫwārizmī sia di al-Battānī, le cui opere furono tradotte in latino, Ḥabaš è quasi del tutto ignorato nell'Occidente medievale. L'attenzione degli storici verso questo autore, al quale spesso si rimanda, si deve all'opera di al-Bīrūnī, fonte infinitamente preziosa e sicura. Dei suoi scritti, che riguardano tutta l'astronomia, resta purtroppo soltanto la sua opera al-Zīǧ al-mumtaḥan (Tavole astronomiche verificate), composta forse poco prima di morire e comunque dopo l'869. Questo testo basta da solo a giustificare il soprannome di al-Ḥāsib (il matematico) dato all'astronomo di Baghdad. Sebbene sia un trattato di astronomia che consta di regole e di tavole, con una composizione propria, e non un commento all'Almagesto, l'opera rivela una riflessione sulle idee matematiche meno evidenti del libro di Tolomeo. A titolo di esempio, si può citare l'applicazione che Ḥabaš fa della formula

,

il cui equivalente geometrico serve a Tolomeo per costruire la tavola delle corde, e dalla quale lo stesso Ḥabaš deduce un procedimento originale di estrazione della radice quadrata utilizzando la tavola dei seni. In tutta l'opera Ḥabaš cerca di migliorare le tecniche dell'Almagesto. Lo vediamo colmare le lacune del calcolo sferico, sviluppare procedimenti ricorsivi attingendo a fonti indiane, generalizzare l'uso delle funzioni di interpolazione che si trovano nelle tavole di equazioni. A quest'ultima idea, molto interessante, di Tolomeo, è forse opportuno collegare l'elaborazione del celebre Ǧadwal al-taqwīm (Tavola delle posizioni esatte), di cui ora parliamo prima di ritornare alla funzione tangente.

Le funzioni di interpolazione dell'Almagesto sono un artificio applicato ad alcune particolari funzioni di due variabili per ridurre, con buona approssimazione, il ruolo della variabile che influisce di meno ai suoi due valori estremi ed evitare così una noiosa tabulazione. Anche le quattro funzioni che compongono il Ǧadwal al-taqwīm di Ḥabaš (che indichiamo qui con f₁, f₂, f₃ e f₄) provengono dal trattamento di espressioni a due parametri; anche se non vengono fornite spiegazioni sulla costruzione della tavola, ciò risulta chiaramente dall'analogia tra le principali applicazioni che ne vengono fatte. Così, sul modello

,

che serve a determinare le coordinate equatoriali (α, δ) di un astro di coordinate eclittiche date (λ, β), Ḥabaš non soltanto opera il cambiamento di coordinate reciproco, ma calcola anche il complementare ν̄ dell'angolo tra eclittica e orizzonte e l'equazione del giorno solare d_⊙, direttamente in funzione dei dati primitivi, la latitudine φ, il tempo siderale α_M e la longitudine solare λ_⊙, mediante le formule

All'origine dell'analogia, comunque sia stata colta, si trova la possibilità di porre gli elementi di un problema in una medesima configurazione formata dall'eclittica, dall'equatore e da due cerchi massimi perpendicolari, passanti per un astro o per lo zenit di un luogo. Di qui deriva anche l'importanza notevole dell'insieme delle funzioni costruite da Ḥabaš. Contrariamente alle solite tavole dei trattati di astronomia, che danno il risultato di un calcolo particolare, o di un passaggio del calcolo, queste funzioni ausiliari si applicano a variabili diverse, fornendo inoltre una semplificazione maggiore di quella che risulta dall'utilizzazione di semplici funzioni trigonometriche, perché fanno intervenire l'obliquità dell'eclittica. Ḥabaš non ne dà la definizione. La quarta funzione coincide, a meno di un coefficiente, con la funzione tangente.

Gli autori arabi hanno commentato e imitato il Ǧadwal al-taqwīm di Ḥabaš. Abū Naṣr, che si ispirò a esso per il suo Ǧadwal al-daqā᾽iq (Tavola dei minuti), un insieme di cinque funzioni ausiliarie, fa un'analisi completa della tavola e delle sue applicazioni. Egli cita un commento di al-Ḫāzin e una tavola dello stesso genere di al-Nayrīzī. Nata dallo sviluppo del calcolo sferico, la ricerca di funzioni ausiliarie, del quale il Ǧadwal al-taqwīm non è forse il primo tentativo, proseguirà assumendo forme diverse. Tra le funzioni tabulate ve ne sono di puramente trigonometriche, come l'inversa del seno, ossia la cosecante. Malgrado le possibili applicazioni al teorema di Menelao, o a certe risoluzioni di triangoli piani, la tangente si distingue quindi poco dalle altre funzioni ausiliarie. Negli zīǧ di Ḥabaš, la nozione di 'ombra' di un arco, definita 'molto utile', è presentata in una breve sezione in occasione di un cambiamento di coordinate. Ḥabaš si serve dei due primi esempi di calcolo per definire l'ombra (qui denotata con Tan) della latitudine φ del luogo e del complementare ¯φ attraverso l'equivalente delle formule seguenti:

Questa definizione, data in un caso particolare, non è nello stile nel quale vengono richiamati altrove il seno e il senoverso. La nozione in sé è generale, in quanto la tavola si applica alla risoluzione di numerosi problemi, tra cui un problema piano relativo all'equazione del Sole. La 'tavola dell'ombra' (corrispondente alla funzione Rtan) dello zīǧ di Ḥabaš è a tre posizioni, a intervalli di mezzo grado, da 0;30° a 89°.

All'epoca del Kitāb Maqālīd ῾ilm al-hay᾽a di al-Bīrūnī, la tangente di un arco non rientrava ancora tra le nozioni più comuni. Vi sono autori, come Ibn Yūnus, che non capirono l'interesse che poteva avere la funzione tabulata da Ḥabaš; infatti, nei suoi Zīǧ al-ḥākimī al-kabīr, nel quale il calcolo sferico ha un posto così importante, l'astronomo del Cairo ritorna alla tavola dell'ombra del Sole e ai soli calcoli reciproci dell'ombra e dell'altezza. Da parte sua, al-Bīrūnī, quando presenta la regola delle tangenti nel Kitāb Maqālīd ῾ilm al-hay᾽a, si sente in dovere di precisare cosa si debba intendere per 'ombra' di un arco, anche se non ne definisce il seno. Egli modifica anche l'esposizione di Abū 'l-Wafā᾽ per meglio distinguere l'ombra di un arco dai due tipi d'ombra dello gnomone definite da quest'ultimo. Si assiste anche in quel periodo al rifiuto del teorema delle tangenti di Abū 'l-Wafā᾽ da parte di al-Ḫuǧandī e di Kūšyār ibn Labbān, i due astronomi di Rayy, sulla base dell'uso giudicato scorretto della tavola delle 'ombre' dovuto al fatto che le differenze crescono rapidamente, come attesta l'allungamento dell'ombra dello gnomone.

Questo termine 'ombra', preso dalla gnomonica, è carico di significati, come dimostra un libro di al-Bīrūnī scritto una ventina d'anni dopo il Kitāb Maqālīd ῾ilm al-hay᾽a il Kitāb fī ifrād al-maqāl fī amr al-aẓlāl (Libro che isola gli argomenti intorno alla questione delle ombre). Esso raccoglie considerazioni di ogni genere sulle ombre e sulle loro misure applicate a diversi problemi, quali il tracciato della linea meridiana, la determinazione delle ore di preghiera o il calcolo delle distanze, prima di menzionare le semplificazioni che esse permettono di ottenere nei calcoli astronomici. Comunque, l'esposizione di Abū 'l-Wafā᾽ sulle 'ombre' riguarda unicamente la funzione tangente.

Nel Libro I della sua opera Kitāb al-Maǧisṭī, dopo il quinto capitolo dedicato ai seni e alle corde, Abū 'l-Wafā᾽ dedica il sesto alle ombre, "per via della necessità di utilizzarle nella maggior parte dei problemi". Egli definisce geometricamente l'ombra di un arco, che egli chiama anche 'prima ombra' o 'ombra versa', identificandola con l'ombra versa di uno gnomone orizzontale coincidente con il raggio di un cerchio di riferimento (ossia, TanBZ=BH, ombra di BE, fig. 6a). La stessa figura gli serve per introdurre l''ombra seconda' o 'ombra estesa' dell'arco considerato (CotanBZ=AY, ombra di AE) e a stabilire tutte le relazioni elementari tra tangente, cotangente, seno e seno del complementare, alcune espresse mediante i due 'diametri dell'ombra' (rispettivamente EH ed EY), ossia le nostre secante e cosecante. Egli osserva anche che, prendendo la norma come unità di misura, l''ombra' è uguale al rapporto tra il seno e il seno del complementare, e lo stesso per l''ombra seconda'. La sua esposizione, ormai classica, fa da pendant alle definizioni geometriche del seno e del senoverso, e si ritrova negli zīǧ con la regola delle tangenti e la tavola dell'ombra. La parola ẓill (ombra) è tuttora usata in arabo per denotare quella che noi chiamiamo 'tangente', con un termine anch'esso ambiguo e per questo criticato da Viète quando fu introdotto, nel 1583, da Thomas Fincke (1561-1656). Prima di lui, Francesco Maurolico (1494-1575), che tradusse dall'arabo gli Sphaerica di Menelao, usa il termine umbra versa nel De sphaera sermo (1558), in particolare a proposito del teorema delle tangenti. Tuttavia, non sappiamo per quali strade l'uso della funzione tangente sia stato introdotto in Occidente.

I trattati di trigonometria

La fine del X sec. segna una vera e propria svolta. Nei testi di astronomia la trigonometria occupa un posto importante, con i capitoli sui seni, le corde, le 'ombre' e le formule del calcolo sferico. Ci si interessa anche alla risoluzione dei triangoli. Lo studio del triangolo si sostituisce in qualche modo agli sviluppi tradizionali sul teorema di Menelao, e si inserisce in un nuovo tipo d'opera del quale il Kašf al-qinā῾ ῾an asrār al-šakl al-qaṭṭā῾ (Trattato sul quadrilatero) di Naṣīr al-Dīn al-Ṭūsī è un tipico esempio. Tale ricerca, pur producendo alcuni risultati, come nuove relazioni del triangolo rettangolo sferico o la nozione di triangolo polare, non arricchisce però il calcolo degli zīǧ con procedimenti nuovi. Espressione di una tecnica che ha già raggiunto i propri obiettivi, la trigonometria dei trattati è essenzialmente una trigonometria sferica che fa largo uso del triangolo rettangolo.

Il problema della risoluzione dei triangoli sferici comincia a emergere nel contesto dell'astronomia nel periodo che precede l'introduzione delle formule del triangolo. Uno scritto di Abū Naṣr a proposito di alcuni errori commessi da al-Ḫāzin negli Zīǧ al-ṣafā᾽iḥ sembra indicare che quest'ultimo aveva effettuato la risoluzione dei triangoli nella maggior parte dei casi, compreso quello in cui sono dati i tre lati. Con l'apporto dei nuovi teoremi la questione inevitabilmente si ripropone.

Al-Bīrūnī sviluppa l'argomento nel Kitāb Maqālīd ῾ilm al-hay᾽a, per dimostrare che i calcoli sferici sono tutti possibili mediante la sola "figura che dispensa [dal quadrilatero]". Divide dapprima i triangoli in dieci classi secondo il tipo di angoli, stabilisce alcune proprietà relative ai lati, poi raggruppa le classi e considera quella formata dai triangoli che hanno un angolo retto e due angoli acuti. Risolve poi i triangoli rettangoli mediante le formule riunite sotto il nome di al-šakl al-muġnī, menzionando le semplificazioni occasionali apportate dall'altra 'figura', al-šakl al-ẓillī, applicate a una configurazione da lui introdotta (fig. 7, triangolo ABG). La sua risoluzione dei triangoli qualunque, ottenuta decomponendo un triangolo in due triangoli rettangoli mediante la sua altezza, è più sommaria. Mancano in particolare i casi in cui sono dati i tre lati o i tre angoli. In sé lo studio di al-Bīrūnī presenta lacune. Lo scopo è diverso, e giustifica d'altronde le applicazioni all'astronomia; tuttavia l'idea sarà ripresa. Del Kitāb Maqālīd ῾ilm al-hay᾽a gli autori arabi conservano i riferimenti al teorema di Menelao, le 'figure' che ne prendono il posto, la classificazione dei triangoli e la loro risoluzione. Sono questi gli elementi che entrano nella composizione di numerose opere puramente matematiche, a margine dei calcoli astronomici che conducono al Kašf al-qinā῾ ῾an asrār al-šakl al-qaṭṭā῾.

Le sei relazioni del triangolo rettangolo compaiono in un testo anonimo della fine del sec. XI, una compilazione che pur non avendo le qualità del libro di al-Ṭūsī ne annuncia già il piano. L'autore del trattato stabilisce quattordici formule più o meno concordanti, delle quali, tuttavia, non fa alcun uso. Riporta però un'interessante risoluzione del triangolo dovuta ad Abū Naṣr; infatti, gli enunciati della sua Risāla sono completati in altri due scritti. Il primo, che raccoglie problemi affrontati su richiesta di al-Bīrūnī, contiene il teorema piano dei seni, il cui enunciato è suggerito dal teorema sferico. Scrive Abū Naṣr: "Quando hai saputo che, nei triangoli formati da archi di cerchio massimo di una sfera, il rapporto tra il seno di un lato e il seno di un altro lato era uguale al rapporto tra il seno dell'angolo opposto al primo lato e il seno dell'angolo opposto al secondo, hai chiesto se la legge valeva per tutti i triangoli, sia che siano formati da archi o da linee rette. La nostra risposta è sì […]". Il teorema, in una forma equivalente a

,

viene poi dimostrato tracciando un'altezza. Il secondo scritto, dal quale è tratto il metodo riportato nel testo anonimo precedentemente citato, è precisamente quello nel quale Abū Naṣr corregge gli errori di al-Ḫāzin. Esso è di notevole importanza perché vi si trova la prima utilizzazione del triangolo polare.

L'uso del triangolo polare, applicato alla risoluzione di un triangolo quando sono dati gli angoli, fu considerato la prima volta nel Kašf al-qinā῾ ῾an asrār al-šakl al-qaṭṭā῾; si trattava della prima utilizzazione conosciuta del principio di dualità che sarebbe stato sviluppato in Europa all'epoca di Viète (1593). Si poteva quindi pensare che Naṣīr al-Dīn avesse perso un'occasione per applicare la nozione introdotta, in particolare allo studio della natura dei lati e degli angoli di un triangolo. Una volta individuato il testo anonimo della fine dell'XI sec., l'idea fu poi attribuita all'autore di questo trattato, e le ricerche successive hanno mostrato che il metodo esposto da Naṣīr al-Dīn è dovuto in realtà ad Abū Naṣr, il quale si richiama a una costruzione di al-Ḫāzin. Eccoci riportati al X sec., ossia all'epoca in cui questo genere di problemi viene elaborato e precisato. Al-Ḫāzin, che si interessò ad argomenti di vario genere, è considerato un autore originale, a volte poco preciso. Il calcolo che egli fa, in realtà sbagliato, ha, tuttavia, il merito di porre abbastanza bene il problema attraverso la costruzione di archi che misurano gli angoli del triangolo dato.

Abū Naṣr rettifica la figura e la completa facendo comparire un triangolo (il triangolo HKS della fig. 9), del quale dimostra che gli angoli e i lati sono i supplementari rispettivamente degli angoli e dei lati del triangolo dato ABG. Il problema è dunque ricondotto alla determinazione degli angoli di un triangolo di lati dati, che egli aveva già risolto mediante le sue formule del triangolo. Lo scritto nel quale Abū Naṣr introduce questa figura notevole si presta male ad altri sviluppi, che d'altra parte non possono essere suggeriti dal solo teorema dei seni, invariante per dualità. Non sembra che gli autori arabi abbiano utilizzato in altri casi il triangolo polare, di cui è nota soltanto un'altra costruzione, più complicata, applicata allo stesso problema ed effettuata a partire dai poli dei lati del triangolo di partenza. Il metodo si trova in un trattato di trigonometria scritto verosimilmente in Spagna ai primi dell'XI secolo. L'autore, Ibn Mu῾āḏ, parla della difficoltà incontrata nella risoluzione di questo problema; ritorneremo sul suo interessante trattato dopo aver studiato la composizione del libro di Naṣīr al-Dīn.

Naṣīr al-Dīn al-Ṭūsī (1201-1274), il fondatore del celebre Osservatorio di Marāġa, visse in un'epoca che vide il crollo del califfato abbaside e nello stesso tempo una certa apertura dell'Islam al mondo dell'Estremo Oriente. Egli è autore di più di sessanta opere, alcune delle quali di filosofia e teologia. La sua opera scientifica, che comprende numerose revisioni di lavori dei suoi predecessori, si presenta come una sorta di aggiornamento del corpus matematico e astronomico. Il Kašf al-qinā῾ ῾an asrār al-šakl al-qaṭṭā῾ in cinque libri, rientra in questa larga sintesi che comprende gli Elementi, gli Sphaerica, l'Almagesto e molte altre opere greche e arabe. I Libri I, II e IV riguardano i rapporti composti e il teorema di Menelao piano e sferico, e sono caratterizzati dalla ricerca continua di esaurire tutti i casi possibili. Il Libro III, sui lemmi necessari al calcolo sferico, evoca brevemente la risoluzione di triangoli piani, senza richiamare altre formule che non siano il teorema dei seni. È soprattutto il Libro V a costituire la parte trigonometrica propriamente detta. I primi quattro capitoli riprendono, completandola, la classificazione di al-Bīrūnī. Vi si trova, dopo aver confrontato gli elementi dei triangoli formati da intersezioni di tre cerchi massimi, una duplice ripartizione dei triangoli sferici in dieci classi secondo la natura dei lati o quella degli angoli e, per entrambe le partizioni, lo studio di ciascuna classe e delle intersezioni alle quali danno luogo.

I capitoli 5 e 6, dedicati alle relazioni del triangolo rettangolo, sviluppano una presentazione parallela a partire dai due teoremi fondamentali, al-šakl al-muġnī e al-šakl al-ẓillī. Infatti, il piano che seguono è lo stesso: enunciato del teorema principale, dimostrazioni classificate secondo il tipo, eventuale estensione a triangoli qualunque, corollari. Le sei relazioni fondamentali, enunciate in generale, nel capitolo 7 sono applicate alla risoluzione dei triangoli rettangoli ottenuta ancora mediante le formule del capitolo 5 o quelle del capitolo 6. Tradotte in simboli, le formule stabilite da Naṣīr al-Dīn per un triangolo ABG rettangolo in G (nella numerazione di A. von Braunmühl) sono le seguenti: nel capitolo 5, la relazione

con l'estensione a triangoli qualunque, e come corollario le relazioni

e

quest'ultima con due varianti, ossia le formule [5] e [6] di Abū Naṣr; nel capitolo 6, la relazione

,

che non può essere generalizzata come la [18] e che ha come corollari le relazioni

e

,

come pure due enunciati analoghi alle [5] e [6]. L'opera termina, nel capitolo 7, con la risoluzione dei triangoli qualunque, che viene riportata a quella dei triangoli rettangoli e comprende l'uso del triangolo polare descritto in precedenza.

Il Kašf al-qinā῾ ῾an asrār al-šakl al-qaṭṭā῾ è un libro costruito benissimo, che riprende evidentemente un'esposizione diventata tradizionale. Conosciamo due trattati, meno elaborati, precedenti al libro di Naṣīr al-Dīn e dello stesso contenuto, quello anonimo già citato e un altro testo, di contenuto prossimo al Kitāb Maqālīd ῾ilm al-hay᾽a di al-Bīrūnī. Invece il Kitāb Maǧhūlāt qisiyy al-kura (Libro delle incognite degli archi della sfera) di Ibn Mu῾āḏ, non rientra esattamente in questa tradizione. La scrittura affrettata e concisa del libro di Ibn Mu῾āḏ contrasta singolarmente con la bella organizzazione del Kašf al-qinā῾ ῾an asrār al-šakl al-qaṭṭā῾. Le idee si susseguono nella scrittura e l'autore non teme di ritornare eventualmente su un punto importante o su qualcosa che ha dimenticato. La recente scoperta di questo piccolo trattato originale genera in verità più interrogativi che risposte riguardo al difficile problema della trasmissione all'Occidente musulmano delle tradizioni scientifiche arabe.

Nato in una famiglia di giuristi dell'Andalus, il qāḍī Abū ῾Abd Allāh Muḥammad ibn Mu῾āḏ al-Ǧayyānī (989-dopo il 1079) aveva soggiornato in gioventù, fra il 1012 e il 1016, al Cairo, dove ebbe probabilmente come maestro Ibn al-Hayṯam. Alcuni lavori di qualità lo fecero considerare nell'Andalus uno dei migliori matematici della sua generazione. Anche se molte sue opere furono tradotte in latino, non vi è traccia di influenza di questo Kitāb Maǧhūlāt qisiyy al-kura, molto diverso dai trattati orientali. All'inizio dell'XI sec. dovevano circolare molti testi che riportavano le nuove tecniche di calcolo degli astronomi. Verosimilmente Ibn Mu῾āḏ scrisse questo libro con una conoscenza frammentaria dei progressi compiuti dagli studiosi mediorientali, basando la propria riflessione sugli Sphaerica di Menelao, la sola opera citata. Vi si stabiliscono le sei relazioni del triangolo rettangolo a partire dal teorema di Menelao, la stessa figura che serve a generalizzare a un triangolo qualunque la relazione [18]. La risoluzione dei triangoli si decompone in un numero di casi uguale al numero degli elementi incogniti da determinare, con una discussione rigorosa della natura dell'arco ottenuto a partire dal seno e dalla tangente. Il triangolo polare è utilizzato nel caso in cui sono dati i tre angoli. Per la tangente, che egli tabula, Ibn Mu῾āḏ non usa il termine 'ombra'; sembra quindi che introduca la tangente in modo indipendente, anche se sotto la forma un po' diversa di 'rapporto del seno al seno del complementare' (tan e non Rtan), e ciò nel corso del calcolo di cui ora trattiamo.

Un aspetto comune a tutti questi trattati è l'assenza quasi totale di trigonometria piana. Un calcolo necessario è la determinazione di due archi conoscendone la somma o la differenza e il rapporto tra i seni. Naṣīr al-Dīn espone due metodi, uno preso dall'Almagesto, dove il problema è trattato con le corde, l'altro attribuito ad Abū Naṣr; in entrambi si usa il teorema di Pitagora. Ibn Mu῾āḏ pone il problema ‒ nel caso in cui è nota la differenza ‒ in una forma equivalente a

con a>b e 0°⟨α⟨180°, e dove gli archi incogniti x e y sono compresi tra 0° e 180°. Dopo aver stabilito geometricamente l'unicità della soluzione, ne dà una costruzione spiegando anche il motivo della scelta a b. Considera poi il caso particolare *** α=90° per introdurre la tangente, deducendo infine dalla figura l'uguaglianza

,

che dà x e y in funzione della somma e della differenza fra a e b. Il metodo di Ibn Mu῾āḏ, interessante per il calcolo finale, è indicativo delle tecniche impiegate: elaborazione geometrica dell'algoritmo, quindi descrizione del calcolo 'indipendentemente dalla figura'. La formula [25] non è ottenuta per trasformazione del rapporto

,

bensì mediante una similitudine; la tangente cercata rappresenta il rapporto dei cateti di un triangolo rettangolo. Questo tipo di applicazione della trigonometria, che fa appello al significato geometrico del seno o della tangente, si ritrova nei testi più diversi, in particolare per il calcolo di distanze. Il Miftāḥ al-ḥisāb (La chiave del calcolo) di al-Kāšī, un compendio di tecniche di calcolo composto nel XV sec., contiene una piccola tavola dei seni per la risoluzione dei triangoli piani e per formule relative alla misura delle superfici, come la seguente

,

che dà il raggio del cerchio inscritto in un triangolo ABG.

Le formule fondamentali della trigonometria piana si trovano nei testi astronomici, dove sono applicate alla costruzione della tavola dei seni. Il capitolo 5 del Libro I del Kitāb al-Maǧisṭī di Abū 'l-Wafā᾽ ne è un buon esempio. Consideriamo le prime sei sezioni, che contengono le definizioni e le formule. Abū 'l-Wafā᾽ descrive dapprima i segmenti che definiscono diametro, corda, seno 'esteso' o seno, senoverso o 'freccia', seno del complementare (denotato qui Cos), corda del 'complementare' (cioè di 180°−α) e massimo seno (R) per R=60. Dopo una breve sezione su seni e corde razionali studia, in successione, la determinazione dei seni e delle corde dei complementari, il calcolo reciproco del seno e della corda, la determinazione dei seni e delle corde degli archi metà e doppio, e quindi somme e differenze; alcune formule sono perciò applicate a calcoli reciproci e tutte sono stabilite geometricamente e accompagnate da esempi.

L'esposizione, molto metodica, di Abū 'l-Wafā᾽ è particolarmente sviluppata, ed è sovraccarica a causa dell'impiego di senoverso e corde. Queste regole, provenienti dall'Almagesto di Tolomeo, sono considerate un insieme che, negli zīǧ, è separato dal capitolo sulle 'ombre'. Per esempio, esse costituiscono uno dei paragrafi del trattato, prevalentemente geometrico, di al-Bīrūnī sulle corde, Istiḫrāǧ al-awtār fī 'l-dā᾽ira (Determinazione delle corde nel cerchio), dedicato ad alcuni teoremi relativi alla spezzata inscritta in un cerchio. Nell'opera al-Qānūn al-mas῾ūdī (Canone [astronomico] dedicato ad al-Mas῾ūd) al-Bīrūnī adopera la semplificazione R=1, già menzionata da Abū 'l-Wafā᾽. Più che il fatto di conservare il valore R=60, comunemente adottato e piuttosto comodo per le tavole, l'assenza di numeri negativi limita e complica un po' l'uso di queste formule. Resta il fatto che, con la tangente e con la formulazione delle relazioni fondamentali, grazie all'apporto delle tecniche algebriche i matematici arabi disponevano delle basi necessarie allo sviluppo del calcolo trigonometrico. Ostacolati probabilmente dal dover ricorrere alla dimostrazione geometrica, ritenuta necessaria, le loro ricerche non hanno però preso questa strada. Fu piuttosto nei lavori di perfezionamento delle tavole che algebra e trigonometria trovarono in qualche modo un punto d'incontro.

La tavola dei seni

La precisione del calcolo astronomico si basa interamente su quella della tavola dei seni. La composizione di questa tavola è connessa con il celebre problema della trisezione dell'angolo. Le ricerche eseguite a partire dal X sec. s'inscrivono nel quadro più generale delle approssimazioni applicate ad alcune categorie di irrazionali. Rigorose oppure soltanto intuitive, sono interessanti per i mezzi che vengono utilizzati: tecniche di interpolazione e procedimenti algoritmici. Le tavole degli zīǧ sono in genere più precise della tavola delle corde dell'Almagesto, sebbene non raggiungano la precisione delle tavole composte in Europa poco tempo prima dell'introduzione dei logaritmi.

La tavola delle corde dell'Almagesto è a tre posizioni sessagesimali e a intervalli di mezzo grado. È esatta, ed è facile verificare che per interpolazione lineare dà l'arcoseno a meno di qualche secondo, salvo nell'intorno di 90° (l'errore supera il minuto oltre gli 89;45°). Le tavole indiane che si conoscevano nel IX sec. non offrivano lo stesso grado di approssimazione. Sembra che la precisione della tavola dell'Almagesto fosse giudicata sufficiente. Ḥabaš, che abbiamo visto riprendere la maggior parte dei calcoli dell'Almagesto, traspone senza modifiche la tavola delle corde che per il seno ha intervalli di 15 minuti e una quarta colonna formata di 0 e di 30. Al-Battānī semplifica, conservando la metà della tavola (intervalli di mezzo grado) e sopprimendo le cifre a partire dalla quarta. I testi non ci dicono se la tavola dei seni sia mai stata calcolata prima della fine del X secolo. Le prime due composizioni originali della tavola conosciute sono dovute a Ibn Yūnus e ad Abū 'l-Wafā᾽. Ibn Yūnus segue più direttamente il procedimento dell'Almagesto.

Ricordiamo che Tolomeo determina un minimo e un massimo per la corda di 1°, grazie a un teorema dimostrato confrontando due aree; esso esprime il fatto che il rapporto Senx/x decresce tra 0° e 90°, nella seguente forma: se a>b, allora Cordaa/Cordab⟨a/b. Ne deduce la doppia disuguaglianza

[28] 2/3 Corda 1;30°⟨Corda 1°⟨4/3 Corda 0;45°,

e poi, con valori approssimati,

[29] 2/3 Corda 1;30°=Corda 1°=4/3 Corda 0;45°=1;2,50.

Il calcolo delle corde di 1;30° e 0;45°, che viene effettuato a partire dai lati del pentagono e dell'esagono regolari inscritti, mediante Corda(72°−60°) seguito da quattro bisezioni, potrebbe essere portato a una precisione maggiore se si facesse comparire una differenza tra i due valori. Appare chiaro che Tolomeo sceglie invece l'ampiezza dell'intervallo (3/4 per la corda, che corrisponde a 3/8 per il seno) in modo tale da ottenere l'uguaglianza con la precisione voluta.

La tavola dei seni compilata da Ibn Yūnus in al-Zīǧ al-ḥākimī al-kabīr è a quattro posizioni sessagesimali a intervalli di un sesto di grado. Il metodo utilizzato è interessante soprattutto per la formula d'interpolazione, che serve a completare la tavola a partire da valori calcolati separatamente per i mezzi gradi. Indipendentemente da questo aspetto, sul quale ritorneremo, vengono apportate modifiche al calcolo di Tolomeo. Ibn Yūnus riduce dapprima della metà l'intervallo che sceglie per Sen1°. I calcoli sono a cinque posizioni, ottenute mediante quattro bisezioni a partire da Sen15° [=Sen(45°−30°)] e da Sen 18° (metà del lato del decagono), ottenendo:

,

cioè 1;2,49,40,4⟨Sen1°⟨1;2,49,45,10. Ne deduce quindi un primo valore di Sen1° dalla relazione

,

che corrisponde all'interpolazione lineare

Apporta infine una piccola correzione al valore trovato, basandosi sull'idea approssimativa che l'errore su Sen1° incide per quantità uguali e contrarie, Sen2,1° e Sen(3°−1°). Ottiene in definitiva:

,

valore che, portando l'approssimazione da cinque a sei cifre, diventa Sen1°=1;2,49,43,11,15.

Il metodo di Ibn Yūnus permette di ottenere facilmente la precisione cercata, ma alcune disattenzioni nei calcoli fanno sì che la tavola non sia molto precisa, con errori che superano talvolta di un'unità la cifra nella quarta posizione.

Abū 'l-Wafā᾽ determina sen(1/2)° in un modo diverso dall'Almagesto e più vantaggioso. Utilizza anche una lenta variazione nell'intorno di (1/2)°, il decrescere delle differenze prime del seno. Nell'Almagesto i trentesimi delle differenze sono tabulati per le corde, allo scopo di facilitare la lettura della tavola per interpolazione lineare. Il decrescere delle differenze prime, messo così in evidenza, è verificato geometricamente da Teone di Alessandria (IV sec. d.C.) nel Commento all'Almagesto. Abū 'l-Wafā᾽ ne dà una diversa dimostrazione per il seno. Con

si ha

da

[35] DY⟨DM⟨DK=GT.

Abū 'l-Wafā᾽ deduce da ciò una maggiorazione e una minorazione per sen(1/2)°, scegliendo tre valori vicini a (1/2)° di seni noti, che sono rappresentati dai punti B, G, Z di una circonferenza:

Con l'arco BG suddiviso in sei archi uguali, Z e il punto H tale che

fanno parte della suddivisione, e l'applicazione ripetuta del teorema porta alla doppia disuguaglianza

cioè

Abū al-Wafā᾽ ottiene così:

[38] 0;31,24,55,52,2⟨Sen(1/2)°⟨0;31,24,55,57,47

e poi, per la semisomma, Sen(1/2)°=0;31,24,55,54,55. Il calcolo non è proprio esatto, ma il metodo dà estremi inferiore e superiore quasi sei volte più precisi dei valori ottenuti col procedimento indicato nell'Almagesto. Nei testi lo si ritrova fino al XV sec.: per esempio, è applicato al calcolo di Sen1° da Muḥyī 'l-Dīn al-Maġribī (XIII sec.), uno degli astronomi di Marāġa all'epoca di Naṣīr al-Dīn, autore di numerosi studi di trigonometria.

La tavola dei seni del Kitāb al-Maǧisṭī di Abū 'l-Wafā᾽ era prevista a quattro posizioni, con dati a intervalli di 15 minuti. Sullo stesso modello, la tavola del Qānūn è praticamente esatta. Quest'opera celeberrima di al-Bīrūnī dà una buona idea della precisione raggiunta in quest'epoca nei calcoli trigonometrici. Riguardo alla costruzione della tavola dei seni, lo studio del Qānūn apre altre prospettive; con la curiosa formula d'interpolazione che utilizza, restiamo in un'impostazione dello stesso tipo. La ricerca di un'approssimazione migliore di quella data dall'interpolazione lineare è stata, a quanto sembra, una preoccupazione costante degli astronomi arabi, abituati a manipolare numerosissime tavole nei loro calcoli. Oggi conosciamo molte formule utilizzate tra il X e il XV secolo. Si pone la questione di sapere come furono elaborate al di fuori di qualunque nozione di rappresentazione grafica. A questo riguardo la regola del Qānūn, che è descritta per il seno e la tangente e poi generalizzata a una tavola qualunque, può essere considerata un esempio di costruzione teorica. Utilizzando la notazione standard

[39] ∆y_-1 = y₀-y_-1,  ∆y₀ = y₁-y₀, ...,  ∆²y_-1 = ∆y₀-∆y_-1, ...,

per x₀−x₋₁=x₁−x₀=…=d, la formula che in al-Bīrūnī sostituisce l'interpolazione lineare y=y₀+[(x−x₀)/d]Δy₀ sull'intervallo [x₀, x₁] è:

Scrivendo la

,

si vede che manca un coefficiente 1/2 davanti al termine

perché la parabola, che al-Bīrūnī sostituisce alla corda che unisce i punti di coordinate (x₀,y₀), (x₁,y₁) passi per un terzo punto della curva, di coordinate (x₋₁,y₋₁); quindi con quest'interpolazione l'errore rimane, approssimativamente e senza considerare il segno, uguale a quello dell'interpolazione lineare. L'iterazione evidente del procedimento è sottolineata da un tentativo di giustificazione, data mediante una figura, per spiegare l'interpolazione applicata a Δy₋₁.

Questa regola del Qānūn ha incuriosito gli storici perché un'espressione corretta dell'interpolazione quadratica, equivalente alla formula di Newton di ordine due, si trova nel Khaṇḍakhādyaka, opera che al-Bīrūnī conosceva bene e che cita spesso nei suoi scritti. La formula dell'opera indiana permette di ottenere per il seno dei valori quasi accettabili a partire da una tavola più che rudimentale, ridotta com'è a sei numeri interi. I numeri sono 39, 36, 31, 24, 15 e 5; essi rappresentano le differenze prime della funzione x → 150senx per i valori di x corrispondenti ai semisegni zodiacali, ossia le quantità 150sen15°, 150(sen30°−sen15°), ..., 150(sen 90°−sen75°). Utilizzando le notazioni precedenti la formula si scrive:

Il suo significato geometrico consiste nel sostituire nell'intervallo [x₀,x₁] la curva con la parabola passante per i tre punti di coordinate (x₋₁,y₋₁), (x₀,y₀), (x₁,y₁). Una forma più elaborata della stessa interpolazione quadratica, corrispondente a intervalli [x₋₁,x₀] e [x₀,x₁] ineguali, fu applicata fin dal X sec. al calcolo della longitudine dei pianeti. Ci furono anche altre formule, ma ci limiteremo a citare la regola di Ibn Yūnus per il seno. Nell'intervallo [x₀,x₂] essa conduce alla parabola passante per i punti (x₀,y₀), (x₁,y₁), (x₂,y₂), con x₀=n, intero, x₁=n+(1/2), x₂=n+1, con la tavola costruita in precedenza, come abbiamo visto, per i mezzi gradi. Ancora una volta l'enunciato della regola mette in evidenza il ragionamento seguito, e Ibn Yūnus corregge l'interpolazione lineare operata su [n,n+1] mediante un termine nullo agli estremi e che dà il valore esatto al centro dell'intervallo. In formule, la regola è la seguente:

equivalente, con le notazioni precedenti e (x−x₀)/d=ξ, per d=1/2, alla formula usuale

nell'intervallo [x₀, x₀+2d].

Dedicato a Mas῾ūd ibn Maḥmūd ibn Sebüktiǧin (r. 1030-1040), il secondo sultano ghaznavide, il Qānūn al-mas῾ūdī è una delle opere principali di al-Bīrūnī. Scritta dopo il soggiorno in India, quando l'autore era sulla sessantina, presenta una grande ricchezza, e con i suoi undici trattati va oltre il quadro abituale delle opere di astronomia. Il terzo trattato, dedicato alla trigonometria piana e sferica, consta di dieci capitoli, uno dei quali riguarda la determinazione dell'ennagono regolare. Due procedimenti geometrici diversi conducono, dopo una riduzione bi-'l-ǧabr wa-'l-muqābala (trattamento algebrico che serve soltanto a semplificare le equazioni ottenute per via geometrica), alle equazioni

vale a dire, a due forme dell'equazione della trisezione. È in questo contesto generale che è affrontata la determinazione della corda di 1°. Vengono posti dodici problemi di costruzione che, se risolti, permetterebbero di realizzare geometricamente la trisezione di un angolo qualunque. Il capitolo termina con quattro calcoli della corda di 1°, due dei quali a partire dal lato dell'ennagono. L'idea dell'equazione di terzo grado, avanzata nel Qānūn, sarà in seguito ripresa. La sua risoluzione per mezzo di un algoritmo rientra nel quadro dei procedimenti di iterazione.

Se ci si attiene al modello dell'Almagesto, la determinazione dell'istante della sizigia vera o apparente è l'esempio tipico di un calcolo da effettuare per iterazione. È così che fa Tolomeo. I testi astronomici arabi forniscono altri esempi. Per restare nel campo della trigonometria, possiamo citare il terzo metodo del Qānūn relativo al lato dell'ennagono. Esso consiste nell'approssimare la corda di 40° con l'undicesimo termine della successione

costruita per ricorrenza, utilizzando le formule di addizione, per mezzo di

[48]

corda u₀ = corda (72°-30°)

corda u₁ = corda [30°+(u₀/4)]

corda u_n = corda [30°+(u_n-1/4)].

Un altro esempio interessante si trova negli zīǧ di Ḥabaš, dove il problema viene posto a proposito della parallasse. Da un punto di vista matematico esso si presenta come la ricerca, nell'intervallo [0°,180°], di una funzione di interpolazione nulla agli estremi dell'intervallo e con un massimo k in un punto 90°−m, cioè spostato di una quantità m rispetto al centro dell'intervallo. La funzione φ considerata da Ḥabaš è tale che φ(t)=ksenθ, dove θ è definito implicitamente in funzione della variabile t dall'equazione t=θ−msenθ, detta equazione di Kepler (è chiaro che la funzione φ soddisfa le condizioni richieste). Quest'equazione, posta nella forma θ=f(θ), ossia θ=t+msenθ, è risolta per t qualunque per mezzo della successione (θ_n) definita da

che converge verso la soluzione cercata. Questo calcolo di Ḥabaš è stato descritto più volte, sia perché è ingegnoso, sia perché introduce l'equazione di Kepler.

Anche l'elegante algoritmo attribuito ad al-Kāšī per il calcolo di Sen1° è stato ben studiato. Si applica a un'equazione della trisezione analoga a quelle del Qānūn e, come il calcolo di Ḥabaš, fa appello a una successione u_n=f(u_n−1). Utilizza inoltre le tecniche degli algebristi, tra cui la disposizione in una tavola usata per lo sviluppo di espressioni del tipo

[50]  (60x_n-1 + q_n)³ - (60x_n-1)³

secondo la

Ǧamšīd Ġiyāṯ al-Dīn al-Kāšī è una delle grandi figure della scienza dell'Islam; direttore dell'importante Osservatorio di Samarcanda all'epoca del sultano Uluġ Beg, fu anche matematico insigne. Questo algoritmo a lui attribuito è conosciuto soltanto attraverso un commento alle tavole astronomiche di Uluġ Beg, ed è quindi difficile sapere quanto al-Kāšī prenda da un predecessore. Il commentatore riporta una dimostrazione geometrica del fatto che sen1° è soluzione dell'equazione:

L'incognita x, della quale è nota la limitazione 1;2⟨x⟨1;3, è poi cercata nella forma x=q₀+60⁻¹q₁+…+60⁻ⁿq_n, cioè, in base 60, x=q₀;q₁,…,q_n, dove le q_i sono minori di 60. Il metodo consiste allora nel determinare successivamente le cifre q₀,q₁,…,q_n mediante una successione convergente, spingendo ogni volta il calcolo alla cifra successiva e prendendo di conseguenza una cifra in più del numero 15∙60Sen3°. Più precisamente, posto x₀=q₀, x₁=q₀;q₁,…, x_k=q₀;q₁,…,q_k, e denotando con [X] la parte intera di X in base 60, il calcolo di al-Kāšī si sviluppa nel modo seguente, a partire dall'equazione [52] per Sen1°, che ora scriviamo

(si è posto N=15∙60 Sen3° e D=45∙60). Al primo passo si ottiene q₀ come parte intera di N/D; allora x₀=q₀, e il resto r₀ della divisione di N per D, cioè r₀=N−Dq₀, serve a mettere l'equazione nella forma:

Si cerca poi q₁ per avere x₁=q₀;q₁=q₀+60⁻¹q₁:

,

da cui si ottiene il nuovo resto r₁=(x₀³+r₀)-60^-1Dq₁ e l'equazione diviene:

In generale, al passo k+1 l'equazione da risolvere è

,

da cui

,

e quindi

[59]  x_k = x_k-1+60^-kq_k, r_k = (x³_k-1 -x³_k-2+r_k-1)-60^-k Dq_k.

Il commentatore si limita a riportare il calcolo delle prime cinque posizioni a partire da un valore di Sen3° esatto a otto posizioni. Al-Kāšī avrebbe determinato le prime dieci posizioni di Sen1°. Possiamo avere un'idea della qualità dei suoi calcoli grazie a un altro scritto, la celebre Risāla al-muḥīṭiyya (Epistola comprensiva sulla circonferenza), dedicato alla determinazione di π, nella quale, con un procedimento diverso da quello di Archimede e che presenta π come il limite di

,

con n radicali sotto il radicale più esterno, al-Kāšī ottiene esattamente le dieci posizioni sessagesimali che cerca aiutandosi con un calcolo dell'errore. La tavola dei seni dei suoi Zīǧ-i Ḫāqānī è esatta a quattro posizioni sessagesimali, con intervalli di un minuto d'arco. Trascurata dagli astronomi dei secc. IX e X, la precisione del calcolo numerico caratterizza quest'ultimo periodo rappresentato dalla Scuola di Samarcanda. Essa si avvale dei progressi dell'algebra, in particolare dei lavori di matematici come al-Samaw᾽al, al-Maġribī o Šaraf al-Dīn al-Ṭūsī.

In conclusione, sarebbe certamente esagerato affermare che prima del IX sec. non esisteva niente in trigonometria. Il concetto di seno è indiano e i fondamenti della disciplina risalgono all'epoca greca, con la tavola delle corde e il teorema sferico di Menelao. Gli studiosi arabi ne fecero quel sapere codificato illustrato dal Kašf al-qinā῾ ῾an asrār al-šakl al-qaṭṭā῾. Nelle loro mani i calcoli geometrici dell'Almagesto con l'uso della tavola delle corde diventarono uno strumento di eccezionale duttilità, mentre si sviluppavano altre tecniche per i calcoli astronomici, come l'uso di funzioni ausiliarie, l'interpolazione e i procedimenti iterativi. La funzione tangente, le prime relazioni del triangolo, la nozione di triangolo polare sono tra le conquiste della scienza dell'epoca. In questo particolare campo, nato dall'attività astronomica, si ritrova il modo di procedere proprio dei matematici arabi, che comincia con una lettura sempre nuova e arricchita dei testi antichi. Questi matematici poterono così dare corso a una nuova disciplina, che avrà ancora bisogno di alcuni sviluppi prima di diventare un elemento indispensabile del calcolo matematico.

Bibliografia

Aaboe 1954: Aaboe, Asger, Al-Kāshī's interaction method for the determination of sin 1°, "Scripta mathematica", 20, 1954, pp. 24-29.

Björnbo 1902: Björnbo, Axel A., Studien über Menelaos' Sphärik. Beiträge zur Geschichte der Sphärik und Trigonometrie der Griechen, Leipzig, Teubner, 1902.

Bond 1921-22: Bond, John D., The development of trigonometric methods down to the close of the XVth century, "Isis", 4, 1921-1922, pp. 295-323.

von Braunmühl 1898: Braunmühl, Anton von, Zur Geschichte des sphärischen Polardreieckes, "Bibliotheca mathematica", 12, 1898, pp. 65-72.

‒ 1900-03: Braunmühl, Anton von, Vorlesungen über Geschichte der Trigonometrie, Leipzig, Teubner, 1900-1903, 2 v.

Debarnot 1978: Debarnot, Marie-Thérèse, Introduction du triangle polaire par Abū Naṣr b. ῾Irāq, "Journal for the history of Arabic science", 2, 1978, pp. 126-136.

‒ 1985: Al-Bīrūnī, Kitāb maqālīd ᾽ilm al-hay᾽a, La trigonométrie sphérique chez les Arabes de l'est à la fin du X^e siècle, édité et traduit par Marie-Thérèse Debarnot, Damasco, Institut Français de Damas, 1985.

Hairetdinova 1966: Hairetdinova, N.G., Trigonometričeskij isfachanskogo anonima, "Istoriko-matematičeskie issledovanija", 17, 1966, pp. 449-464.

Hamadanizadeh 1978: Hamadanizadeh, Javad, Interpolation schemes in Dustūr al-Munajjimīn, "Centaurus", 22, 1978, 1, pp. 44-52.

‒ 1979: Hamadanizadeh, Javad, The interpolation formulae of Islamic mathematicians, in: The second international symposium for the history of Arabic science, University of Aleppo, 5-12 april 1979, Aleppo, Aleppo University Press, 1979.

‒ 1980: Hamadanizadeh, Javad, The trigonometric tables of al-Kāshī in his Zīj-i Khāqānī, "Historia mathematica", 7, 1980, pp. 38-45.

Heath 1921: Heath, Thomas L., A history of Greek mathematics, Oxford, Clarendon, 1921, 2 v. (rist.: New York, Dover, 1981, 2 v.).

Irani 1956: Irani, R., The Jadwal at-taqwīm of Ḥabash al-Ḥāsib (tesi di laurea, Beirut, American University of Beirut, 1956).

Kennedy 1956: Kennedy, Edward S. - Transue, W.R., A medieval iterative algorism, "American mathematical monthly", 63, 1956, 2, pp. 80-83 (rist. in: Kennedy, Edward S. [et al.], Studies in the islamic exact sciences, Beirut, American University of Beirut, 1983).

‒ 1969: Kennedy, Edward S., An early method of successive approximations, "Centaurus", 13, 1969, pp. 248-250 (rist. in: Kennedy, Edward S. [et al.], Studies in the islamic exact sciences, Beirut, American University of Beirut, 1983, pp. 541-543).

‒ 1977-78: Kennedy, Edward S., The motivation of al-Bīrūnī's second order interpolation scheme, in: Proceedings of the first international symposium for the history of Arabic science, Aleppo, Aleppo University Press, 1977-1978, 2 v.; v. II, pp. 67-71 (rist. in: Kennedy, Edward S. [et al.], Studies in the islamic exact sciences, Beirut, American University of Beirut, 1983, pp. 630-634).

‒ 1983: Kennedy, Edward S. [et al.], Studies in the islamic exact sciences, Beirut, American University of Beirut, 1983.

Krause 1936: Krause, Max, Die Sphärik von Menelaos aus Alexandrien in der Verbesserung von Abū Naṣr Manṣūr b. ῾Alī b. ῾Irāq, mit Untersuchungen zur Geschichte des Textes bei den islamischen Mathematikern, Berlin, Weidmann, 1936.

Luckey 1941: Luckey, Paul, Zur Entstehung der Kugeldreiecksrechnung, "Deutsche Mathematik", 5, 1941, pp. 405-446.

‒ 1950: al-Kāšī, Ġiyāṯ al-Dīn Ǧamšīd, Der Lehrbrief über den Kreisumfang, übers. und erläutert von Paul Luckey, "Abhandlungen der deutschen Akademie der Wissenschaften zu Berlin", 6, 1950.

Morelon 1987: Morelon, Régis, Thābit ibn Qurra, Œuvres d'astronomie, Paris, Les Belles Lettres, 1987.

Neugebauer 1975: Neugebauer, Otto, A history of ancient mathematical astronomy, Berlin-New York, Springer, 1975, 3 v.

Rashed 1991: Rashed, Roshdi, Al-Samaw᾽al, al-Bīrūnī et Brahmagupta: les méthodes d'interpolation, "Arabic sciences and philosophy", 1, 1991, pp. 101-160 (rist. in: Rashed, Roshdi, Optique et mathématiques. Recherches sur l'histoire de la pensée scientifique en arabe, Aldershot, Variorum, 1992, XII).

‒ 1999: Rashed, Roshdi - Vahabzadeh, Bijan, Al-Khayyām mathématicien, Paris, Blanchard, 1999 (trad. ingl.: Omar Khayyam. The mathematician, New York, Bibliotheca Persica, 2000).

‒ 2000: Rashed, Roshdi - Bellosta, Hélène, Ibrāhīm ibn Sinān. Logique et géométrie au X^e siècle, Leiden, E.J. Brill, 2000.

‒ 2002: Rashed, Roshdi, Math. inf. IV.

Schoy 1923: Schoy, Carl, Beiträge zur arabischen Trigonometrie, "Isis", 5, 1923, pp. 364-399.

‒ 1927: Schoy, Carl, Die trigonometrischen Lehren des persischen Astronomen Abū 'l-Raiḥān Muḥ. Ibn Aḥmad al-Bīrūnī dargestellt nach al-Qānūn al-Mas῾ūdī, Hannover, Orient-Buchhandlung Lafaire, 1927.

‒ 1988: Schoy, Carl, Beiträge zur arabisch-islamischen Mathematik und Astronomie, Frankfurt a. M., Institut für Geschichte der Arabisch-Islamischen Wissenschaften, 1988, 2 v.

Sédillot 1853: Sédillot, Louis P.E.A., Prolégomènes des tables astronomiques d'Olough Beg, Paris, Didot Frères, 1853.

Suter 1910-11: Suter, Heinrich, Zur Trigonometrie der Araber, "Bibliotheca mathematica", 11, 1910-1911, pp. 156-160.

‒ 1986: Suter, Heinrich, Beiträge zur Geschichte der Mathematik und Astronomie im Islam. Nachdruck seiner Schriften aus den Jahren 1892-1922, hrsg. von Fuat Sezgin, Frankfurt a.M., Institut für Geschichte der Arabisch-Islamischen Wissenschaften, 1986, 2 v.

Villuendas 1979: Villuendas, María V., La trigonometría europea en el siglo XI. Estudio de la obra de Ibn Mu῾ādh, El Kitāb al-maŷhūlāt, Barcelona, Instituto de Historia de la Ciencia de la Real Academia de Buenas Letras, 1979.

Woepcke 1854: Woepcke, Franz, Discussion de deux méthodes arabes pour déterminer une valeur approchée de sin 1°, "Journal de mathématiques pures et appliquées", 19, 1854, pp. 153-176 (v. anche Woepcke 1986, v. I, pp. 614-637).

‒ 1860: Woepcke, Franz, Recherches sur l'histoire des sciences mathématiques chez les orientaux, "Journal asiatique", s. V, 4, 1860, pp. 348-384 (v. anche Woepcke 1986, v. I, pp. 445-481).

‒ 1986: Woepcke, Franz, Études sur les mathématiques arabo-islamiques, hrsg. von Fuat Sezgin, Frankfurt a.M., Institut für Geschichte der Arabisch-Islamischen Wissenschaften, 1986, 2 v.