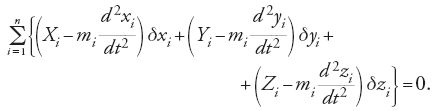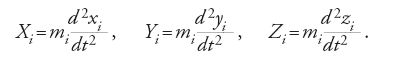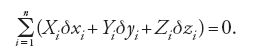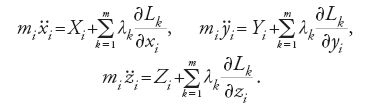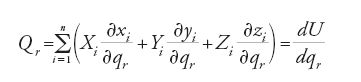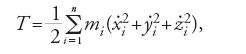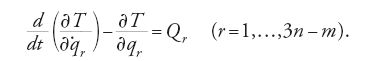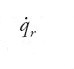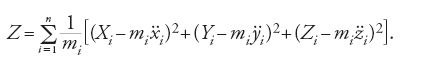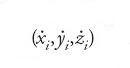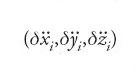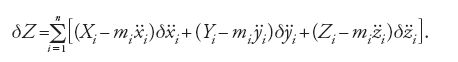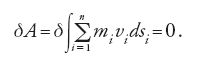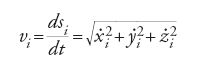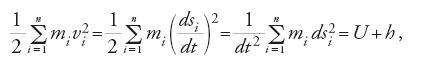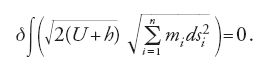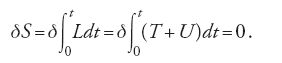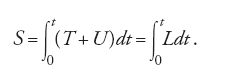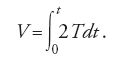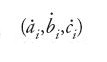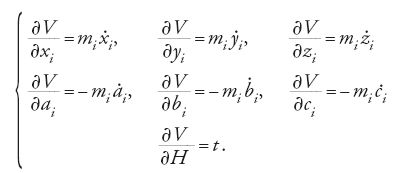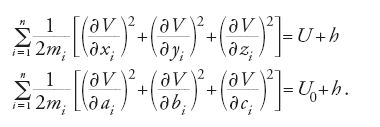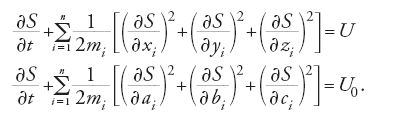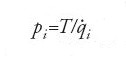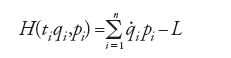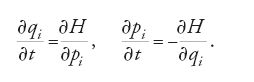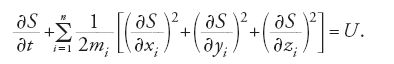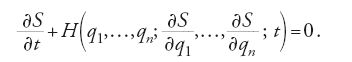L'Ottocento: matematica. Meccanica analitica

L'Ottocento: matematica. Meccanica analitica

Meccanica analitica

La meccanica analitica è una branca della meccanica razionale la quale, dopo i primi passi compiuti nel XVII sec., ebbe un vigoroso sviluppo nel secolo successivo per giungere a forma compiuta nel corso dell'Ottocento. L'aggettivo 'analitico' non si riferisce alla vecchia distinzione, propria della filosofia della scienza, tra metodi analitici e metodi sintetici, come si presenta, per esempio, in Galilei nella distinzione tra 'metodo risolutivo' e metodo compositivo. L'aggettivo si riferisce piuttosto al procedimento matematico che in questa branca della meccanica sarà principalmente (o addirittura, come pretendono alcuni, esclusivamente) utilizzato: la meccanica analitica si avvale del calcolo differenziale e integrale, o 'analisi dell'infinito' come fu chiamata nel XVIII sec. questa importante conquista della matematica dell'Età moderna.

L'analisi matematica ha dato il nome alla meccanica analitica in due sensi: è servita, da un lato, per formularne e rappresentarne i principî primi o assiomi, dall'altro, per derivare da 'principî analitici' risultati che si potevano verificare empiricamente. In particolare qui sta il significato del calcolo delle variazioni ‒ come parte dell'analisi superiore ‒ per questa branca della meccanica.

Una meccanica analitica intesa in questo modo ha come riscontro 'sintetico' la meccanica geometrica, sviluppata anch'essa come parte della meccanica razionale nel XIX sec. (Ziegler 1985). Grazie alla generalità e all'efficacia dei metodi in essa si ravvisa, già a partire dalla metà del XVIII sec., una forte prevalenza della meccanica razionale come canonizzata da Isaac Newton nei Principia (1687), con esplicita eliminazione di ogni meccanica 'pratica', dove la meccanica analitica è considerata "scienza, esattamente spiegata e dimostrata, del moto risultante da forze qualunque, e delle forze che sono richieste per un qualunque moto" (Newton 1687 [1999, p. 3]).

Fu soprattutto per l'ideale di esattezza e per la possibilità di fornire dimostrazioni che la meccanica analitica svolse, con lo sviluppo del calcolo infinitesimale, una funzione chiave nella ricerca matematica. Se Newton si avvaleva di metodi sintetici (nel senso geometrico del termine) ancora preponderanti, Euler fu il primo a insistere con decisione sul significato dell'analisi per la meccanica: quest'ultima non doveva soltanto fornire affermazioni matematiche vere sulla Natura, ma anche "una conoscenza chiara e ben definita della stessa" (Euler 1741, pp. 30-47). Il primo dei principali lavori di matematica di Euler, la Mechanica sive motus scientia analytice exposita (1736), fu successivamente definito da Joseph-Louis Lagrange come "il primo lavoro […] nel quale l'analisi viene applicata alla scienza del moto" (Lagrange 1788 [1853-55, I, p. 243]). Occorre però osservare che nella Mechanica, come pure nella maggior parte dei lavori successivi, come, per esempio, nella Theoria motus del 1765, i metodi geometrici conservavano il loro significato. Fu lo stesso Lagrange, nella Méchanique analitique (1788), il primo a sostenere esplicitamente l'uso sistematico del metodo analitico in meccanica razionale come unico metodo, affermando che si poteva completamente rinunciare ai metodi non analitici e fare della meccanica una "nuova branca" dell'analisi. Le considerazioni di carattere 'geometrico' o 'meccanico' erano superflue, mentre determinante era la 'funzione unificante' dei principî della meccanica esprimibili analiticamente: a partire da un unico principio ‒ quello delle velocità virtuali, da lui stesso formulato ‒ si doveva sviluppare, secondo Legrange, in modo deduttivo tutta la statica e la dinamica.

Da questo punto di vista la Méchanique analitique resta un'opera 'sintetica', nel senso che tale aggettivo aveva nel linguaggio scientifico dell'epoca. Essa si differenzia però dai vecchi e voluminosi trattati di sintesi di meccanica razionale per un aspetto importante: mentre le presentazioni assiomatiche della meccanica sull'esempio degli Elementi di Euclide cominciavano con la spiegazione delle premesse concettuali della meccanica ‒ in particolare i concetti di spazio, tempo, materia, massa e forza ‒ la parte sistematica della Méchanique analitique comincia subito con la discussione dei principî analitici e delle loro relazioni di dipendenza. Il metodo di Lagrange non implica soltanto l'esclusione di altri metodi matematici, non analitici, ma anche di quelli extramatematici. Manca, in particolare, in quest'opera qualunque riflessione di carattere teorico sui fondamenti della meccanica, che fino ad allora avevano invece trovato spazio nei trattati precedenti sull'argomento.

Queste premesse sono importanti perché il testo di Lagrange fu un modello per la meccanica analitica della prima metà del XIX secolo. Tale disciplina, pur appartenendo alla fisica matematica, fu allora considerata principalmente come parte della matematica 'pura', senza riferimento alle applicazioni. Nel seguito si prenderà in esame più da vicino questo aspetto della meccanica analitica e si approfondirà la sua rilevanza in fisica e le sue implicazioni di carattere filosofico. A causa dell'atomismo newtoniano dominante, i rapporti con le applicazioni della meccanica analitica nel XVIII sec. riguardarono soprattutto la dinamica dei punti materiali ideali; nel XIX sec. riguardarono invece soprattutto la meccanica celeste e la teoria delle perturbazioni, a sua volta strumento fondamentale per la meccanica celeste stessa. In particolare dalla prima metà del XIX sec. anche le ricerche sui continui solidi e fluidi divennero un importante campo di applicazione di principî e metodi analitici.

Lo sviluppo dei principî più importanti della meccanica analitica

Alcune differenze concettuali

Parlando di 'principî' non intendiamo né premesse filosofiche, come il principio di causalità, né ipotesi di carattere fisico, come l'azione a distanza, ma soltanto proposizioni generali formulate matematicamente e da assumere come premesse di una meccanica analitica intesa nel senso visto precedentemente. A partire da Lagrange questa branca della meccanica razionale aveva il compito di presentare il complesso dei risultati noti sull'equilibrio e il moto di sistemi in una forma assiomatico-deduttiva. Tali principî, dunque, non dovevano soltanto fornire equazioni per la quiete e il moto di questi sistemi nelle condizioni più generali, ma dovevano anche permettere di dedurre, da condizioni sempre più generali, le leggi della statica e della dinamica già acquisite (come, per es., il teorema del baricentro o il teorema della conservazione del momento cinetico). Nella storiografia sulla meccanica analitica questa impostazione 'costruttiva' spesso non viene presa sufficientemente in considerazione. Poiché la statica è generalmente vista come 'sapere preliminare' oppure quale un semplice caso particolare della dinamica, nel seguito porremo in rilievo i principî dinamici, cioè quelli che riguardano la determinazione del moto.

Dal punto di vista della matematica e della fisica è opportuno premettere alcune distinzioni di carattere concettuale prima di considerare questi principî in dettaglio. Innanzitutto occorre distinguere i principî (o principî variazionali in senso lato) in 'estremali' (o più propriamente integrali) da un lato, e 'differenziali' (o variazionali in senso stretto) dall'altro. I principî analitici estremali determinano le equazioni del moto di un sistema meccanico mediante il confronto tra il moto effettivo risultante e altri moti non realizzati e aventi gli stessi punti iniziali e finali. Il moto realizzato viene così individuato (a fronte di quelli non realizzati, in una classe di moti affini da precisare di volta in volta) dal fatto che per esso una determinata grandezza dipendente dall'intero percorso (in generale l'integrale del tempo o di linea) raggiunge un estremo (in generale un minimo). Quelli differenziali, invece, determinano il moto effettivo non attraverso un confronto globale, bensì, per così dire, locale. Il confronto non viene fatto cioè tra la curva percorsa e altre curve di una classe in un dato periodo di tempo: i singoli punti sono invece confrontati con punti vicini possibili, o 'virtuali', istante per istante. Gli astratti spostamenti virtuali di una massa da una posizione effettiva a una vicina vengono pensati indipendenti dal tempo. I principî estremali, al contrario di quelli differenziali, hanno il vantaggio di essere invarianti per trasformazioni di coordinate (Voss 1901). Una seconda differenza non riguarda i principî analitici, bensì i sistemi meccanici ai quali questi principî vengono applicati. Quando tutte le forze che agiscono sulle masse del sistema si possono dedurre da una 'funzione lavoro' indipendente dal tempo, la somma dell'energia cinetica totale e di quella potenziale (l'opposto della funzione lavoro) resta costante. In questo caso le forze agenti sono dette 'conservative', così come il sistema stesso. Se una tale 'funzione lavoro' non esiste (per es., quando sono presenti forze di attrito o altre forze dissipative) le forze sono dette non conservative.

Anche la terza differenza riguarda il sistema meccanico. Non si tratta di un sistema libero, ma di un sistema nel quale le masse sono soggette a determinati vincoli di movimento che matematicamente si possono classificare in vario modo. Se si possono rappresentare in equazioni dipendenti dalle coordinate delle masse e (anche se non necessariamente) del tempo, si parla di vincoli 'olonomi' (e corrispondentemente di sistemi olonomi). Per esempio, un corpo rigido è un sistema olonomo in quanto le masse sono a distanza fissa, ma lo è anche un sistema di punti materiali vincolati a muoversi su una superficie. Se le condizioni di vincolo non si possono formulare mediante equazioni, si parla di vincoli 'anolonomi'. Questo caso si presenta, per esempio, quando i punti materiali sono vincolati a muoversi fuori di una superficie sferica, una condizione esprimibile soltanto con una disequazione. Infine, se i vincoli non dipendono dal tempo si parla di vincoli 'scleronomi', se invece ne dipendono si parla di vincoli 'reonomi'. Se un punto si muove su un filo circolare fisso il sistema è scleronomo, se il filo ruota attorno a un asse il sistema è reonomo.

Vedremo come lo sviluppo dei più importanti principî analitici della meccanica sia contrassegnato da un graduale venir meno del loro carattere di evidenza e da una conseguente problematizzazione, precisazione e chiarificazione delle condizioni di applicabilità e della estensione dei campi di applicazione.

Il principio generale delle velocità virtuali o principio di d'Alembert

Nella Méchanique analitique Lagrange fonda la statica e la dinamica su una nuova formulazione del principio delle velocità virtuali, che egli stesso definisce una 'combinazione' del vecchio principio con quello di d'Alembert (Lagrange 1788, p. 12). Nella meccanica analitica del XIX e del XX sec. le denominazioni 'principio delle velocità virtuali' e 'principio dei lavori virtuali', sono stati usati ‒ in modo storicamente non corretto ‒ come sinonimi. La seconda denominazione è stata perlopiù utilizzata per la forma generale [1] e la prima per le formulazioni statiche [3] e [4], espresse nel seguito. In una forma leggermente più moderna, la formulazione generale dinamica è la seguente (Lagrange 1788, p. 200 [1853-55, II, p. 274]):

Se su n punti materiali di massa m_i di coordinate (x_i,y_i,z_i) agiscono forze con componenti lungo gli assi cartesiani (X_i,Y_i,Z_i) e se ognuno dei punti è soggetto a uno spostamento virtuale (δx_i,δy_i,δz_i), per la [1] si annulla la somma dei 'momenti', cioè la somma del lavoro virtuale delle forze agenti (X_i,Y_i,Z_i) diminuite delle forze d'inerzia m_id2x_i/dt2, m_id2y_i/dt2, m_id2Z_i/dt2. Per sistemi 'liberi' il principio è banale: gli spostamenti (δx_i,δy_i,δz_i) si possono scegliere a piacere e gli addendi in [1] debbono allora annullarsi. Ne seguono facilmente le equazioni differenziali del moto:

Nel caso di equilibrio la [1] diventa:

Quando non si parta da una decomposizione in componenti lungo gli assi cartesiani ma da forze P,Q,R,… agenti lungo determinate direzioni, si ha la formulazione originale di Lagrange per la statica (Lagrange 1788, p. 15 [1853-55, I, p. 25]):

[4] Pδp+Qδq+Rδr+…=0,

che nel caso di equilibrio esprime ovviamente l'annullarsi della somma dei momenti. Le coordinate (x_i,y_i,z_i) dei punti materiali possono soddisfare globalmente m equazioni del moto (supposte indipendenti):

[5] L_j(x_i,y_i,z_i)=0 [j=1,…,m(m<3n)].

In questo caso di vincoli olonomi (in un primo momento anche scleronomi), gli spostamenti (δx_i,δy_i,δz_i) nella [1] non sono più arbitrari, ma sono da scegliersi conformemente alla [5]. Con il metodo dei moltiplicatori di Lagrange, invece delle equazioni differenziali del moto libero [2] si ottengono le seguenti equazioni del moto, che oggi vanno generalmente sotto il nome 'equazioni di Lagrange del primo tipo':

Gli addendi a destra della [6] si interpretano in senso fisico come 'forze di vincolo' da applicare ai punti m_i in modo che le [5] siano soddisfatte. Soltanto molto tempo dopo Lagrange, Carl Gustav Jacob Jacobi dimostrò che con queste equazioni ‒ dalle quali se è possibile debbono essere eliminati i moltiplicatori ‒ le (x_i,y_i,z_i) si possano effettivamente determinare univocamente mediante la [5]. Lagrange invece aveva affermato che, assieme alle m equazioni indipendenti del moto [5] nelle 3n coordinate (x_i,y_i,z_i) dipendenti dal tempo, si possono introdurre 3n−m variabili indipendenti (quelle che oggi si chiamano 'coordinate lagrangiane' o 'generalizzate') qj=qj(t) che soddisfano la [5] identicamente e utilizzando le quali non compaiono più forze di vincolo. Se si introducono le cosiddette 'forze generalizzate' Q_r mediante la definizione:

dove U denota la 'funzione potenziale' (che nel caso in questione esiste), con l'ulteriore semplificazione

si ottiene, per l''energia cinetica' totale del sistema meccanico, la seguente equazione di Lagrange del secondo tipo (Lagrange 1788, p. 226 [1853-55, II, p. 334]):

Qui

denota la 'velocità generalizzata'.

La deduzione della [9] dalla [1] è una delle conquiste più significative della Méchanique analitique perché grazie alla [9] interi problemi dinamici si possono ridurre alla determinazione delle due funzioni T (energia cinetica) e V (energia potenziale). Lagrange ne dedusse il teorema dell'invarianza del moto del baricentro, la conservazione della quantità di moto e della quantità di moto angolare, come pure, per il caso in cui il sistema meccanico sia soggetto a vincoli indipendenti dal tempo [5] e soltanto a forze centrali, la legge della conservazione delle forze vive (o legge di conservazione dell'energia) e il principio di minima azione. Dal punto di vista dell'organizzazione formale e deduttiva della meccanica si capisce dunque perché egli abbia introdotto il principio delle velocità virtuali già nella parte del suo trattato riguardante la statica come "una sorta di assioma della meccanica" (Lagrange 1788, p. 12).

Tutte le più importanti conseguenze del principio delle velocità virtuali nella prima metà del XIX sec. partono dalla formulazione di Lagrange [1], o, nel caso della statica, dalla [3] o dalla [4]. Un primo importante punto di discussione fu lo status assiomatico del principio. In tarda età, spinto da una critica di Jean-Baptiste-Joseph Fourier, Lagrange stesso non lo considerò più abbastanza evidente da essere preso come assioma e ne diede due diverse 'dimostrazioni' (come egli stesso le definì). Con la prima cercò di conferire al principio statico una chiara evidenza ricorrendo a macchine semplici (1798), con la seconda di rendere 'sicuro' in tal modo il passaggio dalla statica alla dinamica (1813, 1847). Nuovi tentativi di dimostrazione vennero intrapresi da André-Marie Ampère, Lazare Carnot, Antoine-Augustin Cournot, Vittorio Fossombroni, Fourier, Louis Poinsot, Siméon-Denis Poisson, Gaspard-François-Clair-Marie Riche de Prony e altri. Tali tentativi miravano perlopiù a ridurre il principio delle velocità virtuali a quello della leva o alla regola del parallelogramma delle forze o a entrambi. Oggi può sembrare strana l'intenzione di voler dimostrare un principio o assioma meccanico che si trova come premessa di un sistema deduttivo. Essa rivela invece una "crisi dei principî" (Bailhache 1975, p. 7), dovuta al fatto che la meccanica analitica nella tradizione di Lagrange si era spostata nella direzione di un ideale di fondazione ed esattezza proprio della matematica pura. Jacobi fu il primo a rompere nettamente nelle Vorlesungen über analytische Mechanik (Lezioni sulla meccanica analitica, 1847-1848) con questa tradizione della 'certezza', sostituita dalla concezione ‒ che nella seconda metà del secolo andò sempre più imponendosi ‒ secondo la quale un tale principio non può essere garantito né matematicamente né metafisicamente, ma deve essere invece considerato come un'ipotesi (Pulte 1998).

Un secondo punto, strettamente legato al problema della validità del principio, riguarda la sua generalizzazione a sistemi olonomi e scleronomi. Già Fourier nel 1798 aveva richiamato l'attenzione sul fatto che il principio di Lagrange è inadeguato quando i vincoli non possono essere espressi nella forma [5] ma soltanto mediante una disuguaglianza: per esempio, quando un punto materiale è vincolato a muoversi non sopra ma fuori di una superficie sferica. In questo caso la [5] deve essere sostituita dalla:

[5*]  L_j(x_i,y_i,z_i)≤0 j=1,…,m(m<3n).

Il principio delle velocità virtuali nella forma di Lagrange [4] va allora generalizzato nel senso che il momento totale o il lavoro virtuale nel caso dell'equilibrio non si annulla, ma (con un'opportuna scelta dei segni) diventa negativo:

[4*] Pδp+Qδq+Rδr+…≤0.

Un'analoga generalizzazione del principio per la statica fu proposta da Cournot, Carl Friedrich Gauss e Michail Vasil´evič Ostrogradskij, il quale sembra abbia per primo esteso questo principio alla dinamica.

Lo stesso Lagrange auspicò nella prima edizione della Méchanique analitique un'altra generalizzazione (Lagrange 1788, p. 198) e cioè l'estensione del principio a sistemi reonomi, nei quali le equazioni [5] dipendono dal tempo t:

[5**] L_j(x_i,y_i,z_i,t)=0 j=1,…,m(m<3n).

Poisson nel 1833 osservò che l'applicazione del principio [1] a questo caso produceva solamente errori infinitesimali e quindi era lecita. Ostrogradskij nel 1842 sostenne invece che in questo caso il tempo doveva essere considerato come una variabile e quindi nella [1] doveva essere inserita una variazione del tempo; in realtà ciò non è necessario e la [1] si può applicare anche a vincoli reonomi (Schaefer 1919). Un'effettiva chiarificazione del problema, come pure l'estensione del principio a problemi nei quali non può essere data una funzione delle forze (vedi la [7]), come nel caso dell'attrito, o qualora intervengano vincoli non olonomi per i quali le equazioni non contengono le coordinate dei punti materiali bensì le loro derivate prime (come nel caso di un corpo che rotola senza strisciare, per es., una sfera su un piano orizzontale), si avrà però solamente negli ultimi decenni del XIX secolo.

Un terzo punto nella discussione del principio durante il XIX sec. riguarda la sua rilevanza in fisica e in definitiva quella della meccanica analitica nel senso di Lagrange nel suo complesso. Già nella tradizione della fisica matematica francese dopo Lagrange si metteva l'accetto sull'aspetto più propriamente fisico della meccanica, che con Poisson sfociò nell'esplicito rifiuto di una nuova e specifica meccanica fisica nella tradizione della meccanica analitica di Lagrange. Una questione importante riguardava inoltre la natura delle reazioni vincolari, necessarie affinché punti materiali in moto fossero soggetti a limitazioni di tipo quasi geometrico come nella [5] (Duhem 1902). Jacobi, tra gli altri, esaminò in seguito questo problema, studiando il passaggio dalla statica alla dinamica operato da Lagrange tramite il principio delle velocità virtuali. Mentre nel caso dell'equilibrio i vincoli devono compensare i pesi o altre forze delle masse in quiete, nel caso del moto essi dipendono anche dalla velocità e quindi non soddisfano in generale le ipotesi di Lagrange. Infine, nella meccanica analitica Lagrange mescolava forze fisiche (come la gravitazione) con qualcosa di 'totalmente eterogeneo', vale a dire con le condizioni puramente matematiche della forma [5]. Diventava quindi impossibile considerare la forma dinamica generale del principio [1] come una conseguenza del vecchio principio statico [3] o [4]. La critica di Jacobi si rivolgeva soprattutto all'uso fatto da Lagrange di questo principio, uso che ignorava del tutto la struttura fisica dei corpi a vantaggio della 'purezza' della meccanica analitica, che rinuncia così anche alla propria giustificazione pur di rimanere 'pura'. Questa e simili critiche condussero, a partire dalla metà del XIX sec., a conferire al principio delle velocità virtuali una maggiore rilevanza fisica: vincoli del tipo di Lagrange, come quelli presenti nella [5], furono sostituiti con forze esterne, rispondenti a leggi di forza e di potenziale più 'realistiche' e trattate usando la [1]. Carl Neumann e più tardi anche Hermann von Helmholtz avanzarono critiche simili a quelle di Jacobi.

Il principio generale delle velocità virtuali è stato considerato, anche dalla letteratura più recente, uno dei principî più importanti per un'organizzazione della meccanica su base deduttiva. Tuttavia va anche precisato che nella seconda metà del XIX sec., nel confronto con i principî estremali, esso ha visto ridurre la sua importanza: questi ultimi si estendono meglio a campi della fisica teorica al di là della tradizionale meccanica dei punti materiali e dunque hanno potuto superare con successo la decadenza del meccanicismo.

Il principio del minimo vincolo

Riguardo al principio dinamico [1] che abbiamo considerato e alla sua restrizione ai problemi dell'equilibrio ([3] e [4]), Carl Friedrich Gauss osservò che "per la natura stessa della cosa […] non vi può essere alcun nuovo principio fondamentale nella teoria del moto e dell'equilibrio, che non sia già contenuto nei due principî suddetti e non sia da essi derivabile" (Gauss 1829, p. 232). Egli condivideva perciò le idee di molti matematici del suo tempo a proposito dell'evidenza del principio delle velocità virtuali, senza però trarne le medesime conclusioni, e cioè che esso dovesse essere reso certo mediante una 'dimostrazione'. Introduceva invece una nuova 'legge fondamentale della meccanica', che nonostante fosse logicamente equivalente al principio gli appariva però più evidente. Essa gli sembrava caratterizzata da una 'particolare convenienza' che il vecchio principio non aveva (ibidem). Si tratta di un principio variazionale 'differenziale', come quello di Lagrange: analogamente al principio di minima azione esso determina il minimo di una data grandezza meccanica. Secondo Gauss infatti un sistema di masse puntiformi, soggetto a vincoli esterni, si muove sempre in modo "da avvicinarsi il più possibile a un moto libero o il meno possibile vincolato", per cui definisce il vincolo come "la somma dei prodotti dei quadrati della deviazione di ogni punto dal suo moto libero rispetto alla sua massa" (ibidem, p. 233).

Gauss non formula il proprio principio analiticamente. Se però si sviluppano in serie di Taylor rispetto al tempo le posizioni 'effettive' e quelle assunte come 'libere', si ottiene facilmente la seguente espressione analitica per la quantità che egli denota con Z (iniziale del tedesco Zwang, vincolo):

Il principio di Gauss afferma allora che per moti reali la [10] ha un minimo. Per questo è necessario che la variazione di Z si annulli:

[11]  δZ=0.

Che la [11] non sia soltanto necessaria ma anche sufficiente per un minimo, e cioè che Z in queste condizioni non ha unicamente un valore stazionario, ma sempre un valore minimale (in particolare un minimo effettivamente esiste), segue dal fatto che (almeno in tutti i problemi di meccanica rilevanti) la [10] è una forma quadratica definita positiva. Gauss mette poi a confronto sistemi (sotto condizioni di vincolo arbitrarie) per i quali le posizioni istantanee (x_i,y_i,z_i) e le velocità effettive

delle n masse puntiformi m_i sono le stesse. Variano soltanto le accelerazioni

e precisamente in modo da rispettare le condizioni di vincolo. Più tardi Ludwig Boltzmann definirà tutto ciò come "il moto che varia alla maniera di Gauss" (1897-1920, I, p. 210). Per vincoli olonomi [5], e in particolare anche per quelli reonomi [5**], per i quali le condizioni sono date sotto forma di equazioni, si ottiene dalla condizione [11] la seguente forma del principio di Gauss:

La [12] è una rappresentazione logicamente equivalente delle equazioni del moto [1] e [2]. Gauss vedeva una particolare evidenza e 'convenienza' del proprio principio nell'analogia tra la ricerca di un minimo della [10], che si esprime anche nella [12], e il 'metodo dei minimi quadrati' (Gauss 1829, p. 235). Per dare al proprio principio un fondamento intuitivo egli non fece appello a una teleologia materiale della Natura, come era accaduto esplicitamente nel caso del principio della minima azione; si affidò invece a un'interpretazione antropomorfica della Natura: come il ricercatore che calcola fa uso del metodo dei minimi quadrati, così la Natura nei propri calcoli segue il principio del minimo vincolo.

Negli sviluppi successivi del principio questo antropomorfismo della Natura avrà un ruolo sempre minore, anche se August Ritter, allievo di Gauss, nella sua tesi del 1853 dedicava ancora molta attenzione all'analogia con il metodo dei minimi quadrati. Nel 1873 Ritter dimostrerà in particolare che questo principio, come quello delle velocità virtuali, può essere posto quale premessa di una costruzione deduttiva dell'insieme della statica e della dinamica. Già Gauss aveva osservato, incidentalmente e senza approfondire questo punto, che il suo principio valeva in condizioni più generali della [5] e della [5**], e poco dopo Jacobi si sarebbe spinto fino a vederne 'l'importanza caratteristica' nel fatto che esso non si applica soltanto a vincoli dati sotto forma di disequazioni [5*], ma anche a sistemi meccanici nei quali i vincoli possono comparire sotto forma di equazioni e di disequazioni, come per esempio nel caso del moto (non troppo veloce) di una massa puntiforme che, muovendosi all'interno di un cerchio, cade prima di raggiungere lo zenit (Jacobi 1996, pp. 104-105). Generalizzazioni 'formulate analiticamente' del principio di Gauss si avranno verso la fine del XIX sec. per opera di Josiah W. Gibbs, Boltzmann e Paul Appell.

Globalmente il principio di Gauss del minimo vincolo, malgrado la grande generalità (applicabilità anche a sistemi non olonomi) ebbe una scarsa accoglienza al di fuori dell'area tedesca. Ciò potrebbe tra l'altro dipendere dal fatto che il principio richiede una variazione dell'accelerazione, mentre altri principî, come quello di minima azione, raggiungono lo scopo con la variazione della velocità. Malgrado questi inconvenienti di carattere tecnico, esso assunse un significato di principio fondamentale per via dell'impulso dato tra gli altri da Jacobi, Georg Friedrich Bernhard Riemann, Eugenio Beltrami, Joseph J. Thomson, Jean-Gaston Darboux alla cosiddetta geometrizzazione della meccanica nella seconda metà del secolo. 'Geometrizzazione' non significava però una ripresa dei vecchi metodi di geometria sintetica ma l'eliminazione di concetti dinamici fondamentali ‒ come quelli di forza e di energia ‒ dalla meccanica. In particolare, le ricerche di Rudolf Otto Sigismund Lipschitz sui principî variazionali della meccanica e sul principio di Gauss in relazione con la geometria riemanniana (1872, 1877) spinsero Heinrich Rudolf Hertz a sviluppare ulteriormente in Die Prinzipien der Mechanik (I principî della meccanica, 1894) il principio del minimo vincolo nel senso di un semigeometrico 'principio della traiettoria più rettilinea' e porlo come premessa di una meccanica priva del concetto di forza.

Il principio di minima azione

Si tratta del più antico principio estremale della meccanica analitica. Nella sua formulazione più generale, ma anche più indeterminata, esso afferma che in un sistema meccanico con n masse puntiformi m_i e velocità v_i l''azione' del moto effettivo assume un valore stazionario rispetto a quelli di tutte le traiettorie che hanno gli stessi punti iniziali e finali, per cui la variazione prima dell'azione si annulla:

L'azione si esprime spesso non come integrale di linea ma di tempo. Con l'espressione

per la velocità e la forma ridotta [8] per l'energia cinetica T, si ottiene allora, sostituendo:

[15]  δA=δ∫Tdt=0.

Nella seconda metà del XVIII sec., questo principio fu oggetto di ampie discussioni di carattere metafisico, in cui si dibatteva in particolare se fosse necessario supporre il principio di conservazione dell'energia, cioè se il principio di minima azione fosse applicabile soltanto a sistemi 'conservativi', o se viceversa si poteva ottenere da un qualche principio del minimo sforzo. Per molto tempo restò poco chiaro se nella [15] il tempo t dovesse essere considerato una grandezza fissa, invariabile (variazione isocrona), o se, come le posizioni nello spazio, potesse e anzi dovesse essere soggetto a variazione.

Nei suoi primi lavori torinesi Lagrange pose il principio come premessa della meccanica, sviluppando un'altra forma che non presupponeva la conservazione dell'energia. Tuttavia nella Méchanique analitique egli indicherà una direzione che sarà decisiva nel XIX sec., restringendo il principio a una forma valida soltanto per sistemi conservativi. Più precisamente, egli supponeva per le variazioni nelle [13] e [15] traiettorie con energia uguale e costante, per cui l'energia non variava (variazione isoenergetica), mentre non considerava centrale la questione della variazione del tempo nella [15]. L'ipotizzata restrizione del principio a sistemi conservativi lo spinse probabilmente anche a cercare di dedurlo, come corollario, da quello delle velocità virtuali. Questa restrizione, come pure il fatto che i tentativi di fondazione teleologica del XVIII sec. avevano fatto perdere sempre più credito al principio di minima azione, condussero alla sua relativa irrilevanza nei primi decenni del XIX secolo. Poisson lo considerava una "regola oggi inutile per scrivere le equazioni differenziali del moto" (Poisson 1837b, p. 333). Data questa diffusa mancanza di considerazione, si può capire come una pioneristica ricerca di Benjamin Olinde Rodrigues, che aveva chiarito la necessità della variazione del tempo nella formulazione [15] del principio (Rodrigues 1814-15) rimanesse a lungo inosservata. Un'altra eccezione è rappresentata da William R. Hamilton (1805-1865), il quale vedeva il principio di minima azione come la maggiore generalizzazione induttiva della dinamica e dell'ottica e considerava il proprio principio estremale non come equivalente, bensì come (pura) implicazione di quello. Nel 1850 Ostrogradskij affermava nel Mémoire sur les équations différentielles relatives aux problèmes des isopérimètres che il principio di minima azione, se applicato correttamente come tecnica variazionale, coincideva con il principio di Hamilton; ciò ha rilevanza anche per la teoria di Hamilton-Jacobi.

Un'interessante svolta di carattere geometrico alla storia del principio di minima azione fu data da Jacobi nel 1837. Egli faceva risalire esplicitamente a Euler la prima formulazione matematicamente corretta di questo principio (1744), che successivamente verrà "presentato in quasi tutti i libri, anche nei migliori, come quelli di Poisson, Lagrange e Laplace, in un modo che lo rende incomprensibile" (Jacobi 1866 [1884, p. 44]). Jacobi considera soltanto la forma ristretta del principio di minima azione, supponendo cioè la conservazione dell'energia meccanica. Non potendo considerare la variazione del tempo, Jacobi utilizzò il principio di conservazione dell'energia per sostituire il tempo (contenuto non soltanto nella [15] ma anche nella [13] nella forma della velocità v_i=ds_i/dt), esprimendo quindi l'azione solamente mediante la massa e grandezze spaziali. Se U è la 'funzione delle forze' (o, in linguaggio moderno, l'energia potenziale cambiata di segno), questo principio di conservazione si esprime nel modo seguente:

dove h è l'energia meccanica totale. Si può quindi sostituire dt nella (13) e ottenere la nuova forma del principio di minima azione:

In questa forma la determinazione della traiettoria si riduce a un problema geometrico. Per esempio, si vede facilmente che per una massa puntiforme, vincolata a muoversi su una data superficie da condizioni del tipo [5], in assenza di forze (U=0) la condizione [17] si traduce nel caso particolare:

[17*] δ∫ds=δs=0.

Questa equazione esprime soltanto il fatto che la massa si muove su una geodetica della superficie definita dalla [5]. Un altro importante merito di Jacobi è di avere per primo studiato in generale sotto quali condizioni con la [17] si ottiene un minimo. Dal punto di vista della critica dei principî, accanto al nuovo principio fondamentale di Gauss fu soprattutto la nuova formulazione [17] di Jacobi del principio di minima azione che preparò, nella seconda metà del XIX sec., la geometrizzazione della meccanica.

Soltanto nei due ultimi decenni del XIX sec. furono fornite altre formulazioni matematicamente soddisfacenti del principio di minima azione nelle quali, contrariamente alla concezione di Jacobi, era prevista una variazione del tempo e si poteva dimostrare con ineccepibili tecniche di calcolo delle variazioni che accanto alla forma 'ristretta' del principio, come la applica Jacobi, ce n'è un'altra, che non è limitata a sistemi conservativi. Si assiste così alla fine del XIX sec. a una giustificazione delle ampie aspettative riguardo al principio di minima azione, che Pierre-Louis Moreau de Maupertuis ‒ l'altro 'inventore' del principio, insieme a Euler ‒ aveva coltivato e suscitato; non si può però non ricordare che la fondazione metafisica del principio da parte di quest'ultimo era stata del tutto ignorata quando non esplicitamente respinta.

Il principio di Hamilton dell'azione stazionaria

Gli importanti contributi di Hamilton alla meccanica hanno origine nelle sue precedenti ricerche di ottica geometrica. In questo contesto egli introdusse anche la 'funzione caratteristica' V, che più tardi darà luogo alla costruzione della cosiddetta 'funzione principale' S. Egli fece diffusamente uso del principio di minima azione, al quale dava una nuova, particolare interpretazione sotto forma di 'principio dell'azione variabile'. Qui ci interessa un solo principio, affine a questo dal punto di vista fisico, ma matematicamente originale, che Hamilton introdusse soltanto alla fine del suo primo saggio On a general method employed in dynamics e nella Application (entrambi del 1834), e sviluppò dettagliatamente soprattutto nel Second essay on a general method in dynamics (1835). Per un sistema conservativo con energia cinetica T e funzione delle forze U la forma che dà Hamilton a questo principio è la seguente:

La funzione principale S è definita come l'integrale della lagrangiana L preso tra il tempo iniziale t=0 e quello finale t, e quindi in generale può essere vista come una funzione del tempo:

L=T+U è la cosiddetta 'lagrangiana', cioè la differenza tra l'energia cinetica (T) e l'energia potenziale (−U). La [18] dice quindi che l'integrale rispetto al tempo della lagrangiana relativo all'effettiva traiettoria del sistema ‒ integrale che rappresenta, come l'integrale della [13] e della [15] una misura dell'azione ‒ è stazionario.

Nonostante la comune misura dell'azione vi sono importanti differenze con il principio di minima azione 'tradizionale'. Nel processo variazionale [18] Hamilton suppone che il tempo fin da principio non sia soggetto a variazione, come invece non accade per l'altra forma del principio di minima azione. Vengono confrontate anche tutte le traiettorie con tempo iniziale e finale fissati e per le quali sono anche fissate le posizioni iniziali e finali nello spazio. Inoltre Hamilton non suppone nella [18], a differenza della forma ristretta del principio di minima azione, che tutte le traiettorie presentino anche la medesima energia totale T−U. Nel caso in cui le forze agenti derivino da una funzione delle forze (indipendente dal tempo), egli deduce infatti il principio della conservazione dell'energia dalla [18]:

[16*]  T-U=h=cost.

Malgrado le differenze con le vecchie formulazioni del principio di minima azione, nel mondo anglosassone si è continuato a chiamare la [18] principle of least action.

Sulla scia di Jacobi‒ il quale sottolineava con forza la differenza tra questo principio variazionale e la propria formulazione (v. [17]) 'indipendente dal tempo' del principio di minima azione, dimostrando come Hamilton prendesse le mosse dalla forma [18] ‒ si era affermata la denominazione di 'principio di Hamilton', quando in effetti si sarebbe dovuto parlare, per essere più precisi, di 'principio dell'azione stazionaria di Hamilton'.

Questo principio si è rivelato fruttuoso e importante euristicamente non soltanto per l'ulteriore sviluppo della meccanica analitica, ma in generale per la fisica teorica. Esso si è dimostrato indispensabile soprattutto per quei sistemi fisici per i quali non si ha una rappresentazione precisa delle forze agenti, ma solamente delle funzioni delle forze come le U. Inoltre il principio poteva essere esteso a sistemi con funzioni delle forze dipendenti sia dal tempo, sia dalla velocità, e infine anche a sistemi senza funzione delle forze. Contrariamente a quanto postulato nel 1894 da Hertz, tale principio vale anche per sistemi con vincoli non olonomi. In seguito, grazie al nuovo calcolo delle variazioni, si riuscì a chiarire la generalità e applicabilità anche di questo principio.

La teoria di Hamilton-Jacobi

La teoria che prende il nome da Hamilton e Jacobi è una delle più importanti di tutta la fisica matematica, oltre a essere una delle più eleganti. Essa si collega al formalismo della vecchia meccanica analitica sviluppato da Lagrange e Poisson, ma anche all'ulteriore sviluppo dei principî variazionali di minima azione e dell'azione stazionaria, fornendo un metodo generale per l'integrazione delle equazioni del moto nella meccanica. Dal punto di vista matematico essa rappresenta perciò un anello di congiunzione tra la teoria delle equazioni differenziali, ordinarie e alle derivate parziali, e il calcolo delle variazioni. Contrariamente a molte altre denominazioni affermatesi nel tempo, essa porta tale nome a giusto titolo: i concetti più importanti si trovano infatti nei voluminosi On a general method employed in dynamics e nel Second essay di Hamilton e negli sviluppi e nel completamento della teoria che si trovano nella monografia di Jacobi Zur Theorie der Variations-Rechnung (Sulla teoria del calcolo delle variazioni, 1837).

Nella prima opera Hamilton introduce la funzione caratteristica V come misura dell'azione (conformemente al principio di minima azione); quest'ultima è definita come il doppio dell'energia cinetica T di un sistema libero e conservativo di n masse puntiformi m_i

Siano (a_i,b_i,c_i) le coordinate iniziali dei punti m_i e

le velocità iniziali; (x_i,y_i,z_i) le coordinate al tempo t e

le velocità corrispondenti. V si può esprimere come funzione delle coordinate iniziali e finali e del tempo t. Se l'energia totale H è costante, si ha δV=0 (una forma ridotta del principio di minima azione). Prendendo i punti finali come variabili si hanno le seguenti 6n+1 equazioni differenziali ordinarie del primo ordine che determinano completamente il moto del sistema a partire dalla funzione V:

Applicando il principio di conservazione dell'energia [16] Hamilton ottiene poi dalle [21] le due relazioni seguenti:

La determinazione del moto del sistema viene così ridotta al problema matematico di trovare una funzione che soddisfi queste due equazioni differenziali del primo ordine. Hamilton dimostra che dalle [22], assieme alle equazioni originarie [21], si possono dedurre le equazioni del moto [2] e, introducendo le coordinate lagrangiane, anche le equazioni di Lagrange del secondo tipo [9].

Alla fine di On a general method Hamilton sostituisce la funzione caratteristica V con la funzione principale S:

[23] S=V-H∙t.

La funzione principale S si può introdurre anche mediante l'integrale [19]. Poiché essa soddisfa la [18], dalla [20] si ottengono per S equazioni differenziali analoghe alle [21], e alle [22]:

Nel Second essay Hamilton deduce tra l'altro le famose equazioni canoniche del moto: con le coordinate generalizzate q_i e gli impulsi generalizzati

del formalismo di Lagrange e Poisson, e utilizzando l'hamiltoniana

egli trasforma le 3n equazioni differenziali del secondo ordine del moto [6], e rispettivamente [9], per un sistema libero, in un sistema di 2n equazioni differenziali del primo ordine:

Queste equazioni differenziali canoniche di Hamilton sono una formulazione alternativa delle equazioni differenziali del moto di Lagrange; per alcuni problemi esse hanno il vantaggio di essere soltanto del primo ordine.

Tra i tanti importanti risultati del Second essay si sottolinea qui soltanto una notevole proprietà della funzione principale S. Hamilton dimostra che da un lato la variazione di S secondo la [18], cioè per estremi fissati, determina l'equazione differenziale del moto, dall'altro per estremi variabili fornisce l'integrale delle equazioni canoniche. È lui stesso quindi a stabilire la differenza tra la lagrangiana L e la propria funzione principale S in un articolo di rassegna per la British Association: "la funzione di Lagrange enuncia, la funzione di Hamilton risolve il problema; una serve a scrivere le equazioni differenziali dei moti, l'altra a darne gli integrali" (Hamilton 1834b [1931-2000, II, p. 213]).

Jacobi invece, nelle sue ulteriori ricerche e malgrado tutta l'ammirazione per i risultati di Hamilton, non può fare a meno di condannare il fatto che questi "avesse posto la sua bella scoperta sotto una falsa luce" presentandola in modo "inutilmente complicato e limitato" (Jacobi 1837b, p. 73). Egli riesce effettivamente a dimostrare che per determinare l'integrale completo del moto non è necessario introdurre una funzione S come funzione di 6n+1 quantità (coordinate iniziali e finali, (a_i,b_i,c_i) e (x_i,y_i,z_i) oltre al tempo t) e imporre a essa di soddisfare in modo identico le equazioni differenziali alle derivate parziali [21*]. È sufficiente invece considerare S come funzione di 3n+1 quantità (x_i,y_i,z_i e t) e richiedere che essa soddisfi quest'unica equazione differenziale alle derivate parziali:

Jacobi prosegue poi la ricerca iniziata da Hamilton sulle trasformazioni canoniche (cioè le trasformazioni delle coordinate nelle quali si conservano le equazioni canoniche del moto [25]) e dimostra che il problema si riduce alla determinazione di una funzione generatrice, o principale, che soddisfi l'equazione detta oggi 'di Hamilton-Jacobi':

Mentre Hamilton aveva rivolto l'attenzione al fatto che la funzione principale S dà una soluzione parziale delle equazioni differenziali alle derivate parziali, Jacobi può ora dimostrare, in base alle proprie ricerche sulle trasformazioni canoniche, che ogni soluzione completa della [27] fornisce una soluzione delle equazioni canoniche del moto [25].

La relazione qui suggerita tra il calcolo delle variazioni e la teoria delle equazioni differenziali ordinarie e alle derivate parziali ha un significato che va ben oltre la meccanica analitica, e ha per la meccanica stessa un significato più teorico che pratico. In proposito, si può sottolineare un duplice vantaggio del formalismo di Hamilton-Jacobi. Da un lato esso permette una rappresentazione elegante e la determinazione delle quantità che si conservano nel moto (invarianti); la ricerca in questo senso sarà sviluppata nel secolo seguente in particolare da Amalie Emmy Noether (1918). Dall'altro lato, tale formalismo mette in luce ‒ nel modo più chiaro nella forma dell'equazione [27] ‒ un legame tra ottica, meccanica classica e la moderna meccanica quantistica che gli conferisce, al di là del proprio contesto storico, un grande significato anche per la fisica moderna (Dugas 1955).

Principî estremali in fisica teorica

I principî esposti e il formalismo di Hamilton-Jacobi provengono essenzialmente dalla meccanica analitica dei sistemi di masse discrete, ma sono di generalità ancora maggiore, dimostrando, come è accaduto nel corso della seconda metà del XIX sec., di essere strumenti importanti per l'unificazione della fisica. Soprattutto i principî estremali della meccanica (principio di Hamilton e principio di minima azione) acquisteranno, in relazione all'affermarsi del principio di conservazione dell'energia alla metà del XIX sec., un grandissimo significato. Ciò vale in particolare per i campi della fisica teorica che si contrappongono al vecchio riduzionismo meccanicista, che riconduceva tutti i fenomeni fisici a un reciproco effetto di masse discrete sottoposte a forze centrali.

Sono soprattutto i 'dinamisti' britannici come William Thomson (lord Kelvin) o Peter Guthrie Tait e in maggior misura anche i teorici dell'Europa continentale a far uso dei concetti di conservazione dell'energia di campo, potenziale e generale, in relazione ai principî variazionali e al formalismo di Lagrange, di Hamilton e di Jacobi, con l'intento precipuo di dare alla fisica teorica una forma nuova e unitaria. Come esempi si considerino le applicazioni del principio di Hamilton e di quello di minima azione nell'elettrodinamica (comprendente potenziali dipendenti dal tempo) dovute a Riemann, Neumann, Ernst Christian Julius Schering, Enrico Betti, Gustav Holzmüller e altri; nella teoria del calore sono soprattutto da sottolineare i tentativi effettuati da Boltzmann, Rudolf Clausius e Coloman Szily per dedurre il secondo principio della termodinamica da principî estremali; applicazioni in meccanica dei continui sono dovute a Henry Moseley, George Green, Luigi Federico Menabrea, Alberto Castigliano, Gustav Robert Kirchhoff, James H. Cotterill e Boltzmann. Quest'ultimo già nel 1870 sottolineava la grande importanza del principio di Hamilton-Jacobi nella fisica teorica. Che si trattasse di un cambiamento di paradigma all'interno della stessa fisica classica, legato indissolubilmente alla scoperta della forma generale della conservazione dell'energia, fu chiarito in seguito soprattutto dai lavori di fisica teorica di Helmholtz, nei quali il principio di minima azione viene esteso a tutti i campi della fisica. Questo era per Helmholtz il più importante principio di larga applicazione della fisica teorica assieme a quello della conservazione dell'energia, e ne rappresentava una sorta di complemento naturale e necessario: "Tutto ciò che accade si rappresenta mediante un fluire e rifluire dell'energia del mondo, e le leggi di questo fluire sono interamente comprese nel principio della minima azione" (Helmholtz 1900, p. 287).

Alcune implicazioni filosofiche

La meccanica analitica, a causa del suo carattere matematico-formale, è stata spesso considerata una parte della matematica, sterile dal punto di vista fisico, di un'eleganza scolastica, senza rilevanza filosofica e anzi addirittura ignorata dalla filosofia. Le eccezioni della prima metà del secolo, rappresentate dai filosofi Auguste Comte in Francia, William Whewell in Inghilterra o Jacob Friedrich Fries in Germania, non possono che confermare tale giudizio. Sebbene questo quadro cambi leggermente a partire dalla seconda metà dell'Ottocento, da Ernst Mach a Thomas Kuhn prevalse il punto di vista per cui la meccanica analitica è semplicemente una nuova formulazione 'matematicamente' interessante delle ben note leggi di Newton che non solleva nuove questioni filosofiche riguardo ai fondamenti.

In realtà non è così e in conclusione vogliamo indicare almeno alcune delle implicazioni filosofiche. Bisogna infatti tener conto della ricchezza di possibilità di rappresentazione matematica della meccanica analitica, dell'alto grado di formalizzazione e della sua rappresentazione dei fatti empirici più 'simbolica' che 'concettuale'. Questi elementi hanno senza dubbio contribuito al superamento dell'ipostatizzazione, a lungo perdurante, dei concetti fondamentali della meccanica (come quelli di 'spazio assoluto', 'tempo assoluto', 'forza', 'energia') in oggetti reali della Natura. Al tempo stesso, tali elementi hanno portato a prenderne in considerazione il carattere costruttivistico. La critica dello spazio assoluto newtoniano da parte di Neumann nel 1870, per esempio, va vista sullo sfondo della tradizione 'analitica'. Uno sviluppo simile si ha anche, in questa tradizione, con il concetto newtoniano di forza (Jammer 1957). La meccanica analitica avrà inoltre grande influenza nel mutamento che subirà il concetto di 'legge di Natura'. Le vecchie concezioni, secondo le quali si tratta in ultima analisi di leggi del pensiero (razionalismo), di generalizzazioni induttive (empirismo) o di principî sintetici a priori (filosofia critica) ‒ in ogni caso sempre di enunciati generali, certi, univoci e immutabili sulla Natura ‒, sono state messe in dubbio anche grazie alla meccanica analitica. Già in Jacobi, alla metà del XIX sec. compaiono numerosi segni di un'interpretazione convenzionalistica dei principî della meccanica, e Jules-Henri Poincaré, che nella filosofia della scienza fu in primo luogo un sostenitore del convenzionalismo, non si riferisce solo alla geometria, ma anche a quella che egli chiamava la 'fisica dei principî', che inequivocabilmente ha le radici nella meccanica analitica. Anche la Bildtheorie di Hertz, alla quale si riconnette la teoria di Poincaré, non sarebbe stata possibile senza la tradizione analitica della meccanica. La possibilità di sviluppare in un certo campo teorie 'empiricamente equivalenti' a partire da concetti fondamentali differenti rimane, oltre il convenzionalismo, un problema centrale anche per la moderna filosofia della scienza.

Infine singoli principî della meccanica (come quello di minima azione), ma anche l'intero formalismo di Hamilton-Jacobi, trovano analogie al di là della meccanica classica ‒ nella teoria della relatività e in meccanica quantistica.

Bibliografia

Bailhache 1975: Bailhache, Patrice, Introduction et commentaire, in: Poinsot, Louis, La théorie générale de l'équilibre et du mouvement des systèmes, édition critique et commentaires par Patrice Bailhache, Paris, Vrin, 1975, pp. 1-199.

Benvenuto 1991: Benvenuto, Edoardo, An introduction to the history of structural mechanics, New York, Springer, 1991, 2 v. (ed. orig.: La scienza delle costruzioni e il suo sviluppo storico, Firenze, Sansoni, 1981).

Carathéodory 1935: Carathéodory, Constantin, Variationsrechnung und partielle Differentialgleichungen erster Ordnung, Leipzig, Teubner, 1935.

Cassirer 1910: Cassirer, Ernst, Substanzbegriff und Funktionsbegriff. Untersuchungen über die Grundfragen der Erkenntniskritik, Berlin, Cassirer, 1910 (rist. facs.: Darmstadt, Wissenschaftliche Buchgesellschaft, 1994; trad. it.: Sostanza e funzione: ricerche sui problemi fondamentali della critica della conoscenza, introduzione di Massimo Ferrari, traduzione di Eraldo Arnaud, Firenze, La Nuova Italia, 1999).

Costabel 1972: Costabel, Pierre, Fourier et le principe des vitesses virtuelles, "Sciences", 3, 1972, pp. 235-238.

Cyganova 1983-84: Cyganova, N. Ja., Die Entwicklung des Prinzips des kleinsten Zwanges in den Arbeiten deutscher Forscher des 19. Jahrhunderts, "NTM. Schriftenreihe für Geschichte der Naturwissenschaften, Technik und Medizin", 20, 1983, pp. 25-38; 21, 1984, pp. 79-90.

Dugas 1955: Dugas, René, A history of mechanics, Neuchâtel, Édition du Griffon; New York, Central Book Co., 1955.

Fisch 1991: Fisch, Menachem, A philosopher's coming of age. A study in erotetic intellectual history, in: William Whewell: a composite portrait, edited by Menachem Fisch and Simon Schaffer, Oxford, Clarendon, 1991, pp. 31-66.

Fraser 1990: Fraser, Craig, Lagrange's analytical mechanics, its Cartesian origins and reception in Comte's positive philosophy, "Studies in the history and philosophy of science", 21, 1990, pp. 243-256.

Goldstein 1976: Goldstein, Herbert, Klassische Mechanik, 4. ed.,Wiesbaden, Akademische Verlagsgesellschaft, 1976 (ed. orig.: Classical mechanics, Cambridge (Mass.), Addison-Wesley, 1951).

Grattan-Guinness 1990: Grattan-Guinness, Ivor, Convolutions in French mathematics, 1800-1840, Basel, Birkhäuser, 1990, 3 v.

Hankins 1980: Hankins, Thomas L., Sir William Rowan Hamilton, Baltimore, Johns Hopkins University Press, 1980.

Harman 1982: Harman, Peter M., Energy, force, and matter. The conceptual development of nineteenth century physics, Cambridge-New York, Cambridge University Press, 1982.

Jammer 1957: Jammer, Max, Concepts of force. A study in the foundations of dynamics, Cambridge (Mass.), Harvard University Press, 1957.

Jouguet 1908-09: Jouguet, Émile, Lectures de mécanique: la mécanique enseignée par les auteurs originaux, Paris, Gauthier-Villars, 1908-1909, 2 v.

Jungnickel 1986: Jungnickel, Christa - McCormmach, Russell, Intellectual mastery of nature. Theoretical physics from Ohm to Einstein, Chicago-London, University of Chicago Press, 1986, 2 v.

Kuhn 1963: Kuhn, Thomas S., The structure of scientific revolutions, Chicago-London, University of Chicago Press, 1963 (ed. ted.: Die Struktur wissenschaftlicher Revolutionen, 2. reviedierte und um das Postskriptum von 1969 ergänzte Auflage, Frankfurt a.M., Suhrkamp, 1981; trad. it.: La struttura delle rivoluzioni scientifiche, Torino, Einaudi, 1969).

Lanczos 1966: Lanczos, Cornelius, The variational principles of mechanics, 3. ed., Toronto, University of Toronto, 1966 (1. ed.: 1949).

Lindt 1904: Lindt, Richard, Das Prinzip der virtuellen Geschwindigkeiten: seine Beweise und die Unmöglichkeit seiner Umkehrung bei Verwendung des Begriffes 'Gleichgewicht eines Massensystems', "Abhandlungen zur Geschichte der mathematischen Wissenschaften", 18, 1904, pp. 145-196.

Lützen 1995: Lützen, Jesper, Interactions between mechanics and differential geometry in the 19th century, "Archive for history of exact sciences", 49, 1995, pp. 1-72.

Prange 1904-35: Prange, Georg, Die allgemeinen Integrationsmethoden der analytischen Mechanik, in: Enzyklopädie der mathematischen Wissenschaften, mit Einschluss ihrer Anwendungen, redigiert von Wilhelm F. Meyer [et al.], Leipzig, Teubner, 1898-1935, 6 v. in 24 tomi; v. IV/2: Mechanik, redigiert von Felix Klein und Conrad Müller, 1904-1935, pp. 505-804.

Pulte 1989: Pulte, Helmut, Das Prinzip der kleinsten Wirkung und die Kraftkonzeptionen der rationalen Mechanik. Eine Untersuchung zur Grundlegungsproblematik bei Leonhard Euler, Pierre Louis Moreau de Maupertuis und Joseph Louis Lagrange, Stuttgart, Steiner, 1989.

‒ 1994: Pulte, Helmut, C.G.J. Jacobis Vermächtnis einer 'konventionellen' analytischen Mechanik: Vorgeschichte, Nachschriften und Inhalt seiner letzten Mechanik-Vorlesung, "Annals of science", 51, 1994, pp. 498-519.

‒ 1998: Pulte, Helmut, Jacobi's criticism of Lagrange. The changing role of mathematics in the foundations of classical mechanics, "Historia mathematica", 25, 1998, pp. 154-184.

‒ 1999: Pulte, Helmut, Von der Physikotheologie zur Methodologie. Eine wissenschaftstheoriegeschichtliche Analyse der Transformation von nomothetischer Teleologie und Systemdenken bei Kant und Fries, in: Jakob Friedrich Fries, Philosoph, Naturwissenschaftler und Mathematiker, hrsg. von Wolfram Hogrebe und Kay Herrmann, Frankfurt a.M., Lang, 1999, pp. 57-94.

‒ 2002: Pulte, Helmut - Thiele, Rüdiger, Meccanica variazionale, in: Storia della scienza, diretta da Sandro Petruccioli, Roma, Istituto della Enciclopedia Italiana, 2001-; v. VI, 2002, pp. 453-461.

Rund 1966: Rund, Hanno, The Hamilton-Jacobi-theory in the calculus of variations, its role in mathematics and physics, London, van Nostrand, 1966.

Schaefer 1919: Schaefer, Clemens, Die Prinzipe der Dynamik, Berlin, de Gruyter, 1919.

Szabó 1979: Szabó, István, Geschichte der mechanischen Prinzipien und ihrer wichtigsten Anwendungen, 2. neubearbeitete und erweiterte Auflage, Basel, Birkhäuser, 1979 (1. ed.: 1977).

Truesdell 1968: Truesdell, Clifford A., Essays in the history of mechanics, Berlin-Heidelberg-New York, Springer, 1968.

Voss 1901: Voss, Aurel, Die Prinzipien der rationellen Mechanik, in: Enzyklopädie der mathematischen Wissenschaften, mit Einschluss ihrer Anwendungen, redigiert von Wilhelm F. Meyer [et al.], Leipzig, Teubner, 1898-1935, 6 v. in 24 tomi; v. IV/1: Mechanik, redigiert von Felix Klein und Conrad Müller, 1901, pp. 1-121.

Wise 1982: Wise, Norton M., The Maxwell literature and the British dynamical theory, "Historical studies in the physical sciences", 13, 1982, pp. 175-205.

Zermelo 1916: Zermelo, Ernst F. - Hahn, Hans, Weiterentwicklung der Variationsrechnung in den letzten Jahren, in: Enzyklopädie der mathematischen Wissenschaften, mit Einschluss ihrer Anwendungen, redigiert von Wilhelm F. Meyer [et al.], Leipzig, Teubner, 1898-1935, 6 v. in 24 tomi; v. II/1.1: Analysis, redigiert von H. Burkhardt, W. Wirtinger, R. Fricke und E. Hilb, 1916, pp. 626-641.

Ziegler 1985: Ziegler, Renatus, Die Geschichte der geometrischen Mechanik im 19. Jahrhundert. Eine historisch-systematische Untersuchung von Möbius und Plücker bis zu Klein und Lindemann, Stuttgart, Steiner, 1985.